中考数学复习知识梳理第七章尺规作图及图形变换第24课时尺规作图课件(共62张PPT)
文档属性
| 名称 | 中考数学复习知识梳理第七章尺规作图及图形变换第24课时尺规作图课件(共62张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 09:58:38 | ||
图片预览








文档简介
(共62张PPT)
第七章 尺规作图及图形变换
第24课时 尺 规 作 图
课前循环练
(限时5分钟)
1. (广东真题)一元二次方程x2-4x-1=0配方后可化为 ( )
A. (x+2)2=3 B. (x+2)2=5
C. (x-2)2=3 D. (x-2)2=5
2. (广东真题)下列运算正确的是 ( )
A. (-m2n)3=-m6n3 B. m5-m3=m2
C. (m+2)2=m2+4 D. (12m4-3m)÷3m=4m3
D
A
A
图7-24-1
①能用尺规作图:作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线;过一点作已知直线的垂线;过直线外一点作这条直线的平行线; *过圆外一点作圆的切线.
②能用尺规作图:已知三边、两边及其夹角、两角及其夹边作三角形;已知底边及底边上的高线作等腰三角形;已知一直角边和斜边作直角三角形.
③能用尺规作图: 过不在同一直线上的三点作圆;作三角形的外接圆、内切圆;作圆的内接正方形和内接正六边形.
课标要求
对接教材 人教:尺规作图分布在各年级上下册的几何部分
北师:尺规作图分布在各年级上下册的几何部分
考点梳理
考点复习
1.作一条线段等于已知线段
如图7-24-2①,已知线段a,作一条线段AB=a.
步骤(如图7-24-2②):
(1)作射线AM;
(2)在射线AM上截取 ,则线段AB即为所求作的线段
图7-24-2
AB=a
广东省对应考点例题
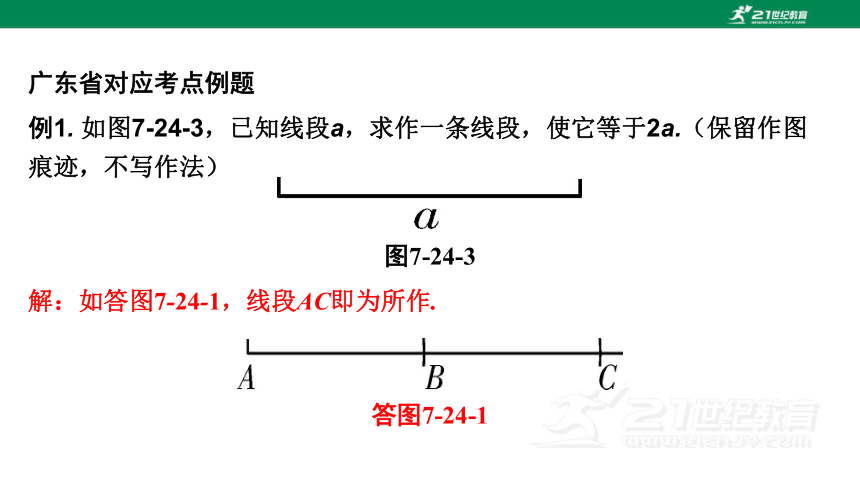
例1. 如图7-24-3,已知线段a,求作一条线段,使它等于2a.(保留作图痕迹,不写作法)
图7-24-3
解:如答图7-24-1,线段AC即为所作.
答图7-24-1
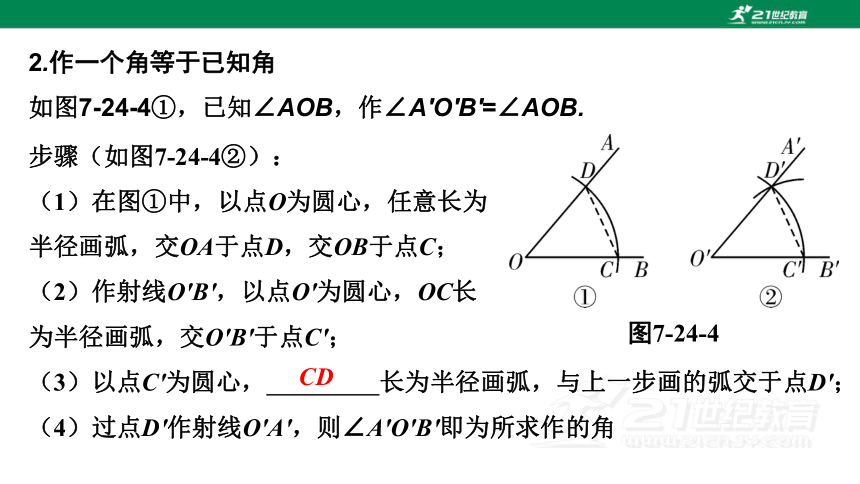
2.作一个角等于已知角
如图7-24-4①,已知∠AOB,作∠A'O'B'=∠AOB.
图7-24-4
步骤(如图7-24-4②):
(1)在图①中,以点O为圆心,任意长为
半径画弧,交OA于点D,交OB于点C;
(2)作射线O'B',以点O'为圆心,OC长
为半径画弧,交O'B'于点C';
(3)以点C'为圆心, 长为半径画弧,与上一步画的弧交于点D';
(4)过点D'作射线O'A',则∠A'O'B'即为所求作的角
CD
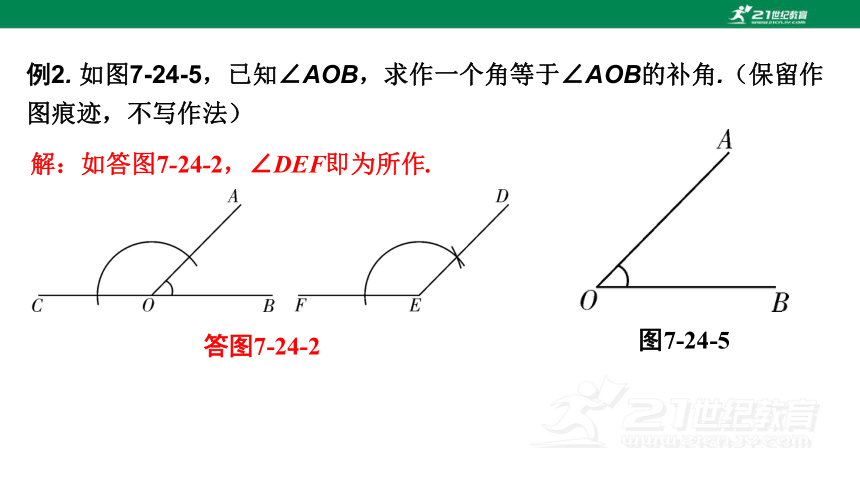
例2. 如图7-24-5,已知∠AOB,求作一个角等于∠AOB的补角.(保留作图痕迹,不写作法)
图7-24-5
解:如答图7-24-2,∠DEF即为所作.
答图7-24-2
3.作一个角的平分线
如图7-24-6①,已知∠AOB,作它的角平分线.
图7-24-6
步骤(如图7-24-6②):
(1)以点O为圆心,适当长为半径画弧,
交OA于点D,交OB于点E;
(2)分别以点D,E为圆心,大于 的长为半径画弧,两弧在∠AOB内部交于点C;
(3)作射线OC,则射线OC即为∠AOB的平分线
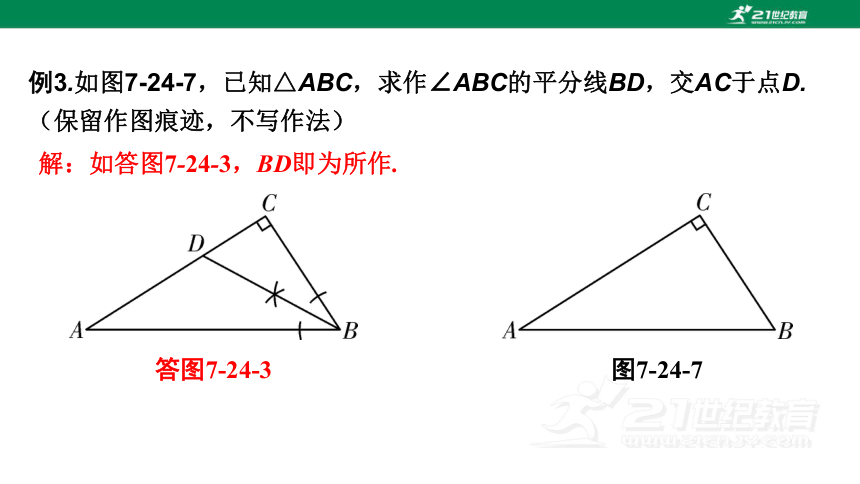
例3.如图7-24-7,已知△ABC,求作∠ABC的平分线BD,交AC于点D.(保留作图痕迹,不写作法)
图7-24-7
解:如答图7-24-3,BD即为所作.
答图7-24-3
4.作一条线段的垂直平分线
如图7-24-8①,已知线段AB,作它的垂直平分线.
步骤(如图7-24-8②):
(1)分别以点A,B为圆心,大于 的长为半径画弧,两弧分别交于点C,D;
(2)作直线CD,则直线CD即为线段AB的垂直平分线
图7-24-8
例4.为了方便居民的生活,计划在三个住宅小区A,B,C(如图7-24-9)之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场的距离相等?请在图中确定购物商场的位置.(保留作图痕迹,不写作法)
图7-24-9
解:如答图7-24-4,点P即为商场的位置.(作法不唯一)
答图7-24-4
图7-24-10
图7-24-11
例5.如图7-24-12,过点P分别向角的两边作垂线.(保留作图痕迹,不写作法)
图7-24-12
解:如答图7-24-5.
答图7-24-5
6.过直线外一点作这条直线的平行线
如图7-24-13①,已知直线l及直线l外一点A,求作直线AD,使得AD∥l.
图7-24-13
步骤(如图7-24-13②):
(1)在直线l上任取一点B,连接AB;
(2)以点B为圆心,AB长为半径画弧,交直线l于点C;
(3)分别以点A,C为圆心,AB长为半径画弧,两弧交于点D(不与点B重合);
(4)作直线AD,则直线AD即为所求作的直线
例6. 如图7-24-14是小明同学完成“过直线外一点P,作直线l的平行线”的尺规作图.
(1)根据作图痕迹,填空:
①AC是∠PAB的 ;
②PA= ;
平分线
PQ
(2)根据作图痕迹,说明直线PQ与l为什么平行?
图7-24-14
解:(2)∵AC平分∠PAB,
∴∠PAC=∠CAB.
∵PA=PQ,∴∠PAC=∠PQA.
∴∠PQA=∠CAB.
∴PQ∥l.
*7. 过圆外一点作圆的切线
如图7-24-15①,已知☉O和圆外一点P,求过点P作☉O的切线.步骤是:
图7-24-15
步骤(如图7-24-15②):
(1)连接OP,作线段OP的垂直平分线交OP于点M;
(2)以点M为圆心,OM的长为半径作圆,交☉O于A,B两点;
(3)作直线PA,PB,则直线PA,PB即为所求作的切线
例7. 如图7-24-16是小海同学设计的“过圆外一点A,作☉O的一条切线AC”的尺规作图.
作法:①连接AO交☉O于点D,并延长AO交☉O于点E;
②以点A为圆心,AO长为半径画弧,以点O为圆心,DE的长为半径画弧,两弧交于点B;
③连接OB交☉O于点C,作直线AC,则直线AC是☉O的一条切线.
请你证明AC是☉O的切线.
图7-24-16
证明:∵OB=DE=2OD=2OC,
∴OC=BC.∵AO=AB,∴AC⊥OB.
又∵OC是☉O的半径,
∴AC是☉O的切线.
8.利用尺规作三角形
(1)已知三角形的三边作三角形
如图7-24-17①,已知线段a,b,c.求作△ABC,使AB=c,AC=b,BC=a.
步骤(如图7-24-17②):
①作射线BM;
②在射线BM上截取BC=a,再分别以点B,
C为圆心,c,b为半径画弧,两弧相交于点A;
③连接AB,AC,则△ABC即为所作.
图7-24-17
(2)已知三角形的两边及夹角作三角形
如图7-24-18①,已知线段m,n和∠β,求作△ABC,使AB=m,BC=n,∠ABC=∠β.
步骤(如图7-24-18②):
①作∠MBN=∠β;
②在BM上截取AB=m,BN上截取BC=n;
③连接AC,则△ABC即为所作.
图7-24-18
(3)已知三角形的两角及其夹边作三角形
如图7-24-19①,已知∠α,∠β和线段a,求作△ABC,使∠A=∠α,∠B=∠β,AB=a.
步骤(如图7-24-19②):
①作射线AM;
②在射线AM上截取AB=a,作∠EAB=∠α,
∠FBA=∠β,射线AE交射线BF于点C,
则△ABC即为所作
图7-24-19
例8.(1)如图7-24-20,已知△ABC,在△ABC下方作△ABD,使得△ABD≌△ABC;(保留作图痕迹,不写作法)
图7-24-20
解:如答图7-24-6,△ABD即为所作.
答图7-24-6
(2)如图7-24-21,已知线段a,b,求作△ABC,使∠A=90°,AB=a,AC=b;(保留作图痕迹,不写作法)
图7-24-21
解:如答图7-24-7,△ABC即为所作.
答图7-24-7
(3)如图7-24-22,已知∠α和线段a,用尺规作△ABC,使∠ABC=∠α,∠ACB=2∠α,BC=a.(保留作图痕迹,不写作法)
图7-24-22
解:如答图7-24-8,△ABC即为所作.
答图7-24-8
9.利用尺规作三角形的外接圆和内切圆
(1)作三角形的外接圆
如图7-24-23①,已知△ABC,求作△ABC的外接圆☉O.
步骤(如图7-24-23②):
①分别作线段AB,BC的 ,它们交于点O;
②以点O为圆心,OB为半径作☉O,则☉O即为所作.
图7-24-23
垂直平分线
(2)作三角形的内切圆
如图7-24-24①,已知△ABC,求作△ABC的内切圆☉O.
步骤(如图7-24-24②):
①分别作∠B,∠C的 ,它们
交于点O;
②过点O作BC的垂线,垂足为D;
③以点O为圆心,OD为半径作☉O,则☉O即为所作
图7-24-24
平分线
例9.(1)如图7-24-25是☉O一段弧,AB和BC是圆弧的两条弦,请你作出圆心O的位置,并把圆补充完整;(保留作图痕迹,不写作法)
图7-24-25
解:如答图7-24-9,点O和☉O即为所作.
答图7-24-9
(2)如图7-24-26,在△ABC中,∠B=∠C,AD是BC边上的中线,求作△ABC的内切圆.(保留作图痕迹,不写作法)
图7-24-26
解:如答图7-24-10,☉O即为所作.
答图7-24-10
广东中考
图7-24-27
45°
2. (2023·广东题19,9分,作图——基本作图;解直角三角形)如图7-24-28,在 ABCD中,∠DAB=30°.
(1)实践与操作:用尺规作图法过点D作AB边上的高DE;(保留作图痕迹,不要求写作法)
图7-24-28
解:(1)如答图7-24-11,DE即为所作.
答图7-24-11
(2)应用与计算:在(1)的条件下,AD=4,AB=6,求BE的长.
答图7-24-11
3. (2024·广东题17,7分,作图—基本作图;角平分线的性质;切线的判定)如图7-24-29,在△ABC中,∠C=90°.
(1)实践与操作:用尺规作图法作∠A的平分线AD交BC于点D;(保留作图痕迹,不要求写作法)
图7-24-29
(1)解:如答图7-24-12,AD即为所作.
答图7-24-12
(2)应用与证明:在(1)的条件下,以点D为圆心,DC长为半径作☉D. 求证:AB与☉D相切.
(2)证明:如答图7-24-12,过点D作DE⊥AB于点E.
∵∠ACB=90°,∴DC⊥AC.
又∵AD平分∠BAC,∴DE=DC,即DE为☉D的半径.
又∵DE⊥AB,∴AB与☉D相切.
答图7-24-12
高分击破
【典型考点】作图—复杂作图;直线与圆的位置关系 得分点分析
1. (2024·广东改编)如图7-24-30,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D.
(1)实践与操作:利用尺规作☉O,使☉O经过点A,D,且圆心O在AB上;(保留作图痕迹,不写作法)
····································································
图7-24-30
解:(1)如图7-24-31,☉O即为所作. ··············2分(尺规作图得2分)
(2)应用与证明:在(1)的条件下,判断直线BC与☉O的位置关系,并说明理由.
(2)直线BC与☉O相切.
理由:如图7-24-31,连接OD.
∵OA=OD,∴∠OAD=∠ODA.
······························3分(利用等边对等角得1分)
∵AD平分∠BAC,∴∠CAD=∠OAD. ··············4分(利用角平分线的定义得1分)
∴∠CAD=∠ODA.∴AC∥OD. ·········5分(利用“内错角相等,两直线平行”得1分)
∴∠ODB=∠C=90°,即OD⊥BC. 6分(利用平行线的性质得出OD⊥BC得1分)
又∵OD是☉O的半径,∴直线BC与☉O相切. ···· 7分(利用切线的判定得1分)
温馨提示:此类考题常见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】由于不理解三角形高的定义导致作图出错
2. 如图7-24-32,利用尺规作图,作△ABC的边BC上的高.(保留作图痕迹,不写作法)
图7-24-32
解:如答图7-24-13,线段AD即为所作.
答图7-24-13
错解分析
错解:如图7-24-33,线段AD即为所作.
剖析:错解①是作BC的垂直平分线;错解②是过点C作BC的垂线;错解③是过点A作AB的垂线.三个解法都没正确理解△ABC的边BC上的高.
图7-24-33
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图7-24-34,已知△ABC.
知识种子:基本概念
(1)若∠B=60°,∠A=80°,以点A为圆心,AB长为半径作弧,交射线CA于点D,连接BD,则∠CBD的度数是 ;
图7-24-34
10°或100°
种子生长:尺规作图
(2)①尺规作图:在图7-24-34中作∠BAC的平分线AD,交BC于点D.作AD的垂直平分线EF,交AB于点E,交AC于点F,连接DE,DF;(保留作图痕迹,不写作法)
图7-24-34
①解:如答图7-24-14.
答图7-24-14
②在①的条件下,求证:四边形AEDF是菱形;
②证明:如答图7-24-14,设AD与EF相交于点O.
∵EF垂直平分AD,∴AE=DE,AF=DF,AD⊥EF.
∴∠AOE=∠AOF=90°.
∵AD平分∠BAC,∴∠EAO=∠FAO.
又∵OA=OA,∴△AOE≌△AOF(ASA).
∴AE=AF,即AE=DE=AF=DF.
∴四边形AEDF是菱形.
答图7-24-14
生长变式:作图变式
(3)①尺规作图:在图7-24-35中AC的右上方确定一点D,使∠DAC=∠ACB,且CD⊥AD;(保留作图痕迹,不写作法)
图7-24-35
解:①如答图7-24-15,点D即为所求.
答图7-24-15
②在①的条件下,若∠B=60°,AB=2,BC=3,求四边形ABCD的面积;
答图7-24-15
种子成树:综合创新
(4)如图7-24-36,在Rt△ABC中,∠A=90°,AB=8,AC=6.
①尺规作图:作☉O,使☉O经过点A,且与BC相切于点D;(保留作图痕迹,不写作法)
图7-24-36
解:①如答图7-24-16,☉O即为所作.
答图7-24-16
②在①的条件下,若D是边BC上的动点,设☉O与边AB,AC分别交于点E,F,求EF的最小值.
答图7-24-17
中考演练
(限时15分钟)
一、选择题
1. (2024·河北)观察图7-24-37中尺规作图的痕迹,可得线段BD一定是△ABC的 ( )
A. 角平分线 B. 高线
C. 中位线 D. 中线
图7-24-37
B
图7-24-38
C
图7-24-39
C
4. (2024·深圳)在如图7-24-40所示的三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是 ( )
A. ①②
B. ①③
C. ②③
D. 只有①
图7-24-40
B
图7-24-41
D
图7-24-42
35
图7-24-43
4
图7-24-44
13
三、解答题
9. (2024·广州)如图7-24-45,Rt△ABC中,∠B=90°.
(1)尺规作图:作AC边上的中线BO;(保留作图痕迹,不写作法)
图7-24-45
(1)解:如答图7-24-18,线段BO为AC边上的中线.
答图7-24-18
(2)在(1)所作的图中,将中线BO绕点O逆时针旋转180°得到DO,连接AD,CD. 求证:四边形ABCD是矩形.
(2)证明:如答图7-24-18.
∵BO是AC边上的中线,∴AO=CO.
∵将中线BO绕点O逆时针旋转180°得到DO,
∴BO=DO.
∴四边形ABCD是平行四边形.
又∵∠ABC=90°,
∴四边形ABCD是矩形.
答图7-24-18
10. (2024·无锡)如图7-24-46,在△ABC中,AB>AC.
(1)尺规作图:作∠BAC的平分线,在角平分线上确定点D,使得DB=DC;(保留作图痕迹,不写作法)
图7-24-46
解:(1)如答图7-24-19,AD即为所作.
答图7-24-19
(2)在(1)的条件下,若∠BAC=90°,AB=7,AC=5,则AD的长是多少?(请直接写出AD的值)
答图7-24-19
命题趋势
( 限时 5 分钟)
(综合探究)如图7-24-47,在Rt△ACB中,∠C=90°.
(1)请按如下要求完成尺规作图.(不写作法,
保留作图痕迹)
①作∠CBD=∠A,交线段AC于点D;
②作线段AD的垂直平分线,交AB于点O;
③以点O为圆心,OA为半径作☉O,交AB于点E;
图7-24-47
解:(1)如答图7-24-20.
答图7-24-20
(2)在(1)的条件下,判断BD所在直线与☉O的位置关系,并说明理由;
(2)BD所在直线与☉O相切.
理由:如答图7-24-20,连接OD,则OD=OA.∴∠ODA=∠A.
又∵∠CBD=∠A,∴∠CBD=∠ODA.
∵∠C=90,∴∠CBD+∠CDB=90°.
∴∠ODA+∠CDB=90°.
∴∠ODB=180°-(∠ODA+∠CDB)=90°,即OD⊥BD.
又∵OD是☉O的半径,∴BD所在直线与☉O相切.
答图7-24-20
答图7-24-20
第七章 尺规作图及图形变换
第24课时 尺 规 作 图
课前循环练
(限时5分钟)
1. (广东真题)一元二次方程x2-4x-1=0配方后可化为 ( )
A. (x+2)2=3 B. (x+2)2=5
C. (x-2)2=3 D. (x-2)2=5
2. (广东真题)下列运算正确的是 ( )
A. (-m2n)3=-m6n3 B. m5-m3=m2
C. (m+2)2=m2+4 D. (12m4-3m)÷3m=4m3
D
A
A
图7-24-1
①能用尺规作图:作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线;过一点作已知直线的垂线;过直线外一点作这条直线的平行线; *过圆外一点作圆的切线.
②能用尺规作图:已知三边、两边及其夹角、两角及其夹边作三角形;已知底边及底边上的高线作等腰三角形;已知一直角边和斜边作直角三角形.
③能用尺规作图: 过不在同一直线上的三点作圆;作三角形的外接圆、内切圆;作圆的内接正方形和内接正六边形.
课标要求
对接教材 人教:尺规作图分布在各年级上下册的几何部分
北师:尺规作图分布在各年级上下册的几何部分
考点梳理
考点复习
1.作一条线段等于已知线段
如图7-24-2①,已知线段a,作一条线段AB=a.
步骤(如图7-24-2②):
(1)作射线AM;
(2)在射线AM上截取 ,则线段AB即为所求作的线段
图7-24-2
AB=a
广东省对应考点例题
例1. 如图7-24-3,已知线段a,求作一条线段,使它等于2a.(保留作图痕迹,不写作法)
图7-24-3
解:如答图7-24-1,线段AC即为所作.
答图7-24-1
2.作一个角等于已知角
如图7-24-4①,已知∠AOB,作∠A'O'B'=∠AOB.
图7-24-4
步骤(如图7-24-4②):
(1)在图①中,以点O为圆心,任意长为
半径画弧,交OA于点D,交OB于点C;
(2)作射线O'B',以点O'为圆心,OC长
为半径画弧,交O'B'于点C';
(3)以点C'为圆心, 长为半径画弧,与上一步画的弧交于点D';
(4)过点D'作射线O'A',则∠A'O'B'即为所求作的角
CD
例2. 如图7-24-5,已知∠AOB,求作一个角等于∠AOB的补角.(保留作图痕迹,不写作法)
图7-24-5
解:如答图7-24-2,∠DEF即为所作.
答图7-24-2
3.作一个角的平分线
如图7-24-6①,已知∠AOB,作它的角平分线.
图7-24-6
步骤(如图7-24-6②):
(1)以点O为圆心,适当长为半径画弧,
交OA于点D,交OB于点E;
(2)分别以点D,E为圆心,大于 的长为半径画弧,两弧在∠AOB内部交于点C;
(3)作射线OC,则射线OC即为∠AOB的平分线
例3.如图7-24-7,已知△ABC,求作∠ABC的平分线BD,交AC于点D.(保留作图痕迹,不写作法)
图7-24-7
解:如答图7-24-3,BD即为所作.
答图7-24-3
4.作一条线段的垂直平分线
如图7-24-8①,已知线段AB,作它的垂直平分线.
步骤(如图7-24-8②):
(1)分别以点A,B为圆心,大于 的长为半径画弧,两弧分别交于点C,D;
(2)作直线CD,则直线CD即为线段AB的垂直平分线
图7-24-8
例4.为了方便居民的生活,计划在三个住宅小区A,B,C(如图7-24-9)之间建购物商场,该购物商场建在何处才能使这三个住宅小区的居民到该购物商场的距离相等?请在图中确定购物商场的位置.(保留作图痕迹,不写作法)
图7-24-9
解:如答图7-24-4,点P即为商场的位置.(作法不唯一)
答图7-24-4
图7-24-10
图7-24-11
例5.如图7-24-12,过点P分别向角的两边作垂线.(保留作图痕迹,不写作法)
图7-24-12
解:如答图7-24-5.
答图7-24-5
6.过直线外一点作这条直线的平行线
如图7-24-13①,已知直线l及直线l外一点A,求作直线AD,使得AD∥l.
图7-24-13
步骤(如图7-24-13②):
(1)在直线l上任取一点B,连接AB;
(2)以点B为圆心,AB长为半径画弧,交直线l于点C;
(3)分别以点A,C为圆心,AB长为半径画弧,两弧交于点D(不与点B重合);
(4)作直线AD,则直线AD即为所求作的直线
例6. 如图7-24-14是小明同学完成“过直线外一点P,作直线l的平行线”的尺规作图.
(1)根据作图痕迹,填空:
①AC是∠PAB的 ;
②PA= ;
平分线
PQ
(2)根据作图痕迹,说明直线PQ与l为什么平行?
图7-24-14
解:(2)∵AC平分∠PAB,
∴∠PAC=∠CAB.
∵PA=PQ,∴∠PAC=∠PQA.
∴∠PQA=∠CAB.
∴PQ∥l.
*7. 过圆外一点作圆的切线
如图7-24-15①,已知☉O和圆外一点P,求过点P作☉O的切线.步骤是:
图7-24-15
步骤(如图7-24-15②):
(1)连接OP,作线段OP的垂直平分线交OP于点M;
(2)以点M为圆心,OM的长为半径作圆,交☉O于A,B两点;
(3)作直线PA,PB,则直线PA,PB即为所求作的切线
例7. 如图7-24-16是小海同学设计的“过圆外一点A,作☉O的一条切线AC”的尺规作图.
作法:①连接AO交☉O于点D,并延长AO交☉O于点E;
②以点A为圆心,AO长为半径画弧,以点O为圆心,DE的长为半径画弧,两弧交于点B;
③连接OB交☉O于点C,作直线AC,则直线AC是☉O的一条切线.
请你证明AC是☉O的切线.
图7-24-16
证明:∵OB=DE=2OD=2OC,
∴OC=BC.∵AO=AB,∴AC⊥OB.
又∵OC是☉O的半径,
∴AC是☉O的切线.
8.利用尺规作三角形
(1)已知三角形的三边作三角形
如图7-24-17①,已知线段a,b,c.求作△ABC,使AB=c,AC=b,BC=a.
步骤(如图7-24-17②):
①作射线BM;
②在射线BM上截取BC=a,再分别以点B,
C为圆心,c,b为半径画弧,两弧相交于点A;
③连接AB,AC,则△ABC即为所作.
图7-24-17
(2)已知三角形的两边及夹角作三角形
如图7-24-18①,已知线段m,n和∠β,求作△ABC,使AB=m,BC=n,∠ABC=∠β.
步骤(如图7-24-18②):
①作∠MBN=∠β;
②在BM上截取AB=m,BN上截取BC=n;
③连接AC,则△ABC即为所作.
图7-24-18
(3)已知三角形的两角及其夹边作三角形
如图7-24-19①,已知∠α,∠β和线段a,求作△ABC,使∠A=∠α,∠B=∠β,AB=a.
步骤(如图7-24-19②):
①作射线AM;
②在射线AM上截取AB=a,作∠EAB=∠α,
∠FBA=∠β,射线AE交射线BF于点C,
则△ABC即为所作
图7-24-19
例8.(1)如图7-24-20,已知△ABC,在△ABC下方作△ABD,使得△ABD≌△ABC;(保留作图痕迹,不写作法)
图7-24-20
解:如答图7-24-6,△ABD即为所作.
答图7-24-6
(2)如图7-24-21,已知线段a,b,求作△ABC,使∠A=90°,AB=a,AC=b;(保留作图痕迹,不写作法)
图7-24-21
解:如答图7-24-7,△ABC即为所作.
答图7-24-7
(3)如图7-24-22,已知∠α和线段a,用尺规作△ABC,使∠ABC=∠α,∠ACB=2∠α,BC=a.(保留作图痕迹,不写作法)
图7-24-22
解:如答图7-24-8,△ABC即为所作.
答图7-24-8
9.利用尺规作三角形的外接圆和内切圆
(1)作三角形的外接圆
如图7-24-23①,已知△ABC,求作△ABC的外接圆☉O.
步骤(如图7-24-23②):
①分别作线段AB,BC的 ,它们交于点O;
②以点O为圆心,OB为半径作☉O,则☉O即为所作.
图7-24-23
垂直平分线
(2)作三角形的内切圆
如图7-24-24①,已知△ABC,求作△ABC的内切圆☉O.
步骤(如图7-24-24②):
①分别作∠B,∠C的 ,它们
交于点O;
②过点O作BC的垂线,垂足为D;
③以点O为圆心,OD为半径作☉O,则☉O即为所作
图7-24-24
平分线
例9.(1)如图7-24-25是☉O一段弧,AB和BC是圆弧的两条弦,请你作出圆心O的位置,并把圆补充完整;(保留作图痕迹,不写作法)
图7-24-25
解:如答图7-24-9,点O和☉O即为所作.
答图7-24-9
(2)如图7-24-26,在△ABC中,∠B=∠C,AD是BC边上的中线,求作△ABC的内切圆.(保留作图痕迹,不写作法)
图7-24-26
解:如答图7-24-10,☉O即为所作.
答图7-24-10
广东中考
图7-24-27
45°
2. (2023·广东题19,9分,作图——基本作图;解直角三角形)如图7-24-28,在 ABCD中,∠DAB=30°.
(1)实践与操作:用尺规作图法过点D作AB边上的高DE;(保留作图痕迹,不要求写作法)
图7-24-28
解:(1)如答图7-24-11,DE即为所作.
答图7-24-11
(2)应用与计算:在(1)的条件下,AD=4,AB=6,求BE的长.
答图7-24-11
3. (2024·广东题17,7分,作图—基本作图;角平分线的性质;切线的判定)如图7-24-29,在△ABC中,∠C=90°.
(1)实践与操作:用尺规作图法作∠A的平分线AD交BC于点D;(保留作图痕迹,不要求写作法)
图7-24-29
(1)解:如答图7-24-12,AD即为所作.
答图7-24-12
(2)应用与证明:在(1)的条件下,以点D为圆心,DC长为半径作☉D. 求证:AB与☉D相切.
(2)证明:如答图7-24-12,过点D作DE⊥AB于点E.
∵∠ACB=90°,∴DC⊥AC.
又∵AD平分∠BAC,∴DE=DC,即DE为☉D的半径.
又∵DE⊥AB,∴AB与☉D相切.
答图7-24-12
高分击破
【典型考点】作图—复杂作图;直线与圆的位置关系 得分点分析
1. (2024·广东改编)如图7-24-30,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D.
(1)实践与操作:利用尺规作☉O,使☉O经过点A,D,且圆心O在AB上;(保留作图痕迹,不写作法)
····································································
图7-24-30
解:(1)如图7-24-31,☉O即为所作. ··············2分(尺规作图得2分)
(2)应用与证明:在(1)的条件下,判断直线BC与☉O的位置关系,并说明理由.
(2)直线BC与☉O相切.
理由:如图7-24-31,连接OD.
∵OA=OD,∴∠OAD=∠ODA.
······························3分(利用等边对等角得1分)
∵AD平分∠BAC,∴∠CAD=∠OAD. ··············4分(利用角平分线的定义得1分)
∴∠CAD=∠ODA.∴AC∥OD. ·········5分(利用“内错角相等,两直线平行”得1分)
∴∠ODB=∠C=90°,即OD⊥BC. 6分(利用平行线的性质得出OD⊥BC得1分)
又∵OD是☉O的半径,∴直线BC与☉O相切. ···· 7分(利用切线的判定得1分)
温馨提示:此类考题常见于广东省中考数学试卷的第17题,分值一般为7分,答题时要注意书写格式,分步书写,慢做会求全对,评卷老师是分步给分的哦!
【典型错例】由于不理解三角形高的定义导致作图出错
2. 如图7-24-32,利用尺规作图,作△ABC的边BC上的高.(保留作图痕迹,不写作法)
图7-24-32
解:如答图7-24-13,线段AD即为所作.
答图7-24-13
错解分析
错解:如图7-24-33,线段AD即为所作.
剖析:错解①是作BC的垂直平分线;错解②是过点C作BC的垂线;错解③是过点A作AB的垂线.三个解法都没正确理解△ABC的边BC上的高.
图7-24-33
【生长式训练】知识生长→变式创新
3. (中考创新,原创题)如图7-24-34,已知△ABC.
知识种子:基本概念
(1)若∠B=60°,∠A=80°,以点A为圆心,AB长为半径作弧,交射线CA于点D,连接BD,则∠CBD的度数是 ;
图7-24-34
10°或100°
种子生长:尺规作图
(2)①尺规作图:在图7-24-34中作∠BAC的平分线AD,交BC于点D.作AD的垂直平分线EF,交AB于点E,交AC于点F,连接DE,DF;(保留作图痕迹,不写作法)
图7-24-34
①解:如答图7-24-14.
答图7-24-14
②在①的条件下,求证:四边形AEDF是菱形;
②证明:如答图7-24-14,设AD与EF相交于点O.
∵EF垂直平分AD,∴AE=DE,AF=DF,AD⊥EF.
∴∠AOE=∠AOF=90°.
∵AD平分∠BAC,∴∠EAO=∠FAO.
又∵OA=OA,∴△AOE≌△AOF(ASA).
∴AE=AF,即AE=DE=AF=DF.
∴四边形AEDF是菱形.
答图7-24-14
生长变式:作图变式
(3)①尺规作图:在图7-24-35中AC的右上方确定一点D,使∠DAC=∠ACB,且CD⊥AD;(保留作图痕迹,不写作法)
图7-24-35
解:①如答图7-24-15,点D即为所求.
答图7-24-15
②在①的条件下,若∠B=60°,AB=2,BC=3,求四边形ABCD的面积;
答图7-24-15
种子成树:综合创新
(4)如图7-24-36,在Rt△ABC中,∠A=90°,AB=8,AC=6.
①尺规作图:作☉O,使☉O经过点A,且与BC相切于点D;(保留作图痕迹,不写作法)
图7-24-36
解:①如答图7-24-16,☉O即为所作.
答图7-24-16
②在①的条件下,若D是边BC上的动点,设☉O与边AB,AC分别交于点E,F,求EF的最小值.
答图7-24-17
中考演练
(限时15分钟)
一、选择题
1. (2024·河北)观察图7-24-37中尺规作图的痕迹,可得线段BD一定是△ABC的 ( )
A. 角平分线 B. 高线
C. 中位线 D. 中线
图7-24-37
B
图7-24-38
C
图7-24-39
C
4. (2024·深圳)在如图7-24-40所示的三个图形中,根据尺规作图的痕迹,能判断射线AD平分∠BAC的是 ( )
A. ①②
B. ①③
C. ②③
D. 只有①
图7-24-40
B
图7-24-41
D
图7-24-42
35
图7-24-43
4
图7-24-44
13
三、解答题
9. (2024·广州)如图7-24-45,Rt△ABC中,∠B=90°.
(1)尺规作图:作AC边上的中线BO;(保留作图痕迹,不写作法)
图7-24-45
(1)解:如答图7-24-18,线段BO为AC边上的中线.
答图7-24-18
(2)在(1)所作的图中,将中线BO绕点O逆时针旋转180°得到DO,连接AD,CD. 求证:四边形ABCD是矩形.
(2)证明:如答图7-24-18.
∵BO是AC边上的中线,∴AO=CO.
∵将中线BO绕点O逆时针旋转180°得到DO,
∴BO=DO.
∴四边形ABCD是平行四边形.
又∵∠ABC=90°,
∴四边形ABCD是矩形.
答图7-24-18
10. (2024·无锡)如图7-24-46,在△ABC中,AB>AC.
(1)尺规作图:作∠BAC的平分线,在角平分线上确定点D,使得DB=DC;(保留作图痕迹,不写作法)
图7-24-46
解:(1)如答图7-24-19,AD即为所作.
答图7-24-19
(2)在(1)的条件下,若∠BAC=90°,AB=7,AC=5,则AD的长是多少?(请直接写出AD的值)
答图7-24-19
命题趋势
( 限时 5 分钟)
(综合探究)如图7-24-47,在Rt△ACB中,∠C=90°.
(1)请按如下要求完成尺规作图.(不写作法,
保留作图痕迹)
①作∠CBD=∠A,交线段AC于点D;
②作线段AD的垂直平分线,交AB于点O;
③以点O为圆心,OA为半径作☉O,交AB于点E;
图7-24-47
解:(1)如答图7-24-20.
答图7-24-20
(2)在(1)的条件下,判断BD所在直线与☉O的位置关系,并说明理由;
(2)BD所在直线与☉O相切.
理由:如答图7-24-20,连接OD,则OD=OA.∴∠ODA=∠A.
又∵∠CBD=∠A,∴∠CBD=∠ODA.
∵∠C=90,∴∠CBD+∠CDB=90°.
∴∠ODA+∠CDB=90°.
∴∠ODB=180°-(∠ODA+∠CDB)=90°,即OD⊥BD.
又∵OD是☉O的半径,∴BD所在直线与☉O相切.
答图7-24-20
答图7-24-20
同课章节目录
