人教版五年级下期末复习——长方体的体积与表面积(含答案)
文档属性
| 名称 | 人教版五年级下期末复习——长方体的体积与表面积(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 655.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-29 19:21:58 | ||
图片预览




文档简介
五年级长方体的体积与表面积
【题型1 切割问题】
【题型2 表面积的实际运用】
【题型3 不规则物体求体积】
【题型4 其它】
【题型1 切割问题】
【练习1】把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积( )。
A.减少110平方厘米 B.减少85平方厘米 C.减少60平方厘米
【练习2】一个长方体的高增加5米后就变成了一个正方体,表面积增加了160平方米。原来长方体的长是( )。
A.3米 B.8米 C.32 平方米
【练习3】把一根长2m的长方体木料,平均截成3段,表面积增加了12dm2,这根木料原来的体积是( )dm3。
A.24 B.36 C.60
【练习4】长方体的高从上面减少3厘米,就变成了一个正方体,表面积比原来减少60平方厘米。原来长方体的体积是( )立方厘米。
A.320 B.300 C.200
【练习5】一个长方体,如果高减少就变成了一个正方体,这时表面积就减少,原来长方体的表面积是( )。
【练习6】把一个长8cm、宽5cm、高4cm的长方体盒子的长减少2cm,那么表面积减少( )cm2,体积减少( )cm3。
【练习7】一个长方体,高增加3厘米后就变成了一个棱长8厘米的正方体(如图),表面积增加了( )平方厘米,体积增加了( )立方厘米。
【练习8】把两个棱长为2分米的正方体拼成一个长方体,表面积减少了( )平方分米,长方体的体积是( )立方分米,长方体的表面积是( )平方分米。
【练习9】一个长方体长a厘米,宽b厘米,高c厘米,如果它的高增加2厘米,那么表面积与原来相比,增加了( )平方厘米。
【练习10】一个长方体,如果高增加3,就成为一个正方体,表面积比原来增加60,原来长方体的体积是( )。
【练习11】一个长方体,高截去了2分米,表面积就减少了48平方分米,剩下部分为一个正方体,原来长方体的表面积是( )。
【练习12】一个长方体,如果宽增加2厘米,就变成一个正方体,这时表面积比原来增加32平方厘米。原来长方体的表面积是( )平方厘米。
【练习13】一个长方体,如果高增加3分米,就变成了一个正方体,这时表面积比原来增加了60平方分米,原来长方体的体积是( )立方分米。
【练习14】将3个棱长为2厘米的正方体拼成一个长方体,拼成的长方体的表面积是( )平方厘米,体积是( )立方厘米。
【题型2 表面积的实际运用】
【练习1】一个长方体的底面是一个正方形,它的侧面展开图正好是一个面积为64平方分米的正方形。这个长方体一个底面的面积是( )平方分米。
A.64 B.16 C.8 D.4
【练习2】如图,在一个透明的无盖的长方体盒子内,放置棱长为1厘米的小正方体。这个透明的长方体盒子的表面积是( )平方厘米。
A.62 B.52 C.47
【练习3】一个长方体,从它上面挖去一个小正方体,这个长方体的表面积( )。
A.不变 B.减少了 C.增加了 D.无法确定
【练习4】如图所示,从一块长方体木料上截去一块小的正方体木料,剩下木料的表面积与原长方体木料的表面积相比,( )。
A.变大 B.不变 C.变小 D.无法比较
【练习5】如图,在一个长方体的一角挖去一个小正方体后,得到一个新的立体图形。新的立体图形和原来长方体相比,下面说法正确的是( )。
A.体积变小,表面积不变 B.体积和表面积都变小
C.体积变小,表面积变大 D.体积和表面积都变大
【练习6】王叔叔打算做一个无盖的长方体鱼缸,已经准备了4块长方形玻璃,其中2块玻璃长6dm,宽4dm,另外2块玻璃长5dm,宽4dm,再加1块( )的玻璃才刚好合适。
A.长6dm;宽5dm B.长4dm;宽4dm C.长6dm;宽4dm
【练习7】将一张边长是20分米的正方形铁皮,沿虚线围成一个底面是正方形的长方体容器,要配上( )大小的铁皮。(焊接处材料损耗忽略不计)
A.40平方分米 B.25平方分米 C.50平方分米
【练习8】一个长方体的底面积为5平方米的正方形,它的侧面展开图正好是一个正方形,这个长方体的侧面积是( )平方米。
A.60 B.80 C.100
【练习9】从两个棱长为5厘米的正方体木块上,分别锯掉长5厘米、宽和高都是1厘米的小长方体木块,得到甲、乙,两种形状的木块,如下图所示。下面关于甲、乙两个木块,描述正确的是( )。
A.甲的体积>乙的体积,甲的表面积>乙的表面积
B.甲的体积=乙的体积,甲的表面积<乙的表面积
C.甲的体积=乙的体积,甲的表面积=乙的表面积
D.甲的体积<乙的体积,甲的表面积<乙的表面积
【练习10】一个长方体,如果把它的高增加2cm,长和宽不变,就变成一个棱长10cm的正方体。原来长方体的体积是( )cm3
A.512 B.800 C.200 D.640
【练习11】笑笑家装修完新居,剩4块玻璃。两块长为5dm,宽为3dm;另外两块长为4dm,宽为3dm。爸爸想做一个长方体的玻璃鱼缸(无盖),还需要配一块长( )dm、宽( )dm的玻璃。
【练习12】如下图,一根3dm长的长方体钢材,把它截成两段后,表面积增加 40cm3。原来钢材的体积是( )dm3
【练习13】把一个正方体木块锯成两个完全一样的长方体,这两个长方体的表面积之和与原正方体木块相比,增加了72cm’。原来正方体木块的表面积是( )cm2,体积是( )cm3
【练习14】把一根长15分米的长方体木料沿横载面截成两个小长方体,表面积增加了100平方厘米,原来这根长方体木料的体积是( )立方厘米。
【练习15】如图,将一根炭20米的长方体木块锯成6段,表面积比原来增加了150平方分米,这根长方体木块原来的体枳是( )立方分米。
【练习16】有一个长方体,从上面截下一个高是2cm的长方体后正好得到一个正方体(如图),正方体的表面积比原来长方体的表面积减少了32cm2求原来长方体的体积( )
【练习17】一根长2.5m的方木锯成4段后,表面积增加 48dm2,原来这根方木的体积是
( )dm3.
【题型3 不规则物体求体积】
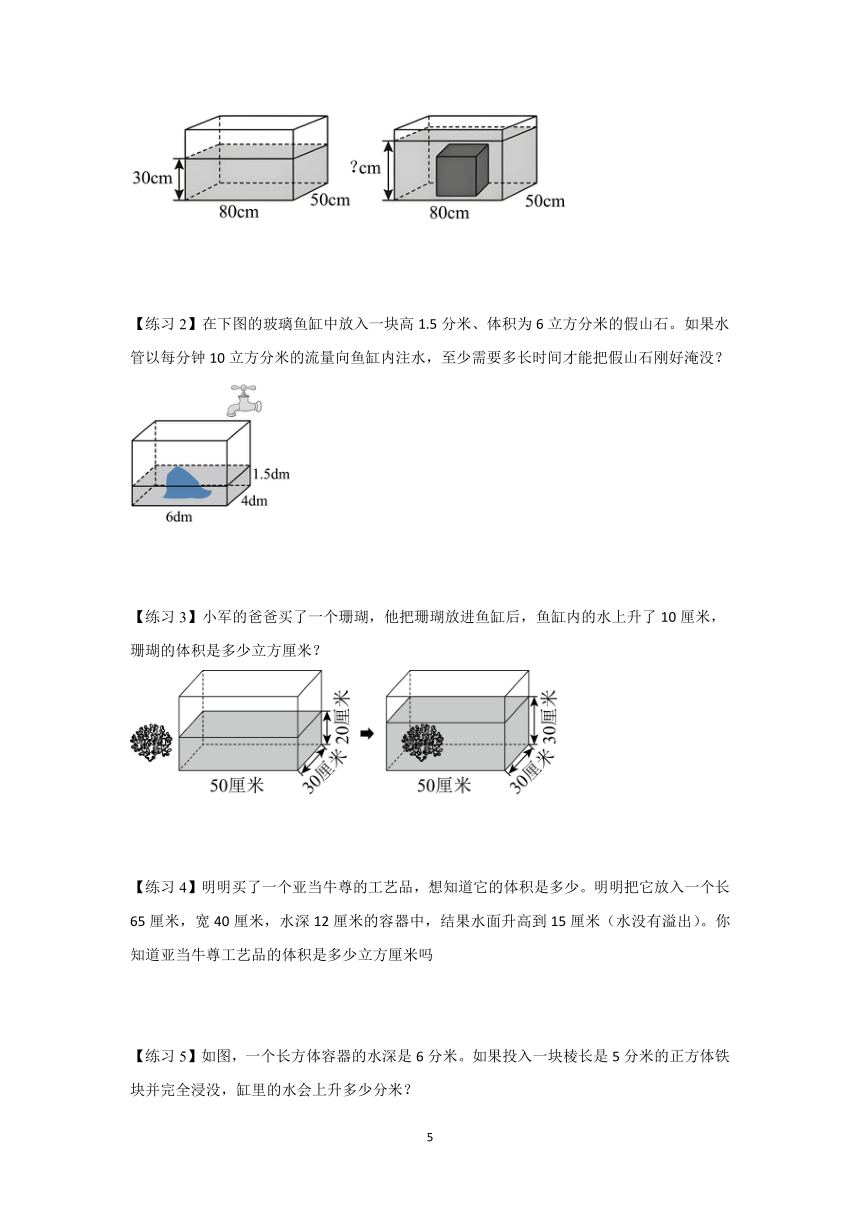
【练习1】在一个长80厘米、宽50厘米、高40厘米的长方体水箱中有30厘米深的水。如果在水中沉入一个棱长为20厘米的正方体铁块,这时水箱中水深多少厘米?
【练习2】在下图的玻璃鱼缸中放入一块高1.5分米、体积为6立方分米的假山石。如果水管以每分钟10立方分米的流量向鱼缸内注水,至少需要多长时间才能把假山石刚好淹没?
【练习3】小军的爸爸买了一个珊瑚,他把珊瑚放进鱼缸后,鱼缸内的水上升了10厘米,珊瑚的体积是多少立方厘米?
【练习4】明明买了一个亚当牛尊的工艺品,想知道它的体积是多少。明明把它放入一个长65厘米,宽40厘米,水深12厘米的容器中,结果水面升高到15厘米(水没有溢出)。你知道亚当牛尊工艺品的体积是多少立方厘米吗
【练习5】如图,一个长方体容器的水深是6分米。如果投入一块棱长是5分米的正方体铁块并完全浸没,缸里的水会上升多少分米?
【练习6】如图,将石块放入A容器中(全部淹没水中),水位上升1.5厘米,如果将其放入B容器中(全部淹没水中),水位会上升几厘米?(水没有溢出)
【练习7】一个量筒,盛有400毫升的水,放入4颗半径相等的钢珠后,水面上升到480毫升的地方。每颗钢珠的体积是多少立方厘米?
【练习8】小明家有一个长12dm、宽8dm、高1m的鱼缸,鱼缸里放入一些鱼后,水深为8dm,爸爸把鱼从鱼缸捞出来换水时,水深下降为6.5dm。这些鱼的体积是多少立方分米
【练习9】如图,一个无盖的长方体玻璃鱼缸,长50厘米、宽30厘米、高25厘米。现将一块高14厘米,体积为1000立方厘米的假石山放入缸内。如果水龙头以每分5000毫升的流量向鱼缸内注水,那么至少需要多少分钟才能将假石山完全淹没
【练习10】图1是一个长方体无盖玻璃容器,容器中水深25cm。
(1)制作这个容器至少需要多大面积的玻璃
(2)如图2,把体积共(600cm3的梨和苹果完全浸入水中,水面上升了几厘米
【练习11】向一个如图所示的长方体空水箱内匀速注水,5分钟后关闭水龙头停止注水,又过了3分钟,放入一块铁块(完全浸没且水没有溢出)。水面高度变化如下图所示。
(1)关团水龙头后,水箱内水面高度是长方体水箱高度的几分之几
(2)铁块的体积是多少立方厘米
【练习12】丁丁将一个小长方体铁块放入一个大长方体空水槽内(如图甲所示),并向水槽内匀速注水,注水速度为每秒20立方厘米,直到注满为止。整个注水过程中水槽内的水深h(厘米)与注水时间t(秒)的关系如图乙所示。
(1)从图中你能获得什么数学信息 (写两条)
(2)从浸没铁块开始到注满水槽,注入的水有多少立方厘米
(3)铁块的体积是多少立方厘米
【练习13】在一个如图所示的空长方体水箱内匀速注水,5分钟后关闭水龙头停止注水,又过了3分钟,放入一块铁块(完全浸没目水没有溢出)。水面高度变化如下图所示。
(1)关闭水龙头后,水箱内水面高度是长方体水箱高的几分之几
(2)铁块的体积是多少立方厘米
【题型4 其它】
【练习1】一个长方体的长、宽、高都扩大3倍,它的表面积扩大( )倍。
A.3 B.6 C.9
【练习2】将正方体的棱长扩大到原来的3倍,则表面积扩大到原来的( )倍;体积扩大到原来的( )倍。
【练习3】如果一个长方体的长变为原来的2倍,宽变为原来的3倍,高变为原来的4倍,那么体积将变为原来的( )倍。
A.10 B.12 C.24
【练习4】如图是一个长方体的展开图,分别计算这个长方体的表面积和体积。
【练习5】如下图,有一个长方体物体,底面是正方形,中间是空心的。(单位:厘米)
(1)这个长方体物体的体积是多少
(2)把这个长方体物体浸没在水中,与水接触的面积是多少
【练习6】如图是一个长方体的展开图,分别计算原来这个长方体的表面积和体积。
五年级长方体的体积与表面积答案
【题型1 切割问题】
【练习1】C
【练习2】B
【练习3】C
【练习4】C
【练习5】480
【练习6】 36 40
【练习7】 96 192
【练习8】 8 16 40
【练习9】4a+4b
【练习10】50
【练习11】264平方分米/264dm2
【练习12】64
【练习13】50
【练习14】56 24
【题型2 表面积的实际运用】
【练习1】D
【练习2】C
【练习3】C
【练习4】A
【练习5】A
【练习6】A
【练习7】C
【练习8】B
【练习9】B
【练习10】 B
【练习11】5 4
【练习12】0.6
【练习13】216 216
【练习14】7500
【练习15】3000
【练习16】96
【练习17】200
【题型3 不规则物体求体积】
【练习1】20×20×20=8000(立方厘米)
8000÷(80×50)
=8000÷4000
=2(厘米)
30+2=32(厘米)
【练习2】(6×4×1.5-6)÷10
=(24×1.5-6)÷10
=(36-6)÷10
=30÷10
=3(分钟)
【练习3】50×30×10
=1500×10
=15000(立方厘米)
【练习4】65×40×(15-12)
=2600×3
=7800(立方厘米)
【练习5】5×5×5÷(10×10)
=125÷100
=1.25(分米)
【练习6】8×8×1.5
=64×1.5
=96(立方厘米)
96÷32=3(厘米)
【练习7】(480-400)÷4
=80÷4
=20(立方厘米)
【练习8】解:12×8×(8-6.5)=96×1.5=144(立方分米 )
【练习9】4分钟
【练习10】1cm
【练习11】 150
【练习12】
(1)小长方体铁块的高为6厘米
在第53秒时水槽内注满水
(2)640 (3)540
【练习13】 150
【题型4 其它】
【练习1】C
【练习2】9 27
【练习3】C
【练习4】解:长:20cm宽:40-25=15(cm)高:(25-15)+2=10÷2=5(cm)
表面积:(20x15+20x5+15x5)x2=(300+100+75)x2=475x2=950cm2
体积20x15x5=300x5=1500cm3
【练习5】(1)解:10x10x25-6x6x25=2500-900
=1600(立方厘米 )
(2)解:10x25x4+10x10x2-6x6x2+6x25x6=1000+200-72+900=2028(平方厘米)
【练习6】解:25-40-2=25-20
=5(厘米)
25-5x2
=25-10=15(厘米 )
(15x5+15x20+5x20)x2=(75+300+100)x2=475x2=950(平方厘米)15x5x20
=75x20
=1500(立方厘米 )
【题型1 切割问题】
【题型2 表面积的实际运用】
【题型3 不规则物体求体积】
【题型4 其它】
【题型1 切割问题】
【练习1】把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积( )。
A.减少110平方厘米 B.减少85平方厘米 C.减少60平方厘米
【练习2】一个长方体的高增加5米后就变成了一个正方体,表面积增加了160平方米。原来长方体的长是( )。
A.3米 B.8米 C.32 平方米
【练习3】把一根长2m的长方体木料,平均截成3段,表面积增加了12dm2,这根木料原来的体积是( )dm3。
A.24 B.36 C.60
【练习4】长方体的高从上面减少3厘米,就变成了一个正方体,表面积比原来减少60平方厘米。原来长方体的体积是( )立方厘米。
A.320 B.300 C.200
【练习5】一个长方体,如果高减少就变成了一个正方体,这时表面积就减少,原来长方体的表面积是( )。
【练习6】把一个长8cm、宽5cm、高4cm的长方体盒子的长减少2cm,那么表面积减少( )cm2,体积减少( )cm3。
【练习7】一个长方体,高增加3厘米后就变成了一个棱长8厘米的正方体(如图),表面积增加了( )平方厘米,体积增加了( )立方厘米。
【练习8】把两个棱长为2分米的正方体拼成一个长方体,表面积减少了( )平方分米,长方体的体积是( )立方分米,长方体的表面积是( )平方分米。
【练习9】一个长方体长a厘米,宽b厘米,高c厘米,如果它的高增加2厘米,那么表面积与原来相比,增加了( )平方厘米。
【练习10】一个长方体,如果高增加3,就成为一个正方体,表面积比原来增加60,原来长方体的体积是( )。
【练习11】一个长方体,高截去了2分米,表面积就减少了48平方分米,剩下部分为一个正方体,原来长方体的表面积是( )。
【练习12】一个长方体,如果宽增加2厘米,就变成一个正方体,这时表面积比原来增加32平方厘米。原来长方体的表面积是( )平方厘米。
【练习13】一个长方体,如果高增加3分米,就变成了一个正方体,这时表面积比原来增加了60平方分米,原来长方体的体积是( )立方分米。
【练习14】将3个棱长为2厘米的正方体拼成一个长方体,拼成的长方体的表面积是( )平方厘米,体积是( )立方厘米。
【题型2 表面积的实际运用】
【练习1】一个长方体的底面是一个正方形,它的侧面展开图正好是一个面积为64平方分米的正方形。这个长方体一个底面的面积是( )平方分米。
A.64 B.16 C.8 D.4
【练习2】如图,在一个透明的无盖的长方体盒子内,放置棱长为1厘米的小正方体。这个透明的长方体盒子的表面积是( )平方厘米。
A.62 B.52 C.47
【练习3】一个长方体,从它上面挖去一个小正方体,这个长方体的表面积( )。
A.不变 B.减少了 C.增加了 D.无法确定
【练习4】如图所示,从一块长方体木料上截去一块小的正方体木料,剩下木料的表面积与原长方体木料的表面积相比,( )。
A.变大 B.不变 C.变小 D.无法比较
【练习5】如图,在一个长方体的一角挖去一个小正方体后,得到一个新的立体图形。新的立体图形和原来长方体相比,下面说法正确的是( )。
A.体积变小,表面积不变 B.体积和表面积都变小
C.体积变小,表面积变大 D.体积和表面积都变大
【练习6】王叔叔打算做一个无盖的长方体鱼缸,已经准备了4块长方形玻璃,其中2块玻璃长6dm,宽4dm,另外2块玻璃长5dm,宽4dm,再加1块( )的玻璃才刚好合适。
A.长6dm;宽5dm B.长4dm;宽4dm C.长6dm;宽4dm
【练习7】将一张边长是20分米的正方形铁皮,沿虚线围成一个底面是正方形的长方体容器,要配上( )大小的铁皮。(焊接处材料损耗忽略不计)
A.40平方分米 B.25平方分米 C.50平方分米
【练习8】一个长方体的底面积为5平方米的正方形,它的侧面展开图正好是一个正方形,这个长方体的侧面积是( )平方米。
A.60 B.80 C.100
【练习9】从两个棱长为5厘米的正方体木块上,分别锯掉长5厘米、宽和高都是1厘米的小长方体木块,得到甲、乙,两种形状的木块,如下图所示。下面关于甲、乙两个木块,描述正确的是( )。
A.甲的体积>乙的体积,甲的表面积>乙的表面积
B.甲的体积=乙的体积,甲的表面积<乙的表面积
C.甲的体积=乙的体积,甲的表面积=乙的表面积
D.甲的体积<乙的体积,甲的表面积<乙的表面积
【练习10】一个长方体,如果把它的高增加2cm,长和宽不变,就变成一个棱长10cm的正方体。原来长方体的体积是( )cm3
A.512 B.800 C.200 D.640
【练习11】笑笑家装修完新居,剩4块玻璃。两块长为5dm,宽为3dm;另外两块长为4dm,宽为3dm。爸爸想做一个长方体的玻璃鱼缸(无盖),还需要配一块长( )dm、宽( )dm的玻璃。
【练习12】如下图,一根3dm长的长方体钢材,把它截成两段后,表面积增加 40cm3。原来钢材的体积是( )dm3
【练习13】把一个正方体木块锯成两个完全一样的长方体,这两个长方体的表面积之和与原正方体木块相比,增加了72cm’。原来正方体木块的表面积是( )cm2,体积是( )cm3
【练习14】把一根长15分米的长方体木料沿横载面截成两个小长方体,表面积增加了100平方厘米,原来这根长方体木料的体积是( )立方厘米。
【练习15】如图,将一根炭20米的长方体木块锯成6段,表面积比原来增加了150平方分米,这根长方体木块原来的体枳是( )立方分米。
【练习16】有一个长方体,从上面截下一个高是2cm的长方体后正好得到一个正方体(如图),正方体的表面积比原来长方体的表面积减少了32cm2求原来长方体的体积( )
【练习17】一根长2.5m的方木锯成4段后,表面积增加 48dm2,原来这根方木的体积是
( )dm3.
【题型3 不规则物体求体积】
【练习1】在一个长80厘米、宽50厘米、高40厘米的长方体水箱中有30厘米深的水。如果在水中沉入一个棱长为20厘米的正方体铁块,这时水箱中水深多少厘米?
【练习2】在下图的玻璃鱼缸中放入一块高1.5分米、体积为6立方分米的假山石。如果水管以每分钟10立方分米的流量向鱼缸内注水,至少需要多长时间才能把假山石刚好淹没?
【练习3】小军的爸爸买了一个珊瑚,他把珊瑚放进鱼缸后,鱼缸内的水上升了10厘米,珊瑚的体积是多少立方厘米?
【练习4】明明买了一个亚当牛尊的工艺品,想知道它的体积是多少。明明把它放入一个长65厘米,宽40厘米,水深12厘米的容器中,结果水面升高到15厘米(水没有溢出)。你知道亚当牛尊工艺品的体积是多少立方厘米吗
【练习5】如图,一个长方体容器的水深是6分米。如果投入一块棱长是5分米的正方体铁块并完全浸没,缸里的水会上升多少分米?
【练习6】如图,将石块放入A容器中(全部淹没水中),水位上升1.5厘米,如果将其放入B容器中(全部淹没水中),水位会上升几厘米?(水没有溢出)
【练习7】一个量筒,盛有400毫升的水,放入4颗半径相等的钢珠后,水面上升到480毫升的地方。每颗钢珠的体积是多少立方厘米?
【练习8】小明家有一个长12dm、宽8dm、高1m的鱼缸,鱼缸里放入一些鱼后,水深为8dm,爸爸把鱼从鱼缸捞出来换水时,水深下降为6.5dm。这些鱼的体积是多少立方分米
【练习9】如图,一个无盖的长方体玻璃鱼缸,长50厘米、宽30厘米、高25厘米。现将一块高14厘米,体积为1000立方厘米的假石山放入缸内。如果水龙头以每分5000毫升的流量向鱼缸内注水,那么至少需要多少分钟才能将假石山完全淹没
【练习10】图1是一个长方体无盖玻璃容器,容器中水深25cm。
(1)制作这个容器至少需要多大面积的玻璃
(2)如图2,把体积共(600cm3的梨和苹果完全浸入水中,水面上升了几厘米
【练习11】向一个如图所示的长方体空水箱内匀速注水,5分钟后关闭水龙头停止注水,又过了3分钟,放入一块铁块(完全浸没且水没有溢出)。水面高度变化如下图所示。
(1)关团水龙头后,水箱内水面高度是长方体水箱高度的几分之几
(2)铁块的体积是多少立方厘米
【练习12】丁丁将一个小长方体铁块放入一个大长方体空水槽内(如图甲所示),并向水槽内匀速注水,注水速度为每秒20立方厘米,直到注满为止。整个注水过程中水槽内的水深h(厘米)与注水时间t(秒)的关系如图乙所示。
(1)从图中你能获得什么数学信息 (写两条)
(2)从浸没铁块开始到注满水槽,注入的水有多少立方厘米
(3)铁块的体积是多少立方厘米
【练习13】在一个如图所示的空长方体水箱内匀速注水,5分钟后关闭水龙头停止注水,又过了3分钟,放入一块铁块(完全浸没目水没有溢出)。水面高度变化如下图所示。
(1)关闭水龙头后,水箱内水面高度是长方体水箱高的几分之几
(2)铁块的体积是多少立方厘米
【题型4 其它】
【练习1】一个长方体的长、宽、高都扩大3倍,它的表面积扩大( )倍。
A.3 B.6 C.9
【练习2】将正方体的棱长扩大到原来的3倍,则表面积扩大到原来的( )倍;体积扩大到原来的( )倍。
【练习3】如果一个长方体的长变为原来的2倍,宽变为原来的3倍,高变为原来的4倍,那么体积将变为原来的( )倍。
A.10 B.12 C.24
【练习4】如图是一个长方体的展开图,分别计算这个长方体的表面积和体积。
【练习5】如下图,有一个长方体物体,底面是正方形,中间是空心的。(单位:厘米)
(1)这个长方体物体的体积是多少
(2)把这个长方体物体浸没在水中,与水接触的面积是多少
【练习6】如图是一个长方体的展开图,分别计算原来这个长方体的表面积和体积。
五年级长方体的体积与表面积答案
【题型1 切割问题】
【练习1】C
【练习2】B
【练习3】C
【练习4】C
【练习5】480
【练习6】 36 40
【练习7】 96 192
【练习8】 8 16 40
【练习9】4a+4b
【练习10】50
【练习11】264平方分米/264dm2
【练习12】64
【练习13】50
【练习14】56 24
【题型2 表面积的实际运用】
【练习1】D
【练习2】C
【练习3】C
【练习4】A
【练习5】A
【练习6】A
【练习7】C
【练习8】B
【练习9】B
【练习10】 B
【练习11】5 4
【练习12】0.6
【练习13】216 216
【练习14】7500
【练习15】3000
【练习16】96
【练习17】200
【题型3 不规则物体求体积】
【练习1】20×20×20=8000(立方厘米)
8000÷(80×50)
=8000÷4000
=2(厘米)
30+2=32(厘米)
【练习2】(6×4×1.5-6)÷10
=(24×1.5-6)÷10
=(36-6)÷10
=30÷10
=3(分钟)
【练习3】50×30×10
=1500×10
=15000(立方厘米)
【练习4】65×40×(15-12)
=2600×3
=7800(立方厘米)
【练习5】5×5×5÷(10×10)
=125÷100
=1.25(分米)
【练习6】8×8×1.5
=64×1.5
=96(立方厘米)
96÷32=3(厘米)
【练习7】(480-400)÷4
=80÷4
=20(立方厘米)
【练习8】解:12×8×(8-6.5)=96×1.5=144(立方分米 )
【练习9】4分钟
【练习10】1cm
【练习11】 150
【练习12】
(1)小长方体铁块的高为6厘米
在第53秒时水槽内注满水
(2)640 (3)540
【练习13】 150
【题型4 其它】
【练习1】C
【练习2】9 27
【练习3】C
【练习4】解:长:20cm宽:40-25=15(cm)高:(25-15)+2=10÷2=5(cm)
表面积:(20x15+20x5+15x5)x2=(300+100+75)x2=475x2=950cm2
体积20x15x5=300x5=1500cm3
【练习5】(1)解:10x10x25-6x6x25=2500-900
=1600(立方厘米 )
(2)解:10x25x4+10x10x2-6x6x2+6x25x6=1000+200-72+900=2028(平方厘米)
【练习6】解:25-40-2=25-20
=5(厘米)
25-5x2
=25-10=15(厘米 )
(15x5+15x20+5x20)x2=(75+300+100)x2=475x2=950(平方厘米)15x5x20
=75x20
=1500(立方厘米 )
同课章节目录
