中考数学复习专练三圆的综合题课件(共41张PPT)
文档属性
| 名称 | 中考数学复习专练三圆的综合题课件(共41张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 10:01:46 | ||
图片预览





文档简介
(共41张PPT)
专练三 圆的综合题
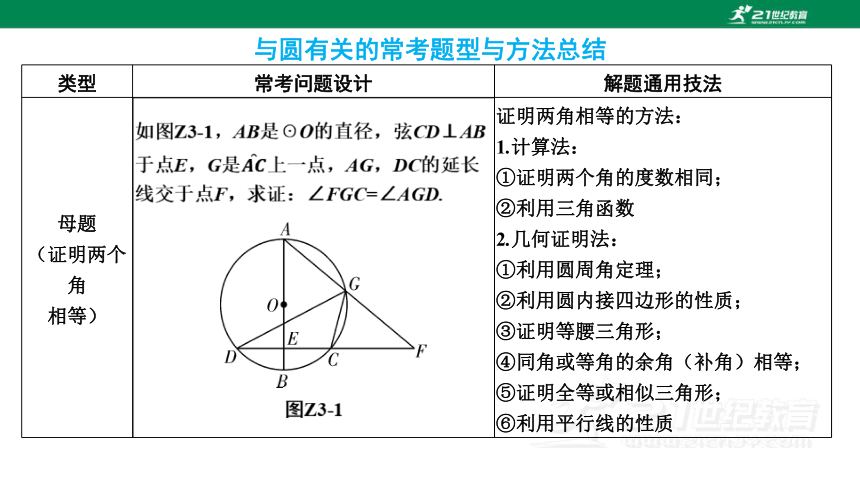
与圆有关的常考题型与方法总结
类型 常考问题设计 解题通用技法
母题
(证明两个角
相等) 证明两角相等的方法:
1.计算法:
①证明两个角的度数相同;
②利用三角函数
2.几何证明法:
①利用圆周角定理;
②利用圆内接四边形的性质;
③证明等腰三角形;
④同角或等角的余角(补角)相等;
⑤证明全等或相似三角形;
⑥利用平行线的性质
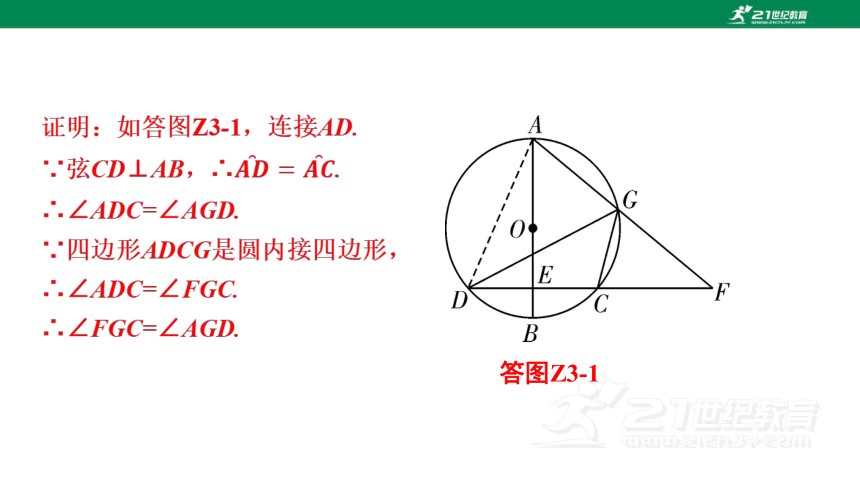
答图Z3-1
以下对于上述母题设计若干常考问题,并进行分析
类型 常考问题设计 解题通用技法
求线段长
(1)如图Z3-2,若BE=2,CD=8,求AD的长.
图Z3-2 求线段长的方法:
1.若题干中作辅助线后有直角三角形存在,考虑用勾股定理求长度;
2.若题中无直角三角形时,考虑用三角形相似或特殊角的三角函数求长度;
3. 若题干中含有30°,45°,60°等角度或出现三角函数sin α,cos α,
tan α时,考虑用三角函数求长度
答图Z3-2
类型 常考问题设计 解题通用技法
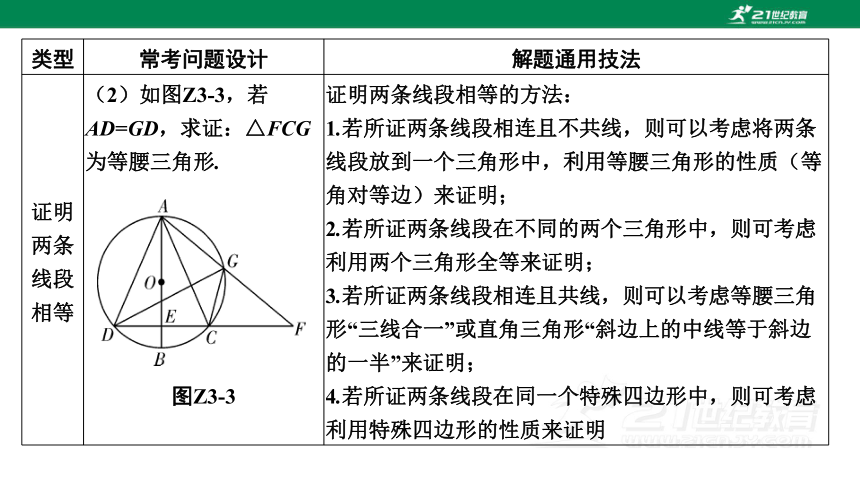
证明两条
线段相等 (2)如图Z3-3,若AD=GD,求证:△FCG为等腰三角形.
图Z3-3 证明两条线段相等的方法:
1.若所证两条线段相连且不共线,则可以考虑将两条线段放到一个三角形中,利用等腰三角形的性质(等角对等边)来证明;
2.若所证两条线段在不同的两个三角形中,则可考虑利用两个三角形全等来证明;
3.若所证两条线段相连且共线,则可以考虑等腰三角形“三线合一”或直角三角形“斜边上的中线等于斜边的一半”来证明;
4.若所证两条线段在同一个特殊四边形中,则可考虑利用特殊四边形的性质来证明
证明:∵A,D,C,G四点共圆,
∴∠FGC=∠ADC=∠AGD,∠FCG=∠GAD.
∵AD=GD,
∴∠GAD=∠DGA.
∴∠FCG=∠FGC.
∴FC=FG.
∴△FCG为等腰三角形.
图Z3-3
类型 常考问题设计 解题通用技法
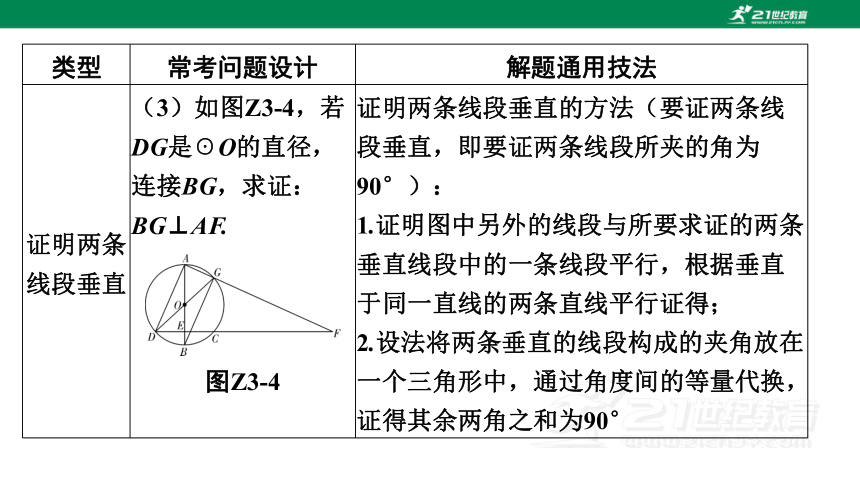
证明两条
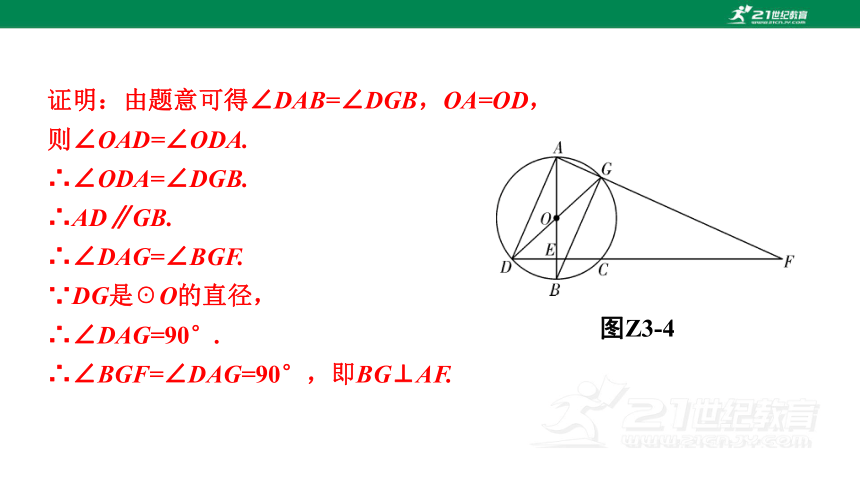
线段垂直 (3)如图Z3-4,若DG是☉O的直径,连接BG,求证:BG⊥AF.
图Z3-4 证明两条线段垂直的方法(要证两条线段垂直,即要证两条线段所夹的角为90°):
1.证明图中另外的线段与所要求证的两条垂直线段中的一条线段平行,根据垂直于同一直线的两条直线平行证得;
2.设法将两条垂直的线段构成的夹角放在一个三角形中,通过角度间的等量代换,证得其余两角之和为90°
证明:由题意可得∠DAB=∠DGB,OA=OD,
则∠OAD=∠ODA.
∴∠ODA=∠DGB.
∴AD∥GB.
∴∠DAG=∠BGF.
∵DG是☉O的直径,
∴∠DAG=90°.
∴∠BGF=∠DAG=90°,即BG⊥AF.
图Z3-4
类型 常考问题设计 解题通用技法
证明两直
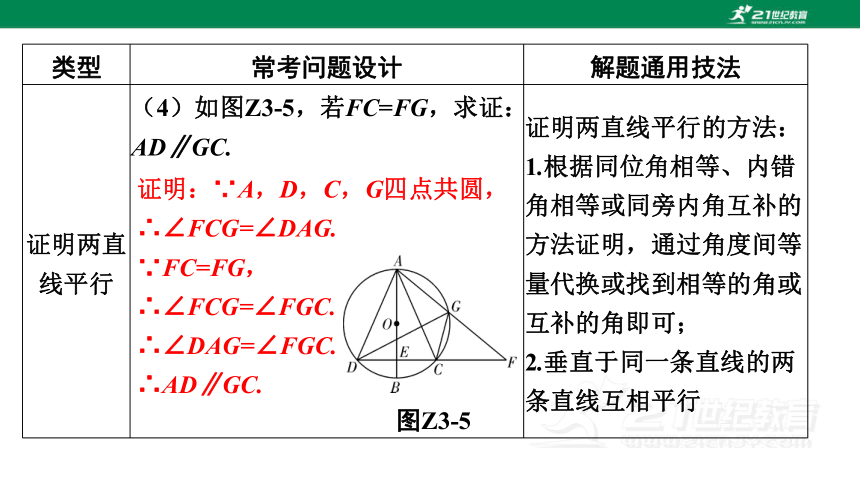
线平行 (4)如图Z3-5,若FC=FG,求证:AD∥GC.
图Z3-5 证明两直线平行的方法:
1.根据同位角相等、内错角相等或同旁内角互补的方法证明,通过角度间等量代换或找到相等的角或互补的角即可;
2.垂直于同一条直线的两条直线互相平行
证明:∵A,D,C,G四点共圆,
∴∠FCG=∠DAG.
∵FC=FG,
∴∠FCG=∠FGC.
∴∠DAG=∠FGC.
∴AD∥GC.
类型 常考问题设计 解题通用技法
证明直线
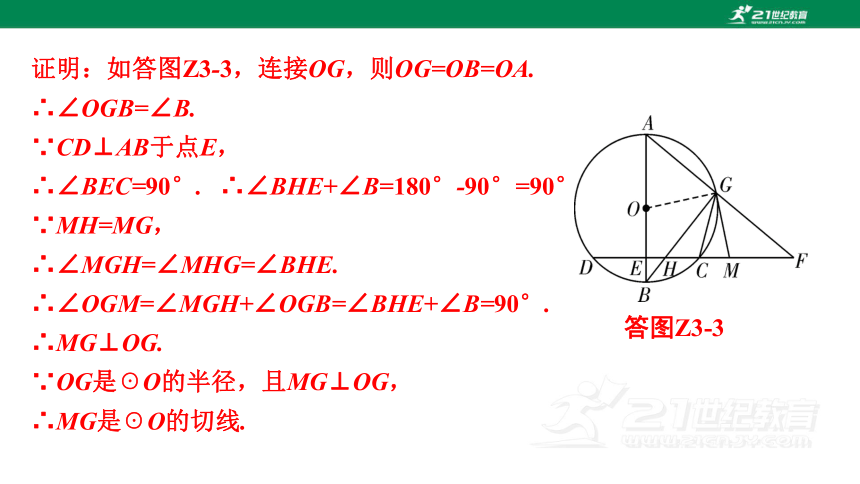
与圆相切 (5)如图Z3-6,设BG与CD交于点H,M是DF上一点,且MH=MG.求证:MG是☉O的切线.
图Z3-6 证明直线与圆相切的方法:
1.定义法:若直线与圆有唯一公共点,则直线与圆相切;
2. d=r法:证明圆心到直线的距离d等于该圆的半径r,就能判定直线与圆相切;
3.利用“切线的判定定理”证明,即经过半径的外端并且垂直于这条半径的直线是圆的切线
证明:如答图Z3-3,连接OG,则OG=OB=OA.
∴∠OGB=∠B.
∵CD⊥AB于点E,
∴∠BEC=90°. ∴∠BHE+∠B=180°-90°=90°.
∵MH=MG,
∴∠MGH=∠MHG=∠BHE.
∴∠OGM=∠MGH+∠OGB=∠BHE+∠B=90°.
∴MG⊥OG.
∵OG是☉O的半径,且MG⊥OG,
∴MG是☉O的切线.
答图Z3-3
题型一:圆的有关性质综合题
例1.如图Z3-7,四边形ABCD内接于☉O,AB=AC,∠ABD=∠CBE,D,C,E三点共线.
图Z3-7
(1)证明:∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,即∠ABC=∠DBE.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠DBE=∠ACB.
∵∠ADB=∠ACB,
∴∠DBE=∠ADB.
∴BE∥AD.
图Z3-7
(1)求证:BE∥AD;
(2)解:如答图Z3-4,设BE与☉O交于点M,连接MC,过点M作MN⊥CE于点N.
∵∠ABC=∠DBE,∠BDE=∠BAC,
∴∠E=∠ACB.
∵∠DBE=∠ACB,
∴∠E=∠DBE.
∵四边形DBMC内接于☉O,
∴∠DBE+∠DCM=180°.
答图Z3-4
答图Z3-4
题型二:圆与相似三角形
例2.如图Z3-8,在☉O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
(1)若∠FGB=∠FBG,求证:BF是☉O的切线;
图Z3-8
(1)证明:∵OA=OB,
∴∠OAB=∠OBA. ∵OA⊥CD,
∴∠OAB+∠AGC=90°.
又∵∠FGB=∠FBG,∠FGB=∠AGC,
∴∠FBG+∠OBA=90°,即∠OBF=90°.∴OB⊥FB.
∵点B在☉O上, ∴BF是☉O的切线.
(2)求证:GB2=GD·GF;
答图Z3-5
图Z3-8
如答图Z3-5,连接OC.
设圆的半径为r,则OC=r,OE=r-9.
在Rt△OCE中,由勾股定理,得CE2+OE2=OC2,
即122+(r-9)2=r2.
解得r=12.5.
∴☉O的半径为12.5.
答图Z3-5
图Z3-9
(1)证明:如答图Z3-6,连接OE.
∵CD为☉O的直径,
∴∠CED=90°. ∴∠OED+∠OEC=90°.
∵OC=OE,
∴∠OEC=∠OCE. ∴∠OCE+∠OED=90°.
∵∠PEF=∠DCE,
∴∠PEF+∠OED=90°.∴∠OEP=180°-∠OED-∠PEF=180°-90°=90°.
∴OE⊥PE.
∵OE为☉O的半径,∴PE是☉O的切线.
答图Z3-6
(1)求证:PE是☉O的切线;
(2)当∠DCE=15°时,求证:AM=2ME;
答图Z3-6
(3)在点E的移动过程中,判断AN·CM是否为定值,若是,求出该定值;若不是,请说明理由.
(3)解:在点E的移动过程中,AN·CM为定值,该定值为2r2.
∵AB⊥CD,∴∠AOC=90°.
∴∠AEC=45°.
∵OA=OC,
∴∠OAC=∠OCA=45°.
∵∠AMC=∠AEC+∠DCE=45°+∠DCE,∠ACN=∠ACO+∠DCE=45°+∠DCE,
∴∠ACN=∠AMC.
图Z3-9
图Z3-9
图Z3-10
答图Z3-7
(1)求该抛物线的解析式;
(2)若☉M的切线交x轴正半轴于点P,交y轴负半轴于点Q,切点为N,且∠OPQ=30°,试判断直线PQ是否经过抛物线的顶点?说明理由;
答图Z3-7
(3)K是☉M位于y轴右侧上的一动点,连接KB交y轴于点H,问是否存在一个常数k始终满足BH·BK=k?如果存在,请求出k的值;如果不存在,请说明理由.
答图Z3-7
图Z3-11
(2)求证:△AEB∽△BEC;
答图Z3-8
∴∠AEB=∠AEO+∠MEB=135°,∠BEC=180°-∠MEB=135°.
∴∠AEB=∠BEC.
∵AB=AC,∠BAC=90°,
∴∠ABC=45°.
∴∠ABM=∠CBE.
∴∠BAE=∠CBE.
∴△AEB∽△BEC.
答图Z3-8
(3)求证:AD与EF互相平分.
答图Z3-8
∴△AOE∽△BDE. ∴∠BED=∠AEO=90°.∴∠DEF=90°.
∴∠AFB=∠DEF.
∴AF∥DE.
由(2)知,∠AEB=135°,
∴∠AEF=180°-∠AEB=45°.
∵∠DFB=∠DAB=45°,
∴∠DFB=∠AEF.
∴AE∥FD.
∴四边形AEDF是平行四边形.
∴AD与EF互相平分.
答图Z3-8
2. (2024·凉山州)如图Z3-12,AB是☉O的直径,点C在☉O上,AD平分∠BAC交☉O于点D,过点D的直线DE⊥AC,交AC的延长线于点E,交AB的延长线于点F.
(1)求证:EF是☉O的切线;
图Z3-12
(1)证明:如答图Z3-9,连接OD.
∵AD平分∠BAC,∴∠DAE=∠OAD.
∵OA=OD,
∴∠OAD=∠ODA. ∴∠DAE=∠ODA.
∴OD∥AC.
∵DE⊥AC,
∴OD⊥DE.
∵OD是☉O的半径,
∴EF是☉O的切线.
答图Z3-9
(2)连接EO并延长,分别交☉O于M、N两点,交AD于点G,若☉O的半径为2,∠F=30°,求GM·GN的值.
答图Z3-9
答图Z3-9
图Z3-13
答图Z3-10
(2)过点D作BC的平行线交AB的延长线于点F.
①判断DF与☉O的位置关系,并说明理由;
答图Z3-10
②若△ABC为锐角三角形,求DF的取值范围.
答图Z3-11
答图Z3-12
专练三 圆的综合题
与圆有关的常考题型与方法总结
类型 常考问题设计 解题通用技法
母题
(证明两个角
相等) 证明两角相等的方法:
1.计算法:
①证明两个角的度数相同;
②利用三角函数
2.几何证明法:
①利用圆周角定理;
②利用圆内接四边形的性质;
③证明等腰三角形;
④同角或等角的余角(补角)相等;
⑤证明全等或相似三角形;
⑥利用平行线的性质
答图Z3-1
以下对于上述母题设计若干常考问题,并进行分析
类型 常考问题设计 解题通用技法
求线段长
(1)如图Z3-2,若BE=2,CD=8,求AD的长.
图Z3-2 求线段长的方法:
1.若题干中作辅助线后有直角三角形存在,考虑用勾股定理求长度;
2.若题中无直角三角形时,考虑用三角形相似或特殊角的三角函数求长度;
3. 若题干中含有30°,45°,60°等角度或出现三角函数sin α,cos α,
tan α时,考虑用三角函数求长度
答图Z3-2
类型 常考问题设计 解题通用技法
证明两条
线段相等 (2)如图Z3-3,若AD=GD,求证:△FCG为等腰三角形.
图Z3-3 证明两条线段相等的方法:
1.若所证两条线段相连且不共线,则可以考虑将两条线段放到一个三角形中,利用等腰三角形的性质(等角对等边)来证明;
2.若所证两条线段在不同的两个三角形中,则可考虑利用两个三角形全等来证明;
3.若所证两条线段相连且共线,则可以考虑等腰三角形“三线合一”或直角三角形“斜边上的中线等于斜边的一半”来证明;
4.若所证两条线段在同一个特殊四边形中,则可考虑利用特殊四边形的性质来证明
证明:∵A,D,C,G四点共圆,
∴∠FGC=∠ADC=∠AGD,∠FCG=∠GAD.
∵AD=GD,
∴∠GAD=∠DGA.
∴∠FCG=∠FGC.
∴FC=FG.
∴△FCG为等腰三角形.
图Z3-3
类型 常考问题设计 解题通用技法
证明两条
线段垂直 (3)如图Z3-4,若DG是☉O的直径,连接BG,求证:BG⊥AF.
图Z3-4 证明两条线段垂直的方法(要证两条线段垂直,即要证两条线段所夹的角为90°):
1.证明图中另外的线段与所要求证的两条垂直线段中的一条线段平行,根据垂直于同一直线的两条直线平行证得;
2.设法将两条垂直的线段构成的夹角放在一个三角形中,通过角度间的等量代换,证得其余两角之和为90°
证明:由题意可得∠DAB=∠DGB,OA=OD,
则∠OAD=∠ODA.
∴∠ODA=∠DGB.
∴AD∥GB.
∴∠DAG=∠BGF.
∵DG是☉O的直径,
∴∠DAG=90°.
∴∠BGF=∠DAG=90°,即BG⊥AF.
图Z3-4
类型 常考问题设计 解题通用技法
证明两直
线平行 (4)如图Z3-5,若FC=FG,求证:AD∥GC.
图Z3-5 证明两直线平行的方法:
1.根据同位角相等、内错角相等或同旁内角互补的方法证明,通过角度间等量代换或找到相等的角或互补的角即可;
2.垂直于同一条直线的两条直线互相平行
证明:∵A,D,C,G四点共圆,
∴∠FCG=∠DAG.
∵FC=FG,
∴∠FCG=∠FGC.
∴∠DAG=∠FGC.
∴AD∥GC.
类型 常考问题设计 解题通用技法
证明直线
与圆相切 (5)如图Z3-6,设BG与CD交于点H,M是DF上一点,且MH=MG.求证:MG是☉O的切线.
图Z3-6 证明直线与圆相切的方法:
1.定义法:若直线与圆有唯一公共点,则直线与圆相切;
2. d=r法:证明圆心到直线的距离d等于该圆的半径r,就能判定直线与圆相切;
3.利用“切线的判定定理”证明,即经过半径的外端并且垂直于这条半径的直线是圆的切线
证明:如答图Z3-3,连接OG,则OG=OB=OA.
∴∠OGB=∠B.
∵CD⊥AB于点E,
∴∠BEC=90°. ∴∠BHE+∠B=180°-90°=90°.
∵MH=MG,
∴∠MGH=∠MHG=∠BHE.
∴∠OGM=∠MGH+∠OGB=∠BHE+∠B=90°.
∴MG⊥OG.
∵OG是☉O的半径,且MG⊥OG,
∴MG是☉O的切线.
答图Z3-3
题型一:圆的有关性质综合题
例1.如图Z3-7,四边形ABCD内接于☉O,AB=AC,∠ABD=∠CBE,D,C,E三点共线.
图Z3-7
(1)证明:∵∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,即∠ABC=∠DBE.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠DBE=∠ACB.
∵∠ADB=∠ACB,
∴∠DBE=∠ADB.
∴BE∥AD.
图Z3-7
(1)求证:BE∥AD;
(2)解:如答图Z3-4,设BE与☉O交于点M,连接MC,过点M作MN⊥CE于点N.
∵∠ABC=∠DBE,∠BDE=∠BAC,
∴∠E=∠ACB.
∵∠DBE=∠ACB,
∴∠E=∠DBE.
∵四边形DBMC内接于☉O,
∴∠DBE+∠DCM=180°.
答图Z3-4
答图Z3-4
题型二:圆与相似三角形
例2.如图Z3-8,在☉O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B的直线与CD的延长线交于点F,AC∥BF.
(1)若∠FGB=∠FBG,求证:BF是☉O的切线;
图Z3-8
(1)证明:∵OA=OB,
∴∠OAB=∠OBA. ∵OA⊥CD,
∴∠OAB+∠AGC=90°.
又∵∠FGB=∠FBG,∠FGB=∠AGC,
∴∠FBG+∠OBA=90°,即∠OBF=90°.∴OB⊥FB.
∵点B在☉O上, ∴BF是☉O的切线.
(2)求证:GB2=GD·GF;
答图Z3-5
图Z3-8
如答图Z3-5,连接OC.
设圆的半径为r,则OC=r,OE=r-9.
在Rt△OCE中,由勾股定理,得CE2+OE2=OC2,
即122+(r-9)2=r2.
解得r=12.5.
∴☉O的半径为12.5.
答图Z3-5
图Z3-9
(1)证明:如答图Z3-6,连接OE.
∵CD为☉O的直径,
∴∠CED=90°. ∴∠OED+∠OEC=90°.
∵OC=OE,
∴∠OEC=∠OCE. ∴∠OCE+∠OED=90°.
∵∠PEF=∠DCE,
∴∠PEF+∠OED=90°.∴∠OEP=180°-∠OED-∠PEF=180°-90°=90°.
∴OE⊥PE.
∵OE为☉O的半径,∴PE是☉O的切线.
答图Z3-6
(1)求证:PE是☉O的切线;
(2)当∠DCE=15°时,求证:AM=2ME;
答图Z3-6
(3)在点E的移动过程中,判断AN·CM是否为定值,若是,求出该定值;若不是,请说明理由.
(3)解:在点E的移动过程中,AN·CM为定值,该定值为2r2.
∵AB⊥CD,∴∠AOC=90°.
∴∠AEC=45°.
∵OA=OC,
∴∠OAC=∠OCA=45°.
∵∠AMC=∠AEC+∠DCE=45°+∠DCE,∠ACN=∠ACO+∠DCE=45°+∠DCE,
∴∠ACN=∠AMC.
图Z3-9
图Z3-9
图Z3-10
答图Z3-7
(1)求该抛物线的解析式;
(2)若☉M的切线交x轴正半轴于点P,交y轴负半轴于点Q,切点为N,且∠OPQ=30°,试判断直线PQ是否经过抛物线的顶点?说明理由;
答图Z3-7
(3)K是☉M位于y轴右侧上的一动点,连接KB交y轴于点H,问是否存在一个常数k始终满足BH·BK=k?如果存在,请求出k的值;如果不存在,请说明理由.
答图Z3-7
图Z3-11
(2)求证:△AEB∽△BEC;
答图Z3-8
∴∠AEB=∠AEO+∠MEB=135°,∠BEC=180°-∠MEB=135°.
∴∠AEB=∠BEC.
∵AB=AC,∠BAC=90°,
∴∠ABC=45°.
∴∠ABM=∠CBE.
∴∠BAE=∠CBE.
∴△AEB∽△BEC.
答图Z3-8
(3)求证:AD与EF互相平分.
答图Z3-8
∴△AOE∽△BDE. ∴∠BED=∠AEO=90°.∴∠DEF=90°.
∴∠AFB=∠DEF.
∴AF∥DE.
由(2)知,∠AEB=135°,
∴∠AEF=180°-∠AEB=45°.
∵∠DFB=∠DAB=45°,
∴∠DFB=∠AEF.
∴AE∥FD.
∴四边形AEDF是平行四边形.
∴AD与EF互相平分.
答图Z3-8
2. (2024·凉山州)如图Z3-12,AB是☉O的直径,点C在☉O上,AD平分∠BAC交☉O于点D,过点D的直线DE⊥AC,交AC的延长线于点E,交AB的延长线于点F.
(1)求证:EF是☉O的切线;
图Z3-12
(1)证明:如答图Z3-9,连接OD.
∵AD平分∠BAC,∴∠DAE=∠OAD.
∵OA=OD,
∴∠OAD=∠ODA. ∴∠DAE=∠ODA.
∴OD∥AC.
∵DE⊥AC,
∴OD⊥DE.
∵OD是☉O的半径,
∴EF是☉O的切线.
答图Z3-9
(2)连接EO并延长,分别交☉O于M、N两点,交AD于点G,若☉O的半径为2,∠F=30°,求GM·GN的值.
答图Z3-9
答图Z3-9
图Z3-13
答图Z3-10
(2)过点D作BC的平行线交AB的延长线于点F.
①判断DF与☉O的位置关系,并说明理由;
答图Z3-10
②若△ABC为锐角三角形,求DF的取值范围.
答图Z3-11
答图Z3-12
同课章节目录
