中考数学复习第九章综合与实践第29课时综合与实践课件(共17张PPT)
文档属性
| 名称 | 中考数学复习第九章综合与实践第29课时综合与实践课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 10:05:07 | ||
图片预览





文档简介
(共17张PPT)
第八章 统计与概率
第29课时 综合与实践
【A组】
1. (2024·云南)某校九年级学生参加社会实践,学习编织圆锥形工艺品.若这种圆锥的母线长为40 cm,底面圆的半径为30 cm,则该圆锥的侧面积为0( )
A. 700π cm2 B. 900π cm2
C. 1 200π cm2 D. 1 600π cm2
C
2. (2023·齐齐哈尔)为提高学生学习兴趣,增强动手实践能力,某校为物理兴趣小组的同学购买了一根长度为150 cm的导线,将其全部截成10 cm和20 cm两种长度的导线用于实验操作(每种长度的导线至少一根),则截取方案共有0( )
A. 5种 B. 6种 C. 7种 D. 8种
C
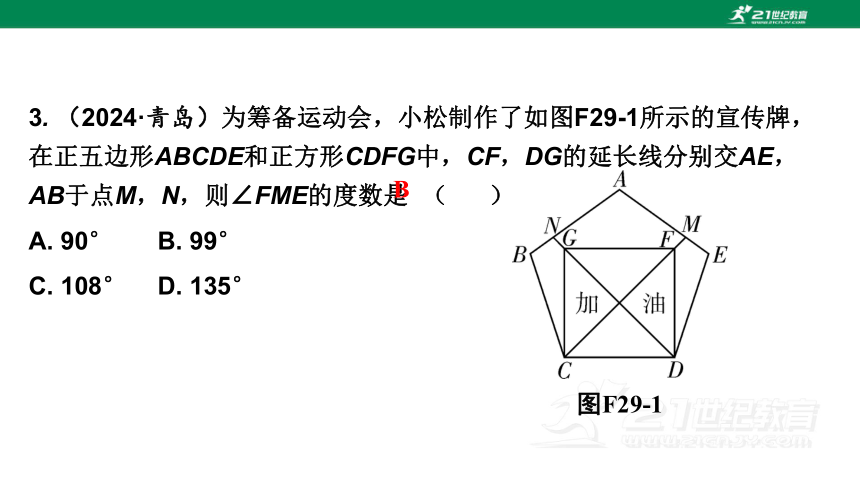
3. (2024·青岛)为筹备运动会,小松制作了如图F29-1所示的宣传牌,在正五边形ABCDE和正方形CDFG中,CF,DG的延长线分别交AE,AB于点M,N,则∠FME的度数是0( )
A. 90° B. 99°
C. 108° D. 135°
图F29-1
B
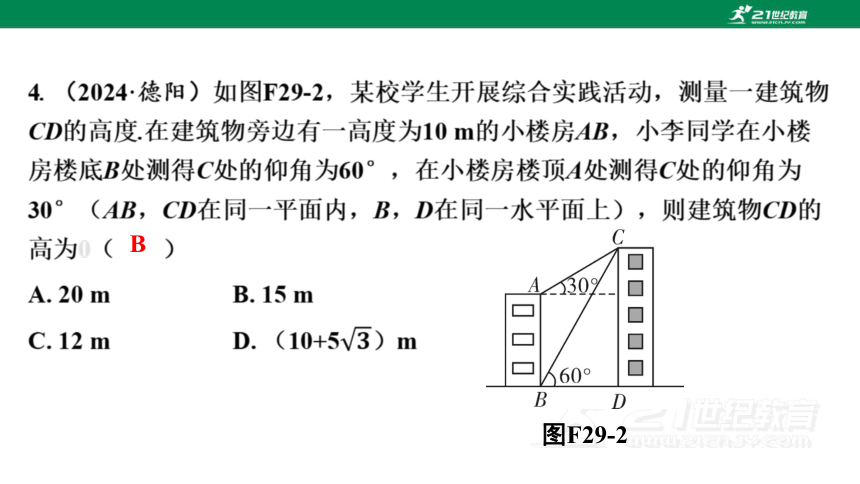
图F29-2
B
5
7. (2023·通辽)综合与实践
在综合与实践课上,老师让同学们以“正方形的折叠”为主题开展数学活动,有一位同学操作过程如下:
操作一:对折正方形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在正方形内部点M处,把纸片展平,连接PM,BM,延长PM交CD于点Q,连接BQ.
(1)如图F29-3①,当点M在EF上时,∠EMB= °;
图F29-3
30
(2)改变点P在AD上的位置(点P不与点A,D重合)如图F29-3②,判断∠MBQ与∠CBQ的数量关系,并说明理由.
解:(2)∠MBQ=∠CBQ.
理由:在正方形ABCD中,BA=BC,∠A=∠C=90°.
由折叠的性质,得BM=BA,∠BMP=∠A=90°.
∴∠BMQ=180°-∠BMP=90°.
∴BM=BA=BC,∠BMQ=∠C.
又∵BQ=BQ,
∴Rt△BMQ≌Rt△BCQ(HL).
∴∠MBQ=∠CBQ.
图F29-3
【B组】
8. (2024·兰州,跨学科融合)综合与实践
单摆是一种能够产生往复摆动的装置.某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验图示
图F29-4
实验说明 如图F29-4①,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计)
如图F29-4②,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,BD⊥OA,∠BOA=64°,BD=20.5 cm;当摆球运动至点C时,∠COA=37°,CE⊥OA.(点O,A,B,C,D,E在同一平面内)
解决问题:根据以上信息,求ED的长.(结果精确到0.1 cm,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 64°≈0.90,
cos 64°≈0.44,tan 64°≈2.05)
图F29-4
【C组】
9. (2023·日照)综合与实践
要制作200个A,B两种规格的顶部无盖木盒,A种规格是长、宽、高都为20 cm的正方体无盖木盒,B种规格是长、宽、高各为20 cm,20 cm,10 cm的长方体无盖木盒,如图F29-5①所示.现有200张规格为40 cm×40 cm的木板材,对该种木板材有甲、乙
两种切割方式,如图F29-5②所示.
切割、拼接等板材损耗忽略不计.
图F29-5
(1)设制作A种木盒x个,则制作B种木盒 个;若使用甲种方式切割的木板材y张,则使用乙种方式切割的木板材 张;
图F29-5
(200-x)
(200-y)
(2)该200张木板材恰好能做成200个A和B两种规格的无盖木盒,请分别求出A,B木盒的个数和使用甲,乙两种方式切割的木板材张数;
图F29-5
图F29-5
图F29-5
第八章 统计与概率
第29课时 综合与实践
【A组】
1. (2024·云南)某校九年级学生参加社会实践,学习编织圆锥形工艺品.若这种圆锥的母线长为40 cm,底面圆的半径为30 cm,则该圆锥的侧面积为0( )
A. 700π cm2 B. 900π cm2
C. 1 200π cm2 D. 1 600π cm2
C
2. (2023·齐齐哈尔)为提高学生学习兴趣,增强动手实践能力,某校为物理兴趣小组的同学购买了一根长度为150 cm的导线,将其全部截成10 cm和20 cm两种长度的导线用于实验操作(每种长度的导线至少一根),则截取方案共有0( )
A. 5种 B. 6种 C. 7种 D. 8种
C
3. (2024·青岛)为筹备运动会,小松制作了如图F29-1所示的宣传牌,在正五边形ABCDE和正方形CDFG中,CF,DG的延长线分别交AE,AB于点M,N,则∠FME的度数是0( )
A. 90° B. 99°
C. 108° D. 135°
图F29-1
B
图F29-2
B
5
7. (2023·通辽)综合与实践
在综合与实践课上,老师让同学们以“正方形的折叠”为主题开展数学活动,有一位同学操作过程如下:
操作一:对折正方形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在正方形内部点M处,把纸片展平,连接PM,BM,延长PM交CD于点Q,连接BQ.
(1)如图F29-3①,当点M在EF上时,∠EMB= °;
图F29-3
30
(2)改变点P在AD上的位置(点P不与点A,D重合)如图F29-3②,判断∠MBQ与∠CBQ的数量关系,并说明理由.
解:(2)∠MBQ=∠CBQ.
理由:在正方形ABCD中,BA=BC,∠A=∠C=90°.
由折叠的性质,得BM=BA,∠BMP=∠A=90°.
∴∠BMQ=180°-∠BMP=90°.
∴BM=BA=BC,∠BMQ=∠C.
又∵BQ=BQ,
∴Rt△BMQ≌Rt△BCQ(HL).
∴∠MBQ=∠CBQ.
图F29-3
【B组】
8. (2024·兰州,跨学科融合)综合与实践
单摆是一种能够产生往复摆动的装置.某兴趣小组利用摆球和摆线进行与单摆相关的实验探究,并撰写实验报告如下.
实验主题 探究摆球运动过程中高度的变化
实验用具 摆球,摆线,支架,摄像机等
实验图示
图F29-4
实验说明 如图F29-4①,在支架的横杆点O处用摆线悬挂一个摆球,将摆球拉高后松手,摆球开始往复运动.(摆线的长度变化忽略不计)
如图F29-4②,摆球静止时的位置为点A,拉紧摆线将摆球拉至点B处,BD⊥OA,∠BOA=64°,BD=20.5 cm;当摆球运动至点C时,∠COA=37°,CE⊥OA.(点O,A,B,C,D,E在同一平面内)
解决问题:根据以上信息,求ED的长.(结果精确到0.1 cm,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,sin 64°≈0.90,
cos 64°≈0.44,tan 64°≈2.05)
图F29-4
【C组】
9. (2023·日照)综合与实践
要制作200个A,B两种规格的顶部无盖木盒,A种规格是长、宽、高都为20 cm的正方体无盖木盒,B种规格是长、宽、高各为20 cm,20 cm,10 cm的长方体无盖木盒,如图F29-5①所示.现有200张规格为40 cm×40 cm的木板材,对该种木板材有甲、乙
两种切割方式,如图F29-5②所示.
切割、拼接等板材损耗忽略不计.
图F29-5
(1)设制作A种木盒x个,则制作B种木盒 个;若使用甲种方式切割的木板材y张,则使用乙种方式切割的木板材 张;
图F29-5
(200-x)
(200-y)
(2)该200张木板材恰好能做成200个A和B两种规格的无盖木盒,请分别求出A,B木盒的个数和使用甲,乙两种方式切割的木板材张数;
图F29-5
图F29-5
图F29-5
同课章节目录
