4.1 第1课时 三角形的内角和 课件(共31张PPT)
文档属性
| 名称 | 4.1 第1课时 三角形的内角和 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:20:52 | ||
图片预览








文档简介
(共31张PPT)
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.1 第1课时 三角形的内角和
4.1 认识三角形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.认识三角形并会用几何符号表示三角形.
2.会用平行线的性质与平角的定义证明三角形内角和等于180°.
3.会运用三角形内角和等于180°进行计算.
4.会按角的大小对三角形进行分类.
5.会表示直角三角形,掌握直角三角形两个锐角互余.
第贰章节
新课导入
新课导入
观察下列图片,你发现了都有什么共同点
为什么设计成三角形
第叁章节
新知探究
新知探究
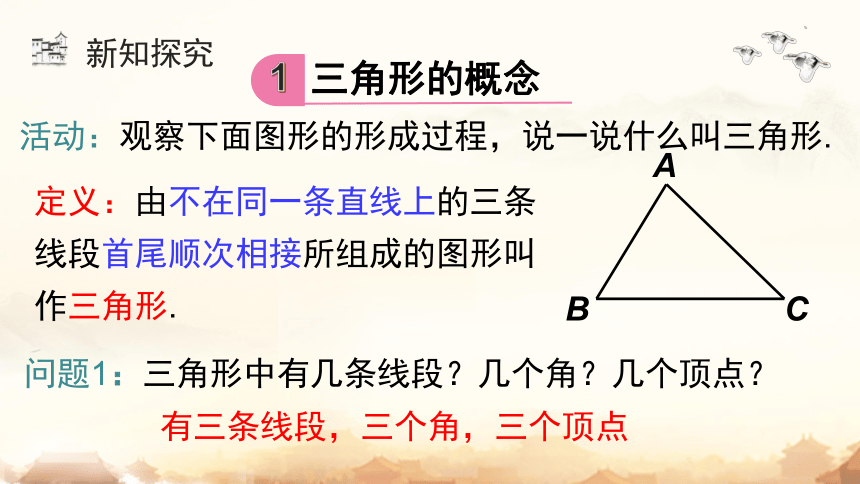
活动:观察下面图形的形成过程,说一说什么叫三角形.
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形.
问题1:三角形中有几条线段?几个角?几个顶点?
A
B
C
有三条线段,三个角,三个顶点
三角形的概念
1
三角形组成元素 三角形 ABC
边
顶点
角(内角)
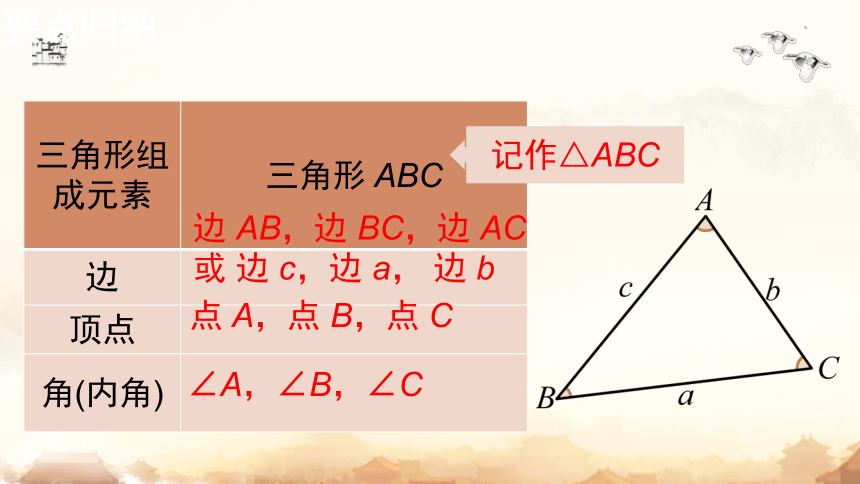
边 AB,边 BC,边 AC
或 边 c,边 a, 边 b
∠A,∠B,∠C
点 A,点 B,点 C
记作△ABC
要点归纳
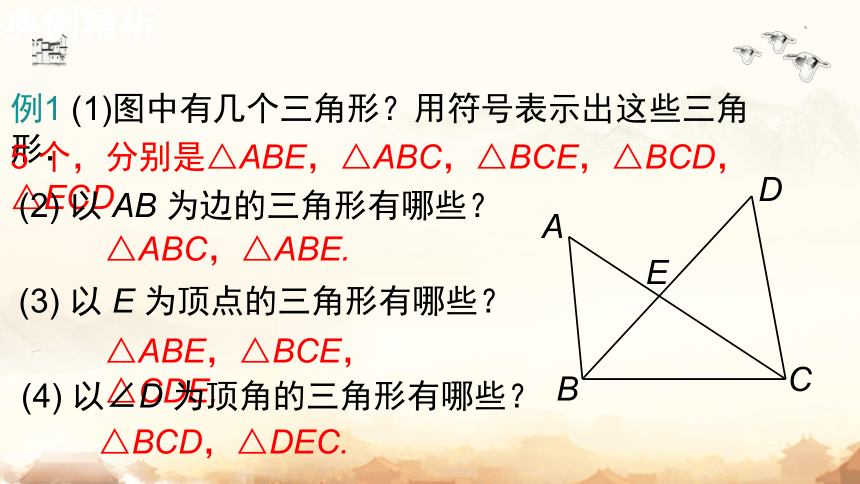
例1 (1)图中有几个三角形?用符号表示出这些三角形.
A
B
C
D
E
5 个,分别是△ABE,△ABC,△BCE,△BCD,△ECD.
(2) 以 AB 为边的三角形有哪些?
△ABC,△ABE.
(3) 以 E 为顶点的三角形有哪些?
△ABE,△BCE,△CDE.
(4) 以∠D 为顶角的三角形有哪些?
△BCD,△DEC.
典例精析
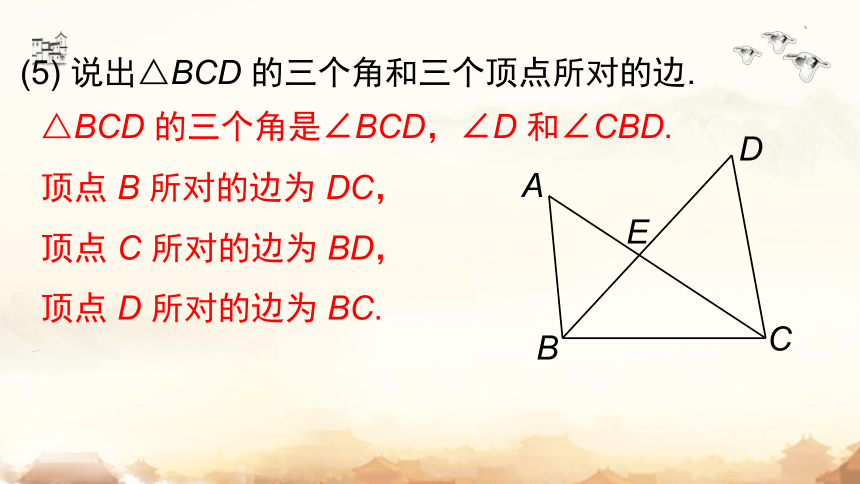
(5) 说出△BCD 的三个角和三个顶点所对的边.
△BCD 的三个角是∠BCD,∠D 和∠CBD.
A
B
C
D
E
顶点 B 所对的边为 DC,
顶点 C 所对的边为 BD,
顶点 D 所对的边为 BC.
三角形的内角和
2
合作探究:如何探索、验证三角形的内角和等于 180° ?说一说理由.
画一画:在准备的三角形硬纸板上画出△ABC,并标出三个内角.
A
B
C
1
2
3
量一量:每个角各是多少度 三个内角的和是多少
动动手:撕下三角形的三个角,拼在一起.
总结:三角形的三个内角拼到一起恰好构成一个平角.
撕拼法:撕下三角形的一个角,拼在一起.
1
3
2
1
a
b
4
此时∠1的另一条边 b 与∠3 的一条边 a 平行吗?为什么?
a∥b
(内错角相等,两直线平行)
∠3与∠4的大小有什么关系?为什么?
∠3 = ∠4
(两直线平行,同位角相等)
自己剪一个三角形纸片,重复上面的过程,你得到同样的结论了吗?与同伴进行交流.
现在,你能够确定这个三角形的内角的和了吗?
C
B
A
E
D
F
三角形三个的内角和等于 180°
动手操作
议一议:猜猜图中三角形被遮住的两个内角是什么角?试着说明理由.
三角形按角分类
3
直角三角形
锐角三角形
钝角三角形
三角形按角的大小分类
三个角都是锐角
有一个角是钝角
有一个角是直角
Rt△ABC
A
B
C
直角边
直角边
斜边
→ 直角三角形的两个锐角互余
三角形的内角和为 180°
观察图中的三角形,你能够按角将它们的形状分类吗?
锐角三角形:
钝角三角形:
直角三角形:
(1)
(2)
(3)
(4)
(5)
(1)、(5)
(2)、(4)
(3)
想一想
例2 一个三角形的三个内角的度数之比为 1∶2∶3,这个三角形一定是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法判定形状
解析:设这个三角形的三个内角的度数分别是 x,2x,3x,根据三角形的内角和为 180°,得 x+2x+3x=180°,解得 x=30°,所以这个三角形的三个内角的度数分别是30°,60°,90°,即这个三角形是直角三角形.
A
典例精析
1.(1)在△ABC 中,∠A = 35°,∠B = 43°,则
∠C =______°;
(2)在△ABC 中,∠C = 90°,∠B = 50°,则
∠A = ______°;
(3)在△ABC 中,∠A = 40°,∠A = 2∠B,则
∠C = ______°.
102
40
120
练一练
第肆章节
随堂练习
随堂练习
1.如图,在△ABC中,∠BAC=60°,∠B=50°,AD∥BC,则∠1的度数为( ).
A.50° B.60°
C.70° D.80°
C
2.物理实验中,小明研究一个小木块在斜坡上滑下时的运动状态,如图,斜坡为Rt△ABC,∠C=90°,∠B=13°,小木块△DEF在斜坡AB上,且DE∥BC,EF∥AC,则∠DFE的度数为( ).
A.13° B.77°
C.87° D.63°
B
3.在直角三角形中,有一个锐角是另外一个锐角的5倍,则这个较大的锐角的度数为 °.
4.如图,x°= ;y°= .
50°
60°
75
5.如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线交于点P,求∠P的度数.
解:∵AB∥CD,
∴∠BEF+∠DFE=180°.
又∵EP平分∠BEF,FP平分∠DFE,
∴∠PEF=∠BEF,∠PFE=∠DFE.
∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°.
∵∠PEF+∠PFE+∠P=180°,∴∠P=90°.
6.如图,在△ABC中,AE,BF是角平分线,它们相交于点O.
(1)若∠C=72°,则∠AOB的度数为 ;
(2)猜想∠AOB的度数与∠C的度数存在的数量关系,并说明理由.
126°
解:(2)∠ABO=90°+∠C,理由如下:∵∠CAB+∠CBA=180°-∠C,
又∵AE,BF是角平分线,∴∠ABO=∠ABC,∠BAO=∠BAC,
∴∠AOB=180°-(∠ABO+∠BAO)
=180°-(∠CAB+∠CBA)=180°-(180°-C)
=180°-90°+∠C=90°+∠C.
第伍章节
课堂小结
课堂小结
认识三角形
三角形三个内角的和等于180°
三角形用符号“△”表示
锐角三角形、直角三角形、钝角三角形
由不在同一直线上的三条线段首尾顺次相接所组成的图形
表示
按角分类
定义
直角三角形的两个锐角互余
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.1 第1课时 三角形的内角和
4.1 认识三角形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.认识三角形并会用几何符号表示三角形.
2.会用平行线的性质与平角的定义证明三角形内角和等于180°.
3.会运用三角形内角和等于180°进行计算.
4.会按角的大小对三角形进行分类.
5.会表示直角三角形,掌握直角三角形两个锐角互余.
第贰章节
新课导入
新课导入
观察下列图片,你发现了都有什么共同点
为什么设计成三角形
第叁章节
新知探究
新知探究
活动:观察下面图形的形成过程,说一说什么叫三角形.
定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫作三角形.
问题1:三角形中有几条线段?几个角?几个顶点?
A
B
C
有三条线段,三个角,三个顶点
三角形的概念
1
三角形组成元素 三角形 ABC
边
顶点
角(内角)
边 AB,边 BC,边 AC
或 边 c,边 a, 边 b
∠A,∠B,∠C
点 A,点 B,点 C
记作△ABC
要点归纳
例1 (1)图中有几个三角形?用符号表示出这些三角形.
A
B
C
D
E
5 个,分别是△ABE,△ABC,△BCE,△BCD,△ECD.
(2) 以 AB 为边的三角形有哪些?
△ABC,△ABE.
(3) 以 E 为顶点的三角形有哪些?
△ABE,△BCE,△CDE.
(4) 以∠D 为顶角的三角形有哪些?
△BCD,△DEC.
典例精析
(5) 说出△BCD 的三个角和三个顶点所对的边.
△BCD 的三个角是∠BCD,∠D 和∠CBD.
A
B
C
D
E
顶点 B 所对的边为 DC,
顶点 C 所对的边为 BD,
顶点 D 所对的边为 BC.
三角形的内角和
2
合作探究:如何探索、验证三角形的内角和等于 180° ?说一说理由.
画一画:在准备的三角形硬纸板上画出△ABC,并标出三个内角.
A
B
C
1
2
3
量一量:每个角各是多少度 三个内角的和是多少
动动手:撕下三角形的三个角,拼在一起.
总结:三角形的三个内角拼到一起恰好构成一个平角.
撕拼法:撕下三角形的一个角,拼在一起.
1
3
2
1
a
b
4
此时∠1的另一条边 b 与∠3 的一条边 a 平行吗?为什么?
a∥b
(内错角相等,两直线平行)
∠3与∠4的大小有什么关系?为什么?
∠3 = ∠4
(两直线平行,同位角相等)
自己剪一个三角形纸片,重复上面的过程,你得到同样的结论了吗?与同伴进行交流.
现在,你能够确定这个三角形的内角的和了吗?
C
B
A
E
D
F
三角形三个的内角和等于 180°
动手操作
议一议:猜猜图中三角形被遮住的两个内角是什么角?试着说明理由.
三角形按角分类
3
直角三角形
锐角三角形
钝角三角形
三角形按角的大小分类
三个角都是锐角
有一个角是钝角
有一个角是直角
Rt△ABC
A
B
C
直角边
直角边
斜边
→ 直角三角形的两个锐角互余
三角形的内角和为 180°
观察图中的三角形,你能够按角将它们的形状分类吗?
锐角三角形:
钝角三角形:
直角三角形:
(1)
(2)
(3)
(4)
(5)
(1)、(5)
(2)、(4)
(3)
想一想
例2 一个三角形的三个内角的度数之比为 1∶2∶3,这个三角形一定是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法判定形状
解析:设这个三角形的三个内角的度数分别是 x,2x,3x,根据三角形的内角和为 180°,得 x+2x+3x=180°,解得 x=30°,所以这个三角形的三个内角的度数分别是30°,60°,90°,即这个三角形是直角三角形.
A
典例精析
1.(1)在△ABC 中,∠A = 35°,∠B = 43°,则
∠C =______°;
(2)在△ABC 中,∠C = 90°,∠B = 50°,则
∠A = ______°;
(3)在△ABC 中,∠A = 40°,∠A = 2∠B,则
∠C = ______°.
102
40
120
练一练
第肆章节
随堂练习
随堂练习
1.如图,在△ABC中,∠BAC=60°,∠B=50°,AD∥BC,则∠1的度数为( ).
A.50° B.60°
C.70° D.80°
C
2.物理实验中,小明研究一个小木块在斜坡上滑下时的运动状态,如图,斜坡为Rt△ABC,∠C=90°,∠B=13°,小木块△DEF在斜坡AB上,且DE∥BC,EF∥AC,则∠DFE的度数为( ).
A.13° B.77°
C.87° D.63°
B
3.在直角三角形中,有一个锐角是另外一个锐角的5倍,则这个较大的锐角的度数为 °.
4.如图,x°= ;y°= .
50°
60°
75
5.如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线交于点P,求∠P的度数.
解:∵AB∥CD,
∴∠BEF+∠DFE=180°.
又∵EP平分∠BEF,FP平分∠DFE,
∴∠PEF=∠BEF,∠PFE=∠DFE.
∴∠PEF+∠PFE=(∠BEF+∠DFE)=90°.
∵∠PEF+∠PFE+∠P=180°,∴∠P=90°.
6.如图,在△ABC中,AE,BF是角平分线,它们相交于点O.
(1)若∠C=72°,则∠AOB的度数为 ;
(2)猜想∠AOB的度数与∠C的度数存在的数量关系,并说明理由.
126°
解:(2)∠ABO=90°+∠C,理由如下:∵∠CAB+∠CBA=180°-∠C,
又∵AE,BF是角平分线,∴∠ABO=∠ABC,∠BAO=∠BAC,
∴∠AOB=180°-(∠ABO+∠BAO)
=180°-(∠CAB+∠CBA)=180°-(180°-C)
=180°-90°+∠C=90°+∠C.
第伍章节
课堂小结
课堂小结
认识三角形
三角形三个内角的和等于180°
三角形用符号“△”表示
锐角三角形、直角三角形、钝角三角形
由不在同一直线上的三条线段首尾顺次相接所组成的图形
表示
按角分类
定义
直角三角形的两个锐角互余
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
