4.2全等三角形 课件(共26张PPT)
文档属性
| 名称 | 4.2全等三角形 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:25:07 | ||
图片预览








文档简介
(共26张PPT)
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.2全等三角形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解全等三角形的概念,能正确表示全等三角形,能识别全等三角形中的对应边、对应角.
2.掌握全等三角形的性质,能利用全等三角形的性质解决相关问题.
第贰章节
新课导入
新课导入
观察下面的图形,它们分别有什么特点?
把它们重叠在一起就能完全重合。
第叁章节
新知探究
新知探究
1
全等三角形的定义
活动 1:观察所给出的图形,它们有什么特点
每个大图形中,都含有若干个形状、大小相同的小三角形.
E
D
F
E
D
F
A
B
C
能够完全重合的两个三角形叫作全等三角形.
例如,在图中,△ABC 与 △DEF 能够完全重合,它们是全等三角形.
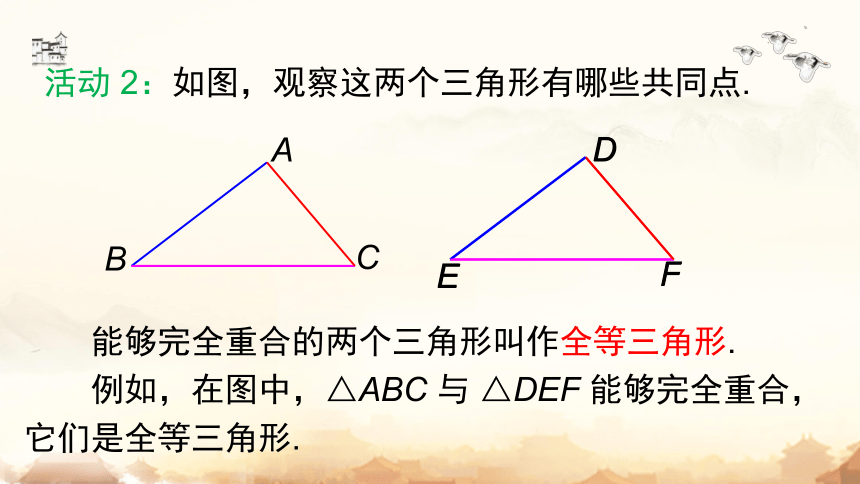
活动 2:如图,观察这两个三角形有哪些共同点.
A
B
C
F
E
D
对应点:点 A,点 D;
对应边:AB 与 DE;
对应角:∠A 与∠D ;
点 B,点 E;
点 C,点 F;
AC 与 DF;
BC 与 EF;
∠B 与∠E ;
∠C 与∠F .
你能找出其他的对应顶点、对应边和对应角吗
全等三角形的对应边相等,对应角相等.
A
B
C
E
D
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
△ABC≌△DEF
△ABC 与 △DEF 全等,记作
因为△ABC≌△DEF,
所以 AB = DE,AC = DF,BC = EF (全等三角形的对应边相等),
∠A =∠D,∠B =∠E,∠C =∠F (全等三角形对应角相等)
全等三角形性质的几何语言
A
B
C
E
D
F
例1 如图,若△BOD≌△COE,指出这两个三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD 与△COE 的对应边为:
BO 与 CO,OD 与 OE,BD 与 CE;
△ADO 与△AEO 的对应角为:
∠DAO 与∠EAO,∠ADO 与∠AEO,
∠AOD 与∠AOE.
典例精析
例2 如图,△ABC≌△EBD,问∠1 与∠2 相等吗 若相等请说明理由.
解:∠l=∠2. 理由如下:
因为△EBD≌△ABC,
所以∠A = ∠E.
在△AOF 与△EOB 中,
∠AOF =∠EOB.
根据三角形内角和为 180°,
所以∠1 =∠2.
典例精析
2
全等三角形的性质
活动 3:准备两个全等的三角形纸片,并画出两个三角形对应边上的高.
(1) 全等三角形对应边的高相等吗 对应边的中线呢
还有哪些相等的线段 举例说明.
A
B
C
E
D
F
M
N
M'
N'
全等三角形的对应线段都相等.
(2) 如图, 已知 △ABC ≌ △A'B'C',你如何在△A'B'C' 中画出与线段 DE 相对应的线段?
A
B
C
D
E
A'
B'
C'
D'
E'
做一做
下图是一个等边三角形,你能把它分成两个全等的三角形吗?三个呢?四个呢?
用 3 个等边三角形纸片画一画,再剪下来试试能否重合!
1. 如图,△ABC≌△ADE,若∠D =∠B,
∠C =∠AED,则∠DAE = ,
∠DAB = .
∠BAC
∠EAC
A
B
C
D
E
练一练
第肆章节
随堂练习
随堂练习
1.如图,将△ABC沿AC对折,点B与点E重合,则全等的三角形有( ).
A.1对 B.2对 C.3对 D.4对
C
2.如图,△ABC≌△ADE,AE∥BC,若∠B=30°,∠C=100°,则∠BAD的度数是 °.
80
3.如图,是一个4×4的正方形网格.根据图中标示的各点位置,在下列三角形中,与△ABC全等的是( ).
A.△ABD B.△ABE
C.△ABF D.△ABG
C
4.如图,AB=12 cm,CA⊥AB于点A,DB⊥AB于点B,且AC=4 cm,点P从点B向点A运动,速度为1 cm/s,点Q从点B向点D运动,速度为2 cm/s,P,Q两点同时出发,则经过 s后,△CAP与△PQB全等.
4
第伍章节
课堂小结
课堂小结
全等三角形
对应边相等
对应角相等
对应边上的高、中线分别相等,对应角的平分线相等
对应元素:对应顶点、对应边、对应角
表示方法:“全等”用符号“≌”表示,读作“全等于”
定义:能够完全重合的两个三角形
性质
相关概念
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.2全等三角形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解全等三角形的概念,能正确表示全等三角形,能识别全等三角形中的对应边、对应角.
2.掌握全等三角形的性质,能利用全等三角形的性质解决相关问题.
第贰章节
新课导入
新课导入
观察下面的图形,它们分别有什么特点?
把它们重叠在一起就能完全重合。
第叁章节
新知探究
新知探究
1
全等三角形的定义
活动 1:观察所给出的图形,它们有什么特点
每个大图形中,都含有若干个形状、大小相同的小三角形.
E
D
F
E
D
F
A
B
C
能够完全重合的两个三角形叫作全等三角形.
例如,在图中,△ABC 与 △DEF 能够完全重合,它们是全等三角形.
活动 2:如图,观察这两个三角形有哪些共同点.
A
B
C
F
E
D
对应点:点 A,点 D;
对应边:AB 与 DE;
对应角:∠A 与∠D ;
点 B,点 E;
点 C,点 F;
AC 与 DF;
BC 与 EF;
∠B 与∠E ;
∠C 与∠F .
你能找出其他的对应顶点、对应边和对应角吗
全等三角形的对应边相等,对应角相等.
A
B
C
E
D
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
△ABC≌△DEF
△ABC 与 △DEF 全等,记作
因为△ABC≌△DEF,
所以 AB = DE,AC = DF,BC = EF (全等三角形的对应边相等),
∠A =∠D,∠B =∠E,∠C =∠F (全等三角形对应角相等)
全等三角形性质的几何语言
A
B
C
E
D
F
例1 如图,若△BOD≌△COE,指出这两个三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD 与△COE 的对应边为:
BO 与 CO,OD 与 OE,BD 与 CE;
△ADO 与△AEO 的对应角为:
∠DAO 与∠EAO,∠ADO 与∠AEO,
∠AOD 与∠AOE.
典例精析
例2 如图,△ABC≌△EBD,问∠1 与∠2 相等吗 若相等请说明理由.
解:∠l=∠2. 理由如下:
因为△EBD≌△ABC,
所以∠A = ∠E.
在△AOF 与△EOB 中,
∠AOF =∠EOB.
根据三角形内角和为 180°,
所以∠1 =∠2.
典例精析
2
全等三角形的性质
活动 3:准备两个全等的三角形纸片,并画出两个三角形对应边上的高.
(1) 全等三角形对应边的高相等吗 对应边的中线呢
还有哪些相等的线段 举例说明.
A
B
C
E
D
F
M
N
M'
N'
全等三角形的对应线段都相等.
(2) 如图, 已知 △ABC ≌ △A'B'C',你如何在△A'B'C' 中画出与线段 DE 相对应的线段?
A
B
C
D
E
A'
B'
C'
D'
E'
做一做
下图是一个等边三角形,你能把它分成两个全等的三角形吗?三个呢?四个呢?
用 3 个等边三角形纸片画一画,再剪下来试试能否重合!
1. 如图,△ABC≌△ADE,若∠D =∠B,
∠C =∠AED,则∠DAE = ,
∠DAB = .
∠BAC
∠EAC
A
B
C
D
E
练一练
第肆章节
随堂练习
随堂练习
1.如图,将△ABC沿AC对折,点B与点E重合,则全等的三角形有( ).
A.1对 B.2对 C.3对 D.4对
C
2.如图,△ABC≌△ADE,AE∥BC,若∠B=30°,∠C=100°,则∠BAD的度数是 °.
80
3.如图,是一个4×4的正方形网格.根据图中标示的各点位置,在下列三角形中,与△ABC全等的是( ).
A.△ABD B.△ABE
C.△ABF D.△ABG
C
4.如图,AB=12 cm,CA⊥AB于点A,DB⊥AB于点B,且AC=4 cm,点P从点B向点A运动,速度为1 cm/s,点Q从点B向点D运动,速度为2 cm/s,P,Q两点同时出发,则经过 s后,△CAP与△PQB全等.
4
第伍章节
课堂小结
课堂小结
全等三角形
对应边相等
对应角相等
对应边上的高、中线分别相等,对应角的平分线相等
对应元素:对应顶点、对应边、对应角
表示方法:“全等”用符号“≌”表示,读作“全等于”
定义:能够完全重合的两个三角形
性质
相关概念
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
