4.3 第3课时 利用“边角边”判定三角形全等 课件(共38张PPT)
文档属性
| 名称 | 4.3 第3课时 利用“边角边”判定三角形全等 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:41:18 | ||
图片预览










文档简介
(共38张PPT)
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.3 第3课时 利用“边角边”判定三角形全等
4.3探究三角形全等的条件
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 探讨出全等三角形的“SAS”的判定方法.
2 . 能运用“SAS”来判定两个三角形全等.
第贰章节
新课导入
新课导入
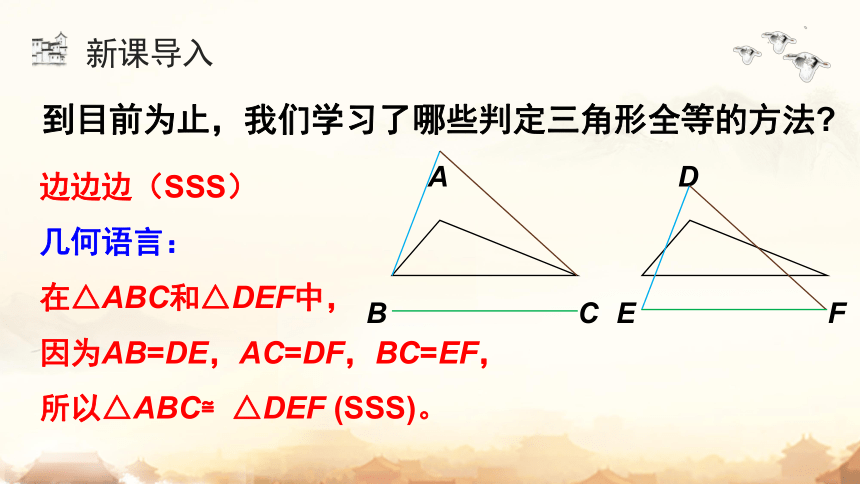
到目前为止,我们学习了哪些判定三角形全等的方法
边边边(SSS)
A
B
C
D
E
F
几何语言:
在△ABC和△DEF中,
所以△ABC≌△DEF (SSS)。
因为AB=DE,AC=DF,BC=EF,
角边角(ASA)
到目前为止,我们学习了哪些判定三角形全等的方法
A
B
C
D
E
F
几何语言:
在△ABC和△DEF中,
所以△ABC≌△DEF (ASA)。
因为∠B=∠E,BC=EF,∠C=∠F,
角角边(AAS)
到目前为止,我们学习了哪些判定三角形全等的方法
A
B
C
D
E
F
几何语言:
在△ABC和△DEF中,
所以△ABC≌△DEF (AAS)。
因为∠A=∠D,∠B=∠E,BC=EF,
第叁章节
新知探究
新知探究
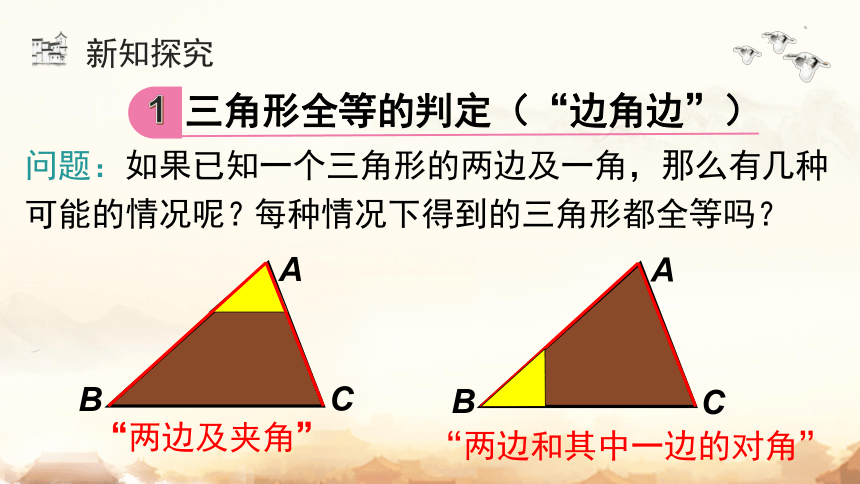
问题:如果已知一个三角形的两边及一角,那么有几种可能的情况呢?
A
B
C
A
B
C
“两边及夹角”
“两边和其中一边的对角”
每种情况下得到的三角形都全等吗?
1
三角形全等的判定(“边角边”)
活动1:如果“两边及一角”条件中的角是两边的夹角,比如三角形两条边分别为 2.5 cm,3.5 cm,它们所夹的角为 40° ,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
40°
3.5 cm
2.5 cm
改变上述条件中的角度和边长,再试一试.
尝试·思考
在△ABC 和△DEF 中,
所以△ABC≌△DEF.
文字语言:两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
几何语言:
因为 AB = DE,∠A =∠D,
AC = DF,
A
B
C
D
E
F
“边角边”判定全等的方法
知识要点
议一议
活动2:如果“两边及一角”条件中的角是其中一边的对角,比如两条边分别为 2.5 cm,3.5 cm;长度为 2.5 cm 的边所对的角为 40° 情况会怎样呢
3.5 cm
40°
2.5 cm
3.5 cm
40°
2.5 cm
结论:两边分别相等且其中一组等边的对角相等时,两个三角形不一定全等.
2
两边及其中一边对角分别相等的两个三角形
解:画出的三角形不都全等.
活动 3:
1.学生根据各小组所画的图形,剪下后对比分析,看图形是否完全重合.
2.小组内合作探究,剪下所画图形后对比分析图形是否全等,并互相补充产生这种情况的原因.
C
A
B
F
D
E
想一想:
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC 和△ABD 满足AB = AB,∠B =∠B,AC = AD,但它们并不全等.
例1 已知三角形的两边及其夹角,求作这个三角形.
已知:线段 a,c,∠α,
求作:△ABC,使 BC=a,AB=c,∠ABC=∠α.
a
c
α
典例精析
解:作法 1:
作法 图示
(1) 作一条线段 BC = a;
B
C
(2)以 B 为顶点,BC 为一边,
作∠DBC =∠a;
(3) 在射线 BD 上截取线段
BA = c;
(4) 连接 AC,△ABC 就是所
求作的三角形.
B
C
D
A
B
C
D
B
C
D
A
B
C
D
A
作法 图示
(1) 作∠MBN =∠a;
(2) 在射线 BM 上截取 BC = a,在射线 BN上截取 BA = c;
(3)连接 AC,则△ABC 为所
求作的三角形.
B
M
N
作法 2:
B
M
N
C
a
c
A
B
M
C
a
c
1.下列条件中,不能说明△ABC≌△DEF 的是 ( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
C
练一练
例3 已知:如图,AB = DB,CB = EB,∠1=∠2,
试说明:∠A =∠D.
解:因为 ∠1=∠2 ,
1
A
2
C
B
D
E
所以∠1 +∠DBC=∠2 +∠DBC ,
即∠ABC=∠DBE.
在△ABC 和△DBE 中,
因为AB=DB,∠ABC=∠DBE,CB=EB,
所以△ABC≌△DBE(SAS) .
所以∠A =∠D .
典例精析
2. 在下列图中找出全等三角形进行连线.
Ⅰ
30°
8 cm
9 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30°
8 cm
5 cm
Ⅲ
30°
8 cm
8 cm
Ⅲ
Ⅶ
30°
8 cm
9 cm
Ⅴ
30°
8 cm
5 cm
Ⅲ
30°
8 cm
8 cm
Ⅵ
Ⅳ
Ⅷ
8 cm
5 cm
练一练
3. 如图,AB = DB,BC = BE,若△ABE≌△DBC,则可以增加的条件是 ( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
D
A
B
D
C
E
4.如图,点 E,F 在 AC 上,AD∥BC,AD = CB,AE = CF. 试说明:△AFD≌△CEB.
F
A
B
D
C
E
解:
因为 AD∥BC,
所以∠A =∠C.
因为 AE = CF,
在△AFD 和△CEB 中,
因为 AD = CB,
∠A = ∠C,
AF = CE ,
所以△AFD≌△CEB .
所以 AE + EF = CF + EF,即 AF = CE.
第肆章节
随堂练习
随堂练习
1.如图,AC与BD相交于点O,且AC=BD,AO=DO,若测得CD=15,则AB= .
15
2.如图,AB=AC,要说明△ADC≌△AEB,添加的条件不能是( ).
A.∠B=∠C B.AD=AE
C.∠ADC=∠AEB D.DC=BE
D
3.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
4.如图,AB=AD,AC=AE,如果增加一个有关角相等的条件,就可以直接得到△ABC≌△ADE,那么这个条件是( ).
A.∠B=∠C
B.∠B=∠D
C.∠C=∠E
D.∠BAC=∠DAE
D
5.如图是由6个边长相等的正方形组合成的图形,则∠1+∠2+∠3=
°.
135
6.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
82°
证明:在线段AE上,截取EF=EB,连接FC,如图.
∵CE⊥AB,∴∠CEB=∠CEF=90°.
在△CBE和△CFE中,
7.如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,并且AE=(AB+AD).求证:∠B+∠D=180°.
答案图
∴△CBE≌△CFE(SAS).
∴∠B=∠CFE.∵AE=(AB+AD),
∴2AE=AB+AD.∴AD=2AE-AB.
∵AE=AF+EF,∴AD=2(AF+EF)-AB=2AF+2EF-AB=AF+AF+EF+EB-AB=AF+AB-AB,
即AD=AF.∵AC平分∠BAD,∴∠FAC=∠DAC.
答案图
在△AFC和△ADC中,∴△AFC≌△ADC(SAS).
∴∠AFC=∠D.∵∠AFC+∠CFE=180°,
∠B=∠CFE,
∴∠AFC+∠B=180°,∠B+∠D=180°.
答案图
8.如图,在△ABC中,∠ACB=90°,AC=BC,点D在AC上,点E在BC的延长线上,CE=CD,BD的延长线交AE于点F.
(1)求证:BF⊥AE.
证明:∵∠ACB=90°,∴∠ACE=180°-90°=90°,
∴∠BCD=∠ACE.在△BCD和△ACE中,
∴△BCD≌△ACE(SAS).∴∠CBD=∠CAE.
∵∠BDC=∠ADF,∴∠AFD=∠BCD=90°,∴BF⊥AE.
解:∵△BCD≌△ACE,∴BD= AE= 8.
∵FD= 2,∴BF= BD+DF= 10.∵BF⊥AE,
∴△ABE的面积为AE·BF= × 8× 10= 40.
(2)若BD=8,DF=2,求△ABE的面积.
第伍章节
课堂小结
课堂小结
三角形全等的条件
两边及其夹角分别相等的两个三角形全等(简写为“SAS”)
两角及其夹边分别相等的两个三角形全等(简写为“ASA”)
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写为“AAS”)
三边分别相等的两个三角形全等(简写为“SSS”)
角角边
边角边
边边边
角边角
相互 转化
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.3 第3课时 利用“边角边”判定三角形全等
4.3探究三角形全等的条件
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 探讨出全等三角形的“SAS”的判定方法.
2 . 能运用“SAS”来判定两个三角形全等.
第贰章节
新课导入
新课导入
到目前为止,我们学习了哪些判定三角形全等的方法
边边边(SSS)
A
B
C
D
E
F
几何语言:
在△ABC和△DEF中,
所以△ABC≌△DEF (SSS)。
因为AB=DE,AC=DF,BC=EF,
角边角(ASA)
到目前为止,我们学习了哪些判定三角形全等的方法
A
B
C
D
E
F
几何语言:
在△ABC和△DEF中,
所以△ABC≌△DEF (ASA)。
因为∠B=∠E,BC=EF,∠C=∠F,
角角边(AAS)
到目前为止,我们学习了哪些判定三角形全等的方法
A
B
C
D
E
F
几何语言:
在△ABC和△DEF中,
所以△ABC≌△DEF (AAS)。
因为∠A=∠D,∠B=∠E,BC=EF,
第叁章节
新知探究
新知探究
问题:如果已知一个三角形的两边及一角,那么有几种可能的情况呢?
A
B
C
A
B
C
“两边及夹角”
“两边和其中一边的对角”
每种情况下得到的三角形都全等吗?
1
三角形全等的判定(“边角边”)
活动1:如果“两边及一角”条件中的角是两边的夹角,比如三角形两条边分别为 2.5 cm,3.5 cm,它们所夹的角为 40° ,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
40°
3.5 cm
2.5 cm
改变上述条件中的角度和边长,再试一试.
尝试·思考
在△ABC 和△DEF 中,
所以△ABC≌△DEF.
文字语言:两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.
几何语言:
因为 AB = DE,∠A =∠D,
AC = DF,
A
B
C
D
E
F
“边角边”判定全等的方法
知识要点
议一议
活动2:如果“两边及一角”条件中的角是其中一边的对角,比如两条边分别为 2.5 cm,3.5 cm;长度为 2.5 cm 的边所对的角为 40° 情况会怎样呢
3.5 cm
40°
2.5 cm
3.5 cm
40°
2.5 cm
结论:两边分别相等且其中一组等边的对角相等时,两个三角形不一定全等.
2
两边及其中一边对角分别相等的两个三角形
解:画出的三角形不都全等.
活动 3:
1.学生根据各小组所画的图形,剪下后对比分析,看图形是否完全重合.
2.小组内合作探究,剪下所画图形后对比分析图形是否全等,并互相补充产生这种情况的原因.
C
A
B
F
D
E
想一想:
如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC 和△ABD 满足AB = AB,∠B =∠B,AC = AD,但它们并不全等.
例1 已知三角形的两边及其夹角,求作这个三角形.
已知:线段 a,c,∠α,
求作:△ABC,使 BC=a,AB=c,∠ABC=∠α.
a
c
α
典例精析
解:作法 1:
作法 图示
(1) 作一条线段 BC = a;
B
C
(2)以 B 为顶点,BC 为一边,
作∠DBC =∠a;
(3) 在射线 BD 上截取线段
BA = c;
(4) 连接 AC,△ABC 就是所
求作的三角形.
B
C
D
A
B
C
D
B
C
D
A
B
C
D
A
作法 图示
(1) 作∠MBN =∠a;
(2) 在射线 BM 上截取 BC = a,在射线 BN上截取 BA = c;
(3)连接 AC,则△ABC 为所
求作的三角形.
B
M
N
作法 2:
B
M
N
C
a
c
A
B
M
C
a
c
1.下列条件中,不能说明△ABC≌△DEF 的是 ( )
A.AB=DE,∠B=∠E,BC=EF
B.AB=DE,∠A=∠D,AC=DF
C.BC=EF,∠B=∠E,AC=DF
D.BC=EF,∠C=∠F,AC=DF
C
练一练
例3 已知:如图,AB = DB,CB = EB,∠1=∠2,
试说明:∠A =∠D.
解:因为 ∠1=∠2 ,
1
A
2
C
B
D
E
所以∠1 +∠DBC=∠2 +∠DBC ,
即∠ABC=∠DBE.
在△ABC 和△DBE 中,
因为AB=DB,∠ABC=∠DBE,CB=EB,
所以△ABC≌△DBE(SAS) .
所以∠A =∠D .
典例精析
2. 在下列图中找出全等三角形进行连线.
Ⅰ
30°
8 cm
9 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30°
8 cm
5 cm
Ⅲ
30°
8 cm
8 cm
Ⅲ
Ⅶ
30°
8 cm
9 cm
Ⅴ
30°
8 cm
5 cm
Ⅲ
30°
8 cm
8 cm
Ⅵ
Ⅳ
Ⅷ
8 cm
5 cm
练一练
3. 如图,AB = DB,BC = BE,若△ABE≌△DBC,则可以增加的条件是 ( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
D
A
B
D
C
E
4.如图,点 E,F 在 AC 上,AD∥BC,AD = CB,AE = CF. 试说明:△AFD≌△CEB.
F
A
B
D
C
E
解:
因为 AD∥BC,
所以∠A =∠C.
因为 AE = CF,
在△AFD 和△CEB 中,
因为 AD = CB,
∠A = ∠C,
AF = CE ,
所以△AFD≌△CEB .
所以 AE + EF = CF + EF,即 AF = CE.
第肆章节
随堂练习
随堂练习
1.如图,AC与BD相交于点O,且AC=BD,AO=DO,若测得CD=15,则AB= .
15
2.如图,AB=AC,要说明△ADC≌△AEB,添加的条件不能是( ).
A.∠B=∠C B.AD=AE
C.∠ADC=∠AEB D.DC=BE
D
3.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
4.如图,AB=AD,AC=AE,如果增加一个有关角相等的条件,就可以直接得到△ABC≌△ADE,那么这个条件是( ).
A.∠B=∠C
B.∠B=∠D
C.∠C=∠E
D.∠BAC=∠DAE
D
5.如图是由6个边长相等的正方形组合成的图形,则∠1+∠2+∠3=
°.
135
6.如图,AC平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
82°
证明:在线段AE上,截取EF=EB,连接FC,如图.
∵CE⊥AB,∴∠CEB=∠CEF=90°.
在△CBE和△CFE中,
7.如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,并且AE=(AB+AD).求证:∠B+∠D=180°.
答案图
∴△CBE≌△CFE(SAS).
∴∠B=∠CFE.∵AE=(AB+AD),
∴2AE=AB+AD.∴AD=2AE-AB.
∵AE=AF+EF,∴AD=2(AF+EF)-AB=2AF+2EF-AB=AF+AF+EF+EB-AB=AF+AB-AB,
即AD=AF.∵AC平分∠BAD,∴∠FAC=∠DAC.
答案图
在△AFC和△ADC中,∴△AFC≌△ADC(SAS).
∴∠AFC=∠D.∵∠AFC+∠CFE=180°,
∠B=∠CFE,
∴∠AFC+∠B=180°,∠B+∠D=180°.
答案图
8.如图,在△ABC中,∠ACB=90°,AC=BC,点D在AC上,点E在BC的延长线上,CE=CD,BD的延长线交AE于点F.
(1)求证:BF⊥AE.
证明:∵∠ACB=90°,∴∠ACE=180°-90°=90°,
∴∠BCD=∠ACE.在△BCD和△ACE中,
∴△BCD≌△ACE(SAS).∴∠CBD=∠CAE.
∵∠BDC=∠ADF,∴∠AFD=∠BCD=90°,∴BF⊥AE.
解:∵△BCD≌△ACE,∴BD= AE= 8.
∵FD= 2,∴BF= BD+DF= 10.∵BF⊥AE,
∴△ABE的面积为AE·BF= × 8× 10= 40.
(2)若BD=8,DF=2,求△ABE的面积.
第伍章节
课堂小结
课堂小结
三角形全等的条件
两边及其夹角分别相等的两个三角形全等(简写为“SAS”)
两角及其夹边分别相等的两个三角形全等(简写为“ASA”)
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写为“AAS”)
三边分别相等的两个三角形全等(简写为“SSS”)
角角边
边角边
边边边
角边角
相互 转化
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
