4.3 第1课时 利用“边边边”判定三角形全等 课件(共33张PPT)
文档属性
| 名称 | 4.3 第1课时 利用“边边边”判定三角形全等 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:41:52 | ||
图片预览








文档简介
(共33张PPT)
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.3 第1课时 利用“边边边”判定三角形全等
4.3探究三角形全等的条件
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解并且会用“边边边”来判断三角形全等.
2.了解三角形的稳定性和实际生活的例子.
第贰章节
新课导入
新课导入
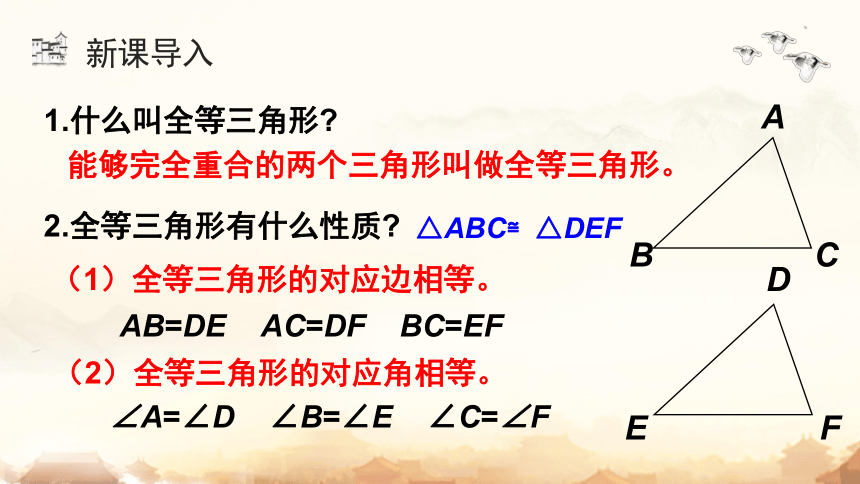
1.什么叫全等三角形
能够完全重合的两个三角形叫做全等三角形。
2.全等三角形有什么性质
△ABC≌△DEF
AB=DE AC=DF BC=EF
(1)全等三角形的对应边相等。
(2)全等三角形的对应角相等。
∠A=∠D ∠B=∠E ∠C=∠F
A
B
C
D
E
F
A
B
C
D
E
F
AB=DE ,AC=DF,BC=EF
∠A=∠D ,∠B=∠E ,∠C=∠F
一定要满足三条边分别相等,三个角也分别相等,才能保证两个三角形全等吗
第叁章节
新知探究
新知探究
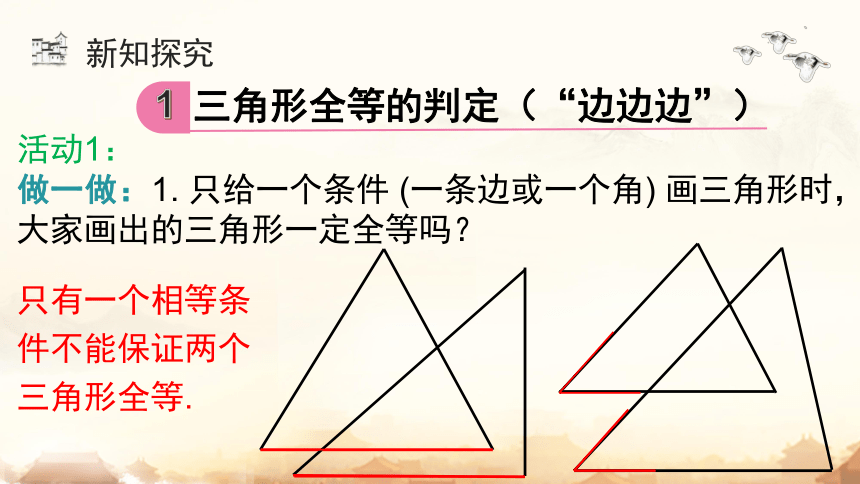
只有一个相等条件不能保证两个三角形全等.
活动1:
做一做:1. 只给一个条件 (一条边或一个角) 画三角形时,大家画出的三角形一定全等吗?
1
三角形全等的判定(“边边边”)
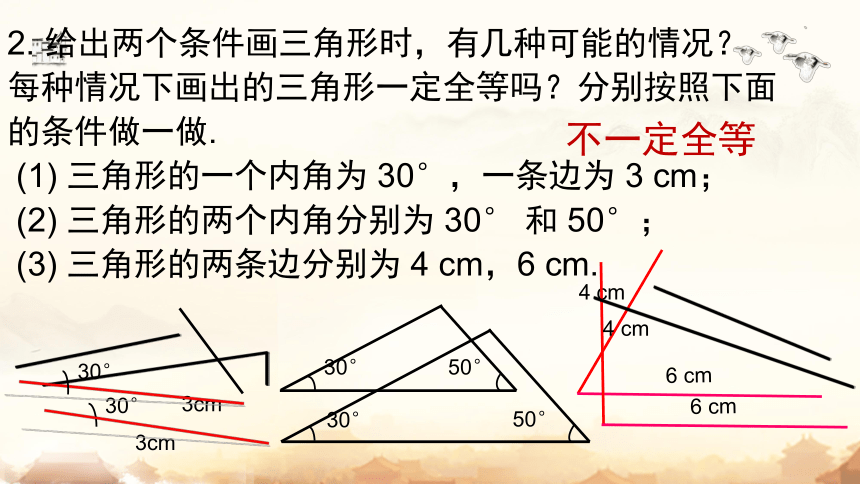
2. 给出两个条件画三角形时,有几种可能的情况?
每种情况下画出的三角形一定全等吗?分别按照下面的条件做一做.
(1) 三角形的一个内角为 30°,一条边为 3 cm;
(2) 三角形的两个内角分别为 30° 和 50°;
(3) 三角形的两条边分别为 4 cm,6 cm.
30°
3cm
3cm
30°
50°
30°
30°
50°
4 cm
6 cm
4 cm
6 cm
不一定全等
如果给出三个条件画三角形,你能说出有哪几种可能的情况?
思考·交流
有四种可能:三条边、三个角、两边一角和两角一边.
做一做
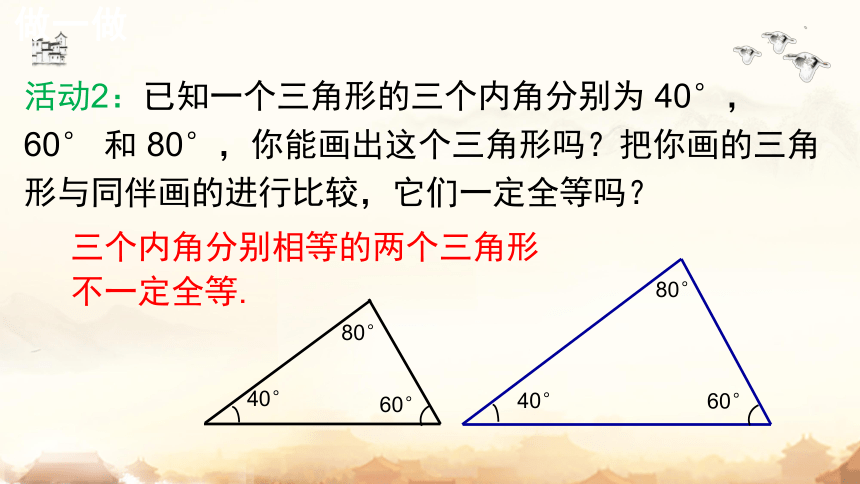
活动2:已知一个三角形的三个内角分别为 40°,60° 和 80°,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
60°
40°
80°
40°
60°
80°
三个内角分别相等的两个三角形不一定全等.
2. 已知一个三角形的三条边分别为 4 cm,5 cm 和 7 cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
改变三边的长度,同桌之间再画一画,比一比吧!
文字语言:三边分别相等的两个三角形全等,
简写为“边边边”或“SSS”.
A
B
C
D
E
F
几何语言:
在△ABC 和△DEF 中,
所以△ABC≌△DEF.
因为 AB = DE,BC = EF,CA = FD,
“边边边”判定方法
知识要点
尺规作图
已知三角形的三边,求作这个三角形.
已知:线段 a,b, c.
求作:△ABC,使 BC = a,AC= b,AB = c.
a
c
b
作法 图示
(1)以B为顶点画一条射线;
(2)以B点为圆心,a为半径画弧交射线于点C
B
C
B
C
B
C
(3)分别以点B,C 为圆心,c ,b为半径作弧交于点 A;
(4)连接AC , AB.△ABC 就是所求作的三角形.
A
A
请按照给出的作法作出相应的图形.
B
例1 如图,有一个三角形钢架,AB = AC,AD 是连接点 A 与 BC 中点 D 的支架.试说明:△ABD≌△ACD;
C
B
D
A
解题思路:
先找隐含条件
公共边 AD
再找现有条件
AB = AC
最后找准备条件
BD = CD
D 是 BC 的中点
典例精析
解:因为 D 是 BC 中点,
所以 BD = DC.
在△ABD 与△ACD 中,
所以△ABD≌△ACD (SSS).
C
B
D
A
因为 AB = AC ,
BD = CD,
AD = AD ,
准备条件
指明范围
摆齐根据
写出结论
A
B
D
C
1. (邻水县期末)如图,AB = DC ,若要用“SSS”证明△ABC≌△DCB,需要补充一个条件,
这个条件是 (填一个条件即可).
AC = BD
练一练
2. 如图,AB = AC,DB = DC,试说明∠B =∠C .
A
B
C
D
在△ABD 和△ACD 中,
因为 AB = AC,DB = DC,AD = AD,
所以△ABD≌△ACD .
解:如图,连接 AD.
所以∠B =∠C .
练一练
由上面的结论可知,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.
探究活动:请同学们动手用三根木条钉成一个三角形框架,再用四根木条钉成框架,看看它们的形状能否改变?
大小和形状固定不变
形状可以改变
四边形具有不稳定性
三角形的稳定性
2
三角形的稳定性
在生活中,我们经常会看到应用三角形稳定性的例子.
你还能举出一些其他的例子吗
3. 如图,桥梁的斜拉钢索是三角形的结构,主要是为了
( )
A. 节省材料,节约成本
B. 保持对称
C. 利用三角形的稳定性
D. 美观漂亮
C
练一练
第肆章节
随堂练习
随堂练习
1.如图,在△ABC中,AB=AC,EB=EC,则由“SSS”可以判定
( ).
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△BDE≌△CDE
D.以上答案都不对
B
2.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA,OB上分别截取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C,D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.这里构造全等三角形的依据是 .
SSS(或边边边)
3.如图,若AB=AC,AD=AE,要判定△ABD≌△ACE,请添加一个条件 .
BD=CE(答案合理即可)
4.如图,已知AB=AC,D为BC的中点,结论:①AD⊥BC;②AD平分∠BAC;③∠B=∠C;④△ABC是等边三角形.其中正确的是
( ).
A.①②
B.②③
C.①②③
D.③④
C
5.如图,在△ABC和△ADE中,AB=AC,AD=AE,BD=CE,求证:∠BAD=∠CAE.
证明:在△ABD和△ACE中,
∴△ABD≌△ACE(SSS).
∴∠BAD=∠CAE(全等三角形的对应角相等).
6.如图,点B,D,C,F在同一条直线上,且BC=FD,AB=EF.
(1)若添加一个条件(不添加辅助线),使得△ABC≌△EFD,则添加的条件是 ;
(2)添加了条件后,试说明△ABC≌△EFD.
AC=ED
解:(2)在△ABC和△EFD中,
∴△ABC≌△EFD(SSS).
第伍章节
课堂小结
课堂小结
由三边长尺规作三角形
三边分别相等的两个三角形全等(简写为“SSS”)
三角形全等的条件
三角形的稳定性
边边边
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.3 第1课时 利用“边边边”判定三角形全等
4.3探究三角形全等的条件
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解并且会用“边边边”来判断三角形全等.
2.了解三角形的稳定性和实际生活的例子.
第贰章节
新课导入
新课导入
1.什么叫全等三角形
能够完全重合的两个三角形叫做全等三角形。
2.全等三角形有什么性质
△ABC≌△DEF
AB=DE AC=DF BC=EF
(1)全等三角形的对应边相等。
(2)全等三角形的对应角相等。
∠A=∠D ∠B=∠E ∠C=∠F
A
B
C
D
E
F
A
B
C
D
E
F
AB=DE ,AC=DF,BC=EF
∠A=∠D ,∠B=∠E ,∠C=∠F
一定要满足三条边分别相等,三个角也分别相等,才能保证两个三角形全等吗
第叁章节
新知探究
新知探究
只有一个相等条件不能保证两个三角形全等.
活动1:
做一做:1. 只给一个条件 (一条边或一个角) 画三角形时,大家画出的三角形一定全等吗?
1
三角形全等的判定(“边边边”)
2. 给出两个条件画三角形时,有几种可能的情况?
每种情况下画出的三角形一定全等吗?分别按照下面的条件做一做.
(1) 三角形的一个内角为 30°,一条边为 3 cm;
(2) 三角形的两个内角分别为 30° 和 50°;
(3) 三角形的两条边分别为 4 cm,6 cm.
30°
3cm
3cm
30°
50°
30°
30°
50°
4 cm
6 cm
4 cm
6 cm
不一定全等
如果给出三个条件画三角形,你能说出有哪几种可能的情况?
思考·交流
有四种可能:三条边、三个角、两边一角和两角一边.
做一做
活动2:已知一个三角形的三个内角分别为 40°,60° 和 80°,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
60°
40°
80°
40°
60°
80°
三个内角分别相等的两个三角形不一定全等.
2. 已知一个三角形的三条边分别为 4 cm,5 cm 和 7 cm,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?
改变三边的长度,同桌之间再画一画,比一比吧!
文字语言:三边分别相等的两个三角形全等,
简写为“边边边”或“SSS”.
A
B
C
D
E
F
几何语言:
在△ABC 和△DEF 中,
所以△ABC≌△DEF.
因为 AB = DE,BC = EF,CA = FD,
“边边边”判定方法
知识要点
尺规作图
已知三角形的三边,求作这个三角形.
已知:线段 a,b, c.
求作:△ABC,使 BC = a,AC= b,AB = c.
a
c
b
作法 图示
(1)以B为顶点画一条射线;
(2)以B点为圆心,a为半径画弧交射线于点C
B
C
B
C
B
C
(3)分别以点B,C 为圆心,c ,b为半径作弧交于点 A;
(4)连接AC , AB.△ABC 就是所求作的三角形.
A
A
请按照给出的作法作出相应的图形.
B
例1 如图,有一个三角形钢架,AB = AC,AD 是连接点 A 与 BC 中点 D 的支架.试说明:△ABD≌△ACD;
C
B
D
A
解题思路:
先找隐含条件
公共边 AD
再找现有条件
AB = AC
最后找准备条件
BD = CD
D 是 BC 的中点
典例精析
解:因为 D 是 BC 中点,
所以 BD = DC.
在△ABD 与△ACD 中,
所以△ABD≌△ACD (SSS).
C
B
D
A
因为 AB = AC ,
BD = CD,
AD = AD ,
准备条件
指明范围
摆齐根据
写出结论
A
B
D
C
1. (邻水县期末)如图,AB = DC ,若要用“SSS”证明△ABC≌△DCB,需要补充一个条件,
这个条件是 (填一个条件即可).
AC = BD
练一练
2. 如图,AB = AC,DB = DC,试说明∠B =∠C .
A
B
C
D
在△ABD 和△ACD 中,
因为 AB = AC,DB = DC,AD = AD,
所以△ABD≌△ACD .
解:如图,连接 AD.
所以∠B =∠C .
练一练
由上面的结论可知,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定了.
探究活动:请同学们动手用三根木条钉成一个三角形框架,再用四根木条钉成框架,看看它们的形状能否改变?
大小和形状固定不变
形状可以改变
四边形具有不稳定性
三角形的稳定性
2
三角形的稳定性
在生活中,我们经常会看到应用三角形稳定性的例子.
你还能举出一些其他的例子吗
3. 如图,桥梁的斜拉钢索是三角形的结构,主要是为了
( )
A. 节省材料,节约成本
B. 保持对称
C. 利用三角形的稳定性
D. 美观漂亮
C
练一练
第肆章节
随堂练习
随堂练习
1.如图,在△ABC中,AB=AC,EB=EC,则由“SSS”可以判定
( ).
A.△ABD≌△ACD
B.△ABE≌△ACE
C.△BDE≌△CDE
D.以上答案都不对
B
2.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA,OB上分别截取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C,D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.这里构造全等三角形的依据是 .
SSS(或边边边)
3.如图,若AB=AC,AD=AE,要判定△ABD≌△ACE,请添加一个条件 .
BD=CE(答案合理即可)
4.如图,已知AB=AC,D为BC的中点,结论:①AD⊥BC;②AD平分∠BAC;③∠B=∠C;④△ABC是等边三角形.其中正确的是
( ).
A.①②
B.②③
C.①②③
D.③④
C
5.如图,在△ABC和△ADE中,AB=AC,AD=AE,BD=CE,求证:∠BAD=∠CAE.
证明:在△ABD和△ACE中,
∴△ABD≌△ACE(SSS).
∴∠BAD=∠CAE(全等三角形的对应角相等).
6.如图,点B,D,C,F在同一条直线上,且BC=FD,AB=EF.
(1)若添加一个条件(不添加辅助线),使得△ABC≌△EFD,则添加的条件是 ;
(2)添加了条件后,试说明△ABC≌△EFD.
AC=ED
解:(2)在△ABC和△EFD中,
∴△ABC≌△EFD(SSS).
第伍章节
课堂小结
课堂小结
由三边长尺规作三角形
三边分别相等的两个三角形全等(简写为“SSS”)
三角形全等的条件
三角形的稳定性
边边边
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
