4.3 第4课时 全等三角形的性质与判定 课件(共30张PPT)
文档属性
| 名称 | 4.3 第4课时 全等三角形的性质与判定 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.3 第4课时 全等三角形的性质与判定
4.3探究三角形全等的条件
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
掌握三角形全等的条件:“SSS”“ASA”“AAS”
“SAS”,并能灵活运用说明问题.
第贰章节
新课导入
新课导入
A
B
C
D
E
F
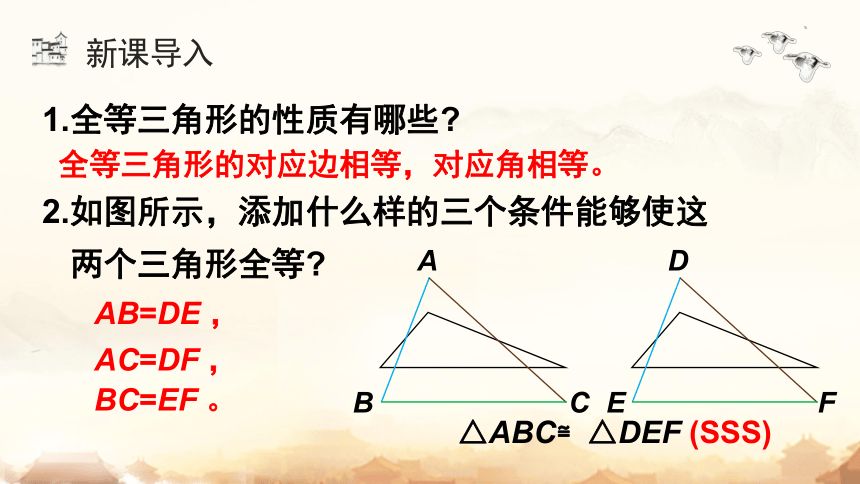
1.全等三角形的性质有哪些
全等三角形的对应边相等,对应角相等。
2.如图所示,添加什么样的三个条件能够使这
两个三角形全等
△ABC≌△DEF (SSS)
AB=DE ,
AC=DF ,
BC=EF 。
A
B
C
D
E
F
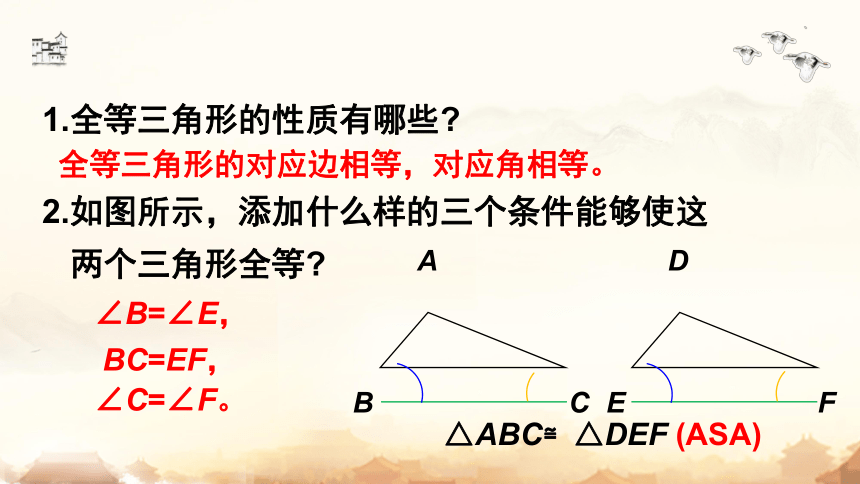
1.全等三角形的性质有哪些
全等三角形的对应边相等,对应角相等。
2.如图所示,添加什么样的三个条件能够使这
两个三角形全等
△ABC≌△DEF (ASA)
∠B=∠E,
BC=EF,
∠C=∠F。
A
B
C
D
E
F
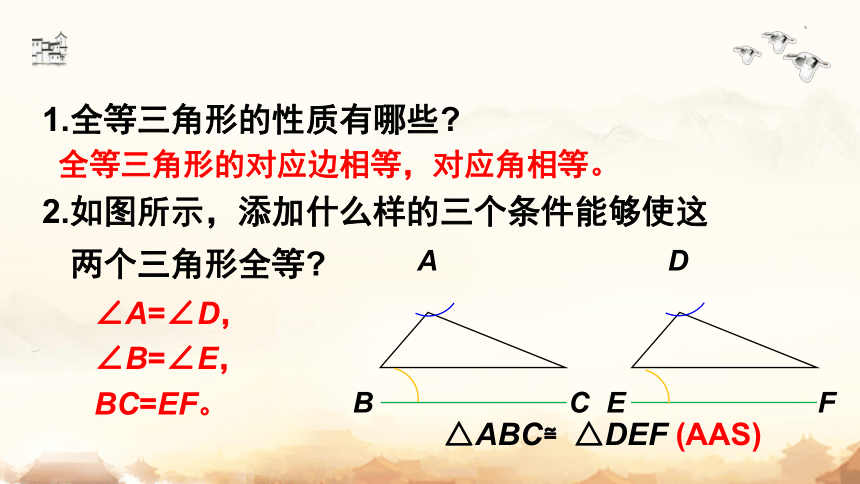
1.全等三角形的性质有哪些
全等三角形的对应边相等,对应角相等。
2.如图所示,添加什么样的三个条件能够使这
两个三角形全等
△ABC≌△DEF (AAS)
∠A=∠D,
∠B=∠E,
BC=EF。
A
B
C
D
E
F
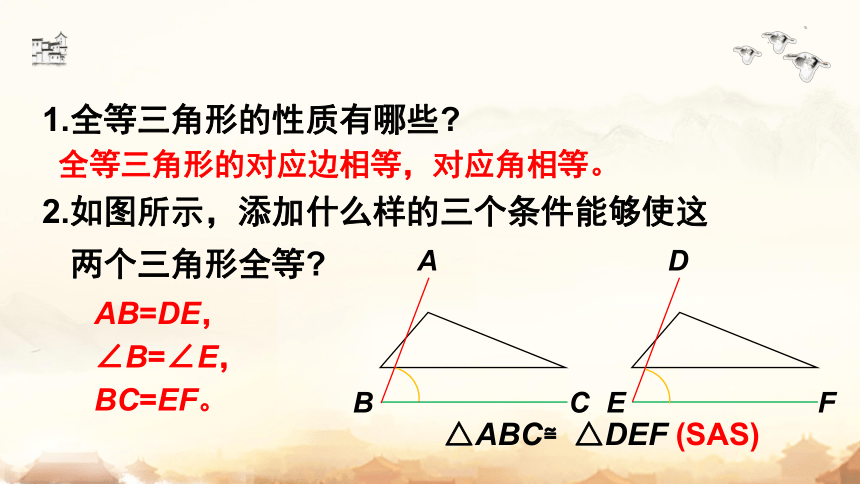
1.全等三角形的性质有哪些
全等三角形的对应边相等,对应角相等。
2.如图所示,添加什么样的三个条件能够使这
两个三角形全等
△ABC≌△DEF (SAS)
AB=DE,
∠B=∠E,
BC=EF。
第叁章节
新知探究
新知探究
1
全等三角形的应用
活动1:已知在△ABC 中,BC = 5 cm,AC = 3 cm,
AB = 3.5 cm,∠B = 36°,∠C = 44°,请你选择适当
数据,画与△ABC 全等的三角形(用三种方法画图,不写作法,但要在所画的三角形中标出用到的数据).
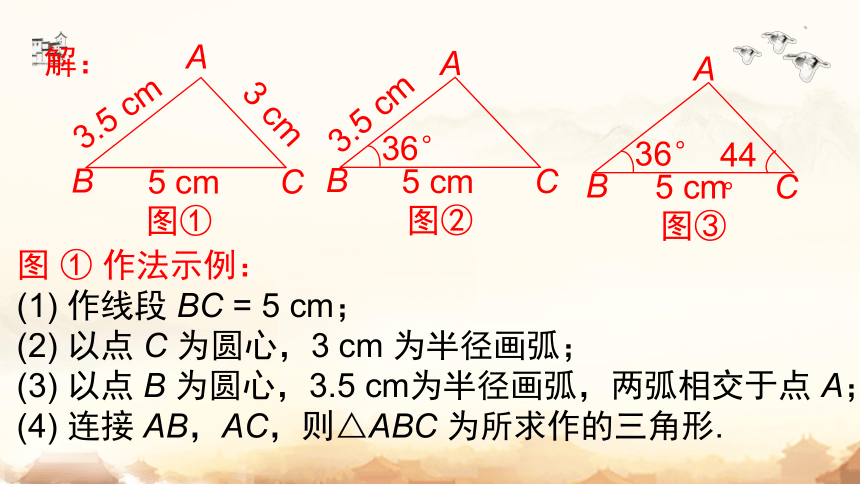
图 ① 作法示例:
(1) 作线段 BC = 5 cm;
(2) 以点 C 为圆心,3 cm 为半径画弧;
(3) 以点 B 为圆心,3.5 cm为半径画弧,两弧相交于点 A;
(4) 连接 AB,AC,则△ABC 为所求作的三角形.
解:
A
B
C
3.5 cm
3 cm
5 cm
图①
A
B
C
3.5 cm
5 cm
图②
36°
A
B
C
5 cm
图③
36°
44°
要点归纳
三角形全等的条件及判定方法:
对应相等
的元素
两边及
其夹角
两角及
其夹边
两角及其中
一角的对边
三边
三角形
全等理由
SAS
ASA
AAS
SSS
2
三角形全等的判定和性质的综合应用
活动 2:如图,点 D,E 分别在线段 AB,AC 上,
AE = AD,不添加新的线段和字母,从下列条件:
①∠B =∠C;② BE = CD;③AB = AC;
④∠ADC = ∠AEB 中选择一个使得△ABE≌△ACD.
小组讨论:你能选择的条件有哪些,请写出证明过程.
解:选择①:在△ABE 和△ACD 中,
A
C
B
D
E
∠B = ∠C,
∠A = ∠A,
AE = AD,
∴△ABE≌△ACD(AAS).
选择②,不能判定△ABE≌△ACD.
A
C
B
D
E
AB = AC,
∠A = ∠A,
AE = AD,
选择③,在△ABE 和△ACD 中,
∴△ABE≌△ACD(SAS).
选择④,在△ABE 和△ACD 中,
∠AEB = ∠ADC,
AE = AD,
∠A = ∠A,
∴△ABE≌△ACD(ASA).
1. 三角形全等书写的三个步骤:
① 写出在哪两个三角形中;
② 摆出三个条件用大括号括起来;
③ 写出全等结论.
要点归纳
2. 怎样寻找已知条件:已知条件包含两部分,
一是已知中给出的,
二是图形中隐含的(如公共边、公共角等).
例1 如图,AB∥CD,并且 AB = CD,
那么△ABD 与△CDB 全等吗 请说明理由.
A
B
C
D
2
1
解:因为 AB∥CD,
根据“两直线平行,内错角相等”,
所以∠1=∠2.
在△ABD 和△CDB 中,
因为 AB = CD,∠1=∠2,BD = DB,
根据三角形全等的判定条件“SAS”,
所以 △ABD≌△CDB.
典例精析
典例精析
例2 如图,AC 与 BD 相交于点 O,且 OA = OB,OC = OD.
(1) △AOD 与△BOC 全等吗 请说明理由.
解: 因为∠AOD 与∠BOC 是对顶角,
根据“对顶角相等”,
所以 ∠AOD =∠BOC.
在△AOD 和△BOC 中,
因为OA = OB,∠AOD =∠BOC,OD = OC,
根据三角形全等的判定条件“SAS”,
所以△AOD≌ △BOC.
A
O
D
C
B
解:由 (1) 可知,△AOD≌△BOC,
根据“全等三角形的对应边相等”,
所以 AD = BC. 因为 OA = OB,OC = OD,
AC = OA + OC,BD = OB + OD,
所以AC = BD.
在△ACD 和△BDC 中,
因为 AD = BC,AC = BD,DC = CD,
根据三角形全等的判定条件“SSS”,
所以△ACD≌△BDC.
(2) △ACD 与△BDC 全等吗 为什么
你还能根据其他的判定条件,判断这两个三角形全等吗
A
O
D
C
B
例3 如图,△ADF 和△BCE 中,∠A =∠B,点 D,E,F,C 在同一直线上,有如下三个关系式:
①AD = BC;② DE = CF;③ BE∥AF.
(1) 请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题(用序号写出命题书写形式,如:如果①②,那么③);
解:如果①③,那么②;
如果②③,那么①.
(2) 选择 (1) 中你写出的一个命题,说明它正确的理由.
解:对于“如果①③,那么②”理由如下:
∵ BE∥AF,∴∠AFD =∠BEC.
又∵AD = BC,∠A =∠B,
∴△ADF≌△BCE (AAS). ∴DF = CE.
∴DF-EF = CE-EF,即 DE = CF.
对于“如果②③,那么①”证明如下:
∵ BE∥AF,∴∠AFD =∠BEC.
∵ DE = CF,∴ DE + EF = CF + EF,即 DF = CE.
∴∠A =∠B,∴△ADF≌△BCE(AAS). ∴AD = BC.
第肆章节
随堂练习
随堂练习
1.如图,根据已知条件填空:(填“SSS”“ASA”
“AAS” 或“SAS”)
(1) 已知BD=CE,CD=BE,利用______可以判定△BCD≌△CBE;
(2) 已知AD=AE,∠ADB=∠AEC,利用______ 可以判定△ABD≌△ACE;
SSS
ASA
(3) 已知OE=OD,OB=OC,利用______可以判定△BOE≌△COD;
(4) 已知∠BEC=∠CDB,∠BCE=∠CBD,利用______ 可以判定△BCE≌△CBD。
SAS
AAS
2.如图,AC=AE,BC=DE,BC的延长线与DE相交
于点F,∠ACF+∠AED=180°。试说明:AB=AD。
解:因为∠ACF +∠AED = 180°,∠ACF +∠ACB=180°,
所以∠ACB=∠AED。
又因为 在△ABC 和△ADE中,
AC=AE,∠ACB=∠AED,BC=DE,
所以△ABC≌△ADE(SAS),
所以AB = AD。
3.如图,D,E分别是 AB,AC 的中点,BE,
CD 相交于点O,∠B=∠C,BD=CE。试说明:
(1)OD=OE; (2)△ABE≌△ACD。
解:(1)在△BOD和△COE中,
因为∠BOD=∠COE,∠B=∠C,BD=CE,
所以△BOD≌△COE (AAS),
所以 OD=OE。
因为BD=CE,
所以 AD = AE,AB = AC。
又因为 在 △ABE 和 △ACD中,∠A =∠A
所以 △ABE ≌ △ACD (SAS)。
3.如图,D,E分别是 AB,AC 的中点,BE,
CD 相交于点O,∠B=∠C,BD=CE。试说明:
(1)OD=OE; (2)△ABE≌△ACD。
(2)因为D,E分别是AB,AC的中点,
所以AD = BD = AB, AE = CE = AC。
第伍章节
课堂小结
课堂小结
三角形全等的条件
两边及其夹角分别相等的两个三角形全等(简写为“SAS”)
两角及其夹边分别相等的两个三角形全等(简写为“ASA”)
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写为“AAS”)
三边分别相等的两个三角形全等(简写为“SSS”)
角角边
边角边
边边边
角边角
相互 转化
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.3 第4课时 全等三角形的性质与判定
4.3探究三角形全等的条件
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
掌握三角形全等的条件:“SSS”“ASA”“AAS”
“SAS”,并能灵活运用说明问题.
第贰章节
新课导入
新课导入
A
B
C
D
E
F
1.全等三角形的性质有哪些
全等三角形的对应边相等,对应角相等。
2.如图所示,添加什么样的三个条件能够使这
两个三角形全等
△ABC≌△DEF (SSS)
AB=DE ,
AC=DF ,
BC=EF 。
A
B
C
D
E
F
1.全等三角形的性质有哪些
全等三角形的对应边相等,对应角相等。
2.如图所示,添加什么样的三个条件能够使这
两个三角形全等
△ABC≌△DEF (ASA)
∠B=∠E,
BC=EF,
∠C=∠F。
A
B
C
D
E
F
1.全等三角形的性质有哪些
全等三角形的对应边相等,对应角相等。
2.如图所示,添加什么样的三个条件能够使这
两个三角形全等
△ABC≌△DEF (AAS)
∠A=∠D,
∠B=∠E,
BC=EF。
A
B
C
D
E
F
1.全等三角形的性质有哪些
全等三角形的对应边相等,对应角相等。
2.如图所示,添加什么样的三个条件能够使这
两个三角形全等
△ABC≌△DEF (SAS)
AB=DE,
∠B=∠E,
BC=EF。
第叁章节
新知探究
新知探究
1
全等三角形的应用
活动1:已知在△ABC 中,BC = 5 cm,AC = 3 cm,
AB = 3.5 cm,∠B = 36°,∠C = 44°,请你选择适当
数据,画与△ABC 全等的三角形(用三种方法画图,不写作法,但要在所画的三角形中标出用到的数据).
图 ① 作法示例:
(1) 作线段 BC = 5 cm;
(2) 以点 C 为圆心,3 cm 为半径画弧;
(3) 以点 B 为圆心,3.5 cm为半径画弧,两弧相交于点 A;
(4) 连接 AB,AC,则△ABC 为所求作的三角形.
解:
A
B
C
3.5 cm
3 cm
5 cm
图①
A
B
C
3.5 cm
5 cm
图②
36°
A
B
C
5 cm
图③
36°
44°
要点归纳
三角形全等的条件及判定方法:
对应相等
的元素
两边及
其夹角
两角及
其夹边
两角及其中
一角的对边
三边
三角形
全等理由
SAS
ASA
AAS
SSS
2
三角形全等的判定和性质的综合应用
活动 2:如图,点 D,E 分别在线段 AB,AC 上,
AE = AD,不添加新的线段和字母,从下列条件:
①∠B =∠C;② BE = CD;③AB = AC;
④∠ADC = ∠AEB 中选择一个使得△ABE≌△ACD.
小组讨论:你能选择的条件有哪些,请写出证明过程.
解:选择①:在△ABE 和△ACD 中,
A
C
B
D
E
∠B = ∠C,
∠A = ∠A,
AE = AD,
∴△ABE≌△ACD(AAS).
选择②,不能判定△ABE≌△ACD.
A
C
B
D
E
AB = AC,
∠A = ∠A,
AE = AD,
选择③,在△ABE 和△ACD 中,
∴△ABE≌△ACD(SAS).
选择④,在△ABE 和△ACD 中,
∠AEB = ∠ADC,
AE = AD,
∠A = ∠A,
∴△ABE≌△ACD(ASA).
1. 三角形全等书写的三个步骤:
① 写出在哪两个三角形中;
② 摆出三个条件用大括号括起来;
③ 写出全等结论.
要点归纳
2. 怎样寻找已知条件:已知条件包含两部分,
一是已知中给出的,
二是图形中隐含的(如公共边、公共角等).
例1 如图,AB∥CD,并且 AB = CD,
那么△ABD 与△CDB 全等吗 请说明理由.
A
B
C
D
2
1
解:因为 AB∥CD,
根据“两直线平行,内错角相等”,
所以∠1=∠2.
在△ABD 和△CDB 中,
因为 AB = CD,∠1=∠2,BD = DB,
根据三角形全等的判定条件“SAS”,
所以 △ABD≌△CDB.
典例精析
典例精析
例2 如图,AC 与 BD 相交于点 O,且 OA = OB,OC = OD.
(1) △AOD 与△BOC 全等吗 请说明理由.
解: 因为∠AOD 与∠BOC 是对顶角,
根据“对顶角相等”,
所以 ∠AOD =∠BOC.
在△AOD 和△BOC 中,
因为OA = OB,∠AOD =∠BOC,OD = OC,
根据三角形全等的判定条件“SAS”,
所以△AOD≌ △BOC.
A
O
D
C
B
解:由 (1) 可知,△AOD≌△BOC,
根据“全等三角形的对应边相等”,
所以 AD = BC. 因为 OA = OB,OC = OD,
AC = OA + OC,BD = OB + OD,
所以AC = BD.
在△ACD 和△BDC 中,
因为 AD = BC,AC = BD,DC = CD,
根据三角形全等的判定条件“SSS”,
所以△ACD≌△BDC.
(2) △ACD 与△BDC 全等吗 为什么
你还能根据其他的判定条件,判断这两个三角形全等吗
A
O
D
C
B
例3 如图,△ADF 和△BCE 中,∠A =∠B,点 D,E,F,C 在同一直线上,有如下三个关系式:
①AD = BC;② DE = CF;③ BE∥AF.
(1) 请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题(用序号写出命题书写形式,如:如果①②,那么③);
解:如果①③,那么②;
如果②③,那么①.
(2) 选择 (1) 中你写出的一个命题,说明它正确的理由.
解:对于“如果①③,那么②”理由如下:
∵ BE∥AF,∴∠AFD =∠BEC.
又∵AD = BC,∠A =∠B,
∴△ADF≌△BCE (AAS). ∴DF = CE.
∴DF-EF = CE-EF,即 DE = CF.
对于“如果②③,那么①”证明如下:
∵ BE∥AF,∴∠AFD =∠BEC.
∵ DE = CF,∴ DE + EF = CF + EF,即 DF = CE.
∴∠A =∠B,∴△ADF≌△BCE(AAS). ∴AD = BC.
第肆章节
随堂练习
随堂练习
1.如图,根据已知条件填空:(填“SSS”“ASA”
“AAS” 或“SAS”)
(1) 已知BD=CE,CD=BE,利用______可以判定△BCD≌△CBE;
(2) 已知AD=AE,∠ADB=∠AEC,利用______ 可以判定△ABD≌△ACE;
SSS
ASA
(3) 已知OE=OD,OB=OC,利用______可以判定△BOE≌△COD;
(4) 已知∠BEC=∠CDB,∠BCE=∠CBD,利用______ 可以判定△BCE≌△CBD。
SAS
AAS
2.如图,AC=AE,BC=DE,BC的延长线与DE相交
于点F,∠ACF+∠AED=180°。试说明:AB=AD。
解:因为∠ACF +∠AED = 180°,∠ACF +∠ACB=180°,
所以∠ACB=∠AED。
又因为 在△ABC 和△ADE中,
AC=AE,∠ACB=∠AED,BC=DE,
所以△ABC≌△ADE(SAS),
所以AB = AD。
3.如图,D,E分别是 AB,AC 的中点,BE,
CD 相交于点O,∠B=∠C,BD=CE。试说明:
(1)OD=OE; (2)△ABE≌△ACD。
解:(1)在△BOD和△COE中,
因为∠BOD=∠COE,∠B=∠C,BD=CE,
所以△BOD≌△COE (AAS),
所以 OD=OE。
因为BD=CE,
所以 AD = AE,AB = AC。
又因为 在 △ABE 和 △ACD中,∠A =∠A
所以 △ABE ≌ △ACD (SAS)。
3.如图,D,E分别是 AB,AC 的中点,BE,
CD 相交于点O,∠B=∠C,BD=CE。试说明:
(1)OD=OE; (2)△ABE≌△ACD。
(2)因为D,E分别是AB,AC的中点,
所以AD = BD = AB, AE = CE = AC。
第伍章节
课堂小结
课堂小结
三角形全等的条件
两边及其夹角分别相等的两个三角形全等(简写为“SAS”)
两角及其夹边分别相等的两个三角形全等(简写为“ASA”)
两角分别相等且其中一组等角的对边相等的两个三角形全等(简写为“AAS”)
三边分别相等的两个三角形全等(简写为“SSS”)
角角边
边角边
边边边
角边角
相互 转化
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
