4.4 利用三角形全等测距离 课件(共33张PPT)
文档属性
| 名称 | 4.4 利用三角形全等测距离 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:43:05 | ||
图片预览









文档简介
(共33张PPT)
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.4 利用三角形全等测距离
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.能利用三角形全等构建数学模型解决实际问题,强化模型观念;在经历解决实际问题的探索过程中,体会数学知识在生活实际中的应用,提升应用意识.
2.能在解决问题的过程中进行有条理的思考与表达.
第贰章节
新课导入
新课导入
判定三角形全等有哪些方法?
①“SSS”:三边对应相等的两个三角形全等。
②“ASA”:两角和它们的夹边对应相等的两个三角形全等。
③“AAS”:两角和其中一角的对边对应相等的两个三角形全等。
④“SAS”:两边和它们的夹角对应相等的两个三角形全等。
第叁章节
新知探究
新知探究
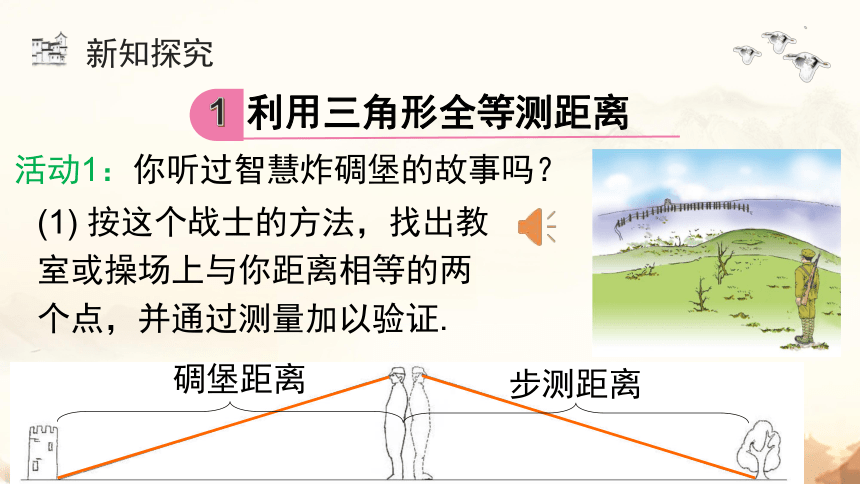
活动1:你听过智慧炸碉堡的故事吗?
步测距离
碉堡距离
(1) 按这个战士的方法,找出教室或操场上与你距离相等的两个点,并通过测量加以验证.
利用三角形全等测距离
1
A
C
B
D
?
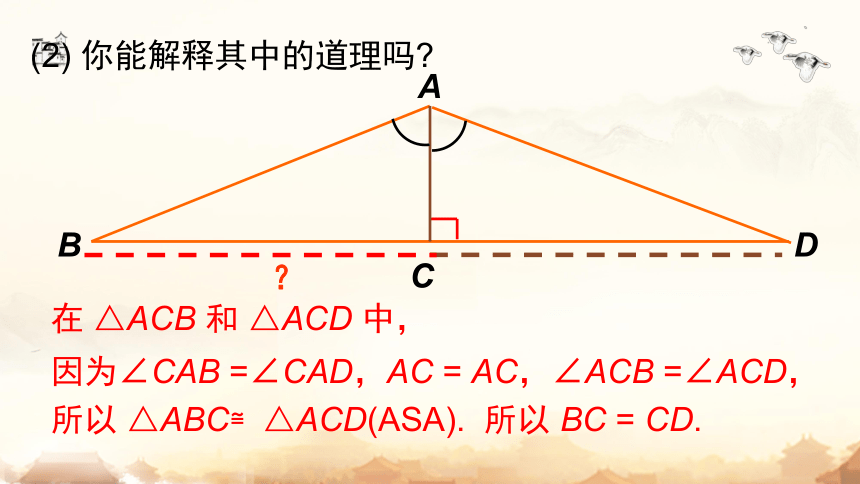
(2) 你能解释其中的道理吗
在 △ACB 和 △ACD 中,
因为∠CAB =∠CAD,AC = AC,∠ACB =∠ACD,
所以 △ABC≌△ACD(ASA).
所以 BC = CD.
1. 利用三角形全等测距离目的:
变不可测距离为可测距离.
2.依据:全等三角形的性质.
3.关键:构造全等三角形.
要点归纳
活动 2:小明在上周末游览风景区时,看到了一个池塘,他想知道池塘最远两点 A,B 之间的距离,但是他没有船,不能直接去测.手里只有两根足够长的绳子和一把尺子,他怎样才能测出点 A,B 之间的距离呢
B
A
·
·
把你的设计方案在图上画出来,并与你的同伴交流你的方案,看看谁的方案更便捷.
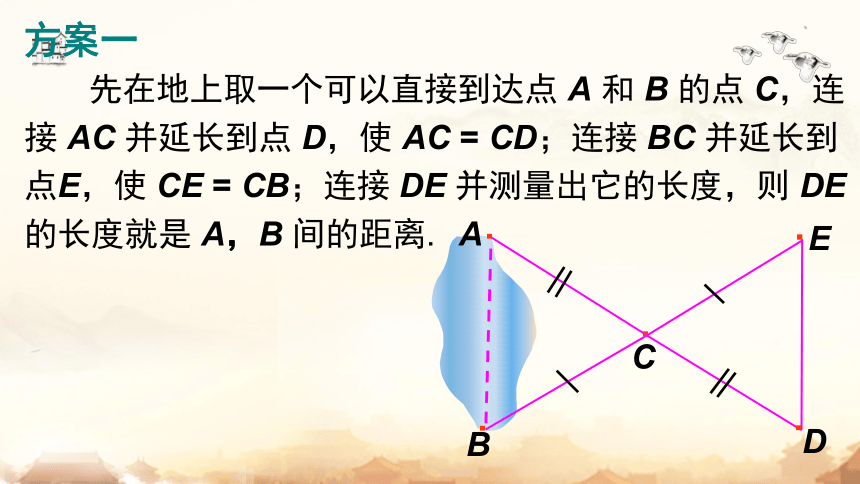
先在地上取一个可以直接到达点 A 和 B 的点 C,连接 AC 并延长到点 D,使 AC = CD;连接 BC 并延长到 点E,使 CE = CB;连接 DE 并测量出它的长度,则 DE 的长度就是 A,B 间的距离.
C
D
E
·
·
·
B
A
·
·
方案一
C
D
E
·
·
·
B
A
·
·
在 △ABC 和 △DEC 中,
因为 AC = DC,
∠ACB =∠DCE,
BC = EC,
所以 △ABC≌△DEC,
所以 AB = DE.
(辅助线)
(对顶角相等)
(辅助线)
(SAS)
(全等三角形,对应边相等)
你能说出每步的道理吗?
你还能设计出其他的方案来吗?(构建全等三角形)
已知条件是什么?结论又是什么?
你能说明设计该方案的道理吗?
B
A
·
·
C
D
E
在△ABC 与△DEC 中,已知 AB⊥BE,BC = CE,DE⊥BE,结论:AB = DE.
·
ASA:两角及其夹边分别相等的两个三角形全等
方案二
·
如图:
方案三
1
2
理由:因为 AD∥CB,
所以∠1=∠2.
如图,先作△ABD,再找一点 C,使 BC∥AD,并使 AD=BC,连接 CD,量 CD 的长即得 AB 的长.
C
D
因为 AD=CB,∠1=∠2,
在△ABD 与△CDB 中,
BD=DB,
所以△ABD≌△CDB (SAS).
所以 AB=CD.
B
A
·
·
如图,找一点 D,使 AD⊥BD,延长 BD 至点C,使CD=BD,连接 AC,量 AC 的长即得 AB 的长.
B
A
D
C
理由: 因为 AD⊥BD,
所以∠ADB=∠ADC=90°.
在 △ADB 与 △ADC 中,
所以△ADB≌△ADC (SAS).
所以 AB=AC.
因为 AD=AD,
∠ADB=∠ADC,
BD=CD,
方案四
C
D
E
B
A
延长法
B
A
C
D
E
B
A
C
D
E
1
2
C
D
B
A
B
A
D
C
1
2
C
D
B
A
平行法
垂直法
SAS
ASA或AAS
SAS
SAS
SAS
ASA或AAS
要点归纳
例1 如图,工人师傅要计算一个圆柱形容器的容积,需要测量其内径. 现在有两根同样长的木棒、一条橡皮绳和一把带有刻度的直尺,你能想法帮助他完成吗?
典例精析
解:如图,在容器外取一点 O,连接 CO,DO 并延长,
使 AO = CO,BO = DO,连接 AB.
∵∠AOB = ∠COD,
∴△ABO≌△CDO(SAS).
∴CD = AB,测出 AB 的长即可知 CD 的长,即可知容器的内径.
·
中点O
A
B
C
D
1. 如图,已知 AC = DB,AO = DO,CD = 100 m,则 A,B 两点间的距离 ( )
A. 大于 100 m B. 等于 100 m
C. 小于 100 m D. 无法确定
B
针对训练
第肆章节
随堂练习
随堂练习
1.如图,为测量河两岸相对的A,B两点间的距离时,先在AB的垂线BF上取两点C,D,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一条直线上时,△EDC≌△ABC,从而得到ED=AB,则测得ED的长即为A,B两点间的距离.判定△EDC≌△ABC的依据是( ).
A.SSS B.ASA
C.三角形全等的定义 D.SAS
B
2.茗茗用同种材料制成的金属框架如图所示,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的长度为( ).
A.51 cm B.48 cm
C.45 cm D.54 cm
C
3.如图,A,B两个建筑物分别位于河的两岸,为了测量它们之间的距离,可以沿河岸作射线BF,且使BF⊥AB,在BF上截取BC=CD,过点D作DE⊥BF,使点E,C,A在一条直线上,则DE的长就是A,B之间的距离,请说明理由.
解:在△ACB和△ECD中,
∴△ACB≌△ECD(ASA).
∴AB=DE.
4.麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B,F,C,E在直线l上(点F,C之间不能直接测量,FC为池塘的长度),点A,D在l的异侧,且AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(1)证明:∵AB∥DE,∴∠ABC=∠DEF,
在△ABC与△DEF中,∴△ABC≌DEF(ASA).
(2)若BE=100 m,BF=30 m,求池塘FC的长.
(2)解:∵△ABC≌△DEF,
∴BC=EF,∴BF+FC=EC+FC,
∴BF=EC.
∵BE=100 m,BF=30 m,
∴FC=100-30-30=40(m).
答:池塘FC的长是40 m.
5.小明利用一根长3 m的竿子来测量路灯AB的高度.他的方法如下:如图,在路灯前选一点P,使BP=3 m,并测得∠APB=70°,然后把竖直的竿子CD(CD=3 m)在BP的延长线上左右移动,使∠CPD=20°,此时测得BD=11.2 m.请根据这些数据,计算出路灯AB的高度.
解:∵∠CPD=20°,∠APB=70°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=70°.
在△CPD和△PAB中,
∴△CPD≌△PAB(ASA).
∴DP=AB.
∵BD=11.2 m,BP=3 m,∴DP=BD-BP=8.2 m,
即AB=8.2 m.
答:路灯AB的高度是8.2 m.
6.某学校花台上有一块如图所示的△ABC地砖现已破损.管理员要对此地砖测量后,再去市场加工一块形状和大小与此完全相同的地砖来换.现在只有直尺和量角器,请你帮他设计一个测量方案,使其加工的地砖能符合要求,并说明理由.
解:①用量角器量出∠A和∠B的度数,用直尺量出边AB的长度;②根据这三个数据,按照原来的位置关系去加工地砖.假设新加工的地砖为△A'B'C'(如图).
∵在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
故形状和大小完全相同.(合理即可)
答案图
第伍章节
课堂小结
课堂小结
测量不能直接测量的两点间的距离
测量不能直接到达的两点间的距离
构造两个全等三角形利用全等三角形的对应边相等解题
利用三角形全等测距离
应用
关键
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第四章 三角形
汇报人:孙老师
汇报班级:X级X班
4.4 利用三角形全等测距离
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.能利用三角形全等构建数学模型解决实际问题,强化模型观念;在经历解决实际问题的探索过程中,体会数学知识在生活实际中的应用,提升应用意识.
2.能在解决问题的过程中进行有条理的思考与表达.
第贰章节
新课导入
新课导入
判定三角形全等有哪些方法?
①“SSS”:三边对应相等的两个三角形全等。
②“ASA”:两角和它们的夹边对应相等的两个三角形全等。
③“AAS”:两角和其中一角的对边对应相等的两个三角形全等。
④“SAS”:两边和它们的夹角对应相等的两个三角形全等。
第叁章节
新知探究
新知探究
活动1:你听过智慧炸碉堡的故事吗?
步测距离
碉堡距离
(1) 按这个战士的方法,找出教室或操场上与你距离相等的两个点,并通过测量加以验证.
利用三角形全等测距离
1
A
C
B
D
?
(2) 你能解释其中的道理吗
在 △ACB 和 △ACD 中,
因为∠CAB =∠CAD,AC = AC,∠ACB =∠ACD,
所以 △ABC≌△ACD(ASA).
所以 BC = CD.
1. 利用三角形全等测距离目的:
变不可测距离为可测距离.
2.依据:全等三角形的性质.
3.关键:构造全等三角形.
要点归纳
活动 2:小明在上周末游览风景区时,看到了一个池塘,他想知道池塘最远两点 A,B 之间的距离,但是他没有船,不能直接去测.手里只有两根足够长的绳子和一把尺子,他怎样才能测出点 A,B 之间的距离呢
B
A
·
·
把你的设计方案在图上画出来,并与你的同伴交流你的方案,看看谁的方案更便捷.
先在地上取一个可以直接到达点 A 和 B 的点 C,连接 AC 并延长到点 D,使 AC = CD;连接 BC 并延长到 点E,使 CE = CB;连接 DE 并测量出它的长度,则 DE 的长度就是 A,B 间的距离.
C
D
E
·
·
·
B
A
·
·
方案一
C
D
E
·
·
·
B
A
·
·
在 △ABC 和 △DEC 中,
因为 AC = DC,
∠ACB =∠DCE,
BC = EC,
所以 △ABC≌△DEC,
所以 AB = DE.
(辅助线)
(对顶角相等)
(辅助线)
(SAS)
(全等三角形,对应边相等)
你能说出每步的道理吗?
你还能设计出其他的方案来吗?(构建全等三角形)
已知条件是什么?结论又是什么?
你能说明设计该方案的道理吗?
B
A
·
·
C
D
E
在△ABC 与△DEC 中,已知 AB⊥BE,BC = CE,DE⊥BE,结论:AB = DE.
·
ASA:两角及其夹边分别相等的两个三角形全等
方案二
·
如图:
方案三
1
2
理由:因为 AD∥CB,
所以∠1=∠2.
如图,先作△ABD,再找一点 C,使 BC∥AD,并使 AD=BC,连接 CD,量 CD 的长即得 AB 的长.
C
D
因为 AD=CB,∠1=∠2,
在△ABD 与△CDB 中,
BD=DB,
所以△ABD≌△CDB (SAS).
所以 AB=CD.
B
A
·
·
如图,找一点 D,使 AD⊥BD,延长 BD 至点C,使CD=BD,连接 AC,量 AC 的长即得 AB 的长.
B
A
D
C
理由: 因为 AD⊥BD,
所以∠ADB=∠ADC=90°.
在 △ADB 与 △ADC 中,
所以△ADB≌△ADC (SAS).
所以 AB=AC.
因为 AD=AD,
∠ADB=∠ADC,
BD=CD,
方案四
C
D
E
B
A
延长法
B
A
C
D
E
B
A
C
D
E
1
2
C
D
B
A
B
A
D
C
1
2
C
D
B
A
平行法
垂直法
SAS
ASA或AAS
SAS
SAS
SAS
ASA或AAS
要点归纳
例1 如图,工人师傅要计算一个圆柱形容器的容积,需要测量其内径. 现在有两根同样长的木棒、一条橡皮绳和一把带有刻度的直尺,你能想法帮助他完成吗?
典例精析
解:如图,在容器外取一点 O,连接 CO,DO 并延长,
使 AO = CO,BO = DO,连接 AB.
∵∠AOB = ∠COD,
∴△ABO≌△CDO(SAS).
∴CD = AB,测出 AB 的长即可知 CD 的长,即可知容器的内径.
·
中点O
A
B
C
D
1. 如图,已知 AC = DB,AO = DO,CD = 100 m,则 A,B 两点间的距离 ( )
A. 大于 100 m B. 等于 100 m
C. 小于 100 m D. 无法确定
B
针对训练
第肆章节
随堂练习
随堂练习
1.如图,为测量河两岸相对的A,B两点间的距离时,先在AB的垂线BF上取两点C,D,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一条直线上时,△EDC≌△ABC,从而得到ED=AB,则测得ED的长即为A,B两点间的距离.判定△EDC≌△ABC的依据是( ).
A.SSS B.ASA
C.三角形全等的定义 D.SAS
B
2.茗茗用同种材料制成的金属框架如图所示,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的长度为( ).
A.51 cm B.48 cm
C.45 cm D.54 cm
C
3.如图,A,B两个建筑物分别位于河的两岸,为了测量它们之间的距离,可以沿河岸作射线BF,且使BF⊥AB,在BF上截取BC=CD,过点D作DE⊥BF,使点E,C,A在一条直线上,则DE的长就是A,B之间的距离,请说明理由.
解:在△ACB和△ECD中,
∴△ACB≌△ECD(ASA).
∴AB=DE.
4.麒麟某数学兴趣小组的同学用数学知识测一池塘的长度,他们所绘如图,点B,F,C,E在直线l上(点F,C之间不能直接测量,FC为池塘的长度),点A,D在l的异侧,且AB∥DE,∠A=∠D,测得AB=DE.
(1)求证:△ABC≌△DEF;
(1)证明:∵AB∥DE,∴∠ABC=∠DEF,
在△ABC与△DEF中,∴△ABC≌DEF(ASA).
(2)若BE=100 m,BF=30 m,求池塘FC的长.
(2)解:∵△ABC≌△DEF,
∴BC=EF,∴BF+FC=EC+FC,
∴BF=EC.
∵BE=100 m,BF=30 m,
∴FC=100-30-30=40(m).
答:池塘FC的长是40 m.
5.小明利用一根长3 m的竿子来测量路灯AB的高度.他的方法如下:如图,在路灯前选一点P,使BP=3 m,并测得∠APB=70°,然后把竖直的竿子CD(CD=3 m)在BP的延长线上左右移动,使∠CPD=20°,此时测得BD=11.2 m.请根据这些数据,计算出路灯AB的高度.
解:∵∠CPD=20°,∠APB=70°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=70°.
在△CPD和△PAB中,
∴△CPD≌△PAB(ASA).
∴DP=AB.
∵BD=11.2 m,BP=3 m,∴DP=BD-BP=8.2 m,
即AB=8.2 m.
答:路灯AB的高度是8.2 m.
6.某学校花台上有一块如图所示的△ABC地砖现已破损.管理员要对此地砖测量后,再去市场加工一块形状和大小与此完全相同的地砖来换.现在只有直尺和量角器,请你帮他设计一个测量方案,使其加工的地砖能符合要求,并说明理由.
解:①用量角器量出∠A和∠B的度数,用直尺量出边AB的长度;②根据这三个数据,按照原来的位置关系去加工地砖.假设新加工的地砖为△A'B'C'(如图).
∵在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(ASA).
故形状和大小完全相同.(合理即可)
答案图
第伍章节
课堂小结
课堂小结
测量不能直接测量的两点间的距离
测量不能直接到达的两点间的距离
构造两个全等三角形利用全等三角形的对应边相等解题
利用三角形全等测距离
应用
关键
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
