5.2 第1课时 等腰三角形的性质 课件(共31张PPT)
文档属性
| 名称 | 5.2 第1课时 等腰三角形的性质 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:44:29 | ||
图片预览










文档简介
(共31张PPT)
北师大版数学七年级下册
第五章 图形的轴对称
汇报人:孙老师
汇报班级:X级X班
5.2 第1课时 等腰三角形的性质
5.2 简单的轴对称图形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.探索并了解等腰三角形的轴对称性和其他性质。
2.根据等腰三角形的性质,探索等边三角形的轴对称性和其他性质。
第贰章节
新课导入
新课导入
等腰三角形是比较常见的图形。
第叁章节
新知探究
新知探究
等腰三角形的性质
1
问题 1:等腰三角形是比较常见的图形. 你有哪些办法可以得到一个等腰三角形 与同伴交流.
1. 折叠法
2. 尺规画图
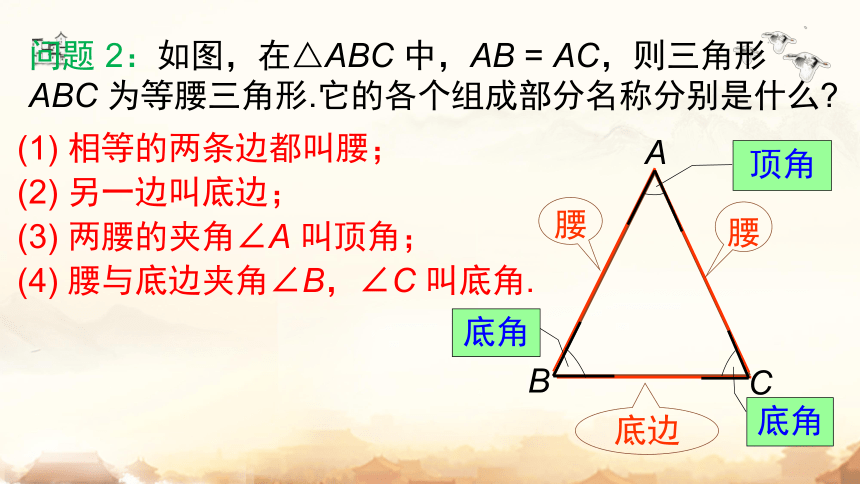
问题 2:如图,在△ABC 中,AB = AC,则三角形 ABC 为等腰三角形.它的各个组成部分名称分别是什么
(1) 相等的两条边都叫腰;
(2) 另一边叫底边;
(3) 两腰的夹角∠A 叫顶角;
(4) 腰与底边夹角∠B,∠C 叫底角.
A
B
C
腰
腰
底边
顶角
底角
底角
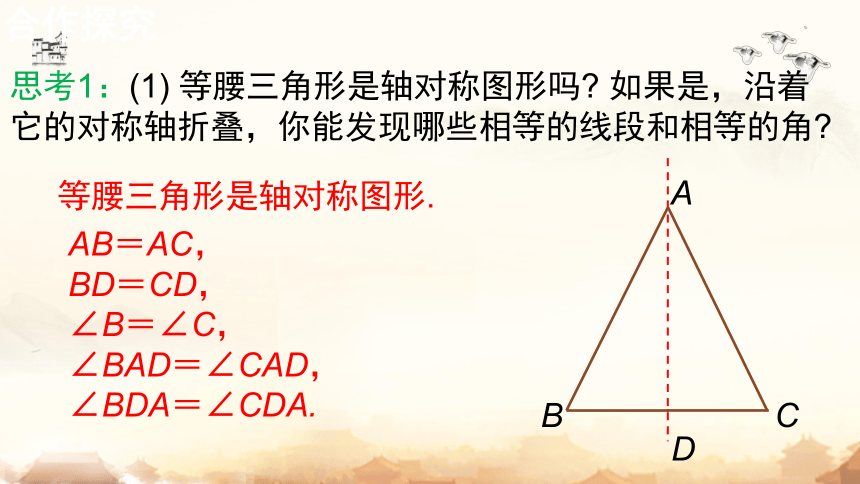
思考1:(1) 等腰三角形是轴对称图形吗 如果是,沿着它的对称轴折叠,你能发现哪些相等的线段和相等的角
A
B
C
等腰三角形是轴对称图形.
AB=AC,
BD=CD,
∠B=∠C,
∠BAD=∠CAD,
∠BDA=∠CDA.
D
合作探究
(2) 等腰三角形的对称轴是一条怎样的直线
你是如何描述的
A
B
C
(3)你认为等腰三角形有哪些特征
与同伴交流.
2.等腰三角形底边上的中线所在的直线是它的对称轴.
3.底边上的高所在的直线是它的对称轴.
1.等腰三角形顶角平分线所在的直线是它的对称轴.
等腰三角形是轴对称图形.
等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(也称“三线合一”),它们所在的直线就是等腰三角形的对称轴.
等腰三角形的两个底角相等.
归纳总结
例1 已知一个等腰三角形的底角是顶角的 2 倍,
求它的各个内角的度数.
解:设这个等腰三角形顶角的度数为 x°,则底角度数为 2x°.
根据“三角形三个内角的和等于180°”,得
x+2x+2x=180.
解得 x=36.
2×36=72.
所以这个三角形的三个内角分别为36°、72°、72°.
典例精析
1.画出任意一个等腰三角形(等边三角形除外)的底角平分线、这个底角所对的腰上的中线和高,看看它们能不能重合
概念辨析
不能重合
2. 如图,△ABC 是一个等腰三角形,直线 l 是它的对称轴. 请在△ABC 中画出以直线 l 为对称轴的一组对应点、一组对应线段、一组对应角,你能发现哪些相等的线段、相等的角,以及形状、大小
完全相同的图形
A
B
C
l
等边三角形的特征
2
思考 2:通过学习我们知道等腰三角形的轴对称性及其特征,那么当等腰三角形的腰与底边相等时它是什么三角形
等边三角形,它是特殊的等腰三角形
(1) 等边三角形有几条对称轴?
(2) 你能发现它的哪些特征?
等边三角形有 3 条对称轴
1.等边三角形三个内角都相等,且均为60°.
2. 等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线或角的平分线所在的直线.
3.等边三角形每条边上的中线、高线和角平分线互相重合.
要点归纳
例2 如图是由大小相等的等边三角形组成的图案,请找出它的对称轴.
典例精析
例3 等腰三角形的一个内角是 50°,则这个三角形的
底角的大小是 ( )
A.65° 或 50° B.80° 或 40°
C.65° 或 80° D.50° 或 80°
解析:当 50° 的角是底角时,三角形的底角就是 50°;当 50° 的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是 65°,综上所述,选 A.
A
例4 如图,在△ABC 中,AB = AC,AD 为 BC 边上的中线,∠CAD = 40°,EF 为过点 A 的一条直线,且 EF∥BC,求∠BAE 的度数.
解:在△ABC 中,因为 AB = AC,
AD 为 BC 边上的中线,
所以 AD⊥BC,且 AD 平分∠BAC,
所以∠ADB = 90°,∠BAD =∠CAD = 40°,
所以∠B = 50°,
因为 EF∥BC,
所以∠BAE =∠B = 50°.
解:因为 OA = AB,
所以∠ABO =∠O = 15°. 所以∠BAO =150°.
所以∠BAC =180°-∠BAO = 30°.
因为 AB = BC,
所以∠ACB =∠BAC = 30°.
所以∠CBO = 135°. 所以∠CBD =180°-∠CBO = 45°.
因为BC=CD,所以∠D =∠CBD = 45°. 所以∠BCD = 90°.
所以∠1 = 180°-∠BCD-∠ACB = 60°.
1. 如图,∠O = 15°,且 OA = AB = BC = CD. 求∠1.
⌒
15°
1
C
D
B
O
A
⌒
练一练
第肆章节
随堂练习
随堂练习
1.如图,在△ABC中,AB=AC,D是BC的中点,∠B=30°,求∠ADB和∠BAD的度数.
∠ADB=90°,
∠BAD=60°
2.如图,点D,E在△ABC的边BC上,AD=AE,BD=EC,求证:AB=AC.
(略.提示:利用等腰三角形的性质得到∠ADE=∠AED,从而得到∠ADB=∠AEC,再证明△ABD≌△ACE得到AB=AC)
A.6个 B.7个
C.8个 D.9个
3.如图所示的正方形网格中,网格线的交点称为格点,已知点A,B是两个格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数可能有( ).
C
4.已知等腰三角形的三边长分别为m-2,2m+1,8,求这个等腰三角形的周长.
∵8+8=16<21,∴不能组成三角形.
∴2m+1=21.∴三边长分别为8,21,8.
②当m-2=8时,解得m=10.
∴m-2=-5(舍去).
①当m-2=2m+1时,解得m=-3.
解:分三种情况,
③当2m+1=8时,解得m=3.5.
∴m-2=1.5.∴三边长分别为1.5,8,8.
∴等腰三角形的周长为1.5+8×2=17.5.
综上所述,等腰三角形的周长为17.5.
5.如图,在△ABC中,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=BE,求∠A的度数.
解:设∠A=x.∵AD=DE=EB,
∴∠DEA=∠A=x,∠EBD=∠EDB.
∵∠DEA+∠DEB=∠EBD+∠EDB+∠DEB=180°,
∴∠DEA=∠EBD+∠EDB.
∴∠EBD=∠EDB=.
∴∠BDC=∠A+∠ABD=x.∵BC=BD,AB=AC,
∴∠BDC=∠BCD=∠ABC=x.
又∵∠A+∠ABC+∠ACB=180°,∴x+x+x=180°.
∴x=45°,即∠A=45°.
第伍章节
课堂小结
课堂小结
等腰三角形
三线合一
两底角相等
轴对称性
性质
等边三角形
性质
轴对称性,有三条对称轴
三个内角相等,并且每个内角都等于60°
三线合一
等腰三角形
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第五章 图形的轴对称
汇报人:孙老师
汇报班级:X级X班
5.2 第1课时 等腰三角形的性质
5.2 简单的轴对称图形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.探索并了解等腰三角形的轴对称性和其他性质。
2.根据等腰三角形的性质,探索等边三角形的轴对称性和其他性质。
第贰章节
新课导入
新课导入
等腰三角形是比较常见的图形。
第叁章节
新知探究
新知探究
等腰三角形的性质
1
问题 1:等腰三角形是比较常见的图形. 你有哪些办法可以得到一个等腰三角形 与同伴交流.
1. 折叠法
2. 尺规画图
问题 2:如图,在△ABC 中,AB = AC,则三角形 ABC 为等腰三角形.它的各个组成部分名称分别是什么
(1) 相等的两条边都叫腰;
(2) 另一边叫底边;
(3) 两腰的夹角∠A 叫顶角;
(4) 腰与底边夹角∠B,∠C 叫底角.
A
B
C
腰
腰
底边
顶角
底角
底角
思考1:(1) 等腰三角形是轴对称图形吗 如果是,沿着它的对称轴折叠,你能发现哪些相等的线段和相等的角
A
B
C
等腰三角形是轴对称图形.
AB=AC,
BD=CD,
∠B=∠C,
∠BAD=∠CAD,
∠BDA=∠CDA.
D
合作探究
(2) 等腰三角形的对称轴是一条怎样的直线
你是如何描述的
A
B
C
(3)你认为等腰三角形有哪些特征
与同伴交流.
2.等腰三角形底边上的中线所在的直线是它的对称轴.
3.底边上的高所在的直线是它的对称轴.
1.等腰三角形顶角平分线所在的直线是它的对称轴.
等腰三角形是轴对称图形.
等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(也称“三线合一”),它们所在的直线就是等腰三角形的对称轴.
等腰三角形的两个底角相等.
归纳总结
例1 已知一个等腰三角形的底角是顶角的 2 倍,
求它的各个内角的度数.
解:设这个等腰三角形顶角的度数为 x°,则底角度数为 2x°.
根据“三角形三个内角的和等于180°”,得
x+2x+2x=180.
解得 x=36.
2×36=72.
所以这个三角形的三个内角分别为36°、72°、72°.
典例精析
1.画出任意一个等腰三角形(等边三角形除外)的底角平分线、这个底角所对的腰上的中线和高,看看它们能不能重合
概念辨析
不能重合
2. 如图,△ABC 是一个等腰三角形,直线 l 是它的对称轴. 请在△ABC 中画出以直线 l 为对称轴的一组对应点、一组对应线段、一组对应角,你能发现哪些相等的线段、相等的角,以及形状、大小
完全相同的图形
A
B
C
l
等边三角形的特征
2
思考 2:通过学习我们知道等腰三角形的轴对称性及其特征,那么当等腰三角形的腰与底边相等时它是什么三角形
等边三角形,它是特殊的等腰三角形
(1) 等边三角形有几条对称轴?
(2) 你能发现它的哪些特征?
等边三角形有 3 条对称轴
1.等边三角形三个内角都相等,且均为60°.
2. 等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线或角的平分线所在的直线.
3.等边三角形每条边上的中线、高线和角平分线互相重合.
要点归纳
例2 如图是由大小相等的等边三角形组成的图案,请找出它的对称轴.
典例精析
例3 等腰三角形的一个内角是 50°,则这个三角形的
底角的大小是 ( )
A.65° 或 50° B.80° 或 40°
C.65° 或 80° D.50° 或 80°
解析:当 50° 的角是底角时,三角形的底角就是 50°;当 50° 的角是顶角时,两底角相等,根据三角形的内角和定理易得底角是 65°,综上所述,选 A.
A
例4 如图,在△ABC 中,AB = AC,AD 为 BC 边上的中线,∠CAD = 40°,EF 为过点 A 的一条直线,且 EF∥BC,求∠BAE 的度数.
解:在△ABC 中,因为 AB = AC,
AD 为 BC 边上的中线,
所以 AD⊥BC,且 AD 平分∠BAC,
所以∠ADB = 90°,∠BAD =∠CAD = 40°,
所以∠B = 50°,
因为 EF∥BC,
所以∠BAE =∠B = 50°.
解:因为 OA = AB,
所以∠ABO =∠O = 15°. 所以∠BAO =150°.
所以∠BAC =180°-∠BAO = 30°.
因为 AB = BC,
所以∠ACB =∠BAC = 30°.
所以∠CBO = 135°. 所以∠CBD =180°-∠CBO = 45°.
因为BC=CD,所以∠D =∠CBD = 45°. 所以∠BCD = 90°.
所以∠1 = 180°-∠BCD-∠ACB = 60°.
1. 如图,∠O = 15°,且 OA = AB = BC = CD. 求∠1.
⌒
15°
1
C
D
B
O
A
⌒
练一练
第肆章节
随堂练习
随堂练习
1.如图,在△ABC中,AB=AC,D是BC的中点,∠B=30°,求∠ADB和∠BAD的度数.
∠ADB=90°,
∠BAD=60°
2.如图,点D,E在△ABC的边BC上,AD=AE,BD=EC,求证:AB=AC.
(略.提示:利用等腰三角形的性质得到∠ADE=∠AED,从而得到∠ADB=∠AEC,再证明△ABD≌△ACE得到AB=AC)
A.6个 B.7个
C.8个 D.9个
3.如图所示的正方形网格中,网格线的交点称为格点,已知点A,B是两个格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数可能有( ).
C
4.已知等腰三角形的三边长分别为m-2,2m+1,8,求这个等腰三角形的周长.
∵8+8=16<21,∴不能组成三角形.
∴2m+1=21.∴三边长分别为8,21,8.
②当m-2=8时,解得m=10.
∴m-2=-5(舍去).
①当m-2=2m+1时,解得m=-3.
解:分三种情况,
③当2m+1=8时,解得m=3.5.
∴m-2=1.5.∴三边长分别为1.5,8,8.
∴等腰三角形的周长为1.5+8×2=17.5.
综上所述,等腰三角形的周长为17.5.
5.如图,在△ABC中,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=BE,求∠A的度数.
解:设∠A=x.∵AD=DE=EB,
∴∠DEA=∠A=x,∠EBD=∠EDB.
∵∠DEA+∠DEB=∠EBD+∠EDB+∠DEB=180°,
∴∠DEA=∠EBD+∠EDB.
∴∠EBD=∠EDB=.
∴∠BDC=∠A+∠ABD=x.∵BC=BD,AB=AC,
∴∠BDC=∠BCD=∠ABC=x.
又∵∠A+∠ABC+∠ACB=180°,∴x+x+x=180°.
∴x=45°,即∠A=45°.
第伍章节
课堂小结
课堂小结
等腰三角形
三线合一
两底角相等
轴对称性
性质
等边三角形
性质
轴对称性,有三条对称轴
三个内角相等,并且每个内角都等于60°
三线合一
等腰三角形
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
