5.2 第2课时 线段垂直平分线的性质 课件(共38张PPT)
文档属性
| 名称 | 5.2 第2课时 线段垂直平分线的性质 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:43:52 | ||
图片预览









文档简介
(共38张PPT)
北师大版数学七年级下册
第五章 图形的轴对称
汇报人:孙老师
汇报班级:X级X班
5.2 第2课时 线段垂直平分线的性质
5.2 简单的轴对称图形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.了解线段的轴对称性。
2.理解并掌握线段垂直平分线的性质。
3.能用尺规作线段的垂直平分线。
第贰章节
新课导入
新课导入
1.什么样的图形叫作轴对称图形
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形。
2. 下列各图中,可看作轴对称图形的是( )
A
B
C
D
B
3.线段是轴对称图形吗
第叁章节
新知探究
新知探究
A
B
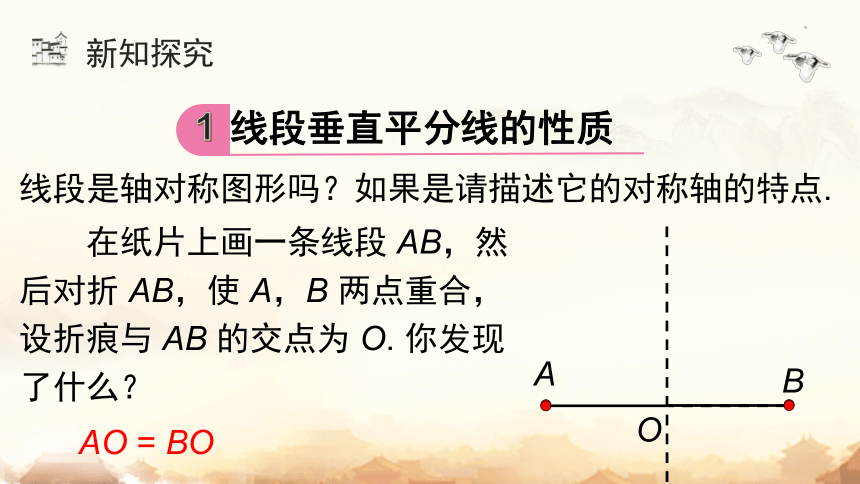
在纸片上画一条线段 AB,然后对折 AB,使 A,B 两点重合,设折痕与 AB 的交点为 O. 你发现了什么?
线段垂直平分线的性质
O
AO = BO
1
线段是轴对称图形吗?如果是请描述它的对称轴的特点.
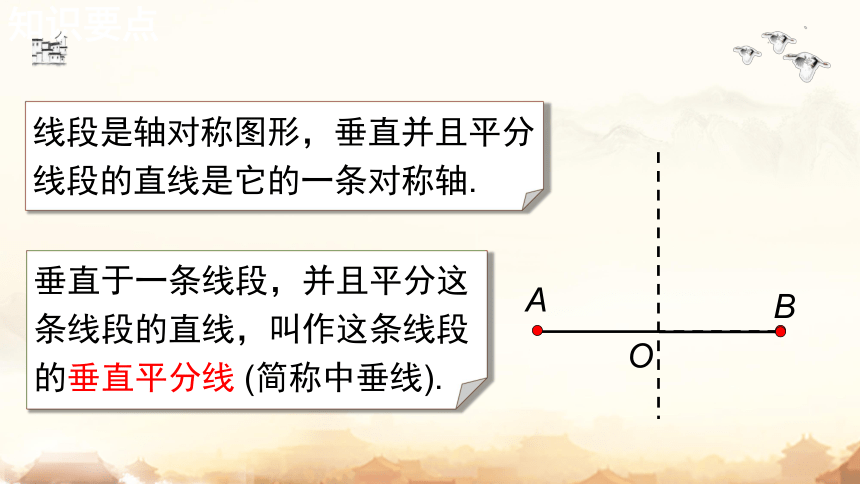
线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴.
垂直于一条线段,并且平分这条线段的直线,叫作这条线段的垂直平分线 (简称中垂线).
A
B
O
知识要点
线段垂直平分线的性质
2
思考1:如图,直线 l 是线段 AB 的垂直平分线,
点 C 是 l 上的任意一点. 在线段 AB 上画出关于直线 l 成轴对称的点 D 和 D',连接 CD 和 CD'.
(1) 你认为线段 CD 和 CD' 之间有什么关系 说说你的理由.
D
D'
C
l
A
B
CD = CD' 且关于直线 l 对称
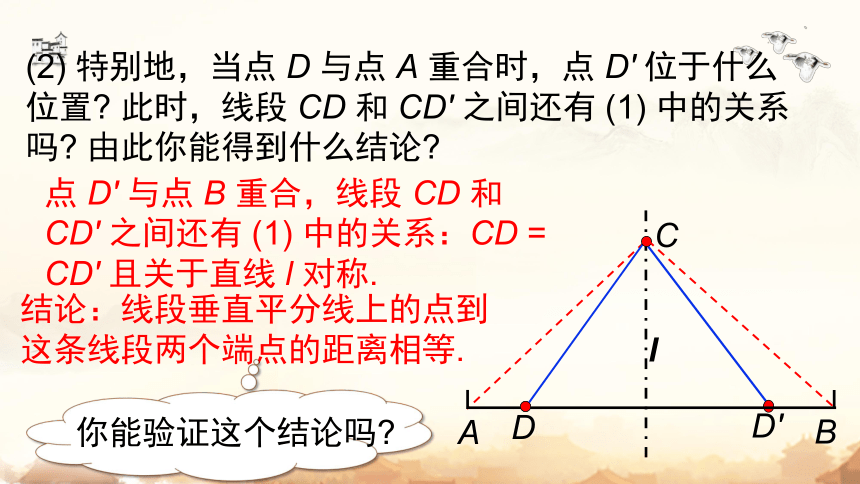
(2) 特别地,当点 D 与点 A 重合时,点 D' 位于什么位置 此时,线段 CD 和 CD' 之间还有 (1) 中的关系吗 由此你能得到什么结论
点 D' 与点 B 重合,线段 CD 和 CD' 之间还有 (1) 中的关系:CD = CD' 且关于直线 l 对称.
D
D'
C
l
A
B
结论:线段垂直平分线上的点到这条线段两个端点的距离相等.
你能验证这个结论吗
已知:如图,MN ⊥ AB,垂足为点 C,AC = BC,点 P 是直线 MN 上的任意一点.
试说明:PA = PB.
证一证
C
B
P
N
A
M
∴△PCA≌△PCB(SAS),∴PA = PB.
解:∵MN⊥AB,
∴∠PCA = ∠PCB = 90°.
在△PCA 和△PCB 中,
AC = BC,
∠PCA =∠PCB,
PC = PC,
知识要点
B
P
A
l
性质:线段垂直平分线上的点到这条线段两个端点的距离相等.
几何语言:
因为点 P 是线段 AB 垂直平分线上的一点,
所以 AP = BP.
利用尺规作线段的垂直平分线
3
思考 2:如图,已知线段 AB,如何作出它的垂直平分线 假设线段 AB 的垂直平分线已作出,那么
(1) 这条直线有什么特征
(2) 如何确定这条直线上的两个点 用三角尺、量角器、圆规等工具试一试.如果只用尺规呢 与同伴进行交流.
A
B
注意:需要确定的点是线段对称轴上的点,因此应当从线段两端进行“对称”的操作.
例1 利用尺规,作线段 AB 的垂直平分线.
作法:
1.分别以点 A 和 B 为圆心,以大
于 AB 的长为半径作弧,
已知:线段 AB.
求作:线段AB 的垂直平分线.
2. 作直线 CD.直线 CD 就是线段 AB 的垂直平分线.
A
B
C
D
两弧相交于点 C 和 D;
典例精析
作法:①以点 P 为圆心,以任意长为半径作弧,与直线 l 相交于点 A,B;
思考3:如图,已知直线 l 和 l 上的一点 P,如何用尺规作 l 的垂线,使它经过点 P 能说明你的作法的道理吗
B
P
A
l
② 分别以点 A 和 B 为圆心,以大
于 AB 的长为半径作弧,
直线MN 即为直线 l 的垂线.
两弧相交于点 M 和 N,
N
M
合作探究
例2 如图,AC 的垂直平分线交 AB 于点 D,交 AC 于点E,AB=12 cm,BC=10 cm,则△BCD 的周长为( )
A.22 cm B.16 cm
C.26 cm D.25 cm
解析:根据线段垂直平分线的性质
得 CD=AD,故△BCD 的周长为
DC+BD+BC=AD+BD+BC
=AB+BC=12+10=22 (cm).故选A
A
典例精析
例3 如图,某地由于居民增多,要在公路 l 边增加一个公共汽车站,A,B 是路边两个新建小区,这个公共汽车站 C 建在什么位置,能使两个小区到车站的路程一样长(要求:尺规作图,保留作图痕迹,不写画法)
解:这个公共汽车站 C 的位置如图所示.
解析:连接 AB,作 AB 的垂直平分线交
直线 l 于点 C,交 AB 于点 E.
因为 EC 是线段 AB 的垂直平分线,
所以点 C 到 A,B 的距离相等.
此时两个小区到车站的路程一样长.
1. 如图,AB 是△ABC 的一条边,DE 是 AB 的垂直平分线,垂足为 E,并交 BC 于点 D,已知 AB = 8 cm,BD = 6 cm,那么 EA =_____cm,DA =_____cm.
A
B
E
D
C
4
6
练一练
第肆章节
随堂练习
随堂练习
1.如图,政府计划在A,B,C三个村庄附近建立一所小学,且小学到三个村庄的距离相等,则小学应建在( ).
A.△ABC三边垂直平分线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条中线的交点
A
2.如图,在△ABC中,已知点D在BC上,且BD+AD=BC,则点D在
( ).
A.AC的垂直平分线上
B.∠BAC的平分线上
C.BC的中点
D.AB的垂直平分线上
A
3.如图,在△ABC中,∠B=40°,∠C=30°,AC的垂直平分线交边AC于点D,交边BC于点E,连接AE,求∠BAE的度数.
80°
4.如图,在△ABC中,将∠B和∠C按如图所示方式折叠,点B,C均落于边BC上一点G处,线段MN,EF为折痕.若∠A=94°,则∠MGE=
.
94°
5.尺规作图:如图,请用圆规和无刻度的直尺作出Rt△ABC中斜边AC上的中线BO.(保留作图痕迹,不要求写作法)
解:如图,线段BO即为所求.
答案图
6.如图,A,B是小河同侧的两个村庄,为解决用水问题,两村合资在河上修建一座水站.(尺规作图,不写作法,保留作图痕迹,写出结论)
(1)为使水站到A村和B村的距离相等,求水站的位置C;
解:(1)如图,点C即为水站的位置.
答案图
(2)如图,点D即为水站的位置.
答案图
(2)为使水站到A村和B村的水管总长最短,求水站的位置D.
7.在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 ;
(2)求BC的长;
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
AD=BD
解:(2)∵l2是线段AC的垂直平分线,
∴EA=EC.∵△ADE的周长为6,
∴AD+DE+AE=6,∴BD+DE+EC=6,即BC=6.
(3)∵l1是线段AB的垂直平分线,∴OA=OB.
∵l2是线段AC的垂直平分线,∴OA=OC,∴OB=OC.
∵△OBC的周长为16,BC=6,∴OB+OC=10,
∴OA=OB=OC=5.
答案图
(1)请用无刻度的直尺和圆规按下列要求作图:在图1中作△ABC的中线AD,延长AD至点E,使DE=AD,连接BE(保留作图痕迹,不写作法).线段AC和线段BE的数量关系和位置关系是 ;
8.已知△ABC.
AC=BE、AC∥BE
解:(1)如图1,AD,DE,BE即为所求.
∵BD=CD,∠BDE=∠CDA,ED=AD,∴△BDE≌△CDA,
∴BE=AC,∠BED=∠CAD,∴BE∥AC.
答案图1
(2)如图2,延长AD至E,使DE=AD,连接BE.
∵BD=CD,∠BDE=∠CDA,ED=AD,∴△BDE≌△CDA,
∴BE=AC,∠DBE=∠DCA.∵∠ABC+∠DCA=90°,
∴∠ABE=∠DBE+∠ABC=90°=∠BAC,又AB=AB,
∴△ABE≌△BAC,∴AE=BC,
∴AD=AE=BC.
(2)当∠BAC=90°时,如图2所示,若AD是△ABC的中线,
试探究AD与BC的数量关系,并说明理由;
答案图2
(3)当∠B=90°时,如图3所示,若AD是△ABC的中线,AB=3,CE⊥BC,∠ADE=90°,CE=5,连接AE,请直接写出AE的长.
(3)如图3,延长ED到点F,使得DF=DE.
∵AD是△ABC的中线,∴BD=CD.
又∵∠BDF=∠CDE,DF=DE,
∴△BDF≌△CDE,
∴BF=EC=5,∠DBF=∠DCE=90°.
∵∠ABC=90°,∴AF=AB+BF=3+5=8.
∵DF=DE,∠ADE=90°,
∴AE=AF=8.
答案图3
第伍章节
课堂小结
课堂小结
线段
作线段的垂直平分线
概念:垂直于一条线段,并且平分这条线段的直线
性质:线段垂直平分线上的点到这条线段两个端点的距离相等
线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴
线段的垂直平分线
尺规作图
轴对称性
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第五章 图形的轴对称
汇报人:孙老师
汇报班级:X级X班
5.2 第2课时 线段垂直平分线的性质
5.2 简单的轴对称图形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.了解线段的轴对称性。
2.理解并掌握线段垂直平分线的性质。
3.能用尺规作线段的垂直平分线。
第贰章节
新课导入
新课导入
1.什么样的图形叫作轴对称图形
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形。
2. 下列各图中,可看作轴对称图形的是( )
A
B
C
D
B
3.线段是轴对称图形吗
第叁章节
新知探究
新知探究
A
B
在纸片上画一条线段 AB,然后对折 AB,使 A,B 两点重合,设折痕与 AB 的交点为 O. 你发现了什么?
线段垂直平分线的性质
O
AO = BO
1
线段是轴对称图形吗?如果是请描述它的对称轴的特点.
线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴.
垂直于一条线段,并且平分这条线段的直线,叫作这条线段的垂直平分线 (简称中垂线).
A
B
O
知识要点
线段垂直平分线的性质
2
思考1:如图,直线 l 是线段 AB 的垂直平分线,
点 C 是 l 上的任意一点. 在线段 AB 上画出关于直线 l 成轴对称的点 D 和 D',连接 CD 和 CD'.
(1) 你认为线段 CD 和 CD' 之间有什么关系 说说你的理由.
D
D'
C
l
A
B
CD = CD' 且关于直线 l 对称
(2) 特别地,当点 D 与点 A 重合时,点 D' 位于什么位置 此时,线段 CD 和 CD' 之间还有 (1) 中的关系吗 由此你能得到什么结论
点 D' 与点 B 重合,线段 CD 和 CD' 之间还有 (1) 中的关系:CD = CD' 且关于直线 l 对称.
D
D'
C
l
A
B
结论:线段垂直平分线上的点到这条线段两个端点的距离相等.
你能验证这个结论吗
已知:如图,MN ⊥ AB,垂足为点 C,AC = BC,点 P 是直线 MN 上的任意一点.
试说明:PA = PB.
证一证
C
B
P
N
A
M
∴△PCA≌△PCB(SAS),∴PA = PB.
解:∵MN⊥AB,
∴∠PCA = ∠PCB = 90°.
在△PCA 和△PCB 中,
AC = BC,
∠PCA =∠PCB,
PC = PC,
知识要点
B
P
A
l
性质:线段垂直平分线上的点到这条线段两个端点的距离相等.
几何语言:
因为点 P 是线段 AB 垂直平分线上的一点,
所以 AP = BP.
利用尺规作线段的垂直平分线
3
思考 2:如图,已知线段 AB,如何作出它的垂直平分线 假设线段 AB 的垂直平分线已作出,那么
(1) 这条直线有什么特征
(2) 如何确定这条直线上的两个点 用三角尺、量角器、圆规等工具试一试.如果只用尺规呢 与同伴进行交流.
A
B
注意:需要确定的点是线段对称轴上的点,因此应当从线段两端进行“对称”的操作.
例1 利用尺规,作线段 AB 的垂直平分线.
作法:
1.分别以点 A 和 B 为圆心,以大
于 AB 的长为半径作弧,
已知:线段 AB.
求作:线段AB 的垂直平分线.
2. 作直线 CD.直线 CD 就是线段 AB 的垂直平分线.
A
B
C
D
两弧相交于点 C 和 D;
典例精析
作法:①以点 P 为圆心,以任意长为半径作弧,与直线 l 相交于点 A,B;
思考3:如图,已知直线 l 和 l 上的一点 P,如何用尺规作 l 的垂线,使它经过点 P 能说明你的作法的道理吗
B
P
A
l
② 分别以点 A 和 B 为圆心,以大
于 AB 的长为半径作弧,
直线MN 即为直线 l 的垂线.
两弧相交于点 M 和 N,
N
M
合作探究
例2 如图,AC 的垂直平分线交 AB 于点 D,交 AC 于点E,AB=12 cm,BC=10 cm,则△BCD 的周长为( )
A.22 cm B.16 cm
C.26 cm D.25 cm
解析:根据线段垂直平分线的性质
得 CD=AD,故△BCD 的周长为
DC+BD+BC=AD+BD+BC
=AB+BC=12+10=22 (cm).故选A
A
典例精析
例3 如图,某地由于居民增多,要在公路 l 边增加一个公共汽车站,A,B 是路边两个新建小区,这个公共汽车站 C 建在什么位置,能使两个小区到车站的路程一样长(要求:尺规作图,保留作图痕迹,不写画法)
解:这个公共汽车站 C 的位置如图所示.
解析:连接 AB,作 AB 的垂直平分线交
直线 l 于点 C,交 AB 于点 E.
因为 EC 是线段 AB 的垂直平分线,
所以点 C 到 A,B 的距离相等.
此时两个小区到车站的路程一样长.
1. 如图,AB 是△ABC 的一条边,DE 是 AB 的垂直平分线,垂足为 E,并交 BC 于点 D,已知 AB = 8 cm,BD = 6 cm,那么 EA =_____cm,DA =_____cm.
A
B
E
D
C
4
6
练一练
第肆章节
随堂练习
随堂练习
1.如图,政府计划在A,B,C三个村庄附近建立一所小学,且小学到三个村庄的距离相等,则小学应建在( ).
A.△ABC三边垂直平分线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条中线的交点
A
2.如图,在△ABC中,已知点D在BC上,且BD+AD=BC,则点D在
( ).
A.AC的垂直平分线上
B.∠BAC的平分线上
C.BC的中点
D.AB的垂直平分线上
A
3.如图,在△ABC中,∠B=40°,∠C=30°,AC的垂直平分线交边AC于点D,交边BC于点E,连接AE,求∠BAE的度数.
80°
4.如图,在△ABC中,将∠B和∠C按如图所示方式折叠,点B,C均落于边BC上一点G处,线段MN,EF为折痕.若∠A=94°,则∠MGE=
.
94°
5.尺规作图:如图,请用圆规和无刻度的直尺作出Rt△ABC中斜边AC上的中线BO.(保留作图痕迹,不要求写作法)
解:如图,线段BO即为所求.
答案图
6.如图,A,B是小河同侧的两个村庄,为解决用水问题,两村合资在河上修建一座水站.(尺规作图,不写作法,保留作图痕迹,写出结论)
(1)为使水站到A村和B村的距离相等,求水站的位置C;
解:(1)如图,点C即为水站的位置.
答案图
(2)如图,点D即为水站的位置.
答案图
(2)为使水站到A村和B村的水管总长最短,求水站的位置D.
7.在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 ;
(2)求BC的长;
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
AD=BD
解:(2)∵l2是线段AC的垂直平分线,
∴EA=EC.∵△ADE的周长为6,
∴AD+DE+AE=6,∴BD+DE+EC=6,即BC=6.
(3)∵l1是线段AB的垂直平分线,∴OA=OB.
∵l2是线段AC的垂直平分线,∴OA=OC,∴OB=OC.
∵△OBC的周长为16,BC=6,∴OB+OC=10,
∴OA=OB=OC=5.
答案图
(1)请用无刻度的直尺和圆规按下列要求作图:在图1中作△ABC的中线AD,延长AD至点E,使DE=AD,连接BE(保留作图痕迹,不写作法).线段AC和线段BE的数量关系和位置关系是 ;
8.已知△ABC.
AC=BE、AC∥BE
解:(1)如图1,AD,DE,BE即为所求.
∵BD=CD,∠BDE=∠CDA,ED=AD,∴△BDE≌△CDA,
∴BE=AC,∠BED=∠CAD,∴BE∥AC.
答案图1
(2)如图2,延长AD至E,使DE=AD,连接BE.
∵BD=CD,∠BDE=∠CDA,ED=AD,∴△BDE≌△CDA,
∴BE=AC,∠DBE=∠DCA.∵∠ABC+∠DCA=90°,
∴∠ABE=∠DBE+∠ABC=90°=∠BAC,又AB=AB,
∴△ABE≌△BAC,∴AE=BC,
∴AD=AE=BC.
(2)当∠BAC=90°时,如图2所示,若AD是△ABC的中线,
试探究AD与BC的数量关系,并说明理由;
答案图2
(3)当∠B=90°时,如图3所示,若AD是△ABC的中线,AB=3,CE⊥BC,∠ADE=90°,CE=5,连接AE,请直接写出AE的长.
(3)如图3,延长ED到点F,使得DF=DE.
∵AD是△ABC的中线,∴BD=CD.
又∵∠BDF=∠CDE,DF=DE,
∴△BDF≌△CDE,
∴BF=EC=5,∠DBF=∠DCE=90°.
∵∠ABC=90°,∴AF=AB+BF=3+5=8.
∵DF=DE,∠ADE=90°,
∴AE=AF=8.
答案图3
第伍章节
课堂小结
课堂小结
线段
作线段的垂直平分线
概念:垂直于一条线段,并且平分这条线段的直线
性质:线段垂直平分线上的点到这条线段两个端点的距离相等
线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴
线段的垂直平分线
尺规作图
轴对称性
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
