3.3 第2课时 与摸球相关的概率 课件(共31张PPT)
文档属性
| 名称 | 3.3 第2课时 与摸球相关的概率 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:46:01 | ||
图片预览










文档简介
(共31张PPT)
北师大版数学七年级下册
第三章 概率初步
汇报人:孙老师
汇报班级:X级X班
3.3 第2课时 与摸球相关的概率
3.3 等可能事件的概率
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.初步理解游戏的公平性,会设计简单的公平的游戏.
2.灵活应用概率的计算方法解决各种类型的实际问题.
第贰章节
新课导入
新课导入
箱子里有 1 个红球和 1 个白球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是多少?
箱子里有 1 个红球和 2 个白球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是多少?
第叁章节
新知探究
新知探究
一个不透明袋中装有 2 个红球和 3 个白球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是多少?
摸出的球不是红球就是白球,所以摸到
红球和白球的可能性相同,P(红球) = .
与摸球相关的等可能事件的概率
你觉得小明说得对吗?
1
小明
从盒中任意摸出一个球,
如果将每一个球都编上号码,
摸出红球可能出现两种等可能的结果:摸出 1 号球或 2 号球.
共有 5 种等可能的结果:1 号球,2 号球,3 号球,4 号球,5 号球.
P (摸到红球) =
1
2
3
4
5
你认为谁说的有道理
小颖
归纳总结
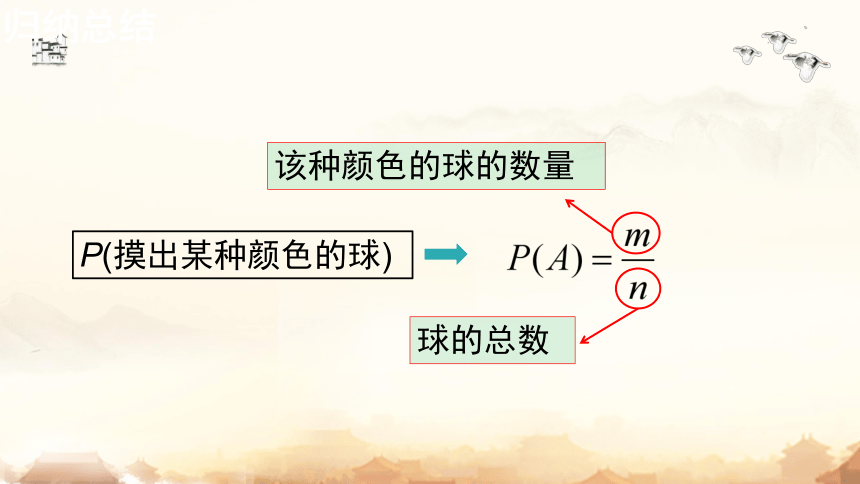
P(摸出某种颜色的球)
该种颜色的球的数量
球的总数
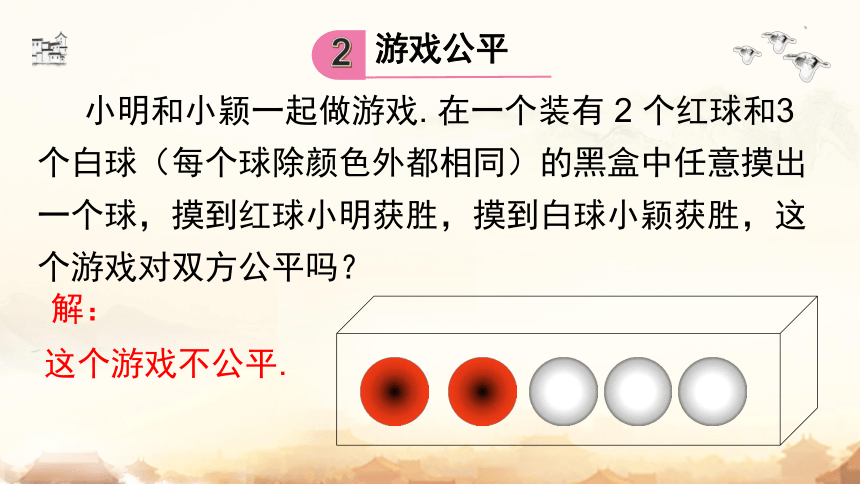
小明和小颖一起做游戏. 在一个装有 2 个红球和3 个白球(每个球除颜色外都相同)的黑盒中任意摸出一个球,摸到红球小明获胜,摸到白球小颖获胜,这个游戏对双方公平吗?
解:
这个游戏不公平.
2
游戏公平
摸出白球可能出现三种等可能的结果:
摸出 3 号球或 4 号球或 5 号球.
因为 所以这个游戏对双方不公平.
理由如下:将小球编号 如图:
小明胜:P (摸到红球) =
小颖胜:P(摸到白球) =
1
2
3
4
5
在一个双人游戏中,你怎样理解游戏对双方
是否公平?
思考
双方赢的可能性相等就公平,否则就不公平.
例1 在一个不透明的袋中有 6 个除颜色外其他都相
同的小球,其中 3 个红球,2 个黄球,1 个白球.
(1) 乐乐从中任意摸出一个小球,摸到的是白球的概率是多少?
解:摸出的求一共有6种情况,
摸出白球只有1种情况
所以 P (摸出白球)=
典例精析
解:该游戏对双方是公平的.理由如下:由题意
可知 P(乐乐获胜)= P(亮亮获胜)=
所以他们获胜的概率相等,即游戏是公平的.
方法总结:判断游戏是否公平,关键是看双方在游戏中所关注的事件发生的概率是否相同.
(2) 乐乐和亮亮商定一个游戏,规则如下:乐乐从中
任意摸出一个小球,摸到红球则乐乐胜,否则亮亮
胜,问该游戏对双方是否公平?为什么?
思考:选取 4 个除颜色外完全相同的球设计一个摸球游戏.
(1) 使得摸到红球的概率是 ,摸到白球的概率也是 .
3
设计简单概率模型
在一个不透明的袋中有 4 个除颜色外其他都相同的小球,其中 2 个红球,2 个白球. 搅匀后,从中任意摸一个球,则摸到红球的概率是,摸到白球的概率也是 .
(2) 使得摸到红球的概率是 ,摸到白球和黄球的概率都是 .
在一个不透明的袋中有 4 个除颜色外其他都相同
的小球,其中 2 个红球,1个白球,1个黄球. 搅匀后,从中任意摸一个球,则摸到红球的概率是 ,摸到白球和黄球的概率都是 .
你能选取 8 个除颜色外完全相同的球分别设计满足如上条件的游戏吗
你能选取 7 个除颜色外完全相同的球分别设计满足如上条件的游戏吗
答:不能,7÷2=3.5,球都是整数个.
答:(1) 4 个红球、4 个白球;
(2) 4个红球、2 个白球、2 个黄球.
合作探究
第肆章节
随堂练习
随堂练习
1.一个不透明的袋子里装有3个绿球、3个黑球和6个红球,它们除颜色外其余均相同.从袋子中任意摸出一个球为绿球的概率为 .
2.围棋起源于中国,棋子分黑白两色.一个不透明的盒子中装有黑色棋子和白色棋子共12个,每个棋子除颜色外其他都相同,任意摸出一个棋子,摸到黑色棋子的概率是,则盒子中黑色棋子有 个.
3
3.联欢会上,小明按照3个红气球,2个黄气球,1个绿气球的顺序把气球串起来装饰教室.第16个气球是 气球,这16个气球中出现黄气球的概率是 .
黄
4.掷一枚质地均匀的骰子,观察向上一面的点数,求下列事件发生的概率:
(1)向上一面的点数为2;
(2)向上一面的点数为奇数;
(3)向上一面的点数大于1且小于6.
5.一个口袋装有a个红球,10个黄球,b个白球,每个球除颜色外其他都相同.如果任意摸出一个球,摸到黄球的概率与不是黄球的概率相同,那么a与b的关系是 .
a+b=10
6.一个口袋装有红、黄、绿三种颜色的球若干个,每个球只有颜色不同,其他都相同.现从口袋中任意摸出一个球,摸到红球的概率为,摸到黄球的概率为.已知绿球有3个,问口袋中有红球、黄球各多少个?
解:摸到绿球的概率为1-,则口袋中三种球共有3÷=18(个).
所以口袋中有红球18×=6(个),口袋中有黄球18×=9(个).
7.在一个不透明的袋子中装有3个红球和5个黄球,每个球除颜色外其余都相同,从中任意摸出一个球.
(1)摸到红球的概率是 ;
(2)请你通过改变袋子中某一种颜色球的数量,设计一种方案,使“摸到红球”和“摸到黄球”的可能性大小相同.
解:(2)∵要使得“摸出红球”和“摸出黄球”的可能性大小相同,
∴使得两种球的数量相同,
∴放入两个红球即可.(合理即可)
8.小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏:小明任意抽取一张牌(不放回),小颖从剩余的牌中任取一张,谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关).然后两人把摸到的牌都放回,重新开始游戏.
(1)现小明已摸到的牌面为4,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?
(1)小明要获胜,则小颖摸到的牌面的数字必须是2,3,四种花色共8张牌,而小明摸完后,剩余51张牌,则小明获胜的概率为;小颖要获胜,则摸的牌的数字必须是5,6,7,8,9,10,J,Q,K,A,共40张牌,则小颖获胜的概率为.
(2)若小明已摸到的牌面为2,情况又如何?
(2)小明摸到的牌面为2,是最小的数字,则小明不可能获胜,获胜概率为0;而小颖要获胜,摸到的牌面的数字必须是3,4,5,6,7,8,9,10,J,Q,K,A,共48张牌,则小颖获胜的概率P=.
第伍章节
课堂小结
课堂小结
若游戏双方获胜的概率相等,则游戏对双方公平;
否则,游戏对双方不公平
游戏的公平性
等可能事件
的概率
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第三章 概率初步
汇报人:孙老师
汇报班级:X级X班
3.3 第2课时 与摸球相关的概率
3.3 等可能事件的概率
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.初步理解游戏的公平性,会设计简单的公平的游戏.
2.灵活应用概率的计算方法解决各种类型的实际问题.
第贰章节
新课导入
新课导入
箱子里有 1 个红球和 1 个白球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是多少?
箱子里有 1 个红球和 2 个白球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是多少?
第叁章节
新知探究
新知探究
一个不透明袋中装有 2 个红球和 3 个白球,每个球除颜色外都相同,任意摸出一个球,摸到红球的概率是多少?
摸出的球不是红球就是白球,所以摸到
红球和白球的可能性相同,P(红球) = .
与摸球相关的等可能事件的概率
你觉得小明说得对吗?
1
小明
从盒中任意摸出一个球,
如果将每一个球都编上号码,
摸出红球可能出现两种等可能的结果:摸出 1 号球或 2 号球.
共有 5 种等可能的结果:1 号球,2 号球,3 号球,4 号球,5 号球.
P (摸到红球) =
1
2
3
4
5
你认为谁说的有道理
小颖
归纳总结
P(摸出某种颜色的球)
该种颜色的球的数量
球的总数
小明和小颖一起做游戏. 在一个装有 2 个红球和3 个白球(每个球除颜色外都相同)的黑盒中任意摸出一个球,摸到红球小明获胜,摸到白球小颖获胜,这个游戏对双方公平吗?
解:
这个游戏不公平.
2
游戏公平
摸出白球可能出现三种等可能的结果:
摸出 3 号球或 4 号球或 5 号球.
因为 所以这个游戏对双方不公平.
理由如下:将小球编号 如图:
小明胜:P (摸到红球) =
小颖胜:P(摸到白球) =
1
2
3
4
5
在一个双人游戏中,你怎样理解游戏对双方
是否公平?
思考
双方赢的可能性相等就公平,否则就不公平.
例1 在一个不透明的袋中有 6 个除颜色外其他都相
同的小球,其中 3 个红球,2 个黄球,1 个白球.
(1) 乐乐从中任意摸出一个小球,摸到的是白球的概率是多少?
解:摸出的求一共有6种情况,
摸出白球只有1种情况
所以 P (摸出白球)=
典例精析
解:该游戏对双方是公平的.理由如下:由题意
可知 P(乐乐获胜)= P(亮亮获胜)=
所以他们获胜的概率相等,即游戏是公平的.
方法总结:判断游戏是否公平,关键是看双方在游戏中所关注的事件发生的概率是否相同.
(2) 乐乐和亮亮商定一个游戏,规则如下:乐乐从中
任意摸出一个小球,摸到红球则乐乐胜,否则亮亮
胜,问该游戏对双方是否公平?为什么?
思考:选取 4 个除颜色外完全相同的球设计一个摸球游戏.
(1) 使得摸到红球的概率是 ,摸到白球的概率也是 .
3
设计简单概率模型
在一个不透明的袋中有 4 个除颜色外其他都相同的小球,其中 2 个红球,2 个白球. 搅匀后,从中任意摸一个球,则摸到红球的概率是,摸到白球的概率也是 .
(2) 使得摸到红球的概率是 ,摸到白球和黄球的概率都是 .
在一个不透明的袋中有 4 个除颜色外其他都相同
的小球,其中 2 个红球,1个白球,1个黄球. 搅匀后,从中任意摸一个球,则摸到红球的概率是 ,摸到白球和黄球的概率都是 .
你能选取 8 个除颜色外完全相同的球分别设计满足如上条件的游戏吗
你能选取 7 个除颜色外完全相同的球分别设计满足如上条件的游戏吗
答:不能,7÷2=3.5,球都是整数个.
答:(1) 4 个红球、4 个白球;
(2) 4个红球、2 个白球、2 个黄球.
合作探究
第肆章节
随堂练习
随堂练习
1.一个不透明的袋子里装有3个绿球、3个黑球和6个红球,它们除颜色外其余均相同.从袋子中任意摸出一个球为绿球的概率为 .
2.围棋起源于中国,棋子分黑白两色.一个不透明的盒子中装有黑色棋子和白色棋子共12个,每个棋子除颜色外其他都相同,任意摸出一个棋子,摸到黑色棋子的概率是,则盒子中黑色棋子有 个.
3
3.联欢会上,小明按照3个红气球,2个黄气球,1个绿气球的顺序把气球串起来装饰教室.第16个气球是 气球,这16个气球中出现黄气球的概率是 .
黄
4.掷一枚质地均匀的骰子,观察向上一面的点数,求下列事件发生的概率:
(1)向上一面的点数为2;
(2)向上一面的点数为奇数;
(3)向上一面的点数大于1且小于6.
5.一个口袋装有a个红球,10个黄球,b个白球,每个球除颜色外其他都相同.如果任意摸出一个球,摸到黄球的概率与不是黄球的概率相同,那么a与b的关系是 .
a+b=10
6.一个口袋装有红、黄、绿三种颜色的球若干个,每个球只有颜色不同,其他都相同.现从口袋中任意摸出一个球,摸到红球的概率为,摸到黄球的概率为.已知绿球有3个,问口袋中有红球、黄球各多少个?
解:摸到绿球的概率为1-,则口袋中三种球共有3÷=18(个).
所以口袋中有红球18×=6(个),口袋中有黄球18×=9(个).
7.在一个不透明的袋子中装有3个红球和5个黄球,每个球除颜色外其余都相同,从中任意摸出一个球.
(1)摸到红球的概率是 ;
(2)请你通过改变袋子中某一种颜色球的数量,设计一种方案,使“摸到红球”和“摸到黄球”的可能性大小相同.
解:(2)∵要使得“摸出红球”和“摸出黄球”的可能性大小相同,
∴使得两种球的数量相同,
∴放入两个红球即可.(合理即可)
8.小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏:小明任意抽取一张牌(不放回),小颖从剩余的牌中任取一张,谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关).然后两人把摸到的牌都放回,重新开始游戏.
(1)现小明已摸到的牌面为4,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?
(1)小明要获胜,则小颖摸到的牌面的数字必须是2,3,四种花色共8张牌,而小明摸完后,剩余51张牌,则小明获胜的概率为;小颖要获胜,则摸的牌的数字必须是5,6,7,8,9,10,J,Q,K,A,共40张牌,则小颖获胜的概率为.
(2)若小明已摸到的牌面为2,情况又如何?
(2)小明摸到的牌面为2,是最小的数字,则小明不可能获胜,获胜概率为0;而小颖要获胜,摸到的牌面的数字必须是3,4,5,6,7,8,9,10,J,Q,K,A,共48张牌,则小颖获胜的概率P=.
第伍章节
课堂小结
课堂小结
若游戏双方获胜的概率相等,则游戏对双方公平;
否则,游戏对双方不公平
游戏的公平性
等可能事件
的概率
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
