湘教版七年级下数学《相交线与平行线》专题复习试卷含答案
文档属性
| 名称 | 湘教版七年级下数学《相交线与平行线》专题复习试卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 81.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-16 19:04:19 | ||
图片预览

文档简介
湘教版七年级数学(下)专题复习卷(三)空间与图形
一、选择题(30分)
1、∠1和∠2是直线AB、CD被直线EF所截得到的同位角,那么∠1和∠2的大小关系是(
)
A.∠1=∠2;
B.∠1>∠2;
C.∠1<∠2;
D.无法确定;
2、在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是(
)
3、一个人从A点出发向北偏东60°方向走到B点,再从B点出发向南偏西15°方向走到C点,那么∠ABC等于(
)
A.75°;
B.105°;
C.45°;
D.135°;
4、下列说法中,正确的是(
)
A.过点P画线段AB的垂线;
B.P是直线AB外一点,Q是直线AB上一点,连接PQ,使PQ⊥AB;
C.过一点有且只有一条直线垂直于已知直线;
D.过一点有且只有一条直线平行于已知直线;
5、下列语句:①三条直线只有两个交点,则其中两条直线互相平行;
②如果两条平行线被第三条直线所截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行;其中(
)
A.①、②是正确的;
B.②、③是正确的;
C.①、③是正确的;
D.以上结论都错;
6、如图所示,在△ABC中,∠C=90°,AC=BC=5,
现将△ABC沿BC方向平移到△DFE的位置,若平移
距离为2,艾尔图中阴影部分面积是(
)
A.9;
B.4.5;
C.8;
D.5;
7、下列说法正确的是(
)
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小;
B.平移和旋转的共同点是改变图形的位置;
C.图形可以向某一方向平移一定距离,也可以向某一方向旋转一定距离;
D.由平移得到的图形也一定可由旋转得到;
8、下列图形中,对称轴有6条的图形是(
)
9、将强一个直角三角板和一把刻度尺如图放置,如果∠α=43°,则∠β是(
)
A.43°;
B.47°;
C.30°;
D.60°;
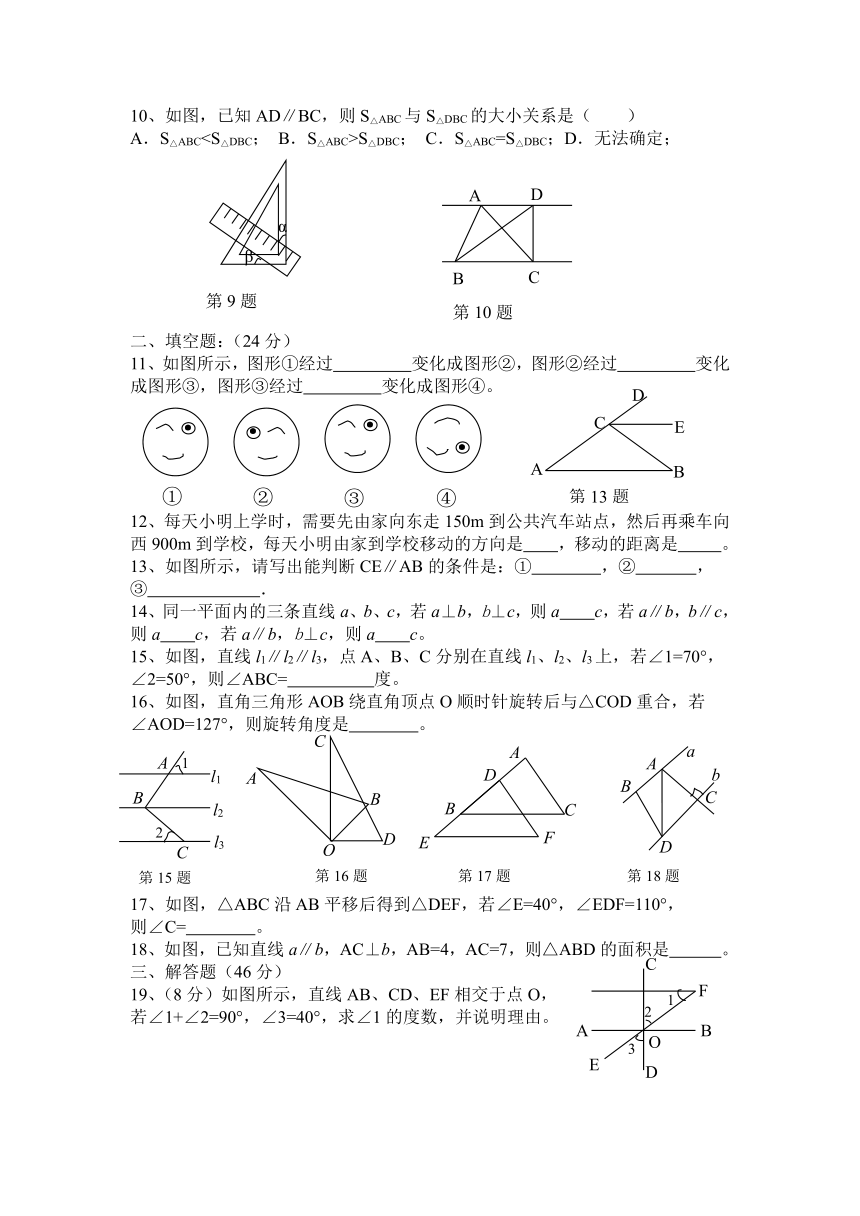
10、如图,已知AD∥BC,则S△ABC与S△DBC的大小关系是(
)
A.S△ABCB.S△ABC>S△DBC;
C.S△ABC=S△DBC;D.无法确定;
二、填空题:(24分)
11、如图所示,图形①经过
变化成图形②,图形②经过
变化成图形③,图形③经过
变化成图形④。
12、每天小明上学时,需要先由家向东走150m到公共汽车站点,然后再乘车向西900m到学校,每天小明由家到学校移动的方向是
,移动的距离是
。
13、如图所示,请写出能判断CE∥AB的条件是:①
,②
,
③
.
14、同一平面内的三条直线a、b、c,若a⊥b,b⊥c,则a
c,若a∥b,b∥c,则a
c,若a∥b,b⊥c,则a
c。
15、如图,直线l1∥l2∥l3,点A、B、C分别在直线l1、l2、l3上,若∠1=70°,
∠2=50°,则∠ABC=
度。
16、如图,直角三角形AOB绕直角顶点O顺时针旋转后与△COD重合,若
∠AOD=127°,则旋转角度是
。
17、如图,△ABC沿AB平移后得到△DEF,若∠E=40°,∠EDF=110°,
则∠C=
。
18、如图,已知直线a∥b,AC⊥b,AB=4,AC=7,则△ABD的面积是
。
三、解答题(46分)
19、(8分)如图所示,直线AB、CD、EF相交于点O,
若∠1+∠2=90°,∠3=40°,求∠1的度数,并说明理由。
20、(8分)已知,如图,ACE,AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,
求证:AD∥BE
证明:∵AB∥CD,(已知)
∴∠4=
。(
)
又∵∠3=∠4,(已知)
∴∠3=
。(
)
∵∠1=∠2,(已知)
∴∠1+∠CAF=∠2+∠CAF,(
)
即:
=∠CAD。
∴∠3=
。(
等量代换)
∴AD∥BE.(
)
21、(10分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,
∠1=∠2,求证:CD⊥AB;
22、(10分)如图,长方形长为8cm,宽为4cm,
求阴影部分面积。
23、(10分)如图,在正方形网格中,△ABC的三个顶点A、B、C均在格点上,将△ABC向右平移5个格,得到△A1B1C1,再将△A1B1C1绕B1按顺时针方向旋转90°,得到△A2B2C2,请在网格中画出△A1B1C1和△A2B2C2(不要求写画法)
参考答案:一、1、D;2、B;3、C;4、C;5、A;
6、C;7、B;8、D;9、B;10、C;
二、11、轴对称,平移,旋转;12、向西,750m;
13、∠DCE=∠A,∠ECB=∠B,∠A+∠ACE=180°;
14、平行,平行,垂直;15、120;16、37°;17、30°;18、14;
三、19、∵∠2=∠3,∠3=40°,∴∠2=40°,又∵∠1+∠2=90°,
∴∠1=50°;
20、∠BAE,两直线平行,同位角相等;∠BAE,等量代换;
等式性质;∠BAE,∠CAD,内错角相等,两直线平行;
21、证明:∵DG⊥BC,AC⊥BC,∴DG∥AC,∠2=∠3,
又∵∠1=∠2,∴∠1=∠3,∴EF∥DC,∴∠AEF=∠ADC,
又∵EF⊥AB,∴∠AEF=90°,∴∠ADC=90°,∴CD⊥AB.
22、由旋转、轴对称变换知,阴影部分面积=长方形面积=8(cm2)
23、作法略,作图如下:
A
B
C
A
B
C
D
A
B
C
D
E
F
G
A
B
C
D
α
β
A
B
C
D
第9题
第10题
A
B
C
D
E
第13题
·
·
·
·
①
②
③
④
l1
l2
l3
A
B
C
1
2
第15题
A
B
C
D
O
第18题
第16题
A
B
C
D
E
F
第17题
A
B
C
D
b
a
O
A
B
C
D
E
F
1
2
3
B
A
C
D
E
F
1
2
3
4
A
B
C
D
E
F
G
1
2
3
一、选择题(30分)
1、∠1和∠2是直线AB、CD被直线EF所截得到的同位角,那么∠1和∠2的大小关系是(
)
A.∠1=∠2;
B.∠1>∠2;
C.∠1<∠2;
D.无法确定;
2、在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是(
)
3、一个人从A点出发向北偏东60°方向走到B点,再从B点出发向南偏西15°方向走到C点,那么∠ABC等于(
)
A.75°;
B.105°;
C.45°;
D.135°;
4、下列说法中,正确的是(
)
A.过点P画线段AB的垂线;
B.P是直线AB外一点,Q是直线AB上一点,连接PQ,使PQ⊥AB;
C.过一点有且只有一条直线垂直于已知直线;
D.过一点有且只有一条直线平行于已知直线;
5、下列语句:①三条直线只有两个交点,则其中两条直线互相平行;
②如果两条平行线被第三条直线所截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行;其中(
)
A.①、②是正确的;
B.②、③是正确的;
C.①、③是正确的;
D.以上结论都错;
6、如图所示,在△ABC中,∠C=90°,AC=BC=5,
现将△ABC沿BC方向平移到△DFE的位置,若平移
距离为2,艾尔图中阴影部分面积是(
)
A.9;
B.4.5;
C.8;
D.5;
7、下列说法正确的是(
)
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小;
B.平移和旋转的共同点是改变图形的位置;
C.图形可以向某一方向平移一定距离,也可以向某一方向旋转一定距离;
D.由平移得到的图形也一定可由旋转得到;
8、下列图形中,对称轴有6条的图形是(
)
9、将强一个直角三角板和一把刻度尺如图放置,如果∠α=43°,则∠β是(
)
A.43°;
B.47°;
C.30°;
D.60°;
10、如图,已知AD∥BC,则S△ABC与S△DBC的大小关系是(
)
A.S△ABC
C.S△ABC=S△DBC;D.无法确定;
二、填空题:(24分)
11、如图所示,图形①经过
变化成图形②,图形②经过
变化成图形③,图形③经过
变化成图形④。
12、每天小明上学时,需要先由家向东走150m到公共汽车站点,然后再乘车向西900m到学校,每天小明由家到学校移动的方向是
,移动的距离是
。
13、如图所示,请写出能判断CE∥AB的条件是:①
,②
,
③
.
14、同一平面内的三条直线a、b、c,若a⊥b,b⊥c,则a
c,若a∥b,b∥c,则a
c,若a∥b,b⊥c,则a
c。
15、如图,直线l1∥l2∥l3,点A、B、C分别在直线l1、l2、l3上,若∠1=70°,
∠2=50°,则∠ABC=
度。
16、如图,直角三角形AOB绕直角顶点O顺时针旋转后与△COD重合,若
∠AOD=127°,则旋转角度是
。
17、如图,△ABC沿AB平移后得到△DEF,若∠E=40°,∠EDF=110°,
则∠C=
。
18、如图,已知直线a∥b,AC⊥b,AB=4,AC=7,则△ABD的面积是
。
三、解答题(46分)
19、(8分)如图所示,直线AB、CD、EF相交于点O,
若∠1+∠2=90°,∠3=40°,求∠1的度数,并说明理由。
20、(8分)已知,如图,ACE,AFE是直线,AB∥CD,∠1=∠2,∠3=∠4,
求证:AD∥BE
证明:∵AB∥CD,(已知)
∴∠4=
。(
)
又∵∠3=∠4,(已知)
∴∠3=
。(
)
∵∠1=∠2,(已知)
∴∠1+∠CAF=∠2+∠CAF,(
)
即:
=∠CAD。
∴∠3=
。(
等量代换)
∴AD∥BE.(
)
21、(10分)如图,已知DG⊥BC,AC⊥BC,EF⊥AB,
∠1=∠2,求证:CD⊥AB;
22、(10分)如图,长方形长为8cm,宽为4cm,
求阴影部分面积。
23、(10分)如图,在正方形网格中,△ABC的三个顶点A、B、C均在格点上,将△ABC向右平移5个格,得到△A1B1C1,再将△A1B1C1绕B1按顺时针方向旋转90°,得到△A2B2C2,请在网格中画出△A1B1C1和△A2B2C2(不要求写画法)
参考答案:一、1、D;2、B;3、C;4、C;5、A;
6、C;7、B;8、D;9、B;10、C;
二、11、轴对称,平移,旋转;12、向西,750m;
13、∠DCE=∠A,∠ECB=∠B,∠A+∠ACE=180°;
14、平行,平行,垂直;15、120;16、37°;17、30°;18、14;
三、19、∵∠2=∠3,∠3=40°,∴∠2=40°,又∵∠1+∠2=90°,
∴∠1=50°;
20、∠BAE,两直线平行,同位角相等;∠BAE,等量代换;
等式性质;∠BAE,∠CAD,内错角相等,两直线平行;
21、证明:∵DG⊥BC,AC⊥BC,∴DG∥AC,∠2=∠3,
又∵∠1=∠2,∴∠1=∠3,∴EF∥DC,∴∠AEF=∠ADC,
又∵EF⊥AB,∴∠AEF=90°,∴∠ADC=90°,∴CD⊥AB.
22、由旋转、轴对称变换知,阴影部分面积=长方形面积=8(cm2)
23、作法略,作图如下:
A
B
C
A
B
C
D
A
B
C
D
E
F
G
A
B
C
D
α
β
A
B
C
D
第9题
第10题
A
B
C
D
E
第13题
·
·
·
·
①
②
③
④
l1
l2
l3
A
B
C
1
2
第15题
A
B
C
D
O
第18题
第16题
A
B
C
D
E
F
第17题
A
B
C
D
b
a
O
A
B
C
D
E
F
1
2
3
B
A
C
D
E
F
1
2
3
4
A
B
C
D
E
F
G
1
2
3
