2025年中考数学二轮复习基础综合卷(九)(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习基础综合卷(九)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 135.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 12:38:02 | ||
图片预览


文档简介
基础综合卷(九)
第一部分 选择题(共30分)
一、选择题(本题共10小题,每小题3分,共30分、在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列各数中,比-1小的数是 ( )
A.1 B.0 C.-0、5 D.-1、5
2.新新考向·情境命题搭载“神舟十六”号载人飞船的长征二号“F遥”十六运载火箭于2023年5月30日成功发射升空、景海鹏、朱杨柱、桂海潮3名航天员开启“太空出差”之旅、展现了中国航天科技的新高度.下列图标中、其文字上方的图案是中心对称图形的是 ( )
3.不等式17-3x>2的解为 ( )
A. x<-5 B. x>5 C. x<5 D. x>-5
4.若一个正多边形的一个内角为144°,则这个图形为 ( )
A.正十一边形 B.正十边形 C.正九边形 D.正八边形
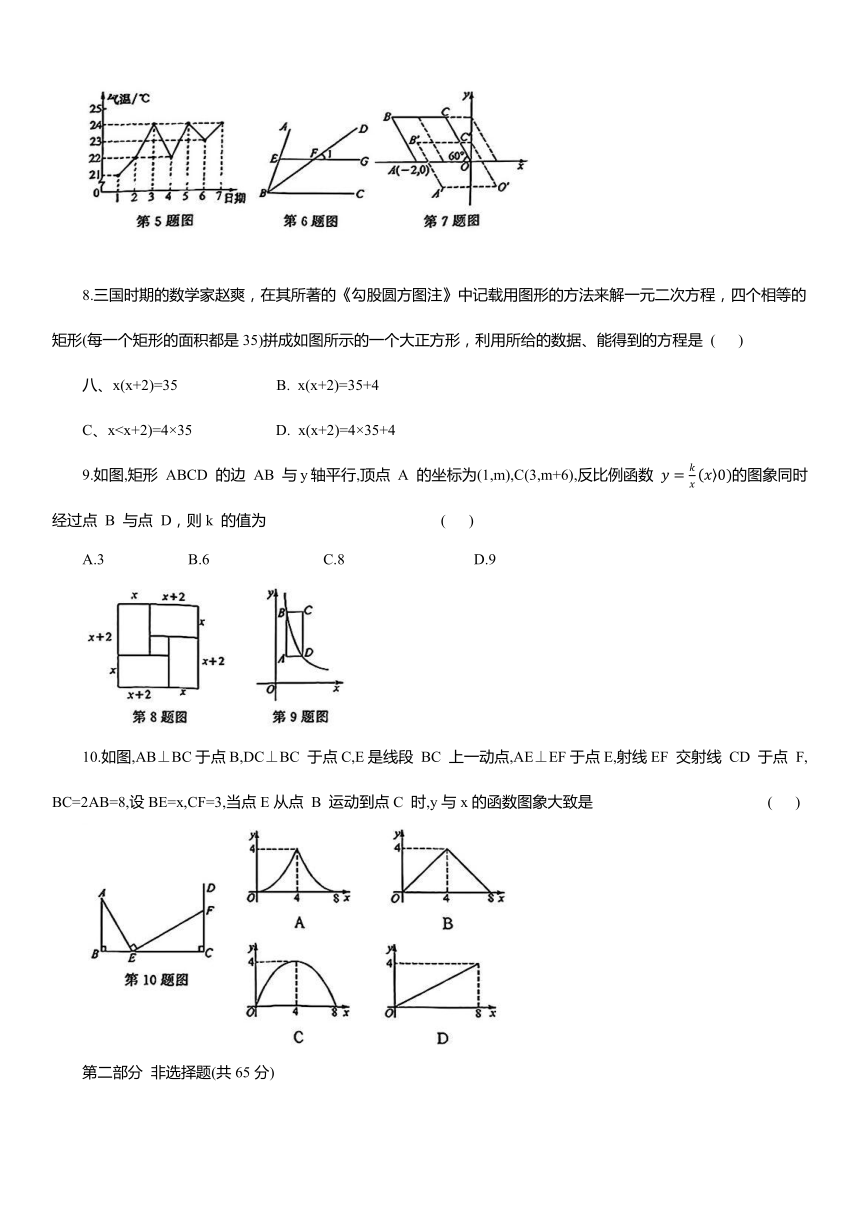
5.某地区连续7天的最高气温统计如图所示,则该地区这7天最高气温的众数为 ( )
A.22℃ B.23℃ C.23.5℃ D.24℃
6.如图,BD平分∠ABC,E为BA 上一点,EG∥BC交BD 于点F.若∠1=35°,则∠AEF 的度数为 ( )
A.70° B.35° C.25° D.17.5°
7.如图,在平面直角坐标系中,菱形OABC 的顶点 A 的坐标为(--2,0),∠AOC=60°.将菱形OABC沿x 轴向右平移1个单位长度,再沿 y 轴向下平移1 个单位长度,得到菱形O'A'B'C',则点 B'的坐标为 ( )
B.(-2,1)
8.三国时期的数学家赵爽,在其所著的《勾股圆方图注》中记载用图形的方法来解一元二次方程,四个相等的矩形(每一个矩形的面积都是35)拼成如图所示的一个大正方形,利用所给的数据、能得到的方程是 ( )
八、x(x+2)=35 B. x(x+2)=35+4
C、x9.如图,矩形 ABCD 的边 AB 与y轴平行,顶点 A 的坐标为(1,m),C(3,m+6),反比例函数 的图象同时经过点 B 与点 D,则k 的值为 ( )
A.3 B.6 C.8 D.9
10.如图,AB⊥BC于点B,DC⊥BC 于点C,E是线段 BC 上一动点,AE⊥EF于点E,射线EF 交射线 CD 于点 F,BC=2AB=8,设BE=x,CF=3,当点E从点 B 运动到点C 时,y与x的函数图象大致是 ( )
第二部分 非选择题(共65分)
二、填空题(本题共5小题,每小题3分,共15分)
11.分解因式: ax-ay= .
12.新新考向·图形操作如图,数轴上点A,B分别对应数1,2,过点 B 作 PQ⊥AB,以点B 为圆心,AB 长为半径画弧,交 PQ于点C,以点A 为圆心,AC 长为半径画弧,交数轴于点M,则点M 对应的数是 .
13.如图,在 中, 将 绕点A 逆时针旋转2α,得到 连接 并延长交AB 于点D,当 时,则 的长是 .
14.新新考向·传统文化我国古代数学经典著作《九章算术》中记载:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之.问几何步及之.”如图是善行者与不善行者的行走路程s(单位:步)关于善行者的行走时间t的函数图象,则两图象交点 P 的纵坐标是 .
15. 如图,在矩形ABCD 中, ,E 是边 BC 上一动点,F是对角线 BD 上一动点,且. 则 的最小值为 .
三、解答题(本题共6小题,共50分、解答应写出文字说明、演算步骤或推理过程)
16.(每题5分,共10分)
(1)计算:
(2)解方程:
17.(本小题8分)
“电梯安全系万家、正确使用靠大家”.某小区的货运电梯限重标志显示,载重总质量禁止超过1000 kg、现需用此货运电梯装运—批设备,每套设备由2个A部件和1个B部件组成、且体积较小.已知1 个 A 部件和2 个 B 部件总质量为150kg.2个A部件和1个B部件的质量相等.
(1)分别求1个A部件和1个B部件的质量;
(2)由于设备需要成套装运、且每次装运都需要两名工人装卸,已知两名装卸工人的质量分别为75 kg和65 kg、货运电梯一次最多可装运多少套设备
18.(本小题8分)
某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取的学生体重情况绘制了如下不完整的频数分布表和扇形统计图.
组别 体重/ kg 学生人数
A 10
B n
C 40
D 20
E 10
请根据图表信息回答下列问题:
(1)填空:( ③在扇形统计图中,C组所在扇形的圆心角度数为 °.
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40kg),求被调查学生的平均体重;
(3)若该校七年级有1000名学生,请估计七年级学生体重低于47.5kg 的人数.
19.(本小题8分)
利川市地处湖北省西南边陲,西靠蜀渝,东接恩施,南邻潇湘,北依三峡,拥有丰富的旅游资源,某景区夏季投放一款纪念品进行销售、每件成本为20元,规定销售单价不低于成本且不高于50元、销售一段时间后,经过调研发现,每天的销售数量y(单位:件)与销售单价x(单位:元/件)满足一次函数关系,部分数据如下表所示:
销售单价x/(元/件) 25 30 35
每天销售数量y/件 150 140 130
(1)求y关于x的函数解析式;
(2)若每天销售所得利润为2400元,则销售单价应定为多少元
(3)当销售单价为多少元时,每天获利最大 最大利润为多少元
20.(本小题8分)
利用无人机测量建筑物两旁B,C两点之间的距离.如图,某同学站在B 处指挥D 处的无人机,飞行高度是41.6m,测得C处的俯角为 若该同学的身高 (点A,B,C,D 在同一平面内)
(1)求该同学抬头看无人机仰角的正弦值;、
(2)求B,C两点之间的距离.(结果精确到1m .参考数据:
21.(本小题8分)
如图,在 中, BD 平分 点O在AB上,以点O为圆心,OB 为半径的圆经过点 D,交BC 于点 E.
(1)求证:AC是⊙O的切线;
(2)若 求图中阴影部分的面积.
第一部分 选择题(共30分)
一、选择题(本题共10小题,每小题3分,共30分、在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列各数中,比-1小的数是 ( )
A.1 B.0 C.-0、5 D.-1、5
2.新新考向·情境命题搭载“神舟十六”号载人飞船的长征二号“F遥”十六运载火箭于2023年5月30日成功发射升空、景海鹏、朱杨柱、桂海潮3名航天员开启“太空出差”之旅、展现了中国航天科技的新高度.下列图标中、其文字上方的图案是中心对称图形的是 ( )
3.不等式17-3x>2的解为 ( )
A. x<-5 B. x>5 C. x<5 D. x>-5
4.若一个正多边形的一个内角为144°,则这个图形为 ( )
A.正十一边形 B.正十边形 C.正九边形 D.正八边形
5.某地区连续7天的最高气温统计如图所示,则该地区这7天最高气温的众数为 ( )
A.22℃ B.23℃ C.23.5℃ D.24℃
6.如图,BD平分∠ABC,E为BA 上一点,EG∥BC交BD 于点F.若∠1=35°,则∠AEF 的度数为 ( )
A.70° B.35° C.25° D.17.5°
7.如图,在平面直角坐标系中,菱形OABC 的顶点 A 的坐标为(--2,0),∠AOC=60°.将菱形OABC沿x 轴向右平移1个单位长度,再沿 y 轴向下平移1 个单位长度,得到菱形O'A'B'C',则点 B'的坐标为 ( )
B.(-2,1)
8.三国时期的数学家赵爽,在其所著的《勾股圆方图注》中记载用图形的方法来解一元二次方程,四个相等的矩形(每一个矩形的面积都是35)拼成如图所示的一个大正方形,利用所给的数据、能得到的方程是 ( )
八、x(x+2)=35 B. x(x+2)=35+4
C、x
A.3 B.6 C.8 D.9
10.如图,AB⊥BC于点B,DC⊥BC 于点C,E是线段 BC 上一动点,AE⊥EF于点E,射线EF 交射线 CD 于点 F,BC=2AB=8,设BE=x,CF=3,当点E从点 B 运动到点C 时,y与x的函数图象大致是 ( )
第二部分 非选择题(共65分)
二、填空题(本题共5小题,每小题3分,共15分)
11.分解因式: ax-ay= .
12.新新考向·图形操作如图,数轴上点A,B分别对应数1,2,过点 B 作 PQ⊥AB,以点B 为圆心,AB 长为半径画弧,交 PQ于点C,以点A 为圆心,AC 长为半径画弧,交数轴于点M,则点M 对应的数是 .
13.如图,在 中, 将 绕点A 逆时针旋转2α,得到 连接 并延长交AB 于点D,当 时,则 的长是 .
14.新新考向·传统文化我国古代数学经典著作《九章算术》中记载:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之.问几何步及之.”如图是善行者与不善行者的行走路程s(单位:步)关于善行者的行走时间t的函数图象,则两图象交点 P 的纵坐标是 .
15. 如图,在矩形ABCD 中, ,E 是边 BC 上一动点,F是对角线 BD 上一动点,且. 则 的最小值为 .
三、解答题(本题共6小题,共50分、解答应写出文字说明、演算步骤或推理过程)
16.(每题5分,共10分)
(1)计算:
(2)解方程:
17.(本小题8分)
“电梯安全系万家、正确使用靠大家”.某小区的货运电梯限重标志显示,载重总质量禁止超过1000 kg、现需用此货运电梯装运—批设备,每套设备由2个A部件和1个B部件组成、且体积较小.已知1 个 A 部件和2 个 B 部件总质量为150kg.2个A部件和1个B部件的质量相等.
(1)分别求1个A部件和1个B部件的质量;
(2)由于设备需要成套装运、且每次装运都需要两名工人装卸,已知两名装卸工人的质量分别为75 kg和65 kg、货运电梯一次最多可装运多少套设备
18.(本小题8分)
某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取的学生体重情况绘制了如下不完整的频数分布表和扇形统计图.
组别 体重/ kg 学生人数
A 10
B n
C 40
D 20
E 10
请根据图表信息回答下列问题:
(1)填空:( ③在扇形统计图中,C组所在扇形的圆心角度数为 °.
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40kg),求被调查学生的平均体重;
(3)若该校七年级有1000名学生,请估计七年级学生体重低于47.5kg 的人数.
19.(本小题8分)
利川市地处湖北省西南边陲,西靠蜀渝,东接恩施,南邻潇湘,北依三峡,拥有丰富的旅游资源,某景区夏季投放一款纪念品进行销售、每件成本为20元,规定销售单价不低于成本且不高于50元、销售一段时间后,经过调研发现,每天的销售数量y(单位:件)与销售单价x(单位:元/件)满足一次函数关系,部分数据如下表所示:
销售单价x/(元/件) 25 30 35
每天销售数量y/件 150 140 130
(1)求y关于x的函数解析式;
(2)若每天销售所得利润为2400元,则销售单价应定为多少元
(3)当销售单价为多少元时,每天获利最大 最大利润为多少元
20.(本小题8分)
利用无人机测量建筑物两旁B,C两点之间的距离.如图,某同学站在B 处指挥D 处的无人机,飞行高度是41.6m,测得C处的俯角为 若该同学的身高 (点A,B,C,D 在同一平面内)
(1)求该同学抬头看无人机仰角的正弦值;、
(2)求B,C两点之间的距离.(结果精确到1m .参考数据:
21.(本小题8分)
如图,在 中, BD 平分 点O在AB上,以点O为圆心,OB 为半径的圆经过点 D,交BC 于点 E.
(1)求证:AC是⊙O的切线;
(2)若 求图中阴影部分的面积.
同课章节目录
