2025年中考数学二轮复习基础综合卷(四)(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习基础综合卷(四)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 137.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 12:39:26 | ||
图片预览




文档简介
基础综合卷(四)
第一部分 选择题(共30分)
一、选择题(本题共10小题,每小题3分,共30分、在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若向东走5m,记作+5m,则向西走5m,可记作 ( )
A.+5m B.---5m C.+10m D.-10m
2.新新考向·传统文化北宋时期的汝窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一,具有极高的历史价值、文化价值、如图,关于它的三视图,下列说法正确的是 ( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
3.下列运算中,结果正确的是 ( )
4.已知方程 的一个根是一1,则另一个根为( )
A.-7 B.-6 C.-2 D.3
5.新新考向·情境命题某市为了方便市民绿色出行,推出某品牌共享单车,如图是其示意图,其中AB,CD 都与地面平行,∠BCD=62°,∠BAC=53°,当AM∥CB 时,∠MAC 的度数为( )
A.62° B.65° C.75° D.115°
6.新新考向·传统文化清代袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”已知 若苔花的花粉直径约为85 000 nm,则85 000 nm用科学记数法表示为( )
7.青少年身体健康问题越来越引起社会的广泛关注.某班50名学生一周体育锻炼时间的统计表如下:
锻炼时间/h 6 7 8 9
学生人数 12 16 17 5
则这些学生一周体育锻炼时间的众数和中位数分别是 ( )
A.8,7 B.17,16.5 C.8,8 D.7.5,8
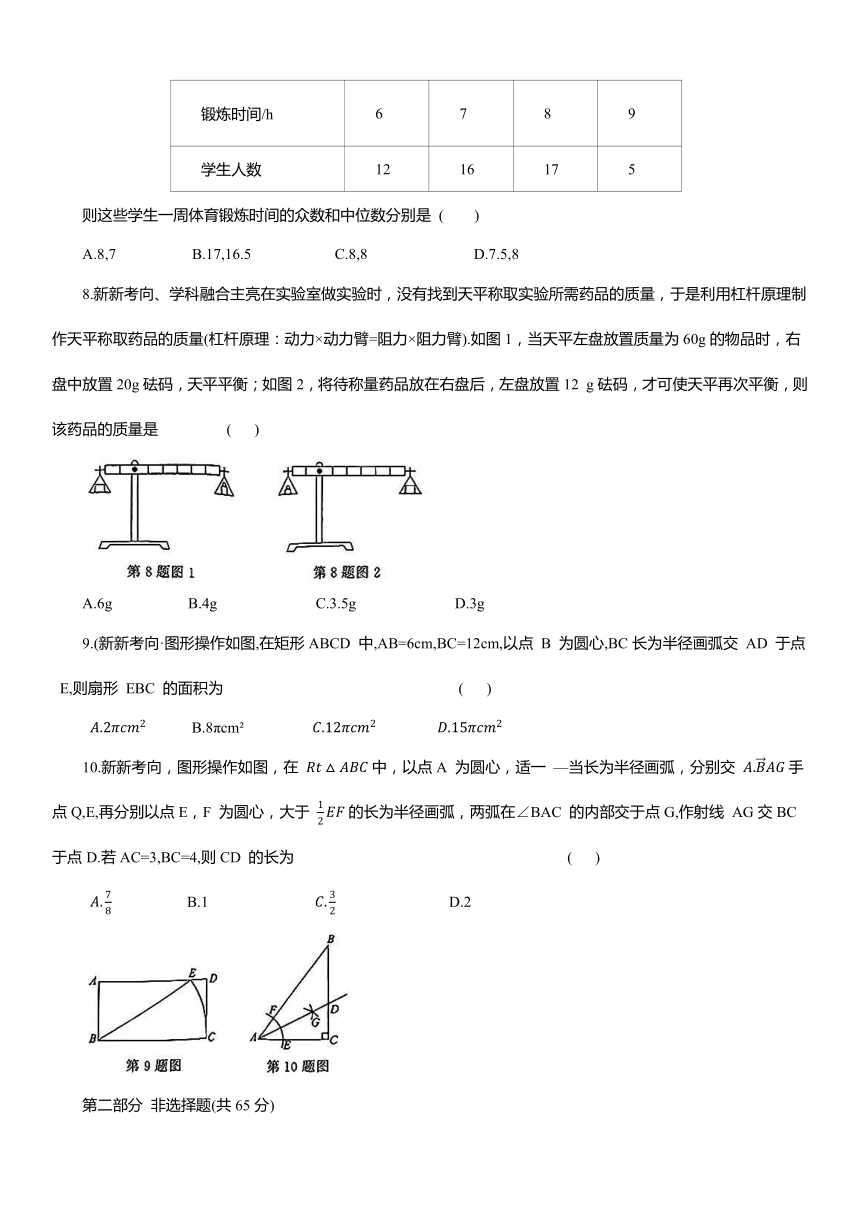
8.新新考向、学科融合主亮在实验室做实验时,没有找到天平称取实验所需药品的质量,于是利用杠杆原理制作天平称取药品的质量(杠杆原理:动力×动力臂=阻力×阻力臂).如图1,当天平左盘放置质量为60g的物品时,右盘中放置20g砝码,天平平衡;如图2,将待称量药品放在右盘后,左盘放置12 g砝码,才可使天平再次平衡,则该药品的质量是 ( )
A.6g B.4g C.3.5g D.3g
9.(新新考向·图形操作如图,在矩形ABCD 中,AB=6cm,BC=12cm,以点 B 为圆心,BC长为半径画弧交 AD 于点 E,则扇形 EBC 的面积为 ( )
B.8πcm
10.新新考向,图形操作如图,在 中,以点A 为圆心,适一 —当长为半径画弧,分别交 手点Q,E,再分别以点E,F 为圆心,大于 的长为半径画弧,两弧在∠BAC 的内部交于点G,作射线 AG交BC于点D.若AC=3,BC=4,则CD 的长为 ( )
B.1 D.2
第二部分 非选择题(共65分)
二、填空题(本题共5小题,每小题3分,共15分)
11.若点 P(m,-1)关于y 轴的对称点是点 则 的值是 .
12.在一个暗箱里放有x个大小相同、质地均匀的白球,为了估计白球的个数,再放入5个除颜色不同外其余均相同的黄球,将球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回暗箱中,通过大量重复试验发现摸到黄球的频率稳定在0.2,则x的值大约是
13.新新考向 学科融合元代数学家朱世杰于1303年编著的《四元玉鉴》中有这样一道题目:“今有绫、罗共三丈,各直钱八百九十六文,只云绫、罗各一尺共直钱一百二十文.问绫、罗尺价各几何.”其大意为:现在有绫布和罗布,布长共3丈(1丈=10尺),已知绫布和罗布分别全部出售后均能收入896文,绫布和罗布各出售一尺共收入120文.问两种布每尺各多少钱.若设绫布有x尺,则可列方程为 .
14.如图,在平面直角坐标系中,点A(0,3),B(4.0),将△AOB向右平移到△CDE 的位置,点A,O分别与点C,D 对应,函数 的图象经过点 C 和CE 的中点 F,则k 的值为
15.(新新考向、图形操作在矩形 ABCD 中,AB=4,BC=3,点 P在边 AB 上.若将 沿 DP 折叠,使点 A 落在矩形ABCD 的对角线上,则AP 的长为
三、解答题(本题共6小题,共50分、解答应写出文字说明、演算步骤或推理过程)
16.(每题5分,共10分)
(1)计算:
(2)化简:
17.(本小题8分)
某校积极开展劳动教育,两次购买A,B两种型号的劳动用品,购买记录如下表:
A 型劳动用品/件 B型劳动用品/件 合计金额/元
第一次 20 25 1150
第二次 10 20 800
(1)求A. B两种型号劳动用品的单价;
(2)若该校计划再次购买 A,B两种型号的劳动用品共40件,其中A型劳动用品的购买数量不少于10件且不多于25件,则该校购买这40件劳动用品至少需要多少元 (备注:A,B两种型号劳动用品的单价保持不变)
18.(本小题8分)
新新考向·开放探索“乡村振兴战略”是在党的十九大报告中提出的战略.十九大报告指出,农业、农村、农民问题是关系国计民生的根本性问题,必须始终把解决好“三农”问题作为全党工作的重中之重,实施乡村振兴战略.某村启动“乡村振兴”项目,为了提高农民的收入,准备在村里大规模种植若干种经济作物.现调查了本村部分村民在过去一年内种植农作物的种类,并根据调查数据绘制成如下两幅不完整的统计图.
请根据统计图提供的信息,解答下列问题:
(1)本次调查村民的总人数是 人,并补全条形统计图;
(2)在扇形统计图中,B种农作物对应扇形的圆心角度数为 ;
(3)经调查,该村准备为240名村民集体建造49个大棚来种植这五种农作物,每个大棚只种植一种农作物.按照统计后的结果分配村民种植农作物,其中种植B,E两种农作物的大棚个数和村民人数已经确定(如下表),在确保每个大棚的人数不低于4人,不高于6人,且种植同种农作物的每个大棚的人数相同的条件下,请你合理安排种植A,C,D三种农作物的大棚个数和村民人数.(写出一种方案即可)
农作物种类 村民人数 大棚个数
A
B 36 9
c
D
E 48 12
19.(本小题8分)
乐乐从甲地到乙地匀速跑步,在途中因故停留了一段时间后,仍按原速跑步,小强骑自行车比乐乐晚出发一段时间,以250 m/min的速度从乙地到甲地匀速骑行,两人路线相同,两人距离乙地的路程y(单位:m)与乐乐出发后所用时间x(单位:min)之间的函数图象如图所示.
(1)求点 D 和点A的坐标:
(2)求乐乐停留结束后享与云之间的函数解析式;(不要求写出自变量x的取值范围)
(3)求乐乐与小强相遇时x的值.
20.(本小题8分)
新新考向·情境命题为了预防近视,要求学生写字姿势应保持“一尺、一拳、一寸”,即眼睛与书本距离约为一尺(约33cm),胸前与课桌距离约为一拳,握笔的手指与笔尖距离约为一寸.如图,BD 为桌面,某同学眼睛 P 看作业本A 的俯角为 身体离书桌距离 ,眼睛到桌面的距离 20cm.
(1)通过计算,请判断这名同学的眼睛与作业本的距离是否符合要求;
(2)为确保符合要求,需将作业本沿BA 方向移动.当眼睛 P 看作业本A 的俯角为 时,求作业本移动的距离.
(结果精确到0.1 cm.参考数据:
21.(本小题8分)
如图,在 中, 以BC 为直径作⊙O,交AB 边于点D,E 是边AC 的中点,直线ED,BC 相交于点F.
(1)求证:DE 是⊙O的切线;
(2)若 求线段 BF 的长.
1. B 2. A 3. D 4. B 5. B 6. C 7. A 8. B 9. C10. C
11.-3 12.20
14.6 解析∵点A(0,3),B(4,0),∴OA=3,OB=4.
根据题意,得CD=OA=3,DE=OB=4.
设OD=a,则C(a,3),E(a+4,0).
∵函数 的图象经过点 C 和CE 的中点 F,
解得a=2.∴k=6.
15. 或
16.解:(1)原式:
(2)原式
17.解:(1)设A 型劳动用品的单价为x 元,B型劳动用品的单价为y元.
根据题意,得 解得
答:A型劳动用品的单价为20元,B型劳动用品的单价为30元.
(2)设购买 A 型劳动用品a 件,则购买 B型劳动用品(40-a)件,购买这40件劳动用品需要 W 元.
根据题意,得10≤a≤25.
∴W=20a+30(40-a)=-10a+1 200.
∵--10<0,∴W 随a的增大而减小.
∴当a=25 时,W 取最小值,最小值为--10×25+1200=950.
答:该校购买这40件劳动用品至少需要950元.
18.解:(1)40
种植 D种农作物的有40-4-6-10-8=12(人).补全条形统计图如图所示.
(2)54°
方案如下:
农作物种类 村民人数 大棚个数
A 24 6
B 36 9
C 60 10
D 72 12
E 48 12
(答案不唯一)
19.解:(1)根据图象,得乐乐的速度为 100(m/ min)、
∴乐乐到达乙地所用时间为 12(min).∴点 D 的坐标为(12,0).
∵小强到达甲地所用时间为
∴6+4=10(min).∴点 F 的坐标为(10,1 000).
(2)设乐乐停留结束后 y 与x 之间的函数解析式为y= kx+b.
将点C(7,500),D(12,0)代入,得 解得
∴乐乐停留结束后 y 与x 之间的函数解析式为y=-100x+1200.
(3)设线段EF 对应的函数解析式为y=mx+n.
将点E(6,0),F(10,1000)代入,得 解得
∴线段 EF 对应的函数解析式为y=250x-1500.
令--100x+1200=250x-1500.
解得 ∴乐乐与小强相遇时x 的值为
20.解:(1)根据题意,得∠ACP=90°.
在 Rt△APC 中, PC=20cm,
∴这名同学的眼睛与作业本的距离不符合要求.
(2)如图,点A'为作业本移动后的位置.
在 Rt△APC 中, PC=20cm,
在Rt△A'PC 中, PC=20cm,
答:作业本移动的距离约为9.9cm.
21.解:(1)证明:如图,连接OD,CD.
∵OD=OC,∴∠ODC=∠OCD.
∵BC 是⊙O的直径,
∴∠BDC=90°,即∠ADC=90°.
∵E 是边AC 的中点,∴DE=AE=EC.
∴∠EDC=∠ECD.
∵∠ACB=90°,
∴∠ECD+∠OCD=90°.∴∠EDC+∠ODC=90°.
∴∠ODE=90°,即OD⊥DE.
∵OD 是⊙O 的半径,∴DE 是⊙O 的切线.
(2)在 Rt△ABC中,
在 Rt△ABC 中,根据勾股定理,得
解得
在 Rt△BCD 中,根据勾股定理,得
∵DE=AE,∴∠A=∠ADE=∠BDF.
∵∠A+∠ACD=∠ACD+∠DCF=90°,
∴∠A=∠DCF=∠BDF.
∵∠F=∠F,∴△BDF∽△DCF.
即
解得
第一部分 选择题(共30分)
一、选择题(本题共10小题,每小题3分,共30分、在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若向东走5m,记作+5m,则向西走5m,可记作 ( )
A.+5m B.---5m C.+10m D.-10m
2.新新考向·传统文化北宋时期的汝窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一,具有极高的历史价值、文化价值、如图,关于它的三视图,下列说法正确的是 ( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
3.下列运算中,结果正确的是 ( )
4.已知方程 的一个根是一1,则另一个根为( )
A.-7 B.-6 C.-2 D.3
5.新新考向·情境命题某市为了方便市民绿色出行,推出某品牌共享单车,如图是其示意图,其中AB,CD 都与地面平行,∠BCD=62°,∠BAC=53°,当AM∥CB 时,∠MAC 的度数为( )
A.62° B.65° C.75° D.115°
6.新新考向·传统文化清代袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”已知 若苔花的花粉直径约为85 000 nm,则85 000 nm用科学记数法表示为( )
7.青少年身体健康问题越来越引起社会的广泛关注.某班50名学生一周体育锻炼时间的统计表如下:
锻炼时间/h 6 7 8 9
学生人数 12 16 17 5
则这些学生一周体育锻炼时间的众数和中位数分别是 ( )
A.8,7 B.17,16.5 C.8,8 D.7.5,8
8.新新考向、学科融合主亮在实验室做实验时,没有找到天平称取实验所需药品的质量,于是利用杠杆原理制作天平称取药品的质量(杠杆原理:动力×动力臂=阻力×阻力臂).如图1,当天平左盘放置质量为60g的物品时,右盘中放置20g砝码,天平平衡;如图2,将待称量药品放在右盘后,左盘放置12 g砝码,才可使天平再次平衡,则该药品的质量是 ( )
A.6g B.4g C.3.5g D.3g
9.(新新考向·图形操作如图,在矩形ABCD 中,AB=6cm,BC=12cm,以点 B 为圆心,BC长为半径画弧交 AD 于点 E,则扇形 EBC 的面积为 ( )
B.8πcm
10.新新考向,图形操作如图,在 中,以点A 为圆心,适一 —当长为半径画弧,分别交 手点Q,E,再分别以点E,F 为圆心,大于 的长为半径画弧,两弧在∠BAC 的内部交于点G,作射线 AG交BC于点D.若AC=3,BC=4,则CD 的长为 ( )
B.1 D.2
第二部分 非选择题(共65分)
二、填空题(本题共5小题,每小题3分,共15分)
11.若点 P(m,-1)关于y 轴的对称点是点 则 的值是 .
12.在一个暗箱里放有x个大小相同、质地均匀的白球,为了估计白球的个数,再放入5个除颜色不同外其余均相同的黄球,将球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回暗箱中,通过大量重复试验发现摸到黄球的频率稳定在0.2,则x的值大约是
13.新新考向 学科融合元代数学家朱世杰于1303年编著的《四元玉鉴》中有这样一道题目:“今有绫、罗共三丈,各直钱八百九十六文,只云绫、罗各一尺共直钱一百二十文.问绫、罗尺价各几何.”其大意为:现在有绫布和罗布,布长共3丈(1丈=10尺),已知绫布和罗布分别全部出售后均能收入896文,绫布和罗布各出售一尺共收入120文.问两种布每尺各多少钱.若设绫布有x尺,则可列方程为 .
14.如图,在平面直角坐标系中,点A(0,3),B(4.0),将△AOB向右平移到△CDE 的位置,点A,O分别与点C,D 对应,函数 的图象经过点 C 和CE 的中点 F,则k 的值为
15.(新新考向、图形操作在矩形 ABCD 中,AB=4,BC=3,点 P在边 AB 上.若将 沿 DP 折叠,使点 A 落在矩形ABCD 的对角线上,则AP 的长为
三、解答题(本题共6小题,共50分、解答应写出文字说明、演算步骤或推理过程)
16.(每题5分,共10分)
(1)计算:
(2)化简:
17.(本小题8分)
某校积极开展劳动教育,两次购买A,B两种型号的劳动用品,购买记录如下表:
A 型劳动用品/件 B型劳动用品/件 合计金额/元
第一次 20 25 1150
第二次 10 20 800
(1)求A. B两种型号劳动用品的单价;
(2)若该校计划再次购买 A,B两种型号的劳动用品共40件,其中A型劳动用品的购买数量不少于10件且不多于25件,则该校购买这40件劳动用品至少需要多少元 (备注:A,B两种型号劳动用品的单价保持不变)
18.(本小题8分)
新新考向·开放探索“乡村振兴战略”是在党的十九大报告中提出的战略.十九大报告指出,农业、农村、农民问题是关系国计民生的根本性问题,必须始终把解决好“三农”问题作为全党工作的重中之重,实施乡村振兴战略.某村启动“乡村振兴”项目,为了提高农民的收入,准备在村里大规模种植若干种经济作物.现调查了本村部分村民在过去一年内种植农作物的种类,并根据调查数据绘制成如下两幅不完整的统计图.
请根据统计图提供的信息,解答下列问题:
(1)本次调查村民的总人数是 人,并补全条形统计图;
(2)在扇形统计图中,B种农作物对应扇形的圆心角度数为 ;
(3)经调查,该村准备为240名村民集体建造49个大棚来种植这五种农作物,每个大棚只种植一种农作物.按照统计后的结果分配村民种植农作物,其中种植B,E两种农作物的大棚个数和村民人数已经确定(如下表),在确保每个大棚的人数不低于4人,不高于6人,且种植同种农作物的每个大棚的人数相同的条件下,请你合理安排种植A,C,D三种农作物的大棚个数和村民人数.(写出一种方案即可)
农作物种类 村民人数 大棚个数
A
B 36 9
c
D
E 48 12
19.(本小题8分)
乐乐从甲地到乙地匀速跑步,在途中因故停留了一段时间后,仍按原速跑步,小强骑自行车比乐乐晚出发一段时间,以250 m/min的速度从乙地到甲地匀速骑行,两人路线相同,两人距离乙地的路程y(单位:m)与乐乐出发后所用时间x(单位:min)之间的函数图象如图所示.
(1)求点 D 和点A的坐标:
(2)求乐乐停留结束后享与云之间的函数解析式;(不要求写出自变量x的取值范围)
(3)求乐乐与小强相遇时x的值.
20.(本小题8分)
新新考向·情境命题为了预防近视,要求学生写字姿势应保持“一尺、一拳、一寸”,即眼睛与书本距离约为一尺(约33cm),胸前与课桌距离约为一拳,握笔的手指与笔尖距离约为一寸.如图,BD 为桌面,某同学眼睛 P 看作业本A 的俯角为 身体离书桌距离 ,眼睛到桌面的距离 20cm.
(1)通过计算,请判断这名同学的眼睛与作业本的距离是否符合要求;
(2)为确保符合要求,需将作业本沿BA 方向移动.当眼睛 P 看作业本A 的俯角为 时,求作业本移动的距离.
(结果精确到0.1 cm.参考数据:
21.(本小题8分)
如图,在 中, 以BC 为直径作⊙O,交AB 边于点D,E 是边AC 的中点,直线ED,BC 相交于点F.
(1)求证:DE 是⊙O的切线;
(2)若 求线段 BF 的长.
1. B 2. A 3. D 4. B 5. B 6. C 7. A 8. B 9. C10. C
11.-3 12.20
14.6 解析∵点A(0,3),B(4,0),∴OA=3,OB=4.
根据题意,得CD=OA=3,DE=OB=4.
设OD=a,则C(a,3),E(a+4,0).
∵函数 的图象经过点 C 和CE 的中点 F,
解得a=2.∴k=6.
15. 或
16.解:(1)原式:
(2)原式
17.解:(1)设A 型劳动用品的单价为x 元,B型劳动用品的单价为y元.
根据题意,得 解得
答:A型劳动用品的单价为20元,B型劳动用品的单价为30元.
(2)设购买 A 型劳动用品a 件,则购买 B型劳动用品(40-a)件,购买这40件劳动用品需要 W 元.
根据题意,得10≤a≤25.
∴W=20a+30(40-a)=-10a+1 200.
∵--10<0,∴W 随a的增大而减小.
∴当a=25 时,W 取最小值,最小值为--10×25+1200=950.
答:该校购买这40件劳动用品至少需要950元.
18.解:(1)40
种植 D种农作物的有40-4-6-10-8=12(人).补全条形统计图如图所示.
(2)54°
方案如下:
农作物种类 村民人数 大棚个数
A 24 6
B 36 9
C 60 10
D 72 12
E 48 12
(答案不唯一)
19.解:(1)根据图象,得乐乐的速度为 100(m/ min)、
∴乐乐到达乙地所用时间为 12(min).∴点 D 的坐标为(12,0).
∵小强到达甲地所用时间为
∴6+4=10(min).∴点 F 的坐标为(10,1 000).
(2)设乐乐停留结束后 y 与x 之间的函数解析式为y= kx+b.
将点C(7,500),D(12,0)代入,得 解得
∴乐乐停留结束后 y 与x 之间的函数解析式为y=-100x+1200.
(3)设线段EF 对应的函数解析式为y=mx+n.
将点E(6,0),F(10,1000)代入,得 解得
∴线段 EF 对应的函数解析式为y=250x-1500.
令--100x+1200=250x-1500.
解得 ∴乐乐与小强相遇时x 的值为
20.解:(1)根据题意,得∠ACP=90°.
在 Rt△APC 中, PC=20cm,
∴这名同学的眼睛与作业本的距离不符合要求.
(2)如图,点A'为作业本移动后的位置.
在 Rt△APC 中, PC=20cm,
在Rt△A'PC 中, PC=20cm,
答:作业本移动的距离约为9.9cm.
21.解:(1)证明:如图,连接OD,CD.
∵OD=OC,∴∠ODC=∠OCD.
∵BC 是⊙O的直径,
∴∠BDC=90°,即∠ADC=90°.
∵E 是边AC 的中点,∴DE=AE=EC.
∴∠EDC=∠ECD.
∵∠ACB=90°,
∴∠ECD+∠OCD=90°.∴∠EDC+∠ODC=90°.
∴∠ODE=90°,即OD⊥DE.
∵OD 是⊙O 的半径,∴DE 是⊙O 的切线.
(2)在 Rt△ABC中,
在 Rt△ABC 中,根据勾股定理,得
解得
在 Rt△BCD 中,根据勾股定理,得
∵DE=AE,∴∠A=∠ADE=∠BDF.
∵∠A+∠ACD=∠ACD+∠DCF=90°,
∴∠A=∠DCF=∠BDF.
∵∠F=∠F,∴△BDF∽△DCF.
即
解得
同课章节目录
