2025年中考数学二轮复习题型练习(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习题型练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 936.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 15:19:12 | ||
图片预览




文档简介
情境题
1.大同阳高栽种杏树有着悠久的历史,阳高杏个大果匀,肉厚味甜,颜色黄里透红,七月果熟开始采摘.图中每筐阳高杏的质量以5kg 为基准,超过的千克数记为正数,不足的千克数记为负数.记录如下,则这4筐中,质量最接近标准质量的是 ( )
2.中国传统纹样产生于人民,寄寓着幸福繁荣的愿景,寄托着平安康乐的期盼.如图,四幅传统纹样中,既是轴对称图形又是中心对称图形的是 ( )
3.“指尖上的非遗——麻柳刺绣”,针线勾勒之间,绣出世间百态,在一幅长80 cm,宽50cm的刺绣风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图,若要使整个挂图的面积是5 400 cm ,设金色纸边的宽度为x cm(风景画四周的金色纸边宽度相同),则列出的方程为 ( )
A.(50+x)(80+x)=5400 B.(50-x)(80-x)=5400
C.(50+2x)(80+2x)=5400 D.(50-2x)(80-2x)=5400
4.筒车是我国古代发明的一种水利灌溉工具,如图1,点M 表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心的圆,且圆心O在水面上方.若圆被水面截得的弦AB 的长为8m,圆心O到AB 的距离为3m ,则tan∠OAB 的值是( )
A. C. D.
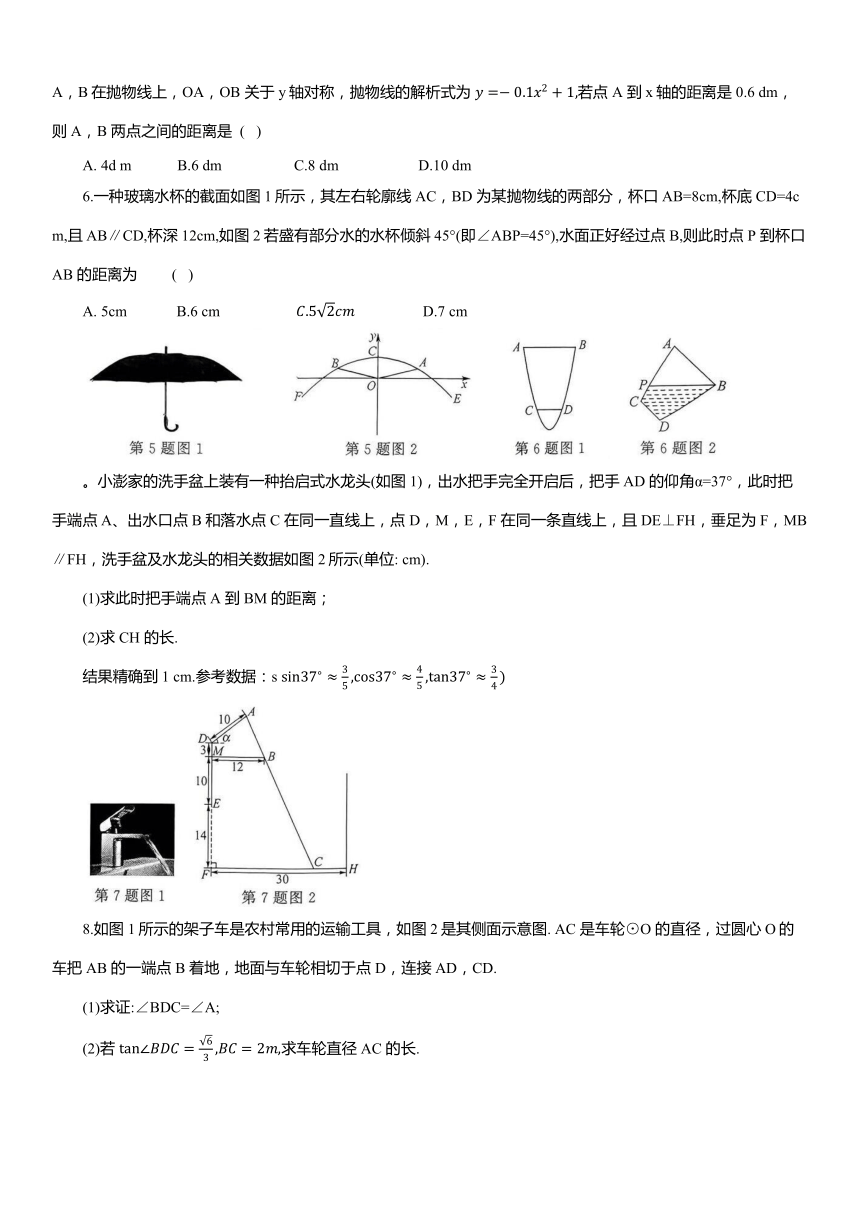
5.数学来源于生活,伞是生活中常见的一种工具,撑开后如图1所示,由此发现数学知识——抛物线.如图2,以伞柄所在的直线为y轴,以伞骨OA,OB 的交点O为坐标原点建立平面直角坐标系.点C 为抛物线的顶点,点A,B在抛物线上,OA,OB 关于y轴对称,抛物线的解析式为 若点 A 到x轴的距离是0.6 dm,则A,B 两点之间的距离是 ( )
A. 4d m B.6 dm C.8 dm D.10 dm
6.一种玻璃水杯的截面如图1所示,其左右轮廓线AC,BD 为某抛物线的两部分,杯口AB=8cm,杯底CD=4cm,且AB∥CD,杯深12cm,如图2若盛有部分水的水杯倾斜45°(即∠ABP=45°),水面正好经过点 B,则此时点 P 到杯口AB 的距离为 ( )
A. 5cm B.6 cm D.7 cm
。小澎家的洗手盆上装有一种抬启式水龙头(如图1),出水把手完全开启后,把手AD 的仰角α=37°,此时把手端点A、出水口点B 和落水点C 在同一直线上,点 D,M,E,F 在同一条直线上,且DE⊥FH,垂足为F,MB∥FH,洗手盆及水龙头的相关数据如图2所示(单位: cm).
(1)求此时把手端点 A 到BM 的距离;
(2)求 CH 的长.
结果精确到1 cm.参考数据:s
8.如图1所示的架子车是农村常用的运输工具,如图2是其侧面示意图. AC 是车轮⊙O 的直径,过圆心O的车把AB 的一端点B 着地,地面与车轮相切于点 D,连接AD,CD.
(1)求证:∠BDC=∠A;
(2)若 求车轮直径AC 的长.
跨学科试题
1.眼镜是利用了凹透镜能使光发散的特点达到矫正视力的目的.如图,平行于主光轴MN 的光线 AB 和CD 经过凹透镜的折射后,折射光线 BE,DF 的反向延长线交于主光轴MN上一点 P.若∠ABE=150°,∠CDF=155°,则∠EPF 的度数是 ( )
A.15° B.25° C.35° D.55°
2.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB 与水杯底部CD 平行,光线EF 从水中射向空气时发生折射,光线变成 FH,点G 在射线 EF 上.已知∠HFB=21°,∠FED=54°,则∠GFH 的度数为 ( )
A.21° B.75° C.33° D.54°
3.伟大的古希腊物理学家阿基米德有句名言:“给我一个支点,我可以撬动地球!”这句名言道出了“杠杆原理”的意义和价值.小明用撬棍撬动一块大石头,运用的就是“杠杆原理”.已知阻力F (单位:N)和阻力臂L (单位:m)的函数图象如图所示,若小明想使动力 F 不超过200 N,则动力臂L 至少为 ( )
A. 2m B. 1m C. 3m D. 4m
4.综合实践小组的同学们利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm )的反比例函数,其图象如图所示(ρ>0).下列说法正确的是 ( )
A.当液体密度ρ≥1时,浸在液体中的高度h≥20
B.当液体密度ρ=2时,浸在液体中的高度h=40
C.当浸在液体中的高度0D.当液体的密度0<ρ≤1时,浸在液体中的高度h≤20
5.生物学研究表明,在一定的温度范围内,酶的活性会随温度的升高逐渐增强,在最适宜温度时,酶的活性最强,超过一定温度范围时,酶的活性又随温度的升高逐渐减弱,甚至会失去活性.现已知某种酶的活性值y(单位:IU)与温度t(单位:℃)的关系可以近似用二次函数 来表示,则当温度为最适宜时,该种酶的活性值为 ( )
A.14 IU B. IU C.240 IU D.44 IU
6.地理学上把两翼指向上风方向,迎风坡平缓前进,背风坡陡呈弧线凸出,平面呈抛物线的沙丘叫做“抛物线形沙丘”.如图1是我国最大沙漠塔克拉玛干沙漠某处的抛物线形沙丘,以抛物线形沙丘最顶端为点O,建立如图所示的平面直角坐标系,若点 A(--15,--100),B(a,-144)是图1中沙丘的两个端点,则a 的值为 ( )
A.15 B.18 C.24 D.36
7.根据物理学规律,如果把一物体从地面以10m/s的速度竖直上抛,那么离地面的高度h(单位:m)与物体运动的时间x(单位:s)的关系满足 根据上述规律,则物体经过 s落回地面.
8.如图是小玲设计用手电来测量家附近“新华大厦”高度的示意图.点P 处放一水平的平面镜(镜的厚度忽略不计),光线从点A 出发经平面镜反射后刚好射到大厦CD 的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2m,BP=1.8m,PD=24 m,那么该大厦的高度为 m.
9.如图1,实验室中存放有A,B两组溶液(均为无色),A组溶液中的两种酸性溶液分别为稀盐酸和稀硫酸,B组溶液中的两种碱性溶液分别为氢氧化钠溶液和氢氧化钙溶液.
(1)彤彤从A组溶液中随机选择一瓶溶液,则选中稀盐酸的概率为 ;
(2)如图2是小杰求“从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液”的概率的部分过程,帮他补全树状图并完成求解.(提示:稀盐酸与氢氧化钙溶液反应可生成氯化钙溶液)
1.写出比 大且比-1小的整数: .(写出一个即可)
2.若关于x的一元二次方程 有两个实数根,则k 的值可以是 .(写出一个即可)
s.在平面直角坐标系中,点O为原点,点B(2,2),点A,C分别在x轴、y轴上,且四边形OABC 为正方形,若一个反比例函数的图象与正方形OABC 有交点,则这个反比例函数的解析式可以为 .(写出一个即可)
4.快递业为商品走进千家万户提供了极大便利,网店店主小张打算从甲、乙两家快递公司中选择一家合作,为此,小张收集了10家网店店主对两家快递公司关于配送速度和服务质量的相关评价,并整理、描述、分析如下:
配送速度得分(满分10分):
甲快递公司:7,6,9,6,7,10,8,8,9,9;
乙快递公司:8,8,6,7,9,7,9,8,8,9.
服务质量统计图如图所示.
配送速度和服务质量得分统计如下表:
快递公司统计量 配送速度得分 服务质量得分
平均数 中位数 众数 平均数 方差
甲快递公司 7.9 8 n 7 s 甲
乙快递公司 7.9 8 8 7 s 乙
根据以上信息,解答下列问题:
(1)n= ,比较大小: (填“>”“<”或“=”);
(2)综合上表中的统计数据,你认为小张应选择哪家快递公司作为合作伙伴,请说明理由.(写出两条理由即可)
5.从“冬日雪暖阳”到“春天花正开”,沈阳魅力更加迷人,相关数据显示,五一小长假期间,南方“小土豆”到沈阳旅游的人数大幅增加.乐乐一家计划暑假来沈阳游玩,为了更好地了解沈阳的景点,乐乐对网友进行了线上调查,想根据调查的数据制定自己一家人的沈阳游玩计划,调查的过程及不完整的统计结果如下表.
调查目的 了解网友最喜爱的沈阳景点
调查方式 抽样调查
调查对象 部分网友
调查内容 你最喜爱的沈阳景点(每名网友只能从下列五个选项中选择一个景点) A.沈阳故宫 B.张学良旧居 C.沈阳世博园 D.中街步行街 E.工业博物馆
调查结果
请解答下列问题:
(1)本次参与线上调查的网友共有多少人
(2)根据上表的调查结果,若有9000名网友参与调查,请你估计最喜爱“沈阳故宫”的人数;
(3)若返程当天还有景点F、景点G 或景点 H 可以去游玩,各景点建议游玩时间和景点间路程用时情况如图2所示.乐乐一家人打算上午9:00到达第一个景点开始游玩,下午18:30坐飞机回家,需要最晚在下午16:40到达机场,如果按图中景点建议游玩时间选择两个景点游玩,请你帮助乐乐设计一个游玩路线.
游玩路线:先到景点 游玩,再到景点 游玩,最后16:40前到达机场.(填“F”“G”或“H”)
操作性试题
1.如图,已知△ABC,用尺规进行如下操作:①以点 A 为圆心,BC 长为半径画弧;②以点C为圆心,BA长为半径画弧;③两弧交于点 D,连接AD,CD.可直接判定四边形ABCD为平行四边形的依据是 ( )
A.两组对边分别相等 B.两组对边分别平行
C.对角线互相平分 D.一组对边平行且相等
2.如图,在△ABC中,∠ACB=90°,按如下步骤操作:①以点 A 为圆心,任意长为半径作弧,分别交AC,AB 于 D,E 两点;②以点C为圆心,AD 长为半径作弧,交AC 的延长线于点F;③以点F 为圆心,DE 长为半径作弧,交②中所画的弧于点G;④作射线CG.若∠B=40°,则∠FCG的度数为 ( )
A.40° B.50° C.60° D.70°
3.如图,在菱形ABCD 中,∠DAB=50°,分别以点A,B 为圆心,大于 AB 的长为半径作弧相交于M,N 两点,过M,N 两点的直线交AD 于点 E,连接BE,则∠EBC 的度数为( )
A.50°
4.如图,在Rt△ABC 中,∠ACB=90°,根据尺规作图的痕迹,判断以下结论错误的是( )
A.∠BDE=∠BAC B.∠BAD=∠B
C. DE=DC D. AE=AC
5.如图,在△ABC 中,∠BAC=90°,以点 A 为圆心,AC长为半径作弧交BC于点D,再分别以点C,D 为圆心,大于 CD的长为半径作弧,两弧交于点 F,作射线 AF 交 BC 于点 E.若AC=3,AB=4,连接AD,则S△ABD= .
6.如图,在△ABC中,D 是边 BC 上一点,AD=AB.
(1)请用尺规作△ABC 绕点A 旋转后得到的△ADE,使旋转后的边 AB 与边AD 重合;(保留作图痕迹,不写作法)
(2)连接CE,若∠B=60°,求证:CE=AE.
7.将矩形纸片ABCD 折叠一次,使点 B 的对应点 B'恰好落在对角线AC上,已知折痕过点A,且与 BC 交于点 E、
(1)用尺规在图中作出折痕AE 和点B 的对应点B';(保留作图痕迹,不写作法)
(2)若AB=5,AD=12,求CE 的长.
8.如图1,在△ABC中, 于点 D.
(1)求证:△ACD≌△BCD;
(2)尺规作图:作Rt△BCD 的外接圆⊙O;(不写作法,保留作图痕迹)
(3)如图2,在(2)的条件下,过点 D 作DE⊥AC,垂足为E.求证:DE 为⊙O 的切线.
新定义试题
1.新定义:若一元二次方程 满足-a+b--1=0,则称这个方程为“美妙方程”.已知 是“美妙方程”,且有两个相等的实数根,则b的值为
A.4
2.新定义:对于函数图象上任意一点P(x,y),y-x称为该点的“坐标差”,函数图象上所有点的“坐标差”的最大值称为该函数的“特征值”.一次函数y=2x+3(-2≤x≤1)的“特征值”为 .
3.新定义:[a,b]为一次函数y= ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”为[3,m--2]的一次函数是正比例函数,则点(1-m,1+m)在第 象限.
4.新定义:在平面直角坐标系中,对于点 P(x ,y ),当点( 满足 y 时,称点Q(x ,y )是点 P(x ,y )的“关联点”.已知点 P (1,2),有下列结论:①点Q (4,8),Q (-2,-4)都是点 P 的“关联点”;②若直线 y=x+2上的点 A 是点 P 的“关联点”,则点 A 的坐标为(2,4);③抛物线 上存在两个点是点 P 的“关联点”.其中正确的是 .(填序号)
5.新定义:若实数m,n满足 则称点 P(m,n)为“雅隽致远点”.
(1)判断点 M(1,2),N(2,1)是不是“雅隽致远点”;
(2)若反比例函数 的图象上存在两个不同的“雅隽致远点”A,B,且AB= ,求反比例函数的解析式.
6.新定义:若实数m,n满足 且m≠n,t为常数,则称点 P(m,n)为“改革创新点”,例如:点(-2,0)是“改革创新点”.
(1)点(1,1),(5,-3),(-3,1)中,是“改革创新点”的是点 ;(填坐标)
(2)设函数 的图象的“改革创新点”分别为点 A,B,过点B作 BC⊥x轴,垂足为C.当△ABC 的面积为3时,求b 的值.
7.新定义:在平面直角坐标系中,点P(a,b),Q(c,d),若c= ka+1,d=-kb+1,其中k为常数,且k≠0,则称点 Q 是点 P 的“k级变换点”.例如:点(-3,7)是点(2,3)的“-2级变换点”.
(1)点(1,1)的“3级变换点”是点 ;
(2)设点 Q(p,q)是点 P(1,1)的“k级变换点”.
①点 M(p,m)在反比例函数 的图象上,当p>0时,m,q的大小关系为 ;
②点A 的坐标为(-3,2),若∠QAO=45°,求点 Q 的坐标.
(3)若以点(n,0)为圆心,1为半径的圆上恰有两个点,这两个点的“1级变换点”都在直线y=-x+5上,求n的取值范围.
滚动练(一)A卷
一、选择题(本题共5小题,每小题3分,共15分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.新新考向·情境命题“早穿棉袄午穿纱,围着火炉吃西瓜”描绘的是我国某地一天内气温变化较大的现象.若该地某天早晨气温上升8℃记作+8℃,则该地傍晚气温下降10℃应记作 ( )
A.+18 ℃ B.-18 ℃ C.+10℃ D.-10℃
2.2020年是我国脱贫攻坚战决胜之年,全国要完成3 900 000贫困人口的搬迁建设任务,数据3 900 000用科学记数法表示为 ( )
3.下列计算正确的是 ( )
C.3a·4a=12a
4.如图,在△ABC中,CD平分∠ACB交AB 于点 D,过点 D 作DE∥BC交AC 于点 E.若∠A=54°,∠B=48°,则∠CDE 的度数为 ( )
A.38° B.39° C.40° D.41°
5.如图,在平面直角坐标系中,矩形OABC 的顶点 A(4,0),C(0,3),连接AC,以点A 为圆心,任意长为半径作弧,交AC 于点 D,交 AB 于点 E;分别以点 D,E 为圆心,大于 DE的长为半径作弧,两弧交于点 F;作射线 AF,交BC 于点 M,则点 M 的坐标为 ( )
A.(
二、填空题(本题共3小题,每小题3分,共9分)
6.不等式7-5x≤2的解集是 .
7.新新考向·传统文化《九章算术》内容丰富,与实际生活联系紧密,在书中讲述了这样一个问题:“今有垣高一丈,倚木于垣,上与垣齐.引木却行一尺,其木至地.问木长几何.”其内容可以表述为:有一面墙,高一丈.将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.若使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆的上端恰好沿着墙滑落到地面上.木杆长多少尺 设木杆长 x 尺,根据题意,可列方程为 .(说明:1丈=10尺)
8.新新考向·图形操作如图,在矩形纸片 ABCD 中, 折叠AD,使它与BC 重合,得到折痕EF,把该矩形纸片展开铺平,再折叠BA,使点A 落在EF上的点G 处,得到折痕 BH,连接CG,则线段CG 的长为 .
三、解答题(本题共3小题,共26分.解答应写出文字说明、演算步骤或推理过程)
9.(每题5分,共10分)
(1)计算:
(2)化简:
10.(本小题8分)
学校为了解学生对新闻、体育、动画、娱乐、戏曲类电视节目的喜爱情况,采用抽样的方法在七年级选取了一个班的学生,通过问卷调查(每名学生必选且只选一类电视节目)、收集数据、整理数据,制作了如下两幅不完整的统计图.
根据统计图中的信息,解答以下问题:
(1)七年级的这个班共有学生 人,图中a= ,b= .在扇形统计图中,“体育”类电视节目对应扇形的圆心角度数为 ;
(2)补全条形统计图;
(3)根据抽样调查的结果,请你估计该校1 750名学生中喜欢“娱乐”类电视节目的人数.
11.(本小题8分)
某校为检测师生体温,在校门安装了某型号的测温门,如图为该“测温门”的截面示意图.身高为1.6m的小聪做了如下实验:当他在地面 M 处时,“测温门”开始显示额头温度,此时在额头B 处测得A 的仰角为30°;当他在地面 N 处时,“测温门”停止显示额头温度,此时在额头C处测得A 的仰角为58°.若“测温门”顶部A 处距地面的高度AD为2.8m,求小聪在有效测温区间MN 的长度.(结果精确到0.01 m.注:额头到地面的距离以身高计.参考数据:s 2
滚动练(一)B卷
一、选择题(本题共5小题,每小题3分,共15分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图是一个立体图形的展开图,该立体图形是 ( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
2.若点 A(-3,2)与点 B 关于x轴对称,则点 B 的坐标是 ( )
A.(-3,2) B.(-3,-2) C.(3,2) D.(3,-2)
3.下列式子错误的是 ( )
4.端午佳节,小明的妈妈准备了豆沙粽2个、红枣粽4个、腊肉粽3个、白米粽2个,它们除了口味其他都相同,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是 ( )
A.
5.新新考向·学科融合光合作用,通常是指绿色植物(包括藻类)吸收光能,把二氧化碳和水合成富能有机物,同时释放氧气的过程,整个过程受光照强度、二氧化碳浓度、温度等多种因素的影响.小星在研究某绿色植物光合作用氧气释放速度v(单位:mg/h)与光照强度L(单位:klx)之间的关系时,设计了如图1的实验装置,并绘制了15℃和25℃时氧气释放速度v(单位:mg/h)与光照强度L(单位:klx)之间的关系如图2所示,下列说法正确的是
( )
A 当L=7时,该绿色植物在25 ℃环境下氧气释放速度比15 ℃环境下的高
B.当L=8时,3h后,该绿色植物在25 ℃环境下比15℃环境下多释放20mg氧气
C.当v=10时,该绿色植物在15℃环境下比25 ℃环境下需要的光照强度高1klx
D.光照强度越大,该绿色植物释放氧气的速度越快
二、填空题(本题共2小题,每小题3分,共6分)
6.某比赛从演讲内容、演讲技巧和演讲效果三个方面打分,最终得分按4:3:3的比例计算.若选手甲在演讲内容、演讲技巧和演讲效果三个方面的得分分别为95分、80分和90 分,则选手甲的最终得分为 分.
7.新新考向·学科融合物理实验课上,同学们分组研究“定滑轮可以改变用力的方向,但不能省力”时,爱动脑筋的小颖发现:重物上升时,滑轮上点 A 的位置在不断改变.已知滑轮的半径为12cm,当重物上升4πcm时,滑轮上点A转过的度数为 .
三、解答题(本题共3小题,共24分.解答应写出文字说明、演算步骤或推理过程)
8.(本小题8分)
“唯有牡丹真国色,花开时节动京城.”在2024年第41届中国洛阳牡丹文化节来临之际,某商店老板计划购进A,B两款牡丹花造型陶瓷手链进行销售.已知A,B两款手链的进价和售价如下表所示.
A 款手链 B款手链
进价(元/个) 15 12
售价(元/个) 24 19
(1)若该商店老板购进A,B两款手链共15个,花费198元,求购进A,B两款手链各多少个;
(2)若该商店老板购进A,B两款手链共40个,卖完全部手链后要保证利润不低于320元,求至少购进 A款手链多少个.
9.(本小题8分)
某厂家生产一批遮阳伞,每把遮阳伞的成本价是20元,试销售时发现:遮阳伞每天的销售量y(单位:把)与销售单价x(单位:元)之间是一次函数关系,当销售单价为28元时,每天的销售量为260把;当销售单价为30元时,每天的销售量为240把.
(1)求遮阳伞每天的销售量y与销售单价x之间的函数解析式;
(1)求遮阳伞每天的销售利润为ω元,当销售单价定为多少元时,才能使每天的销售利润
10.(本小题8分)
如图,△ABC内接于⊙O,AB 为⊙O的直径,过点O 作OD⊥AB 交AC 于点D,交 BC的延长线于点F,E 为线段DF 的中点,连接CE.
(1)求证:CE 为⊙O 的切线;
(2)若OA=4,DF=6,求 AC 的长.
滚动练(二)A卷
一、选择题(本题共5小题,每小题3分,共15分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列四个数中,最小的数是 ( )
A. -(-1) B.0 D.3-1
2.新新考向·情境命题中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作名录.下列四幅作品分别代表“清明”“谷雨”“白露”“大雪”,其中既是中心对称图形又是轴对称图形的是 ( )
3.下列命题是真命题的是 ( )
A.如果 那么a=b
B.如果两个角是同位角,那么这两个角相等
C.相等的两个角是对顶角
D.在同一平面内,垂直于同一条直线的两条直线平行
4.如图,△ABC 的顶点坐标A(2,3),B(1,1),C(4,2),将△ABC 先向左平移3个单位长度,再向下平移1个单位长度,得到△A'B'C',则边 BC上的点 D(m,n)的对应点 D'的坐标是E ( )
A.(m+3,n+1) B.(m-3,n-1)
C.(-1,2) D.(3-m,1-n)
5.2023年2月26日,横琴马拉松在广东珠海横琴金融岛中央公园开跑.小强跑在小海前面,在离终点1 000m时,他以5m/s的速度向终点冲刺,而此时小海在他身后100m,小海需以多快的速度同时冲刺,才能在小强之前到达终点 设此时小海冲刺的速度为 xm/s,可列不等式为 ( )
二、填空题(本题共3小题,每小题3分,共9分)
6.因式分解:
7.新新考向·图形操作如图,正方形ABCD 的边长为8,E是CD 的中点,分别以点 B,E为圆心,大于 BE 的长为半径作弧,两弧分别相交于M,N两点,作直线MN,与AD 相交于点F,则AF= .
8.下列图形都是由相同的小正方形按照一定规律摆放而成的,照此规律排列下去,若第n个图中小正方形的个数比第(n—1)个图中小正方形的个数多41个,则n 的值是 .
三、解答题(本题共3小题,共26分.解答应写出文字说明、演算步骤或推理过程)
9.(每题5分,共10分)
(1)计算:
(2)先化简,再求值: 其中x=-3.
10.(本小题8分)
“双减”政策实施后,某校为丰富学生的课余生活,开设了 A.书法,B.绘画,C.舞蹈,D.跆拳道四类兴趣班.为了解学生对这四类兴趣班的喜爱情况,随机抽取该校部分学生进行问卷调查,并将调查结果整理后绘制成如下两幅不完整的统计图.
根据统计图信息,解答下列问题:
(1)本次抽取调查学生共有 人,估计该校2000名学生喜爱“舞蹈”兴趣班的有 人;
(2)补全两幅统计图;
(3)甲、乙两名学生要选择参加兴趣班,若他们每人从A,B,C,D四类兴趣班中随机选取一类,请用画树状图法或列表法,求两人恰好选择不是同一类的概率.
学习人数24
11.(本小题8分)
为方便市民绿色出行,临沂市政府推出共享单车服务.如图1是某品牌共享单车放在地面上的实物图,如图2 是其示意图,其中AB,CD 均与地面l平行,车轮半径为32 cm,∠BCD=64°,BC=60 cm,坐垫 E 与点B 的距离BE 为15 cm.
(1)求坐垫 E 到地面的距离;
(2)研究表明,当坐垫E到CD的距离为人体腿长的0.8倍时,坐骑比较舒适.小明的腿长约78 cm,现将坐垫 E 调整至坐骑舒适高度E',求 EE'的长.
(结果精确到0.1 cm.参考数据:
滚动练(二)B卷
一、选择题(本题共5小题,每小题3分,共15分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下面图中所示几何体的左视图是 ( )
2.下列计算正确的是 ( )
3.某校为了解学生的课外阅读情况,随机抽取了部分学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则这部分学生一周课外阅读时间的中位数和众数分别是 ( )
读书时间 6 h及以下 7 h 8 h 9 h 10 h及以上
学生人数 6 11 8 8 7
A.8,7 B.8,8
C.8,5,5 D.8.5,7
4.如图,在△ABC中,∠ACB=90°,将△ABC 绕点 C 顺时针旋转得到△EDC,使点 B 的对应点 D 恰好落在边AB 上,AC,ED 交于点 F.若∠BCD=α,则∠EFC 的度数是 ( )
5.新新考向·情境命题如图是蔬菜塑料大棚及其正面的示意图,图中曲线 AGMD 可近似看作一条抛物线,四边形 ABCD 为矩形且支架AB,CD,GH,MN 均垂直于地面 BC.已知BC=6m,AB=2m,以BC 所在的直线为x轴,线段BC 的垂直平分线为y轴,建立平面直角坐标系(规定一个单位长度代表1m),若点M 的坐标为(1,3),则抛物线的解析式为( )
二、填空题(本题共2小题,每小题3分,共6分)
6.新新考向·传统文化我国民间流传的数学名题:“只闻隔壁人分银,不知多少银和人,每人7两少7两,每人半斤多半斤,试问各位善算者,多少人分多少银(1斤等于10两).”其大意是:听见隔壁一些人在分银两,每人7两还缺7两,每人半斤则多半斤,共有多少人 多少两银子 设共有x人,y两银子,根据题意,可列方程组为 .
7.如图,在扇形ABC中,∠BAC=90°,AB=1,若以点C 为圆心,CA 为半径画弧,与 交于点 D,连接CD,则图中阴影部分的面积是 .
三、解答题(本题共3小题,共24分、解答应写出文字说明、演算步骤或推理过程)
8.(本小题8分)
2019年长春国际马拉松于5月26日上午在长春体育中心鸣枪开跑.某公司为赛事赞助了5 000瓶矿泉水,计划以后逐年增加,到2021年将达到7 200瓶,若该公司每年赞助矿泉水数量增加的百分率相同.
(1)求平均每年的增长率;
(2)若2022年该公司赞助矿泉水增长率与前两年相同,请你预计2022年该公司赞助矿泉水的数量.
9.(本小题8分)
甲、乙两车分别从M,N两地出发,沿同一公路相向匀速行驶,两车分别抵达 N,M两地后即停止行驶.已知乙车比甲车提前出发,设甲、乙两车之间的路程为s(单位:km),乙车行驶的时间为t(单位:h),s与t之间的函数关系如图所示.
(1)M,N两地之间的公路路程是 km,乙车的速度是 km/h,m的值为 ;
(2)求线段 EF 的解析式;
(3)求甲车出发多长时间,两车相距140 km.
10.(本小题8分)
如图,△ABC 内接于⊙O,AC 是⊙O 的直径,过OA 上的点 P 作PD⊥AC,交 CB 的延长线于点 D,交AB 于点E,F 为DE 的中点,连接BF.
(1)求证:BF 与⊙O 相切;
(2)若 求 BF 的长.
"情境题
1. A 2. A 3. C 4. A 5. A
6. D解析如图,以AB 所在直线为x轴,玻璃杯的对称轴为y 轴,建立平面直角坐标系,过点 P 作 PE⊥x轴于点E.
根据题意,得A(-4,0),B(4,0),C(-2,-12),D(2,-12).
设抛物线的解析式为y=a(x+4)(x-4)(a≠0).
将点 C(--2,--12)代入,得-12=a(-2+4)(-2-4).解得a=1.
∵∠ABP=45°,∠PEB=90°,
∴EP=EB.
设
解得 (不合题意,舍去),
7.解:(1)如图,过点 A 作AP⊥MB 于点 P,过点 D 作DQ⊥AP 于点Q.
∴∠AQD=∠DQP=∠APB=∠MPQ=90°.
根据题意,得DF⊥FH,MB∥FH.
∴∠DMP=∠DFH=90°.∴四边形 DMPQ 是矩形.
∴MD=PQ=3cm.
在 Rt△ADQ 中, AD=10cm,
∴AP=AQ+PQ=6+3=9(cm).
答:此时把手端点 A 到BM 的距离约为9 cm.
(2)如图,延长AP 交FH 于点G.
∵MB∥FH,∴∠MPQ=∠FGP=90°.
∵∠DFH=90°,∠MPG=∠APB=90°,
∴四边形 MPGF 是矩形.
∴PG=MF=ME+EF=10+14=24(cm).
∴AG=AP+PG=9+24=33(cm).
在Rt△ADQ 中, ‘
∴FG=MP=DQ=8cm.
∴BP=BM--MP=12-8=4(cm).
∵BP∥GC,∴△APB∽△AGC.
即
8.解:(1)证明:如图,连接OD.
∵OD=OC,∴∠ODC=∠OCD.
∵BD 与⊙O 相切,∴OD⊥BD.∴∠ODB=90°.
∴∠ODC+∠BDC=90°.
∵AC 是⊙O 的直径,∴∠ADC=90°.
∴∠A+∠OCD=90°.∴∠A+∠ODC=90°.
∴∠BDC=∠A.
(2)∵∠BDC=∠A,∴tan A=tan∠BDC=
∴在 Rt△ADC 中,
∵∠BDC=∠A,∠DBC=∠ABD,
∴△CBD∽△DBA.
即
解得AC=1.
∴车轮直径AC 的长为1m.
跨学科试题
1. D 2. C 3. C 4. C 5. C (6. B
7. 8.16
9.解:(1)
(2)补全树状图如图所示.
由树状图可知,共有4种等可能的结果,其中能够反应生成氯化钙溶液的结果有1种.
∴P(从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液)
∥开放性试题∥
1.—3(答案不唯一) 2.6(答案不唯一, 即可)
(答案不唯一)
4.解:(1)9;<
(2)小张应选择甲公司,理由如下:
配送速度方面,甲、乙两快递公司的平均分相同,中位数相同,但甲快递公司的众数高于乙快递公司,这说明甲快递公司在配送速度方面可能比乙快递公司表现得更好;服务质量方面,甲、乙两快递公司的平均数相同,但甲快递公司的方差明显小于乙快递公司,说明甲快递公司的服务质量更稳定,因此应该选择甲快递公司.
(答案不唯一,合理即可).
5.解:(1)300÷30%=1 000(人).
答:本次参与线上调查的网友共有 1 000人、
3 600(人).
答:估计最喜爱“沈阳故宫”的有 3 600人.
(3)G;F(答案不唯一,合理即可)
∥操作性试题∥
1. A 2. B 3. D 4. B
5. 解析由作图过程可知,AE 垂直平分CD.
∴CE=DE,∠AEC=90°.
∵∠BAC=90°,AB=4,AC=3,
∴在 Rt△ABC 中,根据勾股定理,得
∴5×AE=4×3,即
在 Rt△ACE 中,根据勾股定理,得
6.解:(1)如图,△ADE 即为所求,
(2)证明:如图,连接CE.
∵AB=AD,∠B=60°,∴△ABD 是等边三角形.
∴∠BAD=60°.
根据旋转的性质,得AC=AE,∠DAE=∠BAC.
∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAD=∠CAE=60°.
∴△ACE 是等边三角形.∴CE=AE.
7.解:(1)如图,折痕 AE 和点B'即为所求.
(2)如图,连接B'E.
∵四边形 ABCD 为矩形,
∴∠B=90°,BC=AD=12.
在 Rt△ABC 中,根据勾股定理,得
根据折叠的性质,得
设CE=x,则
在 Rt△CB'E 中,根据勾股定理,
解得
8.解:(1)证明:∵AC=BC,CD⊥AB,∴BD=AD.在△ACD 和△BCD 中, 学耳∴△ACD≌△BCD(SSS).
(2)作图如图1所示.
(3)证明:如图2,连接OD.
∵OD=OC,∴∠ODC=∠OCD.
∵△ACD≌△BCD,∴∠OCD=∠ACD.
∴∠ODC=∠ACD.∴OD∥AC.∴∠ODE=∠AED.
∵DE⊥AC,∴∠ODE=∠AED=90°.∴OD⊥DE.
∵OD 是⊙O 的半径,∴DE 为⊙O 的切线.
Ⅲ新定义试题〃
1. C 解析∵ 是“美妙方程”,∴--a+b-1=0.∴b=a+1.
∵方程有两个相等的实数根,
解得
∴b=a+1=2.
2.4 解析根据题意,得y-x=2x+3-x=x+3(-2≤x≤1).
设s=y-x=x+3(-2≤x≤1).
∵1>0,∴s随x的增大而增大.
∴当x=1时,s有最大值,最大值为4.
∴该函数的“特征值”为4.
3.二 解析根据题意,得y=3x+m-2是正比例函数.
∴m--2=0.解得m=2.
∴1-m=-1,1+m=3.
∴点(-1,3)在第二象限.
4.①②③ 解析∵2×(1+4)=2+8,∴点 Q (4,8)是点P 的“关联点”.
∵2×[1+(-2)]=2+(-4),∴点 Q (-2,-4)是点P 的“关联点”.故①正确;
根据题意,设点 A 的坐标为(a,a+2).
∵点 A 是点 P 的“关联点”,∴2(1+a)=2+a+2.
解得a=2.
∴a+2=4、∴点A 的坐标为(2,4).故②正确;
设抛物线. 上的点 B 的坐标为 2m+3).
∵点 B 是点 P 的“关联点”,
解得
当m=1时,
当m=3时,
∴点 B 的坐标为(1,2)或(3,6).
∴抛物线. 上存在两个点是点 P 的“关联点”.故③正确.
5.解:①∵M(1,2),且1-2=-1≠1,
不是“雅隽致远点”.
∵N(2,1),且2-1=1,∴N(2,1)是“雅隽致远点”.
(2)∵“雅隽致远点” P(m,n),且m-n=1,
∴n=m-1.∴P(m,m-1).
∵当x=m时,y=m--1=x-1,
∴点 P(m,m-1)在直线y=x-1上.
如图,设直线y=x-1与x轴、y轴分别交于点C,D.
当x=0时,y=-1;当y=0时,x=1.
∴C(1,0),D(0,-1).
∴OC=OD=1.
∴△OCD 是等腰直角三角形.
∴∠OCD=45°.
过点A 作AE∥y 轴,过点 B 作BE∥x轴,AE 与BE 交于点 E,则∠AEB=90°.
∴∠ABE=∠OCD=45°.
在Rt△ABE 中,
设A(x ,y ),B(x ,y ),则
由 得
整理,得
∴1+4k=11.解得
∴反比例函数的解析式为
6.解:(1)(-3,1)
解析对于(1,1),得1=1.∴(1,1)不是“改革创新点”.
对于(5,-3),得5≠-3.
又31≠-1,∴(5,-3)不是“改革创新点”.
对于(-3,1),得-3≠1.
又7=7,∴(-3,1)是“改革创新点”.
(2)根据题意,得
整理,得(m-n)(m+n+2)=0.
∵m≠n,∴m-n≠0.∴m+n+2=0,即n=-m--2.
又m≠n,∴m≠-1,n≠-1.
∴“改革创新点”(m,n)在直线y=-x-2(x≠-1)上.
∴点A,B 分别为y=-x-2与 的交点.
联立方程组,得
解得 或 (不合题意,舍去).
∴A(-3,1).
联立方程组,得 解得
如图,过点 A 作AM⊥BC 于点M.
解得 (不合题意,舍去).
即点 B 在y 轴上.
∴点 C 与点O 重合,点 M 在y 轴上.
∴b=2.
7.解:(1)(4,-2)
(2)①m>q
解析∵点 Q(p,q)是点 P(1,1)的“k 级变换点”,
∴p=k+1,q=-k+1.
∵M(p,m),∴M(k+1,m).
将点 M(k+1,m)代入 得(k+1)m=4.
即m>q.
②根据题意,得p=k+1,q=-k+1.
∴q=-p+2.∴点 Q 在直线y=-x+2上.
如图1,设点 A 绕坐标原点O 按顺时针方向旋转90°至点M,连接OM,AM,交直线 y=-x+2 于点 Q,过点A 作AH⊥x轴于点 H,过点M 作MK⊥x轴于点 K.
根据旋转的性质,得OA=MO,∠AOM=90°.
∴∠AOH+∠MOK=90°.
∵∠AHO=∠OKM=90°,∴∠AOH+∠OAH=90°.
∴∠OAH=∠MOK.
∵∠AHO=∠OKM,OA=MO,∴△OAH≌△MOK.
∴AH=OK,HO=KM.
∵A(-3,2),∴AH=OK=2,HO=KM=3.
∴M(2,3).
设直线 AM 的解析式为y= ax+b(a≠0).
将点A(-3,2),M(2,3)代入,得
解得
∴直线 AM 的解析式为
联立方程组,得 解得
(3)设A(x ,y ),B(x ,y )是圆上两个点,则它们的“1级变换点”为
∵点A',B'在y=-x+5上,
整理,得.
∴A,B 两点在直线y=x-3上.
当直线y=x-3与半径为1的圆相切时,如图2,设该圆的圆心为点 N,直线 y=x-3与x 轴交于点E,与⊙N 相切于点S.
∴NS=1,∠NSE=90°.
在y=x-3中,令y=0,得x=3;令x=0,得y=-3.
∴点 E(3,0),F(0,-3).∴OE=OF=3.
∵∠EOF=90°,∴△EOF 是等腰直角三角形.
∴∠OEF=45°.
,即SE=NS=1.
在 Rt△NSE 中,根据勾股定理,得
当圆心在直线EF 左侧的点N 处时,ON=OE--NE=
当圆心在直线 EF 右侧的点 N'处时,(
∵根据题意,直线 EF 与⊙N 恰有两个交点,
滚动练(一)A卷〃
1. D 2. C 3. A 4. B 5. B
8. 解析如图,连接AG,过点G 作GM⊥BC,垂足为 M.根据折叠的性质,得EF 垂直平分AB,BH 垂直平分AG,∠BAH=∠BGH=90°.
∴AG=BG,AE=BE,∠GEB=90°,AB=BG=2
是等边三角形.
∴∠ABG=60°.
在Rt△BEG 中,
∵四边形 ABCD 是矩形,∴∠ABC=∠BCD=90°=
∴四边形 BCFE 是矩形.
∴EF=BC=5,FC=BE=
∴FG=EF-EG=5-3=2.
∴在 Rt △CGF 中, 根 据勾 股 定 理, 得 CG =
9.解:(1)原式
(2)原式
10.解:(1)50;36%;10;72°
(2)“娱乐”类电视节目的人数为50-4-10-15-3=18(人).
补全条形统计图如图所示.
(人).
答:估计该校 1 750名学生中喜欢“娱乐”类电视节目的有630人.
11.解:如图,延长BC 交AD 于点E.
∴AE=AD-DE=2.8-1.6=1.2= (m).
在Rt△ABE 中,∵∠ABE=30°,t,tan∠ABE=AE/BE,
在 Rt△ACE 中,∵∠ACE=58°,tan∠ACE=AEE,
答:小聪在有效测温区间 MN 的长度约为1.33 m.
滚动练(一)B卷
1. B 2. B 3. B 4. D
5. A 解析根据函数图象,得当L=7时,25 ℃环境下的该绿色植物氧气释放速度比15 ℃环境下的高.故A 选项正确;
当L=8时,该绿色植物在25 ℃、15 ℃环境下氧气释放速度分别为50 mg/h和40 mg/h.
3 h后多释放(50-40)×3=30(mg)氧气.故B选项错误;当v=10时,该绿色植物在25℃环境下比15 ℃环境下需要的光照强度高1 klx.故C选项错误;
该绿色植物释放氧气的速度与光照强度和温度都有关系.故D选项错误.
6.89 7.60°
8.解:(1)设购进 A款手链x个,则购进B款手链(15-x)个.
根据题意,得15x+12(15-x)=198.
解得x=6.∴15-x=15-6=9.
答:购进 A 款手链6个,购进 B款手链9个.
(2)设购进A款手链m个,则购进B款手链(40-m)个.
根据题意,得(24-15)m+(19-12)(40-m)≥320.
解得m≥20.∴m的最小值为20.
答:至少购进 A款手链20个.
9.解:(1)设遮阳伞每天的销售量y 与销售单价x 之间的函数解析式为y= kx+b(k≠0).
根据题意,得 解得
∴遮阳伞每天的销售量y 与销售单价x 之间的函数解析式为y=-10x+540.
(2)根据题意,得ω=(x-20)y=(x-20)(--10x+
∵--10<0,∴当x=37时,ω有最大值为2890.
答:当销售单价定为37元时,才能使每天的销售利润最大.
10.解:(1)证明:如图,连接OC、
∵OA=OC,∴∠A=∠OCA.
∵AB 为⊙O 的直径,
∴∠ACB=90°.
∴∠ACF=90°.
∵E 为线段DF 的中点,
∴∠DCE=∠EDC、
∵OD⊥AO,∴∠AOD=90°、
∴∠ADO+∠A=90°、
∵∠ADO=∠EDC=∠DCE,
∴∠DCE+∠OCA=90°,即∠OCE=90°.∴OC⊥CE.
∵OC 为⊙O 的半径,
∴CE 为⊙O 的切线.
(2)∵DF=6,∴ED=CE=3.
∵OA=4,∴OC=4.
在 Rt△OCE 中,根据勾股定理,得
∵ED=3,∴OD=OE-ED=5-3=2.
在 Rt△AOD 中,根据勾股定理,得
∵∠AOD=∠ACB=90°,∠A=∠A,
滚动练(二)A卷
1. C 2. D 3. D 4. B 5. B
6.(x-2y)(x+2y) 7.1
8.20 解析由所给图形可知,第1个图形中小正方形的个数为 第 2个图形中小正方形的个数为 第3个图形中小正方形的个数为 15=
依次类推,第n个图形中小正方形的个数为 个,第(n-1)个图形中小正方形的个数为 2(n-1)]个.
根据题意,得(
解得n=20.
9.解:(1)原式=2+3-4=1.
(2) 原 式
当x=-3时,原式
10.解:(1)60;500
(2)喜爱“A.书法”的学生有60×35%=21(人).扇形统计图中“C.舞蹈”的百分比为15÷60×100%=25%.补全两幅统计图如图1所示.
(3)画树状图如图2所示.
由树状图可知,共有16种等可能的结果,其中两人恰好选择不是同一类的结果共有12种.
∴P(两人恰好选择不是同一类)
11.解:(1)如图,过点 E 作EH⊥CD,垂足为G,交直线l于点 H.
∵CD∥l,∴EH⊥l,∴GH=32cm.
∵在 Rt△CGE中, 15+60=75(cm),
∴EH=EG+GH=67.5+32=99.5(cm).
答:坐垫 E 到地面的距离约为99.5cm .
(2)如图,在 BE 上取点 E',过点 E'作 E'P⊥CD 于点 P.
∴E'P=78×0.8=62.4(cm).
∵在 Rt△E'CP 中,
答:EE'的长约为5.7 cm.
m滚动练(二)B卷m
1. B 2. C 3. A 4. C
5. A 解析根据题意,得抛物线的对称轴是y轴.
∴设抛物线的解析式为
将点D(3,2),M(1,3)代入,得
解得
∴抛物线的解析式为
8.解:(1)设平均每年的增长率为x.
根据题意,得
解得 (不合题意,舍去).
答:平均每年的增长率为20%.
(2)7 200×(1+20%)=8640(瓶).
答:预计2022年该公司赞助矿泉水的数量为8640瓶.
9.解:(1)300;60;5
(2)设线段 EF 的解析式为
将点( (,210),((3,0)代入s= kt+b,得
解得
∴线段 EF 的解析式为
(3)甲车的速度:
两车相遇前:
两车相遇后:
∴甲车出发 h或 h,两车相距140km.
10.解:(1)证明:如图,连接OB.
∵AC 是⊙O 的直径,∴∠ABC=90°.
∵F 为DE 的中点,
∴∠FEB=∠FBE.
∵∠AEP=∠FEB,∴∠FBE=∠AEP.
∵PD⊥AC,∴∠EPA=90°.
∴∠A+∠AEP=90°.
∵OA=OB,∴∠A=∠OBA.
∴∠OBA+∠FBE=90°,即∠OBF=90°.
∴OB⊥BF.
∵OB 是⊙O 的半径,∴BF 与⊙O 相切.
(2)在 Rt△AEP 中,
根据勾股定理,得
∵AP=OP=4,∴OA=OC=2AP=8.
∴PC=OP+OC=12.
∵∠A+∠AEP=90°,∠A+∠C=90°,
∴∠AEP=∠C.
∵∠APE=∠DPC=90°,∴△APE∽△DPC.
即
∴DE=DP-PE=16-3=13.
1.大同阳高栽种杏树有着悠久的历史,阳高杏个大果匀,肉厚味甜,颜色黄里透红,七月果熟开始采摘.图中每筐阳高杏的质量以5kg 为基准,超过的千克数记为正数,不足的千克数记为负数.记录如下,则这4筐中,质量最接近标准质量的是 ( )
2.中国传统纹样产生于人民,寄寓着幸福繁荣的愿景,寄托着平安康乐的期盼.如图,四幅传统纹样中,既是轴对称图形又是中心对称图形的是 ( )
3.“指尖上的非遗——麻柳刺绣”,针线勾勒之间,绣出世间百态,在一幅长80 cm,宽50cm的刺绣风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图,若要使整个挂图的面积是5 400 cm ,设金色纸边的宽度为x cm(风景画四周的金色纸边宽度相同),则列出的方程为 ( )
A.(50+x)(80+x)=5400 B.(50-x)(80-x)=5400
C.(50+2x)(80+2x)=5400 D.(50-2x)(80-2x)=5400
4.筒车是我国古代发明的一种水利灌溉工具,如图1,点M 表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心的圆,且圆心O在水面上方.若圆被水面截得的弦AB 的长为8m,圆心O到AB 的距离为3m ,则tan∠OAB 的值是( )
A. C. D.
5.数学来源于生活,伞是生活中常见的一种工具,撑开后如图1所示,由此发现数学知识——抛物线.如图2,以伞柄所在的直线为y轴,以伞骨OA,OB 的交点O为坐标原点建立平面直角坐标系.点C 为抛物线的顶点,点A,B在抛物线上,OA,OB 关于y轴对称,抛物线的解析式为 若点 A 到x轴的距离是0.6 dm,则A,B 两点之间的距离是 ( )
A. 4d m B.6 dm C.8 dm D.10 dm
6.一种玻璃水杯的截面如图1所示,其左右轮廓线AC,BD 为某抛物线的两部分,杯口AB=8cm,杯底CD=4cm,且AB∥CD,杯深12cm,如图2若盛有部分水的水杯倾斜45°(即∠ABP=45°),水面正好经过点 B,则此时点 P 到杯口AB 的距离为 ( )
A. 5cm B.6 cm D.7 cm
。小澎家的洗手盆上装有一种抬启式水龙头(如图1),出水把手完全开启后,把手AD 的仰角α=37°,此时把手端点A、出水口点B 和落水点C 在同一直线上,点 D,M,E,F 在同一条直线上,且DE⊥FH,垂足为F,MB∥FH,洗手盆及水龙头的相关数据如图2所示(单位: cm).
(1)求此时把手端点 A 到BM 的距离;
(2)求 CH 的长.
结果精确到1 cm.参考数据:s
8.如图1所示的架子车是农村常用的运输工具,如图2是其侧面示意图. AC 是车轮⊙O 的直径,过圆心O的车把AB 的一端点B 着地,地面与车轮相切于点 D,连接AD,CD.
(1)求证:∠BDC=∠A;
(2)若 求车轮直径AC 的长.
跨学科试题
1.眼镜是利用了凹透镜能使光发散的特点达到矫正视力的目的.如图,平行于主光轴MN 的光线 AB 和CD 经过凹透镜的折射后,折射光线 BE,DF 的反向延长线交于主光轴MN上一点 P.若∠ABE=150°,∠CDF=155°,则∠EPF 的度数是 ( )
A.15° B.25° C.35° D.55°
2.光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB 与水杯底部CD 平行,光线EF 从水中射向空气时发生折射,光线变成 FH,点G 在射线 EF 上.已知∠HFB=21°,∠FED=54°,则∠GFH 的度数为 ( )
A.21° B.75° C.33° D.54°
3.伟大的古希腊物理学家阿基米德有句名言:“给我一个支点,我可以撬动地球!”这句名言道出了“杠杆原理”的意义和价值.小明用撬棍撬动一块大石头,运用的就是“杠杆原理”.已知阻力F (单位:N)和阻力臂L (单位:m)的函数图象如图所示,若小明想使动力 F 不超过200 N,则动力臂L 至少为 ( )
A. 2m B. 1m C. 3m D. 4m
4.综合实践小组的同学们利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm )的反比例函数,其图象如图所示(ρ>0).下列说法正确的是 ( )
A.当液体密度ρ≥1时,浸在液体中的高度h≥20
B.当液体密度ρ=2时,浸在液体中的高度h=40
C.当浸在液体中的高度0
5.生物学研究表明,在一定的温度范围内,酶的活性会随温度的升高逐渐增强,在最适宜温度时,酶的活性最强,超过一定温度范围时,酶的活性又随温度的升高逐渐减弱,甚至会失去活性.现已知某种酶的活性值y(单位:IU)与温度t(单位:℃)的关系可以近似用二次函数 来表示,则当温度为最适宜时,该种酶的活性值为 ( )
A.14 IU B. IU C.240 IU D.44 IU
6.地理学上把两翼指向上风方向,迎风坡平缓前进,背风坡陡呈弧线凸出,平面呈抛物线的沙丘叫做“抛物线形沙丘”.如图1是我国最大沙漠塔克拉玛干沙漠某处的抛物线形沙丘,以抛物线形沙丘最顶端为点O,建立如图所示的平面直角坐标系,若点 A(--15,--100),B(a,-144)是图1中沙丘的两个端点,则a 的值为 ( )
A.15 B.18 C.24 D.36
7.根据物理学规律,如果把一物体从地面以10m/s的速度竖直上抛,那么离地面的高度h(单位:m)与物体运动的时间x(单位:s)的关系满足 根据上述规律,则物体经过 s落回地面.
8.如图是小玲设计用手电来测量家附近“新华大厦”高度的示意图.点P 处放一水平的平面镜(镜的厚度忽略不计),光线从点A 出发经平面镜反射后刚好射到大厦CD 的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2m,BP=1.8m,PD=24 m,那么该大厦的高度为 m.
9.如图1,实验室中存放有A,B两组溶液(均为无色),A组溶液中的两种酸性溶液分别为稀盐酸和稀硫酸,B组溶液中的两种碱性溶液分别为氢氧化钠溶液和氢氧化钙溶液.
(1)彤彤从A组溶液中随机选择一瓶溶液,则选中稀盐酸的概率为 ;
(2)如图2是小杰求“从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液”的概率的部分过程,帮他补全树状图并完成求解.(提示:稀盐酸与氢氧化钙溶液反应可生成氯化钙溶液)
1.写出比 大且比-1小的整数: .(写出一个即可)
2.若关于x的一元二次方程 有两个实数根,则k 的值可以是 .(写出一个即可)
s.在平面直角坐标系中,点O为原点,点B(2,2),点A,C分别在x轴、y轴上,且四边形OABC 为正方形,若一个反比例函数的图象与正方形OABC 有交点,则这个反比例函数的解析式可以为 .(写出一个即可)
4.快递业为商品走进千家万户提供了极大便利,网店店主小张打算从甲、乙两家快递公司中选择一家合作,为此,小张收集了10家网店店主对两家快递公司关于配送速度和服务质量的相关评价,并整理、描述、分析如下:
配送速度得分(满分10分):
甲快递公司:7,6,9,6,7,10,8,8,9,9;
乙快递公司:8,8,6,7,9,7,9,8,8,9.
服务质量统计图如图所示.
配送速度和服务质量得分统计如下表:
快递公司统计量 配送速度得分 服务质量得分
平均数 中位数 众数 平均数 方差
甲快递公司 7.9 8 n 7 s 甲
乙快递公司 7.9 8 8 7 s 乙
根据以上信息,解答下列问题:
(1)n= ,比较大小: (填“>”“<”或“=”);
(2)综合上表中的统计数据,你认为小张应选择哪家快递公司作为合作伙伴,请说明理由.(写出两条理由即可)
5.从“冬日雪暖阳”到“春天花正开”,沈阳魅力更加迷人,相关数据显示,五一小长假期间,南方“小土豆”到沈阳旅游的人数大幅增加.乐乐一家计划暑假来沈阳游玩,为了更好地了解沈阳的景点,乐乐对网友进行了线上调查,想根据调查的数据制定自己一家人的沈阳游玩计划,调查的过程及不完整的统计结果如下表.
调查目的 了解网友最喜爱的沈阳景点
调查方式 抽样调查
调查对象 部分网友
调查内容 你最喜爱的沈阳景点(每名网友只能从下列五个选项中选择一个景点) A.沈阳故宫 B.张学良旧居 C.沈阳世博园 D.中街步行街 E.工业博物馆
调查结果
请解答下列问题:
(1)本次参与线上调查的网友共有多少人
(2)根据上表的调查结果,若有9000名网友参与调查,请你估计最喜爱“沈阳故宫”的人数;
(3)若返程当天还有景点F、景点G 或景点 H 可以去游玩,各景点建议游玩时间和景点间路程用时情况如图2所示.乐乐一家人打算上午9:00到达第一个景点开始游玩,下午18:30坐飞机回家,需要最晚在下午16:40到达机场,如果按图中景点建议游玩时间选择两个景点游玩,请你帮助乐乐设计一个游玩路线.
游玩路线:先到景点 游玩,再到景点 游玩,最后16:40前到达机场.(填“F”“G”或“H”)
操作性试题
1.如图,已知△ABC,用尺规进行如下操作:①以点 A 为圆心,BC 长为半径画弧;②以点C为圆心,BA长为半径画弧;③两弧交于点 D,连接AD,CD.可直接判定四边形ABCD为平行四边形的依据是 ( )
A.两组对边分别相等 B.两组对边分别平行
C.对角线互相平分 D.一组对边平行且相等
2.如图,在△ABC中,∠ACB=90°,按如下步骤操作:①以点 A 为圆心,任意长为半径作弧,分别交AC,AB 于 D,E 两点;②以点C为圆心,AD 长为半径作弧,交AC 的延长线于点F;③以点F 为圆心,DE 长为半径作弧,交②中所画的弧于点G;④作射线CG.若∠B=40°,则∠FCG的度数为 ( )
A.40° B.50° C.60° D.70°
3.如图,在菱形ABCD 中,∠DAB=50°,分别以点A,B 为圆心,大于 AB 的长为半径作弧相交于M,N 两点,过M,N 两点的直线交AD 于点 E,连接BE,则∠EBC 的度数为( )
A.50°
4.如图,在Rt△ABC 中,∠ACB=90°,根据尺规作图的痕迹,判断以下结论错误的是( )
A.∠BDE=∠BAC B.∠BAD=∠B
C. DE=DC D. AE=AC
5.如图,在△ABC 中,∠BAC=90°,以点 A 为圆心,AC长为半径作弧交BC于点D,再分别以点C,D 为圆心,大于 CD的长为半径作弧,两弧交于点 F,作射线 AF 交 BC 于点 E.若AC=3,AB=4,连接AD,则S△ABD= .
6.如图,在△ABC中,D 是边 BC 上一点,AD=AB.
(1)请用尺规作△ABC 绕点A 旋转后得到的△ADE,使旋转后的边 AB 与边AD 重合;(保留作图痕迹,不写作法)
(2)连接CE,若∠B=60°,求证:CE=AE.
7.将矩形纸片ABCD 折叠一次,使点 B 的对应点 B'恰好落在对角线AC上,已知折痕过点A,且与 BC 交于点 E、
(1)用尺规在图中作出折痕AE 和点B 的对应点B';(保留作图痕迹,不写作法)
(2)若AB=5,AD=12,求CE 的长.
8.如图1,在△ABC中, 于点 D.
(1)求证:△ACD≌△BCD;
(2)尺规作图:作Rt△BCD 的外接圆⊙O;(不写作法,保留作图痕迹)
(3)如图2,在(2)的条件下,过点 D 作DE⊥AC,垂足为E.求证:DE 为⊙O 的切线.
新定义试题
1.新定义:若一元二次方程 满足-a+b--1=0,则称这个方程为“美妙方程”.已知 是“美妙方程”,且有两个相等的实数根,则b的值为
A.4
2.新定义:对于函数图象上任意一点P(x,y),y-x称为该点的“坐标差”,函数图象上所有点的“坐标差”的最大值称为该函数的“特征值”.一次函数y=2x+3(-2≤x≤1)的“特征值”为 .
3.新定义:[a,b]为一次函数y= ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”为[3,m--2]的一次函数是正比例函数,则点(1-m,1+m)在第 象限.
4.新定义:在平面直角坐标系中,对于点 P(x ,y ),当点( 满足 y 时,称点Q(x ,y )是点 P(x ,y )的“关联点”.已知点 P (1,2),有下列结论:①点Q (4,8),Q (-2,-4)都是点 P 的“关联点”;②若直线 y=x+2上的点 A 是点 P 的“关联点”,则点 A 的坐标为(2,4);③抛物线 上存在两个点是点 P 的“关联点”.其中正确的是 .(填序号)
5.新定义:若实数m,n满足 则称点 P(m,n)为“雅隽致远点”.
(1)判断点 M(1,2),N(2,1)是不是“雅隽致远点”;
(2)若反比例函数 的图象上存在两个不同的“雅隽致远点”A,B,且AB= ,求反比例函数的解析式.
6.新定义:若实数m,n满足 且m≠n,t为常数,则称点 P(m,n)为“改革创新点”,例如:点(-2,0)是“改革创新点”.
(1)点(1,1),(5,-3),(-3,1)中,是“改革创新点”的是点 ;(填坐标)
(2)设函数 的图象的“改革创新点”分别为点 A,B,过点B作 BC⊥x轴,垂足为C.当△ABC 的面积为3时,求b 的值.
7.新定义:在平面直角坐标系中,点P(a,b),Q(c,d),若c= ka+1,d=-kb+1,其中k为常数,且k≠0,则称点 Q 是点 P 的“k级变换点”.例如:点(-3,7)是点(2,3)的“-2级变换点”.
(1)点(1,1)的“3级变换点”是点 ;
(2)设点 Q(p,q)是点 P(1,1)的“k级变换点”.
①点 M(p,m)在反比例函数 的图象上,当p>0时,m,q的大小关系为 ;
②点A 的坐标为(-3,2),若∠QAO=45°,求点 Q 的坐标.
(3)若以点(n,0)为圆心,1为半径的圆上恰有两个点,这两个点的“1级变换点”都在直线y=-x+5上,求n的取值范围.
滚动练(一)A卷
一、选择题(本题共5小题,每小题3分,共15分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.新新考向·情境命题“早穿棉袄午穿纱,围着火炉吃西瓜”描绘的是我国某地一天内气温变化较大的现象.若该地某天早晨气温上升8℃记作+8℃,则该地傍晚气温下降10℃应记作 ( )
A.+18 ℃ B.-18 ℃ C.+10℃ D.-10℃
2.2020年是我国脱贫攻坚战决胜之年,全国要完成3 900 000贫困人口的搬迁建设任务,数据3 900 000用科学记数法表示为 ( )
3.下列计算正确的是 ( )
C.3a·4a=12a
4.如图,在△ABC中,CD平分∠ACB交AB 于点 D,过点 D 作DE∥BC交AC 于点 E.若∠A=54°,∠B=48°,则∠CDE 的度数为 ( )
A.38° B.39° C.40° D.41°
5.如图,在平面直角坐标系中,矩形OABC 的顶点 A(4,0),C(0,3),连接AC,以点A 为圆心,任意长为半径作弧,交AC 于点 D,交 AB 于点 E;分别以点 D,E 为圆心,大于 DE的长为半径作弧,两弧交于点 F;作射线 AF,交BC 于点 M,则点 M 的坐标为 ( )
A.(
二、填空题(本题共3小题,每小题3分,共9分)
6.不等式7-5x≤2的解集是 .
7.新新考向·传统文化《九章算术》内容丰富,与实际生活联系紧密,在书中讲述了这样一个问题:“今有垣高一丈,倚木于垣,上与垣齐.引木却行一尺,其木至地.问木长几何.”其内容可以表述为:有一面墙,高一丈.将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上.若使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆的上端恰好沿着墙滑落到地面上.木杆长多少尺 设木杆长 x 尺,根据题意,可列方程为 .(说明:1丈=10尺)
8.新新考向·图形操作如图,在矩形纸片 ABCD 中, 折叠AD,使它与BC 重合,得到折痕EF,把该矩形纸片展开铺平,再折叠BA,使点A 落在EF上的点G 处,得到折痕 BH,连接CG,则线段CG 的长为 .
三、解答题(本题共3小题,共26分.解答应写出文字说明、演算步骤或推理过程)
9.(每题5分,共10分)
(1)计算:
(2)化简:
10.(本小题8分)
学校为了解学生对新闻、体育、动画、娱乐、戏曲类电视节目的喜爱情况,采用抽样的方法在七年级选取了一个班的学生,通过问卷调查(每名学生必选且只选一类电视节目)、收集数据、整理数据,制作了如下两幅不完整的统计图.
根据统计图中的信息,解答以下问题:
(1)七年级的这个班共有学生 人,图中a= ,b= .在扇形统计图中,“体育”类电视节目对应扇形的圆心角度数为 ;
(2)补全条形统计图;
(3)根据抽样调查的结果,请你估计该校1 750名学生中喜欢“娱乐”类电视节目的人数.
11.(本小题8分)
某校为检测师生体温,在校门安装了某型号的测温门,如图为该“测温门”的截面示意图.身高为1.6m的小聪做了如下实验:当他在地面 M 处时,“测温门”开始显示额头温度,此时在额头B 处测得A 的仰角为30°;当他在地面 N 处时,“测温门”停止显示额头温度,此时在额头C处测得A 的仰角为58°.若“测温门”顶部A 处距地面的高度AD为2.8m,求小聪在有效测温区间MN 的长度.(结果精确到0.01 m.注:额头到地面的距离以身高计.参考数据:s 2
滚动练(一)B卷
一、选择题(本题共5小题,每小题3分,共15分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图是一个立体图形的展开图,该立体图形是 ( )
A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱
2.若点 A(-3,2)与点 B 关于x轴对称,则点 B 的坐标是 ( )
A.(-3,2) B.(-3,-2) C.(3,2) D.(3,-2)
3.下列式子错误的是 ( )
4.端午佳节,小明的妈妈准备了豆沙粽2个、红枣粽4个、腊肉粽3个、白米粽2个,它们除了口味其他都相同,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是 ( )
A.
5.新新考向·学科融合光合作用,通常是指绿色植物(包括藻类)吸收光能,把二氧化碳和水合成富能有机物,同时释放氧气的过程,整个过程受光照强度、二氧化碳浓度、温度等多种因素的影响.小星在研究某绿色植物光合作用氧气释放速度v(单位:mg/h)与光照强度L(单位:klx)之间的关系时,设计了如图1的实验装置,并绘制了15℃和25℃时氧气释放速度v(单位:mg/h)与光照强度L(单位:klx)之间的关系如图2所示,下列说法正确的是
( )
A 当L=7时,该绿色植物在25 ℃环境下氧气释放速度比15 ℃环境下的高
B.当L=8时,3h后,该绿色植物在25 ℃环境下比15℃环境下多释放20mg氧气
C.当v=10时,该绿色植物在15℃环境下比25 ℃环境下需要的光照强度高1klx
D.光照强度越大,该绿色植物释放氧气的速度越快
二、填空题(本题共2小题,每小题3分,共6分)
6.某比赛从演讲内容、演讲技巧和演讲效果三个方面打分,最终得分按4:3:3的比例计算.若选手甲在演讲内容、演讲技巧和演讲效果三个方面的得分分别为95分、80分和90 分,则选手甲的最终得分为 分.
7.新新考向·学科融合物理实验课上,同学们分组研究“定滑轮可以改变用力的方向,但不能省力”时,爱动脑筋的小颖发现:重物上升时,滑轮上点 A 的位置在不断改变.已知滑轮的半径为12cm,当重物上升4πcm时,滑轮上点A转过的度数为 .
三、解答题(本题共3小题,共24分.解答应写出文字说明、演算步骤或推理过程)
8.(本小题8分)
“唯有牡丹真国色,花开时节动京城.”在2024年第41届中国洛阳牡丹文化节来临之际,某商店老板计划购进A,B两款牡丹花造型陶瓷手链进行销售.已知A,B两款手链的进价和售价如下表所示.
A 款手链 B款手链
进价(元/个) 15 12
售价(元/个) 24 19
(1)若该商店老板购进A,B两款手链共15个,花费198元,求购进A,B两款手链各多少个;
(2)若该商店老板购进A,B两款手链共40个,卖完全部手链后要保证利润不低于320元,求至少购进 A款手链多少个.
9.(本小题8分)
某厂家生产一批遮阳伞,每把遮阳伞的成本价是20元,试销售时发现:遮阳伞每天的销售量y(单位:把)与销售单价x(单位:元)之间是一次函数关系,当销售单价为28元时,每天的销售量为260把;当销售单价为30元时,每天的销售量为240把.
(1)求遮阳伞每天的销售量y与销售单价x之间的函数解析式;
(1)求遮阳伞每天的销售利润为ω元,当销售单价定为多少元时,才能使每天的销售利润
10.(本小题8分)
如图,△ABC内接于⊙O,AB 为⊙O的直径,过点O 作OD⊥AB 交AC 于点D,交 BC的延长线于点F,E 为线段DF 的中点,连接CE.
(1)求证:CE 为⊙O 的切线;
(2)若OA=4,DF=6,求 AC 的长.
滚动练(二)A卷
一、选择题(本题共5小题,每小题3分,共15分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列四个数中,最小的数是 ( )
A. -(-1) B.0 D.3-1
2.新新考向·情境命题中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作名录.下列四幅作品分别代表“清明”“谷雨”“白露”“大雪”,其中既是中心对称图形又是轴对称图形的是 ( )
3.下列命题是真命题的是 ( )
A.如果 那么a=b
B.如果两个角是同位角,那么这两个角相等
C.相等的两个角是对顶角
D.在同一平面内,垂直于同一条直线的两条直线平行
4.如图,△ABC 的顶点坐标A(2,3),B(1,1),C(4,2),将△ABC 先向左平移3个单位长度,再向下平移1个单位长度,得到△A'B'C',则边 BC上的点 D(m,n)的对应点 D'的坐标是E ( )
A.(m+3,n+1) B.(m-3,n-1)
C.(-1,2) D.(3-m,1-n)
5.2023年2月26日,横琴马拉松在广东珠海横琴金融岛中央公园开跑.小强跑在小海前面,在离终点1 000m时,他以5m/s的速度向终点冲刺,而此时小海在他身后100m,小海需以多快的速度同时冲刺,才能在小强之前到达终点 设此时小海冲刺的速度为 xm/s,可列不等式为 ( )
二、填空题(本题共3小题,每小题3分,共9分)
6.因式分解:
7.新新考向·图形操作如图,正方形ABCD 的边长为8,E是CD 的中点,分别以点 B,E为圆心,大于 BE 的长为半径作弧,两弧分别相交于M,N两点,作直线MN,与AD 相交于点F,则AF= .
8.下列图形都是由相同的小正方形按照一定规律摆放而成的,照此规律排列下去,若第n个图中小正方形的个数比第(n—1)个图中小正方形的个数多41个,则n 的值是 .
三、解答题(本题共3小题,共26分.解答应写出文字说明、演算步骤或推理过程)
9.(每题5分,共10分)
(1)计算:
(2)先化简,再求值: 其中x=-3.
10.(本小题8分)
“双减”政策实施后,某校为丰富学生的课余生活,开设了 A.书法,B.绘画,C.舞蹈,D.跆拳道四类兴趣班.为了解学生对这四类兴趣班的喜爱情况,随机抽取该校部分学生进行问卷调查,并将调查结果整理后绘制成如下两幅不完整的统计图.
根据统计图信息,解答下列问题:
(1)本次抽取调查学生共有 人,估计该校2000名学生喜爱“舞蹈”兴趣班的有 人;
(2)补全两幅统计图;
(3)甲、乙两名学生要选择参加兴趣班,若他们每人从A,B,C,D四类兴趣班中随机选取一类,请用画树状图法或列表法,求两人恰好选择不是同一类的概率.
学习人数24
11.(本小题8分)
为方便市民绿色出行,临沂市政府推出共享单车服务.如图1是某品牌共享单车放在地面上的实物图,如图2 是其示意图,其中AB,CD 均与地面l平行,车轮半径为32 cm,∠BCD=64°,BC=60 cm,坐垫 E 与点B 的距离BE 为15 cm.
(1)求坐垫 E 到地面的距离;
(2)研究表明,当坐垫E到CD的距离为人体腿长的0.8倍时,坐骑比较舒适.小明的腿长约78 cm,现将坐垫 E 调整至坐骑舒适高度E',求 EE'的长.
(结果精确到0.1 cm.参考数据:
滚动练(二)B卷
一、选择题(本题共5小题,每小题3分,共15分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下面图中所示几何体的左视图是 ( )
2.下列计算正确的是 ( )
3.某校为了解学生的课外阅读情况,随机抽取了部分学生,对他们一周的课外阅读时间进行了统计,统计数据如下表,则这部分学生一周课外阅读时间的中位数和众数分别是 ( )
读书时间 6 h及以下 7 h 8 h 9 h 10 h及以上
学生人数 6 11 8 8 7
A.8,7 B.8,8
C.8,5,5 D.8.5,7
4.如图,在△ABC中,∠ACB=90°,将△ABC 绕点 C 顺时针旋转得到△EDC,使点 B 的对应点 D 恰好落在边AB 上,AC,ED 交于点 F.若∠BCD=α,则∠EFC 的度数是 ( )
5.新新考向·情境命题如图是蔬菜塑料大棚及其正面的示意图,图中曲线 AGMD 可近似看作一条抛物线,四边形 ABCD 为矩形且支架AB,CD,GH,MN 均垂直于地面 BC.已知BC=6m,AB=2m,以BC 所在的直线为x轴,线段BC 的垂直平分线为y轴,建立平面直角坐标系(规定一个单位长度代表1m),若点M 的坐标为(1,3),则抛物线的解析式为( )
二、填空题(本题共2小题,每小题3分,共6分)
6.新新考向·传统文化我国民间流传的数学名题:“只闻隔壁人分银,不知多少银和人,每人7两少7两,每人半斤多半斤,试问各位善算者,多少人分多少银(1斤等于10两).”其大意是:听见隔壁一些人在分银两,每人7两还缺7两,每人半斤则多半斤,共有多少人 多少两银子 设共有x人,y两银子,根据题意,可列方程组为 .
7.如图,在扇形ABC中,∠BAC=90°,AB=1,若以点C 为圆心,CA 为半径画弧,与 交于点 D,连接CD,则图中阴影部分的面积是 .
三、解答题(本题共3小题,共24分、解答应写出文字说明、演算步骤或推理过程)
8.(本小题8分)
2019年长春国际马拉松于5月26日上午在长春体育中心鸣枪开跑.某公司为赛事赞助了5 000瓶矿泉水,计划以后逐年增加,到2021年将达到7 200瓶,若该公司每年赞助矿泉水数量增加的百分率相同.
(1)求平均每年的增长率;
(2)若2022年该公司赞助矿泉水增长率与前两年相同,请你预计2022年该公司赞助矿泉水的数量.
9.(本小题8分)
甲、乙两车分别从M,N两地出发,沿同一公路相向匀速行驶,两车分别抵达 N,M两地后即停止行驶.已知乙车比甲车提前出发,设甲、乙两车之间的路程为s(单位:km),乙车行驶的时间为t(单位:h),s与t之间的函数关系如图所示.
(1)M,N两地之间的公路路程是 km,乙车的速度是 km/h,m的值为 ;
(2)求线段 EF 的解析式;
(3)求甲车出发多长时间,两车相距140 km.
10.(本小题8分)
如图,△ABC 内接于⊙O,AC 是⊙O 的直径,过OA 上的点 P 作PD⊥AC,交 CB 的延长线于点 D,交AB 于点E,F 为DE 的中点,连接BF.
(1)求证:BF 与⊙O 相切;
(2)若 求 BF 的长.
"情境题
1. A 2. A 3. C 4. A 5. A
6. D解析如图,以AB 所在直线为x轴,玻璃杯的对称轴为y 轴,建立平面直角坐标系,过点 P 作 PE⊥x轴于点E.
根据题意,得A(-4,0),B(4,0),C(-2,-12),D(2,-12).
设抛物线的解析式为y=a(x+4)(x-4)(a≠0).
将点 C(--2,--12)代入,得-12=a(-2+4)(-2-4).解得a=1.
∵∠ABP=45°,∠PEB=90°,
∴EP=EB.
设
解得 (不合题意,舍去),
7.解:(1)如图,过点 A 作AP⊥MB 于点 P,过点 D 作DQ⊥AP 于点Q.
∴∠AQD=∠DQP=∠APB=∠MPQ=90°.
根据题意,得DF⊥FH,MB∥FH.
∴∠DMP=∠DFH=90°.∴四边形 DMPQ 是矩形.
∴MD=PQ=3cm.
在 Rt△ADQ 中, AD=10cm,
∴AP=AQ+PQ=6+3=9(cm).
答:此时把手端点 A 到BM 的距离约为9 cm.
(2)如图,延长AP 交FH 于点G.
∵MB∥FH,∴∠MPQ=∠FGP=90°.
∵∠DFH=90°,∠MPG=∠APB=90°,
∴四边形 MPGF 是矩形.
∴PG=MF=ME+EF=10+14=24(cm).
∴AG=AP+PG=9+24=33(cm).
在Rt△ADQ 中, ‘
∴FG=MP=DQ=8cm.
∴BP=BM--MP=12-8=4(cm).
∵BP∥GC,∴△APB∽△AGC.
即
8.解:(1)证明:如图,连接OD.
∵OD=OC,∴∠ODC=∠OCD.
∵BD 与⊙O 相切,∴OD⊥BD.∴∠ODB=90°.
∴∠ODC+∠BDC=90°.
∵AC 是⊙O 的直径,∴∠ADC=90°.
∴∠A+∠OCD=90°.∴∠A+∠ODC=90°.
∴∠BDC=∠A.
(2)∵∠BDC=∠A,∴tan A=tan∠BDC=
∴在 Rt△ADC 中,
∵∠BDC=∠A,∠DBC=∠ABD,
∴△CBD∽△DBA.
即
解得AC=1.
∴车轮直径AC 的长为1m.
跨学科试题
1. D 2. C 3. C 4. C 5. C (6. B
7. 8.16
9.解:(1)
(2)补全树状图如图所示.
由树状图可知,共有4种等可能的结果,其中能够反应生成氯化钙溶液的结果有1种.
∴P(从两组中各随机选一瓶溶液滴入同一试管中能够反应生成氯化钙溶液)
∥开放性试题∥
1.—3(答案不唯一) 2.6(答案不唯一, 即可)
(答案不唯一)
4.解:(1)9;<
(2)小张应选择甲公司,理由如下:
配送速度方面,甲、乙两快递公司的平均分相同,中位数相同,但甲快递公司的众数高于乙快递公司,这说明甲快递公司在配送速度方面可能比乙快递公司表现得更好;服务质量方面,甲、乙两快递公司的平均数相同,但甲快递公司的方差明显小于乙快递公司,说明甲快递公司的服务质量更稳定,因此应该选择甲快递公司.
(答案不唯一,合理即可).
5.解:(1)300÷30%=1 000(人).
答:本次参与线上调查的网友共有 1 000人、
3 600(人).
答:估计最喜爱“沈阳故宫”的有 3 600人.
(3)G;F(答案不唯一,合理即可)
∥操作性试题∥
1. A 2. B 3. D 4. B
5. 解析由作图过程可知,AE 垂直平分CD.
∴CE=DE,∠AEC=90°.
∵∠BAC=90°,AB=4,AC=3,
∴在 Rt△ABC 中,根据勾股定理,得
∴5×AE=4×3,即
在 Rt△ACE 中,根据勾股定理,得
6.解:(1)如图,△ADE 即为所求,
(2)证明:如图,连接CE.
∵AB=AD,∠B=60°,∴△ABD 是等边三角形.
∴∠BAD=60°.
根据旋转的性质,得AC=AE,∠DAE=∠BAC.
∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAD=∠CAE=60°.
∴△ACE 是等边三角形.∴CE=AE.
7.解:(1)如图,折痕 AE 和点B'即为所求.
(2)如图,连接B'E.
∵四边形 ABCD 为矩形,
∴∠B=90°,BC=AD=12.
在 Rt△ABC 中,根据勾股定理,得
根据折叠的性质,得
设CE=x,则
在 Rt△CB'E 中,根据勾股定理,
解得
8.解:(1)证明:∵AC=BC,CD⊥AB,∴BD=AD.在△ACD 和△BCD 中, 学耳∴△ACD≌△BCD(SSS).
(2)作图如图1所示.
(3)证明:如图2,连接OD.
∵OD=OC,∴∠ODC=∠OCD.
∵△ACD≌△BCD,∴∠OCD=∠ACD.
∴∠ODC=∠ACD.∴OD∥AC.∴∠ODE=∠AED.
∵DE⊥AC,∴∠ODE=∠AED=90°.∴OD⊥DE.
∵OD 是⊙O 的半径,∴DE 为⊙O 的切线.
Ⅲ新定义试题〃
1. C 解析∵ 是“美妙方程”,∴--a+b-1=0.∴b=a+1.
∵方程有两个相等的实数根,
解得
∴b=a+1=2.
2.4 解析根据题意,得y-x=2x+3-x=x+3(-2≤x≤1).
设s=y-x=x+3(-2≤x≤1).
∵1>0,∴s随x的增大而增大.
∴当x=1时,s有最大值,最大值为4.
∴该函数的“特征值”为4.
3.二 解析根据题意,得y=3x+m-2是正比例函数.
∴m--2=0.解得m=2.
∴1-m=-1,1+m=3.
∴点(-1,3)在第二象限.
4.①②③ 解析∵2×(1+4)=2+8,∴点 Q (4,8)是点P 的“关联点”.
∵2×[1+(-2)]=2+(-4),∴点 Q (-2,-4)是点P 的“关联点”.故①正确;
根据题意,设点 A 的坐标为(a,a+2).
∵点 A 是点 P 的“关联点”,∴2(1+a)=2+a+2.
解得a=2.
∴a+2=4、∴点A 的坐标为(2,4).故②正确;
设抛物线. 上的点 B 的坐标为 2m+3).
∵点 B 是点 P 的“关联点”,
解得
当m=1时,
当m=3时,
∴点 B 的坐标为(1,2)或(3,6).
∴抛物线. 上存在两个点是点 P 的“关联点”.故③正确.
5.解:①∵M(1,2),且1-2=-1≠1,
不是“雅隽致远点”.
∵N(2,1),且2-1=1,∴N(2,1)是“雅隽致远点”.
(2)∵“雅隽致远点” P(m,n),且m-n=1,
∴n=m-1.∴P(m,m-1).
∵当x=m时,y=m--1=x-1,
∴点 P(m,m-1)在直线y=x-1上.
如图,设直线y=x-1与x轴、y轴分别交于点C,D.
当x=0时,y=-1;当y=0时,x=1.
∴C(1,0),D(0,-1).
∴OC=OD=1.
∴△OCD 是等腰直角三角形.
∴∠OCD=45°.
过点A 作AE∥y 轴,过点 B 作BE∥x轴,AE 与BE 交于点 E,则∠AEB=90°.
∴∠ABE=∠OCD=45°.
在Rt△ABE 中,
设A(x ,y ),B(x ,y ),则
由 得
整理,得
∴1+4k=11.解得
∴反比例函数的解析式为
6.解:(1)(-3,1)
解析对于(1,1),得1=1.∴(1,1)不是“改革创新点”.
对于(5,-3),得5≠-3.
又31≠-1,∴(5,-3)不是“改革创新点”.
对于(-3,1),得-3≠1.
又7=7,∴(-3,1)是“改革创新点”.
(2)根据题意,得
整理,得(m-n)(m+n+2)=0.
∵m≠n,∴m-n≠0.∴m+n+2=0,即n=-m--2.
又m≠n,∴m≠-1,n≠-1.
∴“改革创新点”(m,n)在直线y=-x-2(x≠-1)上.
∴点A,B 分别为y=-x-2与 的交点.
联立方程组,得
解得 或 (不合题意,舍去).
∴A(-3,1).
联立方程组,得 解得
如图,过点 A 作AM⊥BC 于点M.
解得 (不合题意,舍去).
即点 B 在y 轴上.
∴点 C 与点O 重合,点 M 在y 轴上.
∴b=2.
7.解:(1)(4,-2)
(2)①m>q
解析∵点 Q(p,q)是点 P(1,1)的“k 级变换点”,
∴p=k+1,q=-k+1.
∵M(p,m),∴M(k+1,m).
将点 M(k+1,m)代入 得(k+1)m=4.
即m>q.
②根据题意,得p=k+1,q=-k+1.
∴q=-p+2.∴点 Q 在直线y=-x+2上.
如图1,设点 A 绕坐标原点O 按顺时针方向旋转90°至点M,连接OM,AM,交直线 y=-x+2 于点 Q,过点A 作AH⊥x轴于点 H,过点M 作MK⊥x轴于点 K.
根据旋转的性质,得OA=MO,∠AOM=90°.
∴∠AOH+∠MOK=90°.
∵∠AHO=∠OKM=90°,∴∠AOH+∠OAH=90°.
∴∠OAH=∠MOK.
∵∠AHO=∠OKM,OA=MO,∴△OAH≌△MOK.
∴AH=OK,HO=KM.
∵A(-3,2),∴AH=OK=2,HO=KM=3.
∴M(2,3).
设直线 AM 的解析式为y= ax+b(a≠0).
将点A(-3,2),M(2,3)代入,得
解得
∴直线 AM 的解析式为
联立方程组,得 解得
(3)设A(x ,y ),B(x ,y )是圆上两个点,则它们的“1级变换点”为
∵点A',B'在y=-x+5上,
整理,得.
∴A,B 两点在直线y=x-3上.
当直线y=x-3与半径为1的圆相切时,如图2,设该圆的圆心为点 N,直线 y=x-3与x 轴交于点E,与⊙N 相切于点S.
∴NS=1,∠NSE=90°.
在y=x-3中,令y=0,得x=3;令x=0,得y=-3.
∴点 E(3,0),F(0,-3).∴OE=OF=3.
∵∠EOF=90°,∴△EOF 是等腰直角三角形.
∴∠OEF=45°.
,即SE=NS=1.
在 Rt△NSE 中,根据勾股定理,得
当圆心在直线EF 左侧的点N 处时,ON=OE--NE=
当圆心在直线 EF 右侧的点 N'处时,(
∵根据题意,直线 EF 与⊙N 恰有两个交点,
滚动练(一)A卷〃
1. D 2. C 3. A 4. B 5. B
8. 解析如图,连接AG,过点G 作GM⊥BC,垂足为 M.根据折叠的性质,得EF 垂直平分AB,BH 垂直平分AG,∠BAH=∠BGH=90°.
∴AG=BG,AE=BE,∠GEB=90°,AB=BG=2
是等边三角形.
∴∠ABG=60°.
在Rt△BEG 中,
∵四边形 ABCD 是矩形,∴∠ABC=∠BCD=90°=
∴四边形 BCFE 是矩形.
∴EF=BC=5,FC=BE=
∴FG=EF-EG=5-3=2.
∴在 Rt △CGF 中, 根 据勾 股 定 理, 得 CG =
9.解:(1)原式
(2)原式
10.解:(1)50;36%;10;72°
(2)“娱乐”类电视节目的人数为50-4-10-15-3=18(人).
补全条形统计图如图所示.
(人).
答:估计该校 1 750名学生中喜欢“娱乐”类电视节目的有630人.
11.解:如图,延长BC 交AD 于点E.
∴AE=AD-DE=2.8-1.6=1.2= (m).
在Rt△ABE 中,∵∠ABE=30°,t,tan∠ABE=AE/BE,
在 Rt△ACE 中,∵∠ACE=58°,tan∠ACE=AEE,
答:小聪在有效测温区间 MN 的长度约为1.33 m.
滚动练(一)B卷
1. B 2. B 3. B 4. D
5. A 解析根据函数图象,得当L=7时,25 ℃环境下的该绿色植物氧气释放速度比15 ℃环境下的高.故A 选项正确;
当L=8时,该绿色植物在25 ℃、15 ℃环境下氧气释放速度分别为50 mg/h和40 mg/h.
3 h后多释放(50-40)×3=30(mg)氧气.故B选项错误;当v=10时,该绿色植物在25℃环境下比15 ℃环境下需要的光照强度高1 klx.故C选项错误;
该绿色植物释放氧气的速度与光照强度和温度都有关系.故D选项错误.
6.89 7.60°
8.解:(1)设购进 A款手链x个,则购进B款手链(15-x)个.
根据题意,得15x+12(15-x)=198.
解得x=6.∴15-x=15-6=9.
答:购进 A 款手链6个,购进 B款手链9个.
(2)设购进A款手链m个,则购进B款手链(40-m)个.
根据题意,得(24-15)m+(19-12)(40-m)≥320.
解得m≥20.∴m的最小值为20.
答:至少购进 A款手链20个.
9.解:(1)设遮阳伞每天的销售量y 与销售单价x 之间的函数解析式为y= kx+b(k≠0).
根据题意,得 解得
∴遮阳伞每天的销售量y 与销售单价x 之间的函数解析式为y=-10x+540.
(2)根据题意,得ω=(x-20)y=(x-20)(--10x+
∵--10<0,∴当x=37时,ω有最大值为2890.
答:当销售单价定为37元时,才能使每天的销售利润最大.
10.解:(1)证明:如图,连接OC、
∵OA=OC,∴∠A=∠OCA.
∵AB 为⊙O 的直径,
∴∠ACB=90°.
∴∠ACF=90°.
∵E 为线段DF 的中点,
∴∠DCE=∠EDC、
∵OD⊥AO,∴∠AOD=90°、
∴∠ADO+∠A=90°、
∵∠ADO=∠EDC=∠DCE,
∴∠DCE+∠OCA=90°,即∠OCE=90°.∴OC⊥CE.
∵OC 为⊙O 的半径,
∴CE 为⊙O 的切线.
(2)∵DF=6,∴ED=CE=3.
∵OA=4,∴OC=4.
在 Rt△OCE 中,根据勾股定理,得
∵ED=3,∴OD=OE-ED=5-3=2.
在 Rt△AOD 中,根据勾股定理,得
∵∠AOD=∠ACB=90°,∠A=∠A,
滚动练(二)A卷
1. C 2. D 3. D 4. B 5. B
6.(x-2y)(x+2y) 7.1
8.20 解析由所给图形可知,第1个图形中小正方形的个数为 第 2个图形中小正方形的个数为 第3个图形中小正方形的个数为 15=
依次类推,第n个图形中小正方形的个数为 个,第(n-1)个图形中小正方形的个数为 2(n-1)]个.
根据题意,得(
解得n=20.
9.解:(1)原式=2+3-4=1.
(2) 原 式
当x=-3时,原式
10.解:(1)60;500
(2)喜爱“A.书法”的学生有60×35%=21(人).扇形统计图中“C.舞蹈”的百分比为15÷60×100%=25%.补全两幅统计图如图1所示.
(3)画树状图如图2所示.
由树状图可知,共有16种等可能的结果,其中两人恰好选择不是同一类的结果共有12种.
∴P(两人恰好选择不是同一类)
11.解:(1)如图,过点 E 作EH⊥CD,垂足为G,交直线l于点 H.
∵CD∥l,∴EH⊥l,∴GH=32cm.
∵在 Rt△CGE中, 15+60=75(cm),
∴EH=EG+GH=67.5+32=99.5(cm).
答:坐垫 E 到地面的距离约为99.5cm .
(2)如图,在 BE 上取点 E',过点 E'作 E'P⊥CD 于点 P.
∴E'P=78×0.8=62.4(cm).
∵在 Rt△E'CP 中,
答:EE'的长约为5.7 cm.
m滚动练(二)B卷m
1. B 2. C 3. A 4. C
5. A 解析根据题意,得抛物线的对称轴是y轴.
∴设抛物线的解析式为
将点D(3,2),M(1,3)代入,得
解得
∴抛物线的解析式为
8.解:(1)设平均每年的增长率为x.
根据题意,得
解得 (不合题意,舍去).
答:平均每年的增长率为20%.
(2)7 200×(1+20%)=8640(瓶).
答:预计2022年该公司赞助矿泉水的数量为8640瓶.
9.解:(1)300;60;5
(2)设线段 EF 的解析式为
将点( (,210),((3,0)代入s= kt+b,得
解得
∴线段 EF 的解析式为
(3)甲车的速度:
两车相遇前:
两车相遇后:
∴甲车出发 h或 h,两车相距140km.
10.解:(1)证明:如图,连接OB.
∵AC 是⊙O 的直径,∴∠ABC=90°.
∵F 为DE 的中点,
∴∠FEB=∠FBE.
∵∠AEP=∠FEB,∴∠FBE=∠AEP.
∵PD⊥AC,∴∠EPA=90°.
∴∠A+∠AEP=90°.
∵OA=OB,∴∠A=∠OBA.
∴∠OBA+∠FBE=90°,即∠OBF=90°.
∴OB⊥BF.
∵OB 是⊙O 的半径,∴BF 与⊙O 相切.
(2)在 Rt△AEP 中,
根据勾股定理,得
∵AP=OP=4,∴OA=OC=2AP=8.
∴PC=OP+OC=12.
∵∠A+∠AEP=90°,∠A+∠C=90°,
∴∠AEP=∠C.
∵∠APE=∠DPC=90°,∴△APE∽△DPC.
即
∴DE=DP-PE=16-3=13.
同课章节目录
