2025年中考数学二轮复习解答题专练(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习解答题专练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 267.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 15:21:57 | ||
图片预览



文档简介
解答题专练 (一)
1.(1)计算:
(2)先化简,再求值: ,其中x=-2.
2.某印刷厂每月生产甲、乙两种练习本共40万本,且所有练习本当月全部卖出,其中成本、售价如下表所示.
品种 甲种练习本 乙种练习本
成本 1.2元/本 0.4元/本
售价 1.6元/本 0.6元/本
(1)若该印刷厂五月的利润为11万元,求生产甲、乙两种练习本分别是多少万本;
(2)某学校计划用7680元的经费到该印刷厂采购练习本.经商讨,该印刷厂同意甲种练习本售价打九折,乙种练习本不能让利.若学校能采购到1万本,且不超支,则最多能购买甲种练习本多少本
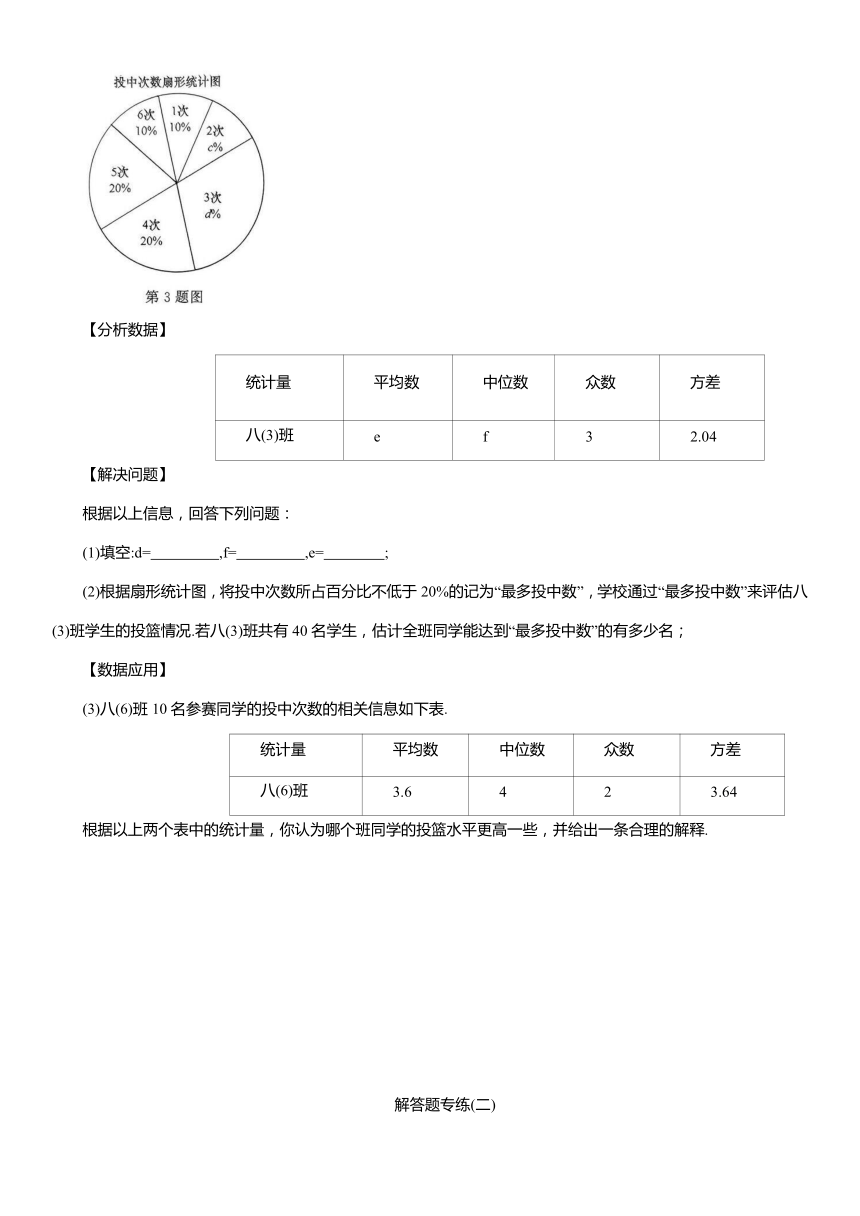
3.新新考向·开放探索某校在“劳动节”期间举行投篮比赛活动.学校在每班随机抽取10名同学参加,规定每人投篮10次.下面对八(3)班10名参赛同学的投中次数进行了收集、整理和分析.
【收集数据】
10名参赛同学的投中次数分别是3,2,1,4,3,5,6,4,3,5.
【整理数据】
投中次数 1 2 3 4 5 6
频数 1 a b 2 2 1
根据上面整理的数据,制作出扇形统计图如图所示.
【分析数据】
统计量 平均数 中位数 众数 方差
八(3)班 e f 3 2.04
【解决问题】
根据以上信息,回答下列问题:
(1)填空:d= ,f= ,e= ;
(2)根据扇形统计图,将投中次数所占百分比不低于20%的记为“最多投中数”,学校通过“最多投中数”来评估八(3)班学生的投篮情况.若八(3)班共有40名学生,估计全班同学能达到“最多投中数”的有多少名;
【数据应用】
(3)八(6)班10名参赛同学的投中次数的相关信息如下表.
统计量 平均数 中位数 众数 方差
八(6)班 3.6 4 2 3.64
根据以上两个表中的统计量,你认为哪个班同学的投篮水平更高一些,并给出一条合理的解释.
解答题专练(二)
1.乌馒头是江北慈城地方特色点心,用麦粉发酵,再掺以白糖、黄糖,蒸制而成.因其用黄糖,颜色暗黄,所以称之谓“乌馒头”.某商店销售乌馒头,通过分析销售情况发现,乌馒头的日销售量y(单位:盒)是销售单价x(单位:元/盒)的一次函数,销售单价、日销售量的部分对应值如下表,已知销售单价不低于成本价且不高于20元/盒,每天销售乌馒头的固定损耗为20元,且成本价为12元/盒,日销售量为200盒.
销售单价x/(元/盒) 15 13
日销售量y/盒 500 700
(1)求乌馒头的日销售量y 与销售单价x 之间的函数解析式;
(2)“端午乌馒重阳粽”是慈城的习俗,端午节期间,商店决定采用降价促销的方式回馈顾客,在顾客获得最大实惠的前提下,当乌馒头每盒降价多少元时,商店日销售纯利润为1480元
(3)当销售单价定为多少时,日销售纯利润最大 并求出日销售最大纯利润.
2.新新考向·情境命题小红在给自建房的楼上安装栏杆时,利用定滑轮设计了如图1的方案帮家人将所需材料运送至该楼层.运送中,小红突发奇想,想利用这个装置测量一下自己所在楼层距离地面的高度AB.如图2,将定滑轮固定在该楼层上方支架点C处(点A,B,C在同一直线上),并利用定滑轮的工作原理拉动水平地面上的箱子,在起始位置点 D 时,测量出绳子和水平面的夹角为30°,拉动一段距离后箱子到达点 F 处,测量出绳子和水平面的夹角为53°.已知定滑轮距离该楼层地面的高度 BC=1.5m,箱子的高度. 移动过程中绳子收回的长度为4.5m,DE,FM,AC 均垂直于地面AE,求AB 的高度.(参考数据:
3.如图,已知AB 为⊙O 的直径,BC 为⊙O 的切线,连接AC 交⊙O 于点 D,F 为 的中点,连接 BF 交 AC 于点 E,过点 C 作( 垂足为G.
(1)求证:CG 平分
(2)若 求 的长.
解答题专练(三)
1.(1)计算:
(2)化简:
2.聚焦“绿色发展,美丽宜居”县城建设,围绕“老旧改造人人参与,和谐家园家家受益”的思路,某市从2021年起连续投入资金用于“建设美丽城市,改造老旧小区”,让小区“旧貌”换“新颜”.已知每年投入资金的增长率相同,其中=2021年投入资金1000万元,2023年投入资金1440万元.
(1)求该市改造小区投入资金的年平均增长率;
(2)2023年每个小区改造的平均费用为80万元,2024年为提高小区品质,每个小区改造的平均费用计划增加20%.如果投入资金年增长率保持不变,那么该市在2024年最多可以改造多少个小区
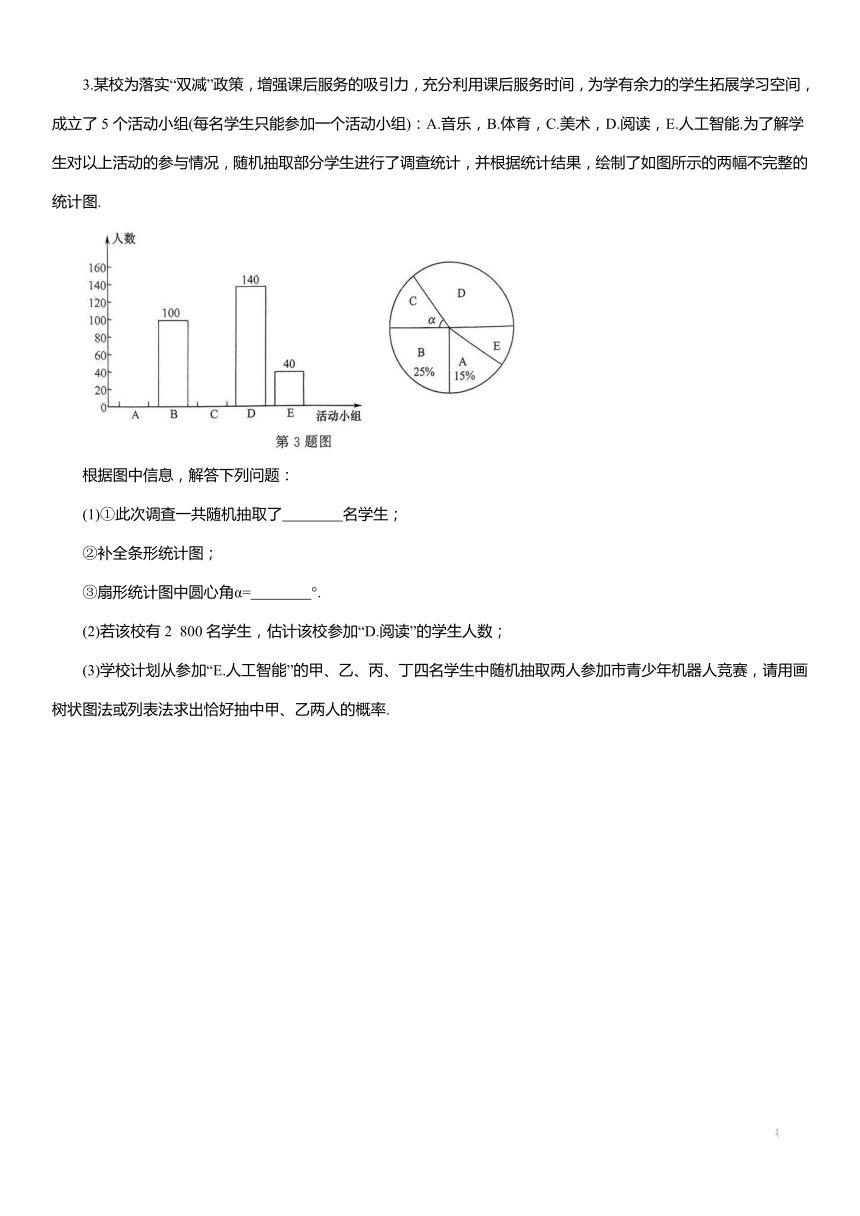
3.某校为落实“双减”政策,增强课后服务的吸引力,充分利用课后服务时间,为学有余力的学生拓展学习空间,成立了5个活动小组(每名学生只能参加一个活动小组):A.音乐,B.体育,C.美术,D.阅读,E.人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
(1)①此次调查一共随机抽取了 名学生;
②补全条形统计图;
③扇形统计图中圆心角α= °.
(2)若该校有2 800名学生,估计该校参加“D.阅读”的学生人数;
(3)学校计划从参加“E.人工智能”的甲、乙、丙、丁四名学生中随机抽取两人参加市青少年机器人竞赛,请用画树状图法或列表法求出恰好抽中甲、乙两人的概率.
解答题专练(四)
1. 新新考向·学科融合在两千四百年前,墨子和他的学生做了世界上第1个小孔成像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”,大意是:影像倒立,在光线交会处有一小孔;关于影像的大小,在于小孔相对物、像的位置.图2 是图1中小孔成像实验的示意图,在图2中,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,图象如图3所示,且当x=6时,y=3.
(1)求y关于x 的函数解析式;
(2)若小孔到蜡烛的距离x为2cm,求火焰的像高y;
(3)根据反比例函数的图象分析,若火焰的像高y不超过6cm,求小孔到蜡烛的距离x至少是多少厘米.
2.新新考向·情境命题水车又称孔明车,是我国最古老的农业灌溉工具.如图1是一种水车的实物图,由立式水轮、竹筒、支撑架和水槽等部件组成.某数学兴趣小组对其进行了研究,示意图如图2所示,⊙O 为立式水轮,水轮在水流的作用下,将水送至C处,再经水槽送至 B处水渠,D 为水轮与水面的交汇处,连接BC,CD,BD,若CD=10m,∠CDF=60°,点C,F 的水平距离为3m,且∠BDF=10°,求水渠离水面的高度 BF.(结果精确到0.01 m.参考数据:
3.新新考向·图形操作如图,已知 AB 为⊙O 的直径,AC 是⊙O 的弦, 的平分线 AD 交⊙O 于点 D、
(1)尺规作图:过点 D 作DE⊥AC 交AC 的延长线于点E,连接OE 交AD 于点 F;(保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:DE 是⊙O 的切线;
(3)在(1)的条件下,若AF=8,求DF 的长.
1.解:(1)原式
(2)原式:
当x=-2时,原式=-8×(-2)+13=29.
2.解:(1)设生产甲种练习本 x 万本,生产乙种练习本y万本.
根据题意,得
解得
答:生产甲种练习本15万本,生产乙种练习本25万本.
(2)设该学校购买甲种练习本m本,则购买乙种练习本(10 000-m)本.
根据题意,得1.6×0.9m+0.6(10 000-m)≤7 680.解得 m≤2000.
∴m的最大值为2000.
答:最多能购买甲种练习本2000本.
3.解:(1)30;3.6;3.5
(2)40×(20%+20%+30%)=28(名).
答:估计全班同学能达到“最多投中数”的有28名.
(3)八(3)班同学的投篮水平更高一些.理由如下:
∵两个班投中次数的平均数相同,八(3)班投中次数的众数比八(6)班的高,投中次数的方差小于八(6)班,水平比较稳定,
∴我认为八(3)班同学的投篮水平更高一些.
(答案不唯一,合理即可)
∥解答题专练(二),
1.解:(1)设乌馒头的日销售量 y 与销售单价x 之间的函数解析式为y= kx+b(k≠0).
将点(15,500),(13,700)代入,得
解得
∴乌馒头的日销售量y 与销售单价x之间的函数解析式为y=-100x+2 000(12≤x≤20).
(2)在 y=--100x+2 000 中,令 y=200,得 200=—100x+2 000.
解得x=18.∴原来销售单价为18元/盒.
设当日销售单价为m 元/盒时,销售利润为1480元.
根据题意,得(-100m+2000)(m-12)=1480+20.
解得
∵为了使顾客获得最大实惠,∴m=15.
∴18-15=3(元).
答:当乌馒头每盒降价3 元时,商店日销售纯利润为1480元.
(3)设日销售纯利润为ω 元.
根据题意,得ω=(--100x+2 000)(x--12)--20=-100x +3200x-24020=-100(x-16) +1580.
∵--100<0,∴当x=16时,ω有最大值1580.
答:当销售单价定为16元/盒时,日销售纯利润最大,日销售最大纯利润为1580元.
2.解:如图,延长DF 交BA 于点 H.
根据题意,得DH⊥AB.
∵DE⊥AE,AB⊥AE,
∴∠DEA=∠EAH=∠DHA=90°.
∴四边形 DEAH 为矩形.∴AH=DE=0.5m .
在Rt△CHD中,∵∠CDH=30°,∴CD=2CH.
在 Rt△CHF 中,
解得CH=6.
∴AB=CH+AH--BC=6+0.5-1.5=5(m).
答:AB 的高度约为5m .
3.解:(1)证明:如图,连接AF.
∵F 为 的中点,∴AF=DF.∴∠FAD=∠ABF.
∵AB 为⊙O 的直径,∴∠AFB=90°.
∵CG⊥BF,∴∠CGF=90°=∠AFB.
∴CG∥AF,∠BCG+∠CBG=90°.
∴∠FAD=∠ACG.∴∠ACG=∠ABF.
∵BC 为⊙O 的切线,
∴∠ABC=90°,即∠ABF+∠CBG=90°.
∴∠BCG=∠ABF.
∴∠ACG=∠BCG,即CG平分∠ACB.
(2)如图,连接OF.
∵∠ECG=∠BCG,CG=CG,∠CGE=∠CGB,
∴△CGE≌△CGB.∴CE=CB.
∴AC=AE+CE=AE+CB=2+CB.
在 Rt△ABC 中,∵根据勾股定理,
解得BC=2.
在 Rt△ABC 中,
∴∠ABF=∠ECG=30°.
∵OF=OB,∴∠OFB=∠ABF=30°.
∴∠FOA=∠OFB+∠ABF=60°.
的长为
∥解答题专练(三).∥
1.解:(1)原式
(2) 原式
2.解:(1)设该市改造小区投入资金的年平均增长率为x.
根据题意,得
解得 (不合题意,舍去).
答:该市改造小区投入资金的年平均增长率为20%.
(2)设该市在2024年可以改造y 个小区.
根据题意,得80×(1+20%)y≤1440×(1+20%).
解得y≤18.
∵y 为整数,∴y 的最大值为18.
答:该市在2024年最多可以改造18个小区.
3.解:(1)①400
②“A.音乐”的人数为400×15%=60(人).
“C.美术”的人数为400-100-140-40-60=60(人).补全条形统计图如图1 所示.
③54
(人)、
答:估计该校参加“D.阅读”的学生有 980人.
(3)画树状图如图2 所示.
由树状图可知,共有12种等可能的结果,其中恰好抽中甲、乙两人的结果有2种.
∴P(恰好抽中甲、乙两人)
解答题专练(四)∥
1.解:(1)设y关于x的函数解析式为
把x=6,y=3代入,得 解得k=18.
∴y关于x的函数解析式为
(2)把x=2代入 得
∴火焰的像高为9 cm.
(3)把y=6代入 得 解得x=3.
由 的图象,得当x>0时,y随x的增大而减小.
∴当y≤6时,x≥3.
∴若火焰的像高 y 不超过6 cm,小孔到蜡烛的距离x至少是3cm.
2.解:如图,过点 C 作CM⊥DF 于点M.
∴∠CMD=90°.
在 Rt△CDM 中,
∵点C,F 的水平距离为3m,∴MF=3m.
∴DF=DM+MF=5+3=8(m).
根据题意,得∠F=90°.
在 Rt△BDF 中,
答:水渠离水面的高度 BF 约为1.44 m.
3.解:(1)作图如图1所示.
(2)证明:如图2,连接OD.
∵OD=OA,∴∠ODA=∠BAD.
∵AD平分∠BAC,∴∠DAC=∠BAD.
∴∠ODA=∠DAC.∴OD∥AC.
∵DE⊥AC,∴∠AED=90°.
,即DE⊥OD.
∵OD 是⊙O 的半径,∴DE 是⊙O 的切线.
(3)如图2,过点 D 作. DQ⊥AB 于点Q.
∵AD=AD,∠EAD=∠QAD,
∴△ADQ≌△ADE.∴AE=AQ.
∵OD∥AC,∴∠BAC=∠QOD.
在 Rt△OQD 中,
设OD=5m,则OQ=3m,OA=5m.
∴AE=AQ=OA+OQ=5m+3m=8m.
∵OD∥EA,∴△DOF∽△AEF、
1.(1)计算:
(2)先化简,再求值: ,其中x=-2.
2.某印刷厂每月生产甲、乙两种练习本共40万本,且所有练习本当月全部卖出,其中成本、售价如下表所示.
品种 甲种练习本 乙种练习本
成本 1.2元/本 0.4元/本
售价 1.6元/本 0.6元/本
(1)若该印刷厂五月的利润为11万元,求生产甲、乙两种练习本分别是多少万本;
(2)某学校计划用7680元的经费到该印刷厂采购练习本.经商讨,该印刷厂同意甲种练习本售价打九折,乙种练习本不能让利.若学校能采购到1万本,且不超支,则最多能购买甲种练习本多少本
3.新新考向·开放探索某校在“劳动节”期间举行投篮比赛活动.学校在每班随机抽取10名同学参加,规定每人投篮10次.下面对八(3)班10名参赛同学的投中次数进行了收集、整理和分析.
【收集数据】
10名参赛同学的投中次数分别是3,2,1,4,3,5,6,4,3,5.
【整理数据】
投中次数 1 2 3 4 5 6
频数 1 a b 2 2 1
根据上面整理的数据,制作出扇形统计图如图所示.
【分析数据】
统计量 平均数 中位数 众数 方差
八(3)班 e f 3 2.04
【解决问题】
根据以上信息,回答下列问题:
(1)填空:d= ,f= ,e= ;
(2)根据扇形统计图,将投中次数所占百分比不低于20%的记为“最多投中数”,学校通过“最多投中数”来评估八(3)班学生的投篮情况.若八(3)班共有40名学生,估计全班同学能达到“最多投中数”的有多少名;
【数据应用】
(3)八(6)班10名参赛同学的投中次数的相关信息如下表.
统计量 平均数 中位数 众数 方差
八(6)班 3.6 4 2 3.64
根据以上两个表中的统计量,你认为哪个班同学的投篮水平更高一些,并给出一条合理的解释.
解答题专练(二)
1.乌馒头是江北慈城地方特色点心,用麦粉发酵,再掺以白糖、黄糖,蒸制而成.因其用黄糖,颜色暗黄,所以称之谓“乌馒头”.某商店销售乌馒头,通过分析销售情况发现,乌馒头的日销售量y(单位:盒)是销售单价x(单位:元/盒)的一次函数,销售单价、日销售量的部分对应值如下表,已知销售单价不低于成本价且不高于20元/盒,每天销售乌馒头的固定损耗为20元,且成本价为12元/盒,日销售量为200盒.
销售单价x/(元/盒) 15 13
日销售量y/盒 500 700
(1)求乌馒头的日销售量y 与销售单价x 之间的函数解析式;
(2)“端午乌馒重阳粽”是慈城的习俗,端午节期间,商店决定采用降价促销的方式回馈顾客,在顾客获得最大实惠的前提下,当乌馒头每盒降价多少元时,商店日销售纯利润为1480元
(3)当销售单价定为多少时,日销售纯利润最大 并求出日销售最大纯利润.
2.新新考向·情境命题小红在给自建房的楼上安装栏杆时,利用定滑轮设计了如图1的方案帮家人将所需材料运送至该楼层.运送中,小红突发奇想,想利用这个装置测量一下自己所在楼层距离地面的高度AB.如图2,将定滑轮固定在该楼层上方支架点C处(点A,B,C在同一直线上),并利用定滑轮的工作原理拉动水平地面上的箱子,在起始位置点 D 时,测量出绳子和水平面的夹角为30°,拉动一段距离后箱子到达点 F 处,测量出绳子和水平面的夹角为53°.已知定滑轮距离该楼层地面的高度 BC=1.5m,箱子的高度. 移动过程中绳子收回的长度为4.5m,DE,FM,AC 均垂直于地面AE,求AB 的高度.(参考数据:
3.如图,已知AB 为⊙O 的直径,BC 为⊙O 的切线,连接AC 交⊙O 于点 D,F 为 的中点,连接 BF 交 AC 于点 E,过点 C 作( 垂足为G.
(1)求证:CG 平分
(2)若 求 的长.
解答题专练(三)
1.(1)计算:
(2)化简:
2.聚焦“绿色发展,美丽宜居”县城建设,围绕“老旧改造人人参与,和谐家园家家受益”的思路,某市从2021年起连续投入资金用于“建设美丽城市,改造老旧小区”,让小区“旧貌”换“新颜”.已知每年投入资金的增长率相同,其中=2021年投入资金1000万元,2023年投入资金1440万元.
(1)求该市改造小区投入资金的年平均增长率;
(2)2023年每个小区改造的平均费用为80万元,2024年为提高小区品质,每个小区改造的平均费用计划增加20%.如果投入资金年增长率保持不变,那么该市在2024年最多可以改造多少个小区
3.某校为落实“双减”政策,增强课后服务的吸引力,充分利用课后服务时间,为学有余力的学生拓展学习空间,成立了5个活动小组(每名学生只能参加一个活动小组):A.音乐,B.体育,C.美术,D.阅读,E.人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
(1)①此次调查一共随机抽取了 名学生;
②补全条形统计图;
③扇形统计图中圆心角α= °.
(2)若该校有2 800名学生,估计该校参加“D.阅读”的学生人数;
(3)学校计划从参加“E.人工智能”的甲、乙、丙、丁四名学生中随机抽取两人参加市青少年机器人竞赛,请用画树状图法或列表法求出恰好抽中甲、乙两人的概率.
解答题专练(四)
1. 新新考向·学科融合在两千四百年前,墨子和他的学生做了世界上第1个小孔成像的实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”,大意是:影像倒立,在光线交会处有一小孔;关于影像的大小,在于小孔相对物、像的位置.图2 是图1中小孔成像实验的示意图,在图2中,根据小孔成像的科学原理,当像距(小孔到像的距离)和物高(蜡烛火焰高度)不变时,火焰的像高y(单位:cm)是物距(小孔到蜡烛的距离)x(单位:cm)的反比例函数,图象如图3所示,且当x=6时,y=3.
(1)求y关于x 的函数解析式;
(2)若小孔到蜡烛的距离x为2cm,求火焰的像高y;
(3)根据反比例函数的图象分析,若火焰的像高y不超过6cm,求小孔到蜡烛的距离x至少是多少厘米.
2.新新考向·情境命题水车又称孔明车,是我国最古老的农业灌溉工具.如图1是一种水车的实物图,由立式水轮、竹筒、支撑架和水槽等部件组成.某数学兴趣小组对其进行了研究,示意图如图2所示,⊙O 为立式水轮,水轮在水流的作用下,将水送至C处,再经水槽送至 B处水渠,D 为水轮与水面的交汇处,连接BC,CD,BD,若CD=10m,∠CDF=60°,点C,F 的水平距离为3m,且∠BDF=10°,求水渠离水面的高度 BF.(结果精确到0.01 m.参考数据:
3.新新考向·图形操作如图,已知 AB 为⊙O 的直径,AC 是⊙O 的弦, 的平分线 AD 交⊙O 于点 D、
(1)尺规作图:过点 D 作DE⊥AC 交AC 的延长线于点E,连接OE 交AD 于点 F;(保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:DE 是⊙O 的切线;
(3)在(1)的条件下,若AF=8,求DF 的长.
1.解:(1)原式
(2)原式:
当x=-2时,原式=-8×(-2)+13=29.
2.解:(1)设生产甲种练习本 x 万本,生产乙种练习本y万本.
根据题意,得
解得
答:生产甲种练习本15万本,生产乙种练习本25万本.
(2)设该学校购买甲种练习本m本,则购买乙种练习本(10 000-m)本.
根据题意,得1.6×0.9m+0.6(10 000-m)≤7 680.解得 m≤2000.
∴m的最大值为2000.
答:最多能购买甲种练习本2000本.
3.解:(1)30;3.6;3.5
(2)40×(20%+20%+30%)=28(名).
答:估计全班同学能达到“最多投中数”的有28名.
(3)八(3)班同学的投篮水平更高一些.理由如下:
∵两个班投中次数的平均数相同,八(3)班投中次数的众数比八(6)班的高,投中次数的方差小于八(6)班,水平比较稳定,
∴我认为八(3)班同学的投篮水平更高一些.
(答案不唯一,合理即可)
∥解答题专练(二),
1.解:(1)设乌馒头的日销售量 y 与销售单价x 之间的函数解析式为y= kx+b(k≠0).
将点(15,500),(13,700)代入,得
解得
∴乌馒头的日销售量y 与销售单价x之间的函数解析式为y=-100x+2 000(12≤x≤20).
(2)在 y=--100x+2 000 中,令 y=200,得 200=—100x+2 000.
解得x=18.∴原来销售单价为18元/盒.
设当日销售单价为m 元/盒时,销售利润为1480元.
根据题意,得(-100m+2000)(m-12)=1480+20.
解得
∵为了使顾客获得最大实惠,∴m=15.
∴18-15=3(元).
答:当乌馒头每盒降价3 元时,商店日销售纯利润为1480元.
(3)设日销售纯利润为ω 元.
根据题意,得ω=(--100x+2 000)(x--12)--20=-100x +3200x-24020=-100(x-16) +1580.
∵--100<0,∴当x=16时,ω有最大值1580.
答:当销售单价定为16元/盒时,日销售纯利润最大,日销售最大纯利润为1580元.
2.解:如图,延长DF 交BA 于点 H.
根据题意,得DH⊥AB.
∵DE⊥AE,AB⊥AE,
∴∠DEA=∠EAH=∠DHA=90°.
∴四边形 DEAH 为矩形.∴AH=DE=0.5m .
在Rt△CHD中,∵∠CDH=30°,∴CD=2CH.
在 Rt△CHF 中,
解得CH=6.
∴AB=CH+AH--BC=6+0.5-1.5=5(m).
答:AB 的高度约为5m .
3.解:(1)证明:如图,连接AF.
∵F 为 的中点,∴AF=DF.∴∠FAD=∠ABF.
∵AB 为⊙O 的直径,∴∠AFB=90°.
∵CG⊥BF,∴∠CGF=90°=∠AFB.
∴CG∥AF,∠BCG+∠CBG=90°.
∴∠FAD=∠ACG.∴∠ACG=∠ABF.
∵BC 为⊙O 的切线,
∴∠ABC=90°,即∠ABF+∠CBG=90°.
∴∠BCG=∠ABF.
∴∠ACG=∠BCG,即CG平分∠ACB.
(2)如图,连接OF.
∵∠ECG=∠BCG,CG=CG,∠CGE=∠CGB,
∴△CGE≌△CGB.∴CE=CB.
∴AC=AE+CE=AE+CB=2+CB.
在 Rt△ABC 中,∵根据勾股定理,
解得BC=2.
在 Rt△ABC 中,
∴∠ABF=∠ECG=30°.
∵OF=OB,∴∠OFB=∠ABF=30°.
∴∠FOA=∠OFB+∠ABF=60°.
的长为
∥解答题专练(三).∥
1.解:(1)原式
(2) 原式
2.解:(1)设该市改造小区投入资金的年平均增长率为x.
根据题意,得
解得 (不合题意,舍去).
答:该市改造小区投入资金的年平均增长率为20%.
(2)设该市在2024年可以改造y 个小区.
根据题意,得80×(1+20%)y≤1440×(1+20%).
解得y≤18.
∵y 为整数,∴y 的最大值为18.
答:该市在2024年最多可以改造18个小区.
3.解:(1)①400
②“A.音乐”的人数为400×15%=60(人).
“C.美术”的人数为400-100-140-40-60=60(人).补全条形统计图如图1 所示.
③54
(人)、
答:估计该校参加“D.阅读”的学生有 980人.
(3)画树状图如图2 所示.
由树状图可知,共有12种等可能的结果,其中恰好抽中甲、乙两人的结果有2种.
∴P(恰好抽中甲、乙两人)
解答题专练(四)∥
1.解:(1)设y关于x的函数解析式为
把x=6,y=3代入,得 解得k=18.
∴y关于x的函数解析式为
(2)把x=2代入 得
∴火焰的像高为9 cm.
(3)把y=6代入 得 解得x=3.
由 的图象,得当x>0时,y随x的增大而减小.
∴当y≤6时,x≥3.
∴若火焰的像高 y 不超过6 cm,小孔到蜡烛的距离x至少是3cm.
2.解:如图,过点 C 作CM⊥DF 于点M.
∴∠CMD=90°.
在 Rt△CDM 中,
∵点C,F 的水平距离为3m,∴MF=3m.
∴DF=DM+MF=5+3=8(m).
根据题意,得∠F=90°.
在 Rt△BDF 中,
答:水渠离水面的高度 BF 约为1.44 m.
3.解:(1)作图如图1所示.
(2)证明:如图2,连接OD.
∵OD=OA,∴∠ODA=∠BAD.
∵AD平分∠BAC,∴∠DAC=∠BAD.
∴∠ODA=∠DAC.∴OD∥AC.
∵DE⊥AC,∴∠AED=90°.
,即DE⊥OD.
∵OD 是⊙O 的半径,∴DE 是⊙O 的切线.
(3)如图2,过点 D 作. DQ⊥AB 于点Q.
∵AD=AD,∠EAD=∠QAD,
∴△ADQ≌△ADE.∴AE=AQ.
∵OD∥AC,∴∠BAC=∠QOD.
在 Rt△OQD 中,
设OD=5m,则OQ=3m,OA=5m.
∴AE=AQ=OA+OQ=5m+3m=8m.
∵OD∥EA,∴△DOF∽△AEF、
同课章节目录
