2025年中考数学二轮复习——二次函数的图象与几何变换(含答案)
文档属性
| 名称 | 2025年中考数学二轮复习——二次函数的图象与几何变换(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 979.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 00:00:00 | ||
图片预览


文档简介
2025年中考数学二轮复习——二次函数的图象与几何变换
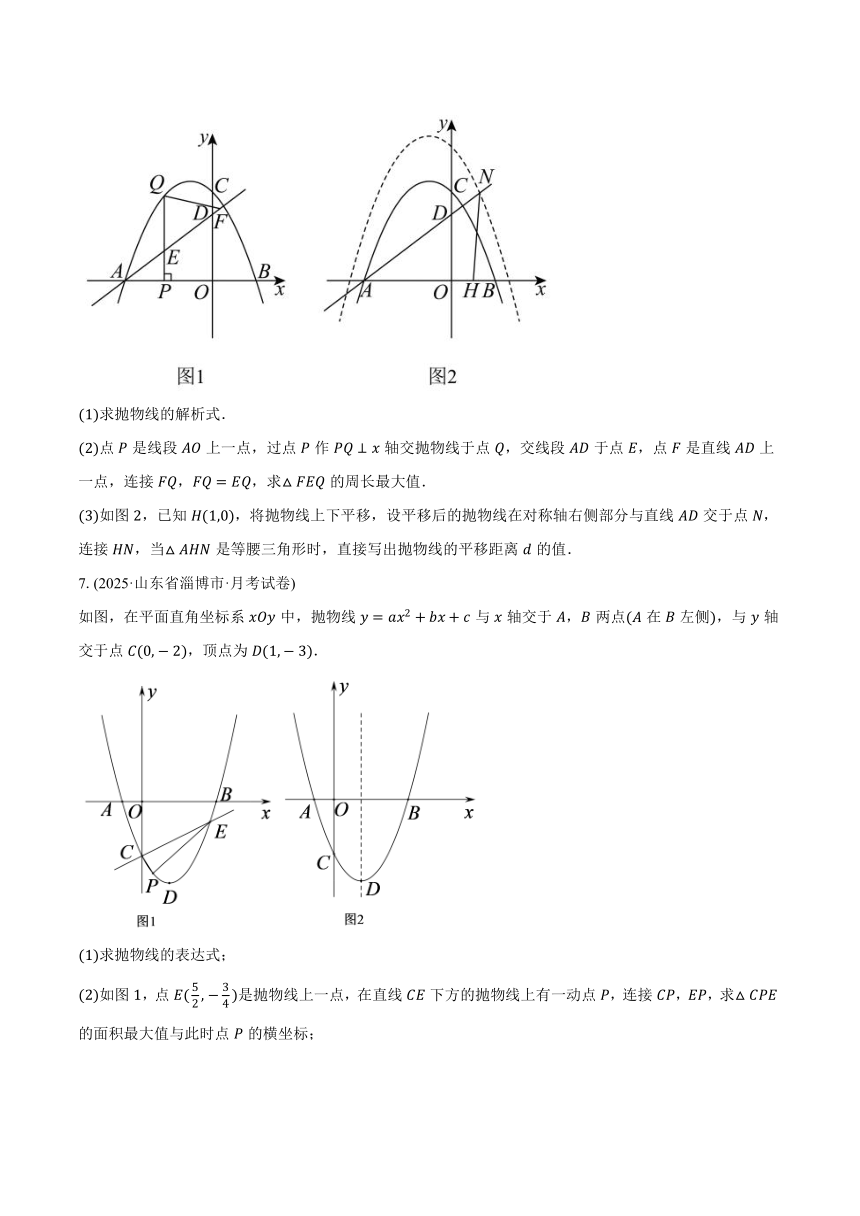
1.(2025·湖北省黄冈市·模拟题)如图,已知抛物线与轴交于,两点,与轴交于,点,关于直线对称.
求抛物线的解析式.
平移抛物线,且平移后抛物线的顶点始终落在直线上,记平移后的新抛物线为,与轴交于点,求点纵坐标的最大值.
在的条件下,记抛物线顶点的横坐标为,长为.
求关于的函数解析式
将点向右平移个单位长度得到点,当随着增大而增大时,若与线段只有一个交点,直接写出的取值范围.
2.(2025·河北省保定市·期末考试)
已知抛物线:.
求抛物线的对称轴;
若点,,均在抛物线上,、、只有一个为正数.
求的取值范围;
直接写出符合条件的一个的取值范围,使得随的增大而减小;
若,将抛物线向左平移个单位,得到抛物线,点为抛物线上一点,且横坐标为,过点作轴交抛物线与点,点在抛物线对称轴的右侧若,求的值.
3.(2025·河北省石家庄市·月考试卷)
如图,在平面直角坐标系中,二次函数的图象与轴交于,两点,且有,与轴交于点,顶点为点.
求,两点的坐标.
将抛物线进行平移,使点恰好落在点关于轴的对称点上.
求出平移后抛物线的解析式,并指出其顶点坐标
求出平移过程中抛物线段所扫过的面积阴影部分.
4.(2025·浙江省·模拟题)
已知抛物线的顶点向右平移个单位长度再向上平移个单位长度后与抛物线为常数的顶点重合.
求,的值;
点在抛物线上,点在抛物线上:
若,求的最大值;
若,且,求的值.
5.(2025·山东省临沂市·模拟题)
已知抛物线:.
当时,求的值;
点是抛物线上一点,若,且时,求的值;
当时,把抛物线向下平移个单位长度得到新抛物线,如果抛物线与轴的一个交点的坐标为,且,请求出的取值范围.
6.(2024·广东省中山市·模拟题)
如图,在平面直角坐标系中,抛物线与轴交于、两点点在点的左侧,与轴交于点,点,连接.
求抛物线的解析式.
点是线段上一点,过点作轴交抛物线于点,交线段于点,点是直线上一点,连接,,求的周长最大值.
如图,已知,将抛物线上下平移,设平移后的抛物线在对称轴右侧部分与直线交于点,连接,当是等腰三角形时,直接写出抛物线的平移距离的值.
7.(2025·山东省淄博市·月考试卷)
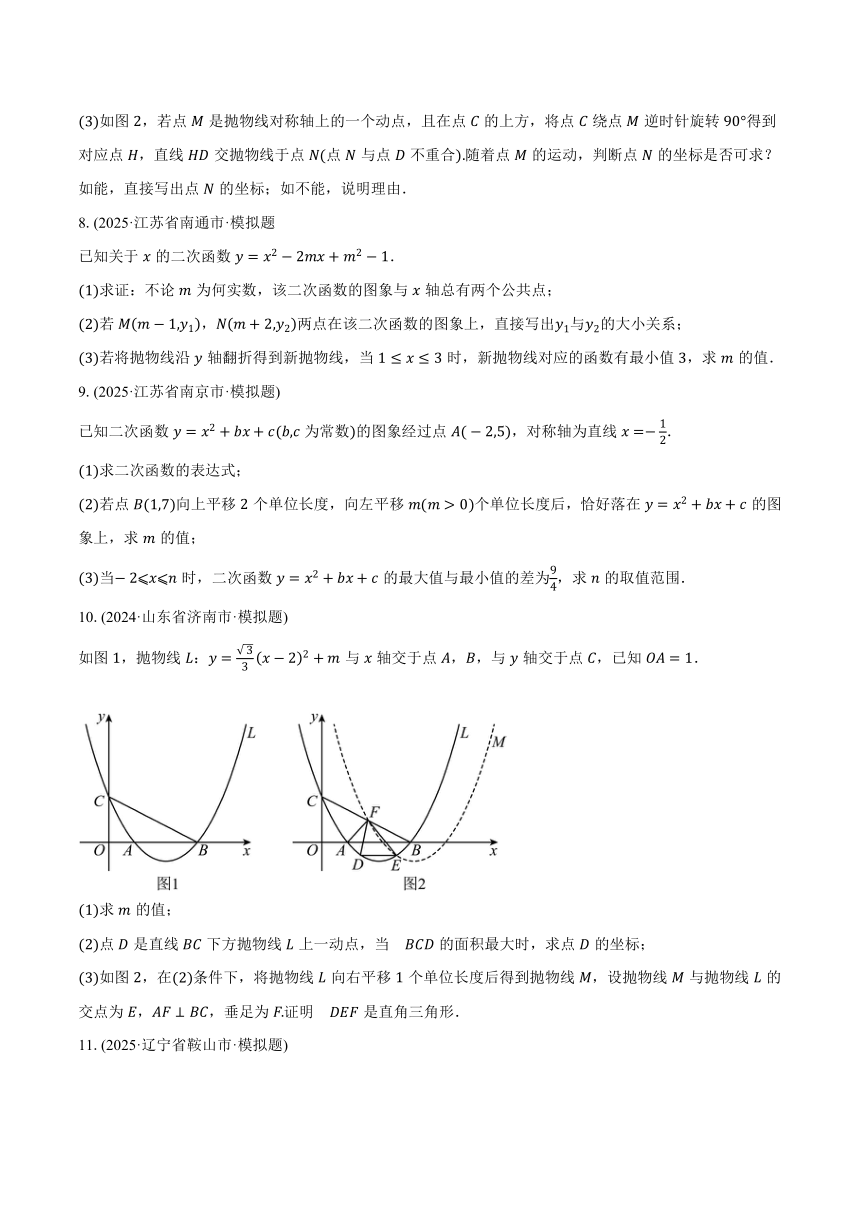
如图,在平面直角坐标系中,抛物线与轴交于,两点在左侧,与轴交于点,顶点为.
求抛物线的表达式;
如图,点是抛物线上一点,在直线下方的抛物线上有一动点,连接,,求的面积最大值与此时点的横坐标;
如图,若点是抛物线对称轴上的一个动点,且在点的上方,将点绕点逆时针旋转得到对应点,直线交抛物线于点点与点不重合随着点的运动,判断点的坐标是否可求?如能,直接写出点的坐标;如不能,说明理由.
8.(2025·江苏省南通市·模拟题
已知关于的二次函数.
求证:不论为何实数,该二次函数的图象与轴总有两个公共点;
若,两点在该二次函数的图象上,直接写出与的大小关系;
若将抛物线沿轴翻折得到新抛物线,当时,新抛物线对应的函数有最小值,求的值.
9.(2025·江苏省南京市·模拟题)
已知二次函数为常数的图象经过点,对称轴为直线.
求二次函数的表达式;
若点向上平移个单位长度,向左平移个单位长度后,恰好落在的图象上,求的值;
当时,二次函数的最大值与最小值的差为,求的取值范围.
10.(2024·山东省济南市·模拟题)
如图,抛物线:与轴交于点,,与轴交于点,已知.
求的值;
点是直线下方抛物线上一动点,当的面积最大时,求点的坐标;
如图,在条件下,将抛物线向右平移个单位长度后得到抛物线,设抛物线与抛物线的交点为,,垂足为证明是直角三角形.
11.(2025·辽宁省鞍山市·模拟题)
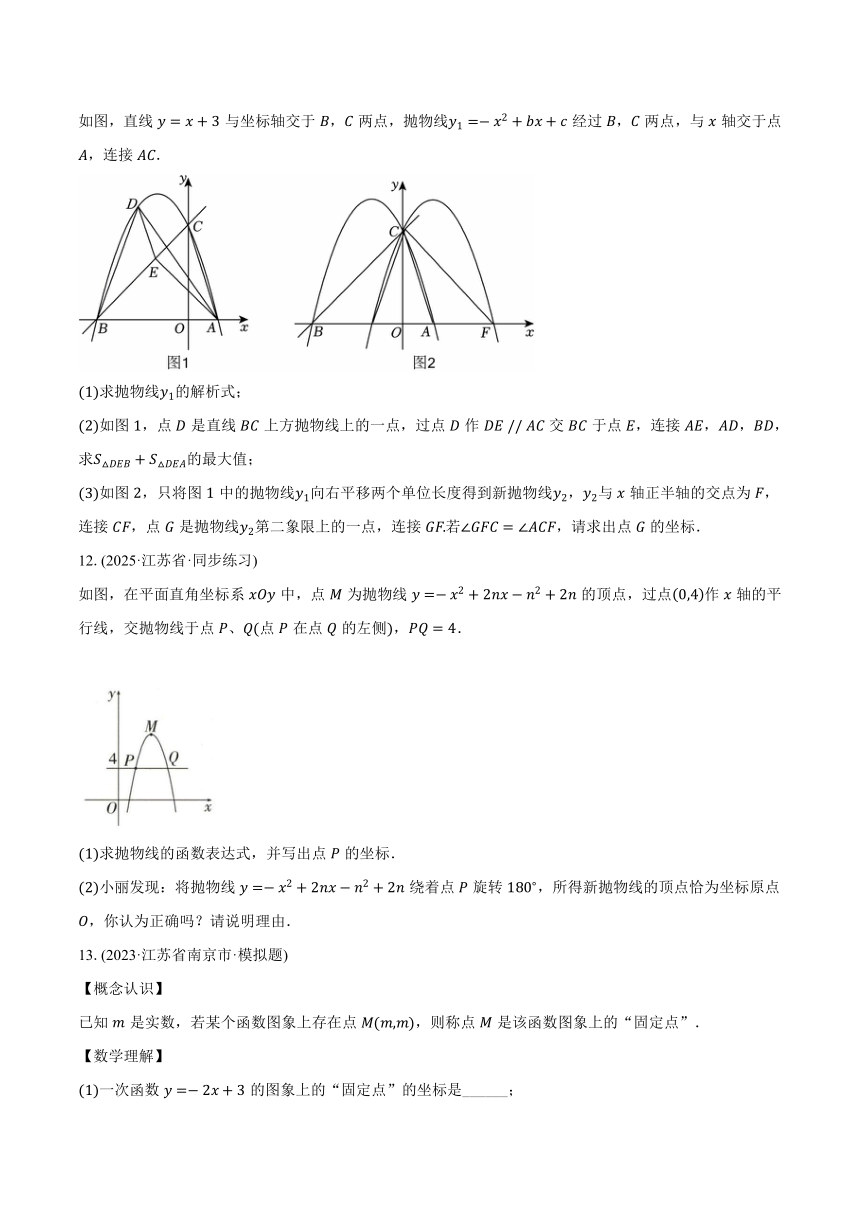
如图,直线与坐标轴交于,两点,抛物线经过,两点,与轴交于点,连接.
求抛物线的解析式;
如图,点是直线上方抛物线上的一点,过点作交于点,连接,,,求的最大值;
如图,只将图中的抛物线向右平移两个单位长度得到新抛物线,与轴正半轴的交点为,连接,点是抛物线第二象限上的一点,连接若,请求出点的坐标.
12.(2025·江苏省·同步练习)
如图,在平面直角坐标系中,点为抛物线的顶点,过点作轴的平行线,交抛物线于点、点在点的左侧,.
求抛物线的函数表达式,并写出点的坐标.
小丽发现:将抛物线绕着点旋转,所得新抛物线的顶点恰为坐标原点,你认为正确吗?请说明理由.
13.(2023·江苏省南京市·模拟题)
【概念认识】
已知是实数,若某个函数图象上存在点,则称点是该函数图象上的“固定点”.
【数学理解】
一次函数的图象上的“固定点”的坐标是______;
求证:反比例函数的图象上存在个“固定点”;
将二次函数的图象在轴下方的部分沿轴翻折到轴上方,图象的其余部分保持不变,翻折后的图象与原图象在轴上方的部分组成一个类似“”形状的新图象若新图象上恰好存在个“固定点”,求的值.
14.(2025·湖北省·模拟题)
如图抛物线与轴交于和两点,与轴交于点,
求抛物线的解析式;
点是轴下方抛物线上一点,设点的横坐标为,过点作轴的平行线交直线于点,过点作轴的垂线交轴于,以,为邻边的矩形的周长记为.
请直接写出关于的函数关系式;
求的最值;
将抛物线向上平移个单位长度,再向左平移个单位长度,若新抛物线的顶点在内不含边界,直接写出的取值范围.
15.(2025·重庆市市辖区·期中考试)
如图,在平面直角坐标系中,抛物线交轴于,两点,交轴于且点,.
求抛物线的表达式;
点是直线上方抛物线上一点,过点作轴于点,过点作于点,点、点分别是直线、轴上的两动点,连接,,当取得最大值时,求三角形周长的最小值;
将抛物线沿射线方向平移个单位得新抛物线,点是轴上方新抛物线上的一点,连接,过点作交直线于点,当时,直接写出所有符合条件的点的横坐标.
16.(2025·江苏省苏州市·模拟题)
抛物线的与轴交于两点点在点的左边,顶点为.
顶点坐标为 ;
如图,若点的坐标是,连接.
把线段沿一定的方向平移,平移后,点的对应点为,点的对应点为,若点,点均在抛物线上,求点的坐标;
将抛物线沿射线方向平移得到抛物线,且抛物线经过点请问在抛物线上是否存在点,使得,若存在,请求出点的坐标;若不存在,请说明理由.
17.(2025·广东省湛江市·模拟题)
如图,抛物线过点,与轴交于点和点点在点左侧,与轴交于点,顶点的坐标为.
求抛物线的表达式和点的坐标.
点是线段上一动点,求周长的最小值.
平移抛物线得到抛物线,已知抛物线过点,顶点为,其对称轴与抛物线交于点若,直接写出点的坐标.
18.(2025·内蒙古自治区·模拟题)
在平面直角坐标系中,抛物线与轴交于,两点点在点的左侧
请求出该二次函数的对称轴和顶点坐标:
当时,二次函数的最大值与最小值的差为,求的取值范围;将抛物线向左平移个单位,再向上平移个单位得到新抛物线与原抛物线交于点直线与原抛物线交于点,与新抛物线交于点.为线段上的动点,过点作轴,垂足为,连接,,当在中的取值范围内,取得最大值时,求的最小值.
19.(2025·山东省·模拟题)
二次函数的图象交轴于点,点,交轴于点,抛物线的顶点为点.
求二次函数的解析式;
如图,点是抛物线上的一点,设点的横坐标为,点在对称轴上,且,若,请求出的值;
如图,将抛物线绕轴正半轴上一点旋转得到新抛物线交轴于,两点,点的对应点为点,点的对应点为点若,求旋转中心点的坐标.
参考答案
1.解:,两点关于直线对称,
抛物线的对称轴为直线.
,
解得.
又抛物线经过点,
.
抛物线的解析式为.
由于抛物线顶点坐标始终落在直线上,
故可设平移后抛物线解析式为.
令,
此时.
当时,有最大值,
即点纵坐标的最大值为.
由题意可知,的解析式为,
点坐标为,点坐标为,
.
关于的图象如图所示.
由图象可知,随着增大而增大部分是或.
由题意可知,的坐标为,
如图,当和只有一个交点时,
若该交点在抛物线对称轴右侧,
则当时,,且当时,,
解得.
若该交点在抛物线对称轴左侧,
则当时,,且当时,,
解得.
综上所述,当或时,符合条件.
2.对称轴为直线;
;;
或.
3.解:设点的坐标为,
由于,则点的坐标为
而二次函数的对称轴为直线,
,
解得,
点的坐标为,点的坐标为.
由于点关于轴的对称点的坐标为,
二次函数的图象向左平移了个单位长度.
,
其向左平移两个单位长度后的解析式为.
平移后的抛物线过点,
,
解得,
平移后的抛物线的解析式为
平移后的抛物线的顶点坐标为.
抛物线向左平移了个单位长度且平移后抛物线的顶点坐标为.
平移过程中,抛物线段所扫过的阴影部分面积等于底边长为,高为的平行四边形的面积
抛物线段所扫过的阴影部分面积为.
4.;
当时,的最大值为;.
5.或;
;
.
6.解:抛物线与轴交于、两点,
,
解得,
抛物线的解析式为;
如图,过点作于点,则,
,,
,
,,
,,
在中,由勾股定理得
轴,
,
,
,
,
,,
,
当最大时,的周长最大.
设,其中.
,,
设直线的解析式为
解得
直线的解析式为,
,
,
,
时,有最大值,最大值为,
周长的最大为.
由题知:平移后的抛物线的解析式为
设,则
又直线的解析式为,点在上,
,
,
,
,,
.
当是等腰三角形时,
若,则,
解得舍去,,
若,
则,
解得:,舍去,
,
若,则,
解得舍去.
综上,抛物线的平移距离的值为或.
7.解:抛物线的顶点为,
可设表达式为,
将点代入,
得,
解得,
,
抛物线的解析式为.
作轴交于.
由,,
设直线表达式为:,
将,的坐标代入,得
解得
直线表达式为:
设点的坐标为,点的坐标为,
当时,
此时点的横坐标为.
点的坐标为.
8.【详解】证明:令,则
不论为何实数,方程有两个不相等的实数根
无论为何实数,该二次函数的图象与轴总有两个公共点
解:二次函数的对称轴为:直线
,抛物线开口向上
抛物线上的点离对称轴越远对应的函数值越大
点到对称轴的距离为:
点到对称轴的距离为:
解:抛物线
沿轴翻折后的函数解析式为
该抛物线的对称轴为直线
若,即,则当时,有最小值
解得,
若,即,则当时,有最小值
不合题意,舍去
若,,则当时,有最小值
解得,
综上,的值为或
9.【小题】
解:设二次函数的解析式为,把代入得,
解得,
【小题】
解:点平移后的点的坐标为,
则,解得或舍,
的值为
【小题】
解:当时,
最大值与最小值的差为,解得:不符合题意,舍去;
当时,
最大值与最小值的差为,符合题意;
当时,
最大值与最小值的差为,解得或,不符合题意;
综上所述,的取值范围为.
10.【小题】
解:,
,
在抛物线:,
,解得:,
故答案为:;
【小题】
令,
解得:或,
,
令,则,
,
;
过点作轴的平行线于点,
设,则,
,
,
当时,的面积最大,
,
;
【小题】
证明:如图,连接,
,
,
,
是的中点,,
,
在中,,
,
过点作于点,
,
点是的中点,
是的中位线,
,
轴,
将抛物线向右平移个单位长度后得到抛物线,
则:,
令,解得:,
,
,
轴,
,即是直角三角形.
11.解:直线与坐标轴交于,两点,
则点、的坐标分别为:、,
由题意得:,
解得,
;
连接,
,
同底等高,
,
过点作轴于点交于点,设,则,
则,
,
,抛物线开口向下,
当时,最大值,
则的最大值是;
当时可得,
,
向右平移两个单位长度得到新抛物线,
则,
当时,解得或,
即,
,
,
如图,设交于点,当时,
,,
≌,
,
则点,
由点、的坐标得,直线的解析式为:,
联立方程组,.
解得:,舍去,
12.【小题】
抛物线过点,点的纵坐标为,,解得,.,,解得,抛物线的表达式为,,解得或,.
【小题】
正确.理由如下:,,绕着点旋转后的对称点为,与正好关于轴对称,所得新抛物线的对称轴是轴.抛物线,抛物线的顶点为,顶点到直线的距离也为,所得新抛物线顶点到直线的距离也为,所得新抛物线的顶点应为坐标原点.
13.;
证明:在中,令,可得.
解得,.
将代入中,得.
将代入中,得.
因此反比例函数的图像上存在个“固定点”,分别为和
图象大致如下:
设固定点为,将代入,
得,即,
,
即原图象翻折前有两个“固定点”,
翻折后图形为:,
将代入:,
即,
依题意,只需该方程有一个根即可对应一个“固定点”,与前两个合成三个,
,
即,
,
当时,不合题意,舍去,
当时,,
综上,.
14.解:将和的坐标分别代入中,得,解得,
抛物线解析式为.
.
点是轴下方抛物线上一点,设点的横坐标为,
,,
对于,令,得,
,
设直线的解析式为,
将,两点的坐标分别代入中,得,解得
直线的解析式为,
根据点的位置分两种情况:
当时,即点在点的左侧,,
,
,
,,
;
当时,点在点的右侧,,
,,
;
;
当时,函数没有最值;
当时,函数,
当时,;
综上所述,当时,的最大值为;
.
,
抛物线的顶点为,将抛物线向上平移个单位长度,再向左平移个单位长度,得到新抛物线的顶点的坐标为,即,
点是直线上的动点,
设直线的解析式为,
将,两点的坐标分别代入中,得,解得
直线的解析式为,
当点在直线上时,,
解得;
当点在直线上时,直线的解析式为,
,解得,
新抛物线的顶点在内不含边界,
.
15.解:对于,令,得,
,
,
在中,,,
,
,
把,分别代入中,得,解得
抛物线的表达式为;
设直线的解析式为,
把点,分别代入中,得
解得
直线的解析式为,
设交于点,如图:
设点,
轴,
,,轴,
,,
,,
,
又,
是等腰直角三角形,
,
轴,
,
,
,
,
,,
,
,
当时,取得最大值,此时点,
作点关于轴的对称点,作点关于直线的对称点,连接,,,,
由对称性得:,,
,
点,
由对称性得,,,
三角形的周长,
由两点之间线段最短可得,,
当、、、四点依次共线时,取得最小值,的最小值为线段的长,即三角形周长的最小值为线段的长,
,,
,
三角形周长的最小值为;
满足条件的点的横坐标为或.
,,,
,,,
将点沿射线方向平移个单位能够与点重合,相当于将点先向右平移个单位,再向上平移个单位得到点,
将抛物线沿射线方向平移个单位得新抛物线,相当于将抛物线先向右平移个单位,再向上平移个单位得新抛物线,
,
新抛物线的解析式为,
当点在直线上方,且在轴上方新抛物线上时,过点作于,过点作轴于,过点作交的延长线于,如图:
,,,,
,,,,,
,
,
在中,,
,
,
,
,
交直线于点,
,
在中,,,
,
设,则,,
,,
,
,
,,
∽,
,
,,
又,
,
把代入中,得,
解得,舍去,
此时点的横坐标为;
当点在直线下方,且在轴上方新抛物线上时,过点作轴的平行线,过点作于,过点作交的延长线于,如图:
则轴,,,,
,
,
由可知,,
在中,,,
设,则,,
,,
∽,
,
,,
又,
,
把代入中,得,
解得,舍去,
此时点的横坐标为;
综上所述,点的横坐标为或.
16.【小题】
【小题】
解:把代入得,,
解得,,
,
设所在直线解析式为,
把,代入得,
解得
直线的解析式为,
平移后所在直线解析式为,
设点坐标为,则点坐标为,
点,点均在抛物线上,
解得
点的坐标为;
设过点平行于的直线解析式为,
把代入得,,
,
过点平行于的直线解析式为,
设沿射线方向平移得到抛物线的解析式为,
把点代入,得,
解得不合题意,舍去或,
抛物线的解析式为,
如图,若与轴交点在点的下方,设交点为,
,
,
点的坐标为,
直线的解析式为,
解得或
点坐标为或
如图,若与轴的交点在点的上方,设交点为,
过点作,垂足分别为点和点,
由题意得,,
过点作轴,过点作,垂足分别为点,点,
则,且相似比,
设,则,
,
.
解得,
点坐标为,
设直线的解析式为,把和代入得,
解得
直线的解析式为,
解得或
点坐标为或;
综上所述,点坐标为或或或.
17.顶点的坐标为,设二次函数表达式为,
将点代入得,
抛物线的表达式为:,
当时,或,
点在点左侧,
点的坐标为;
当时,,
点的坐标为,
直线的表达式为:,
作关于的对称点,则,设垂足为,则点为与的中点,
因为直线的表达式为,,
所以的表达式为,
联立可得点的坐标为,点的坐标为,
,,,
,,
,
即周长的最小值为;
的坐标为或.
18.【小题】
解:,
二次函数的对称轴为直线,
当时,.
即顶点坐标为.
【小题】
解:,
即函数开口向上,对称轴为直线,
即当时,有最小值,为;
当时,;
最大值与最小值的差是,最小值是,
最大值为;
当时,,
解得:,,
.
,
故将抛物线向左平移个单位,再向上平移个单位得到新抛物线为;
当时,
解得,
.
当时,
解得,,
,
设,则,
,
由得,当时,取得最大值,
此时,点的坐标为,点的坐标为;
将点向左平移个单位长度得,连接,与轴交于点,作交于点,连接;
过点作轴,交于点,如图:
,,
是平行四边形,
,
故,此时有最小值;
,,轴,
,
故,,
,
故,
的最小值为.
19.【小题】
将,代入,
得
解得:,.
抛物线的解析式:;
【小题】
如答图,设抛物线对称轴与轴的交点为,过作于,
抛物线的对称轴为,
,,
,
,
,
,
,
即:,.
点的横坐标为,
,,,
则,
代入得:,
解得或舍;
.
【小题】
如答图,过作轴于,过作交的延长线于点,
令,则,
,,
,,,
,,
,
,
在中,
,则,
,,
在中,,
,
则:,
在中,,
则:,
即:,
得.
,
由题意知,、关于点对称,
已知:、,
则.
1.(2025·湖北省黄冈市·模拟题)如图,已知抛物线与轴交于,两点,与轴交于,点,关于直线对称.
求抛物线的解析式.
平移抛物线,且平移后抛物线的顶点始终落在直线上,记平移后的新抛物线为,与轴交于点,求点纵坐标的最大值.
在的条件下,记抛物线顶点的横坐标为,长为.
求关于的函数解析式
将点向右平移个单位长度得到点,当随着增大而增大时,若与线段只有一个交点,直接写出的取值范围.
2.(2025·河北省保定市·期末考试)
已知抛物线:.
求抛物线的对称轴;
若点,,均在抛物线上,、、只有一个为正数.
求的取值范围;
直接写出符合条件的一个的取值范围,使得随的增大而减小;
若,将抛物线向左平移个单位,得到抛物线,点为抛物线上一点,且横坐标为,过点作轴交抛物线与点,点在抛物线对称轴的右侧若,求的值.
3.(2025·河北省石家庄市·月考试卷)
如图,在平面直角坐标系中,二次函数的图象与轴交于,两点,且有,与轴交于点,顶点为点.
求,两点的坐标.
将抛物线进行平移,使点恰好落在点关于轴的对称点上.
求出平移后抛物线的解析式,并指出其顶点坐标
求出平移过程中抛物线段所扫过的面积阴影部分.
4.(2025·浙江省·模拟题)
已知抛物线的顶点向右平移个单位长度再向上平移个单位长度后与抛物线为常数的顶点重合.
求,的值;
点在抛物线上,点在抛物线上:
若,求的最大值;
若,且,求的值.
5.(2025·山东省临沂市·模拟题)
已知抛物线:.
当时,求的值;
点是抛物线上一点,若,且时,求的值;
当时,把抛物线向下平移个单位长度得到新抛物线,如果抛物线与轴的一个交点的坐标为,且,请求出的取值范围.
6.(2024·广东省中山市·模拟题)
如图,在平面直角坐标系中,抛物线与轴交于、两点点在点的左侧,与轴交于点,点,连接.
求抛物线的解析式.
点是线段上一点,过点作轴交抛物线于点,交线段于点,点是直线上一点,连接,,求的周长最大值.
如图,已知,将抛物线上下平移,设平移后的抛物线在对称轴右侧部分与直线交于点,连接,当是等腰三角形时,直接写出抛物线的平移距离的值.
7.(2025·山东省淄博市·月考试卷)
如图,在平面直角坐标系中,抛物线与轴交于,两点在左侧,与轴交于点,顶点为.
求抛物线的表达式;
如图,点是抛物线上一点,在直线下方的抛物线上有一动点,连接,,求的面积最大值与此时点的横坐标;
如图,若点是抛物线对称轴上的一个动点,且在点的上方,将点绕点逆时针旋转得到对应点,直线交抛物线于点点与点不重合随着点的运动,判断点的坐标是否可求?如能,直接写出点的坐标;如不能,说明理由.
8.(2025·江苏省南通市·模拟题
已知关于的二次函数.
求证:不论为何实数,该二次函数的图象与轴总有两个公共点;
若,两点在该二次函数的图象上,直接写出与的大小关系;
若将抛物线沿轴翻折得到新抛物线,当时,新抛物线对应的函数有最小值,求的值.
9.(2025·江苏省南京市·模拟题)
已知二次函数为常数的图象经过点,对称轴为直线.
求二次函数的表达式;
若点向上平移个单位长度,向左平移个单位长度后,恰好落在的图象上,求的值;
当时,二次函数的最大值与最小值的差为,求的取值范围.
10.(2024·山东省济南市·模拟题)
如图,抛物线:与轴交于点,,与轴交于点,已知.
求的值;
点是直线下方抛物线上一动点,当的面积最大时,求点的坐标;
如图,在条件下,将抛物线向右平移个单位长度后得到抛物线,设抛物线与抛物线的交点为,,垂足为证明是直角三角形.
11.(2025·辽宁省鞍山市·模拟题)
如图,直线与坐标轴交于,两点,抛物线经过,两点,与轴交于点,连接.
求抛物线的解析式;
如图,点是直线上方抛物线上的一点,过点作交于点,连接,,,求的最大值;
如图,只将图中的抛物线向右平移两个单位长度得到新抛物线,与轴正半轴的交点为,连接,点是抛物线第二象限上的一点,连接若,请求出点的坐标.
12.(2025·江苏省·同步练习)
如图,在平面直角坐标系中,点为抛物线的顶点,过点作轴的平行线,交抛物线于点、点在点的左侧,.
求抛物线的函数表达式,并写出点的坐标.
小丽发现:将抛物线绕着点旋转,所得新抛物线的顶点恰为坐标原点,你认为正确吗?请说明理由.
13.(2023·江苏省南京市·模拟题)
【概念认识】
已知是实数,若某个函数图象上存在点,则称点是该函数图象上的“固定点”.
【数学理解】
一次函数的图象上的“固定点”的坐标是______;
求证:反比例函数的图象上存在个“固定点”;
将二次函数的图象在轴下方的部分沿轴翻折到轴上方,图象的其余部分保持不变,翻折后的图象与原图象在轴上方的部分组成一个类似“”形状的新图象若新图象上恰好存在个“固定点”,求的值.
14.(2025·湖北省·模拟题)
如图抛物线与轴交于和两点,与轴交于点,
求抛物线的解析式;
点是轴下方抛物线上一点,设点的横坐标为,过点作轴的平行线交直线于点,过点作轴的垂线交轴于,以,为邻边的矩形的周长记为.
请直接写出关于的函数关系式;
求的最值;
将抛物线向上平移个单位长度,再向左平移个单位长度,若新抛物线的顶点在内不含边界,直接写出的取值范围.
15.(2025·重庆市市辖区·期中考试)
如图,在平面直角坐标系中,抛物线交轴于,两点,交轴于且点,.
求抛物线的表达式;
点是直线上方抛物线上一点,过点作轴于点,过点作于点,点、点分别是直线、轴上的两动点,连接,,当取得最大值时,求三角形周长的最小值;
将抛物线沿射线方向平移个单位得新抛物线,点是轴上方新抛物线上的一点,连接,过点作交直线于点,当时,直接写出所有符合条件的点的横坐标.
16.(2025·江苏省苏州市·模拟题)
抛物线的与轴交于两点点在点的左边,顶点为.
顶点坐标为 ;
如图,若点的坐标是,连接.
把线段沿一定的方向平移,平移后,点的对应点为,点的对应点为,若点,点均在抛物线上,求点的坐标;
将抛物线沿射线方向平移得到抛物线,且抛物线经过点请问在抛物线上是否存在点,使得,若存在,请求出点的坐标;若不存在,请说明理由.
17.(2025·广东省湛江市·模拟题)
如图,抛物线过点,与轴交于点和点点在点左侧,与轴交于点,顶点的坐标为.
求抛物线的表达式和点的坐标.
点是线段上一动点,求周长的最小值.
平移抛物线得到抛物线,已知抛物线过点,顶点为,其对称轴与抛物线交于点若,直接写出点的坐标.
18.(2025·内蒙古自治区·模拟题)
在平面直角坐标系中,抛物线与轴交于,两点点在点的左侧
请求出该二次函数的对称轴和顶点坐标:
当时,二次函数的最大值与最小值的差为,求的取值范围;将抛物线向左平移个单位,再向上平移个单位得到新抛物线与原抛物线交于点直线与原抛物线交于点,与新抛物线交于点.为线段上的动点,过点作轴,垂足为,连接,,当在中的取值范围内,取得最大值时,求的最小值.
19.(2025·山东省·模拟题)
二次函数的图象交轴于点,点,交轴于点,抛物线的顶点为点.
求二次函数的解析式;
如图,点是抛物线上的一点,设点的横坐标为,点在对称轴上,且,若,请求出的值;
如图,将抛物线绕轴正半轴上一点旋转得到新抛物线交轴于,两点,点的对应点为点,点的对应点为点若,求旋转中心点的坐标.
参考答案
1.解:,两点关于直线对称,
抛物线的对称轴为直线.
,
解得.
又抛物线经过点,
.
抛物线的解析式为.
由于抛物线顶点坐标始终落在直线上,
故可设平移后抛物线解析式为.
令,
此时.
当时,有最大值,
即点纵坐标的最大值为.
由题意可知,的解析式为,
点坐标为,点坐标为,
.
关于的图象如图所示.
由图象可知,随着增大而增大部分是或.
由题意可知,的坐标为,
如图,当和只有一个交点时,
若该交点在抛物线对称轴右侧,
则当时,,且当时,,
解得.
若该交点在抛物线对称轴左侧,
则当时,,且当时,,
解得.
综上所述,当或时,符合条件.
2.对称轴为直线;
;;
或.
3.解:设点的坐标为,
由于,则点的坐标为
而二次函数的对称轴为直线,
,
解得,
点的坐标为,点的坐标为.
由于点关于轴的对称点的坐标为,
二次函数的图象向左平移了个单位长度.
,
其向左平移两个单位长度后的解析式为.
平移后的抛物线过点,
,
解得,
平移后的抛物线的解析式为
平移后的抛物线的顶点坐标为.
抛物线向左平移了个单位长度且平移后抛物线的顶点坐标为.
平移过程中,抛物线段所扫过的阴影部分面积等于底边长为,高为的平行四边形的面积
抛物线段所扫过的阴影部分面积为.
4.;
当时,的最大值为;.
5.或;
;
.
6.解:抛物线与轴交于、两点,
,
解得,
抛物线的解析式为;
如图,过点作于点,则,
,,
,
,,
,,
在中,由勾股定理得
轴,
,
,
,
,
,,
,
当最大时,的周长最大.
设,其中.
,,
设直线的解析式为
解得
直线的解析式为,
,
,
,
时,有最大值,最大值为,
周长的最大为.
由题知:平移后的抛物线的解析式为
设,则
又直线的解析式为,点在上,
,
,
,
,,
.
当是等腰三角形时,
若,则,
解得舍去,,
若,
则,
解得:,舍去,
,
若,则,
解得舍去.
综上,抛物线的平移距离的值为或.
7.解:抛物线的顶点为,
可设表达式为,
将点代入,
得,
解得,
,
抛物线的解析式为.
作轴交于.
由,,
设直线表达式为:,
将,的坐标代入,得
解得
直线表达式为:
设点的坐标为,点的坐标为,
当时,
此时点的横坐标为.
点的坐标为.
8.【详解】证明:令,则
不论为何实数,方程有两个不相等的实数根
无论为何实数,该二次函数的图象与轴总有两个公共点
解:二次函数的对称轴为:直线
,抛物线开口向上
抛物线上的点离对称轴越远对应的函数值越大
点到对称轴的距离为:
点到对称轴的距离为:
解:抛物线
沿轴翻折后的函数解析式为
该抛物线的对称轴为直线
若,即,则当时,有最小值
解得,
若,即,则当时,有最小值
不合题意,舍去
若,,则当时,有最小值
解得,
综上,的值为或
9.【小题】
解:设二次函数的解析式为,把代入得,
解得,
【小题】
解:点平移后的点的坐标为,
则,解得或舍,
的值为
【小题】
解:当时,
最大值与最小值的差为,解得:不符合题意,舍去;
当时,
最大值与最小值的差为,符合题意;
当时,
最大值与最小值的差为,解得或,不符合题意;
综上所述,的取值范围为.
10.【小题】
解:,
,
在抛物线:,
,解得:,
故答案为:;
【小题】
令,
解得:或,
,
令,则,
,
;
过点作轴的平行线于点,
设,则,
,
,
当时,的面积最大,
,
;
【小题】
证明:如图,连接,
,
,
,
是的中点,,
,
在中,,
,
过点作于点,
,
点是的中点,
是的中位线,
,
轴,
将抛物线向右平移个单位长度后得到抛物线,
则:,
令,解得:,
,
,
轴,
,即是直角三角形.
11.解:直线与坐标轴交于,两点,
则点、的坐标分别为:、,
由题意得:,
解得,
;
连接,
,
同底等高,
,
过点作轴于点交于点,设,则,
则,
,
,抛物线开口向下,
当时,最大值,
则的最大值是;
当时可得,
,
向右平移两个单位长度得到新抛物线,
则,
当时,解得或,
即,
,
,
如图,设交于点,当时,
,,
≌,
,
则点,
由点、的坐标得,直线的解析式为:,
联立方程组,.
解得:,舍去,
12.【小题】
抛物线过点,点的纵坐标为,,解得,.,,解得,抛物线的表达式为,,解得或,.
【小题】
正确.理由如下:,,绕着点旋转后的对称点为,与正好关于轴对称,所得新抛物线的对称轴是轴.抛物线,抛物线的顶点为,顶点到直线的距离也为,所得新抛物线顶点到直线的距离也为,所得新抛物线的顶点应为坐标原点.
13.;
证明:在中,令,可得.
解得,.
将代入中,得.
将代入中,得.
因此反比例函数的图像上存在个“固定点”,分别为和
图象大致如下:
设固定点为,将代入,
得,即,
,
即原图象翻折前有两个“固定点”,
翻折后图形为:,
将代入:,
即,
依题意,只需该方程有一个根即可对应一个“固定点”,与前两个合成三个,
,
即,
,
当时,不合题意,舍去,
当时,,
综上,.
14.解:将和的坐标分别代入中,得,解得,
抛物线解析式为.
.
点是轴下方抛物线上一点,设点的横坐标为,
,,
对于,令,得,
,
设直线的解析式为,
将,两点的坐标分别代入中,得,解得
直线的解析式为,
根据点的位置分两种情况:
当时,即点在点的左侧,,
,
,
,,
;
当时,点在点的右侧,,
,,
;
;
当时,函数没有最值;
当时,函数,
当时,;
综上所述,当时,的最大值为;
.
,
抛物线的顶点为,将抛物线向上平移个单位长度,再向左平移个单位长度,得到新抛物线的顶点的坐标为,即,
点是直线上的动点,
设直线的解析式为,
将,两点的坐标分别代入中,得,解得
直线的解析式为,
当点在直线上时,,
解得;
当点在直线上时,直线的解析式为,
,解得,
新抛物线的顶点在内不含边界,
.
15.解:对于,令,得,
,
,
在中,,,
,
,
把,分别代入中,得,解得
抛物线的表达式为;
设直线的解析式为,
把点,分别代入中,得
解得
直线的解析式为,
设交于点,如图:
设点,
轴,
,,轴,
,,
,,
,
又,
是等腰直角三角形,
,
轴,
,
,
,
,
,,
,
,
当时,取得最大值,此时点,
作点关于轴的对称点,作点关于直线的对称点,连接,,,,
由对称性得:,,
,
点,
由对称性得,,,
三角形的周长,
由两点之间线段最短可得,,
当、、、四点依次共线时,取得最小值,的最小值为线段的长,即三角形周长的最小值为线段的长,
,,
,
三角形周长的最小值为;
满足条件的点的横坐标为或.
,,,
,,,
将点沿射线方向平移个单位能够与点重合,相当于将点先向右平移个单位,再向上平移个单位得到点,
将抛物线沿射线方向平移个单位得新抛物线,相当于将抛物线先向右平移个单位,再向上平移个单位得新抛物线,
,
新抛物线的解析式为,
当点在直线上方,且在轴上方新抛物线上时,过点作于,过点作轴于,过点作交的延长线于,如图:
,,,,
,,,,,
,
,
在中,,
,
,
,
,
交直线于点,
,
在中,,,
,
设,则,,
,,
,
,
,,
∽,
,
,,
又,
,
把代入中,得,
解得,舍去,
此时点的横坐标为;
当点在直线下方,且在轴上方新抛物线上时,过点作轴的平行线,过点作于,过点作交的延长线于,如图:
则轴,,,,
,
,
由可知,,
在中,,,
设,则,,
,,
∽,
,
,,
又,
,
把代入中,得,
解得,舍去,
此时点的横坐标为;
综上所述,点的横坐标为或.
16.【小题】
【小题】
解:把代入得,,
解得,,
,
设所在直线解析式为,
把,代入得,
解得
直线的解析式为,
平移后所在直线解析式为,
设点坐标为,则点坐标为,
点,点均在抛物线上,
解得
点的坐标为;
设过点平行于的直线解析式为,
把代入得,,
,
过点平行于的直线解析式为,
设沿射线方向平移得到抛物线的解析式为,
把点代入,得,
解得不合题意,舍去或,
抛物线的解析式为,
如图,若与轴交点在点的下方,设交点为,
,
,
点的坐标为,
直线的解析式为,
解得或
点坐标为或
如图,若与轴的交点在点的上方,设交点为,
过点作,垂足分别为点和点,
由题意得,,
过点作轴,过点作,垂足分别为点,点,
则,且相似比,
设,则,
,
.
解得,
点坐标为,
设直线的解析式为,把和代入得,
解得
直线的解析式为,
解得或
点坐标为或;
综上所述,点坐标为或或或.
17.顶点的坐标为,设二次函数表达式为,
将点代入得,
抛物线的表达式为:,
当时,或,
点在点左侧,
点的坐标为;
当时,,
点的坐标为,
直线的表达式为:,
作关于的对称点,则,设垂足为,则点为与的中点,
因为直线的表达式为,,
所以的表达式为,
联立可得点的坐标为,点的坐标为,
,,,
,,
,
即周长的最小值为;
的坐标为或.
18.【小题】
解:,
二次函数的对称轴为直线,
当时,.
即顶点坐标为.
【小题】
解:,
即函数开口向上,对称轴为直线,
即当时,有最小值,为;
当时,;
最大值与最小值的差是,最小值是,
最大值为;
当时,,
解得:,,
.
,
故将抛物线向左平移个单位,再向上平移个单位得到新抛物线为;
当时,
解得,
.
当时,
解得,,
,
设,则,
,
由得,当时,取得最大值,
此时,点的坐标为,点的坐标为;
将点向左平移个单位长度得,连接,与轴交于点,作交于点,连接;
过点作轴,交于点,如图:
,,
是平行四边形,
,
故,此时有最小值;
,,轴,
,
故,,
,
故,
的最小值为.
19.【小题】
将,代入,
得
解得:,.
抛物线的解析式:;
【小题】
如答图,设抛物线对称轴与轴的交点为,过作于,
抛物线的对称轴为,
,,
,
,
,
,
,
即:,.
点的横坐标为,
,,,
则,
代入得:,
解得或舍;
.
【小题】
如答图,过作轴于,过作交的延长线于点,
令,则,
,,
,,,
,,
,
,
在中,
,则,
,,
在中,,
,
则:,
在中,,
则:,
即:,
得.
,
由题意知,、关于点对称,
已知:、,
则.
同课章节目录
