1.3 带电粒子在匀强磁场中的运动 课件(共35张PPT)2024-2025学年高二下学期物理人教版(2019)选择性必修第二册
文档属性
| 名称 | 1.3 带电粒子在匀强磁场中的运动 课件(共35张PPT)2024-2025学年高二下学期物理人教版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-30 12:50:10 | ||
图片预览






文档简介
(共35张PPT)
第一章 安培力与洛伦兹力
1.3 带电粒子在匀强磁场中的运动
——选修2——
学习目标
1、知道带电粒子沿着与磁场垂直的方向射入匀强磁场会在磁场中做匀速圆周运动,能推导相关公式。
2、经历实验验证带电粒子在洛伦兹力作用下做匀速圆周运动以及其运动半径与磁感应强度的大小和入射速度大小有关的过程。
3.了解带电粒子在匀强磁场中偏转及应用
情景引入
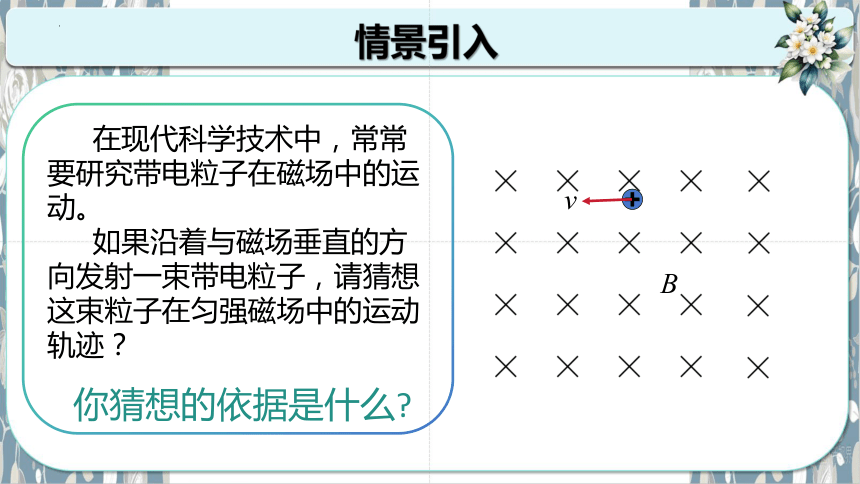
在现代科学技术中,常常要研究带电粒子在磁场中的运动。
如果沿着与磁场垂直的方向发射一束带电粒子,请猜想这束粒子在匀强磁场中的运动轨迹?
你猜想的依据是什么
+
v
B
一、带电粒子在匀强磁场中的运动
+
v
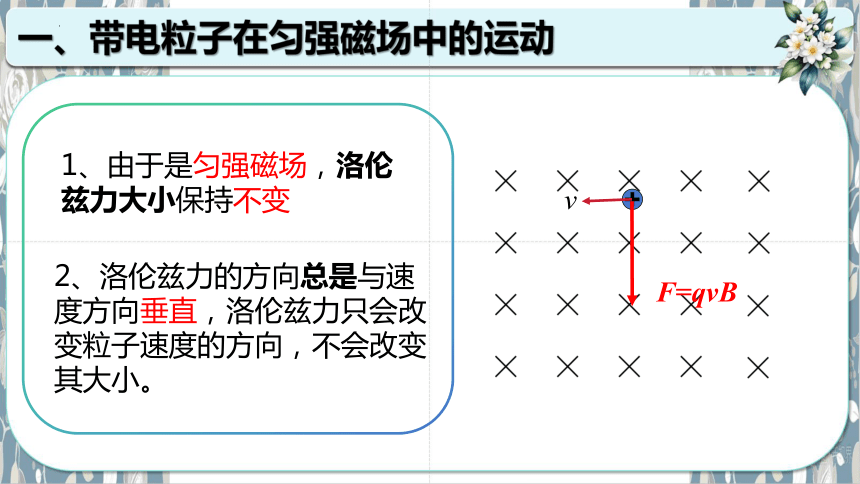
2、洛伦兹力的方向总是与速度方向垂直,洛伦兹力只会改变粒子速度的方向,不会改变其大小。
1、由于是匀强磁场,洛伦兹力大小保持不变
F=qvB
+
一、带电粒子在匀强磁场中的运动
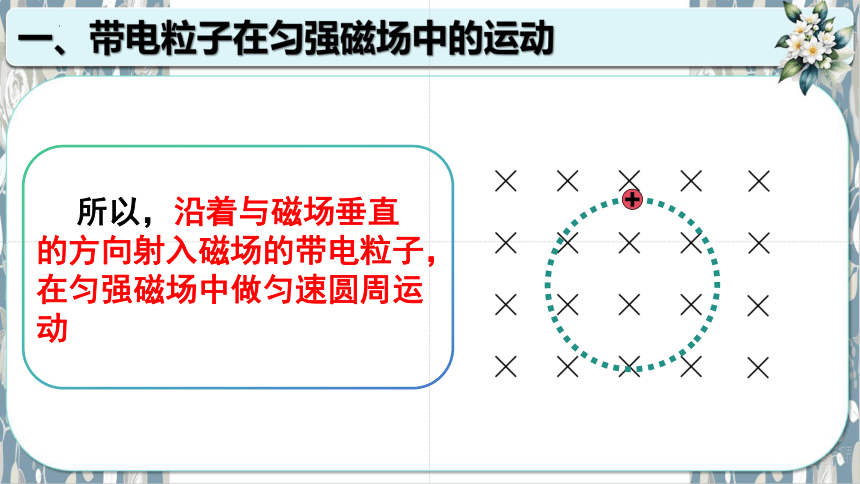
所以,沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动
一、带电粒子在匀强磁场中的运动
思考与讨论
垂直射入磁场的带电粒子在匀强磁场中做匀速圆周运动。
圆周的半径可能与哪些因素有关?
周期可能与哪些因素有关?
二、带电粒子在匀强磁场中运动的半径和周期
匀强磁场中带电粒子运动轨迹的半径与哪些因素有关?
思路: 带电粒子做匀速圆周运动,洛伦兹力提供向心力。
可见r与速度v、磁感应强度B、粒子的比荷有关
二、带电粒子在匀强磁场中运动的半径和周期
实验演示
洛伦兹演示仪
二、带电粒子在匀强磁场中运动的半径和周期
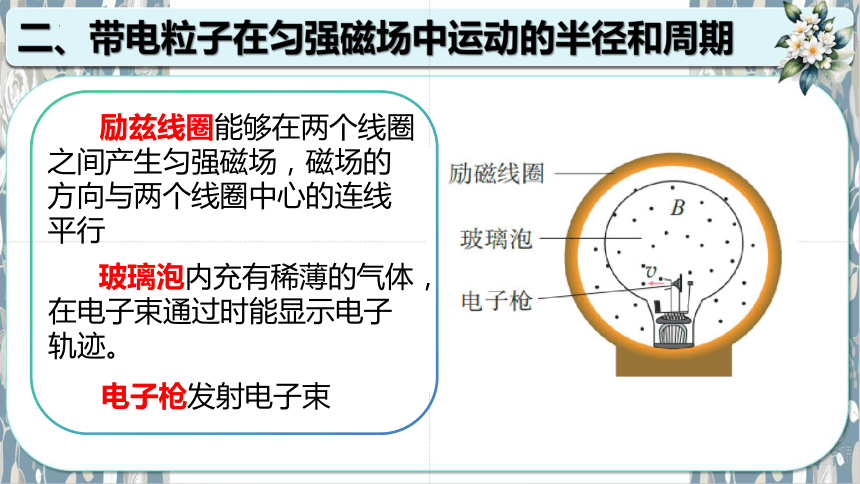
电子枪发射电子束
玻璃泡内充有稀薄的气体,在电子束通过时能显示电子轨迹。
励兹线圈能够在两个线圈之间产生匀强磁场,磁场的方向与两个线圈中心的连线平行
二、带电粒子在匀强磁场中运动的半径和周期
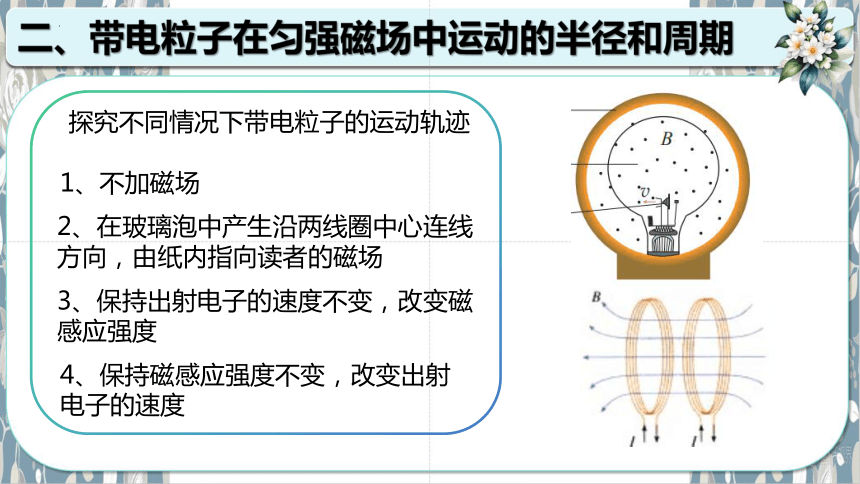
探究不同情况下带电粒子的运动轨迹
1、不加磁场
2、在玻璃泡中产生沿两线圈中心连线方向,由纸内指向读者的磁场
3、保持出射电子的速度不变,改变磁感应强度
4、保持磁感应强度不变,改变出射电子的速度
二、带电粒子在匀强磁场中运动的半径和周期
1.不加磁场时观察电子束的径迹。
2.给励磁线圈通电,在玻璃泡中产生沿两线圈中心连线方向,由纸内指向读者的磁场,观察电子束的径迹。
二、带电粒子在匀强磁场中运动的半径和周期
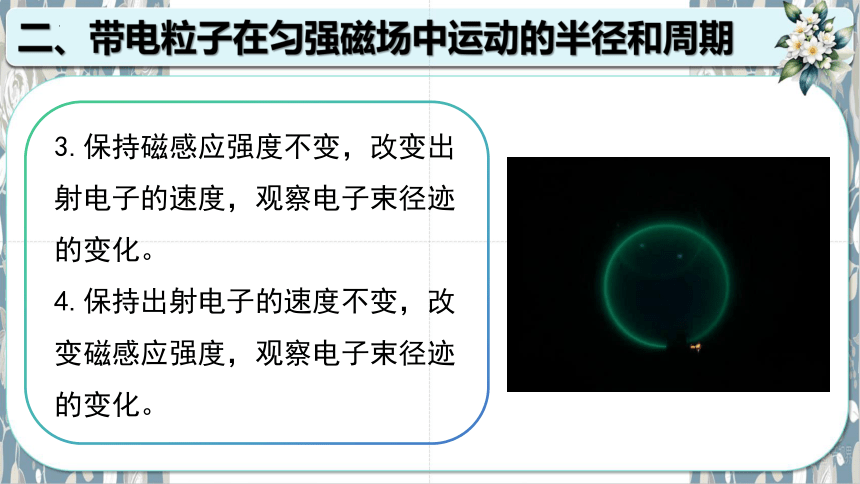
3.保持磁感应强度不变,改变出射电子的速度,观察电子束径迹的变化。
4.保持出射电子的速度不变,改变磁感应强度,观察电子束径迹的变化。
二、带电粒子在匀强磁场中运动的半径和周期
小结
2.给励磁线圈通电,在玻璃泡中产生沿两线圈中心连线方向,由纸内指向读者的磁场,观察电子束的径迹。
1.不加磁场时观察电子束的径迹。
直线
圆周
二、带电粒子在匀强磁场中运动的半径和周期
3.保持磁感应强度不变,改变出射电子的速度,观察电子束径迹的变化。
小结
速度增大时,圆周运动的半径增大;反之半径减小。
二、带电粒子在匀强磁场中运动的半径和周期
小结
4.保持出射电子的速度不变,改变磁感应强度,观察电子束径迹的变化。
B增大时,圆周运动的半径减小;反之半径增大。
二、带电粒子在匀强磁场中运动的半径和周期
带电粒子在匀强磁场中做匀速圆周运动时周期有何特征?
同一个粒子在匀强磁场中做匀速圆周运动的周期与速度无关
二、带电粒子在匀强磁场中运动的半径和周期
一个质量为 1.67×10-27 kg、电荷量为 1.6×10-19 C 的带电粒子,以 5×105m/s 的初速度沿与磁场垂直的方向射入磁感应强度为 0.2 T 的匀强磁场。求:
(1)粒子所受的重力和洛伦兹力的大小之比;
(2)粒子在磁场中运动的轨道半径;
(3)粒子做匀速圆周运动的周期。
例题1
二、带电粒子在匀强磁场中运动的半径和周期
解:
可见,带电粒子在磁场中运动时,洛伦兹力远大于重力,重力作用的影响可以忽略。
重力与洛伦兹力之比
F= qvB = 1.6×10-19×5×105×0.2N = 1.6×10-14N
所受的洛伦兹力
G =mg=1.67×10-27×9.8 N = 1.64×10-26N
(1)粒子所受的重力
二、带电粒子在匀强磁场中运动的半径和周期
(2)带电粒子所受的洛伦兹力为
由此得到粒子在磁场中运动的轨道半径
洛伦兹力提供向心力,故
F = qvB
(3)粒子做匀速圆周运动的周期
三、带电粒子在匀强磁场中运动的情况分析
1. 圆心的确定
(1)若已知入射方向和出射方向,作入射速度出射速度的垂线,两垂线交点就是圆弧轨道的圆心。
v0
P
M
O
v0
三、带电粒子在匀强磁场中运动的情况研究
(2)若已知入射方向和出射点的位置,做入射速度垂线及弦的中垂线,交点就是圆弧轨道的圆心。
v0
P
M
O
1. 圆心的确定
三、带电粒子在匀强磁场中运动的情况研究
(1)已知物理量(q、m、B、v),利用半径公式求半径。
(2)已知其他几何量利用数学图形知识求半径,一般利用几何知识,常用解三角形的方法。
2. 半径的确定
三、带电粒子在匀强磁场中运动的情况研究
3. 运动时间的确定
利用圆心角与弦切角的关系,或者是四边形内角和等计算出圆心角的大小,由公式可求出运动时间。
三、带电粒子在匀强磁场中运动的情况研究
例题2.一束电子(电荷量为 e )以速度 v 垂直射入磁感应强度为 B,宽度为 d 的匀强磁场中,穿过磁场时速度方向与电子原来入射方向的夹角是 30°,则电子的质量是________,穿过磁场的时间是________。
三、带电粒子在匀强磁场中运动的情况研究
解析:
(1) 画轨迹,找圆心。
(2) 定半径。
由几何知识知,弧AB的圆心角 θ=30°,OB 为半径。
所以 r = d/sin 30° = 2d,又由 r = mv/eB,得m = 2dBe/v 。
(3) 定时间。
因为弧 AB 的圆心角是 30° ,所以穿过时间 t = T/12,
故 t = πd/3v 。
答案: 2dBe/v πd/3v
四、课堂检测
1.电子以v=1.6×106m/s的速度沿着与磁场垂直的方向射入B=2.0×10-4T的匀强磁场中,求电子做匀速圆周运动的轨道半径和周期。(电子的电荷量q=1.6×10-19C和质量为m=9.1×10-31kg,π=3.14)
四、课堂检测
解:根据洛伦兹力提供向心力,有
又因为
两式联立可得,电子做匀速圆周运动的轨道半径和周期
代入数据求得
四、课堂检测
2.已知氚核的质量约为质子质量的3倍,带正电荷,电荷量为一个元电荷;α粒子即氦原子核,质量约为质子质量的4倍,带正电荷,电荷量为e的2倍。现在质子、氚核和α粒子在同一匀强磁场中做匀速圆周运动。求下列情况中它们运动的半径之比:
(1)它们的速度大小相等;
(2)它们由静止经过相同的加速电场加速后进入磁场。
四、课堂检测
解:(1)由
可知 r质子∶r氚核∶rα粒子=1∶3∶2
(2)由 qU= mv2
得 r=
∝
所以r质子∶r氚核∶rα粒子=1∶ :
四、课堂检测
3.如图所示,一个质量为m、电荷量为q、不计重力的带电粒子从x轴上的P点以速度v沿与x轴正方向成600的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴从Q点射出第一象限,已知OQ=a。
四、课堂检测
(1)求磁场磁感应强度B的大小;
(2)带电粒子穿过第一象限所用的时间t。
四、课堂检测
解:(1)由洛伦兹力提供向心力得
解得
四、课堂检测
粒子的周期为
则带电粒子穿过第一象限所用的时间为
总结
一、带电粒子在匀强磁场中的运动
二、带电粒子在磁场中做圆周运动的半径
三、带电粒子在磁场中做圆周运动的周期
砥砺前行
不负韶华
第一章 安培力与洛伦兹力
1.3 带电粒子在匀强磁场中的运动
——选修2——
学习目标
1、知道带电粒子沿着与磁场垂直的方向射入匀强磁场会在磁场中做匀速圆周运动,能推导相关公式。
2、经历实验验证带电粒子在洛伦兹力作用下做匀速圆周运动以及其运动半径与磁感应强度的大小和入射速度大小有关的过程。
3.了解带电粒子在匀强磁场中偏转及应用
情景引入
在现代科学技术中,常常要研究带电粒子在磁场中的运动。
如果沿着与磁场垂直的方向发射一束带电粒子,请猜想这束粒子在匀强磁场中的运动轨迹?
你猜想的依据是什么
+
v
B
一、带电粒子在匀强磁场中的运动
+
v
2、洛伦兹力的方向总是与速度方向垂直,洛伦兹力只会改变粒子速度的方向,不会改变其大小。
1、由于是匀强磁场,洛伦兹力大小保持不变
F=qvB
+
一、带电粒子在匀强磁场中的运动
所以,沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动
一、带电粒子在匀强磁场中的运动
思考与讨论
垂直射入磁场的带电粒子在匀强磁场中做匀速圆周运动。
圆周的半径可能与哪些因素有关?
周期可能与哪些因素有关?
二、带电粒子在匀强磁场中运动的半径和周期
匀强磁场中带电粒子运动轨迹的半径与哪些因素有关?
思路: 带电粒子做匀速圆周运动,洛伦兹力提供向心力。
可见r与速度v、磁感应强度B、粒子的比荷有关
二、带电粒子在匀强磁场中运动的半径和周期
实验演示
洛伦兹演示仪
二、带电粒子在匀强磁场中运动的半径和周期
电子枪发射电子束
玻璃泡内充有稀薄的气体,在电子束通过时能显示电子轨迹。
励兹线圈能够在两个线圈之间产生匀强磁场,磁场的方向与两个线圈中心的连线平行
二、带电粒子在匀强磁场中运动的半径和周期
探究不同情况下带电粒子的运动轨迹
1、不加磁场
2、在玻璃泡中产生沿两线圈中心连线方向,由纸内指向读者的磁场
3、保持出射电子的速度不变,改变磁感应强度
4、保持磁感应强度不变,改变出射电子的速度
二、带电粒子在匀强磁场中运动的半径和周期
1.不加磁场时观察电子束的径迹。
2.给励磁线圈通电,在玻璃泡中产生沿两线圈中心连线方向,由纸内指向读者的磁场,观察电子束的径迹。
二、带电粒子在匀强磁场中运动的半径和周期
3.保持磁感应强度不变,改变出射电子的速度,观察电子束径迹的变化。
4.保持出射电子的速度不变,改变磁感应强度,观察电子束径迹的变化。
二、带电粒子在匀强磁场中运动的半径和周期
小结
2.给励磁线圈通电,在玻璃泡中产生沿两线圈中心连线方向,由纸内指向读者的磁场,观察电子束的径迹。
1.不加磁场时观察电子束的径迹。
直线
圆周
二、带电粒子在匀强磁场中运动的半径和周期
3.保持磁感应强度不变,改变出射电子的速度,观察电子束径迹的变化。
小结
速度增大时,圆周运动的半径增大;反之半径减小。
二、带电粒子在匀强磁场中运动的半径和周期
小结
4.保持出射电子的速度不变,改变磁感应强度,观察电子束径迹的变化。
B增大时,圆周运动的半径减小;反之半径增大。
二、带电粒子在匀强磁场中运动的半径和周期
带电粒子在匀强磁场中做匀速圆周运动时周期有何特征?
同一个粒子在匀强磁场中做匀速圆周运动的周期与速度无关
二、带电粒子在匀强磁场中运动的半径和周期
一个质量为 1.67×10-27 kg、电荷量为 1.6×10-19 C 的带电粒子,以 5×105m/s 的初速度沿与磁场垂直的方向射入磁感应强度为 0.2 T 的匀强磁场。求:
(1)粒子所受的重力和洛伦兹力的大小之比;
(2)粒子在磁场中运动的轨道半径;
(3)粒子做匀速圆周运动的周期。
例题1
二、带电粒子在匀强磁场中运动的半径和周期
解:
可见,带电粒子在磁场中运动时,洛伦兹力远大于重力,重力作用的影响可以忽略。
重力与洛伦兹力之比
F= qvB = 1.6×10-19×5×105×0.2N = 1.6×10-14N
所受的洛伦兹力
G =mg=1.67×10-27×9.8 N = 1.64×10-26N
(1)粒子所受的重力
二、带电粒子在匀强磁场中运动的半径和周期
(2)带电粒子所受的洛伦兹力为
由此得到粒子在磁场中运动的轨道半径
洛伦兹力提供向心力,故
F = qvB
(3)粒子做匀速圆周运动的周期
三、带电粒子在匀强磁场中运动的情况分析
1. 圆心的确定
(1)若已知入射方向和出射方向,作入射速度出射速度的垂线,两垂线交点就是圆弧轨道的圆心。
v0
P
M
O
v0
三、带电粒子在匀强磁场中运动的情况研究
(2)若已知入射方向和出射点的位置,做入射速度垂线及弦的中垂线,交点就是圆弧轨道的圆心。
v0
P
M
O
1. 圆心的确定
三、带电粒子在匀强磁场中运动的情况研究
(1)已知物理量(q、m、B、v),利用半径公式求半径。
(2)已知其他几何量利用数学图形知识求半径,一般利用几何知识,常用解三角形的方法。
2. 半径的确定
三、带电粒子在匀强磁场中运动的情况研究
3. 运动时间的确定
利用圆心角与弦切角的关系,或者是四边形内角和等计算出圆心角的大小,由公式可求出运动时间。
三、带电粒子在匀强磁场中运动的情况研究
例题2.一束电子(电荷量为 e )以速度 v 垂直射入磁感应强度为 B,宽度为 d 的匀强磁场中,穿过磁场时速度方向与电子原来入射方向的夹角是 30°,则电子的质量是________,穿过磁场的时间是________。
三、带电粒子在匀强磁场中运动的情况研究
解析:
(1) 画轨迹,找圆心。
(2) 定半径。
由几何知识知,弧AB的圆心角 θ=30°,OB 为半径。
所以 r = d/sin 30° = 2d,又由 r = mv/eB,得m = 2dBe/v 。
(3) 定时间。
因为弧 AB 的圆心角是 30° ,所以穿过时间 t = T/12,
故 t = πd/3v 。
答案: 2dBe/v πd/3v
四、课堂检测
1.电子以v=1.6×106m/s的速度沿着与磁场垂直的方向射入B=2.0×10-4T的匀强磁场中,求电子做匀速圆周运动的轨道半径和周期。(电子的电荷量q=1.6×10-19C和质量为m=9.1×10-31kg,π=3.14)
四、课堂检测
解:根据洛伦兹力提供向心力,有
又因为
两式联立可得,电子做匀速圆周运动的轨道半径和周期
代入数据求得
四、课堂检测
2.已知氚核的质量约为质子质量的3倍,带正电荷,电荷量为一个元电荷;α粒子即氦原子核,质量约为质子质量的4倍,带正电荷,电荷量为e的2倍。现在质子、氚核和α粒子在同一匀强磁场中做匀速圆周运动。求下列情况中它们运动的半径之比:
(1)它们的速度大小相等;
(2)它们由静止经过相同的加速电场加速后进入磁场。
四、课堂检测
解:(1)由
可知 r质子∶r氚核∶rα粒子=1∶3∶2
(2)由 qU= mv2
得 r=
∝
所以r质子∶r氚核∶rα粒子=1∶ :
四、课堂检测
3.如图所示,一个质量为m、电荷量为q、不计重力的带电粒子从x轴上的P点以速度v沿与x轴正方向成600的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴从Q点射出第一象限,已知OQ=a。
四、课堂检测
(1)求磁场磁感应强度B的大小;
(2)带电粒子穿过第一象限所用的时间t。
四、课堂检测
解:(1)由洛伦兹力提供向心力得
解得
四、课堂检测
粒子的周期为
则带电粒子穿过第一象限所用的时间为
总结
一、带电粒子在匀强磁场中的运动
二、带电粒子在磁场中做圆周运动的半径
三、带电粒子在磁场中做圆周运动的周期
砥砺前行
不负韶华
