2025新华东师大版七年级数学下册期末测试卷(含答案)
文档属性
| 名称 | 2025新华东师大版七年级数学下册期末测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 960.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:57:51 | ||
图片预览



文档简介
2025新华东师大版七年级数学下册期末测试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在以下绿色食品、可回收、节能、节水四个标志中,是轴对称图形的是( )
2.下列方程是一元一次方程的是( )
A.x-1= B.3a-3<1
C.2x-3=5 D.2x2+1=5
3.下列四幅图案可以看作是以图案中某部分为基本图形平移得到的是( )
4.不等式组的解集在数轴上表示正确的是( )
5.下列说法不正确的是( )
A.若a>b,则a+2>b+2
B.若a>b,则-a<-b
C.若2a>2b,则a>b
D.若a>b,则ac2>bc2
6.体育课上的侧压腿动作可以抽象为如图所示的几何图形,若∠1=110°,则∠2=( )
A.10° B.20° C.25° D.30°
7.我国古代数学著作《九章算术》中有一道题:“今有五雀六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平;并燕、雀重一斤.问燕、雀一枚各重几何?”其大意是现在有5只雀和6只燕,用秤来称它们,发现雀比较重,燕比较轻.将一只雀和一只燕交换位置后,质量相等;5只雀和6只燕的质量为一斤(斤是古代质量单位).问每只雀和每只燕的质量分别为多少斤?设每只雀的质量为x斤,每只燕的质量为y斤,则可列方程组为( )
A. B.
C. D.
8.若某三角形的三边长分别为3,4,m,则m的值可以是( )
A.9 B.7 C.5 D.1
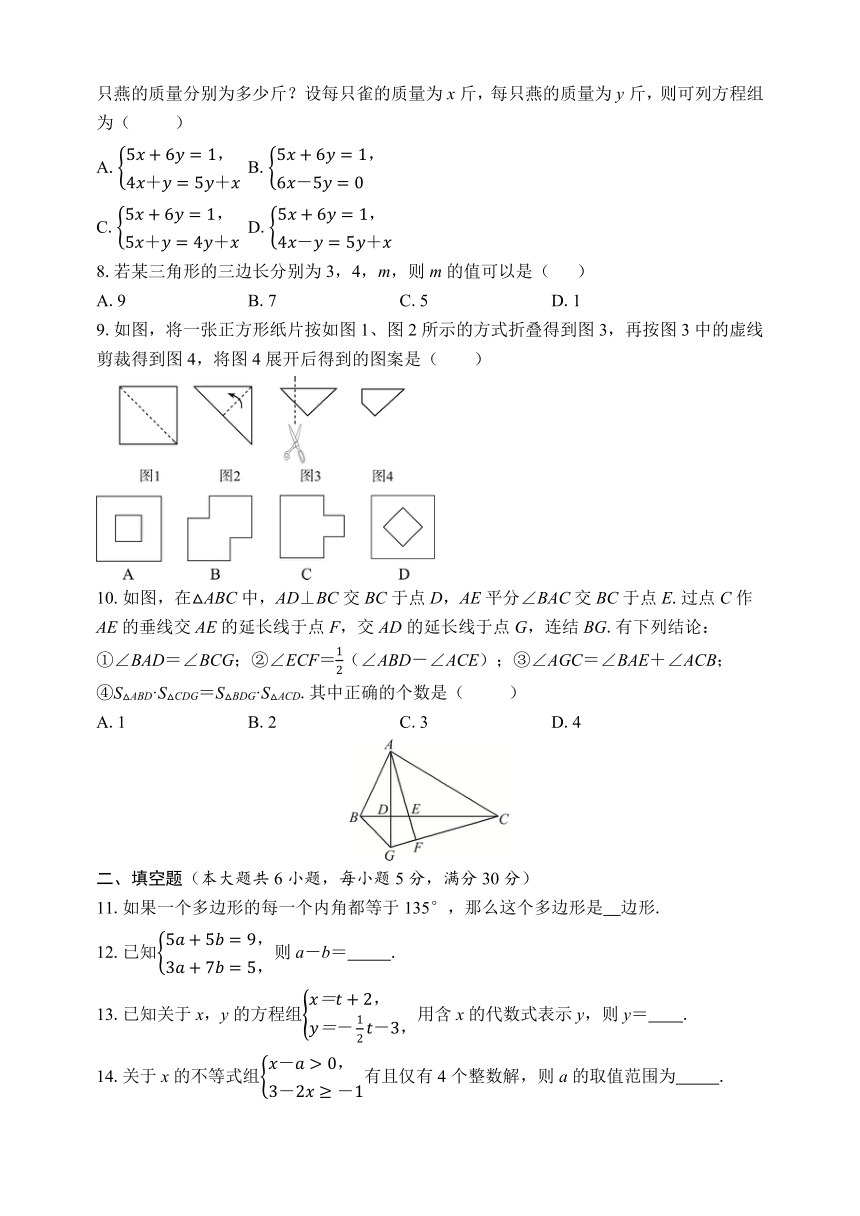
9.如图,将一张正方形纸片按如图1、图2所示的方式折叠得到图3,再按图3中的虚线剪裁得到图4,将图4展开后得到的图案是( )
10.如图,在△ABC中,AD⊥BC交BC于点D,AE平分∠BAC交BC于点E.过点C作AE的垂线交AE的延长线于点F,交AD的延长线于点G,连结BG.有下列结论:
①∠BAD=∠BCG;②∠ECF=(∠ABD-∠ACE);③∠AGC=∠BAE+∠ACB;④S△ABD·S△CDG=S△BDG·S△ACD.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题5分,满分30分)
11.如果一个多边形的每一个内角都等于135°,那么这个多边形是 边形.
12.已知则a-b= .
13.已知关于x,y的方程组用含x的代数式表示y,则y= .
14.关于x的不等式组有且仅有4个整数解,则a的取值范围为 .
15.如图,直线l上摆放着两个大小相同的△ABC和△DEC,∠ACB=∠DCE=90°,∠BAC=∠EDC=30°,将△DEC沿直线l向左平移得到△D'E'C';使点E'落在AB上,E'D'与AC交于点P.有下列结论:
①∠CPD'=60°;
②AB⊥E'D';
③△PEE'和△PCD'的周长之和等于△ABC的周长;
④图中阴影部分的面积之和大于△ABC的面积.
其中正确的是 .(填序号)
16.如图,在△ABC中,∠F=16°,BD,CD分别平分∠ABC,∠ACB,M,N,Q分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ,则∠A= .
三、解答题(本大题共7小题,满分80分)
17.(8分)解下列方程(组):
(1)-=1;
(2)
18.(10分)如图,已知射线AD平分∠BAC.
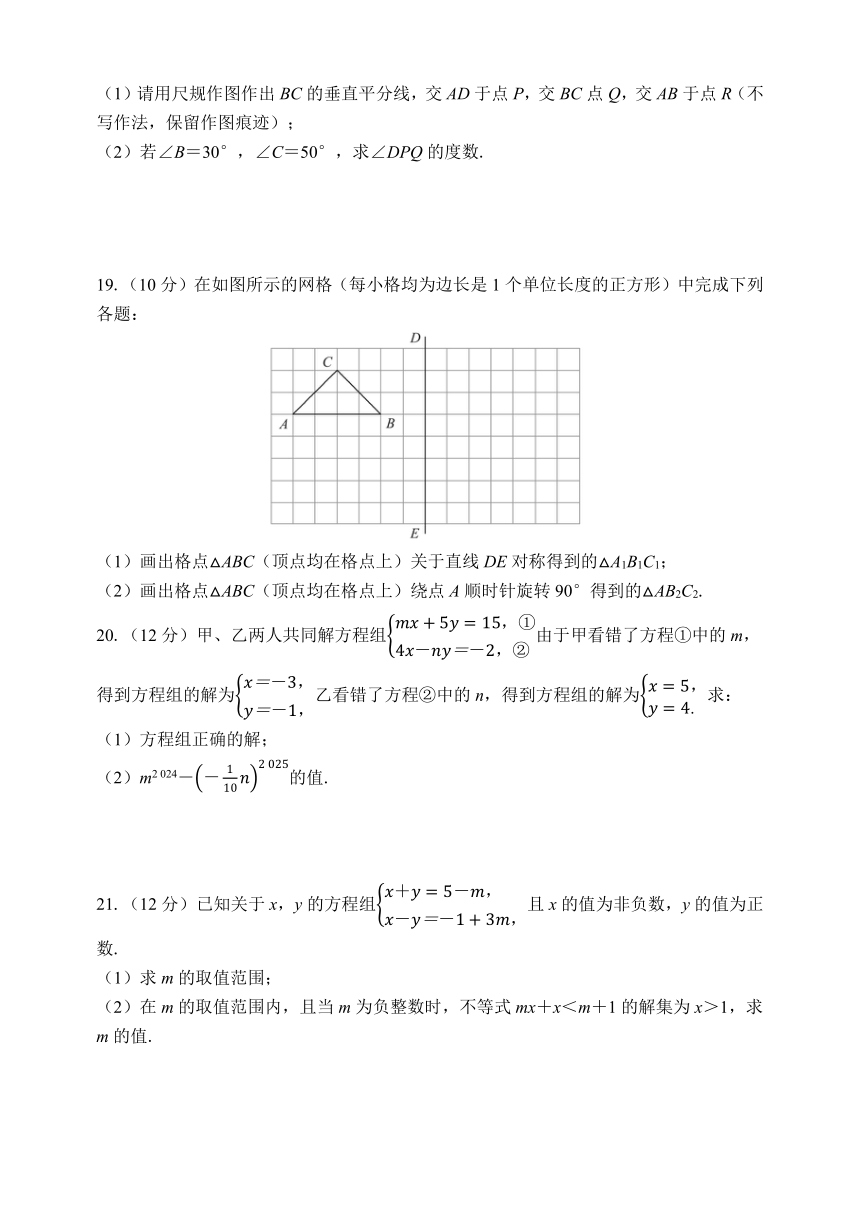
(1)请用尺规作图作出BC的垂直平分线,交AD于点P,交BC点Q,交AB于点R(不写作法,保留作图痕迹);
(2)若∠B=30°,∠C=50°,求∠DPQ的度数.
19.(10分)在如图所示的网格(每小格均为边长是1个单位长度的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称得到的△A1B1C1;
(2)画出格点△ABC(顶点均在格点上)绕点A顺时针旋转90°得到的△AB2C2.
20.(12分)甲、乙两人共同解方程组由于甲看错了方程①中的m,得到方程组的解为乙看错了方程②中的n,得到方程组的解为求:
(1)方程组正确的解;
(2)m2 024-的值.
21.(12分)已知关于x,y的方程组且x的值为非负数,y的值为正数.
(1)求m的取值范围;
(2)在m的取值范围内,且当m为负整数时,不等式mx+x<m+1的解集为x>1,求m的值.
22.(12分)某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果),下表为装运甲、乙、丙三种水果的质量及利润.
水果种类 甲 乙 丙
每辆汽车能装的质量/吨 4 2 3
每吨水果可获利润/千元 5 7 4
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各有多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于1辆车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用含m的式子表示)
(3)在(2)的条件下,如何安排装运的汽车可使水果基地获得最大利润?最大利润是多少?
23.(16分)定义:对任意一个两位数a,如果a满足个位数字比十位数字大3,那么称这个两位数为“慧泉数”.将一个“慧泉数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如,a=14,对调个位数字与十位数字后得到新的两位数为41,新两位数与原两位数的和为14+41=55,其和与11的商为55÷11=5,∴f(14)=5.
根据以上定义,回答下列问题:
(1)f(36)= ;
(2)若f(a)=7,求a的值;
(3)如果一个“慧泉数” m的十位数字是x,另一个“慧泉数”n的个位数字是x,且满足f(m)+f(n)<20,求m,n的值.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在以下绿色食品、可回收、节能、节水四个标志中,是轴对称图形的是( A )
2.下列方程是一元一次方程的是( C )
A.x-1= B.3a-3<1
C.2x-3=5 D.2x2+1=5
3.下列四幅图案可以看作是以图案中某部分为基本图形平移得到的是( B )
4.不等式组的解集在数轴上表示正确的是( B )
5.下列说法不正确的是( D )
A.若a>b,则a+2>b+2
B.若a>b,则-a<-b
C.若2a>2b,则a>b
D.若a>b,则ac2>bc2
6.体育课上的侧压腿动作可以抽象为如图所示的几何图形,若∠1=110°,则∠2=( B )
A.10° B.20° C.25° D.30°
7.我国古代数学著作《九章算术》中有一道题:“今有五雀六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平;并燕、雀重一斤.问燕、雀一枚各重几何?”其大意是现在有5只雀和6只燕,用秤来称它们,发现雀比较重,燕比较轻.将一只雀和一只燕交换位置后,质量相等;5只雀和6只燕的质量为一斤(斤是古代质量单位).问每只雀和每只燕的质量分别为多少斤?设每只雀的质量为x斤,每只燕的质量为y斤,则可列方程组为( A )
A. B.
C. D.
8.若某三角形的三边长分别为3,4,m,则m的值可以是( C )
A.9 B.7 C.5 D.1
9.如图,将一张正方形纸片按如图1、图2所示的方式折叠得到图3,再按图3中的虚线剪裁得到图4,将图4展开后得到的图案是( B )
10.如图,在△ABC中,AD⊥BC交BC于点D,AE平分∠BAC交BC于点E.过点C作AE的垂线交AE的延长线于点F,交AD的延长线于点G,连结BG.有下列结论:
①∠BAD=∠BCG;②∠ECF=(∠ABD-∠ACE);③∠AGC=∠BAE+∠ACB;④S△ABD·S△CDG=S△BDG·S△ACD.其中正确的个数是( C )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题5分,满分30分)
11.如果一个多边形的每一个内角都等于135°,那么这个多边形是 八 边形.
12.已知则a-b= 2 .
13.已知关于x,y的方程组用含x的代数式表示y,则y= -x-2 .
14.关于x的不等式组有且仅有4个整数解,则a的取值范围为 -2≤a<-1 .
15.如图,直线l上摆放着两个大小相同的△ABC和△DEC,∠ACB=∠DCE=90°,∠BAC=∠EDC=30°,将△DEC沿直线l向左平移得到△D'E'C';使点E'落在AB上,E'D'与AC交于点P.有下列结论:
①∠CPD'=60°;
②AB⊥E'D';
③△PEE'和△PCD'的周长之和等于△ABC的周长;
④图中阴影部分的面积之和大于△ABC的面积.
其中正确的是 ①②③ .(填序号)
16.如图,在△ABC中,∠F=16°,BD,CD分别平分∠ABC,∠ACB,M,N,Q分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ,则∠A= 52° .
三、解答题(本大题共7小题,满分80分)
17.(8分)解下列方程(组):
(1)-=1;
解:去分母、去括号,得2x-1+x=4.
移项,得2x+x=4+1.
合并同类项,得3x=5.
系数化为1,得x=.
(2)
解:原方程组化为
①×2-②,得25y=5,解得y=.
把y=代入①,得3x+5×=2,解得x=.
∴原方程组的解为
18.(10分)如图,已知射线AD平分∠BAC.
(1)请用尺规作图作出BC的垂直平分线,交AD于点P,交BC点Q,交AB于点R(不写作法,保留作图痕迹);
(2)若∠B=30°,∠C=50°,求∠DPQ的度数.
解:(1)如图所示,直线RQ即为所求.
(2)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=50°,
∴∠ADC=180°-∠C-∠CAD=80°,
∴∠PDQ=∠ADC=80°.
∵QR垂直平分BC,∴∠PQD=90°,
∴∠DPQ=180°-∠PQD-∠PDQ=10°.
19.(10分)在如图所示的网格(每小格均为边长是1个单位长度的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称得到的△A1B1C1;
(2)画出格点△ABC(顶点均在格点上)绕点A顺时针旋转90°得到的△AB2C2.
解:(1)△A1B1C1如图所示.
(2)△A2B2C2如图所示.
20.(12分)甲、乙两人共同解方程组由于甲看错了方程①中的m,得到方程组的解为乙看错了方程②中的n,得到方程组的解为求:
(1)方程组正确的解;
(2)m2 024-的值.
解:(1)根据题意,得
解得∴原方程组为
①+②,得x=14.
将x=14代入①中,得y=,
∴原方程组的解为
(2)将代入 m2 024-中,
m2 024-=(-1)2 024-
=1-(-1)2 025
=1+1
=2.
21.(12分)已知关于x,y的方程组且x的值为非负数,y的值为正数.
(1)求m的取值范围;
(2)在m的取值范围内,且当m为负整数时,不等式mx+x<m+1的解集为x>1,求m的值.
解:(1)解方程组
得
∵x的值为非负数,y的值为正数,
∴解得-2≤m<,
即m的取值范围为-2≤m<.
(2)∵mx+x<m+1,∴(m+1)x<m+1.
∵不等式mx+x<m+1的解集为x>1,
∴m+1<0,∴m<-1.
∵-2≤m<,∴-2≤m<-1.
∵m为负整数,∴m=-2.
22.(12分)某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果),下表为装运甲、乙、丙三种水果的质量及利润.
水果种类 甲 乙 丙
每辆汽车能装的质量/吨 4 2 3
每吨水果可获利润/千元 5 7 4
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各有多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于1辆车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用含m的式子表示)
(3)在(2)的条件下,如何安排装运的汽车可使水果基地获得最大利润?最大利润是多少?
解:(1)设装运乙、丙两种水果的汽车分别为x辆、y辆.由题意,得解得
答:装运乙种水果的汽车有2辆,装运丙种水果的汽车有6辆.
(2)设装运乙、丙两种水果的汽车分别为a辆、b辆.
由题意,得解得
答:装运乙种水果的汽车有(m-12)辆,装运丙种水果的汽车有(32-2m)辆.
(3)设总利润为W千元.
由题意,得W=5×4m+7×2(m-12)+4×3(32-2m)=10m+216.
∵∴13≤m≤.
∵m为正整数,∴m的值可取13,14,15.
∵当m=13时,W=10×13+216=346(千元);
当m=14时,W=10×14+216=356(千元);
当m=15时,W=10×15+216=366(千元).
∴当m=15时,W最大=366(千元),
m-12=3(辆),32-2m=2(辆).
答:当装运甲水果的汽车15辆,装运乙水果的汽车3辆,装运丙水果的汽车2辆时可使水果基地获得的利润最大,最大利润为366千元.
23.(16分)定义:对任意一个两位数a,如果a满足个位数字比十位数字大3,那么称这个两位数为“慧泉数”.将一个“慧泉数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如,a=14,对调个位数字与十位数字后得到新的两位数为41,新两位数与原两位数的和为14+41=55,其和与11的商为55÷11=5,∴f(14)=5.
根据以上定义,回答下列问题:
(1)f(36)= 9 ;
(2)若f(a)=7,求a的值;
(3)如果一个“慧泉数” m的十位数字是x,另一个“慧泉数”n的个位数字是x,且满足f(m)+f(n)<20,求m,n的值.
解:(1)由题意可得f(36)=(36+63)÷11=99÷11=9.故答案为9.
(2)设a的个位数字为y,则其十位数字为(y-3).
∵f(a)=7,∴=7,
解得y=5,则y-3=5-3=2,
则a=10(y-3)+y=10×2+5=25.
(3)∵一个“慧泉数” m的十位数字是x,另一个“慧泉数”n的个位数字是x,
∴“慧泉数”m的个位数字是(x+3),“慧泉数”n的十位数字是(x-3),
∴f(m)==2x+3,
f(n)==2x-3.
∵f(m)+f(n)<20,
∴2x+3+2x-3<20,解得x<5.
∵x-3>0且x为整数,
∴3<x<5且x为整数,∴x=4,
则x+3=4+3=7,x-3=4-3=1,
即m=10x+(x+3)=10×4+7=47,
n=10(x-3)+x=10×1+4=14.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在以下绿色食品、可回收、节能、节水四个标志中,是轴对称图形的是( )
2.下列方程是一元一次方程的是( )
A.x-1= B.3a-3<1
C.2x-3=5 D.2x2+1=5
3.下列四幅图案可以看作是以图案中某部分为基本图形平移得到的是( )
4.不等式组的解集在数轴上表示正确的是( )
5.下列说法不正确的是( )
A.若a>b,则a+2>b+2
B.若a>b,则-a<-b
C.若2a>2b,则a>b
D.若a>b,则ac2>bc2
6.体育课上的侧压腿动作可以抽象为如图所示的几何图形,若∠1=110°,则∠2=( )
A.10° B.20° C.25° D.30°
7.我国古代数学著作《九章算术》中有一道题:“今有五雀六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平;并燕、雀重一斤.问燕、雀一枚各重几何?”其大意是现在有5只雀和6只燕,用秤来称它们,发现雀比较重,燕比较轻.将一只雀和一只燕交换位置后,质量相等;5只雀和6只燕的质量为一斤(斤是古代质量单位).问每只雀和每只燕的质量分别为多少斤?设每只雀的质量为x斤,每只燕的质量为y斤,则可列方程组为( )
A. B.
C. D.
8.若某三角形的三边长分别为3,4,m,则m的值可以是( )
A.9 B.7 C.5 D.1
9.如图,将一张正方形纸片按如图1、图2所示的方式折叠得到图3,再按图3中的虚线剪裁得到图4,将图4展开后得到的图案是( )
10.如图,在△ABC中,AD⊥BC交BC于点D,AE平分∠BAC交BC于点E.过点C作AE的垂线交AE的延长线于点F,交AD的延长线于点G,连结BG.有下列结论:
①∠BAD=∠BCG;②∠ECF=(∠ABD-∠ACE);③∠AGC=∠BAE+∠ACB;④S△ABD·S△CDG=S△BDG·S△ACD.其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题5分,满分30分)
11.如果一个多边形的每一个内角都等于135°,那么这个多边形是 边形.
12.已知则a-b= .
13.已知关于x,y的方程组用含x的代数式表示y,则y= .
14.关于x的不等式组有且仅有4个整数解,则a的取值范围为 .
15.如图,直线l上摆放着两个大小相同的△ABC和△DEC,∠ACB=∠DCE=90°,∠BAC=∠EDC=30°,将△DEC沿直线l向左平移得到△D'E'C';使点E'落在AB上,E'D'与AC交于点P.有下列结论:
①∠CPD'=60°;
②AB⊥E'D';
③△PEE'和△PCD'的周长之和等于△ABC的周长;
④图中阴影部分的面积之和大于△ABC的面积.
其中正确的是 .(填序号)
16.如图,在△ABC中,∠F=16°,BD,CD分别平分∠ABC,∠ACB,M,N,Q分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ,则∠A= .
三、解答题(本大题共7小题,满分80分)
17.(8分)解下列方程(组):
(1)-=1;
(2)
18.(10分)如图,已知射线AD平分∠BAC.
(1)请用尺规作图作出BC的垂直平分线,交AD于点P,交BC点Q,交AB于点R(不写作法,保留作图痕迹);
(2)若∠B=30°,∠C=50°,求∠DPQ的度数.
19.(10分)在如图所示的网格(每小格均为边长是1个单位长度的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称得到的△A1B1C1;
(2)画出格点△ABC(顶点均在格点上)绕点A顺时针旋转90°得到的△AB2C2.
20.(12分)甲、乙两人共同解方程组由于甲看错了方程①中的m,得到方程组的解为乙看错了方程②中的n,得到方程组的解为求:
(1)方程组正确的解;
(2)m2 024-的值.
21.(12分)已知关于x,y的方程组且x的值为非负数,y的值为正数.
(1)求m的取值范围;
(2)在m的取值范围内,且当m为负整数时,不等式mx+x<m+1的解集为x>1,求m的值.
22.(12分)某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果),下表为装运甲、乙、丙三种水果的质量及利润.
水果种类 甲 乙 丙
每辆汽车能装的质量/吨 4 2 3
每吨水果可获利润/千元 5 7 4
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各有多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于1辆车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用含m的式子表示)
(3)在(2)的条件下,如何安排装运的汽车可使水果基地获得最大利润?最大利润是多少?
23.(16分)定义:对任意一个两位数a,如果a满足个位数字比十位数字大3,那么称这个两位数为“慧泉数”.将一个“慧泉数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如,a=14,对调个位数字与十位数字后得到新的两位数为41,新两位数与原两位数的和为14+41=55,其和与11的商为55÷11=5,∴f(14)=5.
根据以上定义,回答下列问题:
(1)f(36)= ;
(2)若f(a)=7,求a的值;
(3)如果一个“慧泉数” m的十位数字是x,另一个“慧泉数”n的个位数字是x,且满足f(m)+f(n)<20,求m,n的值.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.在以下绿色食品、可回收、节能、节水四个标志中,是轴对称图形的是( A )
2.下列方程是一元一次方程的是( C )
A.x-1= B.3a-3<1
C.2x-3=5 D.2x2+1=5
3.下列四幅图案可以看作是以图案中某部分为基本图形平移得到的是( B )
4.不等式组的解集在数轴上表示正确的是( B )
5.下列说法不正确的是( D )
A.若a>b,则a+2>b+2
B.若a>b,则-a<-b
C.若2a>2b,则a>b
D.若a>b,则ac2>bc2
6.体育课上的侧压腿动作可以抽象为如图所示的几何图形,若∠1=110°,则∠2=( B )
A.10° B.20° C.25° D.30°
7.我国古代数学著作《九章算术》中有一道题:“今有五雀六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平;并燕、雀重一斤.问燕、雀一枚各重几何?”其大意是现在有5只雀和6只燕,用秤来称它们,发现雀比较重,燕比较轻.将一只雀和一只燕交换位置后,质量相等;5只雀和6只燕的质量为一斤(斤是古代质量单位).问每只雀和每只燕的质量分别为多少斤?设每只雀的质量为x斤,每只燕的质量为y斤,则可列方程组为( A )
A. B.
C. D.
8.若某三角形的三边长分别为3,4,m,则m的值可以是( C )
A.9 B.7 C.5 D.1
9.如图,将一张正方形纸片按如图1、图2所示的方式折叠得到图3,再按图3中的虚线剪裁得到图4,将图4展开后得到的图案是( B )
10.如图,在△ABC中,AD⊥BC交BC于点D,AE平分∠BAC交BC于点E.过点C作AE的垂线交AE的延长线于点F,交AD的延长线于点G,连结BG.有下列结论:
①∠BAD=∠BCG;②∠ECF=(∠ABD-∠ACE);③∠AGC=∠BAE+∠ACB;④S△ABD·S△CDG=S△BDG·S△ACD.其中正确的个数是( C )
A.1 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题5分,满分30分)
11.如果一个多边形的每一个内角都等于135°,那么这个多边形是 八 边形.
12.已知则a-b= 2 .
13.已知关于x,y的方程组用含x的代数式表示y,则y= -x-2 .
14.关于x的不等式组有且仅有4个整数解,则a的取值范围为 -2≤a<-1 .
15.如图,直线l上摆放着两个大小相同的△ABC和△DEC,∠ACB=∠DCE=90°,∠BAC=∠EDC=30°,将△DEC沿直线l向左平移得到△D'E'C';使点E'落在AB上,E'D'与AC交于点P.有下列结论:
①∠CPD'=60°;
②AB⊥E'D';
③△PEE'和△PCD'的周长之和等于△ABC的周长;
④图中阴影部分的面积之和大于△ABC的面积.
其中正确的是 ①②③ .(填序号)
16.如图,在△ABC中,∠F=16°,BD,CD分别平分∠ABC,∠ACB,M,N,Q分别在DB,DC,BC的延长线上,BE,CE分别平分∠MBC,∠BCN,BF,CF分别平分∠EBC,∠ECQ,则∠A= 52° .
三、解答题(本大题共7小题,满分80分)
17.(8分)解下列方程(组):
(1)-=1;
解:去分母、去括号,得2x-1+x=4.
移项,得2x+x=4+1.
合并同类项,得3x=5.
系数化为1,得x=.
(2)
解:原方程组化为
①×2-②,得25y=5,解得y=.
把y=代入①,得3x+5×=2,解得x=.
∴原方程组的解为
18.(10分)如图,已知射线AD平分∠BAC.
(1)请用尺规作图作出BC的垂直平分线,交AD于点P,交BC点Q,交AB于点R(不写作法,保留作图痕迹);
(2)若∠B=30°,∠C=50°,求∠DPQ的度数.
解:(1)如图所示,直线RQ即为所求.
(2)∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=50°,
∴∠ADC=180°-∠C-∠CAD=80°,
∴∠PDQ=∠ADC=80°.
∵QR垂直平分BC,∴∠PQD=90°,
∴∠DPQ=180°-∠PQD-∠PDQ=10°.
19.(10分)在如图所示的网格(每小格均为边长是1个单位长度的正方形)中完成下列各题:
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称得到的△A1B1C1;
(2)画出格点△ABC(顶点均在格点上)绕点A顺时针旋转90°得到的△AB2C2.
解:(1)△A1B1C1如图所示.
(2)△A2B2C2如图所示.
20.(12分)甲、乙两人共同解方程组由于甲看错了方程①中的m,得到方程组的解为乙看错了方程②中的n,得到方程组的解为求:
(1)方程组正确的解;
(2)m2 024-的值.
解:(1)根据题意,得
解得∴原方程组为
①+②,得x=14.
将x=14代入①中,得y=,
∴原方程组的解为
(2)将代入 m2 024-中,
m2 024-=(-1)2 024-
=1-(-1)2 025
=1+1
=2.
21.(12分)已知关于x,y的方程组且x的值为非负数,y的值为正数.
(1)求m的取值范围;
(2)在m的取值范围内,且当m为负整数时,不等式mx+x<m+1的解集为x>1,求m的值.
解:(1)解方程组
得
∵x的值为非负数,y的值为正数,
∴解得-2≤m<,
即m的取值范围为-2≤m<.
(2)∵mx+x<m+1,∴(m+1)x<m+1.
∵不等式mx+x<m+1的解集为x>1,
∴m+1<0,∴m<-1.
∵-2≤m<,∴-2≤m<-1.
∵m为负整数,∴m=-2.
22.(12分)某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果),下表为装运甲、乙、丙三种水果的质量及利润.
水果种类 甲 乙 丙
每辆汽车能装的质量/吨 4 2 3
每吨水果可获利润/千元 5 7 4
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各有多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于1辆车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用含m的式子表示)
(3)在(2)的条件下,如何安排装运的汽车可使水果基地获得最大利润?最大利润是多少?
解:(1)设装运乙、丙两种水果的汽车分别为x辆、y辆.由题意,得解得
答:装运乙种水果的汽车有2辆,装运丙种水果的汽车有6辆.
(2)设装运乙、丙两种水果的汽车分别为a辆、b辆.
由题意,得解得
答:装运乙种水果的汽车有(m-12)辆,装运丙种水果的汽车有(32-2m)辆.
(3)设总利润为W千元.
由题意,得W=5×4m+7×2(m-12)+4×3(32-2m)=10m+216.
∵∴13≤m≤.
∵m为正整数,∴m的值可取13,14,15.
∵当m=13时,W=10×13+216=346(千元);
当m=14时,W=10×14+216=356(千元);
当m=15时,W=10×15+216=366(千元).
∴当m=15时,W最大=366(千元),
m-12=3(辆),32-2m=2(辆).
答:当装运甲水果的汽车15辆,装运乙水果的汽车3辆,装运丙水果的汽车2辆时可使水果基地获得的利润最大,最大利润为366千元.
23.(16分)定义:对任意一个两位数a,如果a满足个位数字比十位数字大3,那么称这个两位数为“慧泉数”.将一个“慧泉数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为f(a).例如,a=14,对调个位数字与十位数字后得到新的两位数为41,新两位数与原两位数的和为14+41=55,其和与11的商为55÷11=5,∴f(14)=5.
根据以上定义,回答下列问题:
(1)f(36)= 9 ;
(2)若f(a)=7,求a的值;
(3)如果一个“慧泉数” m的十位数字是x,另一个“慧泉数”n的个位数字是x,且满足f(m)+f(n)<20,求m,n的值.
解:(1)由题意可得f(36)=(36+63)÷11=99÷11=9.故答案为9.
(2)设a的个位数字为y,则其十位数字为(y-3).
∵f(a)=7,∴=7,
解得y=5,则y-3=5-3=2,
则a=10(y-3)+y=10×2+5=25.
(3)∵一个“慧泉数” m的十位数字是x,另一个“慧泉数”n的个位数字是x,
∴“慧泉数”m的个位数字是(x+3),“慧泉数”n的十位数字是(x-3),
∴f(m)==2x+3,
f(n)==2x-3.
∵f(m)+f(n)<20,
∴2x+3+2x-3<20,解得x<5.
∵x-3>0且x为整数,
∴3<x<5且x为整数,∴x=4,
则x+3=4+3=7,x-3=4-3=1,
即m=10x+(x+3)=10×4+7=47,
n=10(x-3)+x=10×1+4=14.
同课章节目录
