2.2第三课时 数轴(共42张PPT)2024-2025学年鲁教版(2024)五四制六年级数学上册
文档属性
| 名称 | 2.2第三课时 数轴(共42张PPT)2024-2025学年鲁教版(2024)五四制六年级数学上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 14:48:08 | ||
图片预览









文档简介
(共42张PPT)
第二章
有理数及其运算
2 认识有理数
(第3课时)
【提问】
(1)温度计上的刻度是怎样表示温度的?
(2)把温度计横放(上温度向右),你觉得它像什么?
(3)你能把温度计的刻度画在纸上吗?
1.了解数轴的概念及其三个要素,会画数轴.
2.理解数轴上的点和有理数的对应关系,会利用数
轴比较有理数的大小.
B
观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)温度计刻度的正负是怎样规定的 以什么为基准
(3)每摄氏度两条刻度线之间的距离有什么特点
A
C
数轴的概念
知识点1
0
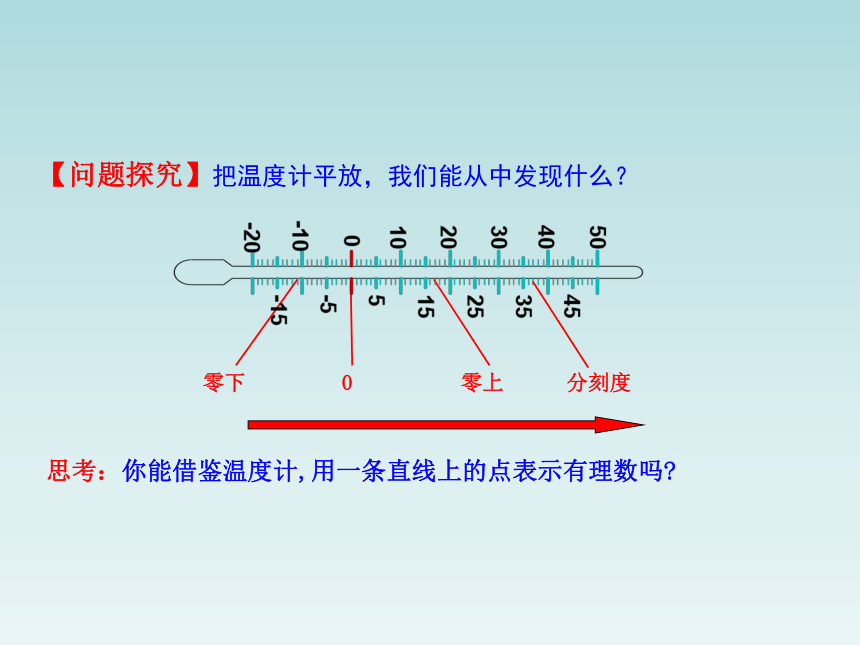
【问题探究】把温度计平放,我们能从中发现什么?
零下
零上
分刻度
思考:你能借鉴温度计,用一条直线上的点表示有理数吗
在一条水平直线上取一点(称为原点)表示0,选取某一长度作为单位长度,规定这条直线上向右的方向为正方向,那么相反方向就是负方向.
【实践操作】
原点右边的点可以表示正数,原点左边的点可以表示负数。
像这样,规定了原点、单位长度、和正方向的直线称为数轴。
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
0
2.规定从原点向右为正方向,那么相反的方向(从
原点向左)则为负方向.
3.选择适当的长度为单位长度.
0
0
1
2
3
-1
-2
-3
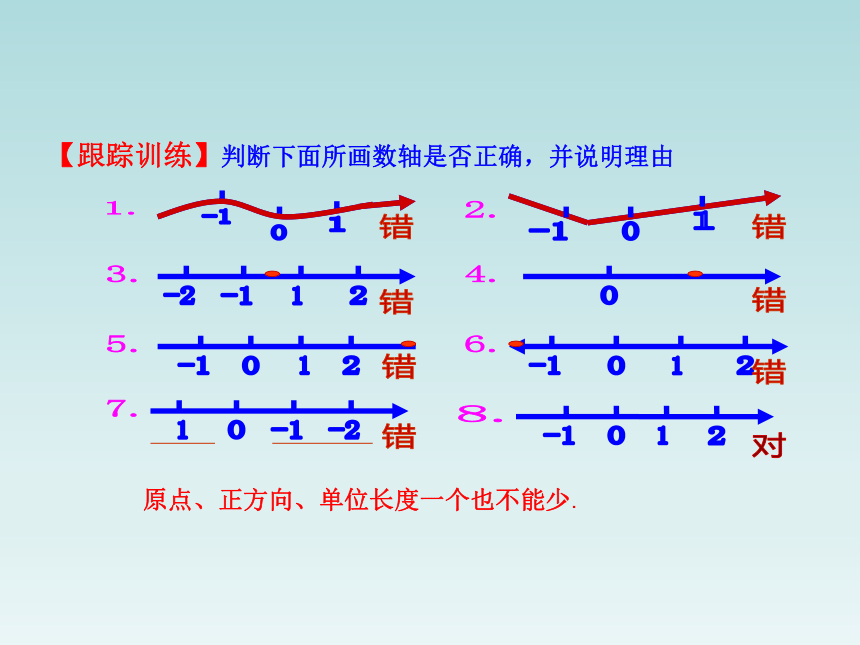
原点、正方向、单位长度一个也不能少.
【跟踪训练】判断下面所画数轴是否正确,并说明理由
新课讲授
2.定原点:在这条直线上的适当位置取一点作为原点(如图),原点表示0;
0
3.定方向:确定正方向,用箭头表示出来(一般规定从原点向右的方向为正方向);
4.定单位长度:确定单位长度,用细短线画出,并对应地标注各数.
0
0
1
2
3
-1
-2
-3
1.先画一条水平的直线;
思考:(3)如何画一条数轴呢?
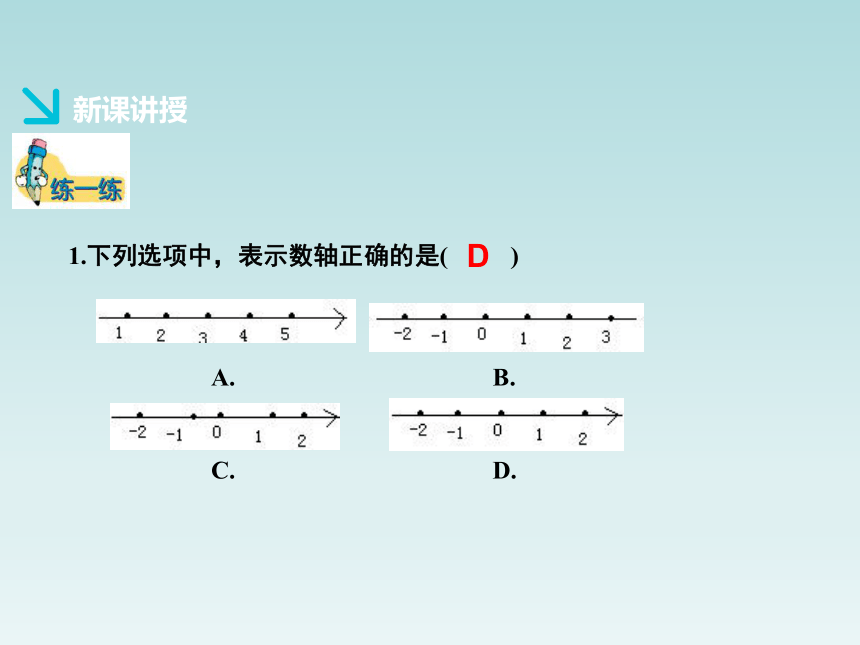
1.下列选项中,表示数轴正确的是( )
A. B.
C. D.
新课讲授
D
尝试·思考:你能用数轴上的点来表示有理数吗?
新课讲授
探究二:用数轴上的点表示有理数
(1)在数轴上,+3可以用位于原点 边 个单位长度的点表示,-4可以用位于原点 边 个单位长度的点表示.
右
3
左
4
-1.5
新课讲授
知识归纳
用数轴上的点表示有理数
任何一个有理数都可以用数轴上的一个点来表示.
正有理数用原点右边的点表示(在数轴上要画出实心的小圆点),负有理数用原点左边的点表示,0用原点表示。
新课讲授
2.(1)指出数轴上A,B,C,D,E各点分别表示什么数.
解:(1)点A表示1.5;点B表示-0.5;
点C表示-3;点D表示3;点E表示-2.
4.已知│a│=3,│b│=2,│c│=2,有理数a,b,c在数轴上的位置如图所示,则a=____;b=_____;c=____.
-3
-2
2
0
巩固练习
2.如图,四个有理数在数轴上的对应点分别为点M,P,N,Q,若点P,Q表示的有理数互为相反数,则图中表示绝对值最大的有理数的点是( )
A.点M B.点P C.点N D.点Q
A
3.已知整数m同时满足下列两个条件,①在数轴上位于原点左侧;
②绝对值大于3且小于6.则m= .
-4,或-5
巩固练习
有一只蚂蚁在数轴上爬行,它从原点开始爬,“+”
表示蚂蚁沿数轴向右爬,“-”表示蚂蚁沿数轴向左爬,
共爬行10次,其数据(单位:cm )统计如下:-7,+5,-3,+2,-1,+6,-4,+4,+7,+3.如果这只蚂蚁每分钟爬 3 cm,那么它在这次爬行过程中一共需要几分钟?
解:|-7|+|+5|+|-3|+|+2|+|-1|+|+6|+|-4|+
|+4|+|+7|+|+3|
=42
42÷3=14
所以它在这次爬行过程中一共需要14分钟。
(cm).
(分钟).
巩固练习
如图,数轴的单位长度为1,且数轴上各点之间的距离均为1.
(1)如果点B与点F表示的数互为相反数,那么点D表示的数是什么?
(2)如果点D与点H表示的数互为相反数,那么点C表示的数是什么?
解:(1)因为BC=CD=DE=EF=1,
所以BD=DF.
因为点B与点F表示的数互为相反数,
所以点D表示的数是0.
当堂检测
如图,数轴的单位长度为1,且数轴上各点之间的距离均为1.
(1)如果点B与点F表示的数互为相反数,那么点D表示的数是什么?
(2)如果点D与点H表示的数互为相反数,那么点C表示的数是什么?
解:(2)因为DE=EF=FG=GH=1, 所以DF=FH.
所以点F表示的数是0.
因为点D与点H表示的数互为相反数,
因为CF=1+1+1=3,所以点C表示的数是-3.
当堂检测
【课堂小测(8分钟)】
1.下列所画的数轴中,正确的是( )
【解析】 A.不符合数轴右边的数总比左边的数大的特点,故本选项错误;
B.有原点、正方向、单位长度,故本选项正确;
C.没有原点,故本选项错误;
D.单位长度不统一,故本选项错误.
B
D
3.(2024·揭阳普宁期末)如图所示,数轴的单位长度为1,如果点A表示的数是-2,那么点B表示的数是( )
A.0 B.1 C.2 D.3
【解析】 点B在点A右侧4个单位长度,即点B所表示的数为-2+4=2.
C
4.(2024·东莞期末)点A为数轴上表示-2的点,点A沿数轴移动4个单位长度到达点B处,
点B所表示的数是__________.
【解析】当点A向右移动时:
所以点B所表示的数是2,
当点A向左移动时:
所以点B所表示的数是-6.
2或-6
13. [2024渭南期末]如图,数轴上从左到右依次有点 A , B , C , D ,其中点 C 为原点, A , D 所对应的数分别 为-4,1, B , D 两点间的距离是3.
(1)在图中标出点 B , C 的位置,并写出点 B 对应的数.
【解】如图所示.点 B 对 应的数是-2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)若在数轴上另取一点 E ,使 B , E 两点间的距离是 7,求点 E 所表示的数.
【解】因为 B , E 两点间的距离是7,点 B 对应的数是-2,所以当点 E 在点 B 的右侧时,点 E 所表示的数为5;当点 E 在点 B 的左侧时,点 E 所表示的数为-9.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. [2024佛山期末]已知 a , b , c 为有理数,且它们在数轴 上的位置如图所示.
(1)试判断 a , b , c 的正负性.
【解】 a <0, b >0, c >0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)在数轴上标出 a , b , c 相反数的位置,用- a ,- b ,- c 表示.
【解】如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)若| a |=5,| b |=2.5,| c |=7.5,求 a , b , c 的值.
【解】因为| a |=5,| b |= 2.5,| c |=7.5, a <0, b > 0, c >0,所以 a =-5, b = 2.5, c =7.5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. [新考法·数形结合法]已知 a , b , c 为有理数,且它们在 数轴上的位置如图所示.
(1)根据数轴填空:
① a 是 数, b - a 是 数(填“正”或 “负”);
②比较大小: a b ,∣ a ∣ ∣ b ∣(填 “>”“<”或“=”);
③根据数轴化简:∣ b ∣= ,| b - c | = .
负
正
<
>
- b
c - b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)在数轴上,表示数 a 的点到原点的距离可表示为| a |,即| a -0|.类似地,表示数 a 的点到表示数2 的点的距离可表示为 .
| a -2|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)应用:①表示数 a 的点到表示数3的点的距离是7,可 记为| a -3|=7,那么 a = .
②当 a 取何值时,| a +4|+| a -3|的值最小, 最小值是多少?请说明理由.
【解】当-4≤ a ≤3时,| a +4|+| a -3|的值最 小,最小值为7.
-4或10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
理由:| a +4|+| a -3|为表示数 a 的点到数-4 的距离和表示数 a 的点到表示数3的点的距离之和.
由数轴可得,当表示数 a 的点在表示数-4的点左侧或 表示数3的点右侧时,距离之和大于7;当表示数 a 的 点在表示数-4和数3(包含-4和3)的点之间时,距离 为7,此时| a +4|+| a -3|的值最小,
所以当-4≤ a ≤3时,| a +4|+| a -3|的值最 小,最小值为7.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例2 如图,数轴上点A表示的数为+3,把点A先向右平移5个单位,再向左平移10个单位到点B,则点B表示的数为 .
-2
0
1
2
3
4
-1
A
·
表示3的点在数轴上原点右侧,距离原点3个单位长度;
表示-3的点在数轴上原点左侧,距离原点3个单位长度;
0
1
2
3
4
-1
-2
-3
-4
-5
5
例3 在数轴上距离原点2.5个单位长度的点所表示的数是 .
±2.5
归纳 一个数的绝对值就是这个数所对应的点到原点的距离。
数轴三要素
数轴
原点、正方向、单位长度
数轴上原点右边的数表示正数,原点左边的数表示负数
表示有理数
比较有理数的大小
数轴上两个点表示的数,右边的总比左边的大
第二章
有理数及其运算
2 认识有理数
(第3课时)
【提问】
(1)温度计上的刻度是怎样表示温度的?
(2)把温度计横放(上温度向右),你觉得它像什么?
(3)你能把温度计的刻度画在纸上吗?
1.了解数轴的概念及其三个要素,会画数轴.
2.理解数轴上的点和有理数的对应关系,会利用数
轴比较有理数的大小.
B
观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)温度计刻度的正负是怎样规定的 以什么为基准
(3)每摄氏度两条刻度线之间的距离有什么特点
A
C
数轴的概念
知识点1
0
【问题探究】把温度计平放,我们能从中发现什么?
零下
零上
分刻度
思考:你能借鉴温度计,用一条直线上的点表示有理数吗
在一条水平直线上取一点(称为原点)表示0,选取某一长度作为单位长度,规定这条直线上向右的方向为正方向,那么相反方向就是负方向.
【实践操作】
原点右边的点可以表示正数,原点左边的点可以表示负数。
像这样,规定了原点、单位长度、和正方向的直线称为数轴。
数轴的画法:
1.画一条水平直线,定原点(如图),原点表示0.
0
2.规定从原点向右为正方向,那么相反的方向(从
原点向左)则为负方向.
3.选择适当的长度为单位长度.
0
0
1
2
3
-1
-2
-3
原点、正方向、单位长度一个也不能少.
【跟踪训练】判断下面所画数轴是否正确,并说明理由
新课讲授
2.定原点:在这条直线上的适当位置取一点作为原点(如图),原点表示0;
0
3.定方向:确定正方向,用箭头表示出来(一般规定从原点向右的方向为正方向);
4.定单位长度:确定单位长度,用细短线画出,并对应地标注各数.
0
0
1
2
3
-1
-2
-3
1.先画一条水平的直线;
思考:(3)如何画一条数轴呢?
1.下列选项中,表示数轴正确的是( )
A. B.
C. D.
新课讲授
D
尝试·思考:你能用数轴上的点来表示有理数吗?
新课讲授
探究二:用数轴上的点表示有理数
(1)在数轴上,+3可以用位于原点 边 个单位长度的点表示,-4可以用位于原点 边 个单位长度的点表示.
右
3
左
4
-1.5
新课讲授
知识归纳
用数轴上的点表示有理数
任何一个有理数都可以用数轴上的一个点来表示.
正有理数用原点右边的点表示(在数轴上要画出实心的小圆点),负有理数用原点左边的点表示,0用原点表示。
新课讲授
2.(1)指出数轴上A,B,C,D,E各点分别表示什么数.
解:(1)点A表示1.5;点B表示-0.5;
点C表示-3;点D表示3;点E表示-2.
4.已知│a│=3,│b│=2,│c│=2,有理数a,b,c在数轴上的位置如图所示,则a=____;b=_____;c=____.
-3
-2
2
0
巩固练习
2.如图,四个有理数在数轴上的对应点分别为点M,P,N,Q,若点P,Q表示的有理数互为相反数,则图中表示绝对值最大的有理数的点是( )
A.点M B.点P C.点N D.点Q
A
3.已知整数m同时满足下列两个条件,①在数轴上位于原点左侧;
②绝对值大于3且小于6.则m= .
-4,或-5
巩固练习
有一只蚂蚁在数轴上爬行,它从原点开始爬,“+”
表示蚂蚁沿数轴向右爬,“-”表示蚂蚁沿数轴向左爬,
共爬行10次,其数据(单位:cm )统计如下:-7,+5,-3,+2,-1,+6,-4,+4,+7,+3.如果这只蚂蚁每分钟爬 3 cm,那么它在这次爬行过程中一共需要几分钟?
解:|-7|+|+5|+|-3|+|+2|+|-1|+|+6|+|-4|+
|+4|+|+7|+|+3|
=42
42÷3=14
所以它在这次爬行过程中一共需要14分钟。
(cm).
(分钟).
巩固练习
如图,数轴的单位长度为1,且数轴上各点之间的距离均为1.
(1)如果点B与点F表示的数互为相反数,那么点D表示的数是什么?
(2)如果点D与点H表示的数互为相反数,那么点C表示的数是什么?
解:(1)因为BC=CD=DE=EF=1,
所以BD=DF.
因为点B与点F表示的数互为相反数,
所以点D表示的数是0.
当堂检测
如图,数轴的单位长度为1,且数轴上各点之间的距离均为1.
(1)如果点B与点F表示的数互为相反数,那么点D表示的数是什么?
(2)如果点D与点H表示的数互为相反数,那么点C表示的数是什么?
解:(2)因为DE=EF=FG=GH=1, 所以DF=FH.
所以点F表示的数是0.
因为点D与点H表示的数互为相反数,
因为CF=1+1+1=3,所以点C表示的数是-3.
当堂检测
【课堂小测(8分钟)】
1.下列所画的数轴中,正确的是( )
【解析】 A.不符合数轴右边的数总比左边的数大的特点,故本选项错误;
B.有原点、正方向、单位长度,故本选项正确;
C.没有原点,故本选项错误;
D.单位长度不统一,故本选项错误.
B
D
3.(2024·揭阳普宁期末)如图所示,数轴的单位长度为1,如果点A表示的数是-2,那么点B表示的数是( )
A.0 B.1 C.2 D.3
【解析】 点B在点A右侧4个单位长度,即点B所表示的数为-2+4=2.
C
4.(2024·东莞期末)点A为数轴上表示-2的点,点A沿数轴移动4个单位长度到达点B处,
点B所表示的数是__________.
【解析】当点A向右移动时:
所以点B所表示的数是2,
当点A向左移动时:
所以点B所表示的数是-6.
2或-6
13. [2024渭南期末]如图,数轴上从左到右依次有点 A , B , C , D ,其中点 C 为原点, A , D 所对应的数分别 为-4,1, B , D 两点间的距离是3.
(1)在图中标出点 B , C 的位置,并写出点 B 对应的数.
【解】如图所示.点 B 对 应的数是-2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)若在数轴上另取一点 E ,使 B , E 两点间的距离是 7,求点 E 所表示的数.
【解】因为 B , E 两点间的距离是7,点 B 对应的数是-2,所以当点 E 在点 B 的右侧时,点 E 所表示的数为5;当点 E 在点 B 的左侧时,点 E 所表示的数为-9.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. [2024佛山期末]已知 a , b , c 为有理数,且它们在数轴 上的位置如图所示.
(1)试判断 a , b , c 的正负性.
【解】 a <0, b >0, c >0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)在数轴上标出 a , b , c 相反数的位置,用- a ,- b ,- c 表示.
【解】如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)若| a |=5,| b |=2.5,| c |=7.5,求 a , b , c 的值.
【解】因为| a |=5,| b |= 2.5,| c |=7.5, a <0, b > 0, c >0,所以 a =-5, b = 2.5, c =7.5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. [新考法·数形结合法]已知 a , b , c 为有理数,且它们在 数轴上的位置如图所示.
(1)根据数轴填空:
① a 是 数, b - a 是 数(填“正”或 “负”);
②比较大小: a b ,∣ a ∣ ∣ b ∣(填 “>”“<”或“=”);
③根据数轴化简:∣ b ∣= ,| b - c | = .
负
正
<
>
- b
c - b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)在数轴上,表示数 a 的点到原点的距离可表示为| a |,即| a -0|.类似地,表示数 a 的点到表示数2 的点的距离可表示为 .
| a -2|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)应用:①表示数 a 的点到表示数3的点的距离是7,可 记为| a -3|=7,那么 a = .
②当 a 取何值时,| a +4|+| a -3|的值最小, 最小值是多少?请说明理由.
【解】当-4≤ a ≤3时,| a +4|+| a -3|的值最 小,最小值为7.
-4或10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
理由:| a +4|+| a -3|为表示数 a 的点到数-4 的距离和表示数 a 的点到表示数3的点的距离之和.
由数轴可得,当表示数 a 的点在表示数-4的点左侧或 表示数3的点右侧时,距离之和大于7;当表示数 a 的 点在表示数-4和数3(包含-4和3)的点之间时,距离 为7,此时| a +4|+| a -3|的值最小,
所以当-4≤ a ≤3时,| a +4|+| a -3|的值最 小,最小值为7.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例2 如图,数轴上点A表示的数为+3,把点A先向右平移5个单位,再向左平移10个单位到点B,则点B表示的数为 .
-2
0
1
2
3
4
-1
A
·
表示3的点在数轴上原点右侧,距离原点3个单位长度;
表示-3的点在数轴上原点左侧,距离原点3个单位长度;
0
1
2
3
4
-1
-2
-3
-4
-5
5
例3 在数轴上距离原点2.5个单位长度的点所表示的数是 .
±2.5
归纳 一个数的绝对值就是这个数所对应的点到原点的距离。
数轴三要素
数轴
原点、正方向、单位长度
数轴上原点右边的数表示正数,原点左边的数表示负数
表示有理数
比较有理数的大小
数轴上两个点表示的数,右边的总比左边的大
同课章节目录
