2.2认识有理数(第三课时)数轴 课件 (40张PPT)2024-2025学年鲁教版(2024)五四制六年级数学上册
文档属性
| 名称 | 2.2认识有理数(第三课时)数轴 课件 (40张PPT)2024-2025学年鲁教版(2024)五四制六年级数学上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 15:56:54 | ||
图片预览









文档简介
(共40张PPT)
2.2认识有理数
(第3课时)
第二章 有理数及其运算
学习目标
通过与温度计的类比认识数轴,理解数轴的三要素并会画数轴
01
知道|a|的含义以及互为相反数的两个数在数轴上的位置关系
02
能利用数轴比较有理数的大小
03
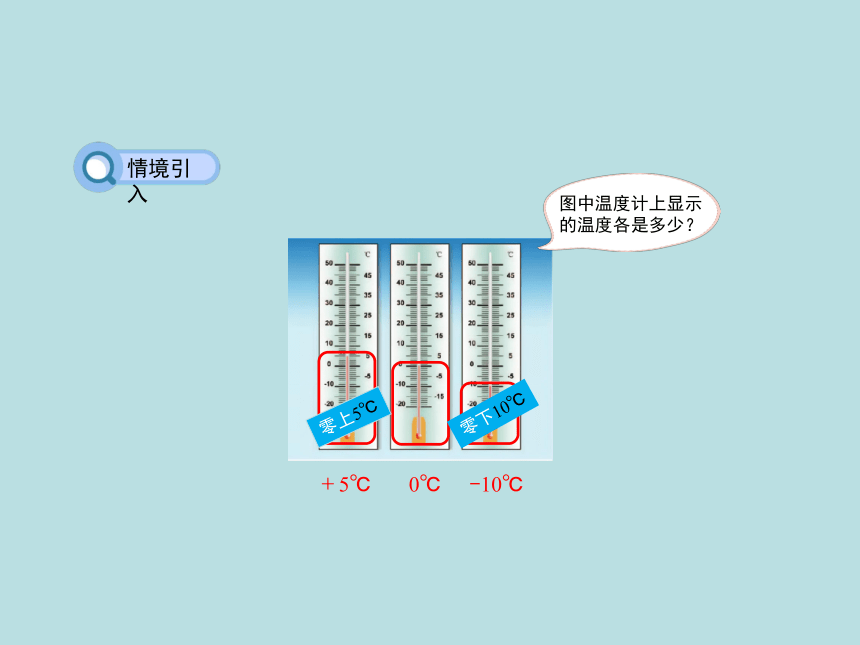
情境引入
图中温度计上显示
的温度各是多少?
﹢5℃
0℃
-10℃
零上5℃
零下10℃
情境引入
温度计上的刻
度有什么特点
①刻度是均匀的,相邻刻度间的距离相等;
③有一点表示0℃;
④0℃以上的刻度表示零上温度,0℃以下的刻度
表示零下温度,即刻度表示温度有方向性.
②刻度都标在一条直线上,刻度数对应有理数;
情境引入
如果我们把温度计放平,大家看看像什么?
像一条直线,直线上有正有理数,0,负有理数.
能否用一条直线来代替温度计表示有理数呢?
在这条数轴上,+3用哪个点表示?
合作探究
画一条水平直线,在直线上取一点表示0(叫做原点),
选取某一长度作为单位长度,
就得到下面的数轴.
规定直线上向右的方向为正方向,
0
单位长度
1
原点
2
3
4
5
-1
-2
-3
-4
-5
→正方向
-4呢?
.
.
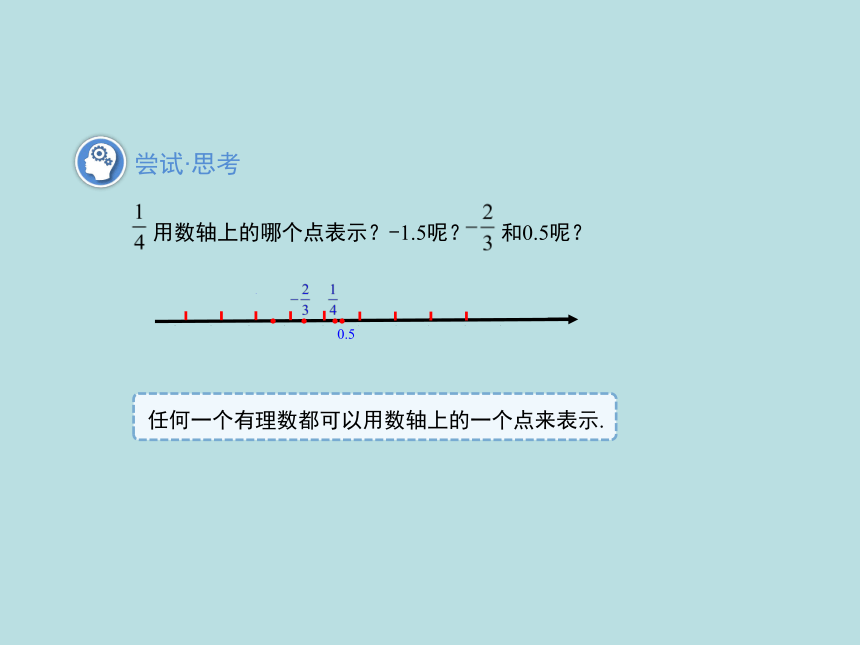
用数轴上的哪个点表示?-1.5呢?
0
1
2
3
4
5
-1
-2
-3
-4
-1.5
和0.5呢?
0.5
任何一个有理数都可以用数轴上的一个点来表示.
.
.
.
.
尝试 思考
归纳
2.任何一个有理数都可以用数轴上的一个点来表示.
1.画数轴的步骤:
(1)画直线定原点,原点表示0;
(2)选择适当的长度作为单位长度;
(3)规定正方向,标箭头.
观察画好的数轴,思考以下问题:
(1)原点表示什么数?
(2)+3, ,-1.5,0分别在数轴的什么位置?
★ 任何一个有理数都可以用数轴上的点来表示.
用数轴上的点表示有理数
知识点2
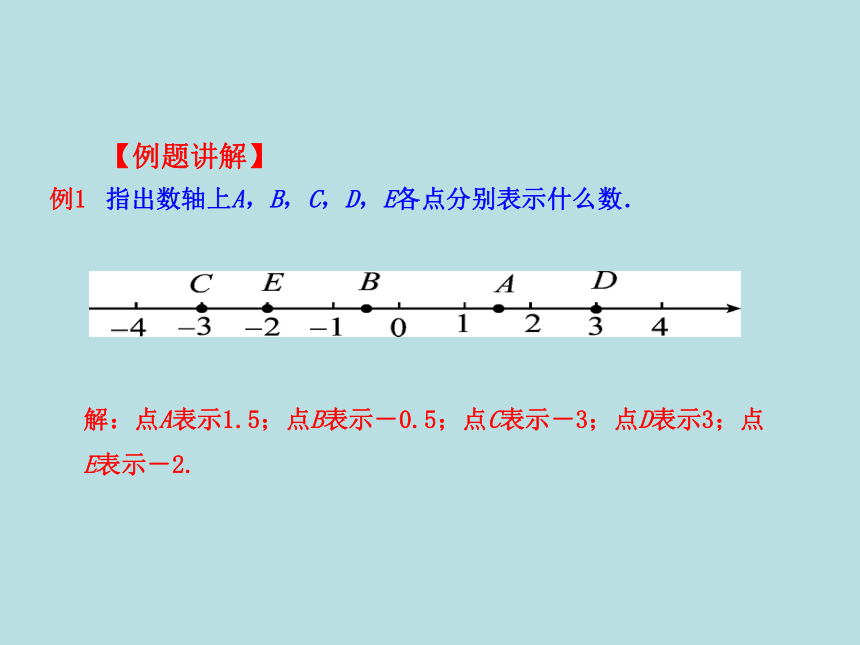
例1 指出数轴上A,B,C,D,E各点分别表示什么数.
解:点A表示1.5;点B表示-0.5;点C表示-3;点D表示3;点E表示-2.
【例题讲解】
例2 画出数轴,并用数轴上的点表示下列各数:
解:如图所示.
1.-3到原点的距离为多少?3到原点的距离为多少?它们有什么关系?
2.-3的绝对值为多少?-2到原点的距离为多少?-2的绝对值为多少?
3
3
3
2
2
【思考】
相等
1.通过思考1和思考2,你有什么发现?
在数轴上,表示互为相反数的两个点,位于原点的两侧,且到原点的距离相等。一个数的绝对值就是这个数所对应的点到原点的距离。
【思考】
1.数轴上表示-6的点在原点的( )侧距原点的距离是(
),表示-1.5的点在原点的( )侧,距原点的距离是(
).
2.(判断)数轴上的两个点可以表示同一个有理数.
左
6个单位
左
单位长度
错,有理数与数轴上的点一一对应.
【跟踪训练】
长度
1.5个
2.如图,在数轴上点M表示的数可能是( )
A.1.5 B.-1.5 C.-2.4 D.2.4
1.如图所示的图形为四名同学画的数轴,其中正确的是( )
学以致用
D
C
学以致用
3.有下列四个地方:死海(海拔-400米),卡达拉低地(海拔-133米),罗讷河三角洲(海拔-2米),吐鲁番盆地(海拔-154米).其中最低的是( )
A.死海 B.卡达拉低地
C.罗讷河三角洲 D.吐鲁番盆地
4.如图所示,将一刻度尺放在数轴上(数轴的单位长度是1 cm),刻度尺上“0 cm”和“3 cm”分别对应数轴上的3和0,那么刻度尺上“4.6 cm”对应数轴上的数为( )
A.-1.6 B.4.6 C.2.6 D.-2.6
A
A
5.如图所示,点A,B,C,D所表示的数分别是:____,____,_____,_____.
学以致用
7.与原点的距离为3个单位长度的点所表示的有理数是_____.
±3
0
-1
-4
<
<
>
-2.5
学以致用
如图,在数轴上有 A , B , C 三个点,请回答下列问题:
(1)点 A 表示的数是 ,点 B 表示的数是 ,点 C 表示的数是 ;
-4
-1
3
【思路导航】(1)根据数轴直接观察出 A , B , C 三点所表 示的数;
【解析】(1)根据图示,知 A , B , C 三点所表示的数分别是 -4,-1,3.故答案为-4,-1,3.
(2) A , B 两点间的距离为 , B , C 两点间的距离 为 , A , C 两点间的距离为 .
【思路导航】(2)根据数轴的定义,结合图示即可求出两点间的距离.
3
4
7
【解析】(2)因为点 A 到原点的距离为4个单位长度,点 B 到原点的距离为1个单位长度,所以 A , B 两点间的距离为4-1=3.因为点 B 到原点的距离为1个单位长度,点 C 到原点的距离为3个单位长度,所以 B , C 两点间的距离为1+3=4.因为点 A 到原点的距离为4个单位长度,点 C 到原点的距离为3个单位长度,所以 A , C 两点间的距离为4+3=7.故答案为3,4,7.
【点拨】利用数形结合的思想,找到点与数的对应关系,正确 表示出数,距离表示的是两个点之间的单位长度.
A. 2 B. -6
C. 2或-6 D. 6
C
2. 已知一条数轴上有点 A , B , C ,其中点 A , B 表示的数分别 是-13和5,现以点 C 为折点,将数轴向右对折,若点 A 对应的 点A'落在点 B 的右边,并且点A'与点 B 间的距离为4,则点 C 表 示的数是 .
-2
【能力练】
6.(2024·汕尾海丰期末)有理数a,b,c在数轴上的位置如图所示,下列结论中,错误的是
( )
A.ca C.b<0,c<0 D.-a>-c
【解析】 根据数轴上点的位置得:ca,b<0,c<0,-a<-c.
D
7.(2024·佛山禅城期末)在数轴上与原点相距5个单位长度的点所表示的数是_______.
【解析】到原点的距离等于5个单位长度的点有2个,它们是±5.
8.(2024·茂名信宜期末)点A是数轴上一点,一只蚂蚁从点A处出发,爬了5个单位长度
到了表示的数为2的点,则点A所表示的数是__________.
【解析】依题意得,该点在2的左侧时所表示的数为2-5=-3,
该点在2的右侧时所表示的数为2+5=7,
因此点A所表示的数是-3或7.
±5
-3或7
【培优练】
9.(几何直观、推理能力)如图所示,在数轴上有A,B,C三个点,回答下列问题:
(1)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(2)在点A左侧找一点E,使点E到点A的距离是点E到点B的距离的2倍,写出点E表示的数.
【解析】(1)点D到A,C两点的距离相等,
故点D为AC的中点,点D表示的数为0.5.
(2)当点E在点A与点B之间时,EA=2EB,从题图上可以看出点E表示的数为-3.
当点E在点B的左侧时,根据题意可知点B是AE的中点,所以点E表示的数是-7.
综上所述,点E表示的数为-3或-7.
11. 小明在写作业时不慎将墨水滴在数轴上,如图,则被墨 迹盖住的整数共有 个.
【点拨】
结合数轴得,第一部分盖住的整数有-6,-5,- 4,-3,-2,第二部分盖住的整数有1,2,3,4,所以 两部分一共盖住9个整数.
9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
在数轴上表示如图:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
13. [2024渭南期末]如图,数轴上从左到右依次有点 A , B , C , D ,其中点 C 为原点, A , D 所对应的数分别 为-4,1, B , D 两点间的距离是3.
(1)在图中标出点 B , C 的位置,并写出点 B 对应的数.
【解】如图所示.点 B 对 应的数是-2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)若在数轴上另取一点 E ,使 B , E 两点间的距离是 7,求点 E 所表示的数.
【解】因为 B , E 两点间的距离是7,点 B 对应的数是-2,所以当点 E 在点 B 的右侧时,点 E 所表示的数为5;当点 E 在点 B 的左侧时,点 E 所表示的数为-9.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. [2024佛山期末]已知 a , b , c 为有理数,且它们在数轴 上的位置如图所示.
(1)试判断 a , b , c 的正负性.
【解】 a <0, b >0, c >0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)在数轴上标出 a , b , c 相反数的位置,用- a ,- b ,- c 表示.
【解】如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)若| a |=5,| b |=2.5,| c |=7.5,求 a , b , c 的值.
【解】因为| a |=5,| b |= 2.5,| c |=7.5, a <0, b > 0, c >0,所以 a =-5, b = 2.5, c =7.5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2.2认识有理数
(第3课时)
第二章 有理数及其运算
学习目标
通过与温度计的类比认识数轴,理解数轴的三要素并会画数轴
01
知道|a|的含义以及互为相反数的两个数在数轴上的位置关系
02
能利用数轴比较有理数的大小
03
情境引入
图中温度计上显示
的温度各是多少?
﹢5℃
0℃
-10℃
零上5℃
零下10℃
情境引入
温度计上的刻
度有什么特点
①刻度是均匀的,相邻刻度间的距离相等;
③有一点表示0℃;
④0℃以上的刻度表示零上温度,0℃以下的刻度
表示零下温度,即刻度表示温度有方向性.
②刻度都标在一条直线上,刻度数对应有理数;
情境引入
如果我们把温度计放平,大家看看像什么?
像一条直线,直线上有正有理数,0,负有理数.
能否用一条直线来代替温度计表示有理数呢?
在这条数轴上,+3用哪个点表示?
合作探究
画一条水平直线,在直线上取一点表示0(叫做原点),
选取某一长度作为单位长度,
就得到下面的数轴.
规定直线上向右的方向为正方向,
0
单位长度
1
原点
2
3
4
5
-1
-2
-3
-4
-5
→正方向
-4呢?
.
.
用数轴上的哪个点表示?-1.5呢?
0
1
2
3
4
5
-1
-2
-3
-4
-1.5
和0.5呢?
0.5
任何一个有理数都可以用数轴上的一个点来表示.
.
.
.
.
尝试 思考
归纳
2.任何一个有理数都可以用数轴上的一个点来表示.
1.画数轴的步骤:
(1)画直线定原点,原点表示0;
(2)选择适当的长度作为单位长度;
(3)规定正方向,标箭头.
观察画好的数轴,思考以下问题:
(1)原点表示什么数?
(2)+3, ,-1.5,0分别在数轴的什么位置?
★ 任何一个有理数都可以用数轴上的点来表示.
用数轴上的点表示有理数
知识点2
例1 指出数轴上A,B,C,D,E各点分别表示什么数.
解:点A表示1.5;点B表示-0.5;点C表示-3;点D表示3;点E表示-2.
【例题讲解】
例2 画出数轴,并用数轴上的点表示下列各数:
解:如图所示.
1.-3到原点的距离为多少?3到原点的距离为多少?它们有什么关系?
2.-3的绝对值为多少?-2到原点的距离为多少?-2的绝对值为多少?
3
3
3
2
2
【思考】
相等
1.通过思考1和思考2,你有什么发现?
在数轴上,表示互为相反数的两个点,位于原点的两侧,且到原点的距离相等。一个数的绝对值就是这个数所对应的点到原点的距离。
【思考】
1.数轴上表示-6的点在原点的( )侧距原点的距离是(
),表示-1.5的点在原点的( )侧,距原点的距离是(
).
2.(判断)数轴上的两个点可以表示同一个有理数.
左
6个单位
左
单位长度
错,有理数与数轴上的点一一对应.
【跟踪训练】
长度
1.5个
2.如图,在数轴上点M表示的数可能是( )
A.1.5 B.-1.5 C.-2.4 D.2.4
1.如图所示的图形为四名同学画的数轴,其中正确的是( )
学以致用
D
C
学以致用
3.有下列四个地方:死海(海拔-400米),卡达拉低地(海拔-133米),罗讷河三角洲(海拔-2米),吐鲁番盆地(海拔-154米).其中最低的是( )
A.死海 B.卡达拉低地
C.罗讷河三角洲 D.吐鲁番盆地
4.如图所示,将一刻度尺放在数轴上(数轴的单位长度是1 cm),刻度尺上“0 cm”和“3 cm”分别对应数轴上的3和0,那么刻度尺上“4.6 cm”对应数轴上的数为( )
A.-1.6 B.4.6 C.2.6 D.-2.6
A
A
5.如图所示,点A,B,C,D所表示的数分别是:____,____,_____,_____.
学以致用
7.与原点的距离为3个单位长度的点所表示的有理数是_____.
±3
0
-1
-4
<
<
>
-2.5
学以致用
如图,在数轴上有 A , B , C 三个点,请回答下列问题:
(1)点 A 表示的数是 ,点 B 表示的数是 ,点 C 表示的数是 ;
-4
-1
3
【思路导航】(1)根据数轴直接观察出 A , B , C 三点所表 示的数;
【解析】(1)根据图示,知 A , B , C 三点所表示的数分别是 -4,-1,3.故答案为-4,-1,3.
(2) A , B 两点间的距离为 , B , C 两点间的距离 为 , A , C 两点间的距离为 .
【思路导航】(2)根据数轴的定义,结合图示即可求出两点间的距离.
3
4
7
【解析】(2)因为点 A 到原点的距离为4个单位长度,点 B 到原点的距离为1个单位长度,所以 A , B 两点间的距离为4-1=3.因为点 B 到原点的距离为1个单位长度,点 C 到原点的距离为3个单位长度,所以 B , C 两点间的距离为1+3=4.因为点 A 到原点的距离为4个单位长度,点 C 到原点的距离为3个单位长度,所以 A , C 两点间的距离为4+3=7.故答案为3,4,7.
【点拨】利用数形结合的思想,找到点与数的对应关系,正确 表示出数,距离表示的是两个点之间的单位长度.
A. 2 B. -6
C. 2或-6 D. 6
C
2. 已知一条数轴上有点 A , B , C ,其中点 A , B 表示的数分别 是-13和5,现以点 C 为折点,将数轴向右对折,若点 A 对应的 点A'落在点 B 的右边,并且点A'与点 B 间的距离为4,则点 C 表 示的数是 .
-2
【能力练】
6.(2024·汕尾海丰期末)有理数a,b,c在数轴上的位置如图所示,下列结论中,错误的是
( )
A.c
【解析】 根据数轴上点的位置得:c
D
7.(2024·佛山禅城期末)在数轴上与原点相距5个单位长度的点所表示的数是_______.
【解析】到原点的距离等于5个单位长度的点有2个,它们是±5.
8.(2024·茂名信宜期末)点A是数轴上一点,一只蚂蚁从点A处出发,爬了5个单位长度
到了表示的数为2的点,则点A所表示的数是__________.
【解析】依题意得,该点在2的左侧时所表示的数为2-5=-3,
该点在2的右侧时所表示的数为2+5=7,
因此点A所表示的数是-3或7.
±5
-3或7
【培优练】
9.(几何直观、推理能力)如图所示,在数轴上有A,B,C三个点,回答下列问题:
(1)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(2)在点A左侧找一点E,使点E到点A的距离是点E到点B的距离的2倍,写出点E表示的数.
【解析】(1)点D到A,C两点的距离相等,
故点D为AC的中点,点D表示的数为0.5.
(2)当点E在点A与点B之间时,EA=2EB,从题图上可以看出点E表示的数为-3.
当点E在点B的左侧时,根据题意可知点B是AE的中点,所以点E表示的数是-7.
综上所述,点E表示的数为-3或-7.
11. 小明在写作业时不慎将墨水滴在数轴上,如图,则被墨 迹盖住的整数共有 个.
【点拨】
结合数轴得,第一部分盖住的整数有-6,-5,- 4,-3,-2,第二部分盖住的整数有1,2,3,4,所以 两部分一共盖住9个整数.
9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
在数轴上表示如图:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
13. [2024渭南期末]如图,数轴上从左到右依次有点 A , B , C , D ,其中点 C 为原点, A , D 所对应的数分别 为-4,1, B , D 两点间的距离是3.
(1)在图中标出点 B , C 的位置,并写出点 B 对应的数.
【解】如图所示.点 B 对 应的数是-2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)若在数轴上另取一点 E ,使 B , E 两点间的距离是 7,求点 E 所表示的数.
【解】因为 B , E 两点间的距离是7,点 B 对应的数是-2,所以当点 E 在点 B 的右侧时,点 E 所表示的数为5;当点 E 在点 B 的左侧时,点 E 所表示的数为-9.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. [2024佛山期末]已知 a , b , c 为有理数,且它们在数轴 上的位置如图所示.
(1)试判断 a , b , c 的正负性.
【解】 a <0, b >0, c >0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)在数轴上标出 a , b , c 相反数的位置,用- a ,- b ,- c 表示.
【解】如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)若| a |=5,| b |=2.5,| c |=7.5,求 a , b , c 的值.
【解】因为| a |=5,| b |= 2.5,| c |=7.5, a <0, b > 0, c >0,所以 a =-5, b = 2.5, c =7.5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
同课章节目录
