2.2认识有理数(第三课时)数轴 复习习题课件 (32张PPT)2024-2025学年鲁教版(2024)五四制六年级数学上册
文档属性
| 名称 | 2.2认识有理数(第三课时)数轴 复习习题课件 (32张PPT)2024-2025学年鲁教版(2024)五四制六年级数学上册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 15:59:05 | ||
图片预览








文档简介
(共32张PPT)
第二章 有理数及其运算
2 认识有理数(第三课时)
数学 七年级上册 BS版
课前预习
典例讲练
目录
CONTENTS
数学 七年级上册 BS版
课前预习
0 1
1. 规定了 、 和 的直线称为数 轴.通常将数轴画成水平直线,并选择向右的方向为正方向.
2. 数轴的三要素: 、 和 .
3. 数轴的画法.
原点
单位长度
正方向
原点
正方向
单位长度
一画:画一条直线(一般是水平直线);
二取:选取原点,并用这个点表示数字0;
三定:确定正方向,用箭头表示(一般规定向右为正方向);
四统一:单位长度应统一;
五标数:在原点左右两边依次标上对应的刻度数.
4. 任何一个有理数都可以用数轴上的 来表示.
5. 数轴上两个点表示的数,右边的总比左边的 .正 数 0,负数 0,正数 负数.
6. 在数轴上,表示互为相反数的两个点,位于原点两侧,且到 原点的距离 ;一个数的绝对值就是这个数所对应的点 到原点的 .
一个点
大
大于
小于
大于
相等
距离
【课堂小测(8分钟)】
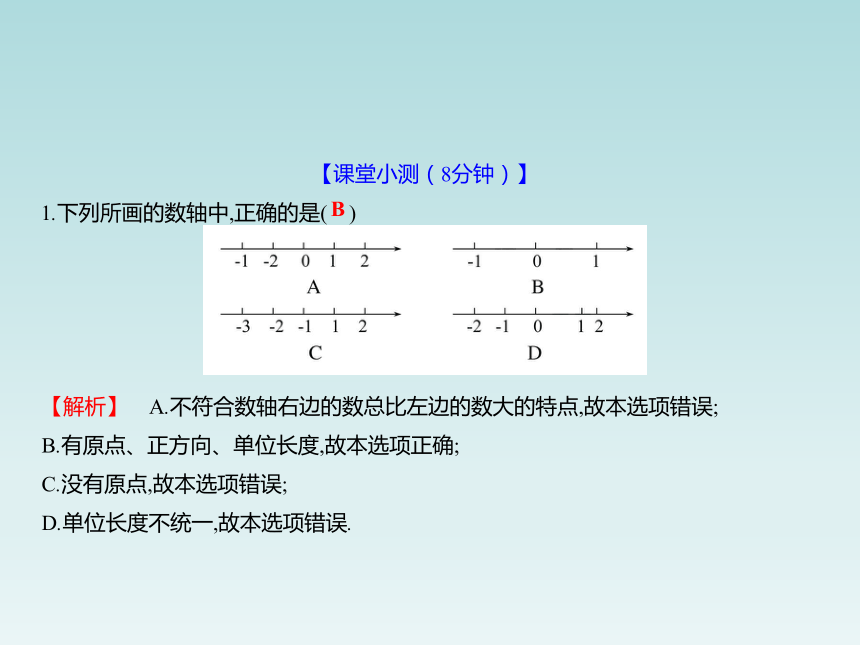
1.下列所画的数轴中,正确的是( )
【解析】 A.不符合数轴右边的数总比左边的数大的特点,故本选项错误;
B.有原点、正方向、单位长度,故本选项正确;
C.没有原点,故本选项错误;
D.单位长度不统一,故本选项错误.
B
D
3.(2024·揭阳普宁期末)如图所示,数轴的单位长度为1,如果点A表示的数是-2,那么点B表示的数是( )
A.0 B.1 C.2 D.3
【解析】 点B在点A右侧4个单位长度,即点B所表示的数为-2+4=2.
C
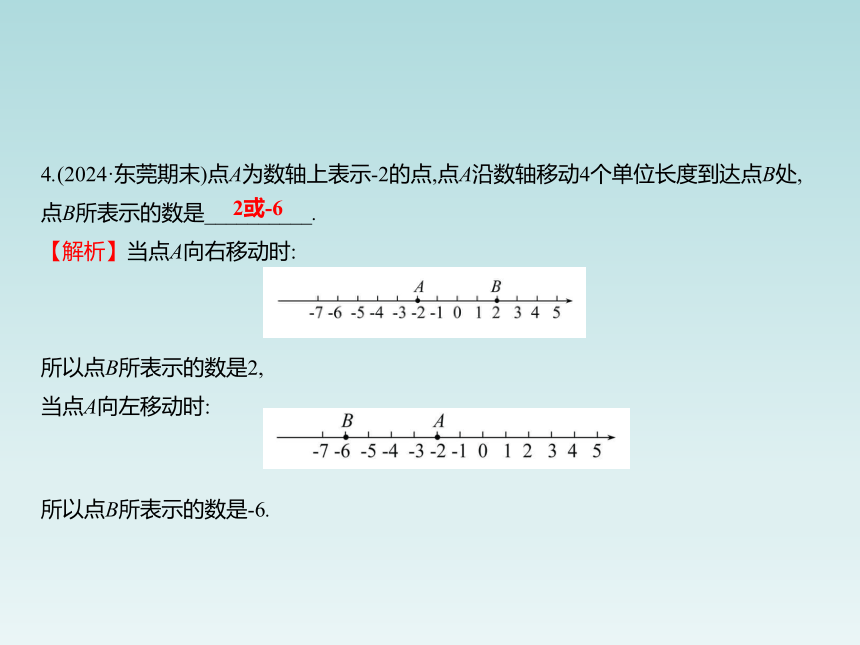
4.(2024·东莞期末)点A为数轴上表示-2的点,点A沿数轴移动4个单位长度到达点B处,
点B所表示的数是__________.
【解析】当点A向右移动时:
所以点B所表示的数是2,
当点A向左移动时:
所以点B所表示的数是-6.
2或-6
A. 3
C. -3
C
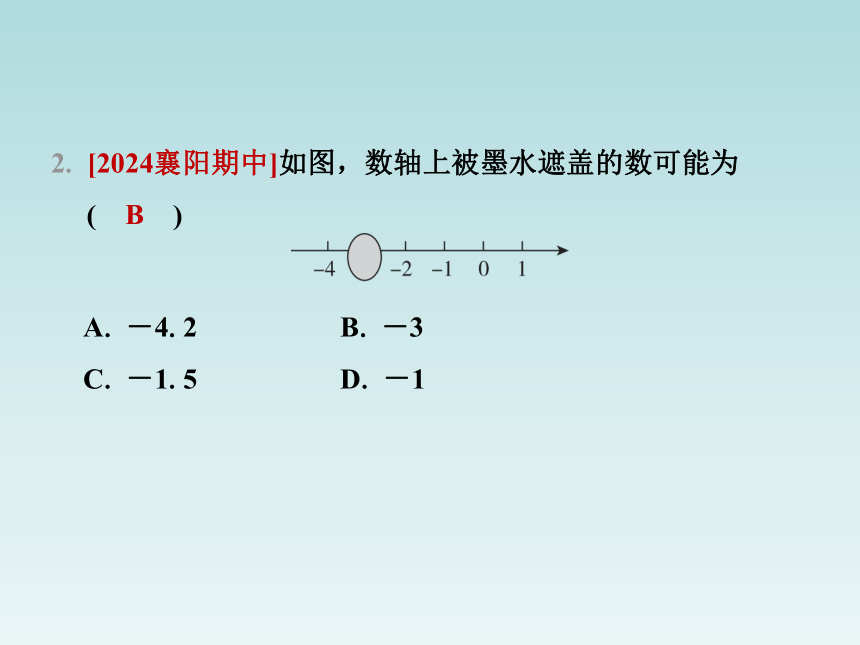
A. -4.2 B. -3
C. -1.5 D. -1
B
A. a < b < c < d B. b < a < d < c
C. a < b < d < c D. d < c < b < a
B
A. -1 B. 0 C. 1 D. 2
C
A. 向东行驶5个单位长度
B. 向西行驶3个单位长度
C. 向东行驶2个单位长度
D. 向西行驶1个单位长度
C
6. 已知有理数 a , b 在数轴上的表示如图,则 a 与- b 的大 小为 a - b .
<
(1)已知数轴上点 A 表示的数是-2,将点 A 在数轴上移动3个 单位长度得到点 B ,则点 B 表示的数是 ;
1或-5
【思路导航】(1)点 A 移动方向不确定可向左也可向右,因此 需要根据点 A 的移动方向及距离分类讨论;
(1)【解析】因为数轴上的点 A 表示的数是-2,
所以当向右移动3个单位长度时,点 B 表示的数为1;
当向左移动3个单位长度时,点 B 表示的数为-5.
所以点 B 表示的数是1或-5.
故答案为1或-5.
(2)在纸上画一条数轴,将这张纸对折后,若该数轴上表示4 的点与表示-1的点恰好重合,则此时与表示-3的点重合的点 所表示的数是多少?
【思路导航】(2)根据题目中的信息可知,将数轴对折,折痕与数轴的交点就是对应点的中点,从而可以求解.
(2)解:因为4与-1相距5个单位长度,
所以表示4与-1的数的点的线段的中点表示的数为4-5÷2= 1.5.
所以表示-3的点与所求点的线段的中点表示的数为1.5.
因为-3与1.5相距4.5个单位长度,
所以所求点表示的数是1.5+4.5=6.
故此时与表示-3的点重合的点所表示的数是6.
1.如图,在单位长度为1的数轴上,点A、B表示的两个数互为相反数,那么点A表示的数是( )
A.2 B.-2 C.3 D.-3
D
2.一个数在数轴上所对应的点向右移动8个单位后,得到它的相反数,则这个数是( )
A.4 B.-4 C.8 D.-8
B
巩固练习
3.有理数a,b在数轴上的对应点的位置如图所示,把
a,-a,b 按照从小到大的顺序排列,正确的是( )
A.a<-a<b B.-a<b<a
C.-a<a<b D.b<-a<a
A
巩固练习
1.已知a,b均为有理数,且它们在数轴上的位置如图所示,
比较大小:
(1)-a -1;
(2)|a| |b|;
(3)-b a;
(4)-a b.
一个数的绝对值就是这个数所对应的点到原点的距离.
>
<
>
>
知识点4 绝对值的几何意义
探究新知
4.在数轴上点A表示7,点B,C表示的数互为相反数,且点C与点A之间的距离为2,求点B与点C表示的数.
解:∵数轴上点A表示7,且点C到点A的距离为2,
∴点C表示的数可能是5或9.
又∵B,C两点所表示的数互为相反数,
∴点B表示的数可能是-5或-9.
故B表示-5,C表示5,或B表示-9,C表示9.
数轴
数轴三要素
表示有理数
相反数与绝对值的几何意义
原点
正方向
单位长度
一个数的绝对值就是这个数所对应的点到原点的距离.
在数轴上,表示互为相反数的两个点,位于原点的两侧,且到原点的距离相等.
数轴上原点右边的数表示正数,原点左边的数表示负数
课堂小结
课后作业
教材第31页习题2.1第8、16题.
第二章 有理数及其运算
2 认识有理数(第三课时)
数学 七年级上册 BS版
课前预习
典例讲练
目录
CONTENTS
数学 七年级上册 BS版
课前预习
0 1
1. 规定了 、 和 的直线称为数 轴.通常将数轴画成水平直线,并选择向右的方向为正方向.
2. 数轴的三要素: 、 和 .
3. 数轴的画法.
原点
单位长度
正方向
原点
正方向
单位长度
一画:画一条直线(一般是水平直线);
二取:选取原点,并用这个点表示数字0;
三定:确定正方向,用箭头表示(一般规定向右为正方向);
四统一:单位长度应统一;
五标数:在原点左右两边依次标上对应的刻度数.
4. 任何一个有理数都可以用数轴上的 来表示.
5. 数轴上两个点表示的数,右边的总比左边的 .正 数 0,负数 0,正数 负数.
6. 在数轴上,表示互为相反数的两个点,位于原点两侧,且到 原点的距离 ;一个数的绝对值就是这个数所对应的点 到原点的 .
一个点
大
大于
小于
大于
相等
距离
【课堂小测(8分钟)】
1.下列所画的数轴中,正确的是( )
【解析】 A.不符合数轴右边的数总比左边的数大的特点,故本选项错误;
B.有原点、正方向、单位长度,故本选项正确;
C.没有原点,故本选项错误;
D.单位长度不统一,故本选项错误.
B
D
3.(2024·揭阳普宁期末)如图所示,数轴的单位长度为1,如果点A表示的数是-2,那么点B表示的数是( )
A.0 B.1 C.2 D.3
【解析】 点B在点A右侧4个单位长度,即点B所表示的数为-2+4=2.
C
4.(2024·东莞期末)点A为数轴上表示-2的点,点A沿数轴移动4个单位长度到达点B处,
点B所表示的数是__________.
【解析】当点A向右移动时:
所以点B所表示的数是2,
当点A向左移动时:
所以点B所表示的数是-6.
2或-6
A. 3
C. -3
C
A. -4.2 B. -3
C. -1.5 D. -1
B
A. a < b < c < d B. b < a < d < c
C. a < b < d < c D. d < c < b < a
B
A. -1 B. 0 C. 1 D. 2
C
A. 向东行驶5个单位长度
B. 向西行驶3个单位长度
C. 向东行驶2个单位长度
D. 向西行驶1个单位长度
C
6. 已知有理数 a , b 在数轴上的表示如图,则 a 与- b 的大 小为 a - b .
<
(1)已知数轴上点 A 表示的数是-2,将点 A 在数轴上移动3个 单位长度得到点 B ,则点 B 表示的数是 ;
1或-5
【思路导航】(1)点 A 移动方向不确定可向左也可向右,因此 需要根据点 A 的移动方向及距离分类讨论;
(1)【解析】因为数轴上的点 A 表示的数是-2,
所以当向右移动3个单位长度时,点 B 表示的数为1;
当向左移动3个单位长度时,点 B 表示的数为-5.
所以点 B 表示的数是1或-5.
故答案为1或-5.
(2)在纸上画一条数轴,将这张纸对折后,若该数轴上表示4 的点与表示-1的点恰好重合,则此时与表示-3的点重合的点 所表示的数是多少?
【思路导航】(2)根据题目中的信息可知,将数轴对折,折痕与数轴的交点就是对应点的中点,从而可以求解.
(2)解:因为4与-1相距5个单位长度,
所以表示4与-1的数的点的线段的中点表示的数为4-5÷2= 1.5.
所以表示-3的点与所求点的线段的中点表示的数为1.5.
因为-3与1.5相距4.5个单位长度,
所以所求点表示的数是1.5+4.5=6.
故此时与表示-3的点重合的点所表示的数是6.
1.如图,在单位长度为1的数轴上,点A、B表示的两个数互为相反数,那么点A表示的数是( )
A.2 B.-2 C.3 D.-3
D
2.一个数在数轴上所对应的点向右移动8个单位后,得到它的相反数,则这个数是( )
A.4 B.-4 C.8 D.-8
B
巩固练习
3.有理数a,b在数轴上的对应点的位置如图所示,把
a,-a,b 按照从小到大的顺序排列,正确的是( )
A.a<-a<b B.-a<b<a
C.-a<a<b D.b<-a<a
A
巩固练习
1.已知a,b均为有理数,且它们在数轴上的位置如图所示,
比较大小:
(1)-a -1;
(2)|a| |b|;
(3)-b a;
(4)-a b.
一个数的绝对值就是这个数所对应的点到原点的距离.
>
<
>
>
知识点4 绝对值的几何意义
探究新知
4.在数轴上点A表示7,点B,C表示的数互为相反数,且点C与点A之间的距离为2,求点B与点C表示的数.
解:∵数轴上点A表示7,且点C到点A的距离为2,
∴点C表示的数可能是5或9.
又∵B,C两点所表示的数互为相反数,
∴点B表示的数可能是-5或-9.
故B表示-5,C表示5,或B表示-9,C表示9.
数轴
数轴三要素
表示有理数
相反数与绝对值的几何意义
原点
正方向
单位长度
一个数的绝对值就是这个数所对应的点到原点的距离.
在数轴上,表示互为相反数的两个点,位于原点的两侧,且到原点的距离相等.
数轴上原点右边的数表示正数,原点左边的数表示负数
课堂小结
课后作业
教材第31页习题2.1第8、16题.
同课章节目录
