小升初复习精讲精练《平面图形的周长与面积》--苏教版(复习课件)
文档属性
| 名称 | 小升初复习精讲精练《平面图形的周长与面积》--苏教版(复习课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 15:29:28 | ||
图片预览






文档简介
(共55张PPT)
图形与几何
平面图形的周长与面积
(苏教版)六年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1.加深对长方形、正方形、平行四边形、梯形、三角形和圆等平面图形基本特征和相关知识的认知。
2.进一步理解各类平面图形之间的关系,能应用知识进行计算或判断。
3.进一步体会平面图形知识的联系,积累学习平面图形知识的经验和方法;能解释自己的判断和应用的方法,发展简单的推理、判断能力;进一步培养空间观念。
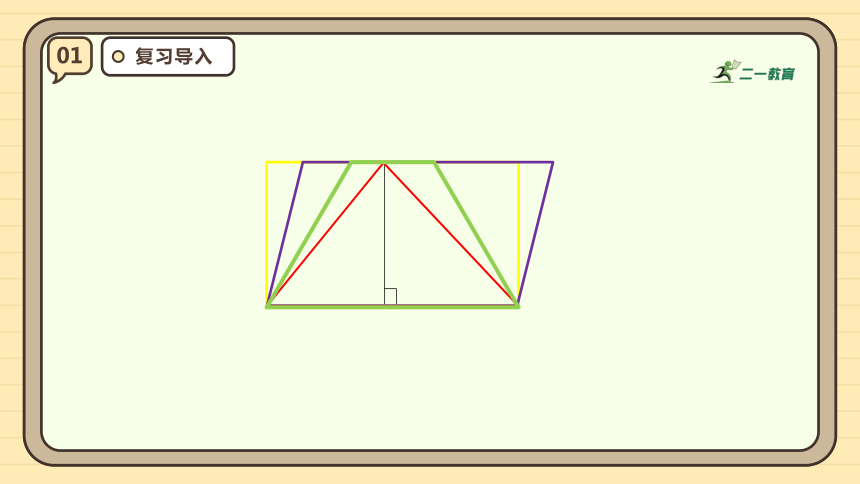
看到这组互相垂直的线段,
你想到了哪些平面图形?
01
复习导入
01
复习导入
01
复习导入
01
复习导入
02
任务一
学习任务一
知识梳理
a
a
a
h
a
h
a
b
h
o
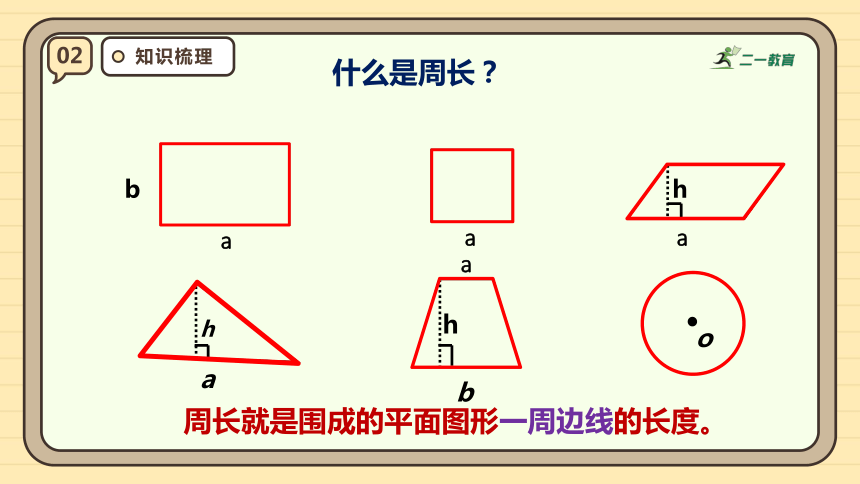
什么是周长?
b
周长就是围成的平面图形一周边线的长度。
02
知识梳理
r
02
知识梳理
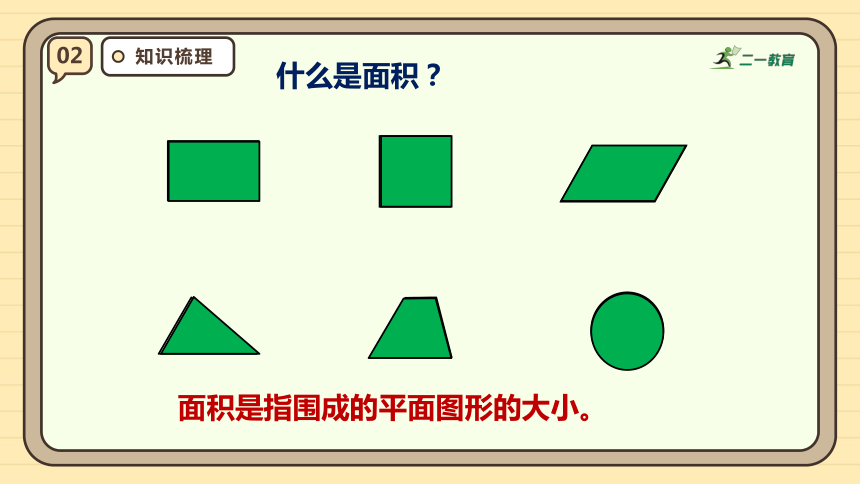
什么是面积?
面积是指围成的平面图形的大小。
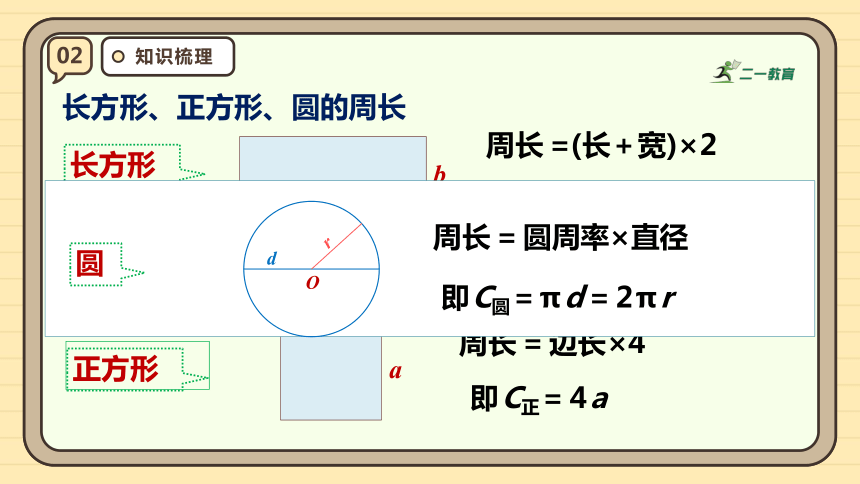
长方形、正方形、圆的周长
长方形
周长=(长+宽)×2
即C长=(a+b)×2
a
b
正方形
a
周长=边长×4
即C正=4a
d
r
O
圆
周长=圆周率×直径
即C圆=πd=2πr
02
知识梳理
平面图形的面积
a
b
a
长方形
用10个1厘米小正方形正好填满,这个长方形的面积是10平方厘米 。
正方形
用4个1厘米小正方形正好填满,这个正方形的面积是4平方厘米 。
由“每行个数×行数=小正方形个数=长方形面积的数值”可得出:长方形的面积=长×宽。
正方形是特殊的长方形,所以正方形的面积计算公式为:正方形的面积=边长×边长。
即S长=ab
即S正=a
02
知识梳理
平行四边形
通过分割移补法
将平行四边形转化成长方形。
a
h
平行四边形的底边=长方形的长
平行四边形的高=长方形的宽
长方形的面积=长×宽
则平行四边形的面积=底×高
即S=ah
02
知识梳理
三角形
两个完全一样的三角形可以拼成一个平行四边形。
拼成的平行四边的底=三角形的底;
拼成的平行四边形的高=三角形的高;
每个三角形的面积=拼成的平行四边形的面积的一半。
则三角形的面积=底×高÷2
a
h
02
知识梳理
即s=ah÷2
梯形
两个完全一样的梯形可以拼成一个平行四边形。
拼成的平行四边形与梯形等高。
拼成的平行四边的底=梯形的上底+下底;
每个梯形的面积=拼成的平行四边形的面积的一半。
b
h
a
则梯形的面积=(上底+下底)×高÷2
02
知识梳理
即s=(a+b)h÷2
d
r
O
圆
O
拼成的图形接近长方形。
长方形的面积与圆的面积相等,长方形的宽是圆的半径,长方形的长是圆周长的一半。
则圆的面积=圆周率×半径×半径
02
知识梳理
平面图形面积
知识网络图
02
知识梳理
03
任务二
学习任务二
不规则图形的面积
不规则图形(选用合适的面积单位)
1格表示1平方厘米
45250+9960÷2=50230(cm2)
1格表示1平方米
1+5÷2
=3.5(m2)
1格表示1平方分米
436+55÷2
=463.5(dm2)
03
知识梳理
测量面积的单位叫做面积单位。
1cm2
1dm2
两张学生
课桌面的面积。
1m2
03
知识梳理
学过的面积单位之间的进率
(cm2) (dm2) (m2) (hm2) (km2)
(平方百米)
100
100
10000
100
平方厘米、 平方分米、 平方米、 公顷、 平方千米
03
知识梳理
04
任务三
学习任务三
典型例题
1、一个长方形农场,长4千米,宽0.06千米。这片农场占地多少平方千米?是多少公顷?
4×0.06=0.24(平方千米)
0.24平方千米=24公顷
答:这片农场占地0.24平方千米,是24公顷。
选择合适的公式
关注题目的细节
04
例题讲解
2.一个梯形茶园,上底是24米,下底是30米,高18米。如果平均每棵茶树占地0.5平方米,这个茶园一共有多少棵茶树?
(24+30)×18÷2
=54×18÷2
=982÷2
=486(平方米)
486 ÷ 0.5 = 972(棵)
答:这个茶园一共有972棵茶树。
总面积÷每棵占地面积=棵树
04
例题讲解
3、有一块0.045公顷的三角形棉田,量得它的底是36米。它的高是多少米?
450×2
36米
÷36=25(米)
0.045公顷=450平方米
答:它的高是25米。
答:它的高是25米。
0.045公顷=450平方米
解:设它的高是x米。
36x÷2=450
36x=900
x=25
?h
多角度思考问题
04
例题讲解
4、有一块正方形土地,它的边长是6米。
要在这块地上造圆形苗圃(如图),
进行花苗的培育和研究。
(1)两个正方形里圆的半径各是多少米?面积呢?
04
例题讲解
大圆的半径:6÷2=3(米)
小圆的半径:6÷4=1.5(米)
大圆的面积:π×3 =9π(平方米)
小圆的面积:π×1.5 ×4=9π(平方米)
3米
1.5米
4、有一块正方形土地,它的边长是6米。
要在这块地上造圆形苗圃(如图),
进行花苗的培育和研究。
(2)两个正方形的利用率是多少?
×=9(平方厘米)
×× 4=9(平方厘米)
04
例题讲解
9π÷(6×6)=0.25π=78.5%
9π÷(6×6)=0.25π=78.5%
3米
1.5米
(3)如果像这样在正方形土地上设计 9 个相同的尽量大的
圆形苗圃,这 9 个苗圃面积的和占正方形土地面积的
百分之几?
4.有一块正方形土地,它的边长是6米。
要在这块地上造圆形的苗圃(如图),
进行花苗的培育和研究。
×9=9(平方厘米)
04
例题讲解
圆的半径:6÷3÷2=1(米)
圆的总面积:π×1 ×9=9π(平方米)
9π÷(6×6)=0.25π=78.5%
4.有一块正方形土地,它的边长是6米。要在这块地上造尽可能大的相同的圆形苗圃(如图)进行花苗的培育和研究。
这块正方形地的利用率是多少?
你发现了什么?
04
例题讲解
3米
1.5米
π×3 =9π(平方米)
π×1.5 ×4=9π(平方米)
π×1 ×9=9π(平方米)
9π÷(6×6)=0.25π=78.5%
05
任务四
学习任务四
培优拓展
(1)如下图(单位:cm),一个长方形框架变形后成了一个平行四边形,原来这个长方形的周长是( )cm,变形后的平行四边形面积是( )cm2。
1.填一填。
26
长方形的周长:
8×4=32(cm2)
(8+5)×2=26(cm)
32
8
4
5
5
平行四边形的面积:
----变式训练
06
课堂练习
(2)如下图的平行四边形中,阴影部分的面积是6cm2,平行四边形的底是直角三角形的3倍,空白部分的面积是( )cm2。
6×2÷4=3(cm)
4 cm
3 cm
3×3=9(cm)
9 cm
9×4-6=30(cm2)
三角形的底:
平行四边形的底:
空白部分的面积:
30
----变式训练
06
课堂练习
(3)如下图,张大爷用24米长的栅栏靠墙围成一块梯形菜地,
这块菜地的面积是( )平方米。
54
6 m
(24-6)×6÷2=54(平方米)
----变式训练
06
课堂练习
2.选一选。
(1)一个平行四边形相邻的两条边分别是6 cm、4 cm,量得一条边上的高是5 cm,这个平行四边形的面积是( )cm2。
A.30 B.24 C.20 D.10
C
4 cm
6 cm
小于4 cm
4 cm
4 cm
6 cm
小于6 cm
6 cm
以4 cm为底的高是5 cm
4×5=20(cm2)
----变式训练
06
课堂练习
(2)一个三角形的底和高相等,如果将底减少2分米,高增加2分米,那么这个三角形的面积会( )。
A.增加 B.减少 C.不变
B
原面积:6×6÷2=18(dm2)
新面积:(6-2)×(6+2)÷2=16(dm2)
16<18,面积减少了。
假设原三角形的底和高都是6分米。
----变式训练
06
课堂练习
(3)如下图,用三张同样大小的正方形纸分别剪掉图中涂色部分的图形,材料的利用率( )。
A.甲最高 B.乙最高 C.丙最高 D.相同
D
甲乙丙
甲:3.14×102÷4÷102=78.5%
乙:3.14×(10÷2)2÷102=78.5%
丙:3.14×(10÷2÷2)2×4÷102=78.5%
假设正方形的边长是10厘米。
----变式训练
06
课堂练习
3.将一根长100米的绳子绕一棵大树20圈,还差48cm,这棵大树的横截面的面积是多少平方米?
再计算大树一圈的周长:
(100+0.48)÷20=5.024m
再计算大树横截面半径:
5.024÷3.14÷2=0.8m
最后计算大树横截面积:
3.14×0.8×0.8=2.0096m2
答:大树的横截面积是2.0096平方米。
先统一单位:48cm=0.48m
----变式训练
06
课堂练习
答:x的值是11.4。
1.已知下图中两块阴影部分的面积相等,求x的值。
扇形面积:3.14×102÷4=78.5(cm2)
10 cm
O
x cm
(10+x)×10÷2-78.5=78.5-50
三角形面积:10×10÷2=50(cm2)
(10+x)×10÷2=107
10+x=21.4
x=11.4
08
培优拓展
=3.14×27+3.14×2
=3.14×29
=91.06(平方米)
答:这只羊能吃到草的面积是91.06平方米。
2.草地上有一间房子,占地形状是边长4米的正方形。一只羊被拴在房子的外墙角处,已知栓羊的绳子长6米,这只羊能吃到草的面积是多少平方米?
2 m
6 m
如图,羊能吃到草的面积由三个扇形组成。
08
培优拓展
3.14×62×
3
4
+3.14×(6-4)2×
1
2
面积是指围成的平面图形的大小。
周长就是围成的平面图形一周边线的长度。
平面图形的周长和面积公式
这节课你们都学会了哪些知识?
07
课堂小结
08
作业布置
作业布置---知识技能类
1.一个长方形的长是12厘米,宽是8厘米。如果长增加3厘米,宽减少2厘米,那么新的长方形的周长是______厘米,面积是______平方厘米。
新的长方形的长:12+3=15(厘米)
新的长方形的宽:8-2=6(厘米)
新的长方形的面积:15×6=90(平方厘米)
新的长方形的周长:(15+6)×2=42(厘米)
42
90
一、填空题
08
作业布置
作业布置---知识技能类
2.一个正方形的边长是10厘米。如果边长扩大到原来的1.5倍,那么新的正方形的周长是______厘米,面积是原来的______倍。
新正方形的边长:10×1.5=15(厘米)
新正方形的周长:15×4=60(厘米)
60
原正方形的面积:10×10=100(平方厘米)
2.25
新正方形的面积:15×15=225(平方厘米)
225÷100=2.25
08
作业布置
作业布置---知识技能类
3.一个圆的半径是5厘米。如果半径增加2厘米,那么新的圆的周长增加了______厘米,面积增加了______平方厘米。(取π=3.14)
新的圆周长:2π×(5+2)=14π(厘米)
原来的圆周长:2π×5=10π(厘米)
14π-10π=4π(厘米)
12.56
4×3.14=12.56(厘米)
原来的圆面积:π×5 =25π(平方厘米)
新的圆面积:π×(5+2) =49π(平方厘米)
49π-25π=24π(平方厘米)
24×3.14=75.36(平方厘米)
75.36
08
作业布置
作业布置---知识技能类
4.一个梯形的上底是6厘米,下底是10厘米,高是4厘米。如果上底和下底都增加2厘米,高不变,那么新的梯形的面积是______平方厘米。
新的梯形上底:6+2=8(厘米)
36
新的梯形下底:10+2=12(厘米)
新的梯形面积:(8+10)×2=36(平方厘米)
5.在一张长24 cm、宽20 cm的长方形纸上画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2;如果改画最大的半圆,这个半圆的面积( )cm2。
62.8
314
圆的周长:3.14×20=62.8(cm)
圆的面积:3.14×(20÷2)2=314(cm2)
半圆的面积:3.14×(24÷2)2÷2=226.08(cm2)
226.08
圆的直径最大为20 cm。
半圆的直径最大为24 cm。
08
作业布置
作业布置---知识技能类
6.如图,在大、小两个正方形中涂色部分的面积比是3∶2,则大、小两个正方形的边长比是( ),面积比是( )。
3∶2
9∶4
08
作业布置
作业布置---知识技能类
08
作业布置
作业布置---知识技能类
1.一个长方形的长是15厘米,宽是10厘米。如果长和宽都增加20%,求新的长方形的周长和面积。
新的长方形的长:15×(1+20%)=18(厘米)
新的长方形的宽:10×(1+20%)=12(厘米)
新的长方形周长:(18+12)×2=60(厘米)
新的长方形面积:18×12=216(平方厘米)
二、计算题
08
作业布置
作业布置---知识技能类
2.如图,圆内三角形的面积是2平方厘米,圆的面积是多少平方厘米?
观察图形可知,这个三角形的底是圆的直径,即2r厘米,高是圆的半径r厘米。根据三角形面积公式S = 底×高÷2,已知三角形面积是2平方厘米,则可列出2r×r ÷2=2 。
r = 2
2r×r ÷2= 2
2r = 2×2
圆的面积公式:S=πr
=2π
=2×3.14=6.28(平方厘米)
答:圆的面积是6.28平方厘米。
(36+52)×42÷2÷1.5
=88×42÷2÷1.5
=1848÷1.5
=1232(棵)
答:这个果园最多可种1232棵果树。
3.一个梯形果园,上底是36米,下底是52米,高是42米。平均每棵果树占地1.5平方米,这个果园最多可种多少棵果树?
梯形的面积=(上底+下底)×高÷2
08
作业布置
作业布置---知识技能类
4.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
3.14×[(28÷2+2)2-(28÷2)2]
=3.14×[162-142]
=3.14×60
=188.4(平方米)
O
28 m
2 m
圆环的面积:S=π(R2-r2)
08
作业布置
作业布置---知识技能类
2×3.14×(28÷2+2)
=2×3.14×16
=100.48(米)
答:这条道路的面积是188.4平方米,外沿周长是100.48米。
O
外沿的周长:C=2πR
28 m
2 m
4.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
08
作业布置
作业布置---知识技能类
09
作业布置---综合实践类作业
5.有一块边长 10 米的正方形空地,要在这块空地上砌一个花坛,使花坛的面积是整块空地的一半,可以怎样设计?
S = πr2
r
a
b
S = ab
a
S = a2
h
S = ah÷2
a
h
S =(a+b)h÷2
a
r
S = ah
09
板书设计
https://www.21cnjy.com/recruitment/home/fine
图形与几何
平面图形的周长与面积
(苏教版)六年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1.加深对长方形、正方形、平行四边形、梯形、三角形和圆等平面图形基本特征和相关知识的认知。
2.进一步理解各类平面图形之间的关系,能应用知识进行计算或判断。
3.进一步体会平面图形知识的联系,积累学习平面图形知识的经验和方法;能解释自己的判断和应用的方法,发展简单的推理、判断能力;进一步培养空间观念。
看到这组互相垂直的线段,
你想到了哪些平面图形?
01
复习导入
01
复习导入
01
复习导入
01
复习导入
02
任务一
学习任务一
知识梳理
a
a
a
h
a
h
a
b
h
o
什么是周长?
b
周长就是围成的平面图形一周边线的长度。
02
知识梳理
r
02
知识梳理
什么是面积?
面积是指围成的平面图形的大小。
长方形、正方形、圆的周长
长方形
周长=(长+宽)×2
即C长=(a+b)×2
a
b
正方形
a
周长=边长×4
即C正=4a
d
r
O
圆
周长=圆周率×直径
即C圆=πd=2πr
02
知识梳理
平面图形的面积
a
b
a
长方形
用10个1厘米小正方形正好填满,这个长方形的面积是10平方厘米 。
正方形
用4个1厘米小正方形正好填满,这个正方形的面积是4平方厘米 。
由“每行个数×行数=小正方形个数=长方形面积的数值”可得出:长方形的面积=长×宽。
正方形是特殊的长方形,所以正方形的面积计算公式为:正方形的面积=边长×边长。
即S长=ab
即S正=a
02
知识梳理
平行四边形
通过分割移补法
将平行四边形转化成长方形。
a
h
平行四边形的底边=长方形的长
平行四边形的高=长方形的宽
长方形的面积=长×宽
则平行四边形的面积=底×高
即S=ah
02
知识梳理
三角形
两个完全一样的三角形可以拼成一个平行四边形。
拼成的平行四边的底=三角形的底;
拼成的平行四边形的高=三角形的高;
每个三角形的面积=拼成的平行四边形的面积的一半。
则三角形的面积=底×高÷2
a
h
02
知识梳理
即s=ah÷2
梯形
两个完全一样的梯形可以拼成一个平行四边形。
拼成的平行四边形与梯形等高。
拼成的平行四边的底=梯形的上底+下底;
每个梯形的面积=拼成的平行四边形的面积的一半。
b
h
a
则梯形的面积=(上底+下底)×高÷2
02
知识梳理
即s=(a+b)h÷2
d
r
O
圆
O
拼成的图形接近长方形。
长方形的面积与圆的面积相等,长方形的宽是圆的半径,长方形的长是圆周长的一半。
则圆的面积=圆周率×半径×半径
02
知识梳理
平面图形面积
知识网络图
02
知识梳理
03
任务二
学习任务二
不规则图形的面积
不规则图形(选用合适的面积单位)
1格表示1平方厘米
45250+9960÷2=50230(cm2)
1格表示1平方米
1+5÷2
=3.5(m2)
1格表示1平方分米
436+55÷2
=463.5(dm2)
03
知识梳理
测量面积的单位叫做面积单位。
1cm2
1dm2
两张学生
课桌面的面积。
1m2
03
知识梳理
学过的面积单位之间的进率
(cm2) (dm2) (m2) (hm2) (km2)
(平方百米)
100
100
10000
100
平方厘米、 平方分米、 平方米、 公顷、 平方千米
03
知识梳理
04
任务三
学习任务三
典型例题
1、一个长方形农场,长4千米,宽0.06千米。这片农场占地多少平方千米?是多少公顷?
4×0.06=0.24(平方千米)
0.24平方千米=24公顷
答:这片农场占地0.24平方千米,是24公顷。
选择合适的公式
关注题目的细节
04
例题讲解
2.一个梯形茶园,上底是24米,下底是30米,高18米。如果平均每棵茶树占地0.5平方米,这个茶园一共有多少棵茶树?
(24+30)×18÷2
=54×18÷2
=982÷2
=486(平方米)
486 ÷ 0.5 = 972(棵)
答:这个茶园一共有972棵茶树。
总面积÷每棵占地面积=棵树
04
例题讲解
3、有一块0.045公顷的三角形棉田,量得它的底是36米。它的高是多少米?
450×2
36米
÷36=25(米)
0.045公顷=450平方米
答:它的高是25米。
答:它的高是25米。
0.045公顷=450平方米
解:设它的高是x米。
36x÷2=450
36x=900
x=25
?h
多角度思考问题
04
例题讲解
4、有一块正方形土地,它的边长是6米。
要在这块地上造圆形苗圃(如图),
进行花苗的培育和研究。
(1)两个正方形里圆的半径各是多少米?面积呢?
04
例题讲解
大圆的半径:6÷2=3(米)
小圆的半径:6÷4=1.5(米)
大圆的面积:π×3 =9π(平方米)
小圆的面积:π×1.5 ×4=9π(平方米)
3米
1.5米
4、有一块正方形土地,它的边长是6米。
要在这块地上造圆形苗圃(如图),
进行花苗的培育和研究。
(2)两个正方形的利用率是多少?
×=9(平方厘米)
×× 4=9(平方厘米)
04
例题讲解
9π÷(6×6)=0.25π=78.5%
9π÷(6×6)=0.25π=78.5%
3米
1.5米
(3)如果像这样在正方形土地上设计 9 个相同的尽量大的
圆形苗圃,这 9 个苗圃面积的和占正方形土地面积的
百分之几?
4.有一块正方形土地,它的边长是6米。
要在这块地上造圆形的苗圃(如图),
进行花苗的培育和研究。
×9=9(平方厘米)
04
例题讲解
圆的半径:6÷3÷2=1(米)
圆的总面积:π×1 ×9=9π(平方米)
9π÷(6×6)=0.25π=78.5%
4.有一块正方形土地,它的边长是6米。要在这块地上造尽可能大的相同的圆形苗圃(如图)进行花苗的培育和研究。
这块正方形地的利用率是多少?
你发现了什么?
04
例题讲解
3米
1.5米
π×3 =9π(平方米)
π×1.5 ×4=9π(平方米)
π×1 ×9=9π(平方米)
9π÷(6×6)=0.25π=78.5%
05
任务四
学习任务四
培优拓展
(1)如下图(单位:cm),一个长方形框架变形后成了一个平行四边形,原来这个长方形的周长是( )cm,变形后的平行四边形面积是( )cm2。
1.填一填。
26
长方形的周长:
8×4=32(cm2)
(8+5)×2=26(cm)
32
8
4
5
5
平行四边形的面积:
----变式训练
06
课堂练习
(2)如下图的平行四边形中,阴影部分的面积是6cm2,平行四边形的底是直角三角形的3倍,空白部分的面积是( )cm2。
6×2÷4=3(cm)
4 cm
3 cm
3×3=9(cm)
9 cm
9×4-6=30(cm2)
三角形的底:
平行四边形的底:
空白部分的面积:
30
----变式训练
06
课堂练习
(3)如下图,张大爷用24米长的栅栏靠墙围成一块梯形菜地,
这块菜地的面积是( )平方米。
54
6 m
(24-6)×6÷2=54(平方米)
----变式训练
06
课堂练习
2.选一选。
(1)一个平行四边形相邻的两条边分别是6 cm、4 cm,量得一条边上的高是5 cm,这个平行四边形的面积是( )cm2。
A.30 B.24 C.20 D.10
C
4 cm
6 cm
小于4 cm
4 cm
4 cm
6 cm
小于6 cm
6 cm
以4 cm为底的高是5 cm
4×5=20(cm2)
----变式训练
06
课堂练习
(2)一个三角形的底和高相等,如果将底减少2分米,高增加2分米,那么这个三角形的面积会( )。
A.增加 B.减少 C.不变
B
原面积:6×6÷2=18(dm2)
新面积:(6-2)×(6+2)÷2=16(dm2)
16<18,面积减少了。
假设原三角形的底和高都是6分米。
----变式训练
06
课堂练习
(3)如下图,用三张同样大小的正方形纸分别剪掉图中涂色部分的图形,材料的利用率( )。
A.甲最高 B.乙最高 C.丙最高 D.相同
D
甲乙丙
甲:3.14×102÷4÷102=78.5%
乙:3.14×(10÷2)2÷102=78.5%
丙:3.14×(10÷2÷2)2×4÷102=78.5%
假设正方形的边长是10厘米。
----变式训练
06
课堂练习
3.将一根长100米的绳子绕一棵大树20圈,还差48cm,这棵大树的横截面的面积是多少平方米?
再计算大树一圈的周长:
(100+0.48)÷20=5.024m
再计算大树横截面半径:
5.024÷3.14÷2=0.8m
最后计算大树横截面积:
3.14×0.8×0.8=2.0096m2
答:大树的横截面积是2.0096平方米。
先统一单位:48cm=0.48m
----变式训练
06
课堂练习
答:x的值是11.4。
1.已知下图中两块阴影部分的面积相等,求x的值。
扇形面积:3.14×102÷4=78.5(cm2)
10 cm
O
x cm
(10+x)×10÷2-78.5=78.5-50
三角形面积:10×10÷2=50(cm2)
(10+x)×10÷2=107
10+x=21.4
x=11.4
08
培优拓展
=3.14×27+3.14×2
=3.14×29
=91.06(平方米)
答:这只羊能吃到草的面积是91.06平方米。
2.草地上有一间房子,占地形状是边长4米的正方形。一只羊被拴在房子的外墙角处,已知栓羊的绳子长6米,这只羊能吃到草的面积是多少平方米?
2 m
6 m
如图,羊能吃到草的面积由三个扇形组成。
08
培优拓展
3.14×62×
3
4
+3.14×(6-4)2×
1
2
面积是指围成的平面图形的大小。
周长就是围成的平面图形一周边线的长度。
平面图形的周长和面积公式
这节课你们都学会了哪些知识?
07
课堂小结
08
作业布置
作业布置---知识技能类
1.一个长方形的长是12厘米,宽是8厘米。如果长增加3厘米,宽减少2厘米,那么新的长方形的周长是______厘米,面积是______平方厘米。
新的长方形的长:12+3=15(厘米)
新的长方形的宽:8-2=6(厘米)
新的长方形的面积:15×6=90(平方厘米)
新的长方形的周长:(15+6)×2=42(厘米)
42
90
一、填空题
08
作业布置
作业布置---知识技能类
2.一个正方形的边长是10厘米。如果边长扩大到原来的1.5倍,那么新的正方形的周长是______厘米,面积是原来的______倍。
新正方形的边长:10×1.5=15(厘米)
新正方形的周长:15×4=60(厘米)
60
原正方形的面积:10×10=100(平方厘米)
2.25
新正方形的面积:15×15=225(平方厘米)
225÷100=2.25
08
作业布置
作业布置---知识技能类
3.一个圆的半径是5厘米。如果半径增加2厘米,那么新的圆的周长增加了______厘米,面积增加了______平方厘米。(取π=3.14)
新的圆周长:2π×(5+2)=14π(厘米)
原来的圆周长:2π×5=10π(厘米)
14π-10π=4π(厘米)
12.56
4×3.14=12.56(厘米)
原来的圆面积:π×5 =25π(平方厘米)
新的圆面积:π×(5+2) =49π(平方厘米)
49π-25π=24π(平方厘米)
24×3.14=75.36(平方厘米)
75.36
08
作业布置
作业布置---知识技能类
4.一个梯形的上底是6厘米,下底是10厘米,高是4厘米。如果上底和下底都增加2厘米,高不变,那么新的梯形的面积是______平方厘米。
新的梯形上底:6+2=8(厘米)
36
新的梯形下底:10+2=12(厘米)
新的梯形面积:(8+10)×2=36(平方厘米)
5.在一张长24 cm、宽20 cm的长方形纸上画一个最大的圆,这个圆的周长是( )cm,面积是( )cm2;如果改画最大的半圆,这个半圆的面积( )cm2。
62.8
314
圆的周长:3.14×20=62.8(cm)
圆的面积:3.14×(20÷2)2=314(cm2)
半圆的面积:3.14×(24÷2)2÷2=226.08(cm2)
226.08
圆的直径最大为20 cm。
半圆的直径最大为24 cm。
08
作业布置
作业布置---知识技能类
6.如图,在大、小两个正方形中涂色部分的面积比是3∶2,则大、小两个正方形的边长比是( ),面积比是( )。
3∶2
9∶4
08
作业布置
作业布置---知识技能类
08
作业布置
作业布置---知识技能类
1.一个长方形的长是15厘米,宽是10厘米。如果长和宽都增加20%,求新的长方形的周长和面积。
新的长方形的长:15×(1+20%)=18(厘米)
新的长方形的宽:10×(1+20%)=12(厘米)
新的长方形周长:(18+12)×2=60(厘米)
新的长方形面积:18×12=216(平方厘米)
二、计算题
08
作业布置
作业布置---知识技能类
2.如图,圆内三角形的面积是2平方厘米,圆的面积是多少平方厘米?
观察图形可知,这个三角形的底是圆的直径,即2r厘米,高是圆的半径r厘米。根据三角形面积公式S = 底×高÷2,已知三角形面积是2平方厘米,则可列出2r×r ÷2=2 。
r = 2
2r×r ÷2= 2
2r = 2×2
圆的面积公式:S=πr
=2π
=2×3.14=6.28(平方厘米)
答:圆的面积是6.28平方厘米。
(36+52)×42÷2÷1.5
=88×42÷2÷1.5
=1848÷1.5
=1232(棵)
答:这个果园最多可种1232棵果树。
3.一个梯形果园,上底是36米,下底是52米,高是42米。平均每棵果树占地1.5平方米,这个果园最多可种多少棵果树?
梯形的面积=(上底+下底)×高÷2
08
作业布置
作业布置---知识技能类
4.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
3.14×[(28÷2+2)2-(28÷2)2]
=3.14×[162-142]
=3.14×60
=188.4(平方米)
O
28 m
2 m
圆环的面积:S=π(R2-r2)
08
作业布置
作业布置---知识技能类
2×3.14×(28÷2+2)
=2×3.14×16
=100.48(米)
答:这条道路的面积是188.4平方米,外沿周长是100.48米。
O
外沿的周长:C=2πR
28 m
2 m
4.一个圆形池塘,直径为28 m,环绕池塘修建一条宽为2 m的道路,这条道路的面积是多少平方米?外沿周长是多少米?
08
作业布置
作业布置---知识技能类
09
作业布置---综合实践类作业
5.有一块边长 10 米的正方形空地,要在这块空地上砌一个花坛,使花坛的面积是整块空地的一半,可以怎样设计?
S = πr2
r
a
b
S = ab
a
S = a2
h
S = ah÷2
a
h
S =(a+b)h÷2
a
r
S = ah
09
板书设计
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
