【小升初真题重组练习】热点命题:平面图形计算题(含答案)-2025年小学数学六年级下册苏教版
文档属性
| 名称 | 【小升初真题重组练习】热点命题:平面图形计算题(含答案)-2025年小学数学六年级下册苏教版 | 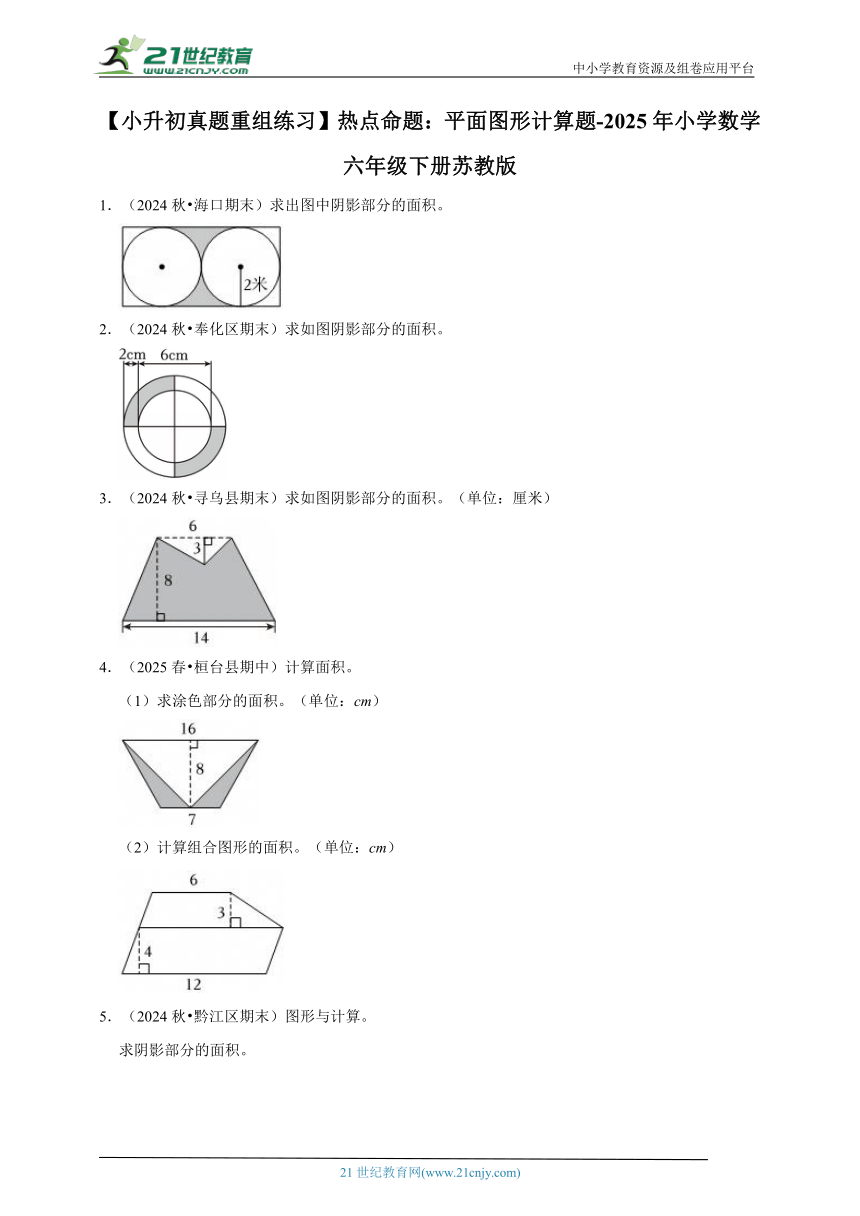 | |
| 格式 | docx | ||
| 文件大小 | 900.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-30 18:31:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【小升初真题重组练习】热点命题:平面图形计算题-2025年小学数学六年级下册苏教版
1.(2024秋 海口期末)求出图中阴影部分的面积。
2.(2024秋 奉化区期末)求如图阴影部分的面积。
3.(2024秋 寻乌县期末)求如图阴影部分的面积。(单位:厘米)
4.(2025春 桓台县期中)计算面积。
(1)求涂色部分的面积。(单位:cm)
(2)计算组合图形的面积。(单位:cm)
5.(2024秋 黔江区期末)图形与计算。
求阴影部分的面积。
6.(2024秋 南岗区期末)如图,求阴影面积(结果保留π)。
7.(2024秋 兰州期末)计算下面涂色部分的周长。
8.(2024秋 南岗区期末)如图,求阴影周长(结果保留π)。
9.(2024秋 鄠邑区期末)计算如图的周长与面积。
10.(2024秋 惠济区期末)求阴影部分的周长。
11.(2024秋 济南期末)计算下面各图中阴影部分的面积。(π取3.14,单位:cm)
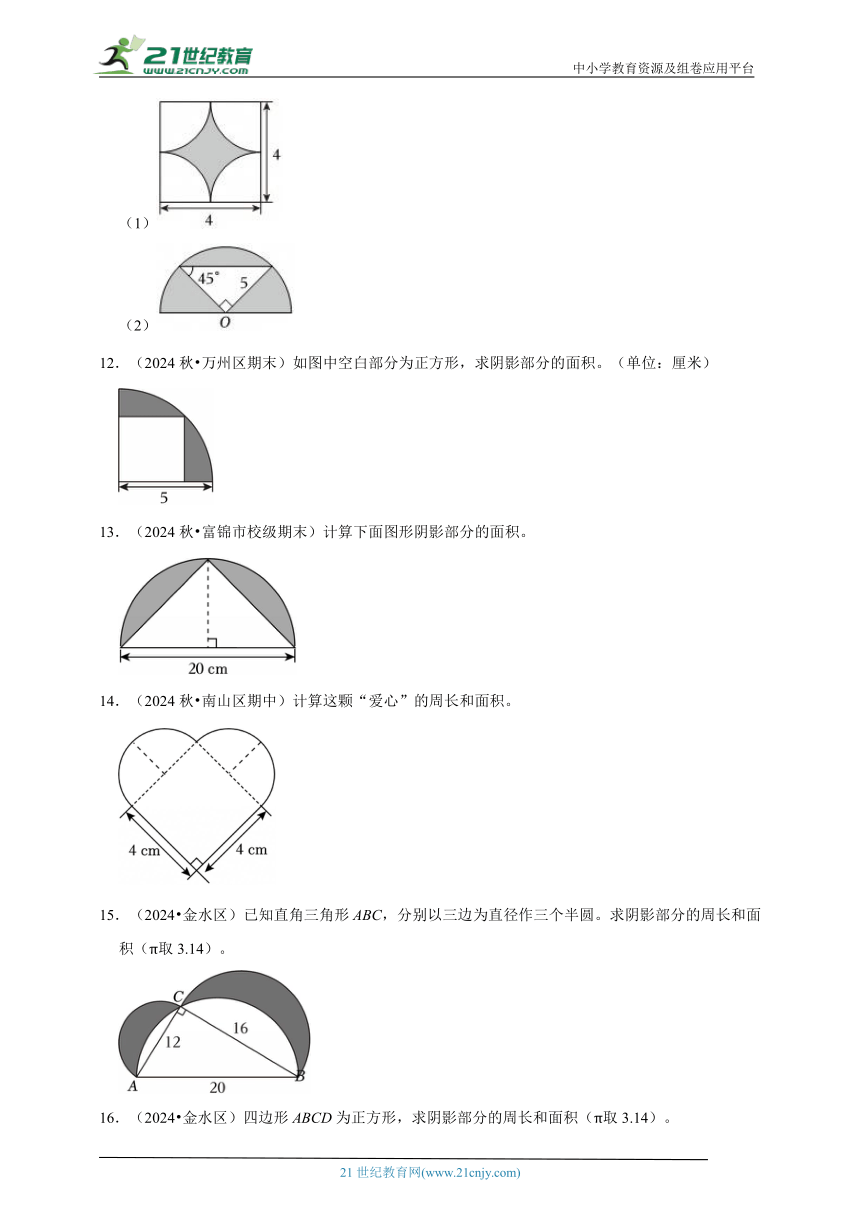
(1)
(2)
12.(2024秋 万州区期末)如图中空白部分为正方形,求阴影部分的面积。(单位:厘米)
13.(2024秋 富锦市校级期末)计算下面图形阴影部分的面积。
14.(2024秋 南山区期中)计算这颗“爱心”的周长和面积。
15.(2024 金水区)已知直角三角形ABC,分别以三边为直径作三个半圆。求阴影部分的周长和面积(π取3.14)。
16.(2024 金水区)四边形ABCD为正方形,求阴影部分的周长和面积(π取3.14)。
17.(2024秋 思明区期末)求图形中阴影部分的周长和面积。
18.(2023秋 石狮市期末)如图中等腰直角三角形的直角边长是6厘米,请计算出阴影部分的面积。
【小升初真题重组练习】热点命题:平面图形计算题-2025年小学数学六年级下册苏教版
参考答案与试题解析
一.计算题(共18小题)
1.(2024秋 海口期末)求出图中阴影部分的面积。
【解答】解:2×2×2=8(米)
2×2=4(米)
8×4=32(平方米)
32÷2=16(平方米)
3.14×22
=3.14×4
=12.56(平方米)
16﹣12.56=3.44(平方米)
答:阴影部分的面积为3.44平方米。
2.(2024秋 奉化区期末)求如图阴影部分的面积。
【解答】解:6÷2=3(cm)
3.14×[(3+2)2﹣32]÷2
=3.14×[52﹣32]÷2
=3.14×16÷2
=50.24÷2
=25.12(cm2)
答:阴影部分的面积是25.12cm2。
3.(2024秋 寻乌县期末)求如图阴影部分的面积。(单位:厘米)
【解答】解:(6+14)×8÷2﹣6×3÷2
=80﹣9
=71(平方厘米)
答:阴影部分的面积是71平方厘米。
4.(2025春 桓台县期中)计算面积。
(1)求涂色部分的面积。(单位:cm)
(2)计算组合图形的面积。(单位:cm)
【解答】解:(1)(16+7)×8÷2﹣16×8÷2
=92﹣64
=28(平方厘米)
答:涂色部分的面积是28平方厘米。
(2)(6+12)×3÷2+12×4
=27+48
=75(平方厘米)
答:组合图形面积是75平方厘米。
5.(2024秋 黔江区期末)图形与计算。
求阴影部分的面积。
【解答】解:3.14×(6÷2)2﹣6×(6÷2)÷2×2
=3.14×9﹣18
=28.26﹣18
=10.26(平方厘米)
答:阴影部分的面积是10.26平方厘米。
6.(2024秋 南岗区期末)如图,求阴影面积(结果保留π)。
【解答】解:2÷2=1
(π×12÷4﹣1×1÷2)×8
=2π﹣4
答:阴影面积是2π﹣4。
7.(2024秋 兰州期末)计算下面涂色部分的周长。
【解答】解:3.14×10×2+10×4
=62.8+40
=102.8(厘米)
答:涂色部分的周长是102.8厘米。
8.(2024秋 南岗区期末)如图,求阴影周长(结果保留π)。
【解答】解:2÷2=1
2+(1+2)×2+2π×1.5
=2+3×2+3π
=2+6+3π
=8+3π
答:阴影部分的周长是(8+3π)。
9.(2024秋 鄠邑区期末)计算如图的周长与面积。
【解答】解:周长:8+10+3.14×6÷2
=18+9.42
=27.42(分米)
面积:8×6÷2+3.14×(6÷2)2÷2
=24+14.13
=38.13(平方分米)
答:图形的周长为27.42分米,面积为38.13平方分米。
10.(2024秋 惠济区期末)求阴影部分的周长。
【解答】解:20﹣14=6(dm)
3.14×6÷2+3.14×14÷2+3.14×20÷2
=9.42+21.98+31.4
=62.8(dm)
答:阴影部分的周长是62.8dm。
11.(2024秋 济南期末)计算下面各图中阴影部分的面积。(π取3.14,单位:cm)
(1)
(2)
【解答】解:(1)4×4﹣3.14×(4÷2)2
=16﹣3.14×22
=16﹣12.56
=3.44(cm2)
答:阴影部分的面积是3.44平方厘米。
(2)3.14×52÷2﹣5×5÷2
=78.5÷2﹣12.5
=39.25﹣12.5
=26.75(cm2)
答:阴影部分的面积是26.75平方厘米。
12.(2024秋 万州区期末)如图中空白部分为正方形,求阴影部分的面积。(单位:厘米)
【解答】解:如图:
5×2=10(厘米)
(3.14×52﹣10×5÷2×2)÷4
=(78.5﹣50)÷4
=28.5÷4
=7.125(平方厘米)
答:阴影部分的面积是7.125平方厘米。
13.(2024秋 富锦市校级期末)计算下面图形阴影部分的面积。
【解答】解:3.14×(20÷2)2÷2﹣20×20÷2÷2
=157﹣100
=57(平方厘米)
答:阴影部分的面积是57平方厘米。
14.(2024秋 南山区期中)计算这颗“爱心”的周长和面积。
【解答】解:周长:4×2+3.14×4
=8+12.56
= 20.56(cm)
面积:4×4+3.14×(4÷2)2
=16+3.14×22
=16+3.14×4
=16+12.56
=28.56(cm2)
答:这个图形的周长是20.56厘米,面积是28.56平方厘米。
15.(2024 金水区)已知直角三角形ABC,分别以三边为直径作三个半圆。求阴影部分的周长和面积(π取3.14)。
【解答】解:(1)3.14×16÷2+3.14×12÷2+3.14×20÷2
=50.24÷2+37.68÷2+62.8÷2
=25.12+18.84+31.4
=75.36
(2)16÷2=8
12÷2=6
20÷2=10
3.14×82÷2+3.14×62÷2+16×12÷2﹣3.14×102÷2
=3.14×64÷2+3.14×36÷2+16×12÷2﹣3.14×100÷2
=100.48+56.52+96﹣157
=96
16.(2024 金水区)四边形ABCD为正方形,求阴影部分的周长和面积(π取3.14)。
【解答】解:(1)3.14×10+2×3.14×10
=31.4+6.28×10
=31.4+62.8
=31.4+15.7
=47.1
(2)3.14×102
=3.14×100
=314
=78.5
17.(2024秋 思明区期末)求图形中阴影部分的周长和面积。
【解答】解:7×2+2×3.14×3
=14+18.84
=14+4.71
=18.71(厘米)
7×3﹣3.14×32
=21﹣3.14×9
=21﹣7.065
=13.935(平方厘米)
答:阴影部分的周长是18.71厘米,面积是13.935平方厘米。
18.(2023秋 石狮市期末)如图中等腰直角三角形的直角边长是6厘米,请计算出阴影部分的面积。
【解答】解:6÷2=3(厘米)
3.14×3×3÷4﹣3×3÷2
=7.065﹣4.5
=2.565(平方厘米)
答:阴影部分的面积是2.565平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【小升初真题重组练习】热点命题:平面图形计算题-2025年小学数学六年级下册苏教版
1.(2024秋 海口期末)求出图中阴影部分的面积。
2.(2024秋 奉化区期末)求如图阴影部分的面积。
3.(2024秋 寻乌县期末)求如图阴影部分的面积。(单位:厘米)
4.(2025春 桓台县期中)计算面积。
(1)求涂色部分的面积。(单位:cm)
(2)计算组合图形的面积。(单位:cm)
5.(2024秋 黔江区期末)图形与计算。
求阴影部分的面积。
6.(2024秋 南岗区期末)如图,求阴影面积(结果保留π)。
7.(2024秋 兰州期末)计算下面涂色部分的周长。
8.(2024秋 南岗区期末)如图,求阴影周长(结果保留π)。
9.(2024秋 鄠邑区期末)计算如图的周长与面积。
10.(2024秋 惠济区期末)求阴影部分的周长。
11.(2024秋 济南期末)计算下面各图中阴影部分的面积。(π取3.14,单位:cm)
(1)
(2)
12.(2024秋 万州区期末)如图中空白部分为正方形,求阴影部分的面积。(单位:厘米)
13.(2024秋 富锦市校级期末)计算下面图形阴影部分的面积。
14.(2024秋 南山区期中)计算这颗“爱心”的周长和面积。
15.(2024 金水区)已知直角三角形ABC,分别以三边为直径作三个半圆。求阴影部分的周长和面积(π取3.14)。
16.(2024 金水区)四边形ABCD为正方形,求阴影部分的周长和面积(π取3.14)。
17.(2024秋 思明区期末)求图形中阴影部分的周长和面积。
18.(2023秋 石狮市期末)如图中等腰直角三角形的直角边长是6厘米,请计算出阴影部分的面积。
【小升初真题重组练习】热点命题:平面图形计算题-2025年小学数学六年级下册苏教版
参考答案与试题解析
一.计算题(共18小题)
1.(2024秋 海口期末)求出图中阴影部分的面积。
【解答】解:2×2×2=8(米)
2×2=4(米)
8×4=32(平方米)
32÷2=16(平方米)
3.14×22
=3.14×4
=12.56(平方米)
16﹣12.56=3.44(平方米)
答:阴影部分的面积为3.44平方米。
2.(2024秋 奉化区期末)求如图阴影部分的面积。
【解答】解:6÷2=3(cm)
3.14×[(3+2)2﹣32]÷2
=3.14×[52﹣32]÷2
=3.14×16÷2
=50.24÷2
=25.12(cm2)
答:阴影部分的面积是25.12cm2。
3.(2024秋 寻乌县期末)求如图阴影部分的面积。(单位:厘米)
【解答】解:(6+14)×8÷2﹣6×3÷2
=80﹣9
=71(平方厘米)
答:阴影部分的面积是71平方厘米。
4.(2025春 桓台县期中)计算面积。
(1)求涂色部分的面积。(单位:cm)
(2)计算组合图形的面积。(单位:cm)
【解答】解:(1)(16+7)×8÷2﹣16×8÷2
=92﹣64
=28(平方厘米)
答:涂色部分的面积是28平方厘米。
(2)(6+12)×3÷2+12×4
=27+48
=75(平方厘米)
答:组合图形面积是75平方厘米。
5.(2024秋 黔江区期末)图形与计算。
求阴影部分的面积。
【解答】解:3.14×(6÷2)2﹣6×(6÷2)÷2×2
=3.14×9﹣18
=28.26﹣18
=10.26(平方厘米)
答:阴影部分的面积是10.26平方厘米。
6.(2024秋 南岗区期末)如图,求阴影面积(结果保留π)。
【解答】解:2÷2=1
(π×12÷4﹣1×1÷2)×8
=2π﹣4
答:阴影面积是2π﹣4。
7.(2024秋 兰州期末)计算下面涂色部分的周长。
【解答】解:3.14×10×2+10×4
=62.8+40
=102.8(厘米)
答:涂色部分的周长是102.8厘米。
8.(2024秋 南岗区期末)如图,求阴影周长(结果保留π)。
【解答】解:2÷2=1
2+(1+2)×2+2π×1.5
=2+3×2+3π
=2+6+3π
=8+3π
答:阴影部分的周长是(8+3π)。
9.(2024秋 鄠邑区期末)计算如图的周长与面积。
【解答】解:周长:8+10+3.14×6÷2
=18+9.42
=27.42(分米)
面积:8×6÷2+3.14×(6÷2)2÷2
=24+14.13
=38.13(平方分米)
答:图形的周长为27.42分米,面积为38.13平方分米。
10.(2024秋 惠济区期末)求阴影部分的周长。
【解答】解:20﹣14=6(dm)
3.14×6÷2+3.14×14÷2+3.14×20÷2
=9.42+21.98+31.4
=62.8(dm)
答:阴影部分的周长是62.8dm。
11.(2024秋 济南期末)计算下面各图中阴影部分的面积。(π取3.14,单位:cm)
(1)
(2)
【解答】解:(1)4×4﹣3.14×(4÷2)2
=16﹣3.14×22
=16﹣12.56
=3.44(cm2)
答:阴影部分的面积是3.44平方厘米。
(2)3.14×52÷2﹣5×5÷2
=78.5÷2﹣12.5
=39.25﹣12.5
=26.75(cm2)
答:阴影部分的面积是26.75平方厘米。
12.(2024秋 万州区期末)如图中空白部分为正方形,求阴影部分的面积。(单位:厘米)
【解答】解:如图:
5×2=10(厘米)
(3.14×52﹣10×5÷2×2)÷4
=(78.5﹣50)÷4
=28.5÷4
=7.125(平方厘米)
答:阴影部分的面积是7.125平方厘米。
13.(2024秋 富锦市校级期末)计算下面图形阴影部分的面积。
【解答】解:3.14×(20÷2)2÷2﹣20×20÷2÷2
=157﹣100
=57(平方厘米)
答:阴影部分的面积是57平方厘米。
14.(2024秋 南山区期中)计算这颗“爱心”的周长和面积。
【解答】解:周长:4×2+3.14×4
=8+12.56
= 20.56(cm)
面积:4×4+3.14×(4÷2)2
=16+3.14×22
=16+3.14×4
=16+12.56
=28.56(cm2)
答:这个图形的周长是20.56厘米,面积是28.56平方厘米。
15.(2024 金水区)已知直角三角形ABC,分别以三边为直径作三个半圆。求阴影部分的周长和面积(π取3.14)。
【解答】解:(1)3.14×16÷2+3.14×12÷2+3.14×20÷2
=50.24÷2+37.68÷2+62.8÷2
=25.12+18.84+31.4
=75.36
(2)16÷2=8
12÷2=6
20÷2=10
3.14×82÷2+3.14×62÷2+16×12÷2﹣3.14×102÷2
=3.14×64÷2+3.14×36÷2+16×12÷2﹣3.14×100÷2
=100.48+56.52+96﹣157
=96
16.(2024 金水区)四边形ABCD为正方形,求阴影部分的周长和面积(π取3.14)。
【解答】解:(1)3.14×10+2×3.14×10
=31.4+6.28×10
=31.4+62.8
=31.4+15.7
=47.1
(2)3.14×102
=3.14×100
=314
=78.5
17.(2024秋 思明区期末)求图形中阴影部分的周长和面积。
【解答】解:7×2+2×3.14×3
=14+18.84
=14+4.71
=18.71(厘米)
7×3﹣3.14×32
=21﹣3.14×9
=21﹣7.065
=13.935(平方厘米)
答:阴影部分的周长是18.71厘米,面积是13.935平方厘米。
18.(2023秋 石狮市期末)如图中等腰直角三角形的直角边长是6厘米,请计算出阴影部分的面积。
【解答】解:6÷2=3(厘米)
3.14×3×3÷4﹣3×3÷2
=7.065﹣4.5
=2.565(平方厘米)
答:阴影部分的面积是2.565平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
