初中数学北师大版八年级下册 第18章《平行四边形》期末知识点复习题(含解析)
文档属性
| 名称 | 初中数学北师大版八年级下册 第18章《平行四边形》期末知识点复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 00:00:00 | ||
图片预览



文档简介
第18章《平行四边形》期末知识点复习题
【题型1 四边形中的多解问题】
1.在正方形中,对角线、交于点,的平分线交于点,交于点.过点作于点,交于点.下列结论:①;②四边形是菱形;③;④若,则.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在菱形中,,,点E为对角线上一动点(不与点B重合),且,连接交延长线于点F.
①;
②当为直角三角形时,;
③当为等腰三角形时,或者;
④连接,当时,平分.
以上结论正确的是 (填正确的序号).
3.如图,在矩形ABCD中,O是对角线的交点,,,过C作于点E,的延长线与的平分线相交于点H,与交于点F,与交于点M.给出下列四个结论:①;②;③;④;⑤.其中正确的结论有 (填写正确的序号).
4.勾股定理是平面几何中一个极为重要的定理,世界上各个文明古国都对勾股定理的发现和研究做出过贡献,特别是定理的证明,据说有400余种.如图是希腊著名数学家欧几里得证明这个定理使用的图形.以的三边为边分别向外作三个正方形:正方形、正方形、正方形,再作垂足为G,交于P,连接,.则结论:①,②,③ ,④ .正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【题型2 四边形中的动点问题】
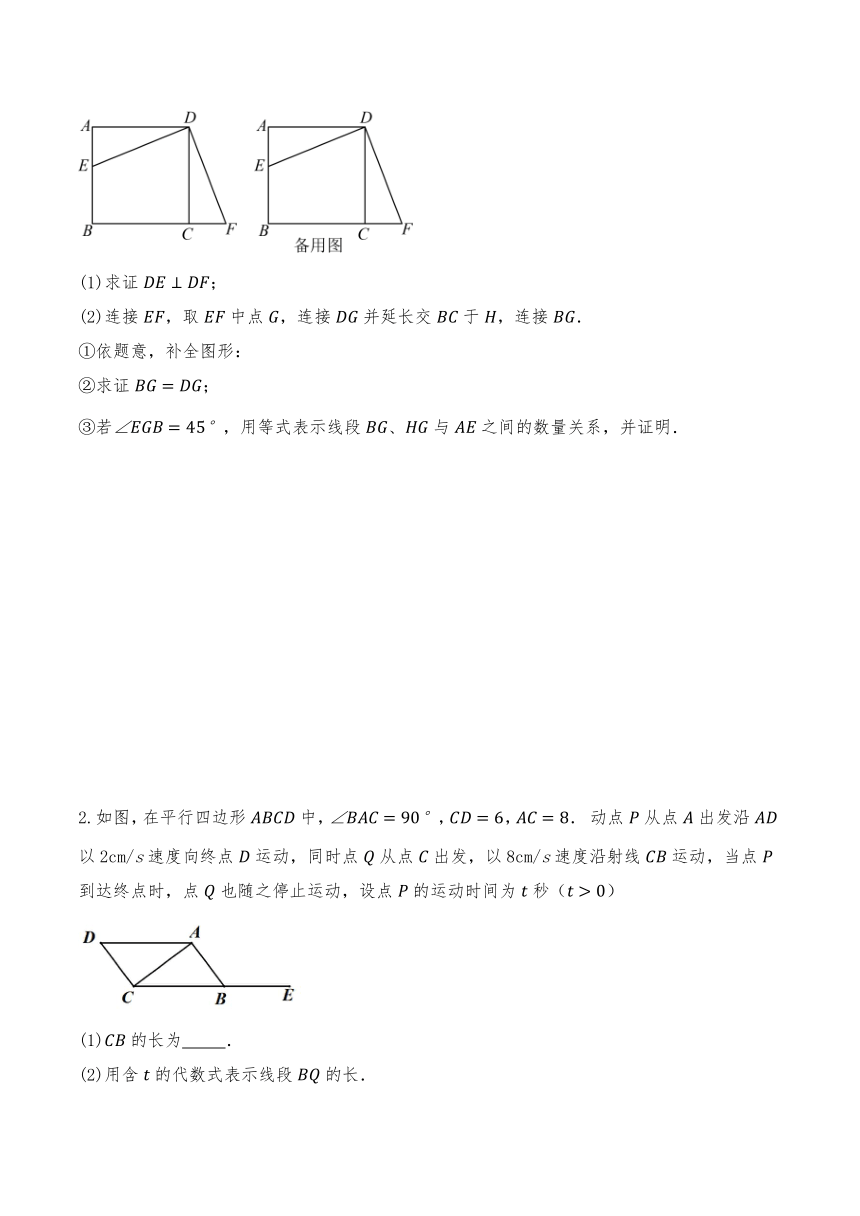
1.如图,在正方形中,E是边上的一动点,点F在边的延长线上,且,连接、.
(1)求证;
(2)连接,取中点,连接并延长交于,连接.
①依题意,补全图形:
②求证;
③若,用等式表示线段、与之间的数量关系,并证明.
2.如图,在平行四边形中,,,. 动点从点出发沿以2cm/s速度向终点运动,同时点从点出发,以8cm/s速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒()
(1)的长为 .
(2)用含的代数式表示线段的长.
(3)连结.是否存在的值,使得与互相平分?若存在,求出的值;若不存在,请说明理由;
(4)若点关于直线对称的点恰好落在直线上,请直接写出的值.
3.如图,已知菱形的边长为,,点、分别是边、上的两个动点,,连接.
(1)是等边三角形吗?如是,请证明;如不是,请说明理由.
(2)在、运动的过程中,的面积存在最大值吗?如存在,请求出该最大值;如不存在,请说明理由.
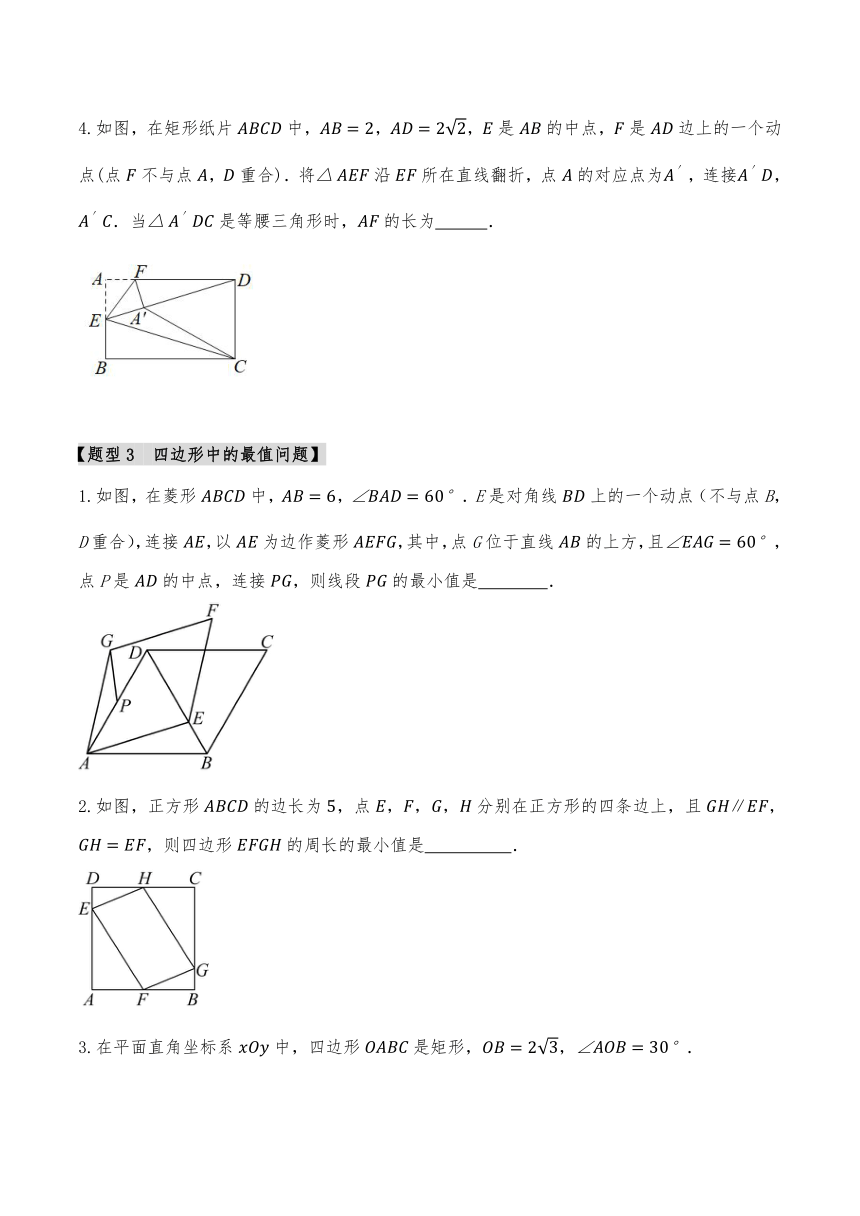
4.如图,在矩形纸片中,,,是的中点,是边上的一个动点(点不与点,重合).将沿所在直线翻折,点的对应点为,连接,.当是等腰三角形时,的长为 .
【题型3 四边形中的最值问题】
1.如图,在菱形中,,.E是对角线上的一个动点(不与点B,D重合),连接,以为边作菱形,其中,点G位于直线的上方,且,点P是的中点,连接,则线段的最小值是 .
2.如图,正方形的边长为,点分别在正方形的四条边上,且,,则四边形的周长的最小值是 .
3.在平面直角坐标系中,四边形是矩形,,.
(1)如图1,点P为射线上的动点,连接,若是等腰三角形,求的长度;
(2)如图2,是否在x轴上存在点E,在直线上存在点F,以O,B,E,F为顶点的四边形是菱形?若存在,求出点E,F的坐标;若不存在,请说明理由;
(3)如图3,点M是边上的动点,过点M作的垂线交直线于点N,求的最小值.
4.如图,矩形中,,E、F分别在边上,并且为等边三角形,则m的取值范围为 ,若点G是边上的一点,且,则随着m的变化,的最小值为 .
【题型4 四边形中的折叠问题】
1.通过对下面几何图形的?作探究,解决下列问题.
【操作发现】
如图1,探究小组将矩形纸片沿对角线所在的直线折叠,点落在点处,与边交于点,再将纸片沿直线折叠,使边落在直线上,点A与点重合.
(1)_______度.
(2)若,,求线段的长.
【迁移应用】
(3)如图2,在正方形纸片中,点为边上一点,探究小组将沿直线折叠得到,再将纸片沿过A的直线折叠,使与重合,折痕为,探究小组继续将正方形纸片沿直线折叠,点的对应点恰好落在折痕上的点处,与相交于点,若,求的面积.
2.如图1,一张矩形纸片,其中,,先沿对角线折叠,点落在点的位置,交于点.
(1)求证:;
(2)求的长;
(3)如图2,再折叠一次,使点与重合,折痕交于,求的长.
3.问题原型
(1)如图1,在菱形中,,于E,F为中点,连结,.试猜想的形状,并说明理由.
(2)如图2,在中,于E,F为中点,连结,.试猜想的形状,并说明理由.
(3)如图3,在中,F为上一点,连结,将沿折叠,点C的对应点为.连结并延长交于G,若,求证:F为中点.
(4)如图4,直角坐标系中有,点A与原点重合,点B在x轴正半轴上,与y轴交于点E.将其沿过A的直线折叠,点B对应点恰好落在y轴上,且折痕交于M,交于点N.若的面积为48,,,求点M的坐标和阴影部分面积(直接写出结果).
4.课本再现:
(1)如图1,是一个正方形花园,E,F是它的两个门,且.要修建两条路和,这两条路等长吗?它们有什么位置关系?和的数量关系是:___________;和的位置关系是___________;(无需证明)
知识应用:
(2)如图2,是一个正方形草地,现要在内部修建两条路,且,
①请问这两条路还相等吗?为什么?
②如图3,将边长为12的正方形纸片沿折叠,点D落在边上的点N处,若折痕的长为13,求此时的长;
拓展延伸:
(3)如图4,将边长为12的正方形纸片沿折叠,点D落在边上的点N处,与交于点P,取的中点M,连接,则的最小值为___________,此时的长度是___________.
【题型5 矩形与等腰三角形】
1.【问题背景】
某“数学学习兴趣小组”在学习了“等腰三角形的性质”和“平行四边形的性质和判定”后,在习题中发现了这样一个问题:如图1,在等腰中,,点D、E分别是边上的点,点P是底边上的点,且,过点B作于点F,请写出线段、、之间满足的数量关系式.
同学们经过交流讨论,得到了如下两种解决思路:
解决思路1:如图2,过点P作于点G;
解决思路2:如图3,过点B作,交的延长线于点H;
(1)上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为______________.
【类比探究】
(2)如图4,在等腰中,,点D、E分别是边上的点,点P是底边上的点,且,过点B作交于点F,请写出线段之间满足的数量关系式,并说明理由.
【拓展应用】
(3)如图5,在与中,,,点A、B、P在同一条直线上,若,,则______________.
2.已知在矩形中,,,为矩形的中心,在等腰中,,.则边上的高为 ;将绕点A按顺时针方向旋转一周,连接,取中点,连接,则的最大值为 .
3.画一个四边形,使得该四边形的面积等于已知图形面积的一半.
(1)如图1,已知等腰,D,E分别是的中点,画四边形;
(2)如图2,已知四边形,.四边的中点分别为E,F,G,H,画四边形;
(3)如图3,已知平行四边形,点E,G分别在上,且.点F,H分别在上,画四边形.
以上三种画法中,所有正确画法的序号是( )
A.(1)(3) B.(2) C.(2)(3) D.(1)(2)(3)
4.如图①,在平面直角坐标系中,一次函数分别与x轴和y轴交于点A、点B,四边形OACB为矩形.
(1)如图②,点F在BC上,连接AF,把沿着AF折叠,点C刚好与线段AB上一点重合.
①求点F的坐标;
②请直接写出直线的解析式:______;
(2)如图③,动点在一次函数的图象上运动,点D在线段AC上,是否存在直角顶点为P的等腰直角,若存在,请求出点P的坐标;若不存在,请说明理由.
【题型6 菱形中的全等三角形的构造】
1.如图,已知菱形的边长为,,点、分别是边、上的两个动点,,连接.
(1)是等边三角形吗?如是,请证明;如不是,请说明理由.
(2)在、运动的过程中,的面积存在最大值吗?如存在,请求出该最大值;如不存在,请说明理由.
2.如图,菱形的一边在x轴的正半轴上,O是坐标原点,B点坐标为,点D是对角线上一点,连结,垂足为E.
(1)求证:;
(2)求菱形的面积;
(3)连接,当时,求点D的坐标.
3.已知在菱形中,,连接对角线.
(1)如图1,为边上一点,为边延长线上一点,且,连接,交于点.
①求证:;
②过点作,垂足为,求证:;
(2)如图2,已知,将沿射线平移,得到,连接,,请直接写出的最小值.
4.如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
【题型7 正方形中线段的和差倍分关系】
1.如图,在正方形中,动点在上,过点作,过点作,点是的中点,连接交于点.
(1)求证:;
(2)请探究线段长度之间的等量关系,并证明你的结论;
(3)设,若点沿着线段从点运动到点,则在该运动过程中,线段所扫过的图形面积为________(直接写出答案).
2.过正方形(四边都相等,四个角都是直角)的顶点A作一条直线.
(1)当不与正方形任何一边相交时,过点B作于点E,过点作于点F,如图(1),请写出,,之间的数量关系,并证明你的结论.
(2)若改变直线的位置,使与边相交如图(2),其它条件不变,,,的关系会发生变化,请直接写出,,的数量关系,不必证明;
(3)若继续改变直线的位置,使与边相交如图(3),其它条件不变,,,的关系又会发生变化,请直接写出,,的数量关系,不必证明.
3.感知:如图(1)所示,四边形是正方形,点是线段上的任意一点,于点,,且交于点,求证:.
探究一:如图(2)所示,若点在的延长线上,上述其余条件不变,则,,存在怎样的等量关系?猜想并证明这一结论.
探究二:若点在的延长线上,上述其余条件不变,则,,又存在怎样的等量关系?直接写出结论.
4.已知:在中,为中线,以、为边向的形外作正方形、正方形.
(1)如图①,当时,求证:.
(2)如图②③,当时,与有怎样的关系?在图②和图③中可任选一个图,证明你的结论.
【题型8 坐标系中的四边形】
1.如图1,在中,,,点是的平分线上一点,于,交的延长线于,交的延长线于,连接.
(1)直接写出的大小;
(2)求证:四边形是平行四边形;
(3)建立如图2所示的坐标系,若,,直线绕点顺时针旋转45°得到直线,求直线的表达式.
2.如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2019次,点B的落点依次为B1,B2,B3,…,则B2019的坐标为 .
3.如图,在坐标系中,正方形的边长为2,点是轴上一动点.若与的两边所组成的角的度数之比为,则点的坐标为 .
4.如图,在△ABC中,AC=BC=1,∠C=90°,E、F是AB上的动点,且∠ECF=45°,分别过E、F作BC、AC的垂线,垂足分别为H、G,两垂线交于点M.
(1)当点E与点B重合时,请直接写出MH与AC的数量关系 ;
(2)探索AF、EF、BE之间的数量关系,并证明你的结论;
(3)以C为坐标原点,以BC所在的直线为x轴,建立直角坐标系,请画出坐标系并利用(2)中的结论证明.
【题型9 四边形中存在性问题】
1.如图,四边形是矩形,点、在坐标轴上,点坐标,是绕点顺时针旋转得到的,点在轴上,直线交轴于点,交于点.
(1)求直线的解析式;
(2)求的面积;
(3)点在轴上,平面内是否存在点,使以点D、F、M、N为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
2.如图,在平面直角坐标系中,矩形的顶点C,A分别在x轴,y轴上,O为坐标原点,B点的坐标为,过A点的直线l与x轴交于点,P是线段上一动点,设.
(1)是第一象限直线l上一点,作轴于E,轴于F,若,.
①求证:;
②求直线l的表达式及D点的坐标;
(2)将直线l向下平移12个单位得到直线,在直线上方的直线上,是否存在这样的点D,使得,且,若存在,请求出点D的坐标,若不存在,请说明理由.
3.如图1所示,在平面直角坐标系中,为坐标原点,四边形是菱形,点的坐标为,点在轴正半轴上,直线交轴于点M,连接,边交轴于点.
(1)求的长;
(2)如图2所示,动点从点出发,沿折线方向以每秒1个单位的速度向终点匀速运动,设的面积为,点的运动时间为秒,求与之间的函数关系式;
(3)在(2)的情况下,当点在线段上运动时,是否存在以为腰的等腰三角形?如存在,直接写出的值;如不存在,说明理由.
4.定义“点对图形的可视度”:在平面直角坐标系中,对于点P和图形,若图形上所有的点都在的内部或的边上,则的最小值称为点对图形的可视度.如图1,点对线段的可视度为的度数.
(1)如图2,已知点,,,.连接,,则的度数为点对的可视度.求证:;
(2)如图3,已知四边形为正方形,其中点,.直线与轴交于点,与轴交于点,其中点对正方形的可视度为.求点的坐标;
(3)在(2)的条件下,在平面直角坐标系内是否存在点,使以点,,,为顶点的四边形为平行四边形 若存在,请直接写出点坐标;若不存在,请说明理由.
参考答案
【题型1 四边形中的多解问题】
1.D
【分析】设,则,可算出,故①正确;先证明,再由得,即,四边形是菱形,故②正确;由,得,可求出,故③正确;由四边形是菱形证明,即可得,故④正确.
【详解】解:平分,,,
,
四边形是正方形,
,
,
设,则,
,故①正确;
在和中,
,
,
,,
四边形是正方形,
,
又
,
,
,
,
,
四边形是菱形,故②正确;
由①②知,,,
,
,故③正确;
,,
,
四边形是菱形,
,
,
,
,
,
,故④正确.
故选:D.
2.①②③④
【分析】连接,交于点O,由题意易得,是等边三角形,,,,则有,则,然后根据等边三角形的性质与判定、全等三角形的性质、勾股定理及等腰三角形的性质可进行求解.
【详解】解:连接,交于点O,如图所示,
∵四边形是菱形,,,
∴,是等边三角形,,,,
∴,则,
∴,则,
∴,
∵,
∴,
∴,
∵,
∴,
∴,故①正确;
当为直角三角形时,即,
∵,,
∴,
∴,
∴,则,
∴;故②正确;
当为等腰三角形时,则可分当时,即,
在菱形中,,
∴,
∵,
∴在中,,
∴
∴;
当时,即,
∵,
∴在中,,
∴
∴;
当时,则,此时点E与点B重合,不符合题意;
故③正确;
连接,当时,则,
∴,
由②可知,
∴,
∴,
∵,
∴是等边三角形,
∴,
∴,
∴平分,故④正确;
故答案为①②③④.
3.①②③⑤
【分析】先证明是等边三角形,得,再证是等腰三角形,得 ,即可得出,可判定①正确;求得,得出,可判定②正确;利用含的直角三角形的性质得出,,再由,,即可求得 ,可判定③正确;过程点M作于N,分别求出,,即可得出,可判定④错误;过点H作交延长线于Q,延长交于P,先求出,从而求得,即可求得,可判定⑤正确.
【详解】解:∵矩形ABCD,
∴,,
∵,
∴是等边三角形,
∴,
∵平分,
∴,
∴,
∴,
∴,
故①正确;
∴,
∴,
∵,
∴,
∴,
∴,
∴,
故②正确;
∵矩形ABCD,
∴,,
∴,
∴,
∴,,
∴,
∵,
∴,
故③正确;
在中,,,
∴,,
∵,
∴,
∴,
过程点M作于N,如图,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故④错误;
过点H作交延长线于Q,延长交于P,
∵,
∴,
∴,
∴,,
∴,
∵
∴四边形是矩形,
∴,,
∴,
∴,
∴,
∴,
故⑤正确,
∴正确的结论有①②③⑤
故答案为:①②③⑤.
4.D
【分析】根据题意,,得到,得到,延长至点,过点做垂线,由题意可知四边形为矩形,求出面积即可,延长至点,过点做垂线,由题意可知四边形为矩形,求出面积即可.
【详解】解:由题意可得,,,
,,
,
∵,
,
故①、②符合题意,正确;
延长至点,过点做垂线,
由题意可知四边形为矩形,
,
故,
,
故 ,③符合题意,正确;
;
延长至点,过点做垂线,
由题意可知四边形为矩形,
故,
,
,
故 ,④符合题意,正确.
.
故选:D.
【题型2 四边形中的动点问题】
1.(1)证明:四边形是正方形,
,,
,
又,
,
,
,
,
即,
;
(2)①解:依题意,补全图形如图所示:
②证明:由(1)可知,和都是直角三角形,
是的中点,
,,
;
③解:,证明如下:
由(1)可知,,,
,
是等腰直角三角形,
,
为的中点,
,,,
,,,,
,
,
,
,
,
又,,
,
,
在中,由勾股定理得:,
,,
,
.
2.(1)∵四边形是平行四边形,
∴,
∵,
∴,
(2)在中,,,
由题意得,,
当点Q与点B重合时,,
∴,
当点Q在线段上时,,
当点Q在线段的延长线上时,,
综上所述,或;
(3)存在,理由如下:
如图,连接,
若与互相平分,则四边形是平行四边形,
∴,
∴,
∴,
∴当时,与
(4)当点P关于直线对称的点落在点A下方时,如图,
由对称得,,
∵,
∴,
∴,即,
∴,
∴,
∴,
解得;
当点P关于直线对称的点落在点A上方时,如图,
由对称得,,
∵,
∴,
∵
∴,
∴,
∴,
∴,
解得,
综上所述,t的值为或2.
3.(1)是,理由如下:
如图,连接,
∵四边形是菱形,
∴,,
∴,都是等边三角形,
∴,,
∴,
在和中,
,
∴,
∴,
∵,
∴是等边三角形;
(2)的面积存在最大值,理由如下:
由(1)得:,
∴,
∴,
∴ ,
∴不发生变化,
则的面积最小时,的面积最大,
∵是等边三角形,根据垂线段最短可知,时,的值最小,的面积最小,
∴,
由(1)得:是等边三角形,则有:,
在中,由勾股定理得:,
∴,
同理:,
在中,由勾股定理得:
∴,即:的面积最小值为,
∴的面积的最大值,
4.或或
【分析】存在三种情况:当 ,连接,勾股定理求得的长,可判断,,三点共线,根据勾股定理即可得到结论;当 ,证明是正方形,于是得到结论;当 时,连接,,证明点,,三点共线,再用勾股定理可得答案.
【详解】解:①当时,连接,如图:
点是的中点,, ,四边形是矩形,
, ,,
,
将沿所在直线翻折,得到 ,
,
,
,
点,,三点共线,
,
,
设则 ,
在 中,
,
解得: ,
;
②当 时,如图:
,
点在线段的垂直平分线上,
点在线段的垂直平分线上,
点是的中点,
是的垂直平分线,
,
将沿所在直线翻折,得到 ,
, ,
四边形 是正方形,
;
③当 时,连接,,如图:
点是的中点,, ,四边形是矩形,
,,
,
将沿所在直线翻折,得到 ,
,
,
,
点,,三点共线,
,
,
设则
在 中,,
在中,,
,
即
解得: ,
;
综上所述,的长为或或,
故答案为:或或.
【题型3 四边形中的最值问题】
1.
【分析】连接,过点P作,则当G点位于点时,有最小值即的长,根据条件证明,可得,进而用勾股定理求解即可.
【详解】解:连接,过点P作,则当G点位于点时,有最小值即的长,如图,
∵四边形是菱形,,
∴,,
∴是等边三角形,,
∴,
∵四边形是菱形,,
∴,
∴,
∴,
∴ ,
∴,
∴C、D、G三点共线,
∵点P是的中点,,
∴,
∵ ,
∴,
∴,
即线段的最小值是,
故答案为:.
2.
【分析】根据垂线段最短及平行四边形的判定与性质可知当时,最短,最短,四边形是正方形即可解答.
【详解】解:∵,,
∴四边形是平行四边形,
∴ ,,即四边形的周长=
∵四边形为正方形,
∴,,
∵,
∴,
∴,即
∴,
过作G点的对应点N,连接,过N点作,交延长线于M,
则
最短为,
∴四边形的周长最短=,
故答案为.
【点睛】本题考查了正方形的判定与性质,全等三角形的性质和判定,轴对称的性质.掌握将军饮马问题是解题关键.
3.(1)解:如图1,
当点P在上时,
∵四边形是矩形,
∴,
∵,
∴,,;
∵是等腰三角形,
∴是等边三角形,
∴,
当点P(图中)在的延长线上时,
∵,
∴,
∵是等腰三角形,
∴,
∴,
∴,
∴,
综上所述:或3;
(2)如图2,
存在点E和F,使以O,B,E,F为顶点的四边形是菱形,理由如下:
是边时,
当点F在的延长线时,
∵,
∴,,
∴,
当点在的延长线上时,
∵,,
∴,
当是对角线时,(菱形)
设,则,
在中,由勾股定理得,,
∴,
∴,,
综上所述:,或,或,;
(3)如图3,
作点O关于的对称点,作B点关于的对称点,
连接,交于点,于点,
此时的最小值为的长,即的长,
作轴,作于T,
∵,,
∴,
∴的最小值为:6.
4.
【分析】当点F与点D重合时,此时有最小值,当点E与点B重合时,此时有最大值,由等边三角形的性质和直角三角形的性质可求的长,即可求m的范围;可证,即, 当点H,点N,点F共线时,有最小值,即可求解.
【详解】解:如图,当点F与点D重合时,此时有最小值,
∵为等边三角形,
∴,,,
∴,,
如图,当点E与点B重合时,此时有最大值,
∵为等边三角形,
∴,,,
∴,,
∴,
∴.
如图,当时,以为边作等边,作,连接,
∴,,
∴,
∴,
∴,
∴当点H,点N,点F共线时,有最小值,
此时,∵ ,
∴四边形是矩形,
∴,
∵是等边三角形,,
∴,
∴.
故答案为:;.
【题型4 四边形中的折叠问题】
1.解:(1)∵四边形是矩形,
∴,
由折叠可知,,
∴,
∴,
故答案为:
(2)∵四边形是矩形,,,
∴,,
由折叠可知, ,,
在和中,
,
∴,
∴,
设,
则
在中,,
即,
解得,
∴;
(3)∵四边形是正方形,
∴,,
由折叠可知,,
∴,
∴,
由折叠可知,,,,,
∴,
∴,
∴,
∴是等腰直角三角形,
∵,,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
由折叠可知,,,
∴,
∴,
∴,
∴,
∴,
∴,,
∴,
即的面积为.
2.(1)证明:∵矩形纸片沿对角线折叠,点落在点的位置,
∴,,
在和中,
,
∴,
∴;
(2)解:∵,,,
∴,
设,则,
∴,
∵在中,,
∴,
解得:,
∴,
∴的长为;
(3)再折叠一次,使点与重合,得折痕,且,,
∴,即点是的中点,
∴在中,,
∵,,
∴,
∴点是的中点,
∴是的中位线,
∴,,
由折叠的性质可知,
在矩形中,,
∴,
∴,
∴,
∴,
设,则,
在中,,
∴,
解得:,
∴,
∴的长为.
3.(1)如图1,
连接,
四边形是菱形,
,
,
是等边三角形,
,,
,
,
同理可得:是等边三角形,
,,
点是的中点,
,,
,
在和中,
,
,
,
是等边三角形;
(2)如图2,
是等腰三角形,理由如下:
取的中点,连接,直线交于,
四边形是平行四边形,
,,
点是的中点,是的中点,
,
,
四边形是平行四边形,
,
点是的中点,
,
,
,
即:是等腰三角形;
(3)证明:由(2)知:,,
,,
,
,
,
四边形是平行四边形,
,
,,
,
,
,
,
即:点是的中点
(4)由得,
,
,
四边形是平行四边形,
,,
,
,
,
,
,
直线的解析式为:,
,
直线的解析式为:,
由得,
,
,,
,
,
直线的解析式为:,
当时,,
,
,
,
,
.
4.解:猜想,,理由如下:
∵四边形是正方形,
∴,
∵,
∴,即,
在和中,,
∴,
∴,
∵,
∴,
∴,
∴,
∴;
故答案为:,;
(2)①,理由如下:
过F点作于点P,过点M作于点Q,与相交于点H,
∵四边形是正方形,
∴,,,,
∵于点P,于点Q,
∴,,
∴,,
∵,
∴,
∴,
∴,
∴,
∴;
②连接,
由折叠可得,,由①中的结论得,
∵四边形是正方形,
∴,
∴在中,,
∴设,则,
∴在中,,
∴,
解得,
∴,
(3)当点P、M、C三点共线时,的值最小,即的长,
根据勾股定理可求得,
由折叠的性质得,
∵四边形是正方形,∴,
∴,,
∴,∴,
同理.
∴由(2)得.
故答案为:;.
【题型5 矩形与等腰三角形】
1.(1)解:PD+PE=BF,理由:
图2:∵BF⊥AC,PG⊥BF,
∴∠PGF=∠GFE=∠PEF=90°,
∴四边形PGFE是矩形,PG∥EF,
∴PE=GE,
∵AB=AC,
∴∠DBP=∠C=∠GPB,
∵∠BDP=∠BGP=90°,BP=BP,
∴△BDP≌△PGB,
∴BG=DP,
∴DP+PE=BG+GF,即PD+PE=BF;
图3:∵,BF⊥AC,
∴∠H=∠BFE=∠PEF=90°,
∴四边形HBFE是矩形,
∴BF=HE,BH∥EF,
∵AB=AC,
∴∠DBP=∠C=∠CBH,
∵∠BDP=∠H=90°,BP=BP,
∴△BDP≌△BHP,
∴PD=PH,
∴PH+PE=PD+PE,即PD+PE=BF;
故答案为:PD+PE=BF;
(2)PD+PE=BF,理由如下:
过点P作PM∥AC,
∵,
∴四边形PEFM是平行四边形,
∴PE=MF,∠PMB=∠MFE=∠PEC,
∴∠PDB=∠PMB,
∵AB=AC,
∴∠DBP=∠C=∠BPM,
∵PB=PB,
∴△BDP≌△PMB,
∴PD=BM,
∴PD+PE=BM+MF,即PD+PE=BF;
(3)延长DP至点N,使PN=PC=2,
∵,
∴∠APN=∠APC,
∵AP=AP,
∴△APC≌△APN,
∴∠PAN=∠PAC=75°,
∵∠ABD=75°,
∴∠PAN=∠ABD,
∴AN∥BD,
过点N作NQ∥AB,交BD的延长线于Q,则四边形ABQN是平行四边形,
∴NQ=AB=6,∠PNQ=∠DPB=60°,∠NQB=∠PBD=75°,
过Q作QR⊥ND于点R,
∴∠NQR=30°,
∴NR=NQ=3,
∴PR=1,RQ=,
∵∠RQD=75°-30°=45°,
∴∠D=45°,
∴RD=RQ=,
∴PD=RP+RD=1+,
故答案为:1+.
2.
【分析】①根据等腰直角三角形的性质和勾股定理即可求出的长度,最后根据三角形面积法即可求出边上的高.
②利用等腰直角三角形的性质求出长度,根据勾股定理求出长度,最后利用旋转的性质可求出取值范围,最后利用中位线定理即可求出取值范围,从而求出最大值.
【详解】解:①为等腰直角三角形,,
.
设边上的高为,
,
,
.
边上的高为.
故答案为:.
②延长至,使,连接,,,过点作于,
如图所示,
由①可知,,,
为等腰三角形,,
.
.
在中,.
矩形中,,,
在中,.
在顺时针旋转一周,
,
,
为中点,为中点,
,
.
最大,
.
故答案为:.
3.C
【分析】如图1所示,连接,证明,进而得到,即可推出;如图2所示,设交于O,先求出 ,利用三角形中位线定理得到,则四边形是平行四边形,再证明,得到四边形是矩形,则;如图3所示,连接,证明四边形是平行四边形,得到,再由,得到,同理可得,则.
【详解】解:如图1所示,连接,
∵E是的中点,
∴,
∴,即,
∵,
∴,故(1)画法错误;
如图2所示,设交于O,
∵,
∴
,
∵分别是的中点,
∴,
同理可得,
∴,
∴四边形是平行四边形,
又∵,
∴,
∴四边形是矩形,
∴,故(2)画法正确;
如图3所示,连接,
∵四边形是平行四边形,
∴,
∵,
∴四边形是平行四边形,
∴,
∵,
∴,
∴,
同理可得,
∴
∴,故(3)画法正确;
故选C.
4.(1)①∵一次函数分别与x轴和y轴交于点A、点B,
可得A(4,0)B(0,3)
∴OA=4,OB=3
∵四边形OABC为矩形,
∴BC=OA=4,OB=AC=3
由折叠可知:
设CF=x,则
在Rt 中,
解得:
∴
∴F的坐标为
②过点作于E,⊥y轴于点G,x轴于M
由(1)可知
∴在Rt中,由等积法可得:
得CE=
∴
∴又F
设为y=kx+b
解得:
所以的解析式为:;
(2)设点P(a,2a-3),
当点P在BC下方时,如图③,过点P作EF//BC,交y轴于E,交AC于F,
,
∵△BPD是等腰直角三角形,
∴BP=PD,∠BPD=90°
∴EF//BC,
∴∠BEP=∠BOA=90°
∴∠PFD=∠CAO=90°
∴∠BPE+∠DPF=∠DPF+∠PDF,
∴∠BPE=∠PDF,
∴△BPE≌△PDF(AAS),
PF=BE=3-(2a-3)=6-2a,EP=DF,
∴EF=EP+PF=a+6-2a=4,
a=2,
∴点P (2,1);
当点P在BC的上方时,如图④,过点P作EF//BC,交y轴于E,交AC的延长线于F,
同理可证△BPE≌△PDF,
BE=PF=2a-3-3=2a-6,
∵EF=EP+PF=a+2a-6=4,
解得:
∴点P,
综上所述:点P坐标为(2,1)或.
【题型6 菱形中的全等三角形的构造】
1.(1)是,理由如下:
如图,连接,
∵四边形是菱形,
∴,,
∴,都是等边三角形,
∴,,
∴,
在和中,
,
∴,
∴,
∵,
∴是等边三角形;
(2)的面积存在最大值,理由如下:
由(1)得:,
∴,
∴,
∴ ,
∴不发生变化,
则的面积最小时,的面积最大,
∵是等边三角形,根据垂线段最短可知,时,的值最小,的面积最小,
∴,
由(1)得:是等边三角形,则有:,
在中,由勾股定理得:,
∴,
同理:,
在中,由勾股定理得:
∴,即:的面积最小值为,
∴的面积的最大值,
2.(1)解:四边形是菱形,
,
,
,
;
(2)解:如图设x轴上的8的点为M
四边形是菱形,B点坐标为,
,,,
设,则,
在中,,即,
解得:即,
菱形OABC的面积:;
(3)设直线的函数解析式:,
将B代入,得,则,
则直线的函数解析式:,
因为四边形是菱形,
,
又 ,
,
,
设点,
,
解得,
.
3.(1)①证明:∵四边形是菱形,,
∴,,
∴和均是等边三角形,
∴,
∴,,
故,
又∵,,
∴,
∴;
②证明:作于,如图:
∵,
∴,
∵,
∴,
即,
∵,,
∴,
∵,
∴,
∴,
∵,
在中,,
∴,
∴,
∴,
∴;
(2)解:设交于点,取的中点,连接,,
由平移可知,,且,
∴,,
∴四边形是平行四边形,
∴,,
是的中点,
,
,
当,,三点共线时,取得最小值,
此时,如图,
∵四边形是菱形,
∴,
∴,
∴,
∴最小值为:.
4.(1)∵MP⊥AB交边CD于点P,∠B=60°,点P与点C重合,
∴∠NPM=30°,∠BMP=90°,
∵N是BC的中点,
∴MN=PN,
∴∠NMP=∠NPM=30°;
(2)如图1,延长MN交DC的延长线于点E,
∵四边形ABCD是菱形,
∴AB∥DC,
∴∠BMN=∠E,
∵点N是线段BC的中点,
∴BN=CN,
在△MNB和△ENC中,
∵∠BMN=∠E,∠MNB=∠ENC,BN=CN,
∴△MNB≌△ENC,
∴MN=EN,即点N是线段ME的中点,
∵MP⊥AB交边CD于点P,AB∥DC,
∴MP⊥DE,
∴∠MPE=90°,
∴PN=MN=ME;
(3)如图2,
∵四边形ABCD是菱形,
∴AB=BC,
又M,N分别是边AB,BC的中点,
∴,,
∴MB=NB,
∴∠BMN=∠BNM,
由(2)知:△MNB≌△ENC,
∴∠BMN=∠BNM=∠E=∠CNE,
又∵PN=MN=NE,
∴∠NPE=∠E,设∠BMN=∠BNM=∠E=∠NCE=∠NPE=x°,则∠NCP=2x°,∠NPC=x°,
①若PN=PC,则∠PNC=∠NCP=2x°,在△PNC中,2x+2x+x=180,解得:x=36,
∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°;
②若PC=NC,则∠PNC=∠NPC=x°,在△PNC中,2x+x+x=180,解得:x=45,
∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°;
综上所述:∠B=108°或90°.
【题型7 正方形中线段的和差倍分关系】
1.(1)证明:连接,如图所示:
∵四边形是正方形,
∴,,
∴,
∵,,
∴,
∴,
∵在中,点E是中点,
∴,
∵,,
∴点B,E在的垂直平分线上,
∴垂直平分,
∴.
(2)解:,理由如下:
∵,,
∴,
∵点E是中点,
∴,
∴是的中位线.
∴,
∵,
∴,
∴.
∵,
∴,
∴,
∴,
在中,,
∴,
∵四边形是正方形,
∴,
∴,
∵,
∴.
(3)解:在点M沿着线段从点C运动到点D的过程中,线段所扫过的图形为四边形,
∵,,
∴,
∴四边形为梯形,
∵,
∴,,
∴.
故答案为:3.
2.(1)解:;
证明:四边形是正方形,
,,
,
又,,
,
∴,
在和中,
∴ ,
∴,,
∴;
(2);
证明:四边形是正方形,
,,
,
又,,
,
∴,
在和中,
∴ ,
∴,,
∴;
(3);
证明:四边形是正方形,
,,
,
又,,
,
∴,
在和中,
∴ ,
∴,,
∴.
3.感知:
证明:四边形是正方形,
,,
,,
,
.
,
在和中
,
(),
,
,
.
探究一:
结论:
理由如下:
四边形是正方形,
,,
,
,
,
,
,
,
,
,
在和中
,
(),
,
,
.
探究二:
结论:,
理由如下:如图:由感知同理可证,
,
,
.
4.(1)证明:∵以、为边向的形外作正方形、正方形,
∴,
又∵,
∴,
∴,
∴,
∴,
∵,为中线,
∴,
∴;
(2),理由如下:
如图②,延长至M,使,连接,延长交于N,
∵为中线,
∴,
又∵,
∴,
∴,
∴,
∴,
∵四边形和四边形都是正方形,
∴,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
∴,
∴.
图③时同理可证.
【题型8 坐标系中的四边形】
1.(1)解:∵CE=CF,∠ECF=90°,
∴∠CEF=45°,
∴∠BEG=45°,
∵AG⊥CE,
∴∠AGC=90°,
∴∠ABF=45°;
(2)∵,
∴,
∵,
∴,
∴.
连接,
∵点是的平分线上一点,
∴,
∴.
又∵.
∴,
∴,
∴.
在和中
,
∴,
∴,
∴,
∴,
∴,
∴四边形是平行四边形;
(3)延长交直线于点,再连接,作轴于点,
∵在中,,,
∴由勾股定理得,,
∴.
∵,四边形是平行四边形,
∴,,
∴,
又∵,
∴,
由题意得,
∴等腰直角三角形,
∴,,
∴,
∴.
在和中
,
∴,
∴,,
∴,
∴,
设直线的表达式为:,
把,代入得,
,解得,
∴直线的表达式为:.
2.(1346,0)
【分析】连接AC,根据条件可以求出AC,画出第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于2019=336×6+3,因此点B3向右平移1344(即336×4)即可到达点B2019,根据点B3的坐标就可求出点B2019的坐标.
【详解】解:连接AC,如图所示.
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB.
∴AC=OA.
∵OA=1,
∴AC=1.
画出第5次、第6次、第7次翻转后的图形,如图所示.
由图可知:每翻转6次,图形向右平移4.
∵2019=336×6+3,
∴点B3向右平移1344(即336×4)到点B2019.
∵B3的坐标为(2,0),
∴B2019的坐标为(2+1344,0),
∴B2019的坐标为(1346,0).
故答案为:(1346,0).
3.(4,0)或(,0)或(,0)
【分析】分三种情况分别画出相应图形,根据正方形、等腰三角形以及直角三角形的边角关系进行计算,求出的长即可.
【详解】解:如图,
①当时,则,
,
,
此时点的坐标为;
②当时,则,
连接,则,,
此时平分,
过点作于,则,
,
此时点的坐标为,;
③当时,则,
,
此时点的坐标为,;
综上所述,点的坐标为或,或,.
故答案为:或,或,.
4.解: (1)结论:,
如图1,当点与点重合时,点与点重合,
,,
,
,
,四边形是矩形,
,
,,
,
又∵
,
;
(2)结论:,
证明:如图2所示,
,,
.
将顺时针旋转至,
则,,,;
,
,
.
在和中,
,
,
.
,
,
,即;
(3)以C为坐标原点,以BC所在的直线为x轴,建立直角坐标系,如图(3):
由(2)易知、、是等腰直角三角形,
∴,
∵,,
∴,
同理可得:,,,
由(2)可得,
∴,
又∵,,
∴.
【题型9 四边形中存在性问题】
1.(1)解: 四边形是矩形,,是由旋转得到,
,
,
设直线的解析式为,根据题意有:
,
解得:,
直线的解析式为:;
(2),
直线的解析式为,
由,
解得:,
,,
,
,
;
(3)由题意可知:,,
,,
,
当为菱形的对角线时,,点与点是关于的对称,此时;
当时,若则,或若,则;
当为对角线时,设,
在中,,即,解得,
此时,,可得,;
综上所述,满足条件的点的坐标为或或或,.
2.(1)解:①证明:轴,轴,
,
,
,
,
,
,
;
②四边形为矩形,,
,
,
设的表达式为,
,
解得,
的表达式为;
四边形是矩形,轴,轴,
四边形是矩形,
,,
,
,,
,,,
,
,
点的坐标为,
在直线上,
,
解得,,
;
(2)存在.如图,过点作轴于,轴于,与直线交于点,
则四边形,都为矩形,
,,,
同(1)可得,,
,
,
,,
点的坐标为,
直线向下平移12个单位得到直线,
直线表达式为,
,
解得:,
,,
点的坐标为,.
3.(1)解:点的坐标为,
由勾股定理得,
四边形是菱形,
,
即点的坐标为,
设直线的解析式为,
则,
解得,
直线的解析式为:,
令得:,即,
;
(2)解:设点M到的距离为,
由,
即,
,
①当在直线上运动时的面积与的运动时间为秒关系为:
,
即;
②当运动到直线上时的面积为与的运动时间为秒关系为:
,
即,
综上所述:与之间的函数关系式为:;
(3)解:存在,
理由如下:
①当时,
点的坐标为,,
,
即,
,
②当时,
即,
,
综上所述,当或时,存在以为腰的等腰三角形.
4.(1)证明:过点作于点,
∵,,,
∴轴,,,,,
∴,,
,
∴,
∴.
(2)解:如图,连接,,令与轴的交点为,则的度数为点对正方形的可视度,即,
∵,,四边形为正方形,
∴,∴,
∴点,关于轴对称,
∴轴垂直平分,
∴,,
∵,∴为等边三角形.,
∴,∴,
∴,
∴点的坐标为,
将点坐标代入中,得,
∴直线的解析式为,
令,得,
∴点的坐标为.
(3)解:存在,如图,
过点作的平行线,在平行线上可取得两点分别为,,使得,,可以得平行四边形和平行四边形,
得, ,
令与轴交点为,则,在轴上取,则,与 互相平分,连接,,,,即得到平行四边形,
点的坐标为或或.
【题型1 四边形中的多解问题】
1.在正方形中,对角线、交于点,的平分线交于点,交于点.过点作于点,交于点.下列结论:①;②四边形是菱形;③;④若,则.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.如图,在菱形中,,,点E为对角线上一动点(不与点B重合),且,连接交延长线于点F.
①;
②当为直角三角形时,;
③当为等腰三角形时,或者;
④连接,当时,平分.
以上结论正确的是 (填正确的序号).
3.如图,在矩形ABCD中,O是对角线的交点,,,过C作于点E,的延长线与的平分线相交于点H,与交于点F,与交于点M.给出下列四个结论:①;②;③;④;⑤.其中正确的结论有 (填写正确的序号).
4.勾股定理是平面几何中一个极为重要的定理,世界上各个文明古国都对勾股定理的发现和研究做出过贡献,特别是定理的证明,据说有400余种.如图是希腊著名数学家欧几里得证明这个定理使用的图形.以的三边为边分别向外作三个正方形:正方形、正方形、正方形,再作垂足为G,交于P,连接,.则结论:①,②,③ ,④ .正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【题型2 四边形中的动点问题】
1.如图,在正方形中,E是边上的一动点,点F在边的延长线上,且,连接、.
(1)求证;
(2)连接,取中点,连接并延长交于,连接.
①依题意,补全图形:
②求证;
③若,用等式表示线段、与之间的数量关系,并证明.
2.如图,在平行四边形中,,,. 动点从点出发沿以2cm/s速度向终点运动,同时点从点出发,以8cm/s速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒()
(1)的长为 .
(2)用含的代数式表示线段的长.
(3)连结.是否存在的值,使得与互相平分?若存在,求出的值;若不存在,请说明理由;
(4)若点关于直线对称的点恰好落在直线上,请直接写出的值.
3.如图,已知菱形的边长为,,点、分别是边、上的两个动点,,连接.
(1)是等边三角形吗?如是,请证明;如不是,请说明理由.
(2)在、运动的过程中,的面积存在最大值吗?如存在,请求出该最大值;如不存在,请说明理由.
4.如图,在矩形纸片中,,,是的中点,是边上的一个动点(点不与点,重合).将沿所在直线翻折,点的对应点为,连接,.当是等腰三角形时,的长为 .
【题型3 四边形中的最值问题】
1.如图,在菱形中,,.E是对角线上的一个动点(不与点B,D重合),连接,以为边作菱形,其中,点G位于直线的上方,且,点P是的中点,连接,则线段的最小值是 .
2.如图,正方形的边长为,点分别在正方形的四条边上,且,,则四边形的周长的最小值是 .
3.在平面直角坐标系中,四边形是矩形,,.
(1)如图1,点P为射线上的动点,连接,若是等腰三角形,求的长度;
(2)如图2,是否在x轴上存在点E,在直线上存在点F,以O,B,E,F为顶点的四边形是菱形?若存在,求出点E,F的坐标;若不存在,请说明理由;
(3)如图3,点M是边上的动点,过点M作的垂线交直线于点N,求的最小值.
4.如图,矩形中,,E、F分别在边上,并且为等边三角形,则m的取值范围为 ,若点G是边上的一点,且,则随着m的变化,的最小值为 .
【题型4 四边形中的折叠问题】
1.通过对下面几何图形的?作探究,解决下列问题.
【操作发现】
如图1,探究小组将矩形纸片沿对角线所在的直线折叠,点落在点处,与边交于点,再将纸片沿直线折叠,使边落在直线上,点A与点重合.
(1)_______度.
(2)若,,求线段的长.
【迁移应用】
(3)如图2,在正方形纸片中,点为边上一点,探究小组将沿直线折叠得到,再将纸片沿过A的直线折叠,使与重合,折痕为,探究小组继续将正方形纸片沿直线折叠,点的对应点恰好落在折痕上的点处,与相交于点,若,求的面积.
2.如图1,一张矩形纸片,其中,,先沿对角线折叠,点落在点的位置,交于点.
(1)求证:;
(2)求的长;
(3)如图2,再折叠一次,使点与重合,折痕交于,求的长.
3.问题原型
(1)如图1,在菱形中,,于E,F为中点,连结,.试猜想的形状,并说明理由.
(2)如图2,在中,于E,F为中点,连结,.试猜想的形状,并说明理由.
(3)如图3,在中,F为上一点,连结,将沿折叠,点C的对应点为.连结并延长交于G,若,求证:F为中点.
(4)如图4,直角坐标系中有,点A与原点重合,点B在x轴正半轴上,与y轴交于点E.将其沿过A的直线折叠,点B对应点恰好落在y轴上,且折痕交于M,交于点N.若的面积为48,,,求点M的坐标和阴影部分面积(直接写出结果).
4.课本再现:
(1)如图1,是一个正方形花园,E,F是它的两个门,且.要修建两条路和,这两条路等长吗?它们有什么位置关系?和的数量关系是:___________;和的位置关系是___________;(无需证明)
知识应用:
(2)如图2,是一个正方形草地,现要在内部修建两条路,且,
①请问这两条路还相等吗?为什么?
②如图3,将边长为12的正方形纸片沿折叠,点D落在边上的点N处,若折痕的长为13,求此时的长;
拓展延伸:
(3)如图4,将边长为12的正方形纸片沿折叠,点D落在边上的点N处,与交于点P,取的中点M,连接,则的最小值为___________,此时的长度是___________.
【题型5 矩形与等腰三角形】
1.【问题背景】
某“数学学习兴趣小组”在学习了“等腰三角形的性质”和“平行四边形的性质和判定”后,在习题中发现了这样一个问题:如图1,在等腰中,,点D、E分别是边上的点,点P是底边上的点,且,过点B作于点F,请写出线段、、之间满足的数量关系式.
同学们经过交流讨论,得到了如下两种解决思路:
解决思路1:如图2,过点P作于点G;
解决思路2:如图3,过点B作,交的延长线于点H;
(1)上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为______________.
【类比探究】
(2)如图4,在等腰中,,点D、E分别是边上的点,点P是底边上的点,且,过点B作交于点F,请写出线段之间满足的数量关系式,并说明理由.
【拓展应用】
(3)如图5,在与中,,,点A、B、P在同一条直线上,若,,则______________.
2.已知在矩形中,,,为矩形的中心,在等腰中,,.则边上的高为 ;将绕点A按顺时针方向旋转一周,连接,取中点,连接,则的最大值为 .
3.画一个四边形,使得该四边形的面积等于已知图形面积的一半.
(1)如图1,已知等腰,D,E分别是的中点,画四边形;
(2)如图2,已知四边形,.四边的中点分别为E,F,G,H,画四边形;
(3)如图3,已知平行四边形,点E,G分别在上,且.点F,H分别在上,画四边形.
以上三种画法中,所有正确画法的序号是( )
A.(1)(3) B.(2) C.(2)(3) D.(1)(2)(3)
4.如图①,在平面直角坐标系中,一次函数分别与x轴和y轴交于点A、点B,四边形OACB为矩形.
(1)如图②,点F在BC上,连接AF,把沿着AF折叠,点C刚好与线段AB上一点重合.
①求点F的坐标;
②请直接写出直线的解析式:______;
(2)如图③,动点在一次函数的图象上运动,点D在线段AC上,是否存在直角顶点为P的等腰直角,若存在,请求出点P的坐标;若不存在,请说明理由.
【题型6 菱形中的全等三角形的构造】
1.如图,已知菱形的边长为,,点、分别是边、上的两个动点,,连接.
(1)是等边三角形吗?如是,请证明;如不是,请说明理由.
(2)在、运动的过程中,的面积存在最大值吗?如存在,请求出该最大值;如不存在,请说明理由.
2.如图,菱形的一边在x轴的正半轴上,O是坐标原点,B点坐标为,点D是对角线上一点,连结,垂足为E.
(1)求证:;
(2)求菱形的面积;
(3)连接,当时,求点D的坐标.
3.已知在菱形中,,连接对角线.
(1)如图1,为边上一点,为边延长线上一点,且,连接,交于点.
①求证:;
②过点作,垂足为,求证:;
(2)如图2,已知,将沿射线平移,得到,连接,,请直接写出的最小值.
4.如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
【题型7 正方形中线段的和差倍分关系】
1.如图,在正方形中,动点在上,过点作,过点作,点是的中点,连接交于点.
(1)求证:;
(2)请探究线段长度之间的等量关系,并证明你的结论;
(3)设,若点沿着线段从点运动到点,则在该运动过程中,线段所扫过的图形面积为________(直接写出答案).
2.过正方形(四边都相等,四个角都是直角)的顶点A作一条直线.
(1)当不与正方形任何一边相交时,过点B作于点E,过点作于点F,如图(1),请写出,,之间的数量关系,并证明你的结论.
(2)若改变直线的位置,使与边相交如图(2),其它条件不变,,,的关系会发生变化,请直接写出,,的数量关系,不必证明;
(3)若继续改变直线的位置,使与边相交如图(3),其它条件不变,,,的关系又会发生变化,请直接写出,,的数量关系,不必证明.
3.感知:如图(1)所示,四边形是正方形,点是线段上的任意一点,于点,,且交于点,求证:.
探究一:如图(2)所示,若点在的延长线上,上述其余条件不变,则,,存在怎样的等量关系?猜想并证明这一结论.
探究二:若点在的延长线上,上述其余条件不变,则,,又存在怎样的等量关系?直接写出结论.
4.已知:在中,为中线,以、为边向的形外作正方形、正方形.
(1)如图①,当时,求证:.
(2)如图②③,当时,与有怎样的关系?在图②和图③中可任选一个图,证明你的结论.
【题型8 坐标系中的四边形】
1.如图1,在中,,,点是的平分线上一点,于,交的延长线于,交的延长线于,连接.
(1)直接写出的大小;
(2)求证:四边形是平行四边形;
(3)建立如图2所示的坐标系,若,,直线绕点顺时针旋转45°得到直线,求直线的表达式.
2.如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2019次,点B的落点依次为B1,B2,B3,…,则B2019的坐标为 .
3.如图,在坐标系中,正方形的边长为2,点是轴上一动点.若与的两边所组成的角的度数之比为,则点的坐标为 .
4.如图,在△ABC中,AC=BC=1,∠C=90°,E、F是AB上的动点,且∠ECF=45°,分别过E、F作BC、AC的垂线,垂足分别为H、G,两垂线交于点M.
(1)当点E与点B重合时,请直接写出MH与AC的数量关系 ;
(2)探索AF、EF、BE之间的数量关系,并证明你的结论;
(3)以C为坐标原点,以BC所在的直线为x轴,建立直角坐标系,请画出坐标系并利用(2)中的结论证明.
【题型9 四边形中存在性问题】
1.如图,四边形是矩形,点、在坐标轴上,点坐标,是绕点顺时针旋转得到的,点在轴上,直线交轴于点,交于点.
(1)求直线的解析式;
(2)求的面积;
(3)点在轴上,平面内是否存在点,使以点D、F、M、N为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
2.如图,在平面直角坐标系中,矩形的顶点C,A分别在x轴,y轴上,O为坐标原点,B点的坐标为,过A点的直线l与x轴交于点,P是线段上一动点,设.
(1)是第一象限直线l上一点,作轴于E,轴于F,若,.
①求证:;
②求直线l的表达式及D点的坐标;
(2)将直线l向下平移12个单位得到直线,在直线上方的直线上,是否存在这样的点D,使得,且,若存在,请求出点D的坐标,若不存在,请说明理由.
3.如图1所示,在平面直角坐标系中,为坐标原点,四边形是菱形,点的坐标为,点在轴正半轴上,直线交轴于点M,连接,边交轴于点.
(1)求的长;
(2)如图2所示,动点从点出发,沿折线方向以每秒1个单位的速度向终点匀速运动,设的面积为,点的运动时间为秒,求与之间的函数关系式;
(3)在(2)的情况下,当点在线段上运动时,是否存在以为腰的等腰三角形?如存在,直接写出的值;如不存在,说明理由.
4.定义“点对图形的可视度”:在平面直角坐标系中,对于点P和图形,若图形上所有的点都在的内部或的边上,则的最小值称为点对图形的可视度.如图1,点对线段的可视度为的度数.
(1)如图2,已知点,,,.连接,,则的度数为点对的可视度.求证:;
(2)如图3,已知四边形为正方形,其中点,.直线与轴交于点,与轴交于点,其中点对正方形的可视度为.求点的坐标;
(3)在(2)的条件下,在平面直角坐标系内是否存在点,使以点,,,为顶点的四边形为平行四边形 若存在,请直接写出点坐标;若不存在,请说明理由.
参考答案
【题型1 四边形中的多解问题】
1.D
【分析】设,则,可算出,故①正确;先证明,再由得,即,四边形是菱形,故②正确;由,得,可求出,故③正确;由四边形是菱形证明,即可得,故④正确.
【详解】解:平分,,,
,
四边形是正方形,
,
,
设,则,
,故①正确;
在和中,
,
,
,,
四边形是正方形,
,
又
,
,
,
,
,
四边形是菱形,故②正确;
由①②知,,,
,
,故③正确;
,,
,
四边形是菱形,
,
,
,
,
,
,故④正确.
故选:D.
2.①②③④
【分析】连接,交于点O,由题意易得,是等边三角形,,,,则有,则,然后根据等边三角形的性质与判定、全等三角形的性质、勾股定理及等腰三角形的性质可进行求解.
【详解】解:连接,交于点O,如图所示,
∵四边形是菱形,,,
∴,是等边三角形,,,,
∴,则,
∴,则,
∴,
∵,
∴,
∴,
∵,
∴,
∴,故①正确;
当为直角三角形时,即,
∵,,
∴,
∴,
∴,则,
∴;故②正确;
当为等腰三角形时,则可分当时,即,
在菱形中,,
∴,
∵,
∴在中,,
∴
∴;
当时,即,
∵,
∴在中,,
∴
∴;
当时,则,此时点E与点B重合,不符合题意;
故③正确;
连接,当时,则,
∴,
由②可知,
∴,
∴,
∵,
∴是等边三角形,
∴,
∴,
∴平分,故④正确;
故答案为①②③④.
3.①②③⑤
【分析】先证明是等边三角形,得,再证是等腰三角形,得 ,即可得出,可判定①正确;求得,得出,可判定②正确;利用含的直角三角形的性质得出,,再由,,即可求得 ,可判定③正确;过程点M作于N,分别求出,,即可得出,可判定④错误;过点H作交延长线于Q,延长交于P,先求出,从而求得,即可求得,可判定⑤正确.
【详解】解:∵矩形ABCD,
∴,,
∵,
∴是等边三角形,
∴,
∵平分,
∴,
∴,
∴,
∴,
故①正确;
∴,
∴,
∵,
∴,
∴,
∴,
∴,
故②正确;
∵矩形ABCD,
∴,,
∴,
∴,
∴,,
∴,
∵,
∴,
故③正确;
在中,,,
∴,,
∵,
∴,
∴,
过程点M作于N,如图,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故④错误;
过点H作交延长线于Q,延长交于P,
∵,
∴,
∴,
∴,,
∴,
∵
∴四边形是矩形,
∴,,
∴,
∴,
∴,
∴,
故⑤正确,
∴正确的结论有①②③⑤
故答案为:①②③⑤.
4.D
【分析】根据题意,,得到,得到,延长至点,过点做垂线,由题意可知四边形为矩形,求出面积即可,延长至点,过点做垂线,由题意可知四边形为矩形,求出面积即可.
【详解】解:由题意可得,,,
,,
,
∵,
,
故①、②符合题意,正确;
延长至点,过点做垂线,
由题意可知四边形为矩形,
,
故,
,
故 ,③符合题意,正确;
;
延长至点,过点做垂线,
由题意可知四边形为矩形,
故,
,
,
故 ,④符合题意,正确.
.
故选:D.
【题型2 四边形中的动点问题】
1.(1)证明:四边形是正方形,
,,
,
又,
,
,
,
,
即,
;
(2)①解:依题意,补全图形如图所示:
②证明:由(1)可知,和都是直角三角形,
是的中点,
,,
;
③解:,证明如下:
由(1)可知,,,
,
是等腰直角三角形,
,
为的中点,
,,,
,,,,
,
,
,
,
,
又,,
,
,
在中,由勾股定理得:,
,,
,
.
2.(1)∵四边形是平行四边形,
∴,
∵,
∴,
(2)在中,,,
由题意得,,
当点Q与点B重合时,,
∴,
当点Q在线段上时,,
当点Q在线段的延长线上时,,
综上所述,或;
(3)存在,理由如下:
如图,连接,
若与互相平分,则四边形是平行四边形,
∴,
∴,
∴,
∴当时,与
(4)当点P关于直线对称的点落在点A下方时,如图,
由对称得,,
∵,
∴,
∴,即,
∴,
∴,
∴,
解得;
当点P关于直线对称的点落在点A上方时,如图,
由对称得,,
∵,
∴,
∵
∴,
∴,
∴,
∴,
解得,
综上所述,t的值为或2.
3.(1)是,理由如下:
如图,连接,
∵四边形是菱形,
∴,,
∴,都是等边三角形,
∴,,
∴,
在和中,
,
∴,
∴,
∵,
∴是等边三角形;
(2)的面积存在最大值,理由如下:
由(1)得:,
∴,
∴,
∴ ,
∴不发生变化,
则的面积最小时,的面积最大,
∵是等边三角形,根据垂线段最短可知,时,的值最小,的面积最小,
∴,
由(1)得:是等边三角形,则有:,
在中,由勾股定理得:,
∴,
同理:,
在中,由勾股定理得:
∴,即:的面积最小值为,
∴的面积的最大值,
4.或或
【分析】存在三种情况:当 ,连接,勾股定理求得的长,可判断,,三点共线,根据勾股定理即可得到结论;当 ,证明是正方形,于是得到结论;当 时,连接,,证明点,,三点共线,再用勾股定理可得答案.
【详解】解:①当时,连接,如图:
点是的中点,, ,四边形是矩形,
, ,,
,
将沿所在直线翻折,得到 ,
,
,
,
点,,三点共线,
,
,
设则 ,
在 中,
,
解得: ,
;
②当 时,如图:
,
点在线段的垂直平分线上,
点在线段的垂直平分线上,
点是的中点,
是的垂直平分线,
,
将沿所在直线翻折,得到 ,
, ,
四边形 是正方形,
;
③当 时,连接,,如图:
点是的中点,, ,四边形是矩形,
,,
,
将沿所在直线翻折,得到 ,
,
,
,
点,,三点共线,
,
,
设则
在 中,,
在中,,
,
即
解得: ,
;
综上所述,的长为或或,
故答案为:或或.
【题型3 四边形中的最值问题】
1.
【分析】连接,过点P作,则当G点位于点时,有最小值即的长,根据条件证明,可得,进而用勾股定理求解即可.
【详解】解:连接,过点P作,则当G点位于点时,有最小值即的长,如图,
∵四边形是菱形,,
∴,,
∴是等边三角形,,
∴,
∵四边形是菱形,,
∴,
∴,
∴,
∴ ,
∴,
∴C、D、G三点共线,
∵点P是的中点,,
∴,
∵ ,
∴,
∴,
即线段的最小值是,
故答案为:.
2.
【分析】根据垂线段最短及平行四边形的判定与性质可知当时,最短,最短,四边形是正方形即可解答.
【详解】解:∵,,
∴四边形是平行四边形,
∴ ,,即四边形的周长=
∵四边形为正方形,
∴,,
∵,
∴,
∴,即
∴,
过作G点的对应点N,连接,过N点作,交延长线于M,
则
最短为,
∴四边形的周长最短=,
故答案为.
【点睛】本题考查了正方形的判定与性质,全等三角形的性质和判定,轴对称的性质.掌握将军饮马问题是解题关键.
3.(1)解:如图1,
当点P在上时,
∵四边形是矩形,
∴,
∵,
∴,,;
∵是等腰三角形,
∴是等边三角形,
∴,
当点P(图中)在的延长线上时,
∵,
∴,
∵是等腰三角形,
∴,
∴,
∴,
∴,
综上所述:或3;
(2)如图2,
存在点E和F,使以O,B,E,F为顶点的四边形是菱形,理由如下:
是边时,
当点F在的延长线时,
∵,
∴,,
∴,
当点在的延长线上时,
∵,,
∴,
当是对角线时,(菱形)
设,则,
在中,由勾股定理得,,
∴,
∴,,
综上所述:,或,或,;
(3)如图3,
作点O关于的对称点,作B点关于的对称点,
连接,交于点,于点,
此时的最小值为的长,即的长,
作轴,作于T,
∵,,
∴,
∴的最小值为:6.
4.
【分析】当点F与点D重合时,此时有最小值,当点E与点B重合时,此时有最大值,由等边三角形的性质和直角三角形的性质可求的长,即可求m的范围;可证,即, 当点H,点N,点F共线时,有最小值,即可求解.
【详解】解:如图,当点F与点D重合时,此时有最小值,
∵为等边三角形,
∴,,,
∴,,
如图,当点E与点B重合时,此时有最大值,
∵为等边三角形,
∴,,,
∴,,
∴,
∴.
如图,当时,以为边作等边,作,连接,
∴,,
∴,
∴,
∴,
∴当点H,点N,点F共线时,有最小值,
此时,∵ ,
∴四边形是矩形,
∴,
∵是等边三角形,,
∴,
∴.
故答案为:;.
【题型4 四边形中的折叠问题】
1.解:(1)∵四边形是矩形,
∴,
由折叠可知,,
∴,
∴,
故答案为:
(2)∵四边形是矩形,,,
∴,,
由折叠可知, ,,
在和中,
,
∴,
∴,
设,
则
在中,,
即,
解得,
∴;
(3)∵四边形是正方形,
∴,,
由折叠可知,,
∴,
∴,
由折叠可知,,,,,
∴,
∴,
∴,
∴是等腰直角三角形,
∵,,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
由折叠可知,,,
∴,
∴,
∴,
∴,
∴,
∴,,
∴,
即的面积为.
2.(1)证明:∵矩形纸片沿对角线折叠,点落在点的位置,
∴,,
在和中,
,
∴,
∴;
(2)解:∵,,,
∴,
设,则,
∴,
∵在中,,
∴,
解得:,
∴,
∴的长为;
(3)再折叠一次,使点与重合,得折痕,且,,
∴,即点是的中点,
∴在中,,
∵,,
∴,
∴点是的中点,
∴是的中位线,
∴,,
由折叠的性质可知,
在矩形中,,
∴,
∴,
∴,
∴,
设,则,
在中,,
∴,
解得:,
∴,
∴的长为.
3.(1)如图1,
连接,
四边形是菱形,
,
,
是等边三角形,
,,
,
,
同理可得:是等边三角形,
,,
点是的中点,
,,
,
在和中,
,
,
,
是等边三角形;
(2)如图2,
是等腰三角形,理由如下:
取的中点,连接,直线交于,
四边形是平行四边形,
,,
点是的中点,是的中点,
,
,
四边形是平行四边形,
,
点是的中点,
,
,
,
即:是等腰三角形;
(3)证明:由(2)知:,,
,,
,
,
,
四边形是平行四边形,
,
,,
,
,
,
,
即:点是的中点
(4)由得,
,
,
四边形是平行四边形,
,,
,
,
,
,
,
直线的解析式为:,
,
直线的解析式为:,
由得,
,
,,
,
,
直线的解析式为:,
当时,,
,
,
,
,
.
4.解:猜想,,理由如下:
∵四边形是正方形,
∴,
∵,
∴,即,
在和中,,
∴,
∴,
∵,
∴,
∴,
∴,
∴;
故答案为:,;
(2)①,理由如下:
过F点作于点P,过点M作于点Q,与相交于点H,
∵四边形是正方形,
∴,,,,
∵于点P,于点Q,
∴,,
∴,,
∵,
∴,
∴,
∴,
∴,
∴;
②连接,
由折叠可得,,由①中的结论得,
∵四边形是正方形,
∴,
∴在中,,
∴设,则,
∴在中,,
∴,
解得,
∴,
(3)当点P、M、C三点共线时,的值最小,即的长,
根据勾股定理可求得,
由折叠的性质得,
∵四边形是正方形,∴,
∴,,
∴,∴,
同理.
∴由(2)得.
故答案为:;.
【题型5 矩形与等腰三角形】
1.(1)解:PD+PE=BF,理由:
图2:∵BF⊥AC,PG⊥BF,
∴∠PGF=∠GFE=∠PEF=90°,
∴四边形PGFE是矩形,PG∥EF,
∴PE=GE,
∵AB=AC,
∴∠DBP=∠C=∠GPB,
∵∠BDP=∠BGP=90°,BP=BP,
∴△BDP≌△PGB,
∴BG=DP,
∴DP+PE=BG+GF,即PD+PE=BF;
图3:∵,BF⊥AC,
∴∠H=∠BFE=∠PEF=90°,
∴四边形HBFE是矩形,
∴BF=HE,BH∥EF,
∵AB=AC,
∴∠DBP=∠C=∠CBH,
∵∠BDP=∠H=90°,BP=BP,
∴△BDP≌△BHP,
∴PD=PH,
∴PH+PE=PD+PE,即PD+PE=BF;
故答案为:PD+PE=BF;
(2)PD+PE=BF,理由如下:
过点P作PM∥AC,
∵,
∴四边形PEFM是平行四边形,
∴PE=MF,∠PMB=∠MFE=∠PEC,
∴∠PDB=∠PMB,
∵AB=AC,
∴∠DBP=∠C=∠BPM,
∵PB=PB,
∴△BDP≌△PMB,
∴PD=BM,
∴PD+PE=BM+MF,即PD+PE=BF;
(3)延长DP至点N,使PN=PC=2,
∵,
∴∠APN=∠APC,
∵AP=AP,
∴△APC≌△APN,
∴∠PAN=∠PAC=75°,
∵∠ABD=75°,
∴∠PAN=∠ABD,
∴AN∥BD,
过点N作NQ∥AB,交BD的延长线于Q,则四边形ABQN是平行四边形,
∴NQ=AB=6,∠PNQ=∠DPB=60°,∠NQB=∠PBD=75°,
过Q作QR⊥ND于点R,
∴∠NQR=30°,
∴NR=NQ=3,
∴PR=1,RQ=,
∵∠RQD=75°-30°=45°,
∴∠D=45°,
∴RD=RQ=,
∴PD=RP+RD=1+,
故答案为:1+.
2.
【分析】①根据等腰直角三角形的性质和勾股定理即可求出的长度,最后根据三角形面积法即可求出边上的高.
②利用等腰直角三角形的性质求出长度,根据勾股定理求出长度,最后利用旋转的性质可求出取值范围,最后利用中位线定理即可求出取值范围,从而求出最大值.
【详解】解:①为等腰直角三角形,,
.
设边上的高为,
,
,
.
边上的高为.
故答案为:.
②延长至,使,连接,,,过点作于,
如图所示,
由①可知,,,
为等腰三角形,,
.
.
在中,.
矩形中,,,
在中,.
在顺时针旋转一周,
,
,
为中点,为中点,
,
.
最大,
.
故答案为:.
3.C
【分析】如图1所示,连接,证明,进而得到,即可推出;如图2所示,设交于O,先求出 ,利用三角形中位线定理得到,则四边形是平行四边形,再证明,得到四边形是矩形,则;如图3所示,连接,证明四边形是平行四边形,得到,再由,得到,同理可得,则.
【详解】解:如图1所示,连接,
∵E是的中点,
∴,
∴,即,
∵,
∴,故(1)画法错误;
如图2所示,设交于O,
∵,
∴
,
∵分别是的中点,
∴,
同理可得,
∴,
∴四边形是平行四边形,
又∵,
∴,
∴四边形是矩形,
∴,故(2)画法正确;
如图3所示,连接,
∵四边形是平行四边形,
∴,
∵,
∴四边形是平行四边形,
∴,
∵,
∴,
∴,
同理可得,
∴
∴,故(3)画法正确;
故选C.
4.(1)①∵一次函数分别与x轴和y轴交于点A、点B,
可得A(4,0)B(0,3)
∴OA=4,OB=3
∵四边形OABC为矩形,
∴BC=OA=4,OB=AC=3
由折叠可知:
设CF=x,则
在Rt 中,
解得:
∴
∴F的坐标为
②过点作于E,⊥y轴于点G,x轴于M
由(1)可知
∴在Rt中,由等积法可得:
得CE=
∴
∴又F
设为y=kx+b
解得:
所以的解析式为:;
(2)设点P(a,2a-3),
当点P在BC下方时,如图③,过点P作EF//BC,交y轴于E,交AC于F,
,
∵△BPD是等腰直角三角形,
∴BP=PD,∠BPD=90°
∴EF//BC,
∴∠BEP=∠BOA=90°
∴∠PFD=∠CAO=90°
∴∠BPE+∠DPF=∠DPF+∠PDF,
∴∠BPE=∠PDF,
∴△BPE≌△PDF(AAS),
PF=BE=3-(2a-3)=6-2a,EP=DF,
∴EF=EP+PF=a+6-2a=4,
a=2,
∴点P (2,1);
当点P在BC的上方时,如图④,过点P作EF//BC,交y轴于E,交AC的延长线于F,
同理可证△BPE≌△PDF,
BE=PF=2a-3-3=2a-6,
∵EF=EP+PF=a+2a-6=4,
解得:
∴点P,
综上所述:点P坐标为(2,1)或.
【题型6 菱形中的全等三角形的构造】
1.(1)是,理由如下:
如图,连接,
∵四边形是菱形,
∴,,
∴,都是等边三角形,
∴,,
∴,
在和中,
,
∴,
∴,
∵,
∴是等边三角形;
(2)的面积存在最大值,理由如下:
由(1)得:,
∴,
∴,
∴ ,
∴不发生变化,
则的面积最小时,的面积最大,
∵是等边三角形,根据垂线段最短可知,时,的值最小,的面积最小,
∴,
由(1)得:是等边三角形,则有:,
在中,由勾股定理得:,
∴,
同理:,
在中,由勾股定理得:
∴,即:的面积最小值为,
∴的面积的最大值,
2.(1)解:四边形是菱形,
,
,
,
;
(2)解:如图设x轴上的8的点为M
四边形是菱形,B点坐标为,
,,,
设,则,
在中,,即,
解得:即,
菱形OABC的面积:;
(3)设直线的函数解析式:,
将B代入,得,则,
则直线的函数解析式:,
因为四边形是菱形,
,
又 ,
,
,
设点,
,
解得,
.
3.(1)①证明:∵四边形是菱形,,
∴,,
∴和均是等边三角形,
∴,
∴,,
故,
又∵,,
∴,
∴;
②证明:作于,如图:
∵,
∴,
∵,
∴,
即,
∵,,
∴,
∵,
∴,
∴,
∵,
在中,,
∴,
∴,
∴,
∴;
(2)解:设交于点,取的中点,连接,,
由平移可知,,且,
∴,,
∴四边形是平行四边形,
∴,,
是的中点,
,
,
当,,三点共线时,取得最小值,
此时,如图,
∵四边形是菱形,
∴,
∴,
∴,
∴最小值为:.
4.(1)∵MP⊥AB交边CD于点P,∠B=60°,点P与点C重合,
∴∠NPM=30°,∠BMP=90°,
∵N是BC的中点,
∴MN=PN,
∴∠NMP=∠NPM=30°;
(2)如图1,延长MN交DC的延长线于点E,
∵四边形ABCD是菱形,
∴AB∥DC,
∴∠BMN=∠E,
∵点N是线段BC的中点,
∴BN=CN,
在△MNB和△ENC中,
∵∠BMN=∠E,∠MNB=∠ENC,BN=CN,
∴△MNB≌△ENC,
∴MN=EN,即点N是线段ME的中点,
∵MP⊥AB交边CD于点P,AB∥DC,
∴MP⊥DE,
∴∠MPE=90°,
∴PN=MN=ME;
(3)如图2,
∵四边形ABCD是菱形,
∴AB=BC,
又M,N分别是边AB,BC的中点,
∴,,
∴MB=NB,
∴∠BMN=∠BNM,
由(2)知:△MNB≌△ENC,
∴∠BMN=∠BNM=∠E=∠CNE,
又∵PN=MN=NE,
∴∠NPE=∠E,设∠BMN=∠BNM=∠E=∠NCE=∠NPE=x°,则∠NCP=2x°,∠NPC=x°,
①若PN=PC,则∠PNC=∠NCP=2x°,在△PNC中,2x+2x+x=180,解得:x=36,
∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°;
②若PC=NC,则∠PNC=∠NPC=x°,在△PNC中,2x+x+x=180,解得:x=45,
∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°;
综上所述:∠B=108°或90°.
【题型7 正方形中线段的和差倍分关系】
1.(1)证明:连接,如图所示:
∵四边形是正方形,
∴,,
∴,
∵,,
∴,
∴,
∵在中,点E是中点,
∴,
∵,,
∴点B,E在的垂直平分线上,
∴垂直平分,
∴.
(2)解:,理由如下:
∵,,
∴,
∵点E是中点,
∴,
∴是的中位线.
∴,
∵,
∴,
∴.
∵,
∴,
∴,
∴,
在中,,
∴,
∵四边形是正方形,
∴,
∴,
∵,
∴.
(3)解:在点M沿着线段从点C运动到点D的过程中,线段所扫过的图形为四边形,
∵,,
∴,
∴四边形为梯形,
∵,
∴,,
∴.
故答案为:3.
2.(1)解:;
证明:四边形是正方形,
,,
,
又,,
,
∴,
在和中,
∴ ,
∴,,
∴;
(2);
证明:四边形是正方形,
,,
,
又,,
,
∴,
在和中,
∴ ,
∴,,
∴;
(3);
证明:四边形是正方形,
,,
,
又,,
,
∴,
在和中,
∴ ,
∴,,
∴.
3.感知:
证明:四边形是正方形,
,,
,,
,
.
,
在和中
,
(),
,
,
.
探究一:
结论:
理由如下:
四边形是正方形,
,,
,
,
,
,
,
,
,
,
在和中
,
(),
,
,
.
探究二:
结论:,
理由如下:如图:由感知同理可证,
,
,
.
4.(1)证明:∵以、为边向的形外作正方形、正方形,
∴,
又∵,
∴,
∴,
∴,
∴,
∵,为中线,
∴,
∴;
(2),理由如下:
如图②,延长至M,使,连接,延长交于N,
∵为中线,
∴,
又∵,
∴,
∴,
∴,
∴,
∵四边形和四边形都是正方形,
∴,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
∴,
∴.
图③时同理可证.
【题型8 坐标系中的四边形】
1.(1)解:∵CE=CF,∠ECF=90°,
∴∠CEF=45°,
∴∠BEG=45°,
∵AG⊥CE,
∴∠AGC=90°,
∴∠ABF=45°;
(2)∵,
∴,
∵,
∴,
∴.
连接,
∵点是的平分线上一点,
∴,
∴.
又∵.
∴,
∴,
∴.
在和中
,
∴,
∴,
∴,
∴,
∴,
∴四边形是平行四边形;
(3)延长交直线于点,再连接,作轴于点,
∵在中,,,
∴由勾股定理得,,
∴.
∵,四边形是平行四边形,
∴,,
∴,
又∵,
∴,
由题意得,
∴等腰直角三角形,
∴,,
∴,
∴.
在和中
,
∴,
∴,,
∴,
∴,
设直线的表达式为:,
把,代入得,
,解得,
∴直线的表达式为:.
2.(1346,0)
【分析】连接AC,根据条件可以求出AC,画出第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于2019=336×6+3,因此点B3向右平移1344(即336×4)即可到达点B2019,根据点B3的坐标就可求出点B2019的坐标.
【详解】解:连接AC,如图所示.
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB.
∴AC=OA.
∵OA=1,
∴AC=1.
画出第5次、第6次、第7次翻转后的图形,如图所示.
由图可知:每翻转6次,图形向右平移4.
∵2019=336×6+3,
∴点B3向右平移1344(即336×4)到点B2019.
∵B3的坐标为(2,0),
∴B2019的坐标为(2+1344,0),
∴B2019的坐标为(1346,0).
故答案为:(1346,0).
3.(4,0)或(,0)或(,0)
【分析】分三种情况分别画出相应图形,根据正方形、等腰三角形以及直角三角形的边角关系进行计算,求出的长即可.
【详解】解:如图,
①当时,则,
,
,
此时点的坐标为;
②当时,则,
连接,则,,
此时平分,
过点作于,则,
,
此时点的坐标为,;
③当时,则,
,
此时点的坐标为,;
综上所述,点的坐标为或,或,.
故答案为:或,或,.
4.解: (1)结论:,
如图1,当点与点重合时,点与点重合,
,,
,
,
,四边形是矩形,
,
,,
,
又∵
,
;
(2)结论:,
证明:如图2所示,
,,
.
将顺时针旋转至,
则,,,;
,
,
.
在和中,
,
,
.
,
,
,即;
(3)以C为坐标原点,以BC所在的直线为x轴,建立直角坐标系,如图(3):
由(2)易知、、是等腰直角三角形,
∴,
∵,,
∴,
同理可得:,,,
由(2)可得,
∴,
又∵,,
∴.
【题型9 四边形中存在性问题】
1.(1)解: 四边形是矩形,,是由旋转得到,
,
,
设直线的解析式为,根据题意有:
,
解得:,
直线的解析式为:;
(2),
直线的解析式为,
由,
解得:,
,,
,
,
;
(3)由题意可知:,,
,,
,
当为菱形的对角线时,,点与点是关于的对称,此时;
当时,若则,或若,则;
当为对角线时,设,
在中,,即,解得,
此时,,可得,;
综上所述,满足条件的点的坐标为或或或,.
2.(1)解:①证明:轴,轴,
,
,
,
,
,
,
;
②四边形为矩形,,
,
,
设的表达式为,
,
解得,
的表达式为;
四边形是矩形,轴,轴,
四边形是矩形,
,,
,
,,
,,,
,
,
点的坐标为,
在直线上,
,
解得,,
;
(2)存在.如图,过点作轴于,轴于,与直线交于点,
则四边形,都为矩形,
,,,
同(1)可得,,
,
,
,,
点的坐标为,
直线向下平移12个单位得到直线,
直线表达式为,
,
解得:,
,,
点的坐标为,.
3.(1)解:点的坐标为,
由勾股定理得,
四边形是菱形,
,
即点的坐标为,
设直线的解析式为,
则,
解得,
直线的解析式为:,
令得:,即,
;
(2)解:设点M到的距离为,
由,
即,
,
①当在直线上运动时的面积与的运动时间为秒关系为:
,
即;
②当运动到直线上时的面积为与的运动时间为秒关系为:
,
即,
综上所述:与之间的函数关系式为:;
(3)解:存在,
理由如下:
①当时,
点的坐标为,,
,
即,
,
②当时,
即,
,
综上所述,当或时,存在以为腰的等腰三角形.
4.(1)证明:过点作于点,
∵,,,
∴轴,,,,,
∴,,
,
∴,
∴.
(2)解:如图,连接,,令与轴的交点为,则的度数为点对正方形的可视度,即,
∵,,四边形为正方形,
∴,∴,
∴点,关于轴对称,
∴轴垂直平分,
∴,,
∵,∴为等边三角形.,
∴,∴,
∴,
∴点的坐标为,
将点坐标代入中,得,
∴直线的解析式为,
令,得,
∴点的坐标为.
(3)解:存在,如图,
过点作的平行线,在平行线上可取得两点分别为,,使得,,可以得平行四边形和平行四边形,
得, ,
令与轴交点为,则,在轴上取,则,与 互相平分,连接,,,,即得到平行四边形,
点的坐标为或或.
