初中数学人教版八年级下册 第19章《一次函数》章节测试卷(含解析)
文档属性
| 名称 | 初中数学人教版八年级下册 第19章《一次函数》章节测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 580.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 14:05:08 | ||
图片预览




文档简介
第19章《一次函数》章节测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.星期一学校举行升国旗仪式,开始国旗与小旗手的肩同高,下列图象能反映国旗距离地面高与升旗时间关系的是( )
A. B. C. D.
2.如果一个正比例函数的图象经过不同象限的两点,那么一定有( )
A. B. C. D.
3.在同一平面直角坐标系中,函数与的图象大致是( )
A. B. C. D.
4.已知二元一次方程与有一组公共解,那么一次函数与的图象在直角坐标系内的交点坐标为( )
A. B. C. D.
5.已知一次函数(为整数)的图象与轴正半轴相交,随的增大而减小,当时,的取值范围是( ).
A. B. C. D.
6.将直线向左平移个单位,再向上平移个单位,得到直线,则( )
A., B., C., D.,
7.平面直角坐标系中,过点的直线l经过一、二、三象限,若点,,都在直线l上,则下列判断正确的是( )
A. B. C. D.
8.若一次函数()的图象经过点,,则下列结论正确的是( )
A.若,则 B.若 ,则
C.若,则 D.若,则
9.如图,点、的坐标分别为、,点是第一象限内直线上一个动点,当点的横坐标逐渐增大时,四边形的面积( )
A.逐渐增大 B.逐渐减少 C.先减少后增大 D.不变
10. 已知:直线y=x+(n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2019( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.已知直线与坐标轴围成的三角形的面积为4,则此直线的解析式为 .
12.一次函数(是常数,且)的图像如图所示,则方程的解为 .
13.在平面直角坐标系xOy中,直线y=﹣x+1与直线y=﹣2x交于点A,点B(m,0)是x轴上的一个动点,过点B作y轴的平行线分别交直线y=﹣x+1、直线y=﹣2x于C、D两点,若,则m的值为 .
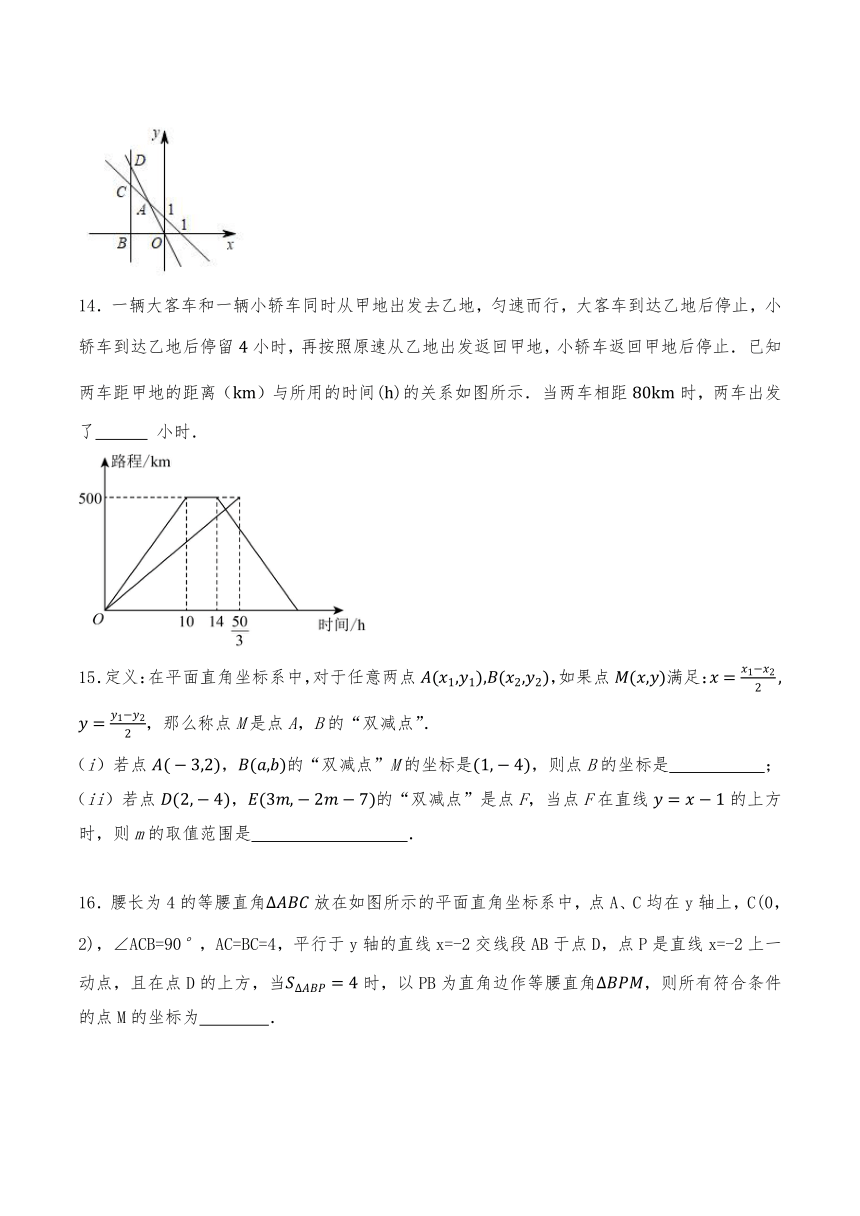
14.一辆大客车和一辆小轿车同时从甲地出发去乙地,匀速而行,大客车到达乙地后停止,小轿车到达乙地后停留小时,再按照原速从乙地出发返回甲地,小轿车返回甲地后停止已知两车距甲地的距离()与所用的时间()的关系如图所示当两车相距时,两车出发了 小时.
15.定义:在平面直角坐标系中,对于任意两点,如果点满足: ,那么称点M是点A,B的“双减点”.
(i)若点,的“双减点”M的坐标是,则点B的坐标是 ;
(ii)若点,的“双减点”是点F,当点F在直线的上方时,则m的取值范围是 .
16.腰长为4的等腰直角放在如图所示的平面直角坐标系中,点A、C均在y轴上,C(0,2),∠ACB=90,AC=BC=4,平行于y轴的直线x=-2交线段AB于点D,点P是直线x=-2上一动点,且在点D的上方,当时,以PB为直角边作等腰直角,则所有符合条件的点M的坐标为 .
三.解答题(共7小题,满分52分)
17.(6分)2023年6月日,由深圳市文化广电旅游体育局和大鹏新区管委会主办的粤港澳大湾区(深圳南澳)海上龙舟赛在深圳大鹏南澳月亮湾举行,参赛队伍有29支.若甲、乙两个龙舟队分别同时从起点出发,划行的路程(米)与划行的时间(分)(其中)之间满足的关系如图所示,根据图象所提供的信息,解答下列问题:
(1)甲队划行的速度为 ;当时,乙队划行的速度为 ;当时,乙队划行的速度为 ;
(2)当 分钟时,甲、乙两队划行的路程相等;
(3)当 分钟时,甲、乙两队划行的路程相差100米.
18.(6分)如图,已知一次函数的图象经过两点,并且交轴于点,交轴于点.
(1)求一次函数的解析式;
(2)求的面积;
(3)点在轴上,当的面积为6时,请求出点的坐标(要求写过程).
19.(8分)某商场准备购进甲乙两种服装进行销售.甲种服装每件进价160元,售价210元;乙种服装每件进价120元,售价150元.现计划购进两种服装共100件,其中甲种服装不少于60件.设购进甲种服装件,两种服装全部售完,商场获利元.
(1)求与之间的函数关系式;
(2)若购进100件服装的总费用不超过15000元,求最大利润为多少元
(3)在(2)的条件下,该服装店对甲种服装以每件优惠元的价格进行优惠促销活动,乙种服装每件进价减少元,售价不变,且,若最大利润为4000元,求的值.
20.(8分)如图,在平面直角坐标系中,一次函数的图象(是常数且)分别与轴和轴交于点和点,一次函数的图象(是常数且)分别与轴和轴交于点和点,直线与交于点.
(1)求和的值;
(2)不等式的解集为________;方程组的解为________;
(3)若点是直线上一点,且,求点的坐标.
21.(8分)从甲地到乙地,先是一段上坡路,然后是一段平路,小冲骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小冲骑车在上坡、平路、下坡时分别保持匀速前进,已知小冲骑车上坡的速度比平路上的速度每小时少,下坡的速度比在平路上的速度每小时多,设小冲出发x h后,到达离乙地的地方,图中的折线ABCDEF表示y与x之间的函数关系.
(1)求小冲在平路上骑车的平均速度以及他在乙地的休息时间;
(2)分别求线段所对应的函数关系式;
(3)从甲地到乙地经过丙地,如果小冲两次经过丙地的时间间隔为,求丙地与甲地之间的路程.
22.(8分)在一次函数的学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数性质及其应用的部分过程,请按要求完成下列各小题.
(1)如表是与的对应值:
0 1 2 3 4
y 3 1 1
①______;
②若点、都在该函数图象上,则______;
(2)在给出的平面直角坐标系中,画出函数图象,并写出这个函数的两条性质:
①__________________
②__________________
(3)已知函数的图象如图所示,结合你所画的函数图象,直接写出时的取值范围______.
23.(8分)在平面直角坐标系中,已知点,对于点给出如下定义:将点P向右()或向左()平移个单位长度,再向上()或向下()平移个单位长度,得到点,点与点M的中点为Q,称点Q为点P的关于点M的“平移中点”.【已知,,则AB中点坐标为】
(1)①若,,则中点坐标为______;
②若,,则点Q的坐标为______
(2)已知,点P在直线l:上.当点Q在第一象限时,点P横坐标t取值范围是______
(3)已知正方形ABCD的边长为2,各边与x轴平行或者垂直,其中心为,点为正方形上的动点
①当时,在点P运动过程中,点Q形成的图形的面积是______
②当点在直线:上,在点P运动过程中,若存在点Q在正方形的边上或者内部,则a的取值范围是______.
参考答案
选择题
1.A
【分析】国旗距离地面高与升旗时间关系应该是直线上升,最后一段时间国旗不再上升,时间仍然增加,得出符合要求的图象即可.
【详解】解:国旗距离地面高与升旗时间关系应该是直线上升,最后一段时间国旗不再上升,
只有A符合要求,
故选:A.
2.D
【分析】本题考查正比例函数图象与性质、平面直角坐标系中点的坐标特征,先根据坐标特征分析点所在象限,从而确定正比例函数的图象所过的象限,再由两点不在同一个象限即可得到答案,熟练掌握一次函数图象与性质及平面直角坐标系中点的坐标特征是解决问题的关键.
【详解】解:∵点的横坐标为,
∴此点在二、三象限;
∵点的纵坐标为,
∴此点在一、二象限,
∴此函数的图象一定经过一、三象限,
∴点在第三象限,点在第一象限,
∴,
故选:D.
3.B
【分析】本题考查了一次函数的图象,根据的值分别判断出一次函数与正比例函数的图象分布位置,两者一致即为正确答案,掌握一次函数的性质是解题的关键.
【详解】解:当时,一次函数的图象经过第二、三、四象限,正比例函数的图象经过第一、三象限,选项中没有符合条件的图象;
当时,一次函数的图象经过第一、二、三象限,正比例函数的图象经过第二、四象限,选项的图象符合要求;
故选:.
4.C
【分析】本题考查了一次函数与二元一次方程的关系.熟练掌握一次函数与二元一次方程的关系是解题的关键.
联立,可求,进而可求两条直线的交点坐标.
【详解】解:联立,
解得,,
∴一次函数与的图象在直角坐标系内的交点坐标为,
故选:C.
5.B
【分析】根据一次函数图象的性质,即中k与b的性质先求出m的值,再根据函数图象的增减性即可求出x的取值范围.
【详解】∵一次函数图象与轴正半轴相交
∴
∴
∵随的增大而减小
∴
∴
∴
∵为整数
∴
∴一次函数解析式为
∴当时,的取值范围是,
故选:B.
6.A
【分析】根据直线向左平移个单位,变为,再向上平移个单位,变为,然后结合得到直线,即可解出和的值.
【详解】解:直线向左平移个单位,变为,
再向上平移个单位,变为,
得到直线,
,,
,,
故选:.
7.D
【分析】本题考查了一次函数的图象和性质,根据直线l经过第一、二、三象限且过点,得出y随x的增大而增大,则,再根据点在直线l上,得出,即可解答.
【详解】解:∵直线l经过第一、二、三象限且过点,
∴y随x的增大而增大.
∵,
∴,
∴A、B、C均错;
∵点在直线l上,
∴.
故选D.
8.A
【分析】本题考查一次函数的图象及性质,熟练掌握一次函数的图象及性质,根据题意得到,再结合一次函数的增减性,分,以及两种情况讨论的取值并判断,即可解题.
【详解】解:一次函数()的图象经过点,,
,解得,
若,即时,则随的增大而增大,
,
,
故若,则 ;
若,即时,则随的增大而减小,
,
,
若,则有可能大于0,也可能小于0;
综上所述,若,则 ;
故选:A.
9.D
【分析】根据点、的坐标求出所在直线解析式,进而得出两直线平行,即可得出是定值,是定值,到直线的距离是定值,进而得出答案.
【详解】解:连接,
点、的坐标分别为、,
设所在直线解析式为:,
,
解得:,
所在直线解析式为:,
将直线:向上平移1个单位即可得直线,
两直线平行,
点是第一象限内直线上的一个动点,
到直线的距离是定值,
是定值,是定值,到直线的距离是定值,
∴是定值,
∴是定值,
当点的横坐标逐渐增大时,四边形的面积不变.
故选:D.
10.D
【分析】依次求出S1、S2、S3,就发现规律:Sn=×,然后求其和即可求得答案.注意.
【详解】解:∵当n=1时,直线为y=x+,
∴直线与两坐标轴的交点为(0,),(-1,0),
∴S1=×1×=;
当n=2时,直线为y=x+,
∴直线与两坐标轴的交点为(0,),(-,0),
∴S2=××=×;
当n=3时,直线为y=x+,
∴直线与两坐标轴的交点为(0,),(-,0),
∴S3=××=×;
…,
Sn=×,
∴S1+S2+S3+…+S2019=×(1-+++…+-)=(1-)=
故选:D.
二.填空题
11.或
【分析】本题考查了一次函数与坐标轴的交点问题,根据平方的定义解方程.
先求出该直线与x轴和y轴的交点坐标,再根据该直线与坐标轴围成的三角形的面积为4,列出方程,根据平方根的定义求解即可.
【详解】解:把代入得:,
∴该直线与y轴交点坐标为,
把代入得:,
解得:,
∴该直线与x轴交点坐标为,
∵该直线与坐标轴围成的三角形的面积为4,
∴,
即,
解得:,
∴此直线的解析式为或.
故答案为:或.
12.
【分析】结合图像,确定与x轴交点的坐标的横坐标,就是方程的解.
【详解】∵一次函数(是常数,且)的图像与x轴交点的坐标的横坐标为,
∴的解为.
故答案为:.
13.或
【分析】分别求出A、C、D三点坐标,根据,利用坐标列式计算即可.
【详解】∵由直线y=﹣x+1与直线y=﹣2x交于点A,
∴点A坐标(-1,2),
∵过点B(m,0)作y轴的平行线分别交直线y=﹣x+1、直线y=﹣2x于C、D两点,
∴点C坐标(m,1-m),点D坐标(m,-2m).
∴,
解得
故答案为或.
14.4或或
【分析】本题考查一次函数的应用,根据图象解决某个问题.要分三种情况讨论:当时,当时,当时.根据数量关系即可求解,该题解答过程比较复杂,利用分类讨论思想解决问题是解题的关键.
【详解】解:由图象可知:
小轿车的速度为:,
大客车的速度为:.
设两车出发后两车相距.
当时,,解得;
当时,,解得;
当时,,解得.
当两车相距时,两车出发了小时或小时或小时.
故答案为:或或.
15.
【分析】(1)根据点是点、的“双减点”的定义可求点坐标;
(2)点,的“双减点”是点,可表示出点的坐标,根据点在直线下方可得出关于的不等式,解不等式即可.
【详解】解:(1)点, “双减点” M的坐标是,
,,
,,
点M坐标,
故答案为:;
(2)点,的“双减点”是点,
,,即,,
点在直线上方,
,
解得,
故答案为:.
16.或或或
【分析】根据等腰直角三角形存在性问题的求解方法,通过分类讨论,借助全等的辅助,即可得解.
【详解】∵,AC=BC=4,平行于y轴的直线交线段AB于点D,
∴
∵
∴
∴PD=2
∴
以PB为直角边作等腰直角
如下图,作⊥于R
∵
,
∴
∴,RP=BS=2
∴;
以PB为直角边作等腰直角
同理可得;
以PB为直角边作等腰直角
同理可得;
以PB为直角边作等腰直角
同理可得,
∴M的坐标为或或或,
故答案为:或或或.
三.解答题
17.(1)由图象可知,甲队划行的速度为:(米分);
当时,乙队划行的速度为:(米分);
当时,乙队划行的速度为:(米分);
(2)设时间为时,甲、乙两队划行的路程相等,
由图象可知,在2分钟后,即划行600米后,甲、乙两队的图象相交,此时对应路程相等,
,
解得,
即分钟时,甲、乙两队划行的路程相等;
(3)根据甲、乙的函数图象可知,
1)当,乙比甲快,在时,两者划行的路程相差最大为,
在存在一个时刻,两者划行的路程相差100米,设时间为,
则,
解得,符合题意;
2)当,由于在时,两者划行的路程相差为200米,甲、乙相遇后,甲超过乙,并在时,两者划行的路程相差为,
在存在两个时刻,两者划行的路程相差100米,设时间为,
则或
解得或,符合题意;
综上所述,即当,3或5分钟时,甲、乙两队划行的路程相差100米.
18.(1)解:把代入得:
,
解得:,
∴一次函数的解析式为;
(2)解:把代入得:,
∴,则,
∴的面积;
(3)解:设,
把代入得:,
解得:,
∴,
∵的面积为6,
∴,即,
解得:,
当点P在点C左边时:,
当点P在点C右边时:,
∴或.
19.(1)解:
(2)解:由题意得:,
∴,
∵中,,
∴随的增大而增大,
∴当时,(元).
(3)解:∵,
∴,
由题意得:
.
∵,
∴当时,,
∴y随x的增大而增大,
∴当时,,
∴,符合题意.
当时,, 不合题意.
当时,, y随x的增大而减小.
∴当时,, ∴,不合题意,舍去.
综上,.
20.(1)解:将点分别代入一次函数和得:,
解得:;
(2)解:两函数的交点坐标为点,
结合图象可得:不等式的解集为;方程组的解为,
故答案为:,;
(3)解:由(1)可得:直线的表达式为,直线的表达式为,
在中,令,则,解得,
,
在中,令,则,解得,
,
,
,
点是直线上一点,
设,
,
,
,
解得:或,
点的坐标为或.
21.解:(1)小冲骑车上坡的速度为:km/h,
平路上的速度为:km/h;
下坡的速度为:km/h,
平路上所用的时间为:h,
下坡所用的时间为:h,
所以小冲在乙地休息了:h;
(2)由题意可知:上坡的速度为km/h,下坡的速度为km/h,
所以线段所对应的函数关系式为:,
即.
线段所对应的函数关系式为.
即;
(3)由题意可知:小冲第一次经过丙地在段,第二次经过丙地在段,
设小冲出发小时第一次经过丙地,则小冲出发后小时第二次经过丙地,
,
解得:.
(千米).
答:丙地与甲地之间的距离为1千米.
22.(1)解:①将代入函数得,
,
,
故答案为:3;
②由表格中数据可知:若,为该函数图象上不同的两点,则;
故答案为:2;
(2)解:画出函数图象如图,
观察图象可知:当时,随的增大而增大;当时,随的增大而减小;
故答案为:当时,随的增大而增大;当时,随的增大而减小;
(3)解:观察图象可知:时的取值范围为或
故答案为:或
23.(1)解:解: ,
中点坐标公式为,即
故答案为:
解: 向右平移2个单位长度,再向上平移1个单位长度得到
与的中点坐标为,即
故答案为:
(2)解:∵点在直线:上,,
∴,
∴,
∵点在第一象限,
∴,
∴
(3)解::当时,
点在正方形上
点的运动形成的图形也是正方形
正方形的边长为2
点形成的正方形边长为1
点形成的图形的面积是1
故答案为:1
解:点在直线:上
点
正方形的中心是,边长为2
∴,,
当时,,
∴,
∴时,存在点在正方形的边上或者内部;
当时,,
∴,
∴时,存在点在正方形的边上或者内部;
综上所述:时,存在点在正方形的边上或者内部.
一.选择题(共10小题,满分30分,每小题3分)
1.星期一学校举行升国旗仪式,开始国旗与小旗手的肩同高,下列图象能反映国旗距离地面高与升旗时间关系的是( )
A. B. C. D.
2.如果一个正比例函数的图象经过不同象限的两点,那么一定有( )
A. B. C. D.
3.在同一平面直角坐标系中,函数与的图象大致是( )
A. B. C. D.
4.已知二元一次方程与有一组公共解,那么一次函数与的图象在直角坐标系内的交点坐标为( )
A. B. C. D.
5.已知一次函数(为整数)的图象与轴正半轴相交,随的增大而减小,当时,的取值范围是( ).
A. B. C. D.
6.将直线向左平移个单位,再向上平移个单位,得到直线,则( )
A., B., C., D.,
7.平面直角坐标系中,过点的直线l经过一、二、三象限,若点,,都在直线l上,则下列判断正确的是( )
A. B. C. D.
8.若一次函数()的图象经过点,,则下列结论正确的是( )
A.若,则 B.若 ,则
C.若,则 D.若,则
9.如图,点、的坐标分别为、,点是第一象限内直线上一个动点,当点的横坐标逐渐增大时,四边形的面积( )
A.逐渐增大 B.逐渐减少 C.先减少后增大 D.不变
10. 已知:直线y=x+(n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2019( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.已知直线与坐标轴围成的三角形的面积为4,则此直线的解析式为 .
12.一次函数(是常数,且)的图像如图所示,则方程的解为 .
13.在平面直角坐标系xOy中,直线y=﹣x+1与直线y=﹣2x交于点A,点B(m,0)是x轴上的一个动点,过点B作y轴的平行线分别交直线y=﹣x+1、直线y=﹣2x于C、D两点,若,则m的值为 .
14.一辆大客车和一辆小轿车同时从甲地出发去乙地,匀速而行,大客车到达乙地后停止,小轿车到达乙地后停留小时,再按照原速从乙地出发返回甲地,小轿车返回甲地后停止已知两车距甲地的距离()与所用的时间()的关系如图所示当两车相距时,两车出发了 小时.
15.定义:在平面直角坐标系中,对于任意两点,如果点满足: ,那么称点M是点A,B的“双减点”.
(i)若点,的“双减点”M的坐标是,则点B的坐标是 ;
(ii)若点,的“双减点”是点F,当点F在直线的上方时,则m的取值范围是 .
16.腰长为4的等腰直角放在如图所示的平面直角坐标系中,点A、C均在y轴上,C(0,2),∠ACB=90,AC=BC=4,平行于y轴的直线x=-2交线段AB于点D,点P是直线x=-2上一动点,且在点D的上方,当时,以PB为直角边作等腰直角,则所有符合条件的点M的坐标为 .
三.解答题(共7小题,满分52分)
17.(6分)2023年6月日,由深圳市文化广电旅游体育局和大鹏新区管委会主办的粤港澳大湾区(深圳南澳)海上龙舟赛在深圳大鹏南澳月亮湾举行,参赛队伍有29支.若甲、乙两个龙舟队分别同时从起点出发,划行的路程(米)与划行的时间(分)(其中)之间满足的关系如图所示,根据图象所提供的信息,解答下列问题:
(1)甲队划行的速度为 ;当时,乙队划行的速度为 ;当时,乙队划行的速度为 ;
(2)当 分钟时,甲、乙两队划行的路程相等;
(3)当 分钟时,甲、乙两队划行的路程相差100米.
18.(6分)如图,已知一次函数的图象经过两点,并且交轴于点,交轴于点.
(1)求一次函数的解析式;
(2)求的面积;
(3)点在轴上,当的面积为6时,请求出点的坐标(要求写过程).
19.(8分)某商场准备购进甲乙两种服装进行销售.甲种服装每件进价160元,售价210元;乙种服装每件进价120元,售价150元.现计划购进两种服装共100件,其中甲种服装不少于60件.设购进甲种服装件,两种服装全部售完,商场获利元.
(1)求与之间的函数关系式;
(2)若购进100件服装的总费用不超过15000元,求最大利润为多少元
(3)在(2)的条件下,该服装店对甲种服装以每件优惠元的价格进行优惠促销活动,乙种服装每件进价减少元,售价不变,且,若最大利润为4000元,求的值.
20.(8分)如图,在平面直角坐标系中,一次函数的图象(是常数且)分别与轴和轴交于点和点,一次函数的图象(是常数且)分别与轴和轴交于点和点,直线与交于点.
(1)求和的值;
(2)不等式的解集为________;方程组的解为________;
(3)若点是直线上一点,且,求点的坐标.
21.(8分)从甲地到乙地,先是一段上坡路,然后是一段平路,小冲骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小冲骑车在上坡、平路、下坡时分别保持匀速前进,已知小冲骑车上坡的速度比平路上的速度每小时少,下坡的速度比在平路上的速度每小时多,设小冲出发x h后,到达离乙地的地方,图中的折线ABCDEF表示y与x之间的函数关系.
(1)求小冲在平路上骑车的平均速度以及他在乙地的休息时间;
(2)分别求线段所对应的函数关系式;
(3)从甲地到乙地经过丙地,如果小冲两次经过丙地的时间间隔为,求丙地与甲地之间的路程.
22.(8分)在一次函数的学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数性质及其应用的部分过程,请按要求完成下列各小题.
(1)如表是与的对应值:
0 1 2 3 4
y 3 1 1
①______;
②若点、都在该函数图象上,则______;
(2)在给出的平面直角坐标系中,画出函数图象,并写出这个函数的两条性质:
①__________________
②__________________
(3)已知函数的图象如图所示,结合你所画的函数图象,直接写出时的取值范围______.
23.(8分)在平面直角坐标系中,已知点,对于点给出如下定义:将点P向右()或向左()平移个单位长度,再向上()或向下()平移个单位长度,得到点,点与点M的中点为Q,称点Q为点P的关于点M的“平移中点”.【已知,,则AB中点坐标为】
(1)①若,,则中点坐标为______;
②若,,则点Q的坐标为______
(2)已知,点P在直线l:上.当点Q在第一象限时,点P横坐标t取值范围是______
(3)已知正方形ABCD的边长为2,各边与x轴平行或者垂直,其中心为,点为正方形上的动点
①当时,在点P运动过程中,点Q形成的图形的面积是______
②当点在直线:上,在点P运动过程中,若存在点Q在正方形的边上或者内部,则a的取值范围是______.
参考答案
选择题
1.A
【分析】国旗距离地面高与升旗时间关系应该是直线上升,最后一段时间国旗不再上升,时间仍然增加,得出符合要求的图象即可.
【详解】解:国旗距离地面高与升旗时间关系应该是直线上升,最后一段时间国旗不再上升,
只有A符合要求,
故选:A.
2.D
【分析】本题考查正比例函数图象与性质、平面直角坐标系中点的坐标特征,先根据坐标特征分析点所在象限,从而确定正比例函数的图象所过的象限,再由两点不在同一个象限即可得到答案,熟练掌握一次函数图象与性质及平面直角坐标系中点的坐标特征是解决问题的关键.
【详解】解:∵点的横坐标为,
∴此点在二、三象限;
∵点的纵坐标为,
∴此点在一、二象限,
∴此函数的图象一定经过一、三象限,
∴点在第三象限,点在第一象限,
∴,
故选:D.
3.B
【分析】本题考查了一次函数的图象,根据的值分别判断出一次函数与正比例函数的图象分布位置,两者一致即为正确答案,掌握一次函数的性质是解题的关键.
【详解】解:当时,一次函数的图象经过第二、三、四象限,正比例函数的图象经过第一、三象限,选项中没有符合条件的图象;
当时,一次函数的图象经过第一、二、三象限,正比例函数的图象经过第二、四象限,选项的图象符合要求;
故选:.
4.C
【分析】本题考查了一次函数与二元一次方程的关系.熟练掌握一次函数与二元一次方程的关系是解题的关键.
联立,可求,进而可求两条直线的交点坐标.
【详解】解:联立,
解得,,
∴一次函数与的图象在直角坐标系内的交点坐标为,
故选:C.
5.B
【分析】根据一次函数图象的性质,即中k与b的性质先求出m的值,再根据函数图象的增减性即可求出x的取值范围.
【详解】∵一次函数图象与轴正半轴相交
∴
∴
∵随的增大而减小
∴
∴
∴
∵为整数
∴
∴一次函数解析式为
∴当时,的取值范围是,
故选:B.
6.A
【分析】根据直线向左平移个单位,变为,再向上平移个单位,变为,然后结合得到直线,即可解出和的值.
【详解】解:直线向左平移个单位,变为,
再向上平移个单位,变为,
得到直线,
,,
,,
故选:.
7.D
【分析】本题考查了一次函数的图象和性质,根据直线l经过第一、二、三象限且过点,得出y随x的增大而增大,则,再根据点在直线l上,得出,即可解答.
【详解】解:∵直线l经过第一、二、三象限且过点,
∴y随x的增大而增大.
∵,
∴,
∴A、B、C均错;
∵点在直线l上,
∴.
故选D.
8.A
【分析】本题考查一次函数的图象及性质,熟练掌握一次函数的图象及性质,根据题意得到,再结合一次函数的增减性,分,以及两种情况讨论的取值并判断,即可解题.
【详解】解:一次函数()的图象经过点,,
,解得,
若,即时,则随的增大而增大,
,
,
故若,则 ;
若,即时,则随的增大而减小,
,
,
若,则有可能大于0,也可能小于0;
综上所述,若,则 ;
故选:A.
9.D
【分析】根据点、的坐标求出所在直线解析式,进而得出两直线平行,即可得出是定值,是定值,到直线的距离是定值,进而得出答案.
【详解】解:连接,
点、的坐标分别为、,
设所在直线解析式为:,
,
解得:,
所在直线解析式为:,
将直线:向上平移1个单位即可得直线,
两直线平行,
点是第一象限内直线上的一个动点,
到直线的距离是定值,
是定值,是定值,到直线的距离是定值,
∴是定值,
∴是定值,
当点的横坐标逐渐增大时,四边形的面积不变.
故选:D.
10.D
【分析】依次求出S1、S2、S3,就发现规律:Sn=×,然后求其和即可求得答案.注意.
【详解】解:∵当n=1时,直线为y=x+,
∴直线与两坐标轴的交点为(0,),(-1,0),
∴S1=×1×=;
当n=2时,直线为y=x+,
∴直线与两坐标轴的交点为(0,),(-,0),
∴S2=××=×;
当n=3时,直线为y=x+,
∴直线与两坐标轴的交点为(0,),(-,0),
∴S3=××=×;
…,
Sn=×,
∴S1+S2+S3+…+S2019=×(1-+++…+-)=(1-)=
故选:D.
二.填空题
11.或
【分析】本题考查了一次函数与坐标轴的交点问题,根据平方的定义解方程.
先求出该直线与x轴和y轴的交点坐标,再根据该直线与坐标轴围成的三角形的面积为4,列出方程,根据平方根的定义求解即可.
【详解】解:把代入得:,
∴该直线与y轴交点坐标为,
把代入得:,
解得:,
∴该直线与x轴交点坐标为,
∵该直线与坐标轴围成的三角形的面积为4,
∴,
即,
解得:,
∴此直线的解析式为或.
故答案为:或.
12.
【分析】结合图像,确定与x轴交点的坐标的横坐标,就是方程的解.
【详解】∵一次函数(是常数,且)的图像与x轴交点的坐标的横坐标为,
∴的解为.
故答案为:.
13.或
【分析】分别求出A、C、D三点坐标,根据,利用坐标列式计算即可.
【详解】∵由直线y=﹣x+1与直线y=﹣2x交于点A,
∴点A坐标(-1,2),
∵过点B(m,0)作y轴的平行线分别交直线y=﹣x+1、直线y=﹣2x于C、D两点,
∴点C坐标(m,1-m),点D坐标(m,-2m).
∴,
解得
故答案为或.
14.4或或
【分析】本题考查一次函数的应用,根据图象解决某个问题.要分三种情况讨论:当时,当时,当时.根据数量关系即可求解,该题解答过程比较复杂,利用分类讨论思想解决问题是解题的关键.
【详解】解:由图象可知:
小轿车的速度为:,
大客车的速度为:.
设两车出发后两车相距.
当时,,解得;
当时,,解得;
当时,,解得.
当两车相距时,两车出发了小时或小时或小时.
故答案为:或或.
15.
【分析】(1)根据点是点、的“双减点”的定义可求点坐标;
(2)点,的“双减点”是点,可表示出点的坐标,根据点在直线下方可得出关于的不等式,解不等式即可.
【详解】解:(1)点, “双减点” M的坐标是,
,,
,,
点M坐标,
故答案为:;
(2)点,的“双减点”是点,
,,即,,
点在直线上方,
,
解得,
故答案为:.
16.或或或
【分析】根据等腰直角三角形存在性问题的求解方法,通过分类讨论,借助全等的辅助,即可得解.
【详解】∵,AC=BC=4,平行于y轴的直线交线段AB于点D,
∴
∵
∴
∴PD=2
∴
以PB为直角边作等腰直角
如下图,作⊥于R
∵
,
∴
∴,RP=BS=2
∴;
以PB为直角边作等腰直角
同理可得;
以PB为直角边作等腰直角
同理可得;
以PB为直角边作等腰直角
同理可得,
∴M的坐标为或或或,
故答案为:或或或.
三.解答题
17.(1)由图象可知,甲队划行的速度为:(米分);
当时,乙队划行的速度为:(米分);
当时,乙队划行的速度为:(米分);
(2)设时间为时,甲、乙两队划行的路程相等,
由图象可知,在2分钟后,即划行600米后,甲、乙两队的图象相交,此时对应路程相等,
,
解得,
即分钟时,甲、乙两队划行的路程相等;
(3)根据甲、乙的函数图象可知,
1)当,乙比甲快,在时,两者划行的路程相差最大为,
在存在一个时刻,两者划行的路程相差100米,设时间为,
则,
解得,符合题意;
2)当,由于在时,两者划行的路程相差为200米,甲、乙相遇后,甲超过乙,并在时,两者划行的路程相差为,
在存在两个时刻,两者划行的路程相差100米,设时间为,
则或
解得或,符合题意;
综上所述,即当,3或5分钟时,甲、乙两队划行的路程相差100米.
18.(1)解:把代入得:
,
解得:,
∴一次函数的解析式为;
(2)解:把代入得:,
∴,则,
∴的面积;
(3)解:设,
把代入得:,
解得:,
∴,
∵的面积为6,
∴,即,
解得:,
当点P在点C左边时:,
当点P在点C右边时:,
∴或.
19.(1)解:
(2)解:由题意得:,
∴,
∵中,,
∴随的增大而增大,
∴当时,(元).
(3)解:∵,
∴,
由题意得:
.
∵,
∴当时,,
∴y随x的增大而增大,
∴当时,,
∴,符合题意.
当时,, 不合题意.
当时,, y随x的增大而减小.
∴当时,, ∴,不合题意,舍去.
综上,.
20.(1)解:将点分别代入一次函数和得:,
解得:;
(2)解:两函数的交点坐标为点,
结合图象可得:不等式的解集为;方程组的解为,
故答案为:,;
(3)解:由(1)可得:直线的表达式为,直线的表达式为,
在中,令,则,解得,
,
在中,令,则,解得,
,
,
,
点是直线上一点,
设,
,
,
,
解得:或,
点的坐标为或.
21.解:(1)小冲骑车上坡的速度为:km/h,
平路上的速度为:km/h;
下坡的速度为:km/h,
平路上所用的时间为:h,
下坡所用的时间为:h,
所以小冲在乙地休息了:h;
(2)由题意可知:上坡的速度为km/h,下坡的速度为km/h,
所以线段所对应的函数关系式为:,
即.
线段所对应的函数关系式为.
即;
(3)由题意可知:小冲第一次经过丙地在段,第二次经过丙地在段,
设小冲出发小时第一次经过丙地,则小冲出发后小时第二次经过丙地,
,
解得:.
(千米).
答:丙地与甲地之间的距离为1千米.
22.(1)解:①将代入函数得,
,
,
故答案为:3;
②由表格中数据可知:若,为该函数图象上不同的两点,则;
故答案为:2;
(2)解:画出函数图象如图,
观察图象可知:当时,随的增大而增大;当时,随的增大而减小;
故答案为:当时,随的增大而增大;当时,随的增大而减小;
(3)解:观察图象可知:时的取值范围为或
故答案为:或
23.(1)解:解: ,
中点坐标公式为,即
故答案为:
解: 向右平移2个单位长度,再向上平移1个单位长度得到
与的中点坐标为,即
故答案为:
(2)解:∵点在直线:上,,
∴,
∴,
∵点在第一象限,
∴,
∴
(3)解::当时,
点在正方形上
点的运动形成的图形也是正方形
正方形的边长为2
点形成的正方形边长为1
点形成的图形的面积是1
故答案为:1
解:点在直线:上
点
正方形的中心是,边长为2
∴,,
当时,,
∴,
∴时,存在点在正方形的边上或者内部;
当时,,
∴,
∴时,存在点在正方形的边上或者内部;
综上所述:时,存在点在正方形的边上或者内部.
