【中考押题预测】2025年中考数学核心考点考前冲刺 一次函数综合题(一)(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 一次函数综合题(一)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
一次函数综合题(一)
一.选择题(共10小题)
1.如图,直线l1与x轴、y轴分别交于A(﹣2,0),B(0,6),直线l2经过点B且与x轴负半轴交于点C,∠ABC=45°.若线段BC上存在一点P,使△ABP是以A为直角顶点的等腰直角三角形,则P点坐标为( )
A.(8,2) B.(﹣6,2) C.(﹣8,2) D.(6,﹣2)
2.已知直线l1:y=kx+b与直线l2:yx+m都经过,直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA,PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法个数有( )
A.1个 B.2个 C.3个 D.4个
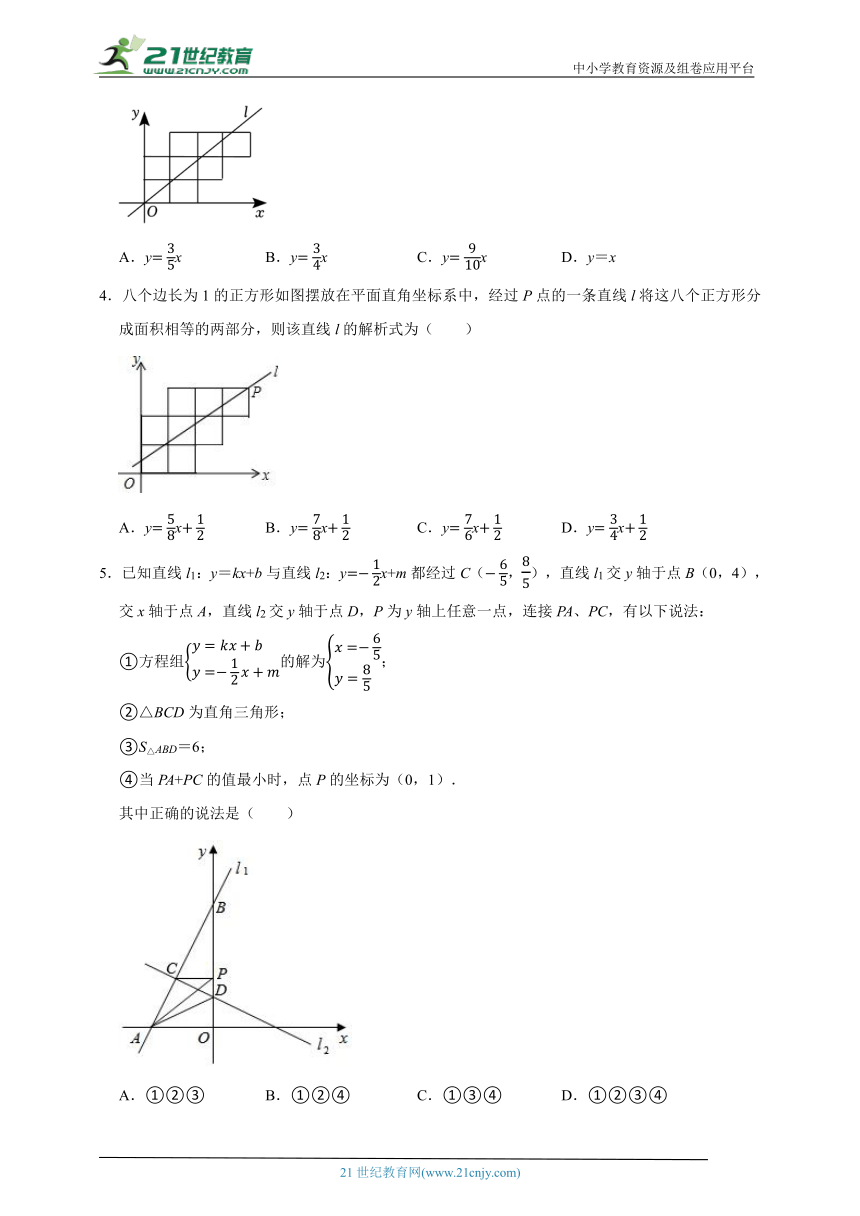
3.八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A.yx B.yx C.yx D.y=x
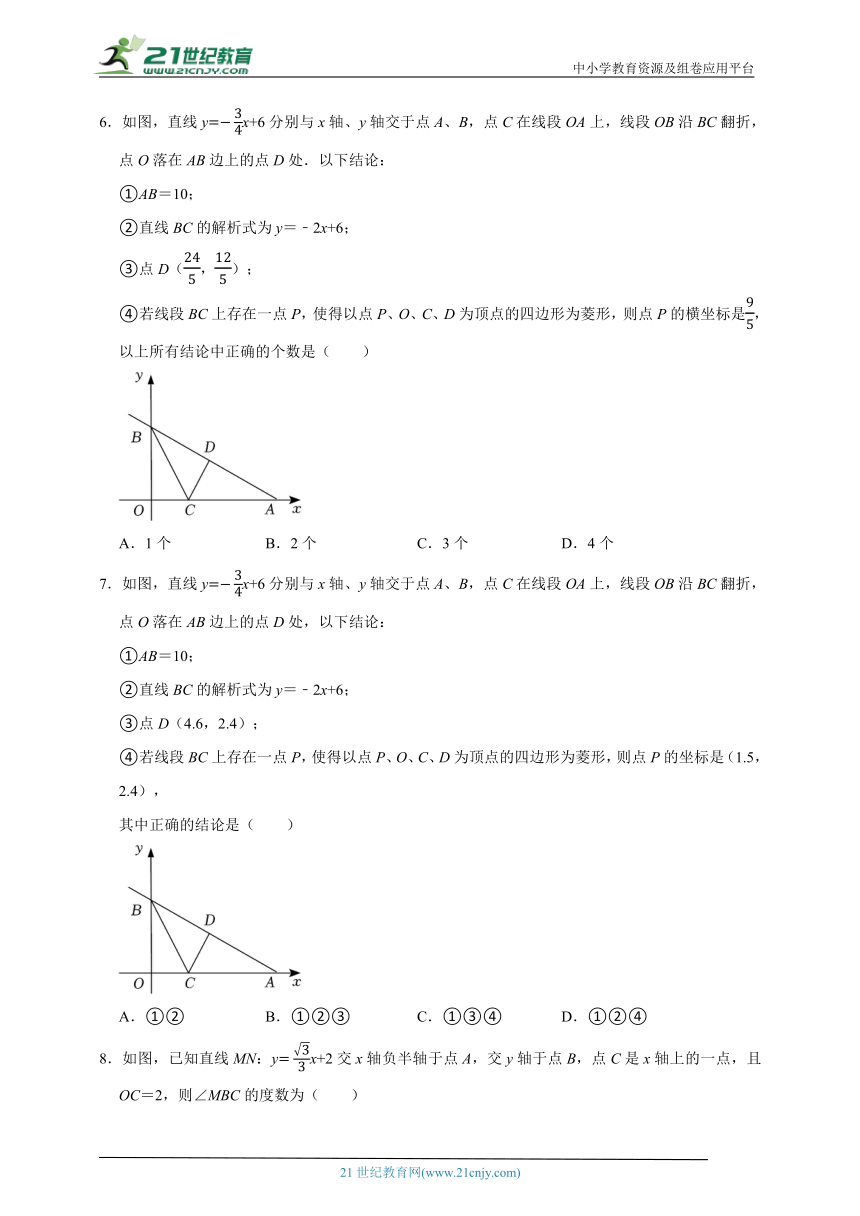
4.八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A.yx B.yx C.yx D.yx
5.已知直线l1:y=kx+b与直线l2:yx+m都经过C(,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
6.如图,直线yx+6分别与x轴、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处.以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(,);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的横坐标是,以上所有结论中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
7.如图,直线yx+6分别与x轴、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处,以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(4.6,2.4);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的坐标是(1.5,2.4),
其中正确的结论是( )
A.①② B.①②③ C.①③④ D.①②④
8.如图,已知直线MN:yx+2交x轴负半轴于点A,交y轴于点B,点C是x轴上的一点,且OC=2,则∠MBC的度数为( )
A.45°或135° B.30°或150° C.60°或120° D.75°或165°
9.如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线yx﹣3与x轴、y轴分别交于点D、E,则点C到直线DE的最小距离为( )
A.1 B. C. D.
10.如图,直线yx+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是( )
A.(4,2) B.(2,4)
C.(,3) D.(22,2)
二.填空题(共10小题)
11.在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足,,则称点T是点A,B的“和谐点”.如图,点D(3,0),点E是直线l:y=2x+3上任意一点,若点T是点D,E的“和谐点”,直线ET交x轴于点H,当∠TDH为直角时,则点H到直线l的距离为 .
12.如图,平面直角坐标系中,⊙P经过点A(8,0),O(0,0),B(0,6),点P关于x轴的对称点是P1,点D是⊙P上的一点.
(1)∠ADB= °;
(2)当点D到弦OB的距离最大时,直线DP1与x轴的交点坐标为 .
13.如图,在平面直角坐标系中,线段AB的端点为A(1,0),B(5,8).
(1)直线AB的函数解析式为 ;
(2)某同学设计了一个动画:在函数y=﹣2x+b中,输入b(b>0)的值,得到直线CD,其中点C在x轴上,点D在y轴上.
①当△OCD的面积为6时,直线CD就会发蓝光,则此时输入的b的值为 ;
②当直线CD与线段AB有交点时,直线CD就会发红光,则此时输入的b的取值范围是 .
14.如图,一次函数的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
(1)△AOB的面积是 ;
(2)点C的坐标是 ;
(3)过B,C两点直线的函数表达式为 .
15.如图,已知一次函数y=kx+2的图象与y轴,x轴分别交于点A、B.
(1)若点(1,1)在函数图象上,则k= ;
(2)若S△OAB=3,则点B的坐标为 ;
(3)一次函数y=kx+2的图象与正比例函数y=2x的图象交于点.点P在x轴上,当△PBC为直角三角形时,点P的坐标为 .
16.如图,在平面直角坐标系中,直线交x轴于点A、交y轴于点B,C点与A点关于y轴对称,动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.当△PQB为等腰三角形时,点P的坐标是 .
17.在平面直角坐标系中,一次函数y=x+4的图象分别与x轴,y轴交于点A,B,点P在一次函数y=x的图象上,则当△ABP为直角三角形时,点P的坐标是 .
18.在平面直角坐标系xOy中,对于P、Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P、Q两点为“友好点”.如图中的P,Q两点即为“友好点”.已知点A的坐标为(﹣3,1).
(1)请在x轴上提供一个点A的“友好点”,它的坐标为 ;
(2)在点R(0,4),S(2,2),T(2,﹣3)中,为点A的“友好点”的是 ;
(3)直线l:y=x﹣5,与x轴相交于点C,与y轴相交于点D,M为线段CD上一点,若第二象限存在点N,使得M,N两点为“友好点”,请你提供一个符合题意的点N,N的坐标为 .
19.如图,直线y=kx+2与x轴,y轴分别交于A,C两点,点B与点A关于y轴对称,连接BC,BC=2,点M,N分别是线段AB,AC上的动点(M不与A,B重合),且满足∠CMN=∠CBA.当△CMN为等腰三角形时,M的坐标为 .
20.如图,直线yx+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A做匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标 ;
(2)若△OQC是等腰直角三角形,则t的值为 .
三.解答题(共10小题)
21.如图1,已知直线l1:y=kx+b交x轴于A(6,0),交y轴于B(0,6).
(1)求直线l的表达式;
(2)如图2,直线CP的表达式为,点P为线段AB的中点,在直线CP上找一点Q,使得OQ+AQ最小,并求出最小值;
(3)如图3,已知点M(﹣2,0),点N(m,2m﹣6)为直线AB右侧一点,且满足∠OBM=∠ABN,求m的值.
22.在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且,直线l2:y=k2x+b经过点,1),与直线AB交于点D.
(1)求直线l1的解析式;
(2)如图2,连接CB、AC,求△ABC的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
23.在平面直角坐标系xOy中,对于点P,Q和图形W,若图形W上存在点K使得∠PQK=α(0°<α<180°),则称图形W与PQ“α关联”.
(1)已知P(0,0),Q(1,0),以下列各点为中心,作边长为1的正方形W,若W与PQ“45°关联”,则这个中心可能是 .
①(1,﹣1);②(2,0);③(0,1).
(2)如图,已知直线l.
①已知P,Q在直线y=﹣2上运动,且点P在点Q左侧.设直线l与x轴,y轴分别交于M,N两点,若线段MN与PQ“α关联”,其中60°<α<90°,求Q点横坐标t的取值范围;
②已知P(﹣1,0),Q(0,0).长度为1的线段ST在l上,以ST上任意一点为圆心作半径为r的圆,对每一个圆总存在α使之与PQ既是“α关联”又是“α+60°关联”但不是“α+90°关联”,直接写出r的取值范围.
24.如图1,一次函数y=k1x+b的图象与x轴交于点A,与y轴交于点B(0,4),与正比例函数y=k2x的图象交于点C(6,12).
(1)直接写出正比例函数与一次函数的表达式;
(2)如图2,点E是直线BC上的一动点(与B,C点不重合),过点E作EP⊥x轴于点P,交直线OC于点F,设点E的横坐标为a,用含a的式子表示EF的长,并求出当EF=2OB时,a的值;
(3)如图3,在(2)的条件下,若E是线段BC上一动点(与B,C点不重合),连接CP,直线OC能否把△CEP分成面积之比为1:3的两部分?若能,请求出E点坐标;若不能,请说明理由.
25.如图①,直线y=2x+b与x轴交于点A(4,0),与y轴交于点B,与直线y=﹣2x交于点C(a,﹣4).
(1)求点C的坐标及直线AB的表达式;
(2)点P在y轴上,若△PBC的面积为6,求点P的坐标;
(3)如图②,过x轴正半轴上的动点D(m,0)作直线l⊥x轴,点Q在直线l上,若以BC为腰的△BCQ是等腰直角三角形,请直接写出相应m的值.
26.如图,在平面直角坐标系xOy中,直线l1:y的图象与x轴、y轴分别交于D,B两点.直线y=kx的图象与x轴交于C.直线l1与直线l2交于点A(a,3).
(1)求点A的坐标及直线l2的表达式;
(2)若点E在直线l2上,且△ADE的面积为,求点E的坐标;
(3)在x轴上是否存在点P,使得∠ACB=2∠APC,若存在,求出点P坐标,若不存在,说明理由.
27.如图,在平面直角坐标系中,一次函数y=k1x+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=k2x的图象交于点C(3,4).
(1)求正比例函数与一次函数的表达式;
(2)求△OBC的面积;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标;
(4)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标.
(5)在y轴上是否存在一点P,使△POC为等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
28.如图,将正比例函数y=﹣2x的图象向上平移2个单位长度后得到的一次函数图象与x轴、y轴分别交于A、B两点,P(m,n)是线段AB(不含端点)上一动点,设△AOP的面积是S.
(1)求点B的坐标;
(2)求S关于m的函数表达式,并写出自变量m的取值范围;
(3)当时,在x轴上是否存在一点Q,使得PQ+BQ的值最小?若存在,求出点Q的坐标;若不存在,请说明理由.
29.如图,在四边形ABCD中,AB∥CD,AB=2CD=6,AD=5,∠DCB=90°,连接BD.点P从点A出发,以每秒一个单位的速度沿折线A→B→D运动,到达D点停止.设点P的运动时间为x秒(0<x<11),△DAP的面积为y.
(1)请直接写出y与x的函数关系式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出y的函数图象,并写出关于函数y的一条性质 ;
(3)若该函数图象与直线y=x+k恰好有一个交点,则常数k的取值范围是 .
30.如图,在平面直角坐标系中,直线y=2x+4与x轴,y轴分别交于点A,C,经过点C的直线与x轴交于点B(4,0),点D是直线AC上一动点.
(1)求直线BC的解析式;
(2)当点D在直线AC上运动时,存在某时刻,使得△DBC为直角三角形且∠CBD=90°,请求出此时点D的坐标;
(3)如备用图所示,当点D运动到线段AC的中点时,此时,在直线BC上是否存在点P,使得∠DAP=45°,若存在,请求出P点坐标;若不存在,请说明理由.
一次函数综合题(一)
参考答案与试题解析
一.选择题(共10小题)
1.如图,直线l1与x轴、y轴分别交于A(﹣2,0),B(0,6),直线l2经过点B且与x轴负半轴交于点C,∠ABC=45°.若线段BC上存在一点P,使△ABP是以A为直角顶点的等腰直角三角形,则P点坐标为( )
A.(8,2) B.(﹣6,2) C.(﹣8,2) D.(6,﹣2)
【分析】过A作AP⊥AB交BC于P,过P作PM⊥AC,可得△ABO≌△PAM,有AM=BO,MP=AO,即可得出结论.
【解答】解:过A作AP⊥AB交BC于P,过P作PM⊥AC,如图:
∵A(﹣2,0),B(0,6),
∴BO=6,AO=2,
∵△ABP是以A为直角顶点的等腰直角三危形,
∴AP=AB,∠PAB=90°,
∴∠BAO=90°﹣∠PAM=∠MPA,
∵∠PMA=90°=∠BOA,
∴△ABO≌△PAM(AAS),
∴AM=BO=6,MP=AO=2,
∴OM=8,
∴P(﹣8,2).
故选:C.
【点评】本题考查一次函数综合应用,涉及旋转变换,全等三角形的判定与旋转,一次函数图象上点坐标的特征等,解题的关键是作辅助线,构造全等三角形解决问题.
2.已知直线l1:y=kx+b与直线l2:yx+m都经过,直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA,PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解即可判断①;根据一次函数的解析式求得交点坐标,求得BD和AO的长,根据三角形面积计算公式,即可得到△ABD的面积,即可判断③;根据勾股定理的逆定理即可判断②;根据轴对称的性质以及两点之间,线段最短,即可得到当PA+PC的值最小时,求得点P的坐标即可判断④,逐一判断即可得出答案.
【解答】解:∵直线l1:y=kx+b与直线都经过,
∴方程组的解为:,故①正确;
把代入直线,可得m=1,
∴,
令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
把B(0,4),代入直线l1:y=kx+b,可得,
解得:,
∴直线l1:y=2x+4,
令y=0,则x=﹣2,
∴A(﹣2,0),
∴OA=2,
∴,故③错误;
∵B(0,4),,D(0,1),
∴,,BD2=(1﹣4)2=9∴BC2+CD2=BD2,
∴△BCD为直角三角形,故②正确;
点A关于y轴对称点为A'(2,0),
设过点C,A'的直线为y=ax+n,则,
解得:,
∴,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),故④正确,
故选:C.
【点评】本题考查了一次函数图象与性质、勾股定理,三角形面积以及最短距离问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
3.八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A.yx B.yx C.yx D.y=x
【分析】设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
【解答】解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴OB AB=5,
∴AB,
∴OC,
由此可知直线l经过(,3),
设直线方程为y=kx,
则3k,
k,
∴直线l解析式为yx,
故选:C.
【点评】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关键是作AB⊥y轴,作AC⊥x轴,根据题意即得到:直角三角形ABO,利用三角形的面积公式求出AB的长.
4.八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A.yx B.yx C.yx D.yx
【分析】直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出点A的坐标,根据待定系数法即可得到该直线l的解析式.
【解答】解:直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过P点的一条直线l将这八个正方形分成面积相等的两部分,
∴三角形ABP面积是8÷2+1=5,
∴BP AB=5,
∴AB=2.5,
∴OA=3﹣2.5=0.5,
由此可知直线l经过(0,0.5),(4,3)
设直线方程为y=kx+b,则,
解得.
∴直线l解析式为yx.
故选:A.
【点评】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关键是作PB⊥y轴,作PC⊥x轴,根据题意即得到:直角三角形ABP面积是5,利用三角形的面积公式求出AB的长.
5.已知直线l1:y=kx+b与直线l2:yx+m都经过C(,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【分析】根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解;根据两直线的系数的积为﹣1,可知两直线互相垂直;求得BD和AO的长,根据三角形面积计算公式,即可得到△ABD的面积;根据轴对称的性质以及两点之间,线段最短,即可得到当PA+PC的值最小时,点P的坐标为(0,1).
【解答】解:①∵直线l1:y=kx+b与直线l2:yx+m都经过C(,),
∴方程组的解为,
故①正确,符合题意;
②把B(0,4),C(,)代入直线l1:y=kx+b,可得,解得,
∴直线l1:y=2x+4,
又∵直线l2:yx+m,
∴直线l1与直线l2互相垂直,即∠BCD=90°,
∴△BCD为直角三角形,
故②正确,符合题意;
③把C(,)代入直线l2:yx+m,可得m=1,
yx+1中,令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
在直线l1:y=2x+4中,令y=0,则x=﹣2,
∴A(﹣2,0),
∴AO=2,
∴S△ABD3×2=3,
故③错误,不符合题意;
④点A关于y轴对称的点为A'(2,0),
由点C、A′的坐标得,直线CA′的表达式为:yx+1,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),
故④正确,符合题意;
故选:B.
【点评】本题为一次函数综合题,主要考查了一次函数图象与性质,三角形面积以及最短距离问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
6.如图,直线yx+6分别与x轴、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处.以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(,);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的横坐标是,以上所有结论中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】先求出点A,点B坐标,由勾股定理可求AB的长,可判断①;由折叠的性质可得OB=BD=6,OC=CD,∠BOC=∠BDC=90°,由勾股定理可求OC的长,可得点C坐标,利用待定系数法可求BC解析式,可判断②;由面积公式可求DH的长,代入解析式可求点D坐标,可判断③;由菱形的性质可得PD∥OC,可得点P纵坐标为,可判断④,即可求解.
【解答】解:∵直线yx+6分别与x、y轴交于点A、B,
∴点A(8,0),点B(0,6),
∴OA=8,OB=6,
∴AB10,故①正确;
∵线段OB沿BC翻折,点O落在AB边上的点D处,
∴OB=BD=6,OC=CD,∠BOC=∠BDC=90°,
∴AD=AB﹣BD=4,
∵AC2=AD2+CD2,
∴(8﹣OC)2=16+OC2,
∴OC=3,
∴点C(3,0),
设直线BC解析式为:y=kx+6,
∴0=3k+6,
∴k=﹣2,
∴直线BC解析式为:y=﹣2x+6,故②正确;
如图,过点D作DH⊥AC于H,
∵CD=OC=3,
∴CA=5,
∵S△ACDAC×DHCD×AD,
∴DH,
∴当y时,x+6,
∴x,
∴点D(,),故③正确;
∵线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,且OC=CD,
∴PD∥OC,PD=OC=3,
∴点P纵坐标为,
∵点D(,),
∵点P(,),
∴点P横坐标为,故④正确,
故选:D.
【点评】本题是一次函数综合题,考查了利用待定系数法求解析式,折叠的性质,面积法,菱形的性质,勾股定理等知识,灵活运用这些性质解决问题是本题的关键.
7.如图,直线yx+6分别与x轴、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处,以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(4.6,2.4);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的坐标是(1.5,2.4),
其中正确的结论是( )
A.①② B.①②③ C.①③④ D.①②④
【分析】根据一次函数的性质和翻折的性质以及勾股定理,菱形的性质对每个结论进行分析后再作出选择.
【解答】解:令y=0,则0x+6,
∴x=8,
∴OA=8,
令x=0,得y=6,
∴OB=6,B(0,6),
在Rt△AOB中,AB,
故①正确;
∵线段OB沿BC翻折,点O落在AB边上的点D处,
∴BD=BO=6,∠ADC=90°,DC=OC,
∴AD=4,
设OC=DC=x,则AC=8﹣x,
在Rt△ACD中,AD2+CD2=AC2,
即42+x2=(8﹣x)2,
解得:x=3,
∴点C(3,0),
设直线BC的解析式为y=kx+b,
把点B(0,6)和C(3,0)分别代入y=kx+b,得:
,
解得:,
∴直线BC的解析式为y=﹣2x+6,
故②正确;
如图1,过D作DE⊥OA于E,
根据三角形面积可得:DE,
在Rt△CDE中,CE,
∴OE=3+1.8=4.8,
∴点D坐标为(4.8,2.4),
故③不正确;
如图2,
当以点P、O、C、D为顶点的四边形为菱形时,PD∥x轴,
∴点P的纵坐标与点D的纵坐标相等,
把y=2.4代入直线y=﹣2x+6中,得x=1.8,
∴点P(1.8,2.4),
故④不正确;
综上,正确的结论有①②,
故选:A.
【点评】本题是一次函数综合题,主要考查一次函数的性质,翻折的性质,勾股定理,菱形的性质等知识点,深入理解题意是解决问题的关键.
8.如图,已知直线MN:yx+2交x轴负半轴于点A,交y轴于点B,点C是x轴上的一点,且OC=2,则∠MBC的度数为( )
A.45°或135° B.30°或150° C.60°或120° D.75°或165°
【分析】令y=0,可得A(﹣2,0),令x=0,可得B(0,2),利用勾股定理求出AB=4,可得∠MAO=30°,分两种情况考虑:①C点在x轴正半轴;②C点在x轴负半轴.分别计算出∠MBO、∠OBC度数,两个角的和差即为所求度数.
【解答】解:∵直线MN:yx+2交x轴负半轴于点A,交y轴于点B,
令y=0,则0x+2,解得x=﹣2,
∴A(﹣2,0),
令x=0,则y=2,
∴B(0,2),
∴AB4,
∴AB=2OB,
∵∠AOB=90°,
∴∠MAO=30°,
∴∠ABO=60°,∠MBO=120°.
∵B(0,2),OC=2,
∴OB=OC,
∴∠CBO=45°,
如图,分两种情况考虑:
①当点C在x轴正半轴上时,
∠C1BO=45°,
∴∠MBC1=120°﹣45°=75°;
②当点C在x轴负半轴上时,
∠MBC2=120°+45°=165°.
故选:D.
【点评】本题是一次函数综合题,考查了一次函数图象上点的坐标特征、含30度角的直角三角形、等腰直角三角形的判定与性质以及坐标与图形性质.分类讨论思想的运用是解题的关键.
9.如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线yx﹣3与x轴、y轴分别交于点D、E,则点C到直线DE的最小距离为( )
A.1 B. C. D.
【分析】连接OC,由垂径定理得OC⊥AB,再由圆周角定理得点C在以OA为直径的圆上(点O、A除外),以OA为直径作⊙P,过P点作直线PH⊥DE于H,交⊙P于M、N,利用一次函数解析式确定E(0,﹣3),D(4,0),则DE=5,然后证△DPH∽△DEO,利用相似比求出PH的长,得MH、NH的长,即可求解.
【解答】解:连接OC,如图,
∵点C为弦AB的中点,
∴OC⊥AB,
∴∠ACO=90°,
∴点C在以OA为直径的圆上(点O、A除外),
以OA为直径作⊙P,过P点作直线PH⊥DE于H,交⊙P于M、N,
当x=0时,yx﹣3=﹣3,则E(0,﹣3),
当y=0时,x﹣3=0,
解得x=4,则D(4,0),
∴OD=4,
∴DE5,
∵⊙O的半径为2,
∴A(2,0),
∴P(1,0),
∴OP=1,
∴PD=OD﹣OP=3,
∵∠PDH=∠EDO,∠PHD=∠EOD=90°,
∴△DPH∽△DEO,
∴PH:OE=DP:DE,
即PH:3=3:5,
解得PH,
∴MH=PH+1,NH=PH﹣1.
∴点C到直线DE的最小距离为.
故选:C.
【点评】本题是一次函数综合题,考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理、相似三角形的判定与性质和一次函数的性质,解题的关键是正确寻找点C的运动轨迹,属于中考选择题中的压轴题.
10.如图,直线yx+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是( )
A.(4,2) B.(2,4)
C.(,3) D.(22,2)
【分析】求得直角△ABO的两条直角边的长,即可利用解直角三角形的方法求得AB,以及∠OAB的度数,则∠OAB′是直角,据此即可求解.
【解答】解:在yx+2中令x=0,解得:y=2;
令y=0,解得:x=2.
则OA=2,OB=2.
∴在直角△ABO中,AB4,∠BAO=30°,
又∵∠BAB′=60°,
∴∠OAB′=90°,
∴B′的坐标是(2,4).
故选:B.
【点评】本题考查了一次函数与解直角三角形,正确证明∠OAB′=90°是关键.
二.填空题(共10小题)
11.在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足,,则称点T是点A,B的“和谐点”.如图,点D(3,0),点E是直线l:y=2x+3上任意一点,若点T是点D,E的“和谐点”,直线ET交x轴于点H,当∠TDH为直角时,则点H到直线l的距离为 .
【分析】设点E的坐标为(x,2x+3),根据点T是点D,E的“和谐点”,表示出点T的坐标,进而根据∠TDH为直角可得点T和点D的横坐标相同得到x的值,即可求得点E和点T的坐标;求得直线ET的解析式,进而求得点H的坐标;作HM⊥l于点M,求得AE和AH的长度,根据△AEH的面积的不同表示方法求出点H到直线l的距离.
【解答】解:设点E的坐标为(x,2x+3),
∵点D(3,0),点T是点D,E的“和谐点”,
∴点T的坐标为(,).
∵∠TDH=90°,
∴点T的横坐标和点D的横坐标相同,
∴3.
解得:x=6.
∴点E的坐标为(6,15),点T的坐标为(3,5).
设直线ET的解析式为y=kx+n(k≠0).
∴,
解得:,
∴直线ET的解析式为yx﹣5.
当y=0时,x=1.5.
∴点H的坐标为(1.5,0).
∴OH.
作HM⊥l于点M.
由题意得:y=2x+3与x轴的交点A为(﹣1.5,0),
∴E点的,横坐标为6+1.5=7.5,
∴AE,AH=3.
∵S△AHEAH×15AE MH.
∴MH.
故答案为:.
【点评】本题考查一次函数的相关知识.理解新定义的意义并灵活应用是解决本题的关键.
12.如图,平面直角坐标系中,⊙P经过点A(8,0),O(0,0),B(0,6),点P关于x轴的对称点是P1,点D是⊙P上的一点.
(1)∠ADB= 90 °;
(2)当点D到弦OB的距离最大时,直线DP1与x轴的交点坐标为 .
【分析】(1)连接AB、AD、BD,利用圆周角定理:90度的圆周角所对的弦是直径,即可得到答案;
(2)由题意,先求出点D和点P的坐标,然后利用待定系数法求出解析式,令y=0,即可求出点C的坐标.
【解答】解:(1)连接AB、AD、BD,如图1:
∵⊙P经过点A(8,0),O(0,0),B(0,6),
又∵∠AOB=90°,
∴AB是直径,
∴,
∴∠ADB=90°,
故答案为:90;
(2)由(1)可知,点P是AB的中点,
∵A(8,0),B(0,6),
∴点P的坐标为(4,3),
∵点P关于x轴的对称点是P,
∴P的坐标为(4,﹣3),
∵当点D到弦OB的距离最大时,即作DE⊥OB,点P在DE上,如图2:连接DP,与x轴交点为C;
∴,
此时,点D的坐标为(9,3);
设直线DP1为y=kx+b,则把点(4,﹣3)和点(9,3)代入,得:
,
解得,
∴;
令y=0,则,
解得:,
∴直线DP与x轴的交点坐标为,
故答案为:.
【点评】本题考查了圆周角定理,轴对称的性质,勾股定理求线段的长度,以及待定系数法求直线的解析式,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行解题.
13.如图,在平面直角坐标系中,线段AB的端点为A(1,0),B(5,8).
(1)直线AB的函数解析式为 y=2x﹣2 ;
(2)某同学设计了一个动画:在函数y=﹣2x+b中,输入b(b>0)的值,得到直线CD,其中点C在x轴上,点D在y轴上.
①当△OCD的面积为6时,直线CD就会发蓝光,则此时输入的b的值为 2 ;
②当直线CD与线段AB有交点时,直线CD就会发红光,则此时输入的b的取值范围是 2≤b≤18 .
【分析】(1)用待定系数法求函数的解析式即可;
(2)①分别求出D(0,b),C(b,0),则S△OCDbb=6,求出b即可;
②当线段CD经过A点时,b=2;当线段CD经过B点时,b=18;则2≤b≤18时,直线CD就会发红光.
【解答】解:(1)设直线AB的解析式为y=kx+b,
∴,
解得,
∴直线AB的解析式为y=2x﹣2,
故答案为:y=2x﹣2;
(2)①当x=0时,y=b,
∴D(0,b),
当y=0时,xb,
∴C(b,0),
∴OCb,OD=b,
∴S△OCDbb=6,
解得b=2或b=﹣2(舍),
故答案为:2;
②当线段CD经过A点时,﹣2+b=0,
解得b=2;
当线段CD经过B点时,﹣10+b=8,
解得b=18;
∴2≤b≤18时,直线CD就会发红光,
故答案为:2≤b≤18.
【点评】本题考查一次函数的图象及性质,熟练掌握一次函数的图象及性质是解题的关键.
14.如图,一次函数的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
(1)△AOB的面积是 3 ;
(2)点C的坐标是 (5,3) ;
(3)过B,C两点直线的函数表达式为 .
【分析】(1)根据题意求得与坐标轴的交点坐标,进而根据三角形的面积公式求解即可;
(2)过点C作CD⊥x轴,垂足为D,证明△AOB≌△CDA,继而求得C的坐标,
(3)待定系数法求解析式即可.
【解答】解:(1)由,令x=0,则y=2,令y=0,则x=3,
∴A(3,0),B(0,2),
∴OA=3,OB=2,
∴,
故答案为:3;
(2)如图,过点C作CD⊥x轴,垂足为D,
∵等腰Rt△ABC,∠BAC=90°,∠ABO=∠CDA=90°,
∴∠BAO+∠CAD=90°,∠BAO+∠ABO=90°,AB=AC,
∴∠CAD=∠ABO,
∴△AOB≌△CDA,
∴AO=CD=3,AD=BO=2,
∴OD=5,
∴C(5,3),
故答案为:(5,3);
(3)设BC直线解析式为y=kx+b,则,
解得,
∴设BC直线解析式为y,
故答案为:.
【点评】本题考查了一次函数与坐标轴交点问题,全等三角形的性质,等腰三角形的性质,数形结合是解题的关键.
15.如图,已知一次函数y=kx+2的图象与y轴,x轴分别交于点A、B.
(1)若点(1,1)在函数图象上,则k= ﹣1 ;
(2)若S△OAB=3,则点B的坐标为 (3,0)或(﹣3,0) ;
(3)一次函数y=kx+2的图象与正比例函数y=2x的图象交于点.点P在x轴上,当△PBC为直角三角形时,点P的坐标为 或 .
【分析】(1)将点(1,1)代入y=kx+2即可得到k的值;
(2)利用解析式求出点A的坐标,再根据面积即可得到点B的坐标;
(3)利用点C的坐标求出一次函数的解析式,再根据等腰直角三角形的性质分两种情况:当∠CPB=90°时,当∠PCB=90°时,分别求解.
【解答】解:(1)∵点(1,1)在函数y=kx+2的图象上,
∴k+2=1,
得k=﹣1,
故答案为:﹣1;
(2)令y=kx+2中x=0,则y=2,
∴A(0,2),
∴OA=2,
∵,
∴OB=3,
∴B(3,0)或B(﹣3,0);
故答案为:(3,0)或(﹣3,0);
(3)将代入y=2x,得,
∴,
∴,
当∠CPB=90°时,点P的横坐标为,即;
当∠PCB=90°时,
将点代入y=kx+2,
∴,
解得k=﹣1,
∴y=﹣x+2,
当y=0时,x=2,
∴B(2,0),
∴OA=OB=2,
∴∠CPB=∠CBP=45°,
过点C作CE⊥OB于点E,
∴,
∴点P的横坐标为,
∴,
故答案为:或.
【点评】此题考查了一次函数与正比例函数的综合应用,待定系数法求解析式,一次函数与图形面积问题,等腰直角三角形的性质,熟练掌握一次函数的综合知识是解题的关键.
16.如图,在平面直角坐标系中,直线交x轴于点A、交y轴于点B,C点与A点关于y轴对称,动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.当△PQB为等腰三角形时,点P的坐标是 (2,0)或(,0) .
【分析】把x=0和y=0分别代入一次函数的解析式,求出B、A的坐标,分为三种情况:①PQ=BP,②BQ=QP,③BQ=BP,分别求解即可.
【解答】解:∵yx+6,
∴当x=0时,y=6,
当y=0时,x=﹣8,
即点A的坐标是(﹣8,0),点B的坐标是(0,6),
∵C点与A点关于y轴对称,
∴C的坐标是(8,0),
分为三种情况:
①当PB=PQ时,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
∵∠BPQ=∠BAO,∠BAO+∠AQP+∠APQ=180°,∠APQ+∠BPQ+∠BPC=180°,
∴∠AQP=∠BPC,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
在△APQ和△CBP中,
,
∴△APQ≌△CBP(AAS),
∴AP=CB,
∵B(0,6),C(8,0),
∴BC10,
∴AP=10,
∴点P的坐标是(2,0);
②当BQ=BP时,则∠BPQ=∠BQP,
∵∠BAO=∠BPQ,
∴∠BAO=∠BQP,
而根据三角形的外角性质得:∠BQP>∠BAO,
∴此种情况不存在;
③当QB=QP时,则∠BPQ=∠QBP=∠BAO,
即BP=AP,
设此时P的坐标是(x,0),
∵在Rt△OBP中,由勾股定理得:BP2=OP2+OB2,
∴(x+8)2=x2+62,
解得:x,
即此时P的坐标是(,0).
∴当△PQB为等腰三角形时,点P的坐标是(2,0)或(,0).
故答案为:(2,0)或(,0).
【点评】本题是一次函数综合题,考查了一次函数图象上点的坐标特征,勾股定理,等腰三角形的性质,全等三角形的性质和判定的应用,解题的关键是分类思想的运用.
17.在平面直角坐标系中,一次函数y=x+4的图象分别与x轴,y轴交于点A,B,点P在一次函数y=x的图象上,则当△ABP为直角三角形时,点P的坐标是 (0,0)或(﹣2,﹣2)或(2,2) .
【分析】设点P的坐标为(x,y),分三种情况:①当∠APB=90°时,②当∠PAB=90°时,③当∠PBA=90°时,根据勾股定理分别求解即可.
【解答】解:∵一次函数y=x+4的图象分别与x轴,y轴交于点A,B,
∴A(﹣4,0),B(0,4),
∴AB2=42+42=32,
设点P的坐标为(x,y),
∵点P在一次函数y=x的图象上,
∴点P的坐标为(x,x),
分三种情况:
①当∠APB=90°时,如图,
∵△ABP为直角三角形,
∴AP2+BP2=AB2,
∴(x+4)2+x2+x2+(4﹣x)2=32,
∴x=0,
∴点P的坐标是(0,0);
②当∠PAB=90°时,如图,
∵△ABP为直角三角形,
∴AP2+AB2=PB2,
∴(x+4)2+x2+32=x2+(4﹣x)2,
∴x=﹣2,
∴点P的坐标是(﹣2,﹣2);
③当∠PBA=90°时,如图,
∵△ABP为直角三角形,
∴AB2+BP2=AP2,
∴x2+(4﹣x)2+32=(x+4)2+x2,
∴x=2,
∴点P的坐标是(2,2).
综上,点P的坐标是(0,0)或(﹣2,﹣2)或(2,2).
【点评】本题是一次函数综合题,考查勾股定理、一次函数的性质等,解决问题的关键是分类思想的运用.
18.在平面直角坐标系xOy中,对于P、Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P、Q两点为“友好点”.如图中的P,Q两点即为“友好点”.已知点A的坐标为(﹣3,1).
(1)请在x轴上提供一个点A的“友好点”,它的坐标为 (﹣4,0)或(4,0) ;
(2)在点R(0,4),S(2,2),T(2,﹣3)中,为点A的“友好点”的是 R,S ;
(3)直线l:y=x﹣5,与x轴相交于点C,与y轴相交于点D,M为线段CD上一点,若第二象限存在点N,使得M,N两点为“友好点”,请你提供一个符合题意的点N,N的坐标为 (3,﹣2)(答案不唯一) .
【分析】(1)因为点A的“友好点”在x轴上,所以|x|=4,可得结论;
(2)把各点的横纵坐标的绝对值相加,得4,则是A的同族点;
(3)首先证明点M的横坐标与纵坐标的绝对值之和为定值5,然后“友好点”的定义即可解决问题.
【解答】解:(1)∵点A(﹣3,1)的“友好点”在x轴上,
∴纵坐标为0,
∴|x|=3+1=4,
∴x=±4,
∴点A的“友好点”的坐标为(﹣4,0)或(4,0);
故答案为:(﹣4,0)或(4,0);
(2)∵点A的坐标为(﹣3,1),
∴3+1=4,
点R(0,4),S(2,2),T(2,﹣3)中,
0+4=4,2+2=4,2+3=5,
∴点A的同族点的是R,S;
故答案为:R,S;
(3)由题意,直线y=x﹣5与x轴交于C(5,0),与y轴交于D(0,﹣5).
点M在线段CD上,设其坐标为(x,y),
则有:x≥0,y≤0,且y=x﹣5.
点M到x轴的距离为|y|,点M到y轴的距离为|x|,
则|x|+|y|=x﹣y=5.
∴点M的“友好点”N满足横纵坐标的绝对值之和为5.
∵第二象限存在点N,使得M,N两点为“友好点”,
∴N的坐标为(3,﹣2)(答案不唯一).
故答案为:(3,﹣2)(答案不唯一)..
【点评】本题是一次函数综合题、考查“友好点”的定义,坐标与图形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考压轴题.
19.如图,直线y=kx+2与x轴,y轴分别交于A,C两点,点B与点A关于y轴对称,连接BC,BC=2,点M,N分别是线段AB,AC上的动点(M不与A,B重合),且满足∠CMN=∠CBA.当△CMN为等腰三角形时,M的坐标为 (24,0)或(,0) .
【分析】先求解点C的坐标为(0,2),可得OC=2,再利用勾股定理求解OB4,可得点B坐标为(4,0),点A坐标为(﹣4,0),由△CMN为等腰三角形,可得CM=MN或CN=CM或NC=NM,当CM=MN时,证明△CBM≌△MAN即可,当CM=CN时,∠CMN=∠CNM≠∠CBA=∠CAB,不符合题意,舍去,当NC=NM时,如图,证明AM=CM,设OM=n,则AM=CM=4﹣n,再利用勾股定理求解即可.
【解答】解:在y=kx+2中,
当x=0时,y=2,
∴点C的坐标为(0,2),
∴OC=2,
在Rt△BOC中,BC=2,OB4,
∴点B坐标为(4,0),
∵点B与点A关于y轴对称,
∴点A坐标为(﹣4,0),
∵点B与点A关于y轴对称,
∴AC=BC,
∵△CMN为等腰三角形,
∴CM=MN或CN=CM或NC=NM,
当CM=MN时,
∵AC=BC,
∴∠CAB=∠CBA,
∵∠CMN=∠CBA,
∴∠BMN=∠BMC+∠CMN=∠BAC+∠ANM,
∴∠ANM=∠BMC,
∵∠MAN=∠CBM,NM=CM,
∴△CBM≌△MAN(AAS),
∴AM=BC=2,
∵OA=4,
∴OM=24,
∴M的坐标为(24,0),
当CM=CN时,
∴∠CMN=∠CNM≠∠CBA=∠CAB,不符合题意,舍去,
当NC=NM时,如图,
∴∠NCM=∠CMN=∠CBA=∠CAB,
∴AM=CM,
设OM=n,则AM=CM=4﹣n,
∴(4﹣n)2=n2+4,
解得:n,
∴M(,0),
综上:点M的坐标为(24,0)或(,0).
故答案为:(24,0)或(,0).
【点评】本题是一次函数综合题,考查的是坐标与图形,轴对称的性质,全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理的应用,分类讨论是解本题的关键.
20.如图,直线yx+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A做匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标 (2,2) ;
(2)若△OQC是等腰直角三角形,则t的值为 2或4 .
【分析】(1)当x+3=x时,求点C的坐标即可;
(2)分两种情况讨论:当CQ⊥OQ时,t=2;当OC⊥CQ时,t=4.
【解答】解:(1)当x+3=x时,解得x=2,
∴C(2,2),
故答案为:(2,2);
(2)∵Q点的运动速度为每秒1个长度单位,运动时间为t秒,
∴OQ=t,
当CQ⊥OQ时,∵∠OCA=45°,
∴△OCQ为等腰直角三角形,
∴t=2;
当OC⊥CQ时,∵∠OCA=45°,
∴△OCQ为等腰直角三角形,
∴Q(4,0),
∴t=4;
综上所述:t的值为2或4,
故答案为:2或4.
【点评】本题考查一次函数的图象及性质,熟练掌握一次函数的图象及性质,等腰直角三角形的性质是解题的关键.
三.解答题(共10小题)
21.如图1,已知直线l1:y=kx+b交x轴于A(6,0),交y轴于B(0,6).
(1)求直线l的表达式;
(2)如图2,直线CP的表达式为,点P为线段AB的中点,在直线CP上找一点Q,使得OQ+AQ最小,并求出最小值;
(3)如图3,已知点M(﹣2,0),点N(m,2m﹣6)为直线AB右侧一点,且满足∠OBM=∠ABN,求m的值.
【分析】(1)把A(6,0),B(0,6)代入y=kx+b,即可求解;
(2)如图:作点O关于CP的对称点R,连接AR交CP于点Q,则此时OQ+AQ最小,即可求解;
(3)作M关于y轴的对称点G(2,0),以G为直角顶点,BG为直角边在BG右侧作等腰直角三角形BGH,过H作HK⊥x轴于K,可证明N在直线BH上,由△BOG≌△GKH(AAS),可得H(8,2),直线BH解析式为yx+6,把N(m,2m﹣6)代入可得答案.
【解答】解:(1)把A(6,0),B(0,6)代入y=kx+b得:,
解得:,
故直线l的表达式为y=﹣x+6;
(2)如图:作点O关于CP的对称点R,连接AR交CP于点Q,则此时OQ+AQ最小,
理由:OQ+AQ=RQ+AQ=RA,
设OR交CP于点T,则点T是OR的中点,
∵A(6,0),B(0,6),
∴线段AB的中点P的坐标为(3,3),
把P(3,3)代入yx+c得:3c,
解得c,
∴直线l2的解析式为yx,
∵CP⊥OR,则直线OR的表达式为:y=﹣2x,
联立上述两个函数表达式得:﹣2xx,
解得:x,即点T(,),
由中点坐标公式得,点R(,),
由点A、R的坐标得,AR,
即OQ+AQ最小值为;
(3)作M关于y轴的对称点G(2,0),以G为直角顶点,BG为直角边在BG右侧作等腰直角三角形BGH,过H作HK⊥x轴于K,如图:
∴∠OBM=∠OBG,
∵A(6,0),B(0,6),
∴△AOB是等腰直角三角形,
∴∠OBG+∠ABG=45°,
∵△BGH是等腰直角三角形,
∴∠ABG+∠ABH=45°,BG=GH,
∴∠OBG=∠ABH,
∴∠OBM=∠ABH,
∴N在直线BH上,
∵∠OGB=90°﹣∠HGK=∠GHK,∠BOG=∠GKH=90°,BG=GH,
∴△BOG≌△GKH(AAS),
∴BO=GK=6,OG=HK=2,
∴H(8,2),
由B(0,6),H(8,2)可得直线BH解析式为yx+6,
把N(m,2m﹣6)代入得:
2m﹣6m+6,
解得m.
【点评】本题考查一次函数的综合应用,涉及待定系数法,三角形面积,全等三角形判定与性质等知识,解题的关键是用含字母的式子表示相关点坐标和相关线段的长度.
22.在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且,直线l2:y=k2x+b经过点,1),与直线AB交于点D.
(1)求直线l1的解析式;
(2)如图2,连接CB、AC,求△ABC的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
【分析】(1)根据待定系数法可得直线l1的解析式;
(2)由△ABC的面积BH×(xC﹣xA)(2)=8,即可求解;
(3)分四种情况:在x轴和y轴上,证明△DMQ≌△QNC(AAS),得DM=QN,QM=CN,设D(m,m+6)(m<0),表示点Q的坐标,根据OQ的长列方程可得m的值,从而得到结论.
【解答】解:(1)y=k1x+6,
当x=0时,y=6,
∴OB=6,
∵OBOA,
∴OA=2,
∴A(﹣2,0),
把A(﹣2,0)代入:y=k1x+6中得:﹣2k1+6=0,
k1,
∴直线l1的解析式为:yx+6;
(2)设AC交x轴于点H,
由点A、C的坐标得,直线AC的表达式为:yx,即点H(0,),
则BH=6,
则△ABC的面积BH×(xC﹣xA)(2)=8;
(3)存在,分四种情况:
①当Q在y轴的正半轴上时,如图2,过D作DM⊥y轴于M,过C作CN⊥y轴于N,
∵△QCD是以CD为底边的等腰直角三角形,
∴∠CQD=90°,CQ=DQ,
∴∠DMQ=∠CNQ=90°,
∴∠MDQ=∠CQN,
∴△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN,
设D(m,m+6)(m<0),则Q(0,﹣m+1),
∴OQ=QN+ON=OM+QM,
即﹣m+1m+6,
m=1﹣2,
∴Q(0,2);
②当Q在x轴的负半轴上时,如图3,过D作DM⊥x轴于M,过C作CN⊥x轴于N,
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=1,
设D(m,m+6)(m<0),则Q(m+1,0),
∴OQ=QN﹣ON=OM﹣QM,
即m+6m﹣1,
m=5﹣4,
∴Q(6﹣4,0);
③当Q在x轴的负半轴上时,如图4,过D作DM⊥x轴于M,过C作CN⊥x轴于N,
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=1,
设D(m,m+6)(m<0),则Q(m﹣1,0),
∴OQ=QN﹣ON=OM+QM,
即m﹣6m+1,
m=﹣45,
∴Q(﹣46,0);
④当Q在y轴的负半轴上时,如图5,过D作DM⊥y轴于M,过C作CN⊥y轴于N,
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN
设D(m,m+6)(m<0),则Q(0,m+1),
∴OQ=QN﹣ON=OM+QM,
即m﹣6m﹣1,
m=﹣21,
∴Q(0,﹣2);
综上,存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2)或(6﹣4,0)或(﹣46,0).
【点评】本题属于一次函数综合题,考查了待定系数法,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考压轴题.
23.在平面直角坐标系xOy中,对于点P,Q和图形W,若图形W上存在点K使得∠PQK=α(0°<α<180°),则称图形W与PQ“α关联”.
(1)已知P(0,0),Q(1,0),以下列各点为中心,作边长为1的正方形W,若W与PQ“45°关联”,则这个中心可能是 ①③ .
①(1,﹣1);②(2,0);③(0,1).
(2)如图,已知直线l.
①已知P,Q在直线y=﹣2上运动,且点P在点Q左侧.设直线l与x轴,y轴分别交于M,N两点,若线段MN与PQ“α关联”,其中60°<α<90°,求Q点横坐标t的取值范围;
②已知P(﹣1,0),Q(0,0).长度为1的线段ST在l上,以ST上任意一点为圆心作半径为r的圆,对每一个圆总存在α使之与PQ既是“α关联”又是“α+60°关联”但不是“α+90°关联”,直接写出r的取值范围.
【分析】(1)根据题意得出,正方形W与射线OK有交点,进而求得边长为1的正方形W的中心到边长的距离的范围,进而判断即可求解;
(2)①根据一次函数与坐标轴交点结合特殊角的三角函数值得出∠NMO=30°,根据P,Q在直线y=﹣2上运动,且点P在点Q左侧.线段MN与PQ“α关联”,其中60°<α<90°,分别画出α=∠PMQ=90°.∠PQN=α=60°时的Q点的位置,进而结合图形,即可求解;
②设R为ST上任意一点,QF、QG分别为⊙R的两条切线,根据ST上任意一点为圆心作半径为r的圆,对每一个圆总存在α使之与PQ既是“a关联”又是a+60°关联”但不是“a+90°关联“得出,进而求得QR的最小值,得出,即可求解.
【解答】解:(1)∵W与PQ“45°关联”,
∴∠PQK=45°,
如图所示,正方形ABCD的边长为1,E是AB的中点,
∴,,
正方形的中心到边上的距离的范围为:,
边长为1的正方形W,W与PQ“45°关联”,
则正方形W与射线OK有交点,
∵①(1,﹣1);②(2,0);③(0,1),
如图所示,
点③(0,1)在射线OK上,
①(1,﹣1)到OK1的距离为,则以(1,﹣1)为中心的正方形W与OK1有交点,
综上所述,若W与PQ“45°关联”,则这个中心可能是①③,
故答案为:①③;
(2)①已知直线l:,直线l与x轴,y轴分别交于M,N两点,
当x=0时,y=3;当y=0时,,
∴,N(0,3),
∴ON=3,,
∴,
∴∠NMO=30°,
∵P,Q在直线y=﹣2上运动,且点P在点Q左侧.线段MN与PQ“a关联”,其中60°<α<90°,
∴当MQ垂直于直线y=﹣2时,Q点的横纵坐标最小(不取等于号),此时α=∠PMQ=90°,
∴,
当∠PQN=α=60°时,如图所示,设PQ与y轴交于点F,则F(0,﹣2),
∴FN=3﹣(﹣2)=5,
∴,
Q点横坐标t的取值范围为:;
②设R为ST上任意一点,QF,QG分别为⊙R的两条切线,
如图所示,当∠FQG=90°时,
∴∠QFR=∠RGQ=∠FQG=90°,
∴四边形QFRG是矩形,
又∵RF=RG,
∴四边形QFRG是正方形,
∴,
当∠MQN=60°时,则∠RQF=30°,则QR=2FR=2r,
∵ST上任意一点为圆心作半径为r的圆,对每一个圆总存在α使之与PQ既是“α关联”又是“α+60°关联”但不是°α+90°关联”,
∴,
∵ST在直线l:上,
∴当QR⊥I时,QR取得最小值,则r取得最小值,如图所示,
由①可得ON=3,,则MN=6,
此时,
∴,
∴.
【点评】本题主要考查了一次函数综合考点,正方形的性质,特殊的三角函数值,圆的切线等相关知识,正确理解相对应的规定并熟练应用是解题的关键.
24.如图1,一次函数y=k1x+b的图象与x轴交于点A,与y轴交于点B(0,4),与正比例函数y=k2x的图象交于点C(6,12).
(1)直接写出正比例函数与一次函数的表达式;
(2)如图2,点E是直线BC上的一动点(与B,C点不重合),过点E作EP⊥x轴于点P,交直线OC于点F,设点E的横坐标为a,用含a的式子表示EF的长,并求出当EF=2OB时,a的值;
(3)如图3,在(2)的条件下,若E是线段BC上一动点(与B,C点不重合),连接CP,直线OC能否把△CEP分成面积之比为1:3的两部分?若能,请求出E点坐标;若不能,请说明理由.
【分析】(1)根据待定系数法求解即可;
(2)根据两点距离公式表示出EF的长,然后求出OB的长,代入数量关系式中,求解a值即可;
(3)根据等高三角形的面积比等于底边长之比,分类讨论求解a的值,从而得到E的坐标即可.
【解答】解:(1)将B,C的坐标代入一次函数解析式:
,
∴k1,b=4,
∴一次函数的表达式:yx+4,
将C点坐标代入正比例函数解析式:
12=6k2,
∴k2=2,
∴正比例函数的表达式:y=2x;
(2)∵点E的横坐标为a,
∴E(a,a+4),
∵EP⊥x轴,
∴F(a,2a),
∴EF=|a+4﹣2a|=|4a|,
∵B(0,4),
∴OB=4,
∵EF=2OB,
∴|4a|=4,
∴a=0或12;
(3)∵E在线段BC上,
∴0<a<6,
∵EP⊥x轴,
∴P(a,0),
∴EPa+4,EF=4a,
∵直线OC能否把△CEP分成面积之比为1:3的两部分,
∴EF:EP=1:4或3:4,
∴4aa+1或16a=4a+12,
解得:a=3或,
∴E(3,8)或(,).
【点评】本题主要考查了一次函数综合题,综合运用待定系数法求一次函数解析式及正比例函数解析式、两点之间的距离以及三角形的面积来解答是本题解题的关键.
25.如图①,直线y=2x+b与x轴交于点A(4,0),与y轴交于点B,与直线y=﹣2x交于点C(a,﹣4).
(1)求点C的坐标及直线AB的表达式;
(2)点P在y轴上,若△PBC的面积为6,求点P的坐标;
(3)如图②,过x轴正半轴上的动点D(m,0)作直线l⊥x轴,点Q在直线l上,若以BC为腰的△BCQ是等腰直角三角形,请直接写出相应m的值.
【分析】(1)将点C的坐标代入直线y=﹣2x可得出a的值,即得C点坐标,再用待定系数法求直线AB的表达式即可;
(2)设点P的坐标为(0,p),根据△PBC的面积为6求解即可;
(3)分三种情况:①当BC=BQ时,过点C作CM⊥y轴于M,过点Q作QN⊥y轴于N,②当BC=CQ时,过点C作CM⊥y轴于M,延长MC交直线l于N,即可得到结论.
【解答】解:(1)∵点C(a,﹣4)在直线y=﹣2x上,
∴﹣2a=﹣4,
解得:a=2,
∴C(2,﹣4),
由点A、C的坐标得,AB的解析式为:y=2x﹣8;
(2)设点P的坐标为(0,p),
∵直线AB的解析式为:y=2x﹣8,
∴B(0,﹣8),
∴BP=|p+8|,
∵△PBC的面积为6,C(2,﹣4),
∴S△PBC2|p+8|=6,
∴p=﹣2或﹣14,
∴点P的坐标为(0,﹣2)或(0,﹣14);
(3)存在,
以B,C,Q为顶点的三角形是等腰直角三角形,分以下三种情况:
①当BC=BQ时,过点C作CM⊥y轴于M,过点Q作QN⊥y轴于N,
∴∠BMC=∠QNB=90°,
∴∠CBM+∠BCM=90°,
∵∠QBC=90°,
∴∠CBM+∠QBN=90°,
∴∠BCM=∠QBN,
∵BC=BQ,
∴△BCM≌△QBN(AAS),
∴QN=BM,BN=CM,
∵B(0,﹣8),C(2,﹣4),
BM=4,CM=2,
∴QN=BM=4,
∴m=4;
②当BC=CQ时,过点C作CM⊥y轴于M,延长MC交直线l于N,
同理:△BCM≌△CQN(AAS),
∴QN=CM=2,BM=CN=4,
∴MN=MC+CN=6
∴m=6;
故m的值为4或6.
【点评】此题是一次函数综合题,考查了一次函数图象上点的坐标特征,两点间的距离,三角形的面积,等腰直角三角形的性质,全等三角形的判定和性质,熟练掌握方程的思想方法及分类讨论思想是解本题的关键.
26.如图,在平面直角坐标系xOy中,直线l1:y的图象与x轴、y轴分别交于D,B两点.直线y=kx的图象与x轴交于C.直线l1与直线l2交于点A(a,3).
(1)求点A的坐标及直线l2的表达式;
(2)若点E在直线l2上,且△ADE的面积为,求点E的坐标;
(3)在x轴上是否存在点P,使得∠ACB=2∠APC,若存在,求出点P坐标,若不存在,说明理由.
【分析】(1)当y=3时,y3,得到点A(1,3),再由待定系数法即可求解;
(2)当点E在y轴左侧时,由△ADE的面积DH×(xA﹣xE)(1﹣m),得到点E(﹣1,);当点E(E′)在y轴右侧时,则此时点E、E关于点A对称,即可求解;
(3)当点P在y轴左侧时,证明PC=AC,设点P(x,0),即可求解;当点P(P′)在y轴右侧时,则点P′、P关于点A对称,即可求解.
【解答】解:(1)当y=3时,y3,
解得:x=1=a,即点A(1,3),
将点A的坐标代入函数表达式得:3=k,则k,
则直线l2的表达式为:yx;
(2)如图1,当点E在y轴左侧时,
设直线l2和y轴交于点H(0,),设点E(m,m),由函数的表达式知,点D(0,),
则DH,
则△ADE的面积DH×(xA﹣xE)(1﹣m),
解得:m=﹣1,即点E(﹣1,);
当点E(E′)在y轴右侧时,
则此时点E、E关于点A对称,
由中点坐标公式得:点E′(3,),
即点E的坐标为:(﹣1,)或(3,);
(3)存在,理由:由函数的表达式知,点C(﹣3,0),
当点P在y轴左侧时,如图2,
∵∠ACB=2∠APC,则∠CPA=∠CAP,
即PC=AC,设点P(x,0),
由点A、P、C的坐标得,AC=5,PC=﹣3﹣x=5,
解得:x=﹣8,即点P(﹣8,0),
当点P(P′)在y轴右侧时,
则点P′、P关于点A对称,
由中点坐标公式得:点P′(10,0),
综上,P(﹣8,0)或(10,0).
【点评】本题考查的是一次函数综合运用,涉及到等腰三角形的性质、面积的计算,数形结合和分类求解是解题的关键.
27.如图,在平面直角坐标系中,一次函数y=k1x+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=k2x的图象交于点C(3,4).
(1)求正比例函数与一次函数的表达式;
(2)求△OBC的面积;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标;
(4)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标.
(5)在y轴上是否存在一点P,使△POC为等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
【分析】(1)由待定系数法即可求解;
(2)由△OBC的面积OB×xC2×3=3,即可求解;
(3)作C关于x轴对称点C',连接BC',交x轴于E,此时△BCE周长最小,即可求解;
(4)①当DA⊥AB时,证明△DAM≌△ABO,则DM=AO=3,AM=BO=2,即D(﹣5,3);②当D′B⊥AB时,同理可解;
(5)当PO=CO时,则y2=25,即可求解;当PO=PC或CO=PC时,同理可解.
【解答】解:(1)∵正比例函数y=kx的图象经过点C(3,4),
∴4=3k,
∴k,
∴正比例函数解析式为yx,
∵一次函数y=k1x+b的图象经过A(﹣3,0),C(3,4),
∴,
∴,
∴一次函数为yx+2;
(2)由一次函数的表达式知,点B(0,2),即OB=2,
则△OBC的面积OB×xC2×3=3;
(3)存在,理由:
如图,
作C关于x轴对称点C',连接BC',交x轴于E,此时△BCE周长最小.
∵C(3,4),
∴C'(3,﹣4),
∵B(0,2)
∴BC'的解析式为:y=﹣2x+2
令y=0,得0=﹣2x+2,
∴x=1
∴E点的坐标为(1,0);
(4)①当DA⊥AB时,如图,作DM⊥x轴垂足为M,
∵∠DAM+∠BAO=90°,∠BAO+∠ABO=90°,
∴∠DAM=∠ABO,
∵DA=AB,∠DMA=∠AOB,
∴△DAM≌△ABO,
∴DM=AO=3,AM=BO=2,
∴D(﹣5,3),
②当D′B⊥AB时,作D′N⊥y轴垂足为N,
同理得△D′BN≌△BAO
∴D′N=BO=2,BN=AO=3,
∴D′(﹣2,5)
∴D点坐标为(﹣5,3)或(﹣2,5);
(5)存在,理由:
设点P(0,y),
由点P、C、O的坐标得:PO2=y2,CO2=25,PC2=9+(y﹣4)2,
当PO=CO时,
则y2=25,则y=±5,
即点P(0,5)或(0,﹣5);
当PO=PC或CO=PC时,
则y2=9+(y﹣4)2或25=9+(y﹣4)2,
解得:y=0(舍去)或8或,
即点P(0,8)或(0,);
综上,P(0,5)或(0,﹣5)或(0,8)或(0,).
【点评】此题是一次函数综合题,主要考查待定系数法求一次函数、全等三角形的判定和性质、勾股定理、添加辅助线构造全等三角形等知识,学会分类讨论的数学思想是正确解题的关键.
28.如图,将正比例函数y=﹣2x的图象向上平移2个单位长度后得到的一次函数图象与x轴、y轴分别交于A、B两点,P(m,n)是线段AB(不含端点)上一动点,设△AOP的面积是S.
(1)求点B的坐标;
(2)求S关于m的函数表达式,并写出自变量m的取值范围;
(3)当时,在x轴上是否存在一点Q,使得PQ+BQ的值最小?若存在,求出点Q的坐标;若不存在,请说明理由.
【分析】(1)从图中不难发现,点B在y轴上,即B点的横坐标为0,且点B在一次函数y=﹣2x+2的图象上,则将x=0代入即可求得y值,B点坐标即可确定;
(2)根据A点为一次函数y=﹣2x+2的图象与x轴的交点,不难确定A点的坐标为(1,0),再运用三角形的面积计算公式,即可用求得;
(3)要使得PQ+BQ最小,找出点P对称点P′,然后连接BP′且求出解析式y=﹣6x+2,当y=0时即可求出点Q的坐标.
【解答】解:(1)将正比例函数y=﹣2x的图象向上平移2个单位长度后得到的一次函数为:y=﹣2x+2,
当x=0,则y=2,
∴点B的坐标为(0,2);
(2)点P(m,﹣2m+2),
由y=﹣2x+2,令y=0,则x=1,
∴点A的坐标为(1,0),
∴OA=1,
∴S△AOPOA y1×(﹣2m+2)=﹣m+1,
即S=﹣m+1(0<m<1);
(3)当S时,在x轴上存在一点Q,使得PQ+BQ最小,理由如下:
当Sx+1,
解得:x,
∴点P的坐标为(,1),
∴点P关于x轴的对称点P′的坐标是(,﹣1),
如图,
设直线BP′的函数表达式为y=kx+b,把点B(0,2)代入,解得:b=2,
将P′(,﹣1)代入y=kx+2,解得:k=﹣6,
∴y=﹣6x+2,
当y=0时,0=﹣6x+2,
解得x,
∴在x轴上存在一点Q(,0),使得PQ+BQ最小.
【点评】此题考查了一次函数的综合应用,待定系数法求函数解析式,最短距离问题,熟练掌握知识点是解题的关键.
29.如图,在四边形ABCD中,AB∥CD,AB=2CD=6,AD=5,∠DCB=90°,连接BD.点P从点A出发,以每秒一个单位的速度沿折线A→B→D运动,到达D点停止.设点P的运动时间为x秒(0<x<11),△DAP的面积为y.
(1)请直接写出y与x的函数关系式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出y的函数图象,并写出关于函数y的一条性质 当0<x≤6时,y随x增大而增大,当6<x<11时,y随x的增大而减小(答案不唯一) ;
(3)若该函数图象与直线y=x+k恰好有一个交点,则常数k的取值范围是 k=6或﹣11<k≤0 .
【分析】(1)当点P在AB上时,则yAP DHx×4=2x;当点P在BD上移动时,同理可解;
(2)当x=0时,y=0,当x=6时,y=12,当x=11时,y=0,根据上述各点绘制函数图象即可;观察函数图象得到函数性质;
(3)当直线y=x+k在m、n、l的位置时,属于临界点,即可求解.
【解答】解:(1)作DH⊥AB于点H,
∵0<x<11,则BD=11﹣6=5,
即△ABD为等腰三角形,则BH=CD=3=AH,
则DH4,
则sin∠DBA,
当点P在AB上时,
则yAP DHx×4=2x;
当点P在BD上移动时,
则y=S△ABD﹣S△ABP6×4AB×PBsin∠DBA=126(x﹣6)x,
则y;
(2)当x=0时,y=0,当x=6时,y=12,当x=11时,y=0,
根据上述各点绘制函数图象如下:
从函数图象看,当0<x≤6时,y随x增大而增大,当6<x<11时,y随x的增大而减小(答案不唯一),
故答案为:当0<x≤6时,y随x增大而增大,当6<x<11时,y随x的增大而减小(答案不唯一);
(3)当直线y=x+k在m、n、l的位置时,属于临界点,
直线m:将点(6,12)代入y=x+k得:12=6+k,则k=6;
直线n:k=0;
直线l:同理可得:k=﹣11,
故k=6或﹣11<k≤0,
故答案为:k=6或﹣11<k≤0.
【点评】此题重点考查平行线的性质、矩形的判定与性质、勾股定理、三角形的面积公式、一次函数的图象与性质、数形结合与分类讨论数学思想的运用等知识与方法,此题综合性强,难度较大,属于考试压轴题.
30.如图,在平面直角坐标系中,直线y=2x+4与x轴,y轴分别交于点A,C,经过点C的直线与x轴交于点B(4,0),点D是直线AC上一动点.
(1)求直线BC的解析式;
(2)当点D在直线AC上运动时,存在某时刻,使得△DBC为直角三角形且∠CBD=90°,请求出此时点D的坐标;
(3)如备用图所示,当点D运动到线段AC的中点时,此时,在直线BC上是否存在点P,使得∠DAP=45°,若存在,请求出P点坐标;若不存在,请说明理由.
【分析】(1)先求出点A(﹣2,0),点C(0,4),设直线BC的解析式为:y=kx+b,将点(4,0),点C(0,4)代入y=kx+b之中求出,由此可得直线BC的解析式;
(2)设直线BD的解析式为:y=mx+n,根据直线BC的解析式为y=﹣x+4,BD⊥BC得m=1,将m=1,点B(4,0)代入y=mx+n求出,则直线BD的解析式为y=x﹣4,解方程组即可得出点D的坐标;
(3)依题意有以下两种情况:①当点P在直线AC的右侧时,过点P作PE⊥x轴于E,PH⊥AC于H,设点P(t,﹣t+4),则PE=﹣t+4,OE=t,显然t>0,AE=2+t,AB=6,由勾股定理得AC,AP,证明△APH为等腰直角三角形则PH=AH,由勾股定理得APPH,则PH,再根据S△ABC=S△APC+S△ABP构造关于t的方程,然后解方程求出t=2.5,进而可得点P的坐标;②当点P在仔细ACDE左侧时,设为P',则PA⊥P'A,先求出直线PA的解析式,进而得直线P'A的解析式为y=﹣3x﹣6,解方程组即可得出点P'的坐标,综上所述即可得出答案.
【解答】解:(1)对于y=2x+4,当x=0时,y=4,当y=0时,x=﹣2,
∴点A(﹣2,0),点C(0,4),
设直线BC的解析式为:y=kx+b,
将点(4,0),点C(0,4)代入y=kx+b,
得:,解得:,
∴直线BC的解析式为:y=﹣x+4;
(2)过点B作BD⊥BC交直线AC于点D,则点D符合条件,如图1所示:
设直线BD的解析式为:y=mx+n,
∵直线BC的解析式为:y=﹣x+4,BD⊥BC,
∴m=1,
将m=1,点B(4,0)代入y=mx+n,
得:,解得:,
∴直线BD的解析式为:y=x﹣4,
解方程组:,得:,
∴点D(﹣8,﹣12);
(3)直线BC上存在点P,使∠DAP=45°,
依题意有以下两种情况:
①当点P在直线AC的右侧时,过点P作PE⊥x轴于E,PH⊥AC于H,如图2所示:
∵点P在直线BC:y=﹣x+4上,
∴设点P(t,﹣t+4),
则PE=﹣t+4,OE=t,显然t>0,
∵点A(﹣2,0),点C(0,4),点B(4,0),
∴OA=2,OC=OB=4,
∴AE=OA+OE=2+t,AB=OA+OB=6,
在Rt△AOC中,由勾股定理得:AC,
在Rt△APE中,由勾股定理得:AP,
∵∠DAP=45°,PH⊥AC,
∴△APH为等腰直角三角形,
∴PH=AH,
由勾股定理得:APPH,
∴PH,
∴PH,
∵S△ABC=S△APC+S△ABP,
∴AB OCAC PH+1AB PE,
即AB OC=AC PH+AB PE,
∴,
即,
整理得:2t2+5t﹣25=0,
解得:t=2.5,t=﹣5(不合题意,舍去),
∴﹣t+4=﹣2.5+4=1.5,
∴点P(2.5,1.5);
②当点P在仔细ACDE左侧时,设为P',如图3所示:
∵∠DAP=∠DAP'=45°,
∴∠PAP'=90°,
即PA⊥P'A,
设直线PA的解析式为:y=k1x+b1,
将A(﹣2,0),点P(2.5,1.5)代入y=k1x+b1,
得:,解得:,
∴直线PA的解析式为:,
设P'A的解析式为:y=k2x+b2,
∵PA⊥P'A,
∴k2=﹣3,
将k2=﹣3,点A(﹣2,0)代入y=k2x+b2,
得:,解得:,
∴直线P'A的解析式为:y=﹣3x﹣6,
解方程组:,得:,
∴点P'的坐标为(﹣5,9).
综上所述:直线BC上是否存在点P,使得∠DAP=45°,此时点P的坐标为(2.5,1.5)或(﹣5,9).
【点评】此题主要考查了一次函数的图象,等腰直角三角形的判定和性质,勾股定理,三角形的面积等知识点,熟练掌握待定系数法求函数的解析式,以及求两个一次函数的图象交点坐标的方法是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
一次函数综合题(一)
一.选择题(共10小题)
1.如图,直线l1与x轴、y轴分别交于A(﹣2,0),B(0,6),直线l2经过点B且与x轴负半轴交于点C,∠ABC=45°.若线段BC上存在一点P,使△ABP是以A为直角顶点的等腰直角三角形,则P点坐标为( )
A.(8,2) B.(﹣6,2) C.(﹣8,2) D.(6,﹣2)
2.已知直线l1:y=kx+b与直线l2:yx+m都经过,直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA,PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法个数有( )
A.1个 B.2个 C.3个 D.4个
3.八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A.yx B.yx C.yx D.y=x
4.八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A.yx B.yx C.yx D.yx
5.已知直线l1:y=kx+b与直线l2:yx+m都经过C(,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
6.如图,直线yx+6分别与x轴、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处.以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(,);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的横坐标是,以上所有结论中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
7.如图,直线yx+6分别与x轴、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处,以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(4.6,2.4);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的坐标是(1.5,2.4),
其中正确的结论是( )
A.①② B.①②③ C.①③④ D.①②④
8.如图,已知直线MN:yx+2交x轴负半轴于点A,交y轴于点B,点C是x轴上的一点,且OC=2,则∠MBC的度数为( )
A.45°或135° B.30°或150° C.60°或120° D.75°或165°
9.如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线yx﹣3与x轴、y轴分别交于点D、E,则点C到直线DE的最小距离为( )
A.1 B. C. D.
10.如图,直线yx+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是( )
A.(4,2) B.(2,4)
C.(,3) D.(22,2)
二.填空题(共10小题)
11.在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足,,则称点T是点A,B的“和谐点”.如图,点D(3,0),点E是直线l:y=2x+3上任意一点,若点T是点D,E的“和谐点”,直线ET交x轴于点H,当∠TDH为直角时,则点H到直线l的距离为 .
12.如图,平面直角坐标系中,⊙P经过点A(8,0),O(0,0),B(0,6),点P关于x轴的对称点是P1,点D是⊙P上的一点.
(1)∠ADB= °;
(2)当点D到弦OB的距离最大时,直线DP1与x轴的交点坐标为 .
13.如图,在平面直角坐标系中,线段AB的端点为A(1,0),B(5,8).
(1)直线AB的函数解析式为 ;
(2)某同学设计了一个动画:在函数y=﹣2x+b中,输入b(b>0)的值,得到直线CD,其中点C在x轴上,点D在y轴上.
①当△OCD的面积为6时,直线CD就会发蓝光,则此时输入的b的值为 ;
②当直线CD与线段AB有交点时,直线CD就会发红光,则此时输入的b的取值范围是 .
14.如图,一次函数的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
(1)△AOB的面积是 ;
(2)点C的坐标是 ;
(3)过B,C两点直线的函数表达式为 .
15.如图,已知一次函数y=kx+2的图象与y轴,x轴分别交于点A、B.
(1)若点(1,1)在函数图象上,则k= ;
(2)若S△OAB=3,则点B的坐标为 ;
(3)一次函数y=kx+2的图象与正比例函数y=2x的图象交于点.点P在x轴上,当△PBC为直角三角形时,点P的坐标为 .
16.如图,在平面直角坐标系中,直线交x轴于点A、交y轴于点B,C点与A点关于y轴对称,动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.当△PQB为等腰三角形时,点P的坐标是 .
17.在平面直角坐标系中,一次函数y=x+4的图象分别与x轴,y轴交于点A,B,点P在一次函数y=x的图象上,则当△ABP为直角三角形时,点P的坐标是 .
18.在平面直角坐标系xOy中,对于P、Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P、Q两点为“友好点”.如图中的P,Q两点即为“友好点”.已知点A的坐标为(﹣3,1).
(1)请在x轴上提供一个点A的“友好点”,它的坐标为 ;
(2)在点R(0,4),S(2,2),T(2,﹣3)中,为点A的“友好点”的是 ;
(3)直线l:y=x﹣5,与x轴相交于点C,与y轴相交于点D,M为线段CD上一点,若第二象限存在点N,使得M,N两点为“友好点”,请你提供一个符合题意的点N,N的坐标为 .
19.如图,直线y=kx+2与x轴,y轴分别交于A,C两点,点B与点A关于y轴对称,连接BC,BC=2,点M,N分别是线段AB,AC上的动点(M不与A,B重合),且满足∠CMN=∠CBA.当△CMN为等腰三角形时,M的坐标为 .
20.如图,直线yx+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A做匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标 ;
(2)若△OQC是等腰直角三角形,则t的值为 .
三.解答题(共10小题)
21.如图1,已知直线l1:y=kx+b交x轴于A(6,0),交y轴于B(0,6).
(1)求直线l的表达式;
(2)如图2,直线CP的表达式为,点P为线段AB的中点,在直线CP上找一点Q,使得OQ+AQ最小,并求出最小值;
(3)如图3,已知点M(﹣2,0),点N(m,2m﹣6)为直线AB右侧一点,且满足∠OBM=∠ABN,求m的值.
22.在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且,直线l2:y=k2x+b经过点,1),与直线AB交于点D.
(1)求直线l1的解析式;
(2)如图2,连接CB、AC,求△ABC的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
23.在平面直角坐标系xOy中,对于点P,Q和图形W,若图形W上存在点K使得∠PQK=α(0°<α<180°),则称图形W与PQ“α关联”.
(1)已知P(0,0),Q(1,0),以下列各点为中心,作边长为1的正方形W,若W与PQ“45°关联”,则这个中心可能是 .
①(1,﹣1);②(2,0);③(0,1).
(2)如图,已知直线l.
①已知P,Q在直线y=﹣2上运动,且点P在点Q左侧.设直线l与x轴,y轴分别交于M,N两点,若线段MN与PQ“α关联”,其中60°<α<90°,求Q点横坐标t的取值范围;
②已知P(﹣1,0),Q(0,0).长度为1的线段ST在l上,以ST上任意一点为圆心作半径为r的圆,对每一个圆总存在α使之与PQ既是“α关联”又是“α+60°关联”但不是“α+90°关联”,直接写出r的取值范围.
24.如图1,一次函数y=k1x+b的图象与x轴交于点A,与y轴交于点B(0,4),与正比例函数y=k2x的图象交于点C(6,12).
(1)直接写出正比例函数与一次函数的表达式;
(2)如图2,点E是直线BC上的一动点(与B,C点不重合),过点E作EP⊥x轴于点P,交直线OC于点F,设点E的横坐标为a,用含a的式子表示EF的长,并求出当EF=2OB时,a的值;
(3)如图3,在(2)的条件下,若E是线段BC上一动点(与B,C点不重合),连接CP,直线OC能否把△CEP分成面积之比为1:3的两部分?若能,请求出E点坐标;若不能,请说明理由.
25.如图①,直线y=2x+b与x轴交于点A(4,0),与y轴交于点B,与直线y=﹣2x交于点C(a,﹣4).
(1)求点C的坐标及直线AB的表达式;
(2)点P在y轴上,若△PBC的面积为6,求点P的坐标;
(3)如图②,过x轴正半轴上的动点D(m,0)作直线l⊥x轴,点Q在直线l上,若以BC为腰的△BCQ是等腰直角三角形,请直接写出相应m的值.
26.如图,在平面直角坐标系xOy中,直线l1:y的图象与x轴、y轴分别交于D,B两点.直线y=kx的图象与x轴交于C.直线l1与直线l2交于点A(a,3).
(1)求点A的坐标及直线l2的表达式;
(2)若点E在直线l2上,且△ADE的面积为,求点E的坐标;
(3)在x轴上是否存在点P,使得∠ACB=2∠APC,若存在,求出点P坐标,若不存在,说明理由.
27.如图,在平面直角坐标系中,一次函数y=k1x+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=k2x的图象交于点C(3,4).
(1)求正比例函数与一次函数的表达式;
(2)求△OBC的面积;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标;
(4)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标.
(5)在y轴上是否存在一点P,使△POC为等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
28.如图,将正比例函数y=﹣2x的图象向上平移2个单位长度后得到的一次函数图象与x轴、y轴分别交于A、B两点,P(m,n)是线段AB(不含端点)上一动点,设△AOP的面积是S.
(1)求点B的坐标;
(2)求S关于m的函数表达式,并写出自变量m的取值范围;
(3)当时,在x轴上是否存在一点Q,使得PQ+BQ的值最小?若存在,求出点Q的坐标;若不存在,请说明理由.
29.如图,在四边形ABCD中,AB∥CD,AB=2CD=6,AD=5,∠DCB=90°,连接BD.点P从点A出发,以每秒一个单位的速度沿折线A→B→D运动,到达D点停止.设点P的运动时间为x秒(0<x<11),△DAP的面积为y.
(1)请直接写出y与x的函数关系式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出y的函数图象,并写出关于函数y的一条性质 ;
(3)若该函数图象与直线y=x+k恰好有一个交点,则常数k的取值范围是 .
30.如图,在平面直角坐标系中,直线y=2x+4与x轴,y轴分别交于点A,C,经过点C的直线与x轴交于点B(4,0),点D是直线AC上一动点.
(1)求直线BC的解析式;
(2)当点D在直线AC上运动时,存在某时刻,使得△DBC为直角三角形且∠CBD=90°,请求出此时点D的坐标;
(3)如备用图所示,当点D运动到线段AC的中点时,此时,在直线BC上是否存在点P,使得∠DAP=45°,若存在,请求出P点坐标;若不存在,请说明理由.
一次函数综合题(一)
参考答案与试题解析
一.选择题(共10小题)
1.如图,直线l1与x轴、y轴分别交于A(﹣2,0),B(0,6),直线l2经过点B且与x轴负半轴交于点C,∠ABC=45°.若线段BC上存在一点P,使△ABP是以A为直角顶点的等腰直角三角形,则P点坐标为( )
A.(8,2) B.(﹣6,2) C.(﹣8,2) D.(6,﹣2)
【分析】过A作AP⊥AB交BC于P,过P作PM⊥AC,可得△ABO≌△PAM,有AM=BO,MP=AO,即可得出结论.
【解答】解:过A作AP⊥AB交BC于P,过P作PM⊥AC,如图:
∵A(﹣2,0),B(0,6),
∴BO=6,AO=2,
∵△ABP是以A为直角顶点的等腰直角三危形,
∴AP=AB,∠PAB=90°,
∴∠BAO=90°﹣∠PAM=∠MPA,
∵∠PMA=90°=∠BOA,
∴△ABO≌△PAM(AAS),
∴AM=BO=6,MP=AO=2,
∴OM=8,
∴P(﹣8,2).
故选:C.
【点评】本题考查一次函数综合应用,涉及旋转变换,全等三角形的判定与旋转,一次函数图象上点坐标的特征等,解题的关键是作辅助线,构造全等三角形解决问题.
2.已知直线l1:y=kx+b与直线l2:yx+m都经过,直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA,PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解即可判断①;根据一次函数的解析式求得交点坐标,求得BD和AO的长,根据三角形面积计算公式,即可得到△ABD的面积,即可判断③;根据勾股定理的逆定理即可判断②;根据轴对称的性质以及两点之间,线段最短,即可得到当PA+PC的值最小时,求得点P的坐标即可判断④,逐一判断即可得出答案.
【解答】解:∵直线l1:y=kx+b与直线都经过,
∴方程组的解为:,故①正确;
把代入直线,可得m=1,
∴,
令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
把B(0,4),代入直线l1:y=kx+b,可得,
解得:,
∴直线l1:y=2x+4,
令y=0,则x=﹣2,
∴A(﹣2,0),
∴OA=2,
∴,故③错误;
∵B(0,4),,D(0,1),
∴,,BD2=(1﹣4)2=9∴BC2+CD2=BD2,
∴△BCD为直角三角形,故②正确;
点A关于y轴对称点为A'(2,0),
设过点C,A'的直线为y=ax+n,则,
解得:,
∴,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),故④正确,
故选:C.
【点评】本题考查了一次函数图象与性质、勾股定理,三角形面积以及最短距离问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
3.八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A.yx B.yx C.yx D.y=x
【分析】设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
【解答】解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴OB AB=5,
∴AB,
∴OC,
由此可知直线l经过(,3),
设直线方程为y=kx,
则3k,
k,
∴直线l解析式为yx,
故选:C.
【点评】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关键是作AB⊥y轴,作AC⊥x轴,根据题意即得到:直角三角形ABO,利用三角形的面积公式求出AB的长.
4.八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
A.yx B.yx C.yx D.yx
【分析】直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出点A的坐标,根据待定系数法即可得到该直线l的解析式.
【解答】解:直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过P点的一条直线l将这八个正方形分成面积相等的两部分,
∴三角形ABP面积是8÷2+1=5,
∴BP AB=5,
∴AB=2.5,
∴OA=3﹣2.5=0.5,
由此可知直线l经过(0,0.5),(4,3)
设直线方程为y=kx+b,则,
解得.
∴直线l解析式为yx.
故选:A.
【点评】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关键是作PB⊥y轴,作PC⊥x轴,根据题意即得到:直角三角形ABP面积是5,利用三角形的面积公式求出AB的长.
5.已知直线l1:y=kx+b与直线l2:yx+m都经过C(,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:
①方程组的解为;
②△BCD为直角三角形;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【分析】根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解;根据两直线的系数的积为﹣1,可知两直线互相垂直;求得BD和AO的长,根据三角形面积计算公式,即可得到△ABD的面积;根据轴对称的性质以及两点之间,线段最短,即可得到当PA+PC的值最小时,点P的坐标为(0,1).
【解答】解:①∵直线l1:y=kx+b与直线l2:yx+m都经过C(,),
∴方程组的解为,
故①正确,符合题意;
②把B(0,4),C(,)代入直线l1:y=kx+b,可得,解得,
∴直线l1:y=2x+4,
又∵直线l2:yx+m,
∴直线l1与直线l2互相垂直,即∠BCD=90°,
∴△BCD为直角三角形,
故②正确,符合题意;
③把C(,)代入直线l2:yx+m,可得m=1,
yx+1中,令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
在直线l1:y=2x+4中,令y=0,则x=﹣2,
∴A(﹣2,0),
∴AO=2,
∴S△ABD3×2=3,
故③错误,不符合题意;
④点A关于y轴对称的点为A'(2,0),
由点C、A′的坐标得,直线CA′的表达式为:yx+1,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),
故④正确,符合题意;
故选:B.
【点评】本题为一次函数综合题,主要考查了一次函数图象与性质,三角形面积以及最短距离问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
6.如图,直线yx+6分别与x轴、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处.以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(,);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的横坐标是,以上所有结论中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】先求出点A,点B坐标,由勾股定理可求AB的长,可判断①;由折叠的性质可得OB=BD=6,OC=CD,∠BOC=∠BDC=90°,由勾股定理可求OC的长,可得点C坐标,利用待定系数法可求BC解析式,可判断②;由面积公式可求DH的长,代入解析式可求点D坐标,可判断③;由菱形的性质可得PD∥OC,可得点P纵坐标为,可判断④,即可求解.
【解答】解:∵直线yx+6分别与x、y轴交于点A、B,
∴点A(8,0),点B(0,6),
∴OA=8,OB=6,
∴AB10,故①正确;
∵线段OB沿BC翻折,点O落在AB边上的点D处,
∴OB=BD=6,OC=CD,∠BOC=∠BDC=90°,
∴AD=AB﹣BD=4,
∵AC2=AD2+CD2,
∴(8﹣OC)2=16+OC2,
∴OC=3,
∴点C(3,0),
设直线BC解析式为:y=kx+6,
∴0=3k+6,
∴k=﹣2,
∴直线BC解析式为:y=﹣2x+6,故②正确;
如图,过点D作DH⊥AC于H,
∵CD=OC=3,
∴CA=5,
∵S△ACDAC×DHCD×AD,
∴DH,
∴当y时,x+6,
∴x,
∴点D(,),故③正确;
∵线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,且OC=CD,
∴PD∥OC,PD=OC=3,
∴点P纵坐标为,
∵点D(,),
∵点P(,),
∴点P横坐标为,故④正确,
故选:D.
【点评】本题是一次函数综合题,考查了利用待定系数法求解析式,折叠的性质,面积法,菱形的性质,勾股定理等知识,灵活运用这些性质解决问题是本题的关键.
7.如图,直线yx+6分别与x轴、y轴交于点A、B,点C在线段OA上,线段OB沿BC翻折,点O落在AB边上的点D处,以下结论:
①AB=10;
②直线BC的解析式为y=﹣2x+6;
③点D(4.6,2.4);
④若线段BC上存在一点P,使得以点P、O、C、D为顶点的四边形为菱形,则点P的坐标是(1.5,2.4),
其中正确的结论是( )
A.①② B.①②③ C.①③④ D.①②④
【分析】根据一次函数的性质和翻折的性质以及勾股定理,菱形的性质对每个结论进行分析后再作出选择.
【解答】解:令y=0,则0x+6,
∴x=8,
∴OA=8,
令x=0,得y=6,
∴OB=6,B(0,6),
在Rt△AOB中,AB,
故①正确;
∵线段OB沿BC翻折,点O落在AB边上的点D处,
∴BD=BO=6,∠ADC=90°,DC=OC,
∴AD=4,
设OC=DC=x,则AC=8﹣x,
在Rt△ACD中,AD2+CD2=AC2,
即42+x2=(8﹣x)2,
解得:x=3,
∴点C(3,0),
设直线BC的解析式为y=kx+b,
把点B(0,6)和C(3,0)分别代入y=kx+b,得:
,
解得:,
∴直线BC的解析式为y=﹣2x+6,
故②正确;
如图1,过D作DE⊥OA于E,
根据三角形面积可得:DE,
在Rt△CDE中,CE,
∴OE=3+1.8=4.8,
∴点D坐标为(4.8,2.4),
故③不正确;
如图2,
当以点P、O、C、D为顶点的四边形为菱形时,PD∥x轴,
∴点P的纵坐标与点D的纵坐标相等,
把y=2.4代入直线y=﹣2x+6中,得x=1.8,
∴点P(1.8,2.4),
故④不正确;
综上,正确的结论有①②,
故选:A.
【点评】本题是一次函数综合题,主要考查一次函数的性质,翻折的性质,勾股定理,菱形的性质等知识点,深入理解题意是解决问题的关键.
8.如图,已知直线MN:yx+2交x轴负半轴于点A,交y轴于点B,点C是x轴上的一点,且OC=2,则∠MBC的度数为( )
A.45°或135° B.30°或150° C.60°或120° D.75°或165°
【分析】令y=0,可得A(﹣2,0),令x=0,可得B(0,2),利用勾股定理求出AB=4,可得∠MAO=30°,分两种情况考虑:①C点在x轴正半轴;②C点在x轴负半轴.分别计算出∠MBO、∠OBC度数,两个角的和差即为所求度数.
【解答】解:∵直线MN:yx+2交x轴负半轴于点A,交y轴于点B,
令y=0,则0x+2,解得x=﹣2,
∴A(﹣2,0),
令x=0,则y=2,
∴B(0,2),
∴AB4,
∴AB=2OB,
∵∠AOB=90°,
∴∠MAO=30°,
∴∠ABO=60°,∠MBO=120°.
∵B(0,2),OC=2,
∴OB=OC,
∴∠CBO=45°,
如图,分两种情况考虑:
①当点C在x轴正半轴上时,
∠C1BO=45°,
∴∠MBC1=120°﹣45°=75°;
②当点C在x轴负半轴上时,
∠MBC2=120°+45°=165°.
故选:D.
【点评】本题是一次函数综合题,考查了一次函数图象上点的坐标特征、含30度角的直角三角形、等腰直角三角形的判定与性质以及坐标与图形性质.分类讨论思想的运用是解题的关键.
9.如图,在平面直角坐标系xOy中,半径为2的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线yx﹣3与x轴、y轴分别交于点D、E,则点C到直线DE的最小距离为( )
A.1 B. C. D.
【分析】连接OC,由垂径定理得OC⊥AB,再由圆周角定理得点C在以OA为直径的圆上(点O、A除外),以OA为直径作⊙P,过P点作直线PH⊥DE于H,交⊙P于M、N,利用一次函数解析式确定E(0,﹣3),D(4,0),则DE=5,然后证△DPH∽△DEO,利用相似比求出PH的长,得MH、NH的长,即可求解.
【解答】解:连接OC,如图,
∵点C为弦AB的中点,
∴OC⊥AB,
∴∠ACO=90°,
∴点C在以OA为直径的圆上(点O、A除外),
以OA为直径作⊙P,过P点作直线PH⊥DE于H,交⊙P于M、N,
当x=0时,yx﹣3=﹣3,则E(0,﹣3),
当y=0时,x﹣3=0,
解得x=4,则D(4,0),
∴OD=4,
∴DE5,
∵⊙O的半径为2,
∴A(2,0),
∴P(1,0),
∴OP=1,
∴PD=OD﹣OP=3,
∵∠PDH=∠EDO,∠PHD=∠EOD=90°,
∴△DPH∽△DEO,
∴PH:OE=DP:DE,
即PH:3=3:5,
解得PH,
∴MH=PH+1,NH=PH﹣1.
∴点C到直线DE的最小距离为.
故选:C.
【点评】本题是一次函数综合题,考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理、相似三角形的判定与性质和一次函数的性质,解题的关键是正确寻找点C的运动轨迹,属于中考选择题中的压轴题.
10.如图,直线yx+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是( )
A.(4,2) B.(2,4)
C.(,3) D.(22,2)
【分析】求得直角△ABO的两条直角边的长,即可利用解直角三角形的方法求得AB,以及∠OAB的度数,则∠OAB′是直角,据此即可求解.
【解答】解:在yx+2中令x=0,解得:y=2;
令y=0,解得:x=2.
则OA=2,OB=2.
∴在直角△ABO中,AB4,∠BAO=30°,
又∵∠BAB′=60°,
∴∠OAB′=90°,
∴B′的坐标是(2,4).
故选:B.
【点评】本题考查了一次函数与解直角三角形,正确证明∠OAB′=90°是关键.
二.填空题(共10小题)
11.在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足,,则称点T是点A,B的“和谐点”.如图,点D(3,0),点E是直线l:y=2x+3上任意一点,若点T是点D,E的“和谐点”,直线ET交x轴于点H,当∠TDH为直角时,则点H到直线l的距离为 .
【分析】设点E的坐标为(x,2x+3),根据点T是点D,E的“和谐点”,表示出点T的坐标,进而根据∠TDH为直角可得点T和点D的横坐标相同得到x的值,即可求得点E和点T的坐标;求得直线ET的解析式,进而求得点H的坐标;作HM⊥l于点M,求得AE和AH的长度,根据△AEH的面积的不同表示方法求出点H到直线l的距离.
【解答】解:设点E的坐标为(x,2x+3),
∵点D(3,0),点T是点D,E的“和谐点”,
∴点T的坐标为(,).
∵∠TDH=90°,
∴点T的横坐标和点D的横坐标相同,
∴3.
解得:x=6.
∴点E的坐标为(6,15),点T的坐标为(3,5).
设直线ET的解析式为y=kx+n(k≠0).
∴,
解得:,
∴直线ET的解析式为yx﹣5.
当y=0时,x=1.5.
∴点H的坐标为(1.5,0).
∴OH.
作HM⊥l于点M.
由题意得:y=2x+3与x轴的交点A为(﹣1.5,0),
∴E点的,横坐标为6+1.5=7.5,
∴AE,AH=3.
∵S△AHEAH×15AE MH.
∴MH.
故答案为:.
【点评】本题考查一次函数的相关知识.理解新定义的意义并灵活应用是解决本题的关键.
12.如图,平面直角坐标系中,⊙P经过点A(8,0),O(0,0),B(0,6),点P关于x轴的对称点是P1,点D是⊙P上的一点.
(1)∠ADB= 90 °;
(2)当点D到弦OB的距离最大时,直线DP1与x轴的交点坐标为 .
【分析】(1)连接AB、AD、BD,利用圆周角定理:90度的圆周角所对的弦是直径,即可得到答案;
(2)由题意,先求出点D和点P的坐标,然后利用待定系数法求出解析式,令y=0,即可求出点C的坐标.
【解答】解:(1)连接AB、AD、BD,如图1:
∵⊙P经过点A(8,0),O(0,0),B(0,6),
又∵∠AOB=90°,
∴AB是直径,
∴,
∴∠ADB=90°,
故答案为:90;
(2)由(1)可知,点P是AB的中点,
∵A(8,0),B(0,6),
∴点P的坐标为(4,3),
∵点P关于x轴的对称点是P,
∴P的坐标为(4,﹣3),
∵当点D到弦OB的距离最大时,即作DE⊥OB,点P在DE上,如图2:连接DP,与x轴交点为C;
∴,
此时,点D的坐标为(9,3);
设直线DP1为y=kx+b,则把点(4,﹣3)和点(9,3)代入,得:
,
解得,
∴;
令y=0,则,
解得:,
∴直线DP与x轴的交点坐标为,
故答案为:.
【点评】本题考查了圆周角定理,轴对称的性质,勾股定理求线段的长度,以及待定系数法求直线的解析式,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行解题.
13.如图,在平面直角坐标系中,线段AB的端点为A(1,0),B(5,8).
(1)直线AB的函数解析式为 y=2x﹣2 ;
(2)某同学设计了一个动画:在函数y=﹣2x+b中,输入b(b>0)的值,得到直线CD,其中点C在x轴上,点D在y轴上.
①当△OCD的面积为6时,直线CD就会发蓝光,则此时输入的b的值为 2 ;
②当直线CD与线段AB有交点时,直线CD就会发红光,则此时输入的b的取值范围是 2≤b≤18 .
【分析】(1)用待定系数法求函数的解析式即可;
(2)①分别求出D(0,b),C(b,0),则S△OCDbb=6,求出b即可;
②当线段CD经过A点时,b=2;当线段CD经过B点时,b=18;则2≤b≤18时,直线CD就会发红光.
【解答】解:(1)设直线AB的解析式为y=kx+b,
∴,
解得,
∴直线AB的解析式为y=2x﹣2,
故答案为:y=2x﹣2;
(2)①当x=0时,y=b,
∴D(0,b),
当y=0时,xb,
∴C(b,0),
∴OCb,OD=b,
∴S△OCDbb=6,
解得b=2或b=﹣2(舍),
故答案为:2;
②当线段CD经过A点时,﹣2+b=0,
解得b=2;
当线段CD经过B点时,﹣10+b=8,
解得b=18;
∴2≤b≤18时,直线CD就会发红光,
故答案为:2≤b≤18.
【点评】本题考查一次函数的图象及性质,熟练掌握一次函数的图象及性质是解题的关键.
14.如图,一次函数的图象分别与x轴、y轴交于点A,B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
(1)△AOB的面积是 3 ;
(2)点C的坐标是 (5,3) ;
(3)过B,C两点直线的函数表达式为 .
【分析】(1)根据题意求得与坐标轴的交点坐标,进而根据三角形的面积公式求解即可;
(2)过点C作CD⊥x轴,垂足为D,证明△AOB≌△CDA,继而求得C的坐标,
(3)待定系数法求解析式即可.
【解答】解:(1)由,令x=0,则y=2,令y=0,则x=3,
∴A(3,0),B(0,2),
∴OA=3,OB=2,
∴,
故答案为:3;
(2)如图,过点C作CD⊥x轴,垂足为D,
∵等腰Rt△ABC,∠BAC=90°,∠ABO=∠CDA=90°,
∴∠BAO+∠CAD=90°,∠BAO+∠ABO=90°,AB=AC,
∴∠CAD=∠ABO,
∴△AOB≌△CDA,
∴AO=CD=3,AD=BO=2,
∴OD=5,
∴C(5,3),
故答案为:(5,3);
(3)设BC直线解析式为y=kx+b,则,
解得,
∴设BC直线解析式为y,
故答案为:.
【点评】本题考查了一次函数与坐标轴交点问题,全等三角形的性质,等腰三角形的性质,数形结合是解题的关键.
15.如图,已知一次函数y=kx+2的图象与y轴,x轴分别交于点A、B.
(1)若点(1,1)在函数图象上,则k= ﹣1 ;
(2)若S△OAB=3,则点B的坐标为 (3,0)或(﹣3,0) ;
(3)一次函数y=kx+2的图象与正比例函数y=2x的图象交于点.点P在x轴上,当△PBC为直角三角形时,点P的坐标为 或 .
【分析】(1)将点(1,1)代入y=kx+2即可得到k的值;
(2)利用解析式求出点A的坐标,再根据面积即可得到点B的坐标;
(3)利用点C的坐标求出一次函数的解析式,再根据等腰直角三角形的性质分两种情况:当∠CPB=90°时,当∠PCB=90°时,分别求解.
【解答】解:(1)∵点(1,1)在函数y=kx+2的图象上,
∴k+2=1,
得k=﹣1,
故答案为:﹣1;
(2)令y=kx+2中x=0,则y=2,
∴A(0,2),
∴OA=2,
∵,
∴OB=3,
∴B(3,0)或B(﹣3,0);
故答案为:(3,0)或(﹣3,0);
(3)将代入y=2x,得,
∴,
∴,
当∠CPB=90°时,点P的横坐标为,即;
当∠PCB=90°时,
将点代入y=kx+2,
∴,
解得k=﹣1,
∴y=﹣x+2,
当y=0时,x=2,
∴B(2,0),
∴OA=OB=2,
∴∠CPB=∠CBP=45°,
过点C作CE⊥OB于点E,
∴,
∴点P的横坐标为,
∴,
故答案为:或.
【点评】此题考查了一次函数与正比例函数的综合应用,待定系数法求解析式,一次函数与图形面积问题,等腰直角三角形的性质,熟练掌握一次函数的综合知识是解题的关键.
16.如图,在平面直角坐标系中,直线交x轴于点A、交y轴于点B,C点与A点关于y轴对称,动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.当△PQB为等腰三角形时,点P的坐标是 (2,0)或(,0) .
【分析】把x=0和y=0分别代入一次函数的解析式,求出B、A的坐标,分为三种情况:①PQ=BP,②BQ=QP,③BQ=BP,分别求解即可.
【解答】解:∵yx+6,
∴当x=0时,y=6,
当y=0时,x=﹣8,
即点A的坐标是(﹣8,0),点B的坐标是(0,6),
∵C点与A点关于y轴对称,
∴C的坐标是(8,0),
分为三种情况:
①当PB=PQ时,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
∵∠BPQ=∠BAO,∠BAO+∠AQP+∠APQ=180°,∠APQ+∠BPQ+∠BPC=180°,
∴∠AQP=∠BPC,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
在△APQ和△CBP中,
,
∴△APQ≌△CBP(AAS),
∴AP=CB,
∵B(0,6),C(8,0),
∴BC10,
∴AP=10,
∴点P的坐标是(2,0);
②当BQ=BP时,则∠BPQ=∠BQP,
∵∠BAO=∠BPQ,
∴∠BAO=∠BQP,
而根据三角形的外角性质得:∠BQP>∠BAO,
∴此种情况不存在;
③当QB=QP时,则∠BPQ=∠QBP=∠BAO,
即BP=AP,
设此时P的坐标是(x,0),
∵在Rt△OBP中,由勾股定理得:BP2=OP2+OB2,
∴(x+8)2=x2+62,
解得:x,
即此时P的坐标是(,0).
∴当△PQB为等腰三角形时,点P的坐标是(2,0)或(,0).
故答案为:(2,0)或(,0).
【点评】本题是一次函数综合题,考查了一次函数图象上点的坐标特征,勾股定理,等腰三角形的性质,全等三角形的性质和判定的应用,解题的关键是分类思想的运用.
17.在平面直角坐标系中,一次函数y=x+4的图象分别与x轴,y轴交于点A,B,点P在一次函数y=x的图象上,则当△ABP为直角三角形时,点P的坐标是 (0,0)或(﹣2,﹣2)或(2,2) .
【分析】设点P的坐标为(x,y),分三种情况:①当∠APB=90°时,②当∠PAB=90°时,③当∠PBA=90°时,根据勾股定理分别求解即可.
【解答】解:∵一次函数y=x+4的图象分别与x轴,y轴交于点A,B,
∴A(﹣4,0),B(0,4),
∴AB2=42+42=32,
设点P的坐标为(x,y),
∵点P在一次函数y=x的图象上,
∴点P的坐标为(x,x),
分三种情况:
①当∠APB=90°时,如图,
∵△ABP为直角三角形,
∴AP2+BP2=AB2,
∴(x+4)2+x2+x2+(4﹣x)2=32,
∴x=0,
∴点P的坐标是(0,0);
②当∠PAB=90°时,如图,
∵△ABP为直角三角形,
∴AP2+AB2=PB2,
∴(x+4)2+x2+32=x2+(4﹣x)2,
∴x=﹣2,
∴点P的坐标是(﹣2,﹣2);
③当∠PBA=90°时,如图,
∵△ABP为直角三角形,
∴AB2+BP2=AP2,
∴x2+(4﹣x)2+32=(x+4)2+x2,
∴x=2,
∴点P的坐标是(2,2).
综上,点P的坐标是(0,0)或(﹣2,﹣2)或(2,2).
【点评】本题是一次函数综合题,考查勾股定理、一次函数的性质等,解决问题的关键是分类思想的运用.
18.在平面直角坐标系xOy中,对于P、Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P、Q两点为“友好点”.如图中的P,Q两点即为“友好点”.已知点A的坐标为(﹣3,1).
(1)请在x轴上提供一个点A的“友好点”,它的坐标为 (﹣4,0)或(4,0) ;
(2)在点R(0,4),S(2,2),T(2,﹣3)中,为点A的“友好点”的是 R,S ;
(3)直线l:y=x﹣5,与x轴相交于点C,与y轴相交于点D,M为线段CD上一点,若第二象限存在点N,使得M,N两点为“友好点”,请你提供一个符合题意的点N,N的坐标为 (3,﹣2)(答案不唯一) .
【分析】(1)因为点A的“友好点”在x轴上,所以|x|=4,可得结论;
(2)把各点的横纵坐标的绝对值相加,得4,则是A的同族点;
(3)首先证明点M的横坐标与纵坐标的绝对值之和为定值5,然后“友好点”的定义即可解决问题.
【解答】解:(1)∵点A(﹣3,1)的“友好点”在x轴上,
∴纵坐标为0,
∴|x|=3+1=4,
∴x=±4,
∴点A的“友好点”的坐标为(﹣4,0)或(4,0);
故答案为:(﹣4,0)或(4,0);
(2)∵点A的坐标为(﹣3,1),
∴3+1=4,
点R(0,4),S(2,2),T(2,﹣3)中,
0+4=4,2+2=4,2+3=5,
∴点A的同族点的是R,S;
故答案为:R,S;
(3)由题意,直线y=x﹣5与x轴交于C(5,0),与y轴交于D(0,﹣5).
点M在线段CD上,设其坐标为(x,y),
则有:x≥0,y≤0,且y=x﹣5.
点M到x轴的距离为|y|,点M到y轴的距离为|x|,
则|x|+|y|=x﹣y=5.
∴点M的“友好点”N满足横纵坐标的绝对值之和为5.
∵第二象限存在点N,使得M,N两点为“友好点”,
∴N的坐标为(3,﹣2)(答案不唯一).
故答案为:(3,﹣2)(答案不唯一)..
【点评】本题是一次函数综合题、考查“友好点”的定义,坐标与图形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考压轴题.
19.如图,直线y=kx+2与x轴,y轴分别交于A,C两点,点B与点A关于y轴对称,连接BC,BC=2,点M,N分别是线段AB,AC上的动点(M不与A,B重合),且满足∠CMN=∠CBA.当△CMN为等腰三角形时,M的坐标为 (24,0)或(,0) .
【分析】先求解点C的坐标为(0,2),可得OC=2,再利用勾股定理求解OB4,可得点B坐标为(4,0),点A坐标为(﹣4,0),由△CMN为等腰三角形,可得CM=MN或CN=CM或NC=NM,当CM=MN时,证明△CBM≌△MAN即可,当CM=CN时,∠CMN=∠CNM≠∠CBA=∠CAB,不符合题意,舍去,当NC=NM时,如图,证明AM=CM,设OM=n,则AM=CM=4﹣n,再利用勾股定理求解即可.
【解答】解:在y=kx+2中,
当x=0时,y=2,
∴点C的坐标为(0,2),
∴OC=2,
在Rt△BOC中,BC=2,OB4,
∴点B坐标为(4,0),
∵点B与点A关于y轴对称,
∴点A坐标为(﹣4,0),
∵点B与点A关于y轴对称,
∴AC=BC,
∵△CMN为等腰三角形,
∴CM=MN或CN=CM或NC=NM,
当CM=MN时,
∵AC=BC,
∴∠CAB=∠CBA,
∵∠CMN=∠CBA,
∴∠BMN=∠BMC+∠CMN=∠BAC+∠ANM,
∴∠ANM=∠BMC,
∵∠MAN=∠CBM,NM=CM,
∴△CBM≌△MAN(AAS),
∴AM=BC=2,
∵OA=4,
∴OM=24,
∴M的坐标为(24,0),
当CM=CN时,
∴∠CMN=∠CNM≠∠CBA=∠CAB,不符合题意,舍去,
当NC=NM时,如图,
∴∠NCM=∠CMN=∠CBA=∠CAB,
∴AM=CM,
设OM=n,则AM=CM=4﹣n,
∴(4﹣n)2=n2+4,
解得:n,
∴M(,0),
综上:点M的坐标为(24,0)或(,0).
故答案为:(24,0)或(,0).
【点评】本题是一次函数综合题,考查的是坐标与图形,轴对称的性质,全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理的应用,分类讨论是解本题的关键.
20.如图,直线yx+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个长度单位的速度从点O出发向点A做匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标 (2,2) ;
(2)若△OQC是等腰直角三角形,则t的值为 2或4 .
【分析】(1)当x+3=x时,求点C的坐标即可;
(2)分两种情况讨论:当CQ⊥OQ时,t=2;当OC⊥CQ时,t=4.
【解答】解:(1)当x+3=x时,解得x=2,
∴C(2,2),
故答案为:(2,2);
(2)∵Q点的运动速度为每秒1个长度单位,运动时间为t秒,
∴OQ=t,
当CQ⊥OQ时,∵∠OCA=45°,
∴△OCQ为等腰直角三角形,
∴t=2;
当OC⊥CQ时,∵∠OCA=45°,
∴△OCQ为等腰直角三角形,
∴Q(4,0),
∴t=4;
综上所述:t的值为2或4,
故答案为:2或4.
【点评】本题考查一次函数的图象及性质,熟练掌握一次函数的图象及性质,等腰直角三角形的性质是解题的关键.
三.解答题(共10小题)
21.如图1,已知直线l1:y=kx+b交x轴于A(6,0),交y轴于B(0,6).
(1)求直线l的表达式;
(2)如图2,直线CP的表达式为,点P为线段AB的中点,在直线CP上找一点Q,使得OQ+AQ最小,并求出最小值;
(3)如图3,已知点M(﹣2,0),点N(m,2m﹣6)为直线AB右侧一点,且满足∠OBM=∠ABN,求m的值.
【分析】(1)把A(6,0),B(0,6)代入y=kx+b,即可求解;
(2)如图:作点O关于CP的对称点R,连接AR交CP于点Q,则此时OQ+AQ最小,即可求解;
(3)作M关于y轴的对称点G(2,0),以G为直角顶点,BG为直角边在BG右侧作等腰直角三角形BGH,过H作HK⊥x轴于K,可证明N在直线BH上,由△BOG≌△GKH(AAS),可得H(8,2),直线BH解析式为yx+6,把N(m,2m﹣6)代入可得答案.
【解答】解:(1)把A(6,0),B(0,6)代入y=kx+b得:,
解得:,
故直线l的表达式为y=﹣x+6;
(2)如图:作点O关于CP的对称点R,连接AR交CP于点Q,则此时OQ+AQ最小,
理由:OQ+AQ=RQ+AQ=RA,
设OR交CP于点T,则点T是OR的中点,
∵A(6,0),B(0,6),
∴线段AB的中点P的坐标为(3,3),
把P(3,3)代入yx+c得:3c,
解得c,
∴直线l2的解析式为yx,
∵CP⊥OR,则直线OR的表达式为:y=﹣2x,
联立上述两个函数表达式得:﹣2xx,
解得:x,即点T(,),
由中点坐标公式得,点R(,),
由点A、R的坐标得,AR,
即OQ+AQ最小值为;
(3)作M关于y轴的对称点G(2,0),以G为直角顶点,BG为直角边在BG右侧作等腰直角三角形BGH,过H作HK⊥x轴于K,如图:
∴∠OBM=∠OBG,
∵A(6,0),B(0,6),
∴△AOB是等腰直角三角形,
∴∠OBG+∠ABG=45°,
∵△BGH是等腰直角三角形,
∴∠ABG+∠ABH=45°,BG=GH,
∴∠OBG=∠ABH,
∴∠OBM=∠ABH,
∴N在直线BH上,
∵∠OGB=90°﹣∠HGK=∠GHK,∠BOG=∠GKH=90°,BG=GH,
∴△BOG≌△GKH(AAS),
∴BO=GK=6,OG=HK=2,
∴H(8,2),
由B(0,6),H(8,2)可得直线BH解析式为yx+6,
把N(m,2m﹣6)代入得:
2m﹣6m+6,
解得m.
【点评】本题考查一次函数的综合应用,涉及待定系数法,三角形面积,全等三角形判定与性质等知识,解题的关键是用含字母的式子表示相关点坐标和相关线段的长度.
22.在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且,直线l2:y=k2x+b经过点,1),与直线AB交于点D.
(1)求直线l1的解析式;
(2)如图2,连接CB、AC,求△ABC的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
【分析】(1)根据待定系数法可得直线l1的解析式;
(2)由△ABC的面积BH×(xC﹣xA)(2)=8,即可求解;
(3)分四种情况:在x轴和y轴上,证明△DMQ≌△QNC(AAS),得DM=QN,QM=CN,设D(m,m+6)(m<0),表示点Q的坐标,根据OQ的长列方程可得m的值,从而得到结论.
【解答】解:(1)y=k1x+6,
当x=0时,y=6,
∴OB=6,
∵OBOA,
∴OA=2,
∴A(﹣2,0),
把A(﹣2,0)代入:y=k1x+6中得:﹣2k1+6=0,
k1,
∴直线l1的解析式为:yx+6;
(2)设AC交x轴于点H,
由点A、C的坐标得,直线AC的表达式为:yx,即点H(0,),
则BH=6,
则△ABC的面积BH×(xC﹣xA)(2)=8;
(3)存在,分四种情况:
①当Q在y轴的正半轴上时,如图2,过D作DM⊥y轴于M,过C作CN⊥y轴于N,
∵△QCD是以CD为底边的等腰直角三角形,
∴∠CQD=90°,CQ=DQ,
∴∠DMQ=∠CNQ=90°,
∴∠MDQ=∠CQN,
∴△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN,
设D(m,m+6)(m<0),则Q(0,﹣m+1),
∴OQ=QN+ON=OM+QM,
即﹣m+1m+6,
m=1﹣2,
∴Q(0,2);
②当Q在x轴的负半轴上时,如图3,过D作DM⊥x轴于M,过C作CN⊥x轴于N,
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=1,
设D(m,m+6)(m<0),则Q(m+1,0),
∴OQ=QN﹣ON=OM﹣QM,
即m+6m﹣1,
m=5﹣4,
∴Q(6﹣4,0);
③当Q在x轴的负半轴上时,如图4,过D作DM⊥x轴于M,过C作CN⊥x轴于N,
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=1,
设D(m,m+6)(m<0),则Q(m﹣1,0),
∴OQ=QN﹣ON=OM+QM,
即m﹣6m+1,
m=﹣45,
∴Q(﹣46,0);
④当Q在y轴的负半轴上时,如图5,过D作DM⊥y轴于M,过C作CN⊥y轴于N,
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN
设D(m,m+6)(m<0),则Q(0,m+1),
∴OQ=QN﹣ON=OM+QM,
即m﹣6m﹣1,
m=﹣21,
∴Q(0,﹣2);
综上,存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2)或(6﹣4,0)或(﹣46,0).
【点评】本题属于一次函数综合题,考查了待定系数法,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考压轴题.
23.在平面直角坐标系xOy中,对于点P,Q和图形W,若图形W上存在点K使得∠PQK=α(0°<α<180°),则称图形W与PQ“α关联”.
(1)已知P(0,0),Q(1,0),以下列各点为中心,作边长为1的正方形W,若W与PQ“45°关联”,则这个中心可能是 ①③ .
①(1,﹣1);②(2,0);③(0,1).
(2)如图,已知直线l.
①已知P,Q在直线y=﹣2上运动,且点P在点Q左侧.设直线l与x轴,y轴分别交于M,N两点,若线段MN与PQ“α关联”,其中60°<α<90°,求Q点横坐标t的取值范围;
②已知P(﹣1,0),Q(0,0).长度为1的线段ST在l上,以ST上任意一点为圆心作半径为r的圆,对每一个圆总存在α使之与PQ既是“α关联”又是“α+60°关联”但不是“α+90°关联”,直接写出r的取值范围.
【分析】(1)根据题意得出,正方形W与射线OK有交点,进而求得边长为1的正方形W的中心到边长的距离的范围,进而判断即可求解;
(2)①根据一次函数与坐标轴交点结合特殊角的三角函数值得出∠NMO=30°,根据P,Q在直线y=﹣2上运动,且点P在点Q左侧.线段MN与PQ“α关联”,其中60°<α<90°,分别画出α=∠PMQ=90°.∠PQN=α=60°时的Q点的位置,进而结合图形,即可求解;
②设R为ST上任意一点,QF、QG分别为⊙R的两条切线,根据ST上任意一点为圆心作半径为r的圆,对每一个圆总存在α使之与PQ既是“a关联”又是a+60°关联”但不是“a+90°关联“得出,进而求得QR的最小值,得出,即可求解.
【解答】解:(1)∵W与PQ“45°关联”,
∴∠PQK=45°,
如图所示,正方形ABCD的边长为1,E是AB的中点,
∴,,
正方形的中心到边上的距离的范围为:,
边长为1的正方形W,W与PQ“45°关联”,
则正方形W与射线OK有交点,
∵①(1,﹣1);②(2,0);③(0,1),
如图所示,
点③(0,1)在射线OK上,
①(1,﹣1)到OK1的距离为,则以(1,﹣1)为中心的正方形W与OK1有交点,
综上所述,若W与PQ“45°关联”,则这个中心可能是①③,
故答案为:①③;
(2)①已知直线l:,直线l与x轴,y轴分别交于M,N两点,
当x=0时,y=3;当y=0时,,
∴,N(0,3),
∴ON=3,,
∴,
∴∠NMO=30°,
∵P,Q在直线y=﹣2上运动,且点P在点Q左侧.线段MN与PQ“a关联”,其中60°<α<90°,
∴当MQ垂直于直线y=﹣2时,Q点的横纵坐标最小(不取等于号),此时α=∠PMQ=90°,
∴,
当∠PQN=α=60°时,如图所示,设PQ与y轴交于点F,则F(0,﹣2),
∴FN=3﹣(﹣2)=5,
∴,
Q点横坐标t的取值范围为:;
②设R为ST上任意一点,QF,QG分别为⊙R的两条切线,
如图所示,当∠FQG=90°时,
∴∠QFR=∠RGQ=∠FQG=90°,
∴四边形QFRG是矩形,
又∵RF=RG,
∴四边形QFRG是正方形,
∴,
当∠MQN=60°时,则∠RQF=30°,则QR=2FR=2r,
∵ST上任意一点为圆心作半径为r的圆,对每一个圆总存在α使之与PQ既是“α关联”又是“α+60°关联”但不是°α+90°关联”,
∴,
∵ST在直线l:上,
∴当QR⊥I时,QR取得最小值,则r取得最小值,如图所示,
由①可得ON=3,,则MN=6,
此时,
∴,
∴.
【点评】本题主要考查了一次函数综合考点,正方形的性质,特殊的三角函数值,圆的切线等相关知识,正确理解相对应的规定并熟练应用是解题的关键.
24.如图1,一次函数y=k1x+b的图象与x轴交于点A,与y轴交于点B(0,4),与正比例函数y=k2x的图象交于点C(6,12).
(1)直接写出正比例函数与一次函数的表达式;
(2)如图2,点E是直线BC上的一动点(与B,C点不重合),过点E作EP⊥x轴于点P,交直线OC于点F,设点E的横坐标为a,用含a的式子表示EF的长,并求出当EF=2OB时,a的值;
(3)如图3,在(2)的条件下,若E是线段BC上一动点(与B,C点不重合),连接CP,直线OC能否把△CEP分成面积之比为1:3的两部分?若能,请求出E点坐标;若不能,请说明理由.
【分析】(1)根据待定系数法求解即可;
(2)根据两点距离公式表示出EF的长,然后求出OB的长,代入数量关系式中,求解a值即可;
(3)根据等高三角形的面积比等于底边长之比,分类讨论求解a的值,从而得到E的坐标即可.
【解答】解:(1)将B,C的坐标代入一次函数解析式:
,
∴k1,b=4,
∴一次函数的表达式:yx+4,
将C点坐标代入正比例函数解析式:
12=6k2,
∴k2=2,
∴正比例函数的表达式:y=2x;
(2)∵点E的横坐标为a,
∴E(a,a+4),
∵EP⊥x轴,
∴F(a,2a),
∴EF=|a+4﹣2a|=|4a|,
∵B(0,4),
∴OB=4,
∵EF=2OB,
∴|4a|=4,
∴a=0或12;
(3)∵E在线段BC上,
∴0<a<6,
∵EP⊥x轴,
∴P(a,0),
∴EPa+4,EF=4a,
∵直线OC能否把△CEP分成面积之比为1:3的两部分,
∴EF:EP=1:4或3:4,
∴4aa+1或16a=4a+12,
解得:a=3或,
∴E(3,8)或(,).
【点评】本题主要考查了一次函数综合题,综合运用待定系数法求一次函数解析式及正比例函数解析式、两点之间的距离以及三角形的面积来解答是本题解题的关键.
25.如图①,直线y=2x+b与x轴交于点A(4,0),与y轴交于点B,与直线y=﹣2x交于点C(a,﹣4).
(1)求点C的坐标及直线AB的表达式;
(2)点P在y轴上,若△PBC的面积为6,求点P的坐标;
(3)如图②,过x轴正半轴上的动点D(m,0)作直线l⊥x轴,点Q在直线l上,若以BC为腰的△BCQ是等腰直角三角形,请直接写出相应m的值.
【分析】(1)将点C的坐标代入直线y=﹣2x可得出a的值,即得C点坐标,再用待定系数法求直线AB的表达式即可;
(2)设点P的坐标为(0,p),根据△PBC的面积为6求解即可;
(3)分三种情况:①当BC=BQ时,过点C作CM⊥y轴于M,过点Q作QN⊥y轴于N,②当BC=CQ时,过点C作CM⊥y轴于M,延长MC交直线l于N,即可得到结论.
【解答】解:(1)∵点C(a,﹣4)在直线y=﹣2x上,
∴﹣2a=﹣4,
解得:a=2,
∴C(2,﹣4),
由点A、C的坐标得,AB的解析式为:y=2x﹣8;
(2)设点P的坐标为(0,p),
∵直线AB的解析式为:y=2x﹣8,
∴B(0,﹣8),
∴BP=|p+8|,
∵△PBC的面积为6,C(2,﹣4),
∴S△PBC2|p+8|=6,
∴p=﹣2或﹣14,
∴点P的坐标为(0,﹣2)或(0,﹣14);
(3)存在,
以B,C,Q为顶点的三角形是等腰直角三角形,分以下三种情况:
①当BC=BQ时,过点C作CM⊥y轴于M,过点Q作QN⊥y轴于N,
∴∠BMC=∠QNB=90°,
∴∠CBM+∠BCM=90°,
∵∠QBC=90°,
∴∠CBM+∠QBN=90°,
∴∠BCM=∠QBN,
∵BC=BQ,
∴△BCM≌△QBN(AAS),
∴QN=BM,BN=CM,
∵B(0,﹣8),C(2,﹣4),
BM=4,CM=2,
∴QN=BM=4,
∴m=4;
②当BC=CQ时,过点C作CM⊥y轴于M,延长MC交直线l于N,
同理:△BCM≌△CQN(AAS),
∴QN=CM=2,BM=CN=4,
∴MN=MC+CN=6
∴m=6;
故m的值为4或6.
【点评】此题是一次函数综合题,考查了一次函数图象上点的坐标特征,两点间的距离,三角形的面积,等腰直角三角形的性质,全等三角形的判定和性质,熟练掌握方程的思想方法及分类讨论思想是解本题的关键.
26.如图,在平面直角坐标系xOy中,直线l1:y的图象与x轴、y轴分别交于D,B两点.直线y=kx的图象与x轴交于C.直线l1与直线l2交于点A(a,3).
(1)求点A的坐标及直线l2的表达式;
(2)若点E在直线l2上,且△ADE的面积为,求点E的坐标;
(3)在x轴上是否存在点P,使得∠ACB=2∠APC,若存在,求出点P坐标,若不存在,说明理由.
【分析】(1)当y=3时,y3,得到点A(1,3),再由待定系数法即可求解;
(2)当点E在y轴左侧时,由△ADE的面积DH×(xA﹣xE)(1﹣m),得到点E(﹣1,);当点E(E′)在y轴右侧时,则此时点E、E关于点A对称,即可求解;
(3)当点P在y轴左侧时,证明PC=AC,设点P(x,0),即可求解;当点P(P′)在y轴右侧时,则点P′、P关于点A对称,即可求解.
【解答】解:(1)当y=3时,y3,
解得:x=1=a,即点A(1,3),
将点A的坐标代入函数表达式得:3=k,则k,
则直线l2的表达式为:yx;
(2)如图1,当点E在y轴左侧时,
设直线l2和y轴交于点H(0,),设点E(m,m),由函数的表达式知,点D(0,),
则DH,
则△ADE的面积DH×(xA﹣xE)(1﹣m),
解得:m=﹣1,即点E(﹣1,);
当点E(E′)在y轴右侧时,
则此时点E、E关于点A对称,
由中点坐标公式得:点E′(3,),
即点E的坐标为:(﹣1,)或(3,);
(3)存在,理由:由函数的表达式知,点C(﹣3,0),
当点P在y轴左侧时,如图2,
∵∠ACB=2∠APC,则∠CPA=∠CAP,
即PC=AC,设点P(x,0),
由点A、P、C的坐标得,AC=5,PC=﹣3﹣x=5,
解得:x=﹣8,即点P(﹣8,0),
当点P(P′)在y轴右侧时,
则点P′、P关于点A对称,
由中点坐标公式得:点P′(10,0),
综上,P(﹣8,0)或(10,0).
【点评】本题考查的是一次函数综合运用,涉及到等腰三角形的性质、面积的计算,数形结合和分类求解是解题的关键.
27.如图,在平面直角坐标系中,一次函数y=k1x+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=k2x的图象交于点C(3,4).
(1)求正比例函数与一次函数的表达式;
(2)求△OBC的面积;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标;
(4)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标.
(5)在y轴上是否存在一点P,使△POC为等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
【分析】(1)由待定系数法即可求解;
(2)由△OBC的面积OB×xC2×3=3,即可求解;
(3)作C关于x轴对称点C',连接BC',交x轴于E,此时△BCE周长最小,即可求解;
(4)①当DA⊥AB时,证明△DAM≌△ABO,则DM=AO=3,AM=BO=2,即D(﹣5,3);②当D′B⊥AB时,同理可解;
(5)当PO=CO时,则y2=25,即可求解;当PO=PC或CO=PC时,同理可解.
【解答】解:(1)∵正比例函数y=kx的图象经过点C(3,4),
∴4=3k,
∴k,
∴正比例函数解析式为yx,
∵一次函数y=k1x+b的图象经过A(﹣3,0),C(3,4),
∴,
∴,
∴一次函数为yx+2;
(2)由一次函数的表达式知,点B(0,2),即OB=2,
则△OBC的面积OB×xC2×3=3;
(3)存在,理由:
如图,
作C关于x轴对称点C',连接BC',交x轴于E,此时△BCE周长最小.
∵C(3,4),
∴C'(3,﹣4),
∵B(0,2)
∴BC'的解析式为:y=﹣2x+2
令y=0,得0=﹣2x+2,
∴x=1
∴E点的坐标为(1,0);
(4)①当DA⊥AB时,如图,作DM⊥x轴垂足为M,
∵∠DAM+∠BAO=90°,∠BAO+∠ABO=90°,
∴∠DAM=∠ABO,
∵DA=AB,∠DMA=∠AOB,
∴△DAM≌△ABO,
∴DM=AO=3,AM=BO=2,
∴D(﹣5,3),
②当D′B⊥AB时,作D′N⊥y轴垂足为N,
同理得△D′BN≌△BAO
∴D′N=BO=2,BN=AO=3,
∴D′(﹣2,5)
∴D点坐标为(﹣5,3)或(﹣2,5);
(5)存在,理由:
设点P(0,y),
由点P、C、O的坐标得:PO2=y2,CO2=25,PC2=9+(y﹣4)2,
当PO=CO时,
则y2=25,则y=±5,
即点P(0,5)或(0,﹣5);
当PO=PC或CO=PC时,
则y2=9+(y﹣4)2或25=9+(y﹣4)2,
解得:y=0(舍去)或8或,
即点P(0,8)或(0,);
综上,P(0,5)或(0,﹣5)或(0,8)或(0,).
【点评】此题是一次函数综合题,主要考查待定系数法求一次函数、全等三角形的判定和性质、勾股定理、添加辅助线构造全等三角形等知识,学会分类讨论的数学思想是正确解题的关键.
28.如图,将正比例函数y=﹣2x的图象向上平移2个单位长度后得到的一次函数图象与x轴、y轴分别交于A、B两点,P(m,n)是线段AB(不含端点)上一动点,设△AOP的面积是S.
(1)求点B的坐标;
(2)求S关于m的函数表达式,并写出自变量m的取值范围;
(3)当时,在x轴上是否存在一点Q,使得PQ+BQ的值最小?若存在,求出点Q的坐标;若不存在,请说明理由.
【分析】(1)从图中不难发现,点B在y轴上,即B点的横坐标为0,且点B在一次函数y=﹣2x+2的图象上,则将x=0代入即可求得y值,B点坐标即可确定;
(2)根据A点为一次函数y=﹣2x+2的图象与x轴的交点,不难确定A点的坐标为(1,0),再运用三角形的面积计算公式,即可用求得;
(3)要使得PQ+BQ最小,找出点P对称点P′,然后连接BP′且求出解析式y=﹣6x+2,当y=0时即可求出点Q的坐标.
【解答】解:(1)将正比例函数y=﹣2x的图象向上平移2个单位长度后得到的一次函数为:y=﹣2x+2,
当x=0,则y=2,
∴点B的坐标为(0,2);
(2)点P(m,﹣2m+2),
由y=﹣2x+2,令y=0,则x=1,
∴点A的坐标为(1,0),
∴OA=1,
∴S△AOPOA y1×(﹣2m+2)=﹣m+1,
即S=﹣m+1(0<m<1);
(3)当S时,在x轴上存在一点Q,使得PQ+BQ最小,理由如下:
当Sx+1,
解得:x,
∴点P的坐标为(,1),
∴点P关于x轴的对称点P′的坐标是(,﹣1),
如图,
设直线BP′的函数表达式为y=kx+b,把点B(0,2)代入,解得:b=2,
将P′(,﹣1)代入y=kx+2,解得:k=﹣6,
∴y=﹣6x+2,
当y=0时,0=﹣6x+2,
解得x,
∴在x轴上存在一点Q(,0),使得PQ+BQ最小.
【点评】此题考查了一次函数的综合应用,待定系数法求函数解析式,最短距离问题,熟练掌握知识点是解题的关键.
29.如图,在四边形ABCD中,AB∥CD,AB=2CD=6,AD=5,∠DCB=90°,连接BD.点P从点A出发,以每秒一个单位的速度沿折线A→B→D运动,到达D点停止.设点P的运动时间为x秒(0<x<11),△DAP的面积为y.
(1)请直接写出y与x的函数关系式,并注明自变量x的取值范围;
(2)在给定的平面直角坐标系中画出y的函数图象,并写出关于函数y的一条性质 当0<x≤6时,y随x增大而增大,当6<x<11时,y随x的增大而减小(答案不唯一) ;
(3)若该函数图象与直线y=x+k恰好有一个交点,则常数k的取值范围是 k=6或﹣11<k≤0 .
【分析】(1)当点P在AB上时,则yAP DHx×4=2x;当点P在BD上移动时,同理可解;
(2)当x=0时,y=0,当x=6时,y=12,当x=11时,y=0,根据上述各点绘制函数图象即可;观察函数图象得到函数性质;
(3)当直线y=x+k在m、n、l的位置时,属于临界点,即可求解.
【解答】解:(1)作DH⊥AB于点H,
∵0<x<11,则BD=11﹣6=5,
即△ABD为等腰三角形,则BH=CD=3=AH,
则DH4,
则sin∠DBA,
当点P在AB上时,
则yAP DHx×4=2x;
当点P在BD上移动时,
则y=S△ABD﹣S△ABP6×4AB×PBsin∠DBA=126(x﹣6)x,
则y;
(2)当x=0时,y=0,当x=6时,y=12,当x=11时,y=0,
根据上述各点绘制函数图象如下:
从函数图象看,当0<x≤6时,y随x增大而增大,当6<x<11时,y随x的增大而减小(答案不唯一),
故答案为:当0<x≤6时,y随x增大而增大,当6<x<11时,y随x的增大而减小(答案不唯一);
(3)当直线y=x+k在m、n、l的位置时,属于临界点,
直线m:将点(6,12)代入y=x+k得:12=6+k,则k=6;
直线n:k=0;
直线l:同理可得:k=﹣11,
故k=6或﹣11<k≤0,
故答案为:k=6或﹣11<k≤0.
【点评】此题重点考查平行线的性质、矩形的判定与性质、勾股定理、三角形的面积公式、一次函数的图象与性质、数形结合与分类讨论数学思想的运用等知识与方法,此题综合性强,难度较大,属于考试压轴题.
30.如图,在平面直角坐标系中,直线y=2x+4与x轴,y轴分别交于点A,C,经过点C的直线与x轴交于点B(4,0),点D是直线AC上一动点.
(1)求直线BC的解析式;
(2)当点D在直线AC上运动时,存在某时刻,使得△DBC为直角三角形且∠CBD=90°,请求出此时点D的坐标;
(3)如备用图所示,当点D运动到线段AC的中点时,此时,在直线BC上是否存在点P,使得∠DAP=45°,若存在,请求出P点坐标;若不存在,请说明理由.
【分析】(1)先求出点A(﹣2,0),点C(0,4),设直线BC的解析式为:y=kx+b,将点(4,0),点C(0,4)代入y=kx+b之中求出,由此可得直线BC的解析式;
(2)设直线BD的解析式为:y=mx+n,根据直线BC的解析式为y=﹣x+4,BD⊥BC得m=1,将m=1,点B(4,0)代入y=mx+n求出,则直线BD的解析式为y=x﹣4,解方程组即可得出点D的坐标;
(3)依题意有以下两种情况:①当点P在直线AC的右侧时,过点P作PE⊥x轴于E,PH⊥AC于H,设点P(t,﹣t+4),则PE=﹣t+4,OE=t,显然t>0,AE=2+t,AB=6,由勾股定理得AC,AP,证明△APH为等腰直角三角形则PH=AH,由勾股定理得APPH,则PH,再根据S△ABC=S△APC+S△ABP构造关于t的方程,然后解方程求出t=2.5,进而可得点P的坐标;②当点P在仔细ACDE左侧时,设为P',则PA⊥P'A,先求出直线PA的解析式,进而得直线P'A的解析式为y=﹣3x﹣6,解方程组即可得出点P'的坐标,综上所述即可得出答案.
【解答】解:(1)对于y=2x+4,当x=0时,y=4,当y=0时,x=﹣2,
∴点A(﹣2,0),点C(0,4),
设直线BC的解析式为:y=kx+b,
将点(4,0),点C(0,4)代入y=kx+b,
得:,解得:,
∴直线BC的解析式为:y=﹣x+4;
(2)过点B作BD⊥BC交直线AC于点D,则点D符合条件,如图1所示:
设直线BD的解析式为:y=mx+n,
∵直线BC的解析式为:y=﹣x+4,BD⊥BC,
∴m=1,
将m=1,点B(4,0)代入y=mx+n,
得:,解得:,
∴直线BD的解析式为:y=x﹣4,
解方程组:,得:,
∴点D(﹣8,﹣12);
(3)直线BC上存在点P,使∠DAP=45°,
依题意有以下两种情况:
①当点P在直线AC的右侧时,过点P作PE⊥x轴于E,PH⊥AC于H,如图2所示:
∵点P在直线BC:y=﹣x+4上,
∴设点P(t,﹣t+4),
则PE=﹣t+4,OE=t,显然t>0,
∵点A(﹣2,0),点C(0,4),点B(4,0),
∴OA=2,OC=OB=4,
∴AE=OA+OE=2+t,AB=OA+OB=6,
在Rt△AOC中,由勾股定理得:AC,
在Rt△APE中,由勾股定理得:AP,
∵∠DAP=45°,PH⊥AC,
∴△APH为等腰直角三角形,
∴PH=AH,
由勾股定理得:APPH,
∴PH,
∴PH,
∵S△ABC=S△APC+S△ABP,
∴AB OCAC PH+1AB PE,
即AB OC=AC PH+AB PE,
∴,
即,
整理得:2t2+5t﹣25=0,
解得:t=2.5,t=﹣5(不合题意,舍去),
∴﹣t+4=﹣2.5+4=1.5,
∴点P(2.5,1.5);
②当点P在仔细ACDE左侧时,设为P',如图3所示:
∵∠DAP=∠DAP'=45°,
∴∠PAP'=90°,
即PA⊥P'A,
设直线PA的解析式为:y=k1x+b1,
将A(﹣2,0),点P(2.5,1.5)代入y=k1x+b1,
得:,解得:,
∴直线PA的解析式为:,
设P'A的解析式为:y=k2x+b2,
∵PA⊥P'A,
∴k2=﹣3,
将k2=﹣3,点A(﹣2,0)代入y=k2x+b2,
得:,解得:,
∴直线P'A的解析式为:y=﹣3x﹣6,
解方程组:,得:,
∴点P'的坐标为(﹣5,9).
综上所述:直线BC上是否存在点P,使得∠DAP=45°,此时点P的坐标为(2.5,1.5)或(﹣5,9).
【点评】此题主要考查了一次函数的图象,等腰直角三角形的判定和性质,勾股定理,三角形的面积等知识点,熟练掌握待定系数法求函数的解析式,以及求两个一次函数的图象交点坐标的方法是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
