【高考押题预测】2025年高考数学核心考点考前冲刺 样本相关系数(填空题)(含解析)
文档属性
| 名称 | 【高考押题预测】2025年高考数学核心考点考前冲刺 样本相关系数(填空题)(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 142.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
样本相关系数(填空题)
一.填空题(共20小题)
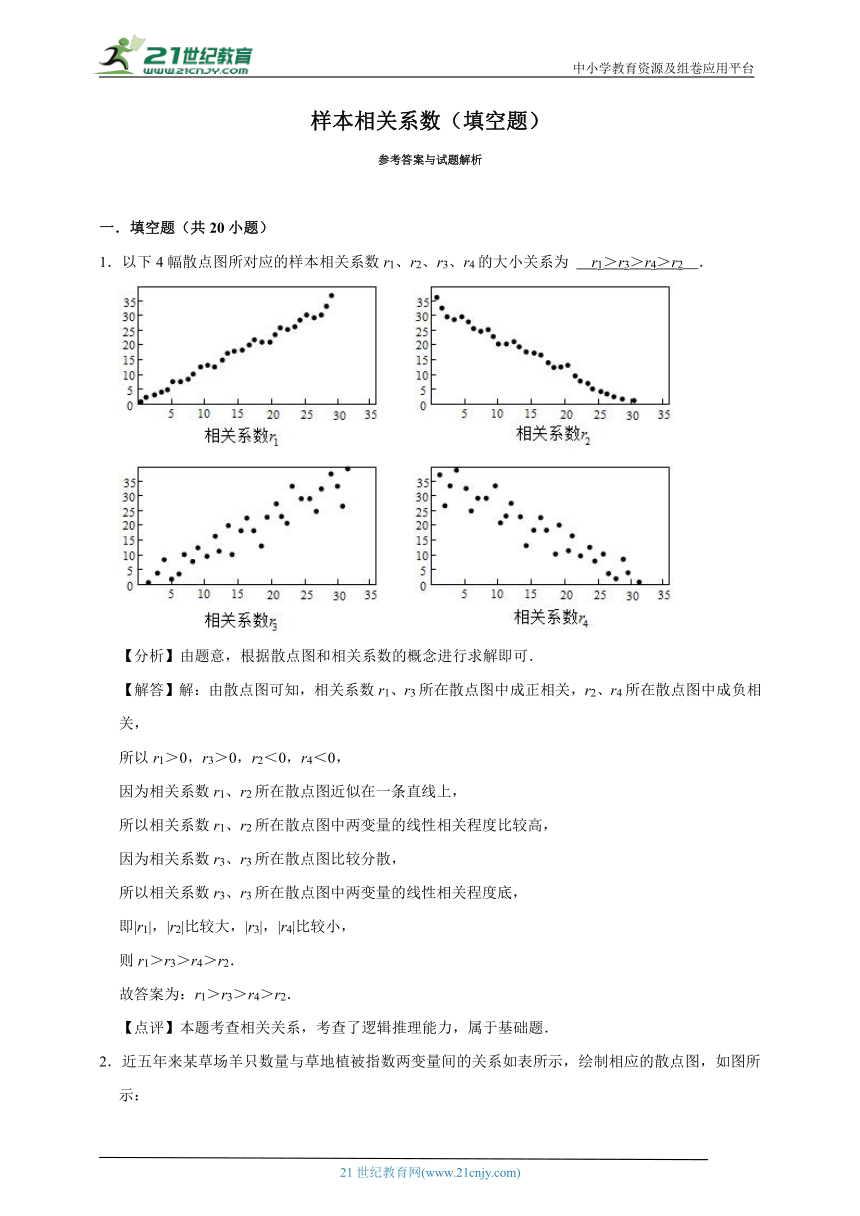
1.以下4幅散点图所对应的样本相关系数r1、r2、r3、r4的大小关系为 .
2.近五年来某草场羊只数量与草地植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 1 2 3 4 5
羊只数量/万只 1.4 0.9 0.75 0.6 0.3
草地植被指数 1.1 4.3 15.6 31.3 49.7
若利用这五组数据得到的两变量间的相关系数为r1,去掉第一年数据(1.4,1.1)后得到的相关系数为r2,则r1 r2(填≥,≤,<,>,=).
3.在一组样本数据(x1,y1),(x2,y2),…,((xn,yn),(n≥2,x1,x2…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线上,则这组样本数据的样本相关系数为 .
4.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2, ,n)都在直线上,则这组样本数据的样本相关系数为 .
5.若已知是的4倍,是的1.5倍,则相关系数r的值为 .
6.已知成对样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥3)中x1,x2,…,xn互不相等,且所有样本点(xi,yi)(i=1,2,…,n)都在直线上,则这组成对样本数据的样本相关系数r= .
7.现调查某地区某种野生动物的数量,将该地区分成面积相近的200个地块,从这些地块中简单随机抽样的方法抽取20个作为样本,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi、yi分别表示第i个样本的植物覆盖面积(单位:公顷)和这种野生动物的数量,构造向量,其中,,并计算得00,由选择性必修二教材中的知识,我们知道n对数据的相关系数,则上述数据(xi,yi)(i=1,2,…,20)的相关系数r= .
8.对于相关系数r,下列说法中错误的是 .
①r=0时,成对样本数据线性相关程度较弱;
②r>0时,表明成对样本数据正相关;
③若线性回归方程中的回归系数,则相关系数r>0;
④|r|越接近1,线性相关程度越强,|r|越接近0,线性相关程度越弱.
9.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)(n≥10)对应的点位于同一直线上,则x,y的相关系数为 .
10.一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2…xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2…n)都在直线y=﹣3x+1上,则这组样本数据相关系数为 .
11.在研究线性回归模型时,样本数据(xi,yi)(i=1,2,3, ,n)所对应的点均在直线上,用r表示解释变量对于反应变量变化的线性相关度,则r= .
12.为了比较甲、乙、丙三组数据的线性相关性强弱,某同学分别计算了甲、乙、丙三组数据的线性相关系数,求得数值依次为0.57,﹣0.93,0.89,则这三组数据中,线性相关性最强的是 组数据.
13.学习于才干信仰,犹如运动于健康体魄,持之已久、行之愈远愈受益.为实现中华民族伟大复兴,全国各行各业掀起了“学习强国”的高潮.某老师很喜欢“学习强国”中“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数如下表:
天数x 1 2 3 4 5 6 7
一次最多答对题数y 12 15 16 18 21 24 27
参考数据:,,,,,,
相关系数
由表中数据可知该老师每天一次最多答对题数y与天数x之间是 相关(填“正”或“负”),其相关系数r≈ (结果保留两位小数)
14.在散点图中,若所有的样本点都落在一条斜率为非0实数的直线上,则相关系数|r|= .
15.已知变量x,y之间的一组相关数据如表所示,则变量x,y之间的相关系数r= .
x 6 8 10 12
y 6 5 3 2
16.已知成对样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2)中x1,x2,…,xn不全相等,且所有样本点(xi,yi)(i=1,2, ,n)都在直线y=﹣2x+1上,则这组成对样本数据的样本相关系数r= .
17.对于两个事件M,N,若0<P(M)<1,0<P(M)<1,称为事件M,N的相关系数.近日重庆酷暑难耐,小张、小李、小王、小刘四人计划周末去避暑,现有四个可出游的景点:南天湖、金佛山、仙女山和黑山谷,若事件M:金佛山景点至少有一人:事件N:仙女山和黑山谷两个景点恰有一个景点无人,则事件M,N的相关系数为 .
18.对于两个事件M,N,若0<P(M)<1,0<P(M)<1,称为事件M,N的相关系数.在春暖花开、风和叶翠的季节,小张、小李、小王、小刘四人都计划周末去踏青,现有四个可出游的景点:南湖、净月、莲花山和天定山,若事件M:净月景点至少有一人:事件N:莲花山和天定山两个景点恰有一个景点无人,则事件M,N的相关系数为 .
19.以下是标号分别为①、②、③、④的四幅散点图,它们的样本相关系数分别为r1,r2,r3,r4,那么相关系数的大小关系为 (按由小到大的顺序排列).
20.甲、乙、丙、丁各自研究两个随机变量的数据,若甲、乙、丙、丁计算得到各自研究的两个随机变量的线性相关系数分别为r1=0.66,r2=﹣0.97,r3=0.92,r4=0.89,则这四人中, 研究的两个随机变量的线性相关程度最高.
样本相关系数(填空题)
参考答案与试题解析
一.填空题(共20小题)
1.以下4幅散点图所对应的样本相关系数r1、r2、r3、r4的大小关系为 r1>r3>r4>r2 .
【分析】由题意,根据散点图和相关系数的概念进行求解即可.
【解答】解:由散点图可知,相关系数r1、r3所在散点图中成正相关,r2、r4所在散点图中成负相关,
所以r1>0,r3>0,r2<0,r4<0,
因为相关系数r1、r2所在散点图近似在一条直线上,
所以相关系数r1、r2所在散点图中两变量的线性相关程度比较高,
因为相关系数r3、r3所在散点图比较分散,
所以相关系数r3、r3所在散点图中两变量的线性相关程度底,
即|r1|,|r2|比较大,|r3|,|r4|比较小,
则r1>r3>r4>r2.
故答案为:r1>r3>r4>r2.
【点评】本题考查相关关系,考查了逻辑推理能力,属于基础题.
2.近五年来某草场羊只数量与草地植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 1 2 3 4 5
羊只数量/万只 1.4 0.9 0.75 0.6 0.3
草地植被指数 1.1 4.3 15.6 31.3 49.7
若利用这五组数据得到的两变量间的相关系数为r1,去掉第一年数据(1.4,1.1)后得到的相关系数为r2,则r1 > r2(填≥,≤,<,>,=).
【分析】因为(1.4,1.1)是离群值,去掉后相关性更强可判断.
【解答】解:用这五组数据得到的两变量间的相关系数为r1,因为第一年数据(1.4,1.1)是离群值,去掉后得到的相关系数为r2,其相关性更强,所以|r1|<|r2|,
又因为数据呈现负相关,所以r1、r2均为负数,
所以r1>r2.
故答案为:r1>r2.
【点评】本题考查相关系数,属于基础题.
3.在一组样本数据(x1,y1),(x2,y2),…,((xn,yn),(n≥2,x1,x2…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线上,则这组样本数据的样本相关系数为 1 .
【分析】根据相关系数的定义可求得结果.
【解答】解:因为在直线方程中,斜率k0,
因为所有样本点(xi,yi)(i=1,2, ,n)都在直线上,
所以,这组样本数据是完全的线性关系,且正相关,
所以,这组样本数据的样本相关系数为1.
故答案为:1.
【点评】本题考查相关系数的定义,属于基础题.
4.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2, ,n)都在直线上,则这组样本数据的样本相关系数为 ﹣1 .
【分析】根据相关系数的定义可求得结果.
【解答】解:因为在直线方程中,斜率k0,
因为所有样本点(xi,yi)(i=1,2, ,n)都在直线上,
所以,这组样本数据是完全的线性关系,且负相关,
所以,这组样本数据的样本相关系数为﹣1.
故答案为:﹣1.
【点评】本题考查相关系数的定义,属于基础题.
5.若已知是的4倍,是的1.5倍,则相关系数r的值为 .
【分析】根据已知条件,结合相关系数的公式,即可求解.
【解答】解:∵是的4倍,是的1.5倍,
∴.
故答案为:.
【点评】本题主要考查相关系数的公式,属于基础题.
6.已知成对样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥3)中x1,x2,…,xn互不相等,且所有样本点(xi,yi)(i=1,2,…,n)都在直线上,则这组成对样本数据的样本相关系数r= ﹣1 .
【分析】根据给定条件,利用相关系数的定义求解作答.
【解答】解:因为所有样本点(xi,yi)(i=1,2,…,n)都在直线上,
显然直线的斜率,
所以样本数据成负相关,相关系数为﹣1.
故答案为:﹣1.
【点评】本题主要考查相关系数的定义,属于基础题.
7.现调查某地区某种野生动物的数量,将该地区分成面积相近的200个地块,从这些地块中简单随机抽样的方法抽取20个作为样本,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi、yi分别表示第i个样本的植物覆盖面积(单位:公顷)和这种野生动物的数量,构造向量,其中,,并计算得00,由选择性必修二教材中的知识,我们知道n对数据的相关系数,则上述数据(xi,yi)(i=1,2,…,20)的相关系数r= .
【分析】由题意,根据题干中相关系数的定义进行计算即可.
【解答】解:因为,1200,
所以3,60,
根据夹角公式的定义,
可得,
所以(xi)(yi)(xiyiyixi)
xiyiyixixiyi﹣20
=4400﹣20×3×60=800,
所以.
故答案为:.
【点评】本题考查相关系数,考查了运算能力.
8.对于相关系数r,下列说法中错误的是 ①③ .
①r=0时,成对样本数据线性相关程度较弱;
②r>0时,表明成对样本数据正相关;
③若线性回归方程中的回归系数,则相关系数r>0;
④|r|越接近1,线性相关程度越强,|r|越接近0,线性相关程度越弱.
【分析】本题根据样本相关系数的性质,即可判断.
【解答】解:根据题意,依次分析4个命题:
对于①,当r=0时,成对样本数据之间不存在任何关系,而不是较弱,错误;
对于②,当r>0时,表明成对样本数据正相关,正确;
对于③,若线性回归方程中的回归系数,说明成对样本数据呈负相关,则相关系数r<0,错误;
对于④,|r|越接近1,线性相关程度越强,|r|越接近0,线性相关程度越弱,正确.
故错误的是:①③.
【点评】本题考查线性回归系数的定义,注意线性回归系数的统计意义,属于基础题.
9.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)(n≥10)对应的点位于同一直线上,则x,y的相关系数为 ±1 .
【分析】根据已知条件,结合相关系数的定义,即可求解.
【解答】解:一组观测值(x1,y1),(x2,y2),…,(xn,yn)(n≥10)对应的点位于同一直线上,
则由相关系数的定义得,x,y的相关系数为±1.
故答案为:±1.
【点评】本题主要考查相关系数的定义,属于基础题.
10.一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2…xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2…n)都在直线y=﹣3x+1上,则这组样本数据相关系数为 ﹣1 .
【分析】根据题意,回归直线方程是y=﹣3x+1,可得这两个变量是负相关,结合相关系数,判断即可.
【解答】解:因为所有样本点(xi,yi),(i=1,2…n)都在直线y=﹣3x+1上,所以回归直线方程是y=﹣3x+1,可得这两个变量是负相关,
故这组样本数据的样本相关系数为负值,且所有样本点(xi,yi),(i=1,2…n)都在直线上,则有|r|=1,
∴相关系数r=﹣1,
故答案为:﹣1.
【点评】本题考查相关系数,属于基础题.
11.在研究线性回归模型时,样本数据(xi,yi)(i=1,2,3, ,n)所对应的点均在直线上,用r表示解释变量对于反应变量变化的线性相关度,则r= ﹣1 .
【分析】根据线性相关系数的定义直接得解.
【解答】解:由题意可知,已知样本数据(xi,yi)(i=1,2,3, ,n)所对应的点均在直线上,
由相关系数的定义可知,|r|=1,
又因为,
所以变量x,y之间是负相关,即r<0,
所以r=﹣1.
故答案为:﹣1.
【点评】本题主要考查了相关系数的性质,属于基础题.
12.为了比较甲、乙、丙三组数据的线性相关性强弱,某同学分别计算了甲、乙、丙三组数据的线性相关系数,求得数值依次为0.57,﹣0.93,0.89,则这三组数据中,线性相关性最强的是 乙 组数据.
【分析】根据相关系数的含义,其绝对值越接近1,线性相关性越强即可得到答案.
【解答】解:根据题意,因为线性相关系数的绝对值越大,线性相关性越强,
由甲、乙、丙三组数据的线性相关系数分别为0.57,﹣0.93,0.89,
所以|0.57|<|0.89|<|﹣0.93|,
故乙组数据的线性相关性最强.
故答案为:乙.
【点评】本题主要考查了相关系数的性质,属于基础题.
13.学习于才干信仰,犹如运动于健康体魄,持之已久、行之愈远愈受益.为实现中华民族伟大复兴,全国各行各业掀起了“学习强国”的高潮.某老师很喜欢“学习强国”中“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数如下表:
天数x 1 2 3 4 5 6 7
一次最多答对题数y 12 15 16 18 21 24 27
参考数据:,,,,,,
相关系数
由表中数据可知该老师每天一次最多答对题数y与天数x之间是 正 相关(填“正”或“负”),其相关系数r≈ 0.99 (结果保留两位小数)
【分析】根据正相关和负相关的定义即可得出结论;根据相关系数公式求相关系数即可.
【解答】解:由表中数据知,y随x的增大而增大,
所以该老师每天一次最多答对题数y与天数x之间是正相关;
计算相关系数为
.
故答案为:正;0.99.
【点评】本题考查了数据分析与相关系数计算问题,是基础题.
14.在散点图中,若所有的样本点都落在一条斜率为非0实数的直线上,则相关系数|r|= 1 .
【分析】根据残差与残差平方和以及相关指数的定义和散点之间的关系即可得出结论.
【解答】解:当散点图的所有点都在一条斜率为非0实数的直线上时,它的残差为0,
所以残差的平方和为0,
由相关系数的公式可得,它的相关系数为1.
故答案为:1.
【点评】本题考查了散点图的应用问题,属于基础题.
15.已知变量x,y之间的一组相关数据如表所示,则变量x,y之间的相关系数r= ﹣0.99 .
x 6 8 10 12
y 6 5 3 2
【分析】根据相关系数公式求解即可.
【解答】解:根据表中数据计算可知(6+8+10+12)=9,(6+5+3+2)=4,
变量x,y之间的相关系数r0.99.
故答案为:﹣0.99.
【点评】本题考查相关系数的定义,属于基础题.
16.已知成对样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2)中x1,x2,…,xn不全相等,且所有样本点(xi,yi)(i=1,2, ,n)都在直线y=﹣2x+1上,则这组成对样本数据的样本相关系数r= ﹣1 .
【分析】根据已知条件,结合相关系数的定义,即可求解.
【解答】解:由题设知,所有样本点(xi,yi)(i=1,2,…,n)都在直线y=﹣2x+1上,
∴这组样本数据完全负相关,故其相关系数为﹣1.
故答案为:﹣1.
【点评】本题考查了相关系数的定义,属于基础题.
17.对于两个事件M,N,若0<P(M)<1,0<P(M)<1,称为事件M,N的相关系数.近日重庆酷暑难耐,小张、小李、小王、小刘四人计划周末去避暑,现有四个可出游的景点:南天湖、金佛山、仙女山和黑山谷,若事件M:金佛山景点至少有一人:事件N:仙女山和黑山谷两个景点恰有一个景点无人,则事件M,N的相关系数为 .
【分析】先求事件M,N,MN的概率,再按定义求事件M,N的的相关系数.
【解答】解:事件M:金佛山景点至少有一人,则事件:金佛山景点无人,
则,所以,
事件N:仙女山和黑山谷两个景点恰有一个景点无人,
所以,
所以,
事件MN:金佛山景点至少有一人,仙女山和黑山谷两个景点恰有一个景点无人,
,
所以.
故答案为:.
【点评】本题主要考查了古典概型的概率公式,考查了相关系数的计算,属于中档题.
18.对于两个事件M,N,若0<P(M)<1,0<P(M)<1,称为事件M,N的相关系数.在春暖花开、风和叶翠的季节,小张、小李、小王、小刘四人都计划周末去踏青,现有四个可出游的景点:南湖、净月、莲花山和天定山,若事件M:净月景点至少有一人:事件N:莲花山和天定山两个景点恰有一个景点无人,则事件M,N的相关系数为 .
【分析】先求事件M,N,MN的概率,再按定义求事件M,N的的相关系数.
【解答】解:事件M:净月景点至少有一人,则事件:净月景点无人,
则,所以,
事件N:莲花山和天定山两个景点恰有一个景点无人,
所以,
所以,
事件MN:净月景点至少有一人,莲花山和天定山两个景点恰有一个景点无人,
,
所以.
故答案为:.
【点评】本题主要考查了古典概型的概率公式,考查了相关系数的计算,属于中档题.
19.以下是标号分别为①、②、③、④的四幅散点图,它们的样本相关系数分别为r1,r2,r3,r4,那么相关系数的大小关系为 r2<r4<r3<r1 (按由小到大的顺序排列).
【分析】利用样本相关系数的性质即可判断出r1,r2,r3,r4的大小关系
【解答】解:根据散点图可知,图①③成正相关,图②④成负相关,
∴r1>0,r2<0,r3>0,r4<0,
又图①②的散点图近似在一条直线上,则图①②两变量的线性相关程度比较高,
图③④的散点图比较分散,故图③④两变量的线性相关程度比较低,
即|r1|与|r2|比较大,|r4|与|r3|比较小,∴r2<r4<r3<r1,
故答案为:r2<r4<r3<r1.
【点评】本题考查相关系数相关知识,属于中档题.
20.甲、乙、丙、丁各自研究两个随机变量的数据,若甲、乙、丙、丁计算得到各自研究的两个随机变量的线性相关系数分别为r1=0.66,r2=﹣0.97,r3=0.92,r4=0.89,则这四人中, 乙 研究的两个随机变量的线性相关程度最高.
【分析】根据相关系数的定义判断即可.
【解答】解:因为|r2|=0.97>|r3|>|r4|>|r1|,所以这四人中,乙研究的两个随机变量的线性相关程度最高.
故答案为:乙.
【点评】本题主要考查相关系数和相关关系,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
样本相关系数(填空题)
一.填空题(共20小题)
1.以下4幅散点图所对应的样本相关系数r1、r2、r3、r4的大小关系为 .
2.近五年来某草场羊只数量与草地植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 1 2 3 4 5
羊只数量/万只 1.4 0.9 0.75 0.6 0.3
草地植被指数 1.1 4.3 15.6 31.3 49.7
若利用这五组数据得到的两变量间的相关系数为r1,去掉第一年数据(1.4,1.1)后得到的相关系数为r2,则r1 r2(填≥,≤,<,>,=).
3.在一组样本数据(x1,y1),(x2,y2),…,((xn,yn),(n≥2,x1,x2…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线上,则这组样本数据的样本相关系数为 .
4.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2, ,n)都在直线上,则这组样本数据的样本相关系数为 .
5.若已知是的4倍,是的1.5倍,则相关系数r的值为 .
6.已知成对样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥3)中x1,x2,…,xn互不相等,且所有样本点(xi,yi)(i=1,2,…,n)都在直线上,则这组成对样本数据的样本相关系数r= .
7.现调查某地区某种野生动物的数量,将该地区分成面积相近的200个地块,从这些地块中简单随机抽样的方法抽取20个作为样本,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi、yi分别表示第i个样本的植物覆盖面积(单位:公顷)和这种野生动物的数量,构造向量,其中,,并计算得00,由选择性必修二教材中的知识,我们知道n对数据的相关系数,则上述数据(xi,yi)(i=1,2,…,20)的相关系数r= .
8.对于相关系数r,下列说法中错误的是 .
①r=0时,成对样本数据线性相关程度较弱;
②r>0时,表明成对样本数据正相关;
③若线性回归方程中的回归系数,则相关系数r>0;
④|r|越接近1,线性相关程度越强,|r|越接近0,线性相关程度越弱.
9.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)(n≥10)对应的点位于同一直线上,则x,y的相关系数为 .
10.一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2…xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2…n)都在直线y=﹣3x+1上,则这组样本数据相关系数为 .
11.在研究线性回归模型时,样本数据(xi,yi)(i=1,2,3, ,n)所对应的点均在直线上,用r表示解释变量对于反应变量变化的线性相关度,则r= .
12.为了比较甲、乙、丙三组数据的线性相关性强弱,某同学分别计算了甲、乙、丙三组数据的线性相关系数,求得数值依次为0.57,﹣0.93,0.89,则这三组数据中,线性相关性最强的是 组数据.
13.学习于才干信仰,犹如运动于健康体魄,持之已久、行之愈远愈受益.为实现中华民族伟大复兴,全国各行各业掀起了“学习强国”的高潮.某老师很喜欢“学习强国”中“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数如下表:
天数x 1 2 3 4 5 6 7
一次最多答对题数y 12 15 16 18 21 24 27
参考数据:,,,,,,
相关系数
由表中数据可知该老师每天一次最多答对题数y与天数x之间是 相关(填“正”或“负”),其相关系数r≈ (结果保留两位小数)
14.在散点图中,若所有的样本点都落在一条斜率为非0实数的直线上,则相关系数|r|= .
15.已知变量x,y之间的一组相关数据如表所示,则变量x,y之间的相关系数r= .
x 6 8 10 12
y 6 5 3 2
16.已知成对样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2)中x1,x2,…,xn不全相等,且所有样本点(xi,yi)(i=1,2, ,n)都在直线y=﹣2x+1上,则这组成对样本数据的样本相关系数r= .
17.对于两个事件M,N,若0<P(M)<1,0<P(M)<1,称为事件M,N的相关系数.近日重庆酷暑难耐,小张、小李、小王、小刘四人计划周末去避暑,现有四个可出游的景点:南天湖、金佛山、仙女山和黑山谷,若事件M:金佛山景点至少有一人:事件N:仙女山和黑山谷两个景点恰有一个景点无人,则事件M,N的相关系数为 .
18.对于两个事件M,N,若0<P(M)<1,0<P(M)<1,称为事件M,N的相关系数.在春暖花开、风和叶翠的季节,小张、小李、小王、小刘四人都计划周末去踏青,现有四个可出游的景点:南湖、净月、莲花山和天定山,若事件M:净月景点至少有一人:事件N:莲花山和天定山两个景点恰有一个景点无人,则事件M,N的相关系数为 .
19.以下是标号分别为①、②、③、④的四幅散点图,它们的样本相关系数分别为r1,r2,r3,r4,那么相关系数的大小关系为 (按由小到大的顺序排列).
20.甲、乙、丙、丁各自研究两个随机变量的数据,若甲、乙、丙、丁计算得到各自研究的两个随机变量的线性相关系数分别为r1=0.66,r2=﹣0.97,r3=0.92,r4=0.89,则这四人中, 研究的两个随机变量的线性相关程度最高.
样本相关系数(填空题)
参考答案与试题解析
一.填空题(共20小题)
1.以下4幅散点图所对应的样本相关系数r1、r2、r3、r4的大小关系为 r1>r3>r4>r2 .
【分析】由题意,根据散点图和相关系数的概念进行求解即可.
【解答】解:由散点图可知,相关系数r1、r3所在散点图中成正相关,r2、r4所在散点图中成负相关,
所以r1>0,r3>0,r2<0,r4<0,
因为相关系数r1、r2所在散点图近似在一条直线上,
所以相关系数r1、r2所在散点图中两变量的线性相关程度比较高,
因为相关系数r3、r3所在散点图比较分散,
所以相关系数r3、r3所在散点图中两变量的线性相关程度底,
即|r1|,|r2|比较大,|r3|,|r4|比较小,
则r1>r3>r4>r2.
故答案为:r1>r3>r4>r2.
【点评】本题考查相关关系,考查了逻辑推理能力,属于基础题.
2.近五年来某草场羊只数量与草地植被指数两变量间的关系如表所示,绘制相应的散点图,如图所示:
年份 1 2 3 4 5
羊只数量/万只 1.4 0.9 0.75 0.6 0.3
草地植被指数 1.1 4.3 15.6 31.3 49.7
若利用这五组数据得到的两变量间的相关系数为r1,去掉第一年数据(1.4,1.1)后得到的相关系数为r2,则r1 > r2(填≥,≤,<,>,=).
【分析】因为(1.4,1.1)是离群值,去掉后相关性更强可判断.
【解答】解:用这五组数据得到的两变量间的相关系数为r1,因为第一年数据(1.4,1.1)是离群值,去掉后得到的相关系数为r2,其相关性更强,所以|r1|<|r2|,
又因为数据呈现负相关,所以r1、r2均为负数,
所以r1>r2.
故答案为:r1>r2.
【点评】本题考查相关系数,属于基础题.
3.在一组样本数据(x1,y1),(x2,y2),…,((xn,yn),(n≥2,x1,x2…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线上,则这组样本数据的样本相关系数为 1 .
【分析】根据相关系数的定义可求得结果.
【解答】解:因为在直线方程中,斜率k0,
因为所有样本点(xi,yi)(i=1,2, ,n)都在直线上,
所以,这组样本数据是完全的线性关系,且正相关,
所以,这组样本数据的样本相关系数为1.
故答案为:1.
【点评】本题考查相关系数的定义,属于基础题.
4.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2, ,n)都在直线上,则这组样本数据的样本相关系数为 ﹣1 .
【分析】根据相关系数的定义可求得结果.
【解答】解:因为在直线方程中,斜率k0,
因为所有样本点(xi,yi)(i=1,2, ,n)都在直线上,
所以,这组样本数据是完全的线性关系,且负相关,
所以,这组样本数据的样本相关系数为﹣1.
故答案为:﹣1.
【点评】本题考查相关系数的定义,属于基础题.
5.若已知是的4倍,是的1.5倍,则相关系数r的值为 .
【分析】根据已知条件,结合相关系数的公式,即可求解.
【解答】解:∵是的4倍,是的1.5倍,
∴.
故答案为:.
【点评】本题主要考查相关系数的公式,属于基础题.
6.已知成对样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥3)中x1,x2,…,xn互不相等,且所有样本点(xi,yi)(i=1,2,…,n)都在直线上,则这组成对样本数据的样本相关系数r= ﹣1 .
【分析】根据给定条件,利用相关系数的定义求解作答.
【解答】解:因为所有样本点(xi,yi)(i=1,2,…,n)都在直线上,
显然直线的斜率,
所以样本数据成负相关,相关系数为﹣1.
故答案为:﹣1.
【点评】本题主要考查相关系数的定义,属于基础题.
7.现调查某地区某种野生动物的数量,将该地区分成面积相近的200个地块,从这些地块中简单随机抽样的方法抽取20个作为样本,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi、yi分别表示第i个样本的植物覆盖面积(单位:公顷)和这种野生动物的数量,构造向量,其中,,并计算得00,由选择性必修二教材中的知识,我们知道n对数据的相关系数,则上述数据(xi,yi)(i=1,2,…,20)的相关系数r= .
【分析】由题意,根据题干中相关系数的定义进行计算即可.
【解答】解:因为,1200,
所以3,60,
根据夹角公式的定义,
可得,
所以(xi)(yi)(xiyiyixi)
xiyiyixixiyi﹣20
=4400﹣20×3×60=800,
所以.
故答案为:.
【点评】本题考查相关系数,考查了运算能力.
8.对于相关系数r,下列说法中错误的是 ①③ .
①r=0时,成对样本数据线性相关程度较弱;
②r>0时,表明成对样本数据正相关;
③若线性回归方程中的回归系数,则相关系数r>0;
④|r|越接近1,线性相关程度越强,|r|越接近0,线性相关程度越弱.
【分析】本题根据样本相关系数的性质,即可判断.
【解答】解:根据题意,依次分析4个命题:
对于①,当r=0时,成对样本数据之间不存在任何关系,而不是较弱,错误;
对于②,当r>0时,表明成对样本数据正相关,正确;
对于③,若线性回归方程中的回归系数,说明成对样本数据呈负相关,则相关系数r<0,错误;
对于④,|r|越接近1,线性相关程度越强,|r|越接近0,线性相关程度越弱,正确.
故错误的是:①③.
【点评】本题考查线性回归系数的定义,注意线性回归系数的统计意义,属于基础题.
9.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)(n≥10)对应的点位于同一直线上,则x,y的相关系数为 ±1 .
【分析】根据已知条件,结合相关系数的定义,即可求解.
【解答】解:一组观测值(x1,y1),(x2,y2),…,(xn,yn)(n≥10)对应的点位于同一直线上,
则由相关系数的定义得,x,y的相关系数为±1.
故答案为:±1.
【点评】本题主要考查相关系数的定义,属于基础题.
10.一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2…xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2…n)都在直线y=﹣3x+1上,则这组样本数据相关系数为 ﹣1 .
【分析】根据题意,回归直线方程是y=﹣3x+1,可得这两个变量是负相关,结合相关系数,判断即可.
【解答】解:因为所有样本点(xi,yi),(i=1,2…n)都在直线y=﹣3x+1上,所以回归直线方程是y=﹣3x+1,可得这两个变量是负相关,
故这组样本数据的样本相关系数为负值,且所有样本点(xi,yi),(i=1,2…n)都在直线上,则有|r|=1,
∴相关系数r=﹣1,
故答案为:﹣1.
【点评】本题考查相关系数,属于基础题.
11.在研究线性回归模型时,样本数据(xi,yi)(i=1,2,3, ,n)所对应的点均在直线上,用r表示解释变量对于反应变量变化的线性相关度,则r= ﹣1 .
【分析】根据线性相关系数的定义直接得解.
【解答】解:由题意可知,已知样本数据(xi,yi)(i=1,2,3, ,n)所对应的点均在直线上,
由相关系数的定义可知,|r|=1,
又因为,
所以变量x,y之间是负相关,即r<0,
所以r=﹣1.
故答案为:﹣1.
【点评】本题主要考查了相关系数的性质,属于基础题.
12.为了比较甲、乙、丙三组数据的线性相关性强弱,某同学分别计算了甲、乙、丙三组数据的线性相关系数,求得数值依次为0.57,﹣0.93,0.89,则这三组数据中,线性相关性最强的是 乙 组数据.
【分析】根据相关系数的含义,其绝对值越接近1,线性相关性越强即可得到答案.
【解答】解:根据题意,因为线性相关系数的绝对值越大,线性相关性越强,
由甲、乙、丙三组数据的线性相关系数分别为0.57,﹣0.93,0.89,
所以|0.57|<|0.89|<|﹣0.93|,
故乙组数据的线性相关性最强.
故答案为:乙.
【点评】本题主要考查了相关系数的性质,属于基础题.
13.学习于才干信仰,犹如运动于健康体魄,持之已久、行之愈远愈受益.为实现中华民族伟大复兴,全国各行各业掀起了“学习强国”的高潮.某老师很喜欢“学习强国”中“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数如下表:
天数x 1 2 3 4 5 6 7
一次最多答对题数y 12 15 16 18 21 24 27
参考数据:,,,,,,
相关系数
由表中数据可知该老师每天一次最多答对题数y与天数x之间是 正 相关(填“正”或“负”),其相关系数r≈ 0.99 (结果保留两位小数)
【分析】根据正相关和负相关的定义即可得出结论;根据相关系数公式求相关系数即可.
【解答】解:由表中数据知,y随x的增大而增大,
所以该老师每天一次最多答对题数y与天数x之间是正相关;
计算相关系数为
.
故答案为:正;0.99.
【点评】本题考查了数据分析与相关系数计算问题,是基础题.
14.在散点图中,若所有的样本点都落在一条斜率为非0实数的直线上,则相关系数|r|= 1 .
【分析】根据残差与残差平方和以及相关指数的定义和散点之间的关系即可得出结论.
【解答】解:当散点图的所有点都在一条斜率为非0实数的直线上时,它的残差为0,
所以残差的平方和为0,
由相关系数的公式可得,它的相关系数为1.
故答案为:1.
【点评】本题考查了散点图的应用问题,属于基础题.
15.已知变量x,y之间的一组相关数据如表所示,则变量x,y之间的相关系数r= ﹣0.99 .
x 6 8 10 12
y 6 5 3 2
【分析】根据相关系数公式求解即可.
【解答】解:根据表中数据计算可知(6+8+10+12)=9,(6+5+3+2)=4,
变量x,y之间的相关系数r0.99.
故答案为:﹣0.99.
【点评】本题考查相关系数的定义,属于基础题.
16.已知成对样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2)中x1,x2,…,xn不全相等,且所有样本点(xi,yi)(i=1,2, ,n)都在直线y=﹣2x+1上,则这组成对样本数据的样本相关系数r= ﹣1 .
【分析】根据已知条件,结合相关系数的定义,即可求解.
【解答】解:由题设知,所有样本点(xi,yi)(i=1,2,…,n)都在直线y=﹣2x+1上,
∴这组样本数据完全负相关,故其相关系数为﹣1.
故答案为:﹣1.
【点评】本题考查了相关系数的定义,属于基础题.
17.对于两个事件M,N,若0<P(M)<1,0<P(M)<1,称为事件M,N的相关系数.近日重庆酷暑难耐,小张、小李、小王、小刘四人计划周末去避暑,现有四个可出游的景点:南天湖、金佛山、仙女山和黑山谷,若事件M:金佛山景点至少有一人:事件N:仙女山和黑山谷两个景点恰有一个景点无人,则事件M,N的相关系数为 .
【分析】先求事件M,N,MN的概率,再按定义求事件M,N的的相关系数.
【解答】解:事件M:金佛山景点至少有一人,则事件:金佛山景点无人,
则,所以,
事件N:仙女山和黑山谷两个景点恰有一个景点无人,
所以,
所以,
事件MN:金佛山景点至少有一人,仙女山和黑山谷两个景点恰有一个景点无人,
,
所以.
故答案为:.
【点评】本题主要考查了古典概型的概率公式,考查了相关系数的计算,属于中档题.
18.对于两个事件M,N,若0<P(M)<1,0<P(M)<1,称为事件M,N的相关系数.在春暖花开、风和叶翠的季节,小张、小李、小王、小刘四人都计划周末去踏青,现有四个可出游的景点:南湖、净月、莲花山和天定山,若事件M:净月景点至少有一人:事件N:莲花山和天定山两个景点恰有一个景点无人,则事件M,N的相关系数为 .
【分析】先求事件M,N,MN的概率,再按定义求事件M,N的的相关系数.
【解答】解:事件M:净月景点至少有一人,则事件:净月景点无人,
则,所以,
事件N:莲花山和天定山两个景点恰有一个景点无人,
所以,
所以,
事件MN:净月景点至少有一人,莲花山和天定山两个景点恰有一个景点无人,
,
所以.
故答案为:.
【点评】本题主要考查了古典概型的概率公式,考查了相关系数的计算,属于中档题.
19.以下是标号分别为①、②、③、④的四幅散点图,它们的样本相关系数分别为r1,r2,r3,r4,那么相关系数的大小关系为 r2<r4<r3<r1 (按由小到大的顺序排列).
【分析】利用样本相关系数的性质即可判断出r1,r2,r3,r4的大小关系
【解答】解:根据散点图可知,图①③成正相关,图②④成负相关,
∴r1>0,r2<0,r3>0,r4<0,
又图①②的散点图近似在一条直线上,则图①②两变量的线性相关程度比较高,
图③④的散点图比较分散,故图③④两变量的线性相关程度比较低,
即|r1|与|r2|比较大,|r4|与|r3|比较小,∴r2<r4<r3<r1,
故答案为:r2<r4<r3<r1.
【点评】本题考查相关系数相关知识,属于中档题.
20.甲、乙、丙、丁各自研究两个随机变量的数据,若甲、乙、丙、丁计算得到各自研究的两个随机变量的线性相关系数分别为r1=0.66,r2=﹣0.97,r3=0.92,r4=0.89,则这四人中, 乙 研究的两个随机变量的线性相关程度最高.
【分析】根据相关系数的定义判断即可.
【解答】解:因为|r2|=0.97>|r3|>|r4|>|r1|,所以这四人中,乙研究的两个随机变量的线性相关程度最高.
故答案为:乙.
【点评】本题主要考查相关系数和相关关系,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
