【高考押题预测】2025年高考数学核心考点考前冲刺 变量间的相关关系(多选题)(含解析)
文档属性
| 名称 | 【高考押题预测】2025年高考数学核心考点考前冲刺 变量间的相关关系(多选题)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 450.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 21:21:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
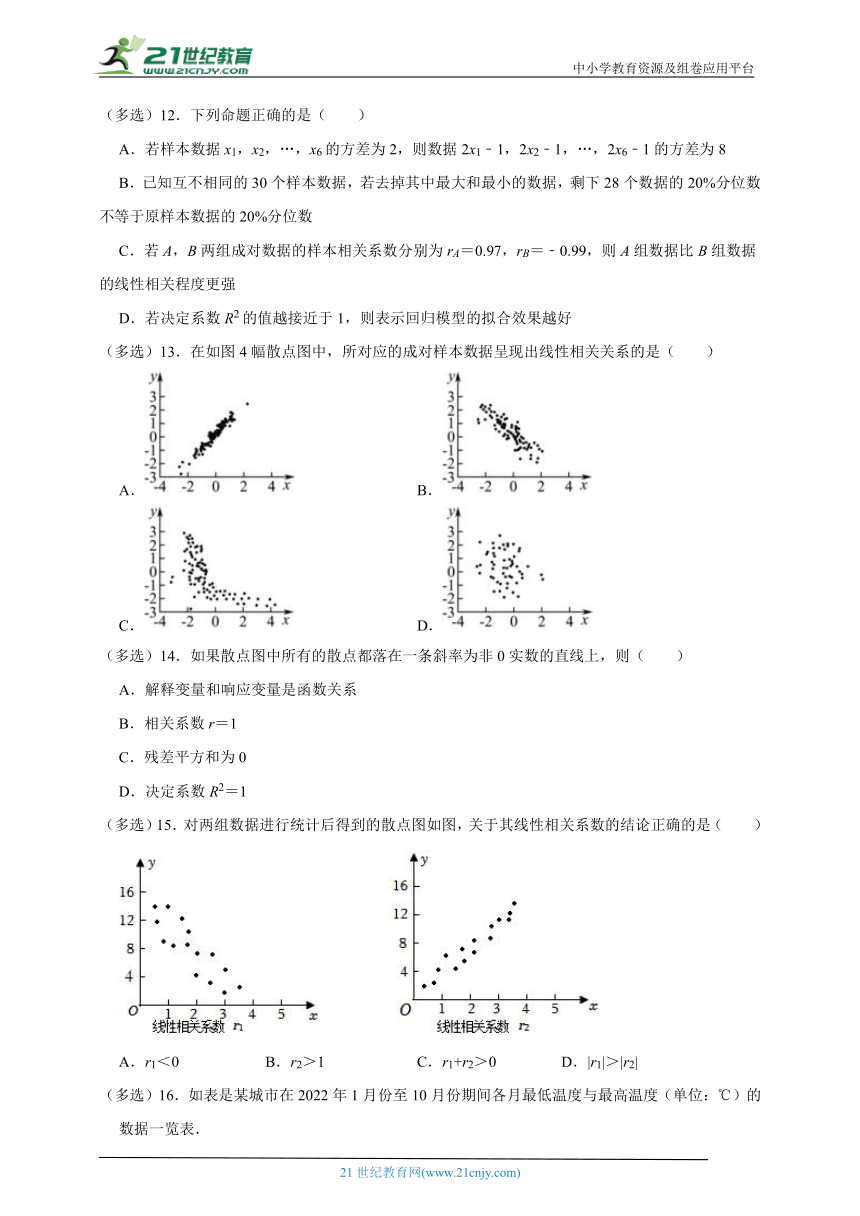
变量间的相关关系(多选题)
一.多选题(共20小题)
(多选)1.下列各组的两个变量中呈正相关关系的是( )
A.学生的身高与学生的化学成绩
B.汽车行驶的里程与它的耗油量
C.人的年龄与年收入
D.水果的重量与它的总价
(多选)2.如图所示,5个(x,y)数据,去掉D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.相关指数R2变小
D.解释变量x与预报变量y的相关性变强
(多选)3.如图,是5个成对数据(x,y)的散点图,若去掉点D(4,3)后,则下列说法正确的是( )
A.变量x与变量y呈负相关
B.解释变量x与响应变量y的相关性变强
C.样本相关系数r变小
D.决定系数R2变小
(多选)4.下列说法中正确的是( )
A.若数据x1,x2,…,xn的方差s2为0,则此组数据的众数唯一
B.已知一组数据2,3,5,7,8,9,9,11,则该组数据的第40百分位数为6
C.若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越大
D.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
(多选)5.下面的散点图与相关系数r一定不符合的是( )
A. B.
C. D.
(多选)6.如图,5个数据(x,y),去掉点D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.变量x与变量y呈正相关
D.变量x与变量y的相关性变强
(多选)7.下列关系中,属于相关关系的为( )
A.正方形的边长和面积之间的关系
B.水稻产量与施肥量之间的关系
C.人的身高与学习成绩之间的关系
D.降雪量与交通事故的发生率之间的关系
(多选)8.关于两个变量x,y与其样本相关系数r的说法中正确的有( )
A.|r|越接近1,x与y的线性相关程度越强
B.若r=1或r=﹣1,则x与y的关系完全对应(即有函数关系)
C.若r<0,则x增大时,y也相应增大
D.若0<r<1,则x与y之间的相关性为正相关
(多选)9.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法错误的是( )
A.利润率与人均销售额成正比例函数关系
B.利润率与人均销售额成反比例函数关系
C.利润率与人均销售额成正相关关系
D.利润率与人均销售额成负相关关系
(多选)10.观察下列散点图的分布规律和特点,其中两个变量存在相关关系的有( )
A. B.
C. D.
(多选)11.为了研究变量y和x的线性相关关系,收集了下图5对样本数据.若已求得,一元线性回归方程为,则下列选项中正确的是( )
x 1 2 3 4 5
y 0.5 0.9 1 1.1 1.5
A.变量y和x正相关
B.变量y和x负相关
C.
D.当x=5时的残差为0.06
(多选)12.下列命题正确的是( )
A.若样本数据x1,x2,…,x6的方差为2,则数据2x1﹣1,2x2﹣1,…,2x6﹣1的方差为8
B.已知互不相同的30个样本数据,若去掉其中最大和最小的数据,剩下28个数据的20%分位数不等于原样本数据的20%分位数
C.若A,B两组成对数据的样本相关系数分别为rA=0.97,rB=﹣0.99,则A组数据比B组数据的线性相关程度更强
D.若决定系数R2的值越接近于1,则表示回归模型的拟合效果越好
(多选)13.在如图4幅散点图中,所对应的成对样本数据呈现出线性相关关系的是( )
A. B.
C. D.
(多选)14.如果散点图中所有的散点都落在一条斜率为非0实数的直线上,则( )
A.解释变量和响应变量是函数关系
B.相关系数r=1
C.残差平方和为0
D.决定系数R2=1
(多选)15.对两组数据进行统计后得到的散点图如图,关于其线性相关系数的结论正确的是( )
A.r1<0 B.r2>1 C.r1+r2>0 D.|r1|>|r2|
(多选)16.如表是某城市在2022年1月份至10月份期间各月最低温度与最高温度(单位:℃)的数据一览表.
月份 1 2 3 4 5 6 7 8 9 10
最高温度/℃ 5 9 9 11 17 24 27 30 31 21
最低温度/℃ ﹣12 ﹣3 1 1 7 17 19 23 25 10
已知该城市的各月最低温度与最高温度具有相关关系,根据该一览表,下列结论正确的是( )
A.最低温度与最高温度为正相关
B.每月最高温度与最低温度的平均值在前8个月逐月增加
C.月温差(最高温度减最低温度)的最大值出现在10月
D.1月至4月的月温差(最高温度减最低温度)相对于7月至10月,波动性更大
(多选)17.下列两个变量之间的关系是函数关系的是( )
A.角度和它的正切值
B.人的右手一柞长和身高
C.正方体的棱长和表面积
D.真空中自由落体运动物体的下落距离和下落时间
(多选)18.已知数据x1<x2<x3<x4<x5<x6<x7,若去掉x4后剩余6个数的平均数比7个数的平均数大,记x1,x2,x3,x4的平均数与方差为,,记x4,x5,x6,x7的平均数与方差为,,则( )
A.
B.
C.[(xk﹣x4)2(xk﹣x4)2]
D.[(xk﹣x4)2(xk﹣x4)2]
(多选)19.下列说法正确的是( )
A.将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a倍
B.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
C.线性相关系数r的绝对值越大,两个变量的线性相关性越强;反之,线性相关性越弱
D.在回归模型中,预报变量y的值不能由解释变量x唯一确定
(多选)20.某校高三1班48名物理方向的学生在一次质量检测中,语文成绩、数学成绩与六科总成绩在全年级中的排名情况如图所示,“★”表示的是该班甲、乙、丙三位同学对应的点.从这次考试的成绩看,下列结论正确的是( )
A.该班六科总成绩排名前6的同学语文成绩比数学成绩排名更好
B.在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是语文
C.数学成绩与六科总成绩的相关性比语文成绩与六科总成绩的相关性更强
D.在甲、乙两人中,其语文成绩名次比其六科总成绩名次靠前的学生是甲
变量间的相关关系(多选题)
参考答案与试题解析
一.多选题(共20小题)
(多选)1.下列各组的两个变量中呈正相关关系的是( )
A.学生的身高与学生的化学成绩
B.汽车行驶的里程与它的耗油量
C.人的年龄与年收入
D.水果的重量与它的总价
【分析】根据已知条件,结合正相关关系的定义,即可求解.
【解答】解:学生的身高与学生的化学成绩没有必然联系,故A错误;
汽车行驶的里程与它的耗油量,呈正相关关系,故B正确;
人的年龄与年收入没有必然联系,故C错误;
水果的重量与它的总价,呈正相关关系,故D正确.
故选:BD.
【点评】本题主要考查正相关关系的定义,属于基础题.
(多选)2.如图所示,5个(x,y)数据,去掉D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.相关指数R2变小
D.解释变量x与预报变量y的相关性变强
【分析】由散点图知,去掉离群点D后,x与y的相关性变强,且为正相关,由此判断即可.
【解答】解:由散点图知,去掉离群点D后,x与y的相关性变强,且为正相关,
所以相关系数r的值变大,相关指数R2的值变大,残差平方和变小.
故选:AD.
【点评】本题考查了线性相关问题的判断问题,也考查了识图与用图能力,是基础题.
(多选)3.如图,是5个成对数据(x,y)的散点图,若去掉点D(4,3)后,则下列说法正确的是( )
A.变量x与变量y呈负相关
B.解释变量x与响应变量y的相关性变强
C.样本相关系数r变小
D.决定系数R2变小
【分析】由题意,结合所给散点图所给信息以及变量间的相关关系,判断即可.
【解答】解:由散点图知,只有D(4,3)偏离直线最远,
当去掉点D(4,3)后,变量x与变量y的线性相关变强,且为负相关,
所以选项A和选项B正确;
此时相关系数r变小,选项C正确,
决定系数R2变大,选项D错误.
故选:ABC.
【点评】本题考查了散点图的应用以及相关系数,也考查了逻辑推理和数据分析,是基础题.
(多选)4.下列说法中正确的是( )
A.若数据x1,x2,…,xn的方差s2为0,则此组数据的众数唯一
B.已知一组数据2,3,5,7,8,9,9,11,则该组数据的第40百分位数为6
C.若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越大
D.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
【分析】根据方差和平均数、众数,百分位数,相关系数和残差图的意义,对选项中的问题分析判断即可.
【解答】解:对于A,数据x1,x2,…,xn的方差s2为0时,则此组数据与平均数相同,所以众数唯一,选项A正确;
对于B,数据2,3,5,7,8,9,9,11,且8×40%=3.2,所以该组数据的第40百分位数为第4个数,是7,选项B错误;
对于C,若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的绝对值越接近1,所以选项C错误;
对于D,残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高,选项D正确.
故选:AD.
【点评】本题考查了方差与平均数、众数和百分位数以及相关系数和残差图的应用问题,是基础题.
(多选)5.下面的散点图与相关系数r一定不符合的是( )
A. B.
C. D.
【分析】根据题意,由相关系数r的意义依次分析选项,即可得答案.
【解答】解:根据题意,依次分析选项,
对于A,散点图中,各点散布在从左上角到右下角的区域里,所以样本相关系数r<0,与相关系数r一定不符合;
对于B,散点图中,各点散布在从左下角到右上角的区域里,所以样本相关系数r>0;
对于C,散点图中,变量x,y的散点图从左到右是向下的带状分布,所以相关系数﹣1<r<0,不可能是﹣1,与相关系数r一定不符合;
对于D,散点图中,各点散布在从左下角到右上角的带状区域里,所以样本相关系数0<r<1,不可能是1,与相关系数r一定不符合;
故选:ACD.
【点评】本题考查散点图的判断,根据|r|的值越接近于1时,两个变量的相关关系越明显进行判断是解决本题的关键,是基础题.
(多选)6.如图,5个数据(x,y),去掉点D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.变量x与变量y呈正相关
D.变量x与变量y的相关性变强
【分析】根据已知条件,结合变量间的相关关系,结合图象,即可求解.
【解答】解:由散点图可知,去掉D(3,10)后,y与x的线性相关加强,且为正相关,故AC正确,
相关系数r变大,误差变小,故B错误,
解释变量x与预报变量y的相关性变强.
故选:ACD.
【点评】本题主要考查变量间的相关关系,考查数形结合的能力,属于基础题.
(多选)7.下列关系中,属于相关关系的为( )
A.正方形的边长和面积之间的关系
B.水稻产量与施肥量之间的关系
C.人的身高与学习成绩之间的关系
D.降雪量与交通事故的发生率之间的关系
【分析】根据已知条件,结合变量间相关关系的定义,即可求解.
【解答】解:对于A,正方形的边长与面积之间的关系是函数关系,不是相关关系,故A错误,
对于B,水稻的产量与施肥量之间不具有严格的函数关系,但具有相关关系,故B正确,
对于C,人的身高与体重之间的关系既不是函数关系,也不是相关关系,
因为人的体重达到一定时期身高就不发生明显变化,因而它们不具有相关关系,故C错误,
对于D,降雪量与交通事故的发生率之间具有相关关系,故D正确.
故选:BD.
【点评】本题主要考查变量间相关关系的定义,属于基础题.
(多选)8.关于两个变量x,y与其样本相关系数r的说法中正确的有( )
A.|r|越接近1,x与y的线性相关程度越强
B.若r=1或r=﹣1,则x与y的关系完全对应(即有函数关系)
C.若r<0,则x增大时,y也相应增大
D.若0<r<1,则x与y之间的相关性为正相关
【分析】根据相关系数的定义,变量之间的相关关系,逐一判断即可.
【解答】解:根据相关系数的定义,变量之间的相关关系可利用相关系数r进行判断:
当r为正数时,表示变量x,y正相关;
当r为负数时,表示两个变量x,y负相关;
|r|越接近于1,相关程度越强;
|r|越接近于0,相关程度越弱.
故ABD正确,
若r>0,则x增大时,y也相应增大,故C错误.
故选:ABD.
【点评】本题考查变量间的相关关系,属于基础题.
(多选)9.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法错误的是( )
A.利润率与人均销售额成正比例函数关系
B.利润率与人均销售额成反比例函数关系
C.利润率与人均销售额成正相关关系
D.利润率与人均销售额成负相关关系
【分析】根据题意画出利润与人均销售额的散点图,由散点图得出利润率与人均销售额成正相关关系.
【解答】解:根据题意,画出利润与人均销售额的散点图,如图所示;
由散点图知,利润率与人均销售额成正相关关系.
故选:ABD.
【点评】本题考查了利用散点图判断两变量的线性相关关系应用问题,是基础题.
(多选)10.观察下列散点图的分布规律和特点,其中两个变量存在相关关系的有( )
A.
B.
C.
D.
【分析】由相关关系对应的图形是散点图,能反映两个变量的变化规律才具有相关关系直接可以判断.
【解答】解:相关关系对应的图形是散点图,
D中的点散乱地分布在坐标平面内,不能反映两个变量的变化规律,不具有相关关系;
ABC都能反映两个变量的变化规律,它们都具有相关关系.
故选:ABC.
【点评】本题主要考查散点图的应用,考查计算能力,属于基础题.
(多选)11.为了研究变量y和x的线性相关关系,收集了下图5对样本数据.若已求得,一元线性回归方程为,则下列选项中正确的是( )
x 1 2 3 4 5
y 0.5 0.9 1 1.1 1.5
A.变量y和x正相关
B.变量y和x负相关
C.
D.当x=5时的残差为0.06
【分析】根据表中数据,即可判断出选项A和B的正误,选C,利用中心点在回归方程上,即可求解;选项D,根据条件直接求出残差,即可求解.
【解答】解:根据表中数据可知,选项A正确,选项B错误,
对于选项C,将(3,1)代入,得,
解得,所以选项C正确,
对于选项D,由C可知,y=0.22x+0.34,
当x=5时,,
所以残差为,故选项D正确.
故选:ACD.
【点评】本题主要考查了线性回归方程的性质,考查了残差的定义,属于基础题.
(多选)12.下列命题正确的是( )
A.若样本数据x1,x2,…,x6的方差为2,则数据2x1﹣1,2x2﹣1,…,2x6﹣1的方差为8
B.已知互不相同的30个样本数据,若去掉其中最大和最小的数据,剩下28个数据的20%分位数不等于原样本数据的20%分位数
C.若A,B两组成对数据的样本相关系数分别为rA=0.97,rB=﹣0.99,则A组数据比B组数据的线性相关程度更强
D.若决定系数R2的值越接近于1,则表示回归模型的拟合效果越好
【分析】根据方差的性质可判断A,根据百分位数的定义可判断B,根据相关系数的性质可判断C,根据决定系数的性质可判断D.
【解答】解:对于A,由方差的性质可知,数据2x1﹣1,2x2﹣1,…,2x6﹣1的方差为22×2=8,故A正确;
对于B,设原数据从小到大排列为x1,x2,…,x30,则去掉最大值x30和最小值x1后,剩余数据按从小到大排列为x2,x3,…,x29,
又因为30×20%=6,28×20%=5.6,
所以原样本数据的20%分位数为,剩下28个数据的20%分位数为x7,
又因为30个样本数据互不相同,所以剩下28个数据的20%分位数不等于原样本数据的20%分位数,故B正确;
对于C,因为|rB|>|rA|,所以B组数据比A组数据的线性相关程度更强,故C错误;
对于D,由决定系数R2的性质可知,D正确.
故选:ABD.
【点评】本题主要考查了方差的性质,考查了百分位数的定义,以及变量间相关关系的判断,属于基础题.
(多选)13.在如图4幅散点图中,所对应的成对样本数据呈现出线性相关关系的是( )
A. B.
C. D.
【分析】根据数据点的分布情况直观判断是否有线性相关关系即可.
【解答】解:A、B中各点都有线性拟合趋势,其中A样本数据正相关,B样本数据负相关;
C中各点有非线性拟合趋势,D中各点分布比较分散,它们不具有线性相关.
故选:AB.
【点评】本题主要考查了散点图的应用,考查了变量间相关关系的判断,属于基础题.
(多选)14.如果散点图中所有的散点都落在一条斜率为非0实数的直线上,则( )
A.解释变量和响应变量是函数关系
B.相关系数r=1
C.残差平方和为0
D.决定系数R2=1
【分析】根据变量间的关系可解.
【解答】解:因为样本点都落在直线上,所以样本相关系数|r|=1,
若直线的斜率为正,则r=1,若斜率为负,则r=﹣1,故B错误;
直线对应的函数为一次函数,故解释变量和响应变量是一次函数关系,故A选项说法正确;
决定系数和残差平方和都能反映模型的拟合程度,故决定系数数R =1,残差平方和为0,故C,D选项说法正确.
故选:ACD.
【点评】本题考查变量间的相关关系,属于基础题.
(多选)15.对两组数据进行统计后得到的散点图如图,关于其线性相关系数的结论正确的是( )
A.r1<0 B.r2>1 C.r1+r2>0 D.|r1|>|r2|
【分析】根据y与x成正相关或负相关可判断相关系数的正负,根据点的密集程度可比较相关性的大小,从而比较相关系数绝对值的大小.
【解答】解:由散点图可知,线性相关系数r1的图像表示y与x成负相关,故﹣1<r1<0,故A正确;
线性相关系数r2的图像表示y与x正相关,故1>r2>0,故B错误;
线性相关系数r2的点较线性相关系数r1的点密集,故|r2|>|r1|,故r1+r2>0,故C正确,D错误.
故选:AC.
【点评】本题考查相关系数,考查学生的推理能力,属于基础题.
(多选)16.如表是某城市在2022年1月份至10月份期间各月最低温度与最高温度(单位:℃)的数据一览表.
月份 1 2 3 4 5 6 7 8 9 10
最高温度/℃ 5 9 9 11 17 24 27 30 31 21
最低温度/℃ ﹣12 ﹣3 1 1 7 17 19 23 25 10
已知该城市的各月最低温度与最高温度具有相关关系,根据该一览表,下列结论正确的是( )
A.最低温度与最高温度为正相关
B.每月最高温度与最低温度的平均值在前8个月逐月增加
C.月温差(最高温度减最低温度)的最大值出现在10月
D.1月至4月的月温差(最高温度减最低温度)相对于7月至10月,波动性更大
【分析】根据题意,依次分析选项,综合即可得答案.
【解答】解:根据题意依次分析选项:
A.由表中数据,最低气温大致随着最高气温的升高而升高,故该城市的各月最低温与最高温具有相关关系,且最低温与最高温为正相关,则A正确;
B.由表中数据,前8个月每月最高温与最低温的平均值依次为:﹣3.5,3,5,6,12,20.5,23,26.5,
故前8个月是逐月增加,则B正确;
C.由表中数据,月温差依次为:17,12,8,10,10,7,8,7,6,11,月温差的最大值出现在1月,则C错误;
D.由C的结论分析可得1月至4月的月温差相对于7月至10月波动性更大,D正确.
故选:ABD.
【点评】本题考查变量间的相关关系,属于基础题.
(多选)17.下列两个变量之间的关系是函数关系的是( )
A.角度和它的正切值
B.人的右手一柞长和身高
C.正方体的棱长和表面积
D.真空中自由落体运动物体的下落距离和下落时间
【分析】由函数的定义知,两个变量具有确定的关系,利用这一点可知B不是函数关系,再由正切函数、正方体的表面积公式和物理知识知A、C、D是函数关系.
【解答】解:由正切函数y=tanx知,A是函数关系;
人的右手一柞长和身高不是确定的关系,故不是函数关系;
设正方体的棱长为a,则它的表面积S=6a2,C是函数关系;
由物理知识知,自由落体运动物体的下落距离h和下落时间t满足hgt2(t>0),D是函数关系.
故选:ACD.
【点评】本题主要考查了函数的概念,属于基础题.
(多选)18.已知数据x1<x2<x3<x4<x5<x6<x7,若去掉x4后剩余6个数的平均数比7个数的平均数大,记x1,x2,x3,x4的平均数与方差为,,记x4,x5,x6,x7的平均数与方差为,,则( )
A.
B.
C.[(xk﹣x4)2(xk﹣x4)2]
D.[(xk﹣x4)2(xk﹣x4)2]
【分析】根据平均数的大小列出不等式变形即可判断AB,根据方差公式作差后变形,利用,即可判断CD.
【解答】解:因为,
所以x1+x2+x3+x5+x6+x7>6x4,
所以(x1+x2+x3+x4)+(x4+x5+x6+x7)>8x4,所以,故A正确,B错误;
,故C正确,D错误.
故选:AC.
【点评】本题考查了平均数和方差的计算,属于中档题.
(多选)19.下列说法正确的是( )
A.将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a倍
B.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
C.线性相关系数r的绝对值越大,两个变量的线性相关性越强;反之,线性相关性越弱
D.在回归模型中,预报变量y的值不能由解释变量x唯一确定
【分析】根据方差性质判断A;根据残差图的意义判断B;根据相关系数的含义判断C;根据回归模型中,预报变量y的值与解释变量的关系判断D.
【解答】解:对于A,将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a2倍,故A错误;
对于B,在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高,故B正确;
对于C,线性相关系数r的绝对值越接近于1,两个变量的线性相关性越强;
反之,相关系数r的绝对值越接近于0,线性相关性越弱,故C错误;
对于D,预报变量y的值由解释变量x和随机误差e共同确定,x只能解释部分y的变化,
即在回归模型中,预报变量y的值不能由解释变量x唯一确定,故D正确.
故选:BD.
【点评】本题主要考查了方差的性质,考查了变量间的相关关系,属于中档题.
(多选)20.某校高三1班48名物理方向的学生在一次质量检测中,语文成绩、数学成绩与六科总成绩在全年级中的排名情况如图所示,“★”表示的是该班甲、乙、丙三位同学对应的点.从这次考试的成绩看,下列结论正确的是( )
A.该班六科总成绩排名前6的同学语文成绩比数学成绩排名更好
B.在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是语文
C.数学成绩与六科总成绩的相关性比语文成绩与六科总成绩的相关性更强
D.在甲、乙两人中,其语文成绩名次比其六科总成绩名次靠前的学生是甲
【分析】结合图形可分析出答案.
【解答】解:A:由图可得,该班六科总成绩排名前6的同学数学成绩比语文成绩排名更好,故A错误;
B:由右图可得丙同学的总成绩排在班上倒数第三名,其语文成绩排在250到300名之间,
从左图可得其数学成绩排在400名左右,故B正确;
C:数学成绩与六科总成绩的相关性比语文成绩与六科总成绩的相关性更强,因为右图的点的分布较左图更分散,故C正确;
D:由左图可得甲的总成绩排在班上第7名,年级名次100多一点,
对应到右图可得,其语文成绩排在年级近100名,故甲的语文成绩名次比其六科总成绩名次靠前;
由左图可得甲的总成绩排在班上第27名,年级名次接近250名,
对应到右图可得,其语文成绩排在年级250名之后,故乙的语文成绩名次比其六科总成绩名次靠后,故D正确;
故选:BCD.
【点评】本题考查了根据图形解决实际问题,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
变量间的相关关系(多选题)
一.多选题(共20小题)
(多选)1.下列各组的两个变量中呈正相关关系的是( )
A.学生的身高与学生的化学成绩
B.汽车行驶的里程与它的耗油量
C.人的年龄与年收入
D.水果的重量与它的总价
(多选)2.如图所示,5个(x,y)数据,去掉D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.相关指数R2变小
D.解释变量x与预报变量y的相关性变强
(多选)3.如图,是5个成对数据(x,y)的散点图,若去掉点D(4,3)后,则下列说法正确的是( )
A.变量x与变量y呈负相关
B.解释变量x与响应变量y的相关性变强
C.样本相关系数r变小
D.决定系数R2变小
(多选)4.下列说法中正确的是( )
A.若数据x1,x2,…,xn的方差s2为0,则此组数据的众数唯一
B.已知一组数据2,3,5,7,8,9,9,11,则该组数据的第40百分位数为6
C.若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越大
D.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
(多选)5.下面的散点图与相关系数r一定不符合的是( )
A. B.
C. D.
(多选)6.如图,5个数据(x,y),去掉点D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.变量x与变量y呈正相关
D.变量x与变量y的相关性变强
(多选)7.下列关系中,属于相关关系的为( )
A.正方形的边长和面积之间的关系
B.水稻产量与施肥量之间的关系
C.人的身高与学习成绩之间的关系
D.降雪量与交通事故的发生率之间的关系
(多选)8.关于两个变量x,y与其样本相关系数r的说法中正确的有( )
A.|r|越接近1,x与y的线性相关程度越强
B.若r=1或r=﹣1,则x与y的关系完全对应(即有函数关系)
C.若r<0,则x增大时,y也相应增大
D.若0<r<1,则x与y之间的相关性为正相关
(多选)9.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法错误的是( )
A.利润率与人均销售额成正比例函数关系
B.利润率与人均销售额成反比例函数关系
C.利润率与人均销售额成正相关关系
D.利润率与人均销售额成负相关关系
(多选)10.观察下列散点图的分布规律和特点,其中两个变量存在相关关系的有( )
A. B.
C. D.
(多选)11.为了研究变量y和x的线性相关关系,收集了下图5对样本数据.若已求得,一元线性回归方程为,则下列选项中正确的是( )
x 1 2 3 4 5
y 0.5 0.9 1 1.1 1.5
A.变量y和x正相关
B.变量y和x负相关
C.
D.当x=5时的残差为0.06
(多选)12.下列命题正确的是( )
A.若样本数据x1,x2,…,x6的方差为2,则数据2x1﹣1,2x2﹣1,…,2x6﹣1的方差为8
B.已知互不相同的30个样本数据,若去掉其中最大和最小的数据,剩下28个数据的20%分位数不等于原样本数据的20%分位数
C.若A,B两组成对数据的样本相关系数分别为rA=0.97,rB=﹣0.99,则A组数据比B组数据的线性相关程度更强
D.若决定系数R2的值越接近于1,则表示回归模型的拟合效果越好
(多选)13.在如图4幅散点图中,所对应的成对样本数据呈现出线性相关关系的是( )
A. B.
C. D.
(多选)14.如果散点图中所有的散点都落在一条斜率为非0实数的直线上,则( )
A.解释变量和响应变量是函数关系
B.相关系数r=1
C.残差平方和为0
D.决定系数R2=1
(多选)15.对两组数据进行统计后得到的散点图如图,关于其线性相关系数的结论正确的是( )
A.r1<0 B.r2>1 C.r1+r2>0 D.|r1|>|r2|
(多选)16.如表是某城市在2022年1月份至10月份期间各月最低温度与最高温度(单位:℃)的数据一览表.
月份 1 2 3 4 5 6 7 8 9 10
最高温度/℃ 5 9 9 11 17 24 27 30 31 21
最低温度/℃ ﹣12 ﹣3 1 1 7 17 19 23 25 10
已知该城市的各月最低温度与最高温度具有相关关系,根据该一览表,下列结论正确的是( )
A.最低温度与最高温度为正相关
B.每月最高温度与最低温度的平均值在前8个月逐月增加
C.月温差(最高温度减最低温度)的最大值出现在10月
D.1月至4月的月温差(最高温度减最低温度)相对于7月至10月,波动性更大
(多选)17.下列两个变量之间的关系是函数关系的是( )
A.角度和它的正切值
B.人的右手一柞长和身高
C.正方体的棱长和表面积
D.真空中自由落体运动物体的下落距离和下落时间
(多选)18.已知数据x1<x2<x3<x4<x5<x6<x7,若去掉x4后剩余6个数的平均数比7个数的平均数大,记x1,x2,x3,x4的平均数与方差为,,记x4,x5,x6,x7的平均数与方差为,,则( )
A.
B.
C.[(xk﹣x4)2(xk﹣x4)2]
D.[(xk﹣x4)2(xk﹣x4)2]
(多选)19.下列说法正确的是( )
A.将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a倍
B.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
C.线性相关系数r的绝对值越大,两个变量的线性相关性越强;反之,线性相关性越弱
D.在回归模型中,预报变量y的值不能由解释变量x唯一确定
(多选)20.某校高三1班48名物理方向的学生在一次质量检测中,语文成绩、数学成绩与六科总成绩在全年级中的排名情况如图所示,“★”表示的是该班甲、乙、丙三位同学对应的点.从这次考试的成绩看,下列结论正确的是( )
A.该班六科总成绩排名前6的同学语文成绩比数学成绩排名更好
B.在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是语文
C.数学成绩与六科总成绩的相关性比语文成绩与六科总成绩的相关性更强
D.在甲、乙两人中,其语文成绩名次比其六科总成绩名次靠前的学生是甲
变量间的相关关系(多选题)
参考答案与试题解析
一.多选题(共20小题)
(多选)1.下列各组的两个变量中呈正相关关系的是( )
A.学生的身高与学生的化学成绩
B.汽车行驶的里程与它的耗油量
C.人的年龄与年收入
D.水果的重量与它的总价
【分析】根据已知条件,结合正相关关系的定义,即可求解.
【解答】解:学生的身高与学生的化学成绩没有必然联系,故A错误;
汽车行驶的里程与它的耗油量,呈正相关关系,故B正确;
人的年龄与年收入没有必然联系,故C错误;
水果的重量与它的总价,呈正相关关系,故D正确.
故选:BD.
【点评】本题主要考查正相关关系的定义,属于基础题.
(多选)2.如图所示,5个(x,y)数据,去掉D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.相关指数R2变小
D.解释变量x与预报变量y的相关性变强
【分析】由散点图知,去掉离群点D后,x与y的相关性变强,且为正相关,由此判断即可.
【解答】解:由散点图知,去掉离群点D后,x与y的相关性变强,且为正相关,
所以相关系数r的值变大,相关指数R2的值变大,残差平方和变小.
故选:AD.
【点评】本题考查了线性相关问题的判断问题,也考查了识图与用图能力,是基础题.
(多选)3.如图,是5个成对数据(x,y)的散点图,若去掉点D(4,3)后,则下列说法正确的是( )
A.变量x与变量y呈负相关
B.解释变量x与响应变量y的相关性变强
C.样本相关系数r变小
D.决定系数R2变小
【分析】由题意,结合所给散点图所给信息以及变量间的相关关系,判断即可.
【解答】解:由散点图知,只有D(4,3)偏离直线最远,
当去掉点D(4,3)后,变量x与变量y的线性相关变强,且为负相关,
所以选项A和选项B正确;
此时相关系数r变小,选项C正确,
决定系数R2变大,选项D错误.
故选:ABC.
【点评】本题考查了散点图的应用以及相关系数,也考查了逻辑推理和数据分析,是基础题.
(多选)4.下列说法中正确的是( )
A.若数据x1,x2,…,xn的方差s2为0,则此组数据的众数唯一
B.已知一组数据2,3,5,7,8,9,9,11,则该组数据的第40百分位数为6
C.若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越大
D.在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
【分析】根据方差和平均数、众数,百分位数,相关系数和残差图的意义,对选项中的问题分析判断即可.
【解答】解:对于A,数据x1,x2,…,xn的方差s2为0时,则此组数据与平均数相同,所以众数唯一,选项A正确;
对于B,数据2,3,5,7,8,9,9,11,且8×40%=3.2,所以该组数据的第40百分位数为第4个数,是7,选项B错误;
对于C,若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的绝对值越接近1,所以选项C错误;
对于D,残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高,选项D正确.
故选:AD.
【点评】本题考查了方差与平均数、众数和百分位数以及相关系数和残差图的应用问题,是基础题.
(多选)5.下面的散点图与相关系数r一定不符合的是( )
A. B.
C. D.
【分析】根据题意,由相关系数r的意义依次分析选项,即可得答案.
【解答】解:根据题意,依次分析选项,
对于A,散点图中,各点散布在从左上角到右下角的区域里,所以样本相关系数r<0,与相关系数r一定不符合;
对于B,散点图中,各点散布在从左下角到右上角的区域里,所以样本相关系数r>0;
对于C,散点图中,变量x,y的散点图从左到右是向下的带状分布,所以相关系数﹣1<r<0,不可能是﹣1,与相关系数r一定不符合;
对于D,散点图中,各点散布在从左下角到右上角的带状区域里,所以样本相关系数0<r<1,不可能是1,与相关系数r一定不符合;
故选:ACD.
【点评】本题考查散点图的判断,根据|r|的值越接近于1时,两个变量的相关关系越明显进行判断是解决本题的关键,是基础题.
(多选)6.如图,5个数据(x,y),去掉点D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.变量x与变量y呈正相关
D.变量x与变量y的相关性变强
【分析】根据已知条件,结合变量间的相关关系,结合图象,即可求解.
【解答】解:由散点图可知,去掉D(3,10)后,y与x的线性相关加强,且为正相关,故AC正确,
相关系数r变大,误差变小,故B错误,
解释变量x与预报变量y的相关性变强.
故选:ACD.
【点评】本题主要考查变量间的相关关系,考查数形结合的能力,属于基础题.
(多选)7.下列关系中,属于相关关系的为( )
A.正方形的边长和面积之间的关系
B.水稻产量与施肥量之间的关系
C.人的身高与学习成绩之间的关系
D.降雪量与交通事故的发生率之间的关系
【分析】根据已知条件,结合变量间相关关系的定义,即可求解.
【解答】解:对于A,正方形的边长与面积之间的关系是函数关系,不是相关关系,故A错误,
对于B,水稻的产量与施肥量之间不具有严格的函数关系,但具有相关关系,故B正确,
对于C,人的身高与体重之间的关系既不是函数关系,也不是相关关系,
因为人的体重达到一定时期身高就不发生明显变化,因而它们不具有相关关系,故C错误,
对于D,降雪量与交通事故的发生率之间具有相关关系,故D正确.
故选:BD.
【点评】本题主要考查变量间相关关系的定义,属于基础题.
(多选)8.关于两个变量x,y与其样本相关系数r的说法中正确的有( )
A.|r|越接近1,x与y的线性相关程度越强
B.若r=1或r=﹣1,则x与y的关系完全对应(即有函数关系)
C.若r<0,则x增大时,y也相应增大
D.若0<r<1,则x与y之间的相关性为正相关
【分析】根据相关系数的定义,变量之间的相关关系,逐一判断即可.
【解答】解:根据相关系数的定义,变量之间的相关关系可利用相关系数r进行判断:
当r为正数时,表示变量x,y正相关;
当r为负数时,表示两个变量x,y负相关;
|r|越接近于1,相关程度越强;
|r|越接近于0,相关程度越弱.
故ABD正确,
若r>0,则x增大时,y也相应增大,故C错误.
故选:ABD.
【点评】本题考查变量间的相关关系,属于基础题.
(多选)9.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法错误的是( )
A.利润率与人均销售额成正比例函数关系
B.利润率与人均销售额成反比例函数关系
C.利润率与人均销售额成正相关关系
D.利润率与人均销售额成负相关关系
【分析】根据题意画出利润与人均销售额的散点图,由散点图得出利润率与人均销售额成正相关关系.
【解答】解:根据题意,画出利润与人均销售额的散点图,如图所示;
由散点图知,利润率与人均销售额成正相关关系.
故选:ABD.
【点评】本题考查了利用散点图判断两变量的线性相关关系应用问题,是基础题.
(多选)10.观察下列散点图的分布规律和特点,其中两个变量存在相关关系的有( )
A.
B.
C.
D.
【分析】由相关关系对应的图形是散点图,能反映两个变量的变化规律才具有相关关系直接可以判断.
【解答】解:相关关系对应的图形是散点图,
D中的点散乱地分布在坐标平面内,不能反映两个变量的变化规律,不具有相关关系;
ABC都能反映两个变量的变化规律,它们都具有相关关系.
故选:ABC.
【点评】本题主要考查散点图的应用,考查计算能力,属于基础题.
(多选)11.为了研究变量y和x的线性相关关系,收集了下图5对样本数据.若已求得,一元线性回归方程为,则下列选项中正确的是( )
x 1 2 3 4 5
y 0.5 0.9 1 1.1 1.5
A.变量y和x正相关
B.变量y和x负相关
C.
D.当x=5时的残差为0.06
【分析】根据表中数据,即可判断出选项A和B的正误,选C,利用中心点在回归方程上,即可求解;选项D,根据条件直接求出残差,即可求解.
【解答】解:根据表中数据可知,选项A正确,选项B错误,
对于选项C,将(3,1)代入,得,
解得,所以选项C正确,
对于选项D,由C可知,y=0.22x+0.34,
当x=5时,,
所以残差为,故选项D正确.
故选:ACD.
【点评】本题主要考查了线性回归方程的性质,考查了残差的定义,属于基础题.
(多选)12.下列命题正确的是( )
A.若样本数据x1,x2,…,x6的方差为2,则数据2x1﹣1,2x2﹣1,…,2x6﹣1的方差为8
B.已知互不相同的30个样本数据,若去掉其中最大和最小的数据,剩下28个数据的20%分位数不等于原样本数据的20%分位数
C.若A,B两组成对数据的样本相关系数分别为rA=0.97,rB=﹣0.99,则A组数据比B组数据的线性相关程度更强
D.若决定系数R2的值越接近于1,则表示回归模型的拟合效果越好
【分析】根据方差的性质可判断A,根据百分位数的定义可判断B,根据相关系数的性质可判断C,根据决定系数的性质可判断D.
【解答】解:对于A,由方差的性质可知,数据2x1﹣1,2x2﹣1,…,2x6﹣1的方差为22×2=8,故A正确;
对于B,设原数据从小到大排列为x1,x2,…,x30,则去掉最大值x30和最小值x1后,剩余数据按从小到大排列为x2,x3,…,x29,
又因为30×20%=6,28×20%=5.6,
所以原样本数据的20%分位数为,剩下28个数据的20%分位数为x7,
又因为30个样本数据互不相同,所以剩下28个数据的20%分位数不等于原样本数据的20%分位数,故B正确;
对于C,因为|rB|>|rA|,所以B组数据比A组数据的线性相关程度更强,故C错误;
对于D,由决定系数R2的性质可知,D正确.
故选:ABD.
【点评】本题主要考查了方差的性质,考查了百分位数的定义,以及变量间相关关系的判断,属于基础题.
(多选)13.在如图4幅散点图中,所对应的成对样本数据呈现出线性相关关系的是( )
A. B.
C. D.
【分析】根据数据点的分布情况直观判断是否有线性相关关系即可.
【解答】解:A、B中各点都有线性拟合趋势,其中A样本数据正相关,B样本数据负相关;
C中各点有非线性拟合趋势,D中各点分布比较分散,它们不具有线性相关.
故选:AB.
【点评】本题主要考查了散点图的应用,考查了变量间相关关系的判断,属于基础题.
(多选)14.如果散点图中所有的散点都落在一条斜率为非0实数的直线上,则( )
A.解释变量和响应变量是函数关系
B.相关系数r=1
C.残差平方和为0
D.决定系数R2=1
【分析】根据变量间的关系可解.
【解答】解:因为样本点都落在直线上,所以样本相关系数|r|=1,
若直线的斜率为正,则r=1,若斜率为负,则r=﹣1,故B错误;
直线对应的函数为一次函数,故解释变量和响应变量是一次函数关系,故A选项说法正确;
决定系数和残差平方和都能反映模型的拟合程度,故决定系数数R =1,残差平方和为0,故C,D选项说法正确.
故选:ACD.
【点评】本题考查变量间的相关关系,属于基础题.
(多选)15.对两组数据进行统计后得到的散点图如图,关于其线性相关系数的结论正确的是( )
A.r1<0 B.r2>1 C.r1+r2>0 D.|r1|>|r2|
【分析】根据y与x成正相关或负相关可判断相关系数的正负,根据点的密集程度可比较相关性的大小,从而比较相关系数绝对值的大小.
【解答】解:由散点图可知,线性相关系数r1的图像表示y与x成负相关,故﹣1<r1<0,故A正确;
线性相关系数r2的图像表示y与x正相关,故1>r2>0,故B错误;
线性相关系数r2的点较线性相关系数r1的点密集,故|r2|>|r1|,故r1+r2>0,故C正确,D错误.
故选:AC.
【点评】本题考查相关系数,考查学生的推理能力,属于基础题.
(多选)16.如表是某城市在2022年1月份至10月份期间各月最低温度与最高温度(单位:℃)的数据一览表.
月份 1 2 3 4 5 6 7 8 9 10
最高温度/℃ 5 9 9 11 17 24 27 30 31 21
最低温度/℃ ﹣12 ﹣3 1 1 7 17 19 23 25 10
已知该城市的各月最低温度与最高温度具有相关关系,根据该一览表,下列结论正确的是( )
A.最低温度与最高温度为正相关
B.每月最高温度与最低温度的平均值在前8个月逐月增加
C.月温差(最高温度减最低温度)的最大值出现在10月
D.1月至4月的月温差(最高温度减最低温度)相对于7月至10月,波动性更大
【分析】根据题意,依次分析选项,综合即可得答案.
【解答】解:根据题意依次分析选项:
A.由表中数据,最低气温大致随着最高气温的升高而升高,故该城市的各月最低温与最高温具有相关关系,且最低温与最高温为正相关,则A正确;
B.由表中数据,前8个月每月最高温与最低温的平均值依次为:﹣3.5,3,5,6,12,20.5,23,26.5,
故前8个月是逐月增加,则B正确;
C.由表中数据,月温差依次为:17,12,8,10,10,7,8,7,6,11,月温差的最大值出现在1月,则C错误;
D.由C的结论分析可得1月至4月的月温差相对于7月至10月波动性更大,D正确.
故选:ABD.
【点评】本题考查变量间的相关关系,属于基础题.
(多选)17.下列两个变量之间的关系是函数关系的是( )
A.角度和它的正切值
B.人的右手一柞长和身高
C.正方体的棱长和表面积
D.真空中自由落体运动物体的下落距离和下落时间
【分析】由函数的定义知,两个变量具有确定的关系,利用这一点可知B不是函数关系,再由正切函数、正方体的表面积公式和物理知识知A、C、D是函数关系.
【解答】解:由正切函数y=tanx知,A是函数关系;
人的右手一柞长和身高不是确定的关系,故不是函数关系;
设正方体的棱长为a,则它的表面积S=6a2,C是函数关系;
由物理知识知,自由落体运动物体的下落距离h和下落时间t满足hgt2(t>0),D是函数关系.
故选:ACD.
【点评】本题主要考查了函数的概念,属于基础题.
(多选)18.已知数据x1<x2<x3<x4<x5<x6<x7,若去掉x4后剩余6个数的平均数比7个数的平均数大,记x1,x2,x3,x4的平均数与方差为,,记x4,x5,x6,x7的平均数与方差为,,则( )
A.
B.
C.[(xk﹣x4)2(xk﹣x4)2]
D.[(xk﹣x4)2(xk﹣x4)2]
【分析】根据平均数的大小列出不等式变形即可判断AB,根据方差公式作差后变形,利用,即可判断CD.
【解答】解:因为,
所以x1+x2+x3+x5+x6+x7>6x4,
所以(x1+x2+x3+x4)+(x4+x5+x6+x7)>8x4,所以,故A正确,B错误;
,故C正确,D错误.
故选:AC.
【点评】本题考查了平均数和方差的计算,属于中档题.
(多选)19.下列说法正确的是( )
A.将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a倍
B.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
C.线性相关系数r的绝对值越大,两个变量的线性相关性越强;反之,线性相关性越弱
D.在回归模型中,预报变量y的值不能由解释变量x唯一确定
【分析】根据方差性质判断A;根据残差图的意义判断B;根据相关系数的含义判断C;根据回归模型中,预报变量y的值与解释变量的关系判断D.
【解答】解:对于A,将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a2倍,故A错误;
对于B,在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高,故B正确;
对于C,线性相关系数r的绝对值越接近于1,两个变量的线性相关性越强;
反之,相关系数r的绝对值越接近于0,线性相关性越弱,故C错误;
对于D,预报变量y的值由解释变量x和随机误差e共同确定,x只能解释部分y的变化,
即在回归模型中,预报变量y的值不能由解释变量x唯一确定,故D正确.
故选:BD.
【点评】本题主要考查了方差的性质,考查了变量间的相关关系,属于中档题.
(多选)20.某校高三1班48名物理方向的学生在一次质量检测中,语文成绩、数学成绩与六科总成绩在全年级中的排名情况如图所示,“★”表示的是该班甲、乙、丙三位同学对应的点.从这次考试的成绩看,下列结论正确的是( )
A.该班六科总成绩排名前6的同学语文成绩比数学成绩排名更好
B.在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是语文
C.数学成绩与六科总成绩的相关性比语文成绩与六科总成绩的相关性更强
D.在甲、乙两人中,其语文成绩名次比其六科总成绩名次靠前的学生是甲
【分析】结合图形可分析出答案.
【解答】解:A:由图可得,该班六科总成绩排名前6的同学数学成绩比语文成绩排名更好,故A错误;
B:由右图可得丙同学的总成绩排在班上倒数第三名,其语文成绩排在250到300名之间,
从左图可得其数学成绩排在400名左右,故B正确;
C:数学成绩与六科总成绩的相关性比语文成绩与六科总成绩的相关性更强,因为右图的点的分布较左图更分散,故C正确;
D:由左图可得甲的总成绩排在班上第7名,年级名次100多一点,
对应到右图可得,其语文成绩排在年级近100名,故甲的语文成绩名次比其六科总成绩名次靠前;
由左图可得甲的总成绩排在班上第27名,年级名次接近250名,
对应到右图可得,其语文成绩排在年级250名之后,故乙的语文成绩名次比其六科总成绩名次靠后,故D正确;
故选:BCD.
【点评】本题考查了根据图形解决实际问题,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
