【高考押题预测】2025年高考物理核心考点考前冲刺 匀变速直线运动位移与时间的关系(含解析)
文档属性
| 名称 | 【高考押题预测】2025年高考物理核心考点考前冲刺 匀变速直线运动位移与时间的关系(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 175.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-01 09:42:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
匀变速直线运动位移与时间的关系
一.选择题(共10小题)
1.一辆汽车以54km/h的速度在平直公路上匀速行驶,司机发现前方有异常情况而紧急刹车,刹车后汽车以6m/s2的加速度做匀减速直线运动。从汽车开始做减速运动开始计时,3s内汽车的位移为( )
A.18m B.18.75m C.22.5m D.81m
2.伽利略设计了如图所示的“斜面实验”,当时只能靠滴水计时。他说:“为了测时间,我们把一只盛水的大容器置于高处,在容器底部焊上一根口径很细的管子,用小杯子收集每次下降时由细管流出的水,然后称出水的重量”,若将小球由静止滚下的距离记为L,对应时间内收集的水的质量记为m,则L与m的比例关系为( )
A.L∝ B.L∝ C.L∝m2 D.L∝m
3.一辆汽车做匀加速直线运动,经过路旁两棵相距50m的树共用时间5s,它经过第二棵树时的速度是15m/s,则它经过第一棵树时的速度是( )
A.2m/s B.10m/s C.5m/s D.2.5m/s
4.某汽车以速度10m/s匀速行驶,刹车后第1个2s内位移与最后一个2s内位移之比为3:2,设汽车做匀减速直线运动,则刹车后4s内汽车通过的距离是( )
A.2.5 m B.4 m C.12 m D.12.5 m
5.交警在处理某次交通事故时,把监控仪器记录的数据输入计算机,得到肇事汽车在平直路面上紧急刹车(且遇车轮抱死)过程中的位移随时间变化的规律为x=24t﹣3t2(x的单位是m,t的单位是s),则下列说法不正确的是( )
A.该汽车刹车的初速度为24m/s
B.该汽车刹车的加速度为﹣3m/s2
C.刹车后2s末的速度为12m/s
D.刹车后5s内的平均速度为9.6m/s
6.如图是某小区单扇自动感应门,人进出时,门从静止开始以加速度a匀加速运动,后以匀减速运动,完全打开时速度恰好为零。已知单扇门的宽度为d,则门完全打开所用时间为( )
A. B. C. D.
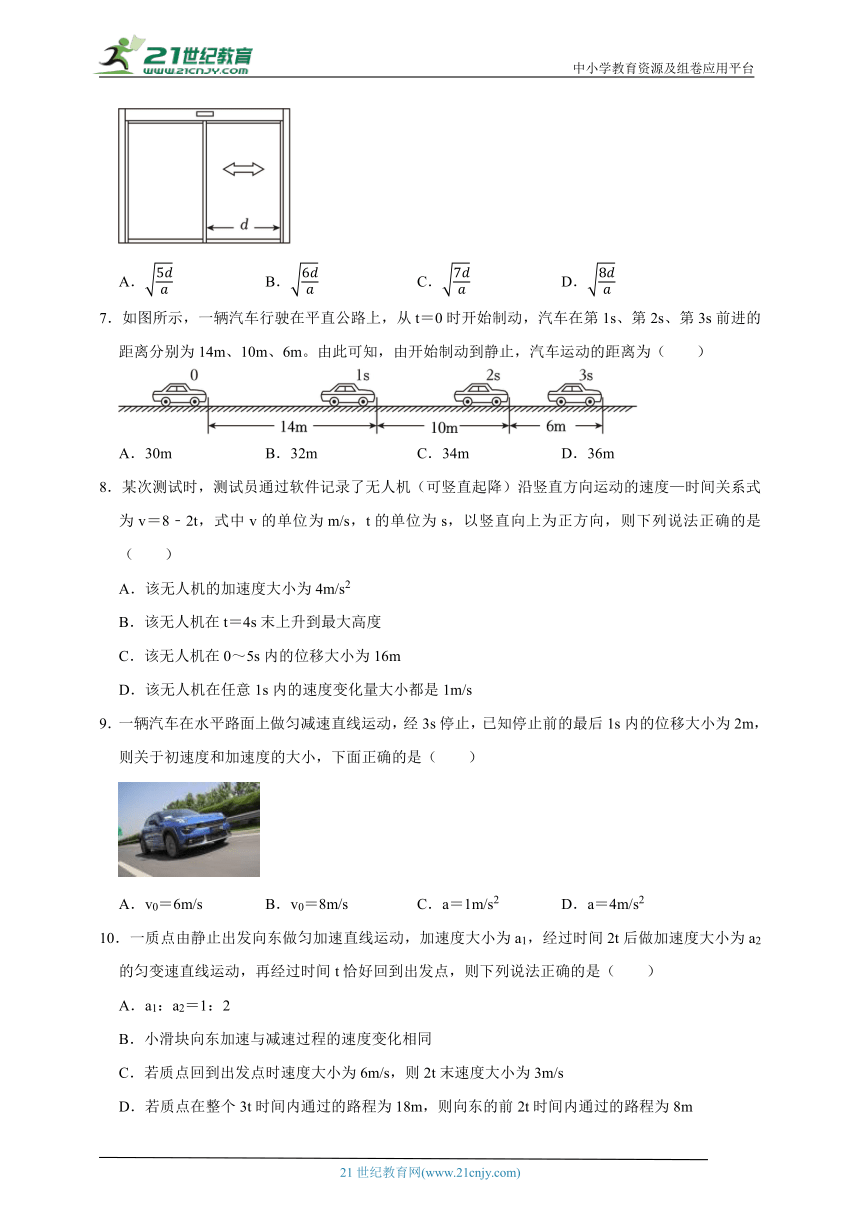
7.如图所示,一辆汽车行驶在平直公路上,从t=0时开始制动,汽车在第1s、第2s、第3s前进的距离分别为14m、10m、6m。由此可知,由开始制动到静止,汽车运动的距离为( )
A.30m B.32m C.34m D.36m
8.某次测试时,测试员通过软件记录了无人机(可竖直起降)沿竖直方向运动的速度—时间关系式为v=8﹣2t,式中v的单位为m/s,t的单位为s,以竖直向上为正方向,则下列说法正确的是( )
A.该无人机的加速度大小为4m/s2
B.该无人机在t=4s末上升到最大高度
C.该无人机在0~5s内的位移大小为16m
D.该无人机在任意1s内的速度变化量大小都是1m/s
9.一辆汽车在水平路面上做匀减速直线运动,经3s停止,已知停止前的最后1s内的位移大小为2m,则关于初速度和加速度的大小,下面正确的是( )
A.v0=6m/s B.v0=8m/s C.a=1m/s2 D.a=4m/s2
10.一质点由静止出发向东做匀加速直线运动,加速度大小为a1,经过时间2t后做加速度大小为a2的匀变速直线运动,再经过时间t恰好回到出发点,则下列说法正确的是( )
A.a1:a2=1:2
B.小滑块向东加速与减速过程的速度变化相同
C.若质点回到出发点时速度大小为6m/s,则2t末速度大小为3m/s
D.若质点在整个3t时间内通过的路程为18m,则向东的前2t时间内通过的路程为8m
二.多选题(共10小题)
(多选)11.平直公路上,一辆自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标,它们的位移x随时间t变化的规律分别为:汽车,自行车x2=4t,则下列说法正确的( )
A.汽车做匀减速直线运动,自行车做匀速直线运动
B.自行车追上汽车之前二者的最大距离为36m
C.经过路标后较短时间内自行车在前,汽车在后
D.当自行车追上汽车时,它们距路标100m
(多选)12.一辆汽车在水平路面上做匀减速直线运动,经3s停止,已知停止前最后1s内汽车的位移大小为2m,则关于汽车的初速度和加速度的大小,下列说法正确的是( )
A.v0=6m/s B.v0=12m/s C.a=1m/s2 D.a=4m/s2
(多选)13.北京冬奥会的成功举办极大地促进了我国民众对冰雪运动的热爱。如图为某滑冰场的滑雪轨道,该轨道是由倾斜直轨道AB和水平轨道BC组成。t=0时某滑雪爱好者从A点由静止开始匀加速下滑,经过B点前后速度大小不变,之后在BC上做匀减速直线运动,最后停在C点。若第2s末和第6s末速度大小均为8m/s,第4s末速度大小为12m/s,则( )
A.运动员在第4s末恰好经过B点
B.运动员经过B点的速度为
C.运动员在第8s末恰好停在C点
D.运动员在第10s末恰好停在C点
(多选)14.绿灯亮起后,一汽车由静止开始沿直线匀加速通过路口。对汽车匀加速通过路口过程,下列说法正确的是( )
A.加速度方向与其速度方向相同
B.加速度随时间均匀增大
C.速度随时间均匀增大
D.位移随时间均匀增大
(多选)15.某物体做直线运动的t图像如图所示。下列说法正确的是( )
A.物体的加速度大小为10m/s2
B.物体的初速度大小为10m/s
C.1s时,物体的速度大小为10m/s
D.在0~3s内,物体的位移大小为30m
(多选)16.汽车正以17m/s的速度在平直公路上前进,突然发现前方距离车头21m处有险情。司机立即刹车,刹车时加速度大小为8.5m/s2,下列说法正确的是( )
A.汽车刚刹车至刚停止的过程所需时间为3s
B.汽车运动的位移大小为17m
C.汽车停止的位置离险情处还有3m
D.汽车最后1s的位移大小为4.25m
(多选)17.甲、乙两车在平直公路上同向做匀变速直线运动,如图所示为计算机生成的图像,x为车辆运动位移,t为对应时间。已知两车在3s时并排行驶,则( )
A.t=0时,甲车在乙车前7.5m处
B.t=0时,甲车在乙车前15m处
C.在2s时,两车第一次并排行驶
D.甲车初速度大小为10m/s
(多选)18.物理的研究过程中科学家们创造了许多物理学研究方法,下列叙述中正确的是( )
A.在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法
B.根据速度定义式,当Δt非常小时,就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法
C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法
D.定义加速度用到比值定义法,加速度与Δv和Δt无关
(多选)19.一质点沿x轴运动,其位移x时间t变化的规律为x=2t+t2(m),t的单位为s。关于该质点的初速度和加速度判断正确的是( )
A.初速度为1m/s B.初速度为2m/s
C.加速度为1m/s2 D.加速度为2m/s2
(多选)20.物体做匀加速直线运动,已知第1s末的速度是6m/s,第2s末的速度是8m/s,则下面结论正确的是( )
A.物体的加速度是2m/s2
B.物体零时刻的速度是3m/s
C.第1s内的平均速度为4m/s
D.第2s内的位移为7m
三.填空题(共10小题)
21.芜湖轨道交通开通两年来,已成为市民生活中不可或缺的通勤工具,客流呈稳步上升趋势。现一位同学正好站立在轻轨列车的第一节车厢前端平齐处,轻轨列车启动后做匀加速直线运动,该同学测出第一节车厢通过他所用的时间是4s,则第一节车厢通过他的时间与第二节车厢通过他的时间之比是 ;若这列车共有4节车厢,则全部车厢通过这位同学历时 s。
22.质量为m=1kg的物体在水平力作用下沿着粗糙水平面做匀变速直线运动,物体与水平面间的动摩擦因数μ=0.1,其位移随时间变化的关系式为x=16t﹣2t2(m),则物体的初速度大小是 m/s,水平力的大小为 N。
23.一个物体做匀加速直线运动,位移随时间变化关系式为s=3t+t2(位移单位为m,时间单位为s),则该物体运动的加速度大小为 m/s2,3秒末的速度大小为 m/s。
24.由静止开始做匀加速直线运动的汽车,第1s内通过0.4m位移,汽车在第1s末的速度为 m/s;汽车在第2s内通过的位移为 m.
25.早在16世纪末,伽利略就猜想落体运动的速度应该是均匀变化的,一种为速度随时间均匀变化,一种速度随位移均匀变化。为此他设计了的“斜面实验”,反复做了上百次,验证了他的猜想。若伽利略研究小球沿斜面下滑时小球的位移与时间的关系式为x=kt2(k为一定值),则小球速度随 (填“时间”或“位移”)均匀变化。小球运动的加速度大小为 。
26.汽车以20m/s的速度在平直公路上匀减速行驶,刹车后经3s速度变为8m/s,则刹车过程中加速度为 m/s2,刹车8s后位移为 m。
27.汽车初速为20m/s,关闭发动机后做匀减速运动,加速度大小为4m/s2,汽车在第4s初的速度为 ;前6s内位移为 。
28.一质点沿直线Ox方向做变速运动,它离开O点的距离随时间变化的关系为x=5+2t3(m),它的速度随时间t变化的关系为v=6t2(m/s)。该质点在前2秒内的平均速度为 m/s,第2秒内的平均加速度为 m/s2。
29.汽车以大小为30m/s的速度做匀速直线运动,刹车后,前2s内(车未停)的平均速度大小为25m/s,则刹车后,汽车获得的加速度的大小为 m/s2。刹车后2s内与刹车后7s内汽车通过的位移之比为 。
30.海滨浴场的滑梯从顶端到入水处长12.5m,一人由滑梯顶端开始做初速度为零的匀加速直线运动,开始运动后的第一秒通过的位移是0.5m,则人的加速度大小是 。从顶端开始到入水所需的时间为 ,人入水时的速度大小是 ,从顶端开始到入水的平均速度大小是 。
匀变速直线运动位移与时间的关系
参考答案与试题解析
一.选择题(共10小题)
1.一辆汽车以54km/h的速度在平直公路上匀速行驶,司机发现前方有异常情况而紧急刹车,刹车后汽车以6m/s2的加速度做匀减速直线运动。从汽车开始做减速运动开始计时,3s内汽车的位移为( )
A.18m B.18.75m C.22.5m D.81m
【分析】汽车刹车过程做匀减速直线运动,根据加速度和初速度,由速度—时间公式求出刹车的时间,然后判断4s内汽车是否停止运动,再根据汽车的运动状态求汽车的位移。
【解答】解:汽车的初速度v0=54km/h=15m/s,加速度大小a=6m/s2,
汽车刹车后减速到零需要的时间t0s=2.5s<t=3s
汽车刹车后经过2.5s停止运动,因此汽车刹车后3s内的位移:
xm=18.75m,故B正确,ACD错误。
故选:B。
【点评】对于汽车刹车这种匀减速直线运动,不能死套公式,要注意检验解题结果的合理性,往往要先求出汽车刹车的时间,然后再进行其他计算。
2.伽利略设计了如图所示的“斜面实验”,当时只能靠滴水计时。他说:“为了测时间,我们把一只盛水的大容器置于高处,在容器底部焊上一根口径很细的管子,用小杯子收集每次下降时由细管流出的水,然后称出水的重量”,若将小球由静止滚下的距离记为L,对应时间内收集的水的质量记为m,则L与m的比例关系为( )
A.L∝ B.L∝ C.L∝m2 D.L∝m
【分析】明确该实验的实验原理是初速度为零的匀变速直线运动,位移与时间的二次方成正比,由于水是均匀稳定的流出,水的体积和时间成正比,则水的质量和时间成正比,由此解答。
【解答】解:球做初速度为零的匀变速直线运动,由位移公式有:L,得:L∝t2;
由于水是均匀稳定的流出,水的体积和时间成正比,又:m=ρV,所以水的质量与时间成正比,即:m∝t;
所以量筒中收集的水量可以间接的测量时间,即:t∝m
所以可得:L∝m2,故C正确,ABD错误。
故选:C。
【点评】解决该问题的关键是明确实验原理,根据流入小杯子中水的质量与时间成正比,将时间问题转化为水的质量问题。
3.一辆汽车做匀加速直线运动,经过路旁两棵相距50m的树共用时间5s,它经过第二棵树时的速度是15m/s,则它经过第一棵树时的速度是( )
A.2m/s B.10m/s C.5m/s D.2.5m/s
【分析】根据位移和时间,结合匀变速直线运动的平均速度推论求出汽车经过第一棵树时的速度.
【解答】解:汽车的平均速度为:,
因为,则汽车经过第一棵树时的速度为:.故C正确,A、B、D错误。
故选:C。
【点评】解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.
4.某汽车以速度10m/s匀速行驶,刹车后第1个2s内位移与最后一个2s内位移之比为3:2,设汽车做匀减速直线运动,则刹车后4s内汽车通过的距离是( )
A.2.5 m B.4 m C.12 m D.12.5 m
【分析】根据匀变速直线运动的位移—时间公式求出第1个2s内的位移与最后一个2s内的位移,通过比值求出加速度的大小,从而运动学公式求出刹车后4s内的位移.
【解答】解:设加速度的大小为a,则第1个2s内的位移大小为:x1=v0tat2=20﹣2a。
根据逆向思维,最后1个2s内的位移大小为:x2at2a×4=2a
根据:x1:x2=3:2,解得:a=4m/s2。
汽车刹车到停止所需的时间 ts=2.5s
可知刹车后4s内的位移等于2.5s内的位移,则有:
xm=12.5m。故D正确,A、B、C错误。
故选:D。
【点评】解决本题的关键掌握匀变速直线运动的运动学公式,并能灵活运用,注意汽车刹车速度减为零后不再运动.
5.交警在处理某次交通事故时,把监控仪器记录的数据输入计算机,得到肇事汽车在平直路面上紧急刹车(且遇车轮抱死)过程中的位移随时间变化的规律为x=24t﹣3t2(x的单位是m,t的单位是s),则下列说法不正确的是( )
A.该汽车刹车的初速度为24m/s
B.该汽车刹车的加速度为﹣3m/s2
C.刹车后2s末的速度为12m/s
D.刹车后5s内的平均速度为9.6m/s
【分析】AB.根据题中的表达式结合匀变速直线运动的位移公式求解初速度和加速度;
CD.根据匀变速直线运动的瞬时速度和平均速度规律求解。
【解答】解:AB.由匀变速直线运动的位移—时间关系
及汽车刹车过程中的位移规律
x=24t﹣3t2
可知,汽车刹车时的初速度为
v0=24m/s
加速度为
a=﹣6m/s2
故A正确,B错误;
C.由v=v0+at得汽车刹车时间
t0s=4s
刹车后2s末的速度为
v=v0+at=24m/s+(﹣6×2)m/s=12m/s
故C正确;
D.刹车后5s内的位移即为4s的位移为
x2 t04m=48m
刹车后5s内的平均速度为
m/s=9.6m/s
故D正确。
本题选不正确的,故选:B。
【点评】考查匀变速直线运动的速度、加速度、平均速度等规律,会根据题中数据进行相关的计算解答。
6.如图是某小区单扇自动感应门,人进出时,门从静止开始以加速度a匀加速运动,后以匀减速运动,完全打开时速度恰好为零。已知单扇门的宽度为d,则门完全打开所用时间为( )
A. B. C. D.
【分析】根据用平均速度表示的位移公式和速度—时间公式求解。
【解答】解:设门的最大速度为v,根据匀变速直线运动的规律可知加速过程和减速过程的平均速度均为
设加速和减速的时间分别为t1、t2,则v
又d
解得t
故ABC错误,D正确。
故选:D。
【点评】本题考查匀变速直线运动的求解,学生要熟练掌握,属于简单题。
7.如图所示,一辆汽车行驶在平直公路上,从t=0时开始制动,汽车在第1s、第2s、第3s前进的距离分别为14m、10m、6m。由此可知,由开始制动到静止,汽车运动的距离为( )
A.30m B.32m C.34m D.36m
【分析】利用逐差法求出加速度,然后求出1s末速度大小,结合速度—位移公式可求出距离。
【解答】解:根据匀变速直线运动相邻的相等时间间隔内的位移差相等,可知汽车做匀变速直线运动根据逐差法有x2﹣x1=aT2,解得a=﹣4m/s2,1s末的速度大小为vm/s=12m/s,由开始制动到静止,汽车运动的距离为s=14 m,得到s=32m,故B正确,ACD错误。
故选:B。
【点评】学生在解决本题时,应注意要灵活运用运动学公式,尤其是逐差法公式的利用。
8.某次测试时,测试员通过软件记录了无人机(可竖直起降)沿竖直方向运动的速度—时间关系式为v=8﹣2t,式中v的单位为m/s,t的单位为s,以竖直向上为正方向,则下列说法正确的是( )
A.该无人机的加速度大小为4m/s2
B.该无人机在t=4s末上升到最大高度
C.该无人机在0~5s内的位移大小为16m
D.该无人机在任意1s内的速度变化量大小都是1m/s
【分析】A.根据匀变速直线运动的速度公式结合给出的表达式分析初速度和加速度;
B.根据匀减速直线运动的减速时间分析计算;
C.根据匀减速直线运动的位移公式求解;
D.根据匀变速直线运动公式Δv=aΔt代入数据求解其大小。
【解答】解:A.根据匀变速直线运动速度—时间公式
v=v0+at
结合v=8﹣2t
可得
v0=8m/s,a=﹣2m/s2
故该无人机的加速度大小为2m/s2,故A错误;
B.该无人机上升到最大高度时,速度为零,所用的时间为
故B正确;
C.该无人机在0~5s内的位移大小为
故C错误;
D.根据Δv=aΔt,该无人机在任意1s内的速度变化量大小都是
Δv=|a|Δt=2×1m/s=2m/s
故D错误。
故选:B。
【点评】考查匀变速直线运动速度、位移、时间等规律,要求学生熟练掌握这些基本概念会进行相关的计算。
9.一辆汽车在水平路面上做匀减速直线运动,经3s停止,已知停止前的最后1s内的位移大小为2m,则关于初速度和加速度的大小,下面正确的是( )
A.v0=6m/s B.v0=8m/s C.a=1m/s2 D.a=4m/s2
【分析】根据匀变速直线运动的位移—时间公式和速度—时间公式解答即可。
【解答】解:因为停止前的最后1s内的位移大小为2m,运用逆向思维有:,其中t=1s
代入数据得:a=4m/s2
根据v=v0+at',代入数据可得速度大小为:v=12m/s,即初速度为12m/s,故ABC错误,D正确;
故选:D。
【点评】本题主要考查了匀变速直线运动的位移—时间公式和速度—时间公式,选用逆向思维使问题简单化。
10.一质点由静止出发向东做匀加速直线运动,加速度大小为a1,经过时间2t后做加速度大小为a2的匀变速直线运动,再经过时间t恰好回到出发点,则下列说法正确的是( )
A.a1:a2=1:2
B.小滑块向东加速与减速过程的速度变化相同
C.若质点回到出发点时速度大小为6m/s,则2t末速度大小为3m/s
D.若质点在整个3t时间内通过的路程为18m,则向东的前2t时间内通过的路程为8m
【分析】A、根据位移与时间公式解答;
B、速度是矢量,有大小有方向;
C、根据速度公式解答;
D、求解滑块向右减速的时间,运用速度公式解答。
【解答】解:A、由题意可知,解得a1:a2=1:8,故A错误;
B.小滑块向东加速与减速过程的速度变化大小相同,方向相反,故B错误;
C.若质点回到出发点时速度大小为v2,2t末速度大小为v1,则,可得v2=3v1,若质点回到出发点时速度大小为6m/s,则2t末速度大小为2m/s,故C错误;
D.滑块向右减速的时间为t1,则a1 2t=a2t1,可得,则整个过程的路程为,则向东的前2t时间内通过的路程为,故D正确。
故选:D。
【点评】考查对匀变速直线运动规律的理解,熟练运用运动学公式。
二.多选题(共10小题)
(多选)11.平直公路上,一辆自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标,它们的位移x随时间t变化的规律分别为:汽车,自行车x2=4t,则下列说法正确的( )
A.汽车做匀减速直线运动,自行车做匀速直线运动
B.自行车追上汽车之前二者的最大距离为36m
C.经过路标后较短时间内自行车在前,汽车在后
D.当自行车追上汽车时,它们距路标100m
【分析】A、由运动学公式,x=vt推导;
B、两车速度相等时相距最远;
CD、根据关系式分析。
【解答】解:A.根据汽车可知其初速度v0=10m/s,加速度a=﹣0.5m/s2,做匀减速直线运动,自行车x2=4t,则乙做速度为v=4m/s的匀速直线运动,故A正确;
B.汽车速度为v'=v0+at=v=4m/s,即在t12s时两车速度相等,此时两车相距最远,最大距离为,故B正确;
C.经过路标后,在速度相等前,汽车的速度大于自行车的速度,可知汽车在前,自行车在后,故C错误;
D.两车相遇时,有,解得t=24s,汽车刹车时间为,即20s时,车已停止运动,刹车距离为,所以当自行车追上汽车时,它们距路标100m,故D正确;
故选:ABD。
【点评】考查对匀变速直线运动规律的理解,熟悉运动学公式。
(多选)12.一辆汽车在水平路面上做匀减速直线运动,经3s停止,已知停止前最后1s内汽车的位移大小为2m,则关于汽车的初速度和加速度的大小,下列说法正确的是( )
A.v0=6m/s B.v0=12m/s C.a=1m/s2 D.a=4m/s2
【分析】根据逆向思维法把汽车的运动看作初速度为零的匀加速直线运动,根据位移—时间公式计算加速度,根据速度—时间关系计算初速度即可。
【解答】解:利用逆向思维可知汽车看作反向的初速度为零的匀加速直线运动,
汽车在第1s内的位移大小为2m,则加速度
a=4m/s2
初速度大小为
v0=at=4×3m/s=12m/s,故BD正确,AC错误。
故选:BD。
【点评】知道把汽车看作初速度为零的反向匀加速直线运动可以简化解题步骤。
(多选)13.北京冬奥会的成功举办极大地促进了我国民众对冰雪运动的热爱。如图为某滑冰场的滑雪轨道,该轨道是由倾斜直轨道AB和水平轨道BC组成。t=0时某滑雪爱好者从A点由静止开始匀加速下滑,经过B点前后速度大小不变,之后在BC上做匀减速直线运动,最后停在C点。若第2s末和第6s末速度大小均为8m/s,第4s末速度大小为12m/s,则( )
A.运动员在第4s末恰好经过B点
B.运动员经过B点的速度为
C.运动员在第8s末恰好停在C点
D.运动员在第10s末恰好停在C点
【分析】在斜面上和水平面上分别列速度—时间公式和位移—时间公式,需要判断第4s是在斜面上还是在水平面上,然后分别求出在斜面上和水平面上的加速度,进而联立,分段求解。
【解答】解:A、依题意,运动员在第2s末和第6s末速度大小相等,且第2s末速度为8m/s,
则运动员加速过程的加速度大小为
代入数据解得
a1=4m/s2
若运动员在第4s末恰好经过B点,则运动员在第4s末的速度应该为
v=a1t4=4×4m/s=16m/s
而实际上,第4s末速度大小为12m/s,说明运动员第4s末已经越过B点做减速运动了,故A错误;
B、第4s末到第6s末过程中,运动员做减速运动,
加速度大小为
a2
代入数据解得
a2=2m/s2
根据运动学公式有v2+a1t1+(﹣a1t2)=v4
又t1+t2=2s
代入数据解得
运动员到达B点的时间为
B点的速度为
vB=a1t
代入数据解得
vB
故B错误;
CD、设运动员在t′时间恰好停在C点,则有v6=a2t′
代入数据解得t′=4s
所以到C点的时间为10s末。
故选:BD。
【点评】本题考查了匀变速直线运动的位移—时间公式、速度—时间公式的熟练应用,判断第4s末在斜面还是水平面是关键,可假设来判断。
(多选)14.绿灯亮起后,一汽车由静止开始沿直线匀加速通过路口。对汽车匀加速通过路口过程,下列说法正确的是( )
A.加速度方向与其速度方向相同
B.加速度随时间均匀增大
C.速度随时间均匀增大
D.位移随时间均匀增大
【分析】根据加速度恒定,速度与加速度同向运动时为匀加速直线运动。
【解答】解:A.汽车由静止开始沿直线匀加速通过路口,即汽车做初速度为零的匀加速直线运动,则加速度方向与其速度方向相同,故A正确;
B.汽车做初速度为零的匀加速直线运动,加速度大小和方向均不变的运动,故B错误;
C.根据速度—时间公式v = at,加速度不变,所以速度随时间均匀增大,故C正确;
D.根据位移—时间公式可知位移与时间是二次函数关系,故D错误。
故选:AC。
【点评】本题主要考查了匀加速直线运动的理解,解题关键是掌握加速度恒定,速度与加速度同向运动时为匀加速直线运动。
(多选)15.某物体做直线运动的t图像如图所示。下列说法正确的是( )
A.物体的加速度大小为10m/s2
B.物体的初速度大小为10m/s
C.1s时,物体的速度大小为10m/s
D.在0~3s内,物体的位移大小为30m
【分析】根据图像得到与t的关系式,将匀变速直线运动位移—时间公式x=v0tat2变形得到与t的关系式,两式对比得到物体的加速度、初速度,再根据运动学公式求解其他量。
【解答】解:AB、由图可得
由匀变速直线运动的位移—时间公式变形得
对比可得,物体初速度为v0=﹣5m/s,a=10m/s2,故A正确,B错误;
C、物体做匀变速直线运动,1s时,物体的速度为v=v0+at=(﹣5+10×1)m/s=5m/s,故C错误;
D、根据得x=﹣5t+5t2,则在0~3s内,物体的位移大小为x=(﹣5×3+5×32)m=30m,故D正确。
故选:AD。
【点评】解决本题的关键要根据数学知识写出图像的解析式,分析位移与时间的关系,结合匀变速直线运动位移—时间公式,得到加速度、初速度,从而分析物体的运动情况。
(多选)16.汽车正以17m/s的速度在平直公路上前进,突然发现前方距离车头21m处有险情。司机立即刹车,刹车时加速度大小为8.5m/s2,下列说法正确的是( )
A.汽车刚刹车至刚停止的过程所需时间为3s
B.汽车运动的位移大小为17m
C.汽车停止的位置离险情处还有3m
D.汽车最后1s的位移大小为4.25m
【分析】根据运动学公式分析各选项。
【解答】解:A、汽车减速至0的时间为,故A错误;
BC、汽车运动的位移大小 ,汽车停止的位置离险情处还有21m﹣17m=4m,故B正确、C错误;
D、将汽车的运动视为反向的从静止开始的匀加速直线运动,可得汽车最后1s的位移大小 ,故D正确。
故选:BD。
【点评】考查对匀变速直线运动规律的理解和运动学公式的运用,运用逆向思维法解答。
(多选)17.甲、乙两车在平直公路上同向做匀变速直线运动,如图所示为计算机生成的图像,x为车辆运动位移,t为对应时间。已知两车在3s时并排行驶,则( )
A.t=0时,甲车在乙车前7.5m处
B.t=0时,甲车在乙车前15m处
C.在2s时,两车第一次并排行驶
D.甲车初速度大小为10m/s
【分析】根据可得:,则可知图像的纵轴截距表示初速度,斜率为,可求两车的初速度与加速度的大小;根据3s内位移之差求解t=0时刻两者位置关系;分析2s内两车位移关系,从而判断t=2s时两车位置关系。
【解答】解:ABC,根据图像的纵轴截距表示初速度,斜率为可知:甲车的初速度为:v甲=10m/s,,乙车的初速度为v乙=0,加速度为,甲车在3s内的位移为:,乙车在3s内发生的位移为:,由题知3s时两车并排行驶,则在t=0时,甲车在乙车前的距离为:Δx=x乙﹣x甲=67.5m﹣52.5m=15m;故BD正确,A错误;
C、甲车在2s内的位移为:,乙车在2s内发生的位移为:,由于x甲1+Δx=30m+15m=45m>x乙1=30m,则甲、乙两车在2s时没有并排,故C错误。
故选:BD。
【点评】本题是图像的应用,解题的关键是要知道在速度一时间图像中,图像与纵轴的截距表示初速度,斜率的2倍表示加速度,然后通过位移关系来分析并排问题。
(多选)18.物理的研究过程中科学家们创造了许多物理学研究方法,下列叙述中正确的是( )
A.在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法
B.根据速度定义式,当Δt非常小时,就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法
C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法
D.定义加速度用到比值定义法,加速度与Δv和Δt无关
【分析】根据理想化模型法,极限思想方法,微元法以及比值定义法的特点分析求解。
【解答】解:A.在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫理想化模型法,故A错误;
B.根据速度定义式,当Δt非常小时,就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法,故B正确;
C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法,故C正确;
D.定义加速度用到比值定义法,加速度与Δv和Δt无关,故D正确;
故选:BCD。
【点评】本题考查了物理学方法,理解各个物理量推导或定义背后所蕴含的物理学方法是解决此类问题的关键。
(多选)19.一质点沿x轴运动,其位移x时间t变化的规律为x=2t+t2(m),t的单位为s。关于该质点的初速度和加速度判断正确的是( )
A.初速度为1m/s B.初速度为2m/s
C.加速度为1m/s2 D.加速度为2m/s2
【分析】根据匀变速直线运动的位移—时间公式得出质点的初速度和加速度。
【解答】解:质点的位移x时间t变化的规律为x=2t+t2(m),
结合匀变速直线运动位移—时间关系x=v0tat2
对比可知该质点的初速度和加速度分别为v0=2m/s,a=2m/s2
故AC错误,BD正确。
故选:BD。
【点评】解决本题的关键掌握匀变速直线运动的位移—时间公式,并能灵活运用,基础题。
(多选)20.物体做匀加速直线运动,已知第1s末的速度是6m/s,第2s末的速度是8m/s,则下面结论正确的是( )
A.物体的加速度是2m/s2
B.物体零时刻的速度是3m/s
C.第1s内的平均速度为4m/s
D.第2s内的位移为7m
【分析】根据加速度的定义求解加速度,并结合速度—时间公式求解初速度;
根据平均速度公式求解第1s内的平均速度和第2s内位移。
【解答】解:AB、规定初速度方向为正方向,根据加速度定义式得:物体的加速度a2m/s2,根据v1=v0+at代入数据得:v0=4m/s。故A正确,B错误;
C、第1s内的平均速度,故C错误;
D、第2s内的位移为,故D正确。
故选:AD。
【点评】解决本题的关键掌握匀变速直线运动的速度—时间公式和平均速度公式,并能灵活运用。
三.填空题(共10小题)
21.芜湖轨道交通开通两年来,已成为市民生活中不可或缺的通勤工具,客流呈稳步上升趋势。现一位同学正好站立在轻轨列车的第一节车厢前端平齐处,轻轨列车启动后做匀加速直线运动,该同学测出第一节车厢通过他所用的时间是4s,则第一节车厢通过他的时间与第二节车厢通过他的时间之比是 ;若这列车共有4节车厢,则全部车厢通过这位同学历时 8 s。
【分析】根据位移公式列方程得出全部通过这位工作人员历时和前2节车厢运动的时间,从而得出第二节车厢运动的时间,即可求出第二节车厢通过它的时间与第一节车厢通过他的时间之比。
【解答】解:设每一节车厢的长度为L,第一节通过时间满足,解得:
前2节车厢通过他的时间为:,解得:
联立解得:
则第2节车厢通过他的时间为:
第一节车厢通过他的时间与第二节车厢通过他的时间之比为:
则全部列车通过的时间为:
又,
联立解得:。
故答案为:;8。
【点评】本题考查匀变速直线运动规律的应用,基础题目。
22.质量为m=1kg的物体在水平力作用下沿着粗糙水平面做匀变速直线运动,物体与水平面间的动摩擦因数μ=0.1,其位移随时间变化的关系式为x=16t﹣2t2(m),则物体的初速度大小是 16 m/s,水平力的大小为 3 N。
【分析】结合物体做匀变速直线运动时的位移—时间公式与题干中所给的位移与时间的关系进行对比,求出加速度和初速;根据牛顿第二定律求出物体所受的合力即水平拉力的大小。
【解答】解:根据匀变速直线运动位移与时间变化的关系式可得:x=v0t,与x=16t﹣2t2(m)对照可得
初速度:v0=16m/s,加速度大小为:a=4m/s2
取加速度方向为正方向,由牛顿第二定律可得:F+μmg=ma
代入数据可得:F=3N,说明F方向向后,大小为3N。
故答案为:16;3。
【点评】本题考查匀变速直线运动的规律与牛顿运动定律的应用,关键是运用位移—时间公式求出初速度和加速度,再由牛顿第二定律求出未知力。
23.一个物体做匀加速直线运动,位移随时间变化关系式为s=3t+t2(位移单位为m,时间单位为s),则该物体运动的加速度大小为 2 m/s2,3秒末的速度大小为 9 m/s。
【分析】根据位移—时间公式可求出初速度和加速度,利用速度公式可求出3s末的速度。
【解答】解:根据位移—时间公式,s=v0tat2,结合题干中s=3t+t2可知v0=3m/s,a=1m/s2,解得a=2m/s2,利用公式v=v0+at,当t=3s时,解得v=9m/s
故答案为:2,9。
【点评】学生在解答本题时,应注意利用原始公式对比题干中的公式,得到相关物理量。
24.由静止开始做匀加速直线运动的汽车,第1s内通过0.4m位移,汽车在第1s末的速度为 0.8 m/s;汽车在第2s内通过的位移为 1.2 m.
【分析】小车做初速度为零的匀加速直线运动,根据位移—时间关系求出加速度,根据速度—时间公式求出速度;
根据初速度为0的匀加速直线运动,第一秒内和第二秒内位移之比为1:3即可求解.
【解答】解:小车做初速度为零的匀加速直线运动
由,得:
则汽车在第1s末的速度为v1=at=0.8×1m/s=0.8m/s
由s1:s2=1:3,得:
汽车在第2s内通过的位移为s2=3s1=3×0.4m=1.2m
故答案为:0.8,1.2
【点评】本题主要考查了初速度为0的匀加速直线运动的基本规律以及推论,难度不大,属于基础题.
25.早在16世纪末,伽利略就猜想落体运动的速度应该是均匀变化的,一种为速度随时间均匀变化,一种速度随位移均匀变化。为此他设计了的“斜面实验”,反复做了上百次,验证了他的猜想。若伽利略研究小球沿斜面下滑时小球的位移与时间的关系式为x=kt2(k为一定值),则小球速度随 时间 (填“时间”或“位移”)均匀变化。小球运动的加速度大小为 2k 。
【分析】根据位移与时间的关系式为x = kt2,结合匀变速直线运动位移—时间公式分析求解。
【解答】解:伽利略研究小球沿斜面下滑时小球的位移与时间的关系式为x = kt2,由匀变速直线运动位移—时间公式:,可知小球运动的加速度大小为:a=2k
则小球运动的加速度为定值,小球的速度随时间均匀变化。
故答案为:时间;2k。
【点评】本题考查了匀变速直线运动相关知识,理解物体运动状态,合理选取运动学公式是解决此类问题的关键。
26.汽车以20m/s的速度在平直公路上匀减速行驶,刹车后经3s速度变为8m/s,则刹车过程中加速度为 ﹣4 m/s2,刹车8s后位移为 50 m。
【分析】(1)根据速度一时间公式求出刹车的加速度,
(2)根据速度一时间公式求出刹车速度减为零的时间,判断汽车是否停止,再结合位移公式求出刹车后的位移。
【解答】解:(1)汽车刹车时的加速度为:
am/s2=﹣4m/s2;
(2)汽车速度减为零的时间为:
t0s=5s;
则刹车后8s内的位移等于5s内的位移为:
xm=50m;
故答案为:﹣4;50。
【点评】解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,注意本题考查运动学中的刹车问题,是道易错题,汽车速度减为0后不再运动。
27.汽车初速为20m/s,关闭发动机后做匀减速运动,加速度大小为4m/s2,汽车在第4s初的速度为 8m/s ;前6s内位移为 50m 。
【分析】先计算出汽车的刹车时间,然后根据情况判断汽车是否已经停止运动,根据速度—时间公式计算出汽车的速度;然后根据位移与时间的关系得到汽车的位移大小。
【解答】解:汽车的刹车时间为,4s初即为3s末,此时汽车还没有停止,所以汽车在第4s初的速度为v=v0﹣at=20m/s﹣4×3m/s=8m/s。在5s末已经停止运动,所以汽车在前6s内位移为。
故答案为:8m/s,50m。
【点评】本题注意两点,一个是避免掉进刹车陷阱;第二个是第4s初的速度即为3s末的速度,汽车是减速3s时的速度。
28.一质点沿直线Ox方向做变速运动,它离开O点的距离随时间变化的关系为x=5+2t3(m),它的速度随时间t变化的关系为v=6t2(m/s)。该质点在前2秒内的平均速度为 8 m/s,第2秒内的平均加速度为 18 m/s2。
【分析】将t=0s、t=2s代入距离随时间变化的关系式x=5+2t3(m),可求出两个时刻质点离O点的距离,求得位移,再求解平均速度;将t=1s、t=2s代入速度表达式即可求得1s末、2s末的瞬时速度,根据加速度定义式求解平均加速度。
【解答】解:一质点沿直线Ox方向做变速运动,它离开O点的距离x随时间变化的关系为:x=5+2t3m;
t0=0时,位置坐标为x0=5m;
t2=2s时,位置坐标为x2=21m;
前2s内的位移Δx=21m﹣5m=16m
前2s内的平均速度:m/s=8m/s;
质点沿直线Ox方向做变速运动,它的速度随时间t变化的关系为:v=6t2m/s;
t1=1s时,速度为v1=6m/s;
t2=2s时,速度为v2=24m/s;
第2秒内的平均加速度为:am/s2=18m/s2。
故答案为:8;18。
【点评】题中物体的运动不是匀变速运动,根据平均速度的定义公式和平均加速度的定义公式列式求解即可。
29.汽车以大小为30m/s的速度做匀速直线运动,刹车后,前2s内(车未停)的平均速度大小为25m/s,则刹车后,汽车获得的加速度的大小为 5 m/s2。刹车后2s内与刹车后7s内汽车通过的位移之比为 5:9 。
【分析】根据匀变速直线运动的速度—时间公式求出汽车速度减为零的时间,判断汽车是否停止,再结合位移公式求出刹车后的位移,从而得出位移之比.
【解答】解:根据匀变速直线运动的规律可知,前2s内的平均速度等于中间时刻的瞬时速度,即刹车1s末的速度:v1=25m/s
根据匀变速直线运动速度一时间公式可知,v1=v0﹣at1
代入数据解得:a=5m/s2
停车时间:ts=6s
刹车后2s内的位移:x2=v1t2=25×2m=50m
刹车后7s内的位移即6s内的位移:x7m=90m,两者之比为5:9.
故答案为:5;5:9。
【点评】本题考查了运动学中的刹车问题,是道易错题,注意汽车速度减为零后不再运动.
30.海滨浴场的滑梯从顶端到入水处长12.5m,一人由滑梯顶端开始做初速度为零的匀加速直线运动,开始运动后的第一秒通过的位移是0.5m,则人的加速度大小是 1m/s2 。从顶端开始到入水所需的时间为 5s ,人入水时的速度大小是 5m/s ,从顶端开始到入水的平均速度大小是 2.5m/s 。
【分析】根据匀变速直线运动的位移—时间公式,结合速度—时间公式和平均速度分析求解。
【解答】解:根据匀变速直线运动的位移—时间公式:x,可得am/s2=1m/s2
从顶端开始到入水所需的时间有:t′s=5s
入水的速度:v=at=1×5m/s=5m/s
平均速度:m/s=2.5m/s
故答案为:1m/s2;5s;5m/s;2.5m/s。
【点评】本题考查了运动学相关知识,理解匀变速直线运动的位移—时间公式和速度—时间公式是解决此类问题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
匀变速直线运动位移与时间的关系
一.选择题(共10小题)
1.一辆汽车以54km/h的速度在平直公路上匀速行驶,司机发现前方有异常情况而紧急刹车,刹车后汽车以6m/s2的加速度做匀减速直线运动。从汽车开始做减速运动开始计时,3s内汽车的位移为( )
A.18m B.18.75m C.22.5m D.81m
2.伽利略设计了如图所示的“斜面实验”,当时只能靠滴水计时。他说:“为了测时间,我们把一只盛水的大容器置于高处,在容器底部焊上一根口径很细的管子,用小杯子收集每次下降时由细管流出的水,然后称出水的重量”,若将小球由静止滚下的距离记为L,对应时间内收集的水的质量记为m,则L与m的比例关系为( )
A.L∝ B.L∝ C.L∝m2 D.L∝m
3.一辆汽车做匀加速直线运动,经过路旁两棵相距50m的树共用时间5s,它经过第二棵树时的速度是15m/s,则它经过第一棵树时的速度是( )
A.2m/s B.10m/s C.5m/s D.2.5m/s
4.某汽车以速度10m/s匀速行驶,刹车后第1个2s内位移与最后一个2s内位移之比为3:2,设汽车做匀减速直线运动,则刹车后4s内汽车通过的距离是( )
A.2.5 m B.4 m C.12 m D.12.5 m
5.交警在处理某次交通事故时,把监控仪器记录的数据输入计算机,得到肇事汽车在平直路面上紧急刹车(且遇车轮抱死)过程中的位移随时间变化的规律为x=24t﹣3t2(x的单位是m,t的单位是s),则下列说法不正确的是( )
A.该汽车刹车的初速度为24m/s
B.该汽车刹车的加速度为﹣3m/s2
C.刹车后2s末的速度为12m/s
D.刹车后5s内的平均速度为9.6m/s
6.如图是某小区单扇自动感应门,人进出时,门从静止开始以加速度a匀加速运动,后以匀减速运动,完全打开时速度恰好为零。已知单扇门的宽度为d,则门完全打开所用时间为( )
A. B. C. D.
7.如图所示,一辆汽车行驶在平直公路上,从t=0时开始制动,汽车在第1s、第2s、第3s前进的距离分别为14m、10m、6m。由此可知,由开始制动到静止,汽车运动的距离为( )
A.30m B.32m C.34m D.36m
8.某次测试时,测试员通过软件记录了无人机(可竖直起降)沿竖直方向运动的速度—时间关系式为v=8﹣2t,式中v的单位为m/s,t的单位为s,以竖直向上为正方向,则下列说法正确的是( )
A.该无人机的加速度大小为4m/s2
B.该无人机在t=4s末上升到最大高度
C.该无人机在0~5s内的位移大小为16m
D.该无人机在任意1s内的速度变化量大小都是1m/s
9.一辆汽车在水平路面上做匀减速直线运动,经3s停止,已知停止前的最后1s内的位移大小为2m,则关于初速度和加速度的大小,下面正确的是( )
A.v0=6m/s B.v0=8m/s C.a=1m/s2 D.a=4m/s2
10.一质点由静止出发向东做匀加速直线运动,加速度大小为a1,经过时间2t后做加速度大小为a2的匀变速直线运动,再经过时间t恰好回到出发点,则下列说法正确的是( )
A.a1:a2=1:2
B.小滑块向东加速与减速过程的速度变化相同
C.若质点回到出发点时速度大小为6m/s,则2t末速度大小为3m/s
D.若质点在整个3t时间内通过的路程为18m,则向东的前2t时间内通过的路程为8m
二.多选题(共10小题)
(多选)11.平直公路上,一辆自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标,它们的位移x随时间t变化的规律分别为:汽车,自行车x2=4t,则下列说法正确的( )
A.汽车做匀减速直线运动,自行车做匀速直线运动
B.自行车追上汽车之前二者的最大距离为36m
C.经过路标后较短时间内自行车在前,汽车在后
D.当自行车追上汽车时,它们距路标100m
(多选)12.一辆汽车在水平路面上做匀减速直线运动,经3s停止,已知停止前最后1s内汽车的位移大小为2m,则关于汽车的初速度和加速度的大小,下列说法正确的是( )
A.v0=6m/s B.v0=12m/s C.a=1m/s2 D.a=4m/s2
(多选)13.北京冬奥会的成功举办极大地促进了我国民众对冰雪运动的热爱。如图为某滑冰场的滑雪轨道,该轨道是由倾斜直轨道AB和水平轨道BC组成。t=0时某滑雪爱好者从A点由静止开始匀加速下滑,经过B点前后速度大小不变,之后在BC上做匀减速直线运动,最后停在C点。若第2s末和第6s末速度大小均为8m/s,第4s末速度大小为12m/s,则( )
A.运动员在第4s末恰好经过B点
B.运动员经过B点的速度为
C.运动员在第8s末恰好停在C点
D.运动员在第10s末恰好停在C点
(多选)14.绿灯亮起后,一汽车由静止开始沿直线匀加速通过路口。对汽车匀加速通过路口过程,下列说法正确的是( )
A.加速度方向与其速度方向相同
B.加速度随时间均匀增大
C.速度随时间均匀增大
D.位移随时间均匀增大
(多选)15.某物体做直线运动的t图像如图所示。下列说法正确的是( )
A.物体的加速度大小为10m/s2
B.物体的初速度大小为10m/s
C.1s时,物体的速度大小为10m/s
D.在0~3s内,物体的位移大小为30m
(多选)16.汽车正以17m/s的速度在平直公路上前进,突然发现前方距离车头21m处有险情。司机立即刹车,刹车时加速度大小为8.5m/s2,下列说法正确的是( )
A.汽车刚刹车至刚停止的过程所需时间为3s
B.汽车运动的位移大小为17m
C.汽车停止的位置离险情处还有3m
D.汽车最后1s的位移大小为4.25m
(多选)17.甲、乙两车在平直公路上同向做匀变速直线运动,如图所示为计算机生成的图像,x为车辆运动位移,t为对应时间。已知两车在3s时并排行驶,则( )
A.t=0时,甲车在乙车前7.5m处
B.t=0时,甲车在乙车前15m处
C.在2s时,两车第一次并排行驶
D.甲车初速度大小为10m/s
(多选)18.物理的研究过程中科学家们创造了许多物理学研究方法,下列叙述中正确的是( )
A.在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法
B.根据速度定义式,当Δt非常小时,就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法
C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法
D.定义加速度用到比值定义法,加速度与Δv和Δt无关
(多选)19.一质点沿x轴运动,其位移x时间t变化的规律为x=2t+t2(m),t的单位为s。关于该质点的初速度和加速度判断正确的是( )
A.初速度为1m/s B.初速度为2m/s
C.加速度为1m/s2 D.加速度为2m/s2
(多选)20.物体做匀加速直线运动,已知第1s末的速度是6m/s,第2s末的速度是8m/s,则下面结论正确的是( )
A.物体的加速度是2m/s2
B.物体零时刻的速度是3m/s
C.第1s内的平均速度为4m/s
D.第2s内的位移为7m
三.填空题(共10小题)
21.芜湖轨道交通开通两年来,已成为市民生活中不可或缺的通勤工具,客流呈稳步上升趋势。现一位同学正好站立在轻轨列车的第一节车厢前端平齐处,轻轨列车启动后做匀加速直线运动,该同学测出第一节车厢通过他所用的时间是4s,则第一节车厢通过他的时间与第二节车厢通过他的时间之比是 ;若这列车共有4节车厢,则全部车厢通过这位同学历时 s。
22.质量为m=1kg的物体在水平力作用下沿着粗糙水平面做匀变速直线运动,物体与水平面间的动摩擦因数μ=0.1,其位移随时间变化的关系式为x=16t﹣2t2(m),则物体的初速度大小是 m/s,水平力的大小为 N。
23.一个物体做匀加速直线运动,位移随时间变化关系式为s=3t+t2(位移单位为m,时间单位为s),则该物体运动的加速度大小为 m/s2,3秒末的速度大小为 m/s。
24.由静止开始做匀加速直线运动的汽车,第1s内通过0.4m位移,汽车在第1s末的速度为 m/s;汽车在第2s内通过的位移为 m.
25.早在16世纪末,伽利略就猜想落体运动的速度应该是均匀变化的,一种为速度随时间均匀变化,一种速度随位移均匀变化。为此他设计了的“斜面实验”,反复做了上百次,验证了他的猜想。若伽利略研究小球沿斜面下滑时小球的位移与时间的关系式为x=kt2(k为一定值),则小球速度随 (填“时间”或“位移”)均匀变化。小球运动的加速度大小为 。
26.汽车以20m/s的速度在平直公路上匀减速行驶,刹车后经3s速度变为8m/s,则刹车过程中加速度为 m/s2,刹车8s后位移为 m。
27.汽车初速为20m/s,关闭发动机后做匀减速运动,加速度大小为4m/s2,汽车在第4s初的速度为 ;前6s内位移为 。
28.一质点沿直线Ox方向做变速运动,它离开O点的距离随时间变化的关系为x=5+2t3(m),它的速度随时间t变化的关系为v=6t2(m/s)。该质点在前2秒内的平均速度为 m/s,第2秒内的平均加速度为 m/s2。
29.汽车以大小为30m/s的速度做匀速直线运动,刹车后,前2s内(车未停)的平均速度大小为25m/s,则刹车后,汽车获得的加速度的大小为 m/s2。刹车后2s内与刹车后7s内汽车通过的位移之比为 。
30.海滨浴场的滑梯从顶端到入水处长12.5m,一人由滑梯顶端开始做初速度为零的匀加速直线运动,开始运动后的第一秒通过的位移是0.5m,则人的加速度大小是 。从顶端开始到入水所需的时间为 ,人入水时的速度大小是 ,从顶端开始到入水的平均速度大小是 。
匀变速直线运动位移与时间的关系
参考答案与试题解析
一.选择题(共10小题)
1.一辆汽车以54km/h的速度在平直公路上匀速行驶,司机发现前方有异常情况而紧急刹车,刹车后汽车以6m/s2的加速度做匀减速直线运动。从汽车开始做减速运动开始计时,3s内汽车的位移为( )
A.18m B.18.75m C.22.5m D.81m
【分析】汽车刹车过程做匀减速直线运动,根据加速度和初速度,由速度—时间公式求出刹车的时间,然后判断4s内汽车是否停止运动,再根据汽车的运动状态求汽车的位移。
【解答】解:汽车的初速度v0=54km/h=15m/s,加速度大小a=6m/s2,
汽车刹车后减速到零需要的时间t0s=2.5s<t=3s
汽车刹车后经过2.5s停止运动,因此汽车刹车后3s内的位移:
xm=18.75m,故B正确,ACD错误。
故选:B。
【点评】对于汽车刹车这种匀减速直线运动,不能死套公式,要注意检验解题结果的合理性,往往要先求出汽车刹车的时间,然后再进行其他计算。
2.伽利略设计了如图所示的“斜面实验”,当时只能靠滴水计时。他说:“为了测时间,我们把一只盛水的大容器置于高处,在容器底部焊上一根口径很细的管子,用小杯子收集每次下降时由细管流出的水,然后称出水的重量”,若将小球由静止滚下的距离记为L,对应时间内收集的水的质量记为m,则L与m的比例关系为( )
A.L∝ B.L∝ C.L∝m2 D.L∝m
【分析】明确该实验的实验原理是初速度为零的匀变速直线运动,位移与时间的二次方成正比,由于水是均匀稳定的流出,水的体积和时间成正比,则水的质量和时间成正比,由此解答。
【解答】解:球做初速度为零的匀变速直线运动,由位移公式有:L,得:L∝t2;
由于水是均匀稳定的流出,水的体积和时间成正比,又:m=ρV,所以水的质量与时间成正比,即:m∝t;
所以量筒中收集的水量可以间接的测量时间,即:t∝m
所以可得:L∝m2,故C正确,ABD错误。
故选:C。
【点评】解决该问题的关键是明确实验原理,根据流入小杯子中水的质量与时间成正比,将时间问题转化为水的质量问题。
3.一辆汽车做匀加速直线运动,经过路旁两棵相距50m的树共用时间5s,它经过第二棵树时的速度是15m/s,则它经过第一棵树时的速度是( )
A.2m/s B.10m/s C.5m/s D.2.5m/s
【分析】根据位移和时间,结合匀变速直线运动的平均速度推论求出汽车经过第一棵树时的速度.
【解答】解:汽车的平均速度为:,
因为,则汽车经过第一棵树时的速度为:.故C正确,A、B、D错误。
故选:C。
【点评】解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.
4.某汽车以速度10m/s匀速行驶,刹车后第1个2s内位移与最后一个2s内位移之比为3:2,设汽车做匀减速直线运动,则刹车后4s内汽车通过的距离是( )
A.2.5 m B.4 m C.12 m D.12.5 m
【分析】根据匀变速直线运动的位移—时间公式求出第1个2s内的位移与最后一个2s内的位移,通过比值求出加速度的大小,从而运动学公式求出刹车后4s内的位移.
【解答】解:设加速度的大小为a,则第1个2s内的位移大小为:x1=v0tat2=20﹣2a。
根据逆向思维,最后1个2s内的位移大小为:x2at2a×4=2a
根据:x1:x2=3:2,解得:a=4m/s2。
汽车刹车到停止所需的时间 ts=2.5s
可知刹车后4s内的位移等于2.5s内的位移,则有:
xm=12.5m。故D正确,A、B、C错误。
故选:D。
【点评】解决本题的关键掌握匀变速直线运动的运动学公式,并能灵活运用,注意汽车刹车速度减为零后不再运动.
5.交警在处理某次交通事故时,把监控仪器记录的数据输入计算机,得到肇事汽车在平直路面上紧急刹车(且遇车轮抱死)过程中的位移随时间变化的规律为x=24t﹣3t2(x的单位是m,t的单位是s),则下列说法不正确的是( )
A.该汽车刹车的初速度为24m/s
B.该汽车刹车的加速度为﹣3m/s2
C.刹车后2s末的速度为12m/s
D.刹车后5s内的平均速度为9.6m/s
【分析】AB.根据题中的表达式结合匀变速直线运动的位移公式求解初速度和加速度;
CD.根据匀变速直线运动的瞬时速度和平均速度规律求解。
【解答】解:AB.由匀变速直线运动的位移—时间关系
及汽车刹车过程中的位移规律
x=24t﹣3t2
可知,汽车刹车时的初速度为
v0=24m/s
加速度为
a=﹣6m/s2
故A正确,B错误;
C.由v=v0+at得汽车刹车时间
t0s=4s
刹车后2s末的速度为
v=v0+at=24m/s+(﹣6×2)m/s=12m/s
故C正确;
D.刹车后5s内的位移即为4s的位移为
x2 t04m=48m
刹车后5s内的平均速度为
m/s=9.6m/s
故D正确。
本题选不正确的,故选:B。
【点评】考查匀变速直线运动的速度、加速度、平均速度等规律,会根据题中数据进行相关的计算解答。
6.如图是某小区单扇自动感应门,人进出时,门从静止开始以加速度a匀加速运动,后以匀减速运动,完全打开时速度恰好为零。已知单扇门的宽度为d,则门完全打开所用时间为( )
A. B. C. D.
【分析】根据用平均速度表示的位移公式和速度—时间公式求解。
【解答】解:设门的最大速度为v,根据匀变速直线运动的规律可知加速过程和减速过程的平均速度均为
设加速和减速的时间分别为t1、t2,则v
又d
解得t
故ABC错误,D正确。
故选:D。
【点评】本题考查匀变速直线运动的求解,学生要熟练掌握,属于简单题。
7.如图所示,一辆汽车行驶在平直公路上,从t=0时开始制动,汽车在第1s、第2s、第3s前进的距离分别为14m、10m、6m。由此可知,由开始制动到静止,汽车运动的距离为( )
A.30m B.32m C.34m D.36m
【分析】利用逐差法求出加速度,然后求出1s末速度大小,结合速度—位移公式可求出距离。
【解答】解:根据匀变速直线运动相邻的相等时间间隔内的位移差相等,可知汽车做匀变速直线运动根据逐差法有x2﹣x1=aT2,解得a=﹣4m/s2,1s末的速度大小为vm/s=12m/s,由开始制动到静止,汽车运动的距离为s=14 m,得到s=32m,故B正确,ACD错误。
故选:B。
【点评】学生在解决本题时,应注意要灵活运用运动学公式,尤其是逐差法公式的利用。
8.某次测试时,测试员通过软件记录了无人机(可竖直起降)沿竖直方向运动的速度—时间关系式为v=8﹣2t,式中v的单位为m/s,t的单位为s,以竖直向上为正方向,则下列说法正确的是( )
A.该无人机的加速度大小为4m/s2
B.该无人机在t=4s末上升到最大高度
C.该无人机在0~5s内的位移大小为16m
D.该无人机在任意1s内的速度变化量大小都是1m/s
【分析】A.根据匀变速直线运动的速度公式结合给出的表达式分析初速度和加速度;
B.根据匀减速直线运动的减速时间分析计算;
C.根据匀减速直线运动的位移公式求解;
D.根据匀变速直线运动公式Δv=aΔt代入数据求解其大小。
【解答】解:A.根据匀变速直线运动速度—时间公式
v=v0+at
结合v=8﹣2t
可得
v0=8m/s,a=﹣2m/s2
故该无人机的加速度大小为2m/s2,故A错误;
B.该无人机上升到最大高度时,速度为零,所用的时间为
故B正确;
C.该无人机在0~5s内的位移大小为
故C错误;
D.根据Δv=aΔt,该无人机在任意1s内的速度变化量大小都是
Δv=|a|Δt=2×1m/s=2m/s
故D错误。
故选:B。
【点评】考查匀变速直线运动速度、位移、时间等规律,要求学生熟练掌握这些基本概念会进行相关的计算。
9.一辆汽车在水平路面上做匀减速直线运动,经3s停止,已知停止前的最后1s内的位移大小为2m,则关于初速度和加速度的大小,下面正确的是( )
A.v0=6m/s B.v0=8m/s C.a=1m/s2 D.a=4m/s2
【分析】根据匀变速直线运动的位移—时间公式和速度—时间公式解答即可。
【解答】解:因为停止前的最后1s内的位移大小为2m,运用逆向思维有:,其中t=1s
代入数据得:a=4m/s2
根据v=v0+at',代入数据可得速度大小为:v=12m/s,即初速度为12m/s,故ABC错误,D正确;
故选:D。
【点评】本题主要考查了匀变速直线运动的位移—时间公式和速度—时间公式,选用逆向思维使问题简单化。
10.一质点由静止出发向东做匀加速直线运动,加速度大小为a1,经过时间2t后做加速度大小为a2的匀变速直线运动,再经过时间t恰好回到出发点,则下列说法正确的是( )
A.a1:a2=1:2
B.小滑块向东加速与减速过程的速度变化相同
C.若质点回到出发点时速度大小为6m/s,则2t末速度大小为3m/s
D.若质点在整个3t时间内通过的路程为18m,则向东的前2t时间内通过的路程为8m
【分析】A、根据位移与时间公式解答;
B、速度是矢量,有大小有方向;
C、根据速度公式解答;
D、求解滑块向右减速的时间,运用速度公式解答。
【解答】解:A、由题意可知,解得a1:a2=1:8,故A错误;
B.小滑块向东加速与减速过程的速度变化大小相同,方向相反,故B错误;
C.若质点回到出发点时速度大小为v2,2t末速度大小为v1,则,可得v2=3v1,若质点回到出发点时速度大小为6m/s,则2t末速度大小为2m/s,故C错误;
D.滑块向右减速的时间为t1,则a1 2t=a2t1,可得,则整个过程的路程为,则向东的前2t时间内通过的路程为,故D正确。
故选:D。
【点评】考查对匀变速直线运动规律的理解,熟练运用运动学公式。
二.多选题(共10小题)
(多选)11.平直公路上,一辆自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标,它们的位移x随时间t变化的规律分别为:汽车,自行车x2=4t,则下列说法正确的( )
A.汽车做匀减速直线运动,自行车做匀速直线运动
B.自行车追上汽车之前二者的最大距离为36m
C.经过路标后较短时间内自行车在前,汽车在后
D.当自行车追上汽车时,它们距路标100m
【分析】A、由运动学公式,x=vt推导;
B、两车速度相等时相距最远;
CD、根据关系式分析。
【解答】解:A.根据汽车可知其初速度v0=10m/s,加速度a=﹣0.5m/s2,做匀减速直线运动,自行车x2=4t,则乙做速度为v=4m/s的匀速直线运动,故A正确;
B.汽车速度为v'=v0+at=v=4m/s,即在t12s时两车速度相等,此时两车相距最远,最大距离为,故B正确;
C.经过路标后,在速度相等前,汽车的速度大于自行车的速度,可知汽车在前,自行车在后,故C错误;
D.两车相遇时,有,解得t=24s,汽车刹车时间为,即20s时,车已停止运动,刹车距离为,所以当自行车追上汽车时,它们距路标100m,故D正确;
故选:ABD。
【点评】考查对匀变速直线运动规律的理解,熟悉运动学公式。
(多选)12.一辆汽车在水平路面上做匀减速直线运动,经3s停止,已知停止前最后1s内汽车的位移大小为2m,则关于汽车的初速度和加速度的大小,下列说法正确的是( )
A.v0=6m/s B.v0=12m/s C.a=1m/s2 D.a=4m/s2
【分析】根据逆向思维法把汽车的运动看作初速度为零的匀加速直线运动,根据位移—时间公式计算加速度,根据速度—时间关系计算初速度即可。
【解答】解:利用逆向思维可知汽车看作反向的初速度为零的匀加速直线运动,
汽车在第1s内的位移大小为2m,则加速度
a=4m/s2
初速度大小为
v0=at=4×3m/s=12m/s,故BD正确,AC错误。
故选:BD。
【点评】知道把汽车看作初速度为零的反向匀加速直线运动可以简化解题步骤。
(多选)13.北京冬奥会的成功举办极大地促进了我国民众对冰雪运动的热爱。如图为某滑冰场的滑雪轨道,该轨道是由倾斜直轨道AB和水平轨道BC组成。t=0时某滑雪爱好者从A点由静止开始匀加速下滑,经过B点前后速度大小不变,之后在BC上做匀减速直线运动,最后停在C点。若第2s末和第6s末速度大小均为8m/s,第4s末速度大小为12m/s,则( )
A.运动员在第4s末恰好经过B点
B.运动员经过B点的速度为
C.运动员在第8s末恰好停在C点
D.运动员在第10s末恰好停在C点
【分析】在斜面上和水平面上分别列速度—时间公式和位移—时间公式,需要判断第4s是在斜面上还是在水平面上,然后分别求出在斜面上和水平面上的加速度,进而联立,分段求解。
【解答】解:A、依题意,运动员在第2s末和第6s末速度大小相等,且第2s末速度为8m/s,
则运动员加速过程的加速度大小为
代入数据解得
a1=4m/s2
若运动员在第4s末恰好经过B点,则运动员在第4s末的速度应该为
v=a1t4=4×4m/s=16m/s
而实际上,第4s末速度大小为12m/s,说明运动员第4s末已经越过B点做减速运动了,故A错误;
B、第4s末到第6s末过程中,运动员做减速运动,
加速度大小为
a2
代入数据解得
a2=2m/s2
根据运动学公式有v2+a1t1+(﹣a1t2)=v4
又t1+t2=2s
代入数据解得
运动员到达B点的时间为
B点的速度为
vB=a1t
代入数据解得
vB
故B错误;
CD、设运动员在t′时间恰好停在C点,则有v6=a2t′
代入数据解得t′=4s
所以到C点的时间为10s末。
故选:BD。
【点评】本题考查了匀变速直线运动的位移—时间公式、速度—时间公式的熟练应用,判断第4s末在斜面还是水平面是关键,可假设来判断。
(多选)14.绿灯亮起后,一汽车由静止开始沿直线匀加速通过路口。对汽车匀加速通过路口过程,下列说法正确的是( )
A.加速度方向与其速度方向相同
B.加速度随时间均匀增大
C.速度随时间均匀增大
D.位移随时间均匀增大
【分析】根据加速度恒定,速度与加速度同向运动时为匀加速直线运动。
【解答】解:A.汽车由静止开始沿直线匀加速通过路口,即汽车做初速度为零的匀加速直线运动,则加速度方向与其速度方向相同,故A正确;
B.汽车做初速度为零的匀加速直线运动,加速度大小和方向均不变的运动,故B错误;
C.根据速度—时间公式v = at,加速度不变,所以速度随时间均匀增大,故C正确;
D.根据位移—时间公式可知位移与时间是二次函数关系,故D错误。
故选:AC。
【点评】本题主要考查了匀加速直线运动的理解,解题关键是掌握加速度恒定,速度与加速度同向运动时为匀加速直线运动。
(多选)15.某物体做直线运动的t图像如图所示。下列说法正确的是( )
A.物体的加速度大小为10m/s2
B.物体的初速度大小为10m/s
C.1s时,物体的速度大小为10m/s
D.在0~3s内,物体的位移大小为30m
【分析】根据图像得到与t的关系式,将匀变速直线运动位移—时间公式x=v0tat2变形得到与t的关系式,两式对比得到物体的加速度、初速度,再根据运动学公式求解其他量。
【解答】解:AB、由图可得
由匀变速直线运动的位移—时间公式变形得
对比可得,物体初速度为v0=﹣5m/s,a=10m/s2,故A正确,B错误;
C、物体做匀变速直线运动,1s时,物体的速度为v=v0+at=(﹣5+10×1)m/s=5m/s,故C错误;
D、根据得x=﹣5t+5t2,则在0~3s内,物体的位移大小为x=(﹣5×3+5×32)m=30m,故D正确。
故选:AD。
【点评】解决本题的关键要根据数学知识写出图像的解析式,分析位移与时间的关系,结合匀变速直线运动位移—时间公式,得到加速度、初速度,从而分析物体的运动情况。
(多选)16.汽车正以17m/s的速度在平直公路上前进,突然发现前方距离车头21m处有险情。司机立即刹车,刹车时加速度大小为8.5m/s2,下列说法正确的是( )
A.汽车刚刹车至刚停止的过程所需时间为3s
B.汽车运动的位移大小为17m
C.汽车停止的位置离险情处还有3m
D.汽车最后1s的位移大小为4.25m
【分析】根据运动学公式分析各选项。
【解答】解:A、汽车减速至0的时间为,故A错误;
BC、汽车运动的位移大小 ,汽车停止的位置离险情处还有21m﹣17m=4m,故B正确、C错误;
D、将汽车的运动视为反向的从静止开始的匀加速直线运动,可得汽车最后1s的位移大小 ,故D正确。
故选:BD。
【点评】考查对匀变速直线运动规律的理解和运动学公式的运用,运用逆向思维法解答。
(多选)17.甲、乙两车在平直公路上同向做匀变速直线运动,如图所示为计算机生成的图像,x为车辆运动位移,t为对应时间。已知两车在3s时并排行驶,则( )
A.t=0时,甲车在乙车前7.5m处
B.t=0时,甲车在乙车前15m处
C.在2s时,两车第一次并排行驶
D.甲车初速度大小为10m/s
【分析】根据可得:,则可知图像的纵轴截距表示初速度,斜率为,可求两车的初速度与加速度的大小;根据3s内位移之差求解t=0时刻两者位置关系;分析2s内两车位移关系,从而判断t=2s时两车位置关系。
【解答】解:ABC,根据图像的纵轴截距表示初速度,斜率为可知:甲车的初速度为:v甲=10m/s,,乙车的初速度为v乙=0,加速度为,甲车在3s内的位移为:,乙车在3s内发生的位移为:,由题知3s时两车并排行驶,则在t=0时,甲车在乙车前的距离为:Δx=x乙﹣x甲=67.5m﹣52.5m=15m;故BD正确,A错误;
C、甲车在2s内的位移为:,乙车在2s内发生的位移为:,由于x甲1+Δx=30m+15m=45m>x乙1=30m,则甲、乙两车在2s时没有并排,故C错误。
故选:BD。
【点评】本题是图像的应用,解题的关键是要知道在速度一时间图像中,图像与纵轴的截距表示初速度,斜率的2倍表示加速度,然后通过位移关系来分析并排问题。
(多选)18.物理的研究过程中科学家们创造了许多物理学研究方法,下列叙述中正确的是( )
A.在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法
B.根据速度定义式,当Δt非常小时,就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法
C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法
D.定义加速度用到比值定义法,加速度与Δv和Δt无关
【分析】根据理想化模型法,极限思想方法,微元法以及比值定义法的特点分析求解。
【解答】解:A.在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫理想化模型法,故A错误;
B.根据速度定义式,当Δt非常小时,就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法,故B正确;
C.在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法,故C正确;
D.定义加速度用到比值定义法,加速度与Δv和Δt无关,故D正确;
故选:BCD。
【点评】本题考查了物理学方法,理解各个物理量推导或定义背后所蕴含的物理学方法是解决此类问题的关键。
(多选)19.一质点沿x轴运动,其位移x时间t变化的规律为x=2t+t2(m),t的单位为s。关于该质点的初速度和加速度判断正确的是( )
A.初速度为1m/s B.初速度为2m/s
C.加速度为1m/s2 D.加速度为2m/s2
【分析】根据匀变速直线运动的位移—时间公式得出质点的初速度和加速度。
【解答】解:质点的位移x时间t变化的规律为x=2t+t2(m),
结合匀变速直线运动位移—时间关系x=v0tat2
对比可知该质点的初速度和加速度分别为v0=2m/s,a=2m/s2
故AC错误,BD正确。
故选:BD。
【点评】解决本题的关键掌握匀变速直线运动的位移—时间公式,并能灵活运用,基础题。
(多选)20.物体做匀加速直线运动,已知第1s末的速度是6m/s,第2s末的速度是8m/s,则下面结论正确的是( )
A.物体的加速度是2m/s2
B.物体零时刻的速度是3m/s
C.第1s内的平均速度为4m/s
D.第2s内的位移为7m
【分析】根据加速度的定义求解加速度,并结合速度—时间公式求解初速度;
根据平均速度公式求解第1s内的平均速度和第2s内位移。
【解答】解:AB、规定初速度方向为正方向,根据加速度定义式得:物体的加速度a2m/s2,根据v1=v0+at代入数据得:v0=4m/s。故A正确,B错误;
C、第1s内的平均速度,故C错误;
D、第2s内的位移为,故D正确。
故选:AD。
【点评】解决本题的关键掌握匀变速直线运动的速度—时间公式和平均速度公式,并能灵活运用。
三.填空题(共10小题)
21.芜湖轨道交通开通两年来,已成为市民生活中不可或缺的通勤工具,客流呈稳步上升趋势。现一位同学正好站立在轻轨列车的第一节车厢前端平齐处,轻轨列车启动后做匀加速直线运动,该同学测出第一节车厢通过他所用的时间是4s,则第一节车厢通过他的时间与第二节车厢通过他的时间之比是 ;若这列车共有4节车厢,则全部车厢通过这位同学历时 8 s。
【分析】根据位移公式列方程得出全部通过这位工作人员历时和前2节车厢运动的时间,从而得出第二节车厢运动的时间,即可求出第二节车厢通过它的时间与第一节车厢通过他的时间之比。
【解答】解:设每一节车厢的长度为L,第一节通过时间满足,解得:
前2节车厢通过他的时间为:,解得:
联立解得:
则第2节车厢通过他的时间为:
第一节车厢通过他的时间与第二节车厢通过他的时间之比为:
则全部列车通过的时间为:
又,
联立解得:。
故答案为:;8。
【点评】本题考查匀变速直线运动规律的应用,基础题目。
22.质量为m=1kg的物体在水平力作用下沿着粗糙水平面做匀变速直线运动,物体与水平面间的动摩擦因数μ=0.1,其位移随时间变化的关系式为x=16t﹣2t2(m),则物体的初速度大小是 16 m/s,水平力的大小为 3 N。
【分析】结合物体做匀变速直线运动时的位移—时间公式与题干中所给的位移与时间的关系进行对比,求出加速度和初速;根据牛顿第二定律求出物体所受的合力即水平拉力的大小。
【解答】解:根据匀变速直线运动位移与时间变化的关系式可得:x=v0t,与x=16t﹣2t2(m)对照可得
初速度:v0=16m/s,加速度大小为:a=4m/s2
取加速度方向为正方向,由牛顿第二定律可得:F+μmg=ma
代入数据可得:F=3N,说明F方向向后,大小为3N。
故答案为:16;3。
【点评】本题考查匀变速直线运动的规律与牛顿运动定律的应用,关键是运用位移—时间公式求出初速度和加速度,再由牛顿第二定律求出未知力。
23.一个物体做匀加速直线运动,位移随时间变化关系式为s=3t+t2(位移单位为m,时间单位为s),则该物体运动的加速度大小为 2 m/s2,3秒末的速度大小为 9 m/s。
【分析】根据位移—时间公式可求出初速度和加速度,利用速度公式可求出3s末的速度。
【解答】解:根据位移—时间公式,s=v0tat2,结合题干中s=3t+t2可知v0=3m/s,a=1m/s2,解得a=2m/s2,利用公式v=v0+at,当t=3s时,解得v=9m/s
故答案为:2,9。
【点评】学生在解答本题时,应注意利用原始公式对比题干中的公式,得到相关物理量。
24.由静止开始做匀加速直线运动的汽车,第1s内通过0.4m位移,汽车在第1s末的速度为 0.8 m/s;汽车在第2s内通过的位移为 1.2 m.
【分析】小车做初速度为零的匀加速直线运动,根据位移—时间关系求出加速度,根据速度—时间公式求出速度;
根据初速度为0的匀加速直线运动,第一秒内和第二秒内位移之比为1:3即可求解.
【解答】解:小车做初速度为零的匀加速直线运动
由,得:
则汽车在第1s末的速度为v1=at=0.8×1m/s=0.8m/s
由s1:s2=1:3,得:
汽车在第2s内通过的位移为s2=3s1=3×0.4m=1.2m
故答案为:0.8,1.2
【点评】本题主要考查了初速度为0的匀加速直线运动的基本规律以及推论,难度不大,属于基础题.
25.早在16世纪末,伽利略就猜想落体运动的速度应该是均匀变化的,一种为速度随时间均匀变化,一种速度随位移均匀变化。为此他设计了的“斜面实验”,反复做了上百次,验证了他的猜想。若伽利略研究小球沿斜面下滑时小球的位移与时间的关系式为x=kt2(k为一定值),则小球速度随 时间 (填“时间”或“位移”)均匀变化。小球运动的加速度大小为 2k 。
【分析】根据位移与时间的关系式为x = kt2,结合匀变速直线运动位移—时间公式分析求解。
【解答】解:伽利略研究小球沿斜面下滑时小球的位移与时间的关系式为x = kt2,由匀变速直线运动位移—时间公式:,可知小球运动的加速度大小为:a=2k
则小球运动的加速度为定值,小球的速度随时间均匀变化。
故答案为:时间;2k。
【点评】本题考查了匀变速直线运动相关知识,理解物体运动状态,合理选取运动学公式是解决此类问题的关键。
26.汽车以20m/s的速度在平直公路上匀减速行驶,刹车后经3s速度变为8m/s,则刹车过程中加速度为 ﹣4 m/s2,刹车8s后位移为 50 m。
【分析】(1)根据速度一时间公式求出刹车的加速度,
(2)根据速度一时间公式求出刹车速度减为零的时间,判断汽车是否停止,再结合位移公式求出刹车后的位移。
【解答】解:(1)汽车刹车时的加速度为:
am/s2=﹣4m/s2;
(2)汽车速度减为零的时间为:
t0s=5s;
则刹车后8s内的位移等于5s内的位移为:
xm=50m;
故答案为:﹣4;50。
【点评】解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,注意本题考查运动学中的刹车问题,是道易错题,汽车速度减为0后不再运动。
27.汽车初速为20m/s,关闭发动机后做匀减速运动,加速度大小为4m/s2,汽车在第4s初的速度为 8m/s ;前6s内位移为 50m 。
【分析】先计算出汽车的刹车时间,然后根据情况判断汽车是否已经停止运动,根据速度—时间公式计算出汽车的速度;然后根据位移与时间的关系得到汽车的位移大小。
【解答】解:汽车的刹车时间为,4s初即为3s末,此时汽车还没有停止,所以汽车在第4s初的速度为v=v0﹣at=20m/s﹣4×3m/s=8m/s。在5s末已经停止运动,所以汽车在前6s内位移为。
故答案为:8m/s,50m。
【点评】本题注意两点,一个是避免掉进刹车陷阱;第二个是第4s初的速度即为3s末的速度,汽车是减速3s时的速度。
28.一质点沿直线Ox方向做变速运动,它离开O点的距离随时间变化的关系为x=5+2t3(m),它的速度随时间t变化的关系为v=6t2(m/s)。该质点在前2秒内的平均速度为 8 m/s,第2秒内的平均加速度为 18 m/s2。
【分析】将t=0s、t=2s代入距离随时间变化的关系式x=5+2t3(m),可求出两个时刻质点离O点的距离,求得位移,再求解平均速度;将t=1s、t=2s代入速度表达式即可求得1s末、2s末的瞬时速度,根据加速度定义式求解平均加速度。
【解答】解:一质点沿直线Ox方向做变速运动,它离开O点的距离x随时间变化的关系为:x=5+2t3m;
t0=0时,位置坐标为x0=5m;
t2=2s时,位置坐标为x2=21m;
前2s内的位移Δx=21m﹣5m=16m
前2s内的平均速度:m/s=8m/s;
质点沿直线Ox方向做变速运动,它的速度随时间t变化的关系为:v=6t2m/s;
t1=1s时,速度为v1=6m/s;
t2=2s时,速度为v2=24m/s;
第2秒内的平均加速度为:am/s2=18m/s2。
故答案为:8;18。
【点评】题中物体的运动不是匀变速运动,根据平均速度的定义公式和平均加速度的定义公式列式求解即可。
29.汽车以大小为30m/s的速度做匀速直线运动,刹车后,前2s内(车未停)的平均速度大小为25m/s,则刹车后,汽车获得的加速度的大小为 5 m/s2。刹车后2s内与刹车后7s内汽车通过的位移之比为 5:9 。
【分析】根据匀变速直线运动的速度—时间公式求出汽车速度减为零的时间,判断汽车是否停止,再结合位移公式求出刹车后的位移,从而得出位移之比.
【解答】解:根据匀变速直线运动的规律可知,前2s内的平均速度等于中间时刻的瞬时速度,即刹车1s末的速度:v1=25m/s
根据匀变速直线运动速度一时间公式可知,v1=v0﹣at1
代入数据解得:a=5m/s2
停车时间:ts=6s
刹车后2s内的位移:x2=v1t2=25×2m=50m
刹车后7s内的位移即6s内的位移:x7m=90m,两者之比为5:9.
故答案为:5;5:9。
【点评】本题考查了运动学中的刹车问题,是道易错题,注意汽车速度减为零后不再运动.
30.海滨浴场的滑梯从顶端到入水处长12.5m,一人由滑梯顶端开始做初速度为零的匀加速直线运动,开始运动后的第一秒通过的位移是0.5m,则人的加速度大小是 1m/s2 。从顶端开始到入水所需的时间为 5s ,人入水时的速度大小是 5m/s ,从顶端开始到入水的平均速度大小是 2.5m/s 。
【分析】根据匀变速直线运动的位移—时间公式,结合速度—时间公式和平均速度分析求解。
【解答】解:根据匀变速直线运动的位移—时间公式:x,可得am/s2=1m/s2
从顶端开始到入水所需的时间有:t′s=5s
入水的速度:v=at=1×5m/s=5m/s
平均速度:m/s=2.5m/s
故答案为:1m/s2;5s;5m/s;2.5m/s。
【点评】本题考查了运动学相关知识,理解匀变速直线运动的位移—时间公式和速度—时间公式是解决此类问题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
