15.3.2等边三角形(课时1) 课件(共26张PPT) 人教版(2024)数学八年级上册
文档属性
| 名称 | 15.3.2等边三角形(课时1) 课件(共26张PPT) 人教版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 09:09:30 | ||
图片预览





文档简介
(共26张PPT)
15.3.2等边三角形
(课时1)
第十五章 轴对称
人教版(2024)
素养目标
2.能运用等边三角形的性质和判定进行计算和证明;
1.探索并掌握等边三角形的性质、判定方法;
重点
重难点
知识回顾
回顾关于等腰三角形的知识:
名称 图形 定义 性质 判定
等腰三角形 有两条边相等的三角形是等腰三角形 等边对等角
等角对等边
三线合一 轴对称图形
新知导入
在等腰三角形中,有一种特殊的情况,就是底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫等边三角形.
底边=腰
等边三角形具有等腰三角形的所有性质,除此之外,等边三角形还具有哪些性质?
探究新知
把等腰三角形的性质用于等边三角形,能得到什么结论?
图形
定义 有两条边相等的三角形 三边都相等的三角形
性质 边 两腰相等 等边三角形三边相等
角 等边对等角
?
探究新知
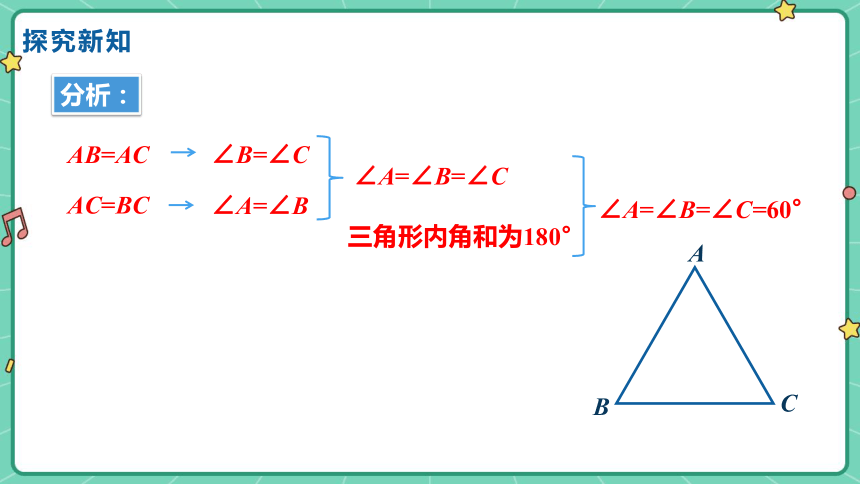
三角形内角和为180°
AB=AC
∠B=∠C
AC=BC
∠A=∠B
∠A=∠B=∠C
∠A=∠B=∠C=60°
分析:
A
B
C
归纳总结
等边三角形的性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
几何语言:
如图,在 △ABC 中,
∵AB = BC = AC,
∴∠A =∠B = ∠C = 60°
A
B
C
探究新知
A
B
C
A
B
C
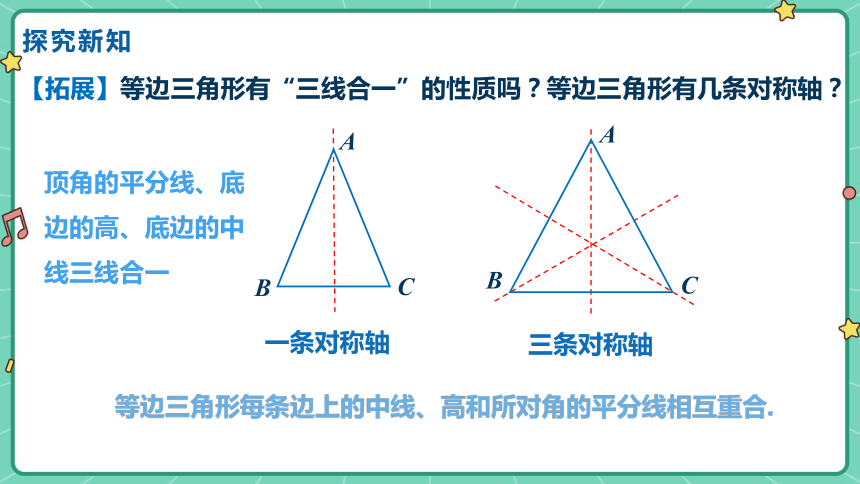
【拓展】等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?
等边三角形每条边上的中线、高和所对角的平分线相互重合.
顶角的平分线、底边的高、底边的中线三线合一
一条对称轴
三条对称轴
探究新知
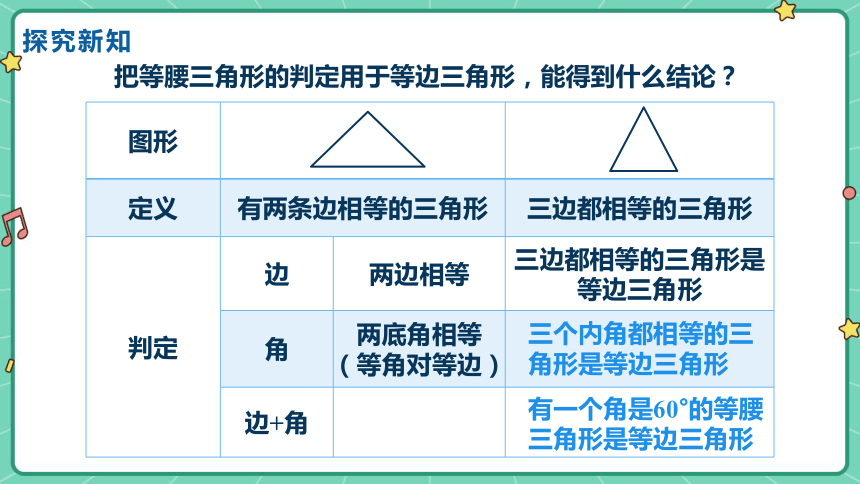
把等腰三角形的判定用于等边三角形,能得到什么结论?
图形
定义 有两条边相等的三角形 三边都相等的三角形
判定 边 两边相等 三边都相等的三角形是等边三角形
角 两底角相等 (等角对等边)
边+角
三个内角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
探究新知
已知:在△ABC中,∠A=∠B=∠C
求证:△ABC是等边三角形
A
B
C
证明:∵∠A=∠B,∠B=∠C,
∴BC=AC,AC=AB(等角对等边)
∴AB = BC = AC
∴△ABC是等边三角形
归纳总结
等边三角形的判定1:三个角都相等的三角形是等边三角形.
几何语言:
如图,在 △ABC 中,
∵∠A=∠B=∠C
∴△ABC是等边三角形
A
B
C
探究新知
已知:在△ABC中,AC=BC 且 ∠A=60°
求证:△ABC是等边三角形
∴∠C = 60°
证明:
∵AC=BC
∴∠A =∠B
又∵∠A=60°
∴∠B = 60°
A
B
C
∴△ABC是等边三角形
归纳总结
等边三角形的判定2:一个角为60°的等腰三角形是等边三角形.
几何语言:
如图,在 △ABC 中
∵BC = AC,∠A = 60°,∴△ABC是等边三角形
A
B
C
探究新知
如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形
证明:
∵△ABC 是等边三角形,
∴∠A =∠B =∠C.
∵ DE∥BC,
∴∠ADE =∠B,∠AED =∠C.
∴∠A =∠ADE =∠AED.
∴△ADE 是等边三角形.
A
C
B
D
E
探究新知
若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明:∵△ABC 是等边三角形,
∴∠BAC =∠B =∠C
∵DE∥BC,
∴∠B =∠D,∠C =∠E.
∴∠EAD =∠D =∠E.
∴△ADE 是等边三角形.
A
D
E
B
C
D
D
A
B
C
9
小结
定义
等边三角形
__________的三角形是等边三角形
判定
性质
____________的三角形是等边三角形
等边三角形的三个内角______,并且每一个内角________
三个角都相等
都相等
有____个角是___的______三角形是等边三角形
一
60°
等腰
三边都相等
等于 60°
谢谢同学们的聆听
15.3.2等边三角形
(课时1)
第十五章 轴对称
人教版(2024)
素养目标
2.能运用等边三角形的性质和判定进行计算和证明;
1.探索并掌握等边三角形的性质、判定方法;
重点
重难点
知识回顾
回顾关于等腰三角形的知识:
名称 图形 定义 性质 判定
等腰三角形 有两条边相等的三角形是等腰三角形 等边对等角
等角对等边
三线合一 轴对称图形
新知导入
在等腰三角形中,有一种特殊的情况,就是底与腰相等,即三角形的三边相等,我们把三条边都相等的三角形叫等边三角形.
底边=腰
等边三角形具有等腰三角形的所有性质,除此之外,等边三角形还具有哪些性质?
探究新知
把等腰三角形的性质用于等边三角形,能得到什么结论?
图形
定义 有两条边相等的三角形 三边都相等的三角形
性质 边 两腰相等 等边三角形三边相等
角 等边对等角
?
探究新知
三角形内角和为180°
AB=AC
∠B=∠C
AC=BC
∠A=∠B
∠A=∠B=∠C
∠A=∠B=∠C=60°
分析:
A
B
C
归纳总结
等边三角形的性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
几何语言:
如图,在 △ABC 中,
∵AB = BC = AC,
∴∠A =∠B = ∠C = 60°
A
B
C
探究新知
A
B
C
A
B
C
【拓展】等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?
等边三角形每条边上的中线、高和所对角的平分线相互重合.
顶角的平分线、底边的高、底边的中线三线合一
一条对称轴
三条对称轴
探究新知
把等腰三角形的判定用于等边三角形,能得到什么结论?
图形
定义 有两条边相等的三角形 三边都相等的三角形
判定 边 两边相等 三边都相等的三角形是等边三角形
角 两底角相等 (等角对等边)
边+角
三个内角都相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
探究新知
已知:在△ABC中,∠A=∠B=∠C
求证:△ABC是等边三角形
A
B
C
证明:∵∠A=∠B,∠B=∠C,
∴BC=AC,AC=AB(等角对等边)
∴AB = BC = AC
∴△ABC是等边三角形
归纳总结
等边三角形的判定1:三个角都相等的三角形是等边三角形.
几何语言:
如图,在 △ABC 中,
∵∠A=∠B=∠C
∴△ABC是等边三角形
A
B
C
探究新知
已知:在△ABC中,AC=BC 且 ∠A=60°
求证:△ABC是等边三角形
∴∠C = 60°
证明:
∵AC=BC
∴∠A =∠B
又∵∠A=60°
∴∠B = 60°
A
B
C
∴△ABC是等边三角形
归纳总结
等边三角形的判定2:一个角为60°的等腰三角形是等边三角形.
几何语言:
如图,在 △ABC 中
∵BC = AC,∠A = 60°,∴△ABC是等边三角形
A
B
C
探究新知
如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形
证明:
∵△ABC 是等边三角形,
∴∠A =∠B =∠C.
∵ DE∥BC,
∴∠ADE =∠B,∠AED =∠C.
∴∠A =∠ADE =∠AED.
∴△ADE 是等边三角形.
A
C
B
D
E
探究新知
若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然成立吗?
证明:∵△ABC 是等边三角形,
∴∠BAC =∠B =∠C
∵DE∥BC,
∴∠B =∠D,∠C =∠E.
∴∠EAD =∠D =∠E.
∴△ADE 是等边三角形.
A
D
E
B
C
D
D
A
B
C
9
小结
定义
等边三角形
__________的三角形是等边三角形
判定
性质
____________的三角形是等边三角形
等边三角形的三个内角______,并且每一个内角________
三个角都相等
都相等
有____个角是___的______三角形是等边三角形
一
60°
等腰
三边都相等
等于 60°
谢谢同学们的聆听
同课章节目录
