16.1.2幂的乘方与积的乘方 课件(共27张PPT) 人教版(2024)数学八年级上册
文档属性
| 名称 | 16.1.2幂的乘方与积的乘方 课件(共27张PPT) 人教版(2024)数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 09:16:57 | ||
图片预览







文档简介
(共27张PPT)
16.1.2幂的乘方与积的乘方
第十六章 整式的乘法
人教版(2024)
素养目标
2.能够运用幂的乘方与积的乘方的运算法则进行相关运算.
1. 理解并掌握幂的乘方与积的乘方的运算法则;
重点
知识回顾
1.回顾同底数幂的乘法的运算法则:
am · an = (m,n 都是正整数).
同底数幂相乘,底数 ,指数 .
相加
不变
am+n
2.计算:(1) x4·x8 (2) a·a3·a5.
解:(1) x4·x8 = x4+8 = x12;
(2) a·a3·a5 = a1+3+5= a9.
新知导入
6
6
3m
【探究】根据乘方的意义及同底数幂的乘法填空,观察计算结果,你能发现什么规律?
(1)(32)3 = 32×32 ×32 = 3( )
(2)(a2)3 = a2·a2 ·a2 = a( )
(3)(am)3 = am·am ·am = a( )
(m是正整数)
【发现】1.结果的底数与原来的底数相同;
2.结果的指数等于原来两个指数的积.
(32)3表示3个32相乘
(a2)3表示3个a2相乘
(am)3表示3个am相乘
探究新知
验证
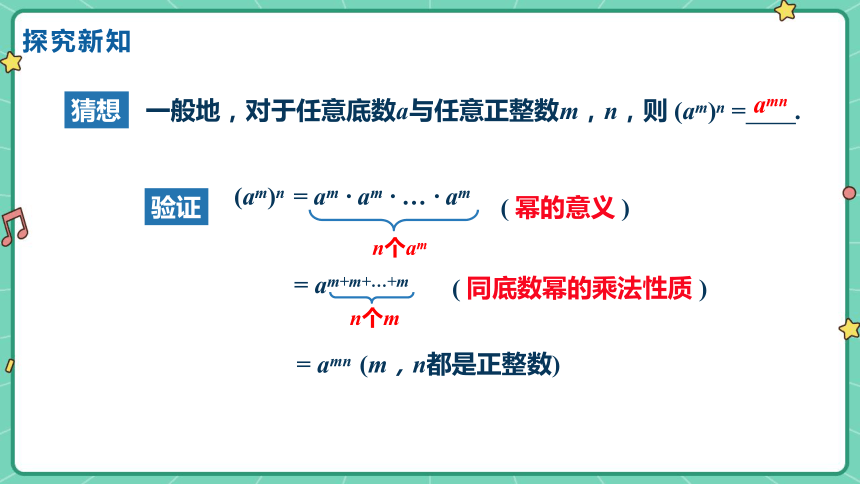
一般地,对于任意底数a与任意正整数m,n,则 (am)n = .
猜想
(am)n = am · am · … · am
= am+m+…+m
= amn (m,n都是正整数)
n个am
n个m
( 幂的意义 )
( 同底数幂的乘法性质 )
amn
归纳总结
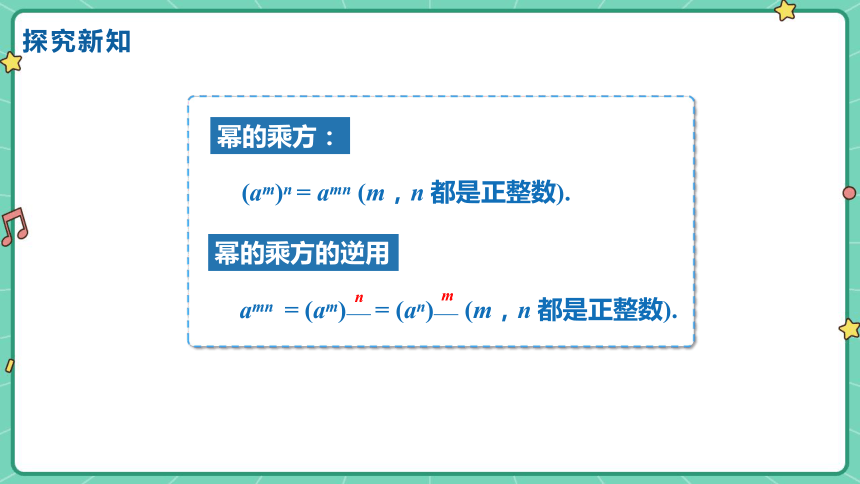
幂的乘方运算法则:(am)n = amn (m,n 都是正整数).
幂的乘方,底数______,指数 .
不变
相乘
幂的底数和指数不仅仅是单独字母或数字,也可以是某个单项式和多项式.
注意
探究新知
幂的乘方的逆用
amn = (am) = (an) (m,n 都是正整数).
幂的乘方:
(am)n = amn (m,n 都是正整数).
n
m
探究新知
(-a5)2表示2个-a5相乘,结果没有负号.
【思考】(-a2)5和(-a5)2的结果相同吗?为什么?
不相同.
(-a2)5表示5个-a2相乘,其结果带有负号.
n为偶数
n为奇数
探究新知
【拓展】下面这道题该怎么进行计算呢?
= (a6)4
= a24
[(y5)2]2=______=________
[(x5)m]n=______=________
练一练:
(y10)2
y20
(x5m)n
x5mn
[(am)n] p = am·n·p (m,n,p 都是正整数)
当幂进行三次或三次以上乘方运算时,依旧满足底数不变,指数相乘.
[(a2)3]4
例题练习
(1) ( 103 )5 ; (2) ( a4 )4 ; (3) ( am )2 ; (4) -( x4 )3 .
计算:
解:(1) (103)5 = 103×5 = 1015.
(2) (a4)4 = a4×4 = a16.
(3) (am)2 = am·2 = a2m.
(4) -( x4 )3 = -x4×3 = -x12.
探究新知
【探究】下面的运算过程用到了哪些运算律,你能发现结果又什么规律?
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
(ab)·(ab)
(ab)2
(a·a)·(b·b)
a( )b( )
2
2
(ab)·(ab)·(ab)
(ab)3
a( )b( )
3
3
(a·a·a)·(b·b·b)
【发现】结果把积的每一个因式分别乘方,再把所得的幂相乘.
探究新知
验证
若n是正整数,则 (ab)n = .
猜想
anbn
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn.
归纳总结
积的乘方运算法则:(ab)n = anbn ( n 为正整数).
积的乘方,等于把积的每个因式分别乘方,在把所得的幂相乘.
底数中的a、b不仅可以代表数、单项式,还可以代表多项式等其他式子.
注意
归纳总结
积的乘方的逆用
积的乘方:
anbn (ab)n(n是正整数).
(ab)n = anbn ( n 为正整数).
探究新知
对三个或三个以上因式进行积的乘方,积的乘方的性质是否仍然成立?
成立,(abc)n = anbncn (n 为正整数).
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
积的乘方的性质也适用于三个及三个以上因式的积的乘方
例题练习
计算:
(1) ( 2a )3; (2) ( -5b )3; (3) ( xy2 )2; (4) ( -2x3y )4.
解:(1) (2a)3
(2) ( 5b)3
(3) (xy2)2
(4) ( 2x3y)4
23·a3
( 5)3·b3
x2·(y2)2
( 2)4·(x3)4·y4
8a3 ;
125b3 ;
x2y4 ;
16x12y4.
D
B
C
小结
幂的乘方,底数不变,指数相乘
(am)n=amn (m,n都是正整数)
积的乘方,等于把积的每个因式分别乘方,在把所得的幂相乘.
(ab)n = anbn ( n为正整数).
幂的乘方与积的乘方
幂的乘方
积的乘方
谢谢同学们的聆听
16.1.2幂的乘方与积的乘方
第十六章 整式的乘法
人教版(2024)
素养目标
2.能够运用幂的乘方与积的乘方的运算法则进行相关运算.
1. 理解并掌握幂的乘方与积的乘方的运算法则;
重点
知识回顾
1.回顾同底数幂的乘法的运算法则:
am · an = (m,n 都是正整数).
同底数幂相乘,底数 ,指数 .
相加
不变
am+n
2.计算:(1) x4·x8 (2) a·a3·a5.
解:(1) x4·x8 = x4+8 = x12;
(2) a·a3·a5 = a1+3+5= a9.
新知导入
6
6
3m
【探究】根据乘方的意义及同底数幂的乘法填空,观察计算结果,你能发现什么规律?
(1)(32)3 = 32×32 ×32 = 3( )
(2)(a2)3 = a2·a2 ·a2 = a( )
(3)(am)3 = am·am ·am = a( )
(m是正整数)
【发现】1.结果的底数与原来的底数相同;
2.结果的指数等于原来两个指数的积.
(32)3表示3个32相乘
(a2)3表示3个a2相乘
(am)3表示3个am相乘
探究新知
验证
一般地,对于任意底数a与任意正整数m,n,则 (am)n = .
猜想
(am)n = am · am · … · am
= am+m+…+m
= amn (m,n都是正整数)
n个am
n个m
( 幂的意义 )
( 同底数幂的乘法性质 )
amn
归纳总结
幂的乘方运算法则:(am)n = amn (m,n 都是正整数).
幂的乘方,底数______,指数 .
不变
相乘
幂的底数和指数不仅仅是单独字母或数字,也可以是某个单项式和多项式.
注意
探究新知
幂的乘方的逆用
amn = (am) = (an) (m,n 都是正整数).
幂的乘方:
(am)n = amn (m,n 都是正整数).
n
m
探究新知
(-a5)2表示2个-a5相乘,结果没有负号.
【思考】(-a2)5和(-a5)2的结果相同吗?为什么?
不相同.
(-a2)5表示5个-a2相乘,其结果带有负号.
n为偶数
n为奇数
探究新知
【拓展】下面这道题该怎么进行计算呢?
= (a6)4
= a24
[(y5)2]2=______=________
[(x5)m]n=______=________
练一练:
(y10)2
y20
(x5m)n
x5mn
[(am)n] p = am·n·p (m,n,p 都是正整数)
当幂进行三次或三次以上乘方运算时,依旧满足底数不变,指数相乘.
[(a2)3]4
例题练习
(1) ( 103 )5 ; (2) ( a4 )4 ; (3) ( am )2 ; (4) -( x4 )3 .
计算:
解:(1) (103)5 = 103×5 = 1015.
(2) (a4)4 = a4×4 = a16.
(3) (am)2 = am·2 = a2m.
(4) -( x4 )3 = -x4×3 = -x12.
探究新知
【探究】下面的运算过程用到了哪些运算律,你能发现结果又什么规律?
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
(ab)·(ab)
(ab)2
(a·a)·(b·b)
a( )b( )
2
2
(ab)·(ab)·(ab)
(ab)3
a( )b( )
3
3
(a·a·a)·(b·b·b)
【发现】结果把积的每一个因式分别乘方,再把所得的幂相乘.
探究新知
验证
若n是正整数,则 (ab)n = .
猜想
anbn
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn.
归纳总结
积的乘方运算法则:(ab)n = anbn ( n 为正整数).
积的乘方,等于把积的每个因式分别乘方,在把所得的幂相乘.
底数中的a、b不仅可以代表数、单项式,还可以代表多项式等其他式子.
注意
归纳总结
积的乘方的逆用
积的乘方:
anbn (ab)n(n是正整数).
(ab)n = anbn ( n 为正整数).
探究新知
对三个或三个以上因式进行积的乘方,积的乘方的性质是否仍然成立?
成立,(abc)n = anbncn (n 为正整数).
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
积的乘方的性质也适用于三个及三个以上因式的积的乘方
例题练习
计算:
(1) ( 2a )3; (2) ( -5b )3; (3) ( xy2 )2; (4) ( -2x3y )4.
解:(1) (2a)3
(2) ( 5b)3
(3) (xy2)2
(4) ( 2x3y)4
23·a3
( 5)3·b3
x2·(y2)2
( 2)4·(x3)4·y4
8a3 ;
125b3 ;
x2y4 ;
16x12y4.
D
B
C
小结
幂的乘方,底数不变,指数相乘
(am)n=amn (m,n都是正整数)
积的乘方,等于把积的每个因式分别乘方,在把所得的幂相乘.
(ab)n = anbn ( n为正整数).
幂的乘方与积的乘方
幂的乘方
积的乘方
谢谢同学们的聆听
同课章节目录
