15.2画轴对称的图形(课时2) 课件(共24张PPT) 人教版(2024)八年级上册
文档属性
| 名称 | 15.2画轴对称的图形(课时2) 课件(共24张PPT) 人教版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 09:20:08 | ||
图片预览






文档简介
(共24张PPT)
15.2画轴对称的图形
(课时2)
第十五章 轴对称
人教版(2024)
素养目标
2.能利用坐标的变化规律在平面直角坐标系中画出一个图形的轴对称图形,加深对轴对称的理解和掌握.
1.理解在平面直角坐标系中,已知点关于x轴、y轴对称的点的坐标的变化规律;
重点
重点
新知导入
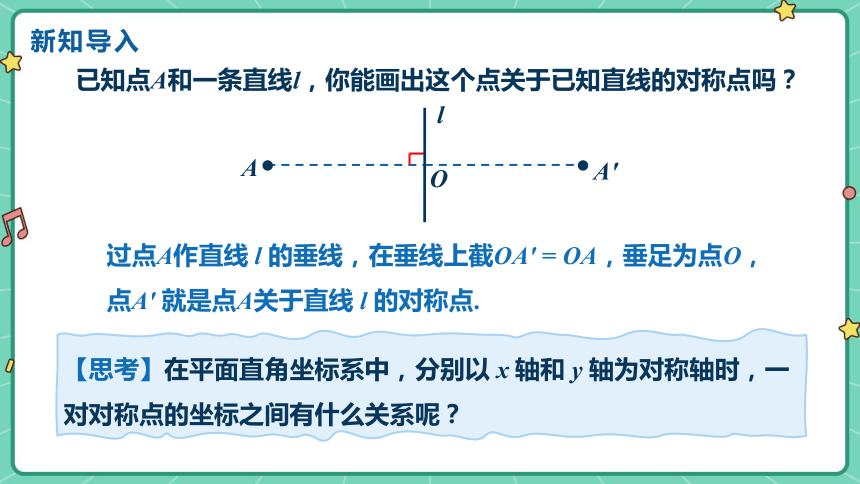
已知点A和一条直线l,你能画出这个点关于已知直线的对称点吗?
A
A′
l
O
过点A作直线 l 的垂线,在垂线上截OA′ = OA,垂足为点O,
点A′ 就是点A关于直线 l 的对称点.
【思考】在平面直角坐标系中,分别以 x 轴和 y 轴为对称轴时,一对对称点的坐标之间有什么关系呢?
探究新知
在平面直角坐标系中,画出下列已知点及其关于 x 轴对称的点,把它们的坐标填入表格中,观察每对对称点的坐标,你能发现什么规律?
已知点 A(2,-3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于 x 轴对称的点
探究新知
x
y
1
1
O
A
B
C
D
E
A′
B′
C′
D′
E′
已知点 A(2,-3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于 x 轴对称的点
A′(2,3)
B′(-1,-2)
C′(-6, 5)
D′( ,-1)
E′(4,0)
关于 x 轴对称的每对对称点的横坐标相等,纵坐标互为相反数.
归纳总结
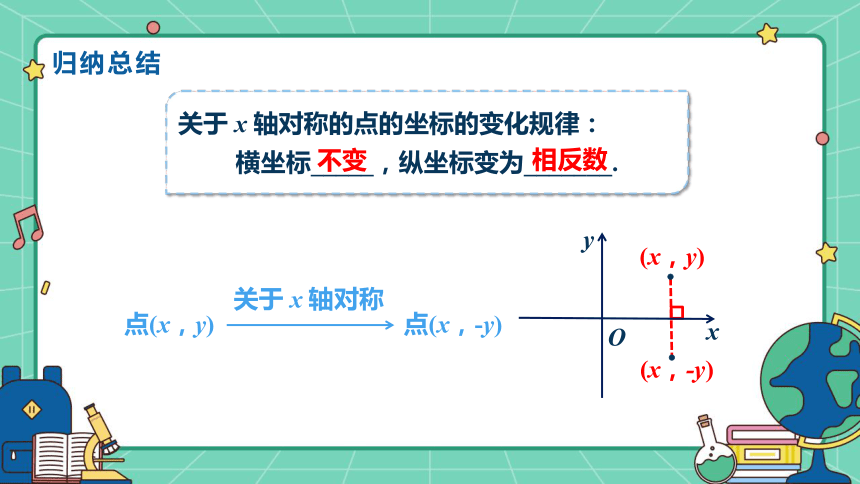
关于 x 轴对称的点的坐标的变化规律:
横坐标_____,纵坐标变为_______.
点(x,y)
关于 x 轴对称
点(x,-y)
不变
相反数
(x,-y)
y
x
O
(x,y)
探究新知
在平面直角坐标系中,画出下列已知点及其关于 y 轴对称的点,把它们的坐标填入表格中,观察每对对称点的坐标,你能发现什么规律?
已知点 A(2,-3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于 y 轴对称的点
探究新知
已知点 A(2,-3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于 y 轴对称的点
A′′(-2,-3)
B′′(1,2)
C′′(6,-5)
D′′( ,1)
E′′(-4,0)
x
y
1
1
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
关于y 轴对称的每对对称点的横坐标互为相反数,纵坐标相等.
归纳总结
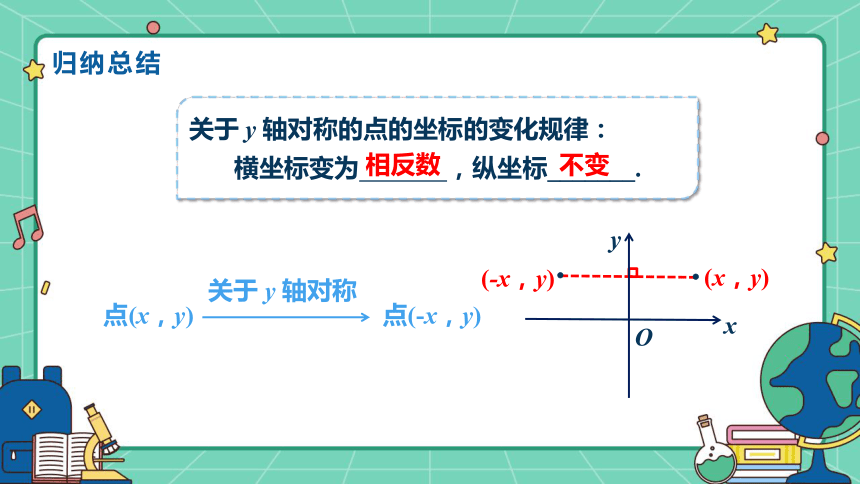
关于 y 轴对称的点的坐标的变化规律:
横坐标变为 ,纵坐标_______.
点(x,y)
关于 y 轴对称
点(-x,y)
不变
相反数
(-x,y)
y
x
O
(x,y)
探究新知
在平面直角坐标系中,我们可以利用关于x轴、y轴对称的点的坐标的变化规律画出与一个图形关于x轴或y轴对称的图形.
对于一些规则的几何图形,只要先求出已知图形中的一些关键点(如三角形的顶点)关于坐标轴对称的点的坐标,描出并连接这些点,就可以得到与这个图形关于坐标轴对称的图形.
探究新知
如图,四边形 ABCD 的四个顶点的坐标分别为 A(-5,1),B(-2,1),C(-2,5),D(-5,4),画出与四边形ABCD 关于 y 轴对称的图形.
解:点(x,y)关于y轴对称的点的坐标为(-x,y),因此四边形ABCD 的顶点A,B,C,D 关于y轴对称的点分别为:
A′( , ),
B′( , ),
C′( , ),
D′( , ),
探究新知
2 5
5 1
2 1
5 4
依次连接 A′B′ ,B′C′, C′D′ ,D′A′就可得到与四边形ABCD 关于y轴对称的四边A′B′C′D′
探究新知
类似地,可以画出与四边形ABCD关于x轴对称的图形.
依次连接 A′′B′′ ,B′′C′′ , C′′D′′ ,D′′A′′就可得到与四边形ABCD 关于y轴对称的四边A′′B′′C′′D′′
解:点(x,y)关于x 轴对称的点的坐标为(x,-y),因此四边形
ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为:
A′′( , ),
B′′ ( , ),
C′′( , ),
D′′( , ),
-2 -5
-5 -1
-2 -1
-5 -4
A
A
A
0
三
(4,2)
4
小结
画轴对称图形
点(x,y)
关于 y 轴对称
点(-x,y)
点(x,y)
关于 x 轴对称
点(x,-y)
谢谢同学们的聆听
15.2画轴对称的图形
(课时2)
第十五章 轴对称
人教版(2024)
素养目标
2.能利用坐标的变化规律在平面直角坐标系中画出一个图形的轴对称图形,加深对轴对称的理解和掌握.
1.理解在平面直角坐标系中,已知点关于x轴、y轴对称的点的坐标的变化规律;
重点
重点
新知导入
已知点A和一条直线l,你能画出这个点关于已知直线的对称点吗?
A
A′
l
O
过点A作直线 l 的垂线,在垂线上截OA′ = OA,垂足为点O,
点A′ 就是点A关于直线 l 的对称点.
【思考】在平面直角坐标系中,分别以 x 轴和 y 轴为对称轴时,一对对称点的坐标之间有什么关系呢?
探究新知
在平面直角坐标系中,画出下列已知点及其关于 x 轴对称的点,把它们的坐标填入表格中,观察每对对称点的坐标,你能发现什么规律?
已知点 A(2,-3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于 x 轴对称的点
探究新知
x
y
1
1
O
A
B
C
D
E
A′
B′
C′
D′
E′
已知点 A(2,-3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于 x 轴对称的点
A′(2,3)
B′(-1,-2)
C′(-6, 5)
D′( ,-1)
E′(4,0)
关于 x 轴对称的每对对称点的横坐标相等,纵坐标互为相反数.
归纳总结
关于 x 轴对称的点的坐标的变化规律:
横坐标_____,纵坐标变为_______.
点(x,y)
关于 x 轴对称
点(x,-y)
不变
相反数
(x,-y)
y
x
O
(x,y)
探究新知
在平面直角坐标系中,画出下列已知点及其关于 y 轴对称的点,把它们的坐标填入表格中,观察每对对称点的坐标,你能发现什么规律?
已知点 A(2,-3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于 y 轴对称的点
探究新知
已知点 A(2,-3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于 y 轴对称的点
A′′(-2,-3)
B′′(1,2)
C′′(6,-5)
D′′( ,1)
E′′(-4,0)
x
y
1
1
O
A
B
C
D
E
A〞
B〞
C〞
D〞
E〞
关于y 轴对称的每对对称点的横坐标互为相反数,纵坐标相等.
归纳总结
关于 y 轴对称的点的坐标的变化规律:
横坐标变为 ,纵坐标_______.
点(x,y)
关于 y 轴对称
点(-x,y)
不变
相反数
(-x,y)
y
x
O
(x,y)
探究新知
在平面直角坐标系中,我们可以利用关于x轴、y轴对称的点的坐标的变化规律画出与一个图形关于x轴或y轴对称的图形.
对于一些规则的几何图形,只要先求出已知图形中的一些关键点(如三角形的顶点)关于坐标轴对称的点的坐标,描出并连接这些点,就可以得到与这个图形关于坐标轴对称的图形.
探究新知
如图,四边形 ABCD 的四个顶点的坐标分别为 A(-5,1),B(-2,1),C(-2,5),D(-5,4),画出与四边形ABCD 关于 y 轴对称的图形.
解:点(x,y)关于y轴对称的点的坐标为(-x,y),因此四边形ABCD 的顶点A,B,C,D 关于y轴对称的点分别为:
A′( , ),
B′( , ),
C′( , ),
D′( , ),
探究新知
2 5
5 1
2 1
5 4
依次连接 A′B′ ,B′C′, C′D′ ,D′A′就可得到与四边形ABCD 关于y轴对称的四边A′B′C′D′
探究新知
类似地,可以画出与四边形ABCD关于x轴对称的图形.
依次连接 A′′B′′ ,B′′C′′ , C′′D′′ ,D′′A′′就可得到与四边形ABCD 关于y轴对称的四边A′′B′′C′′D′′
解:点(x,y)关于x 轴对称的点的坐标为(x,-y),因此四边形
ABCD 的顶点A,B,C,D 关于x 轴对称的点分别为:
A′′( , ),
B′′ ( , ),
C′′( , ),
D′′( , ),
-2 -5
-5 -1
-2 -1
-5 -4
A
A
A
0
三
(4,2)
4
小结
画轴对称图形
点(x,y)
关于 y 轴对称
点(-x,y)
点(x,y)
关于 x 轴对称
点(x,-y)
谢谢同学们的聆听
同课章节目录
