15.1.2线段的垂直平分线(课时2)(教学课件)(共23张PPT)-初中数学人教版(2024)八年级上册
文档属性
| 名称 | 15.1.2线段的垂直平分线(课时2)(教学课件)(共23张PPT)-初中数学人教版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 20:57:33 | ||
图片预览







文档简介
(共23张PPT)
15.1.2线段的垂直平分线
(课时2)
第十五章 轴对称
人教版(2024)
素养目标
2.通过尺规作图,提升学生的动手操作能力.
1.能用尺规作图:作线段的垂直平分线,作轴对称图形的对称轴,过一点作已知直线的垂线;
重点
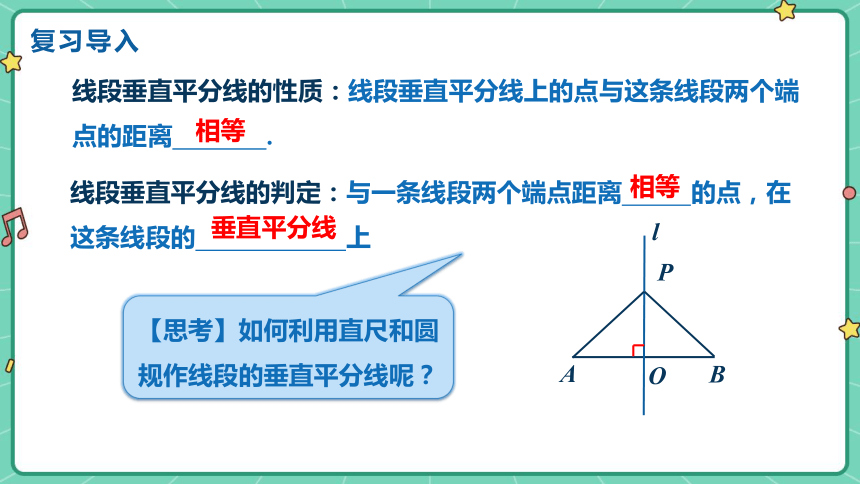
复习导入
线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离 .
线段垂直平分线的判定:与一条线段两个端点距离 的点,在这条线段的 上
A
B
l
O
P
相等
垂直平分线
相等
【思考】如何利用直尺和圆规作线段的垂直平分线呢?
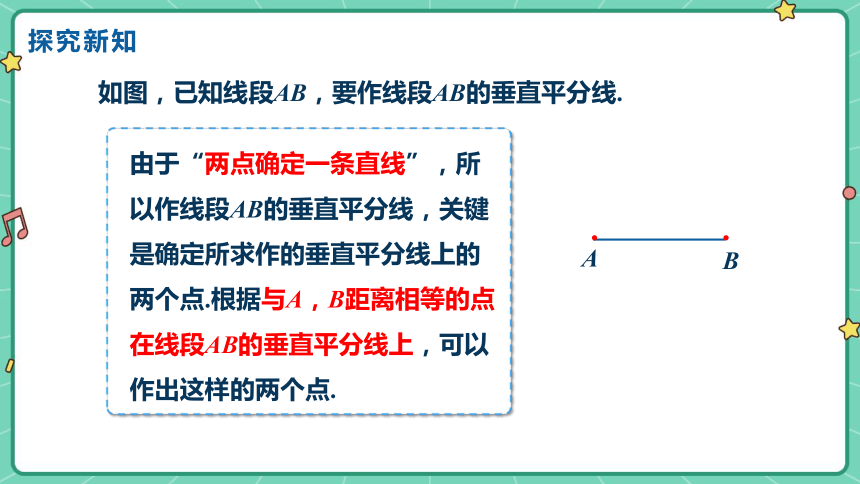
探究新知
A
B
如图,已知线段AB,要作线段AB的垂直平分线.
由于“两点确定一条直线”,所以作线段AB的垂直平分线,关键是确定所求作的垂直平分线上的两个点.根据与A,B距离相等的点在线段AB的垂直平分线上,可以作出这样的两个点.
探究新知
C
D
B
A
作法:如图所示:
(1)分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧线相交于C,D两点;
(2)作直线CD, CD就是线段AB的垂直平分线.
可以用这种方法确定线段的中点
探究新知
以小于 AB的长为半径,两弧无交点;
以等于 AB的长为半径,不易操作.
【思考】为什么以大于 AB的长为半径作弧?
探究新知
【思考】在作线段的垂直平分线的基础上,你能作出成轴对称的两个图形的对称轴吗?
由于成轴对称的两个图形的对称轴是其任意一对对称点所连线段的垂直平分线,所以只要任意找一对对称点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
探究新知
同样地,对于轴对称图形,只要任意找一对对称点,作出连接它们的线段的垂直平分线,就得到此图形的对称轴.
如图中的五角星,请作出它的一条对称轴.
B
找出一对对称点A和A′,连接AA′,作出线段AA′的垂直平分线 l,则 l 就是这个五角星的一条对称轴.
l
类似地,请你尝试作出这个五角星的其他对称轴.
A
归纳总结
作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对称点;
②连:连接这对对称点;
③作:做出对称点所连线段的垂直平分线.
探究新知
利用作线段的垂直平分线,还可以完成其他尺规作图.
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.
A
B
C
探究新知
分析:假设所求作直线已经作出,则它不仅过点C与直线AB垂直,而且是连接AB上与垂足距离相等的两点的线段的垂直平分线.我们已经会作线段的垂直平分线,因此需要首先在直线AB上确定这两点.根据前面关于线段垂直平分线的定理,这两点只需满足与点C的距离相等即可.
A
B
C
探究新知
作法:(1)以点C为圆心,适当长为半径作弧,交直线AB于点D和E.
(2)分别以点D和E为圆心,以大于 DE的长为半径作弧,两弧相交于点F.
(3)作直线CF.直线CF 就是所求作的垂线.
A
B
C
D
E
F
由(1)可知,点C在线段 DE的垂直平分线上,因而再作出与D,E距离相等的另一点F,就能得到线段DE 的垂直平分线.
C
D
D
C
A
如图,点P为所作.
谢谢同学们的聆听
15.1.2线段的垂直平分线
(课时2)
第十五章 轴对称
人教版(2024)
素养目标
2.通过尺规作图,提升学生的动手操作能力.
1.能用尺规作图:作线段的垂直平分线,作轴对称图形的对称轴,过一点作已知直线的垂线;
重点
复习导入
线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离 .
线段垂直平分线的判定:与一条线段两个端点距离 的点,在这条线段的 上
A
B
l
O
P
相等
垂直平分线
相等
【思考】如何利用直尺和圆规作线段的垂直平分线呢?
探究新知
A
B
如图,已知线段AB,要作线段AB的垂直平分线.
由于“两点确定一条直线”,所以作线段AB的垂直平分线,关键是确定所求作的垂直平分线上的两个点.根据与A,B距离相等的点在线段AB的垂直平分线上,可以作出这样的两个点.
探究新知
C
D
B
A
作法:如图所示:
(1)分别以点A和点B为圆心,大于 AB的长为半径作弧,两弧线相交于C,D两点;
(2)作直线CD, CD就是线段AB的垂直平分线.
可以用这种方法确定线段的中点
探究新知
以小于 AB的长为半径,两弧无交点;
以等于 AB的长为半径,不易操作.
【思考】为什么以大于 AB的长为半径作弧?
探究新知
【思考】在作线段的垂直平分线的基础上,你能作出成轴对称的两个图形的对称轴吗?
由于成轴对称的两个图形的对称轴是其任意一对对称点所连线段的垂直平分线,所以只要任意找一对对称点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
探究新知
同样地,对于轴对称图形,只要任意找一对对称点,作出连接它们的线段的垂直平分线,就得到此图形的对称轴.
如图中的五角星,请作出它的一条对称轴.
B
找出一对对称点A和A′,连接AA′,作出线段AA′的垂直平分线 l,则 l 就是这个五角星的一条对称轴.
l
类似地,请你尝试作出这个五角星的其他对称轴.
A
归纳总结
作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对称点;
②连:连接这对对称点;
③作:做出对称点所连线段的垂直平分线.
探究新知
利用作线段的垂直平分线,还可以完成其他尺规作图.
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线AB和AB外一点C.求作:AB的垂线,使它经过点C.
A
B
C
探究新知
分析:假设所求作直线已经作出,则它不仅过点C与直线AB垂直,而且是连接AB上与垂足距离相等的两点的线段的垂直平分线.我们已经会作线段的垂直平分线,因此需要首先在直线AB上确定这两点.根据前面关于线段垂直平分线的定理,这两点只需满足与点C的距离相等即可.
A
B
C
探究新知
作法:(1)以点C为圆心,适当长为半径作弧,交直线AB于点D和E.
(2)分别以点D和E为圆心,以大于 DE的长为半径作弧,两弧相交于点F.
(3)作直线CF.直线CF 就是所求作的垂线.
A
B
C
D
E
F
由(1)可知,点C在线段 DE的垂直平分线上,因而再作出与D,E距离相等的另一点F,就能得到线段DE 的垂直平分线.
C
D
D
C
A
如图,点P为所作.
谢谢同学们的聆听
同课章节目录
