11.2 课时2 一元一次不等式实际应用(1) 课件(共35张PPT) 2024—2025学年人教版七年级数学下册
文档属性
| 名称 | 11.2 课时2 一元一次不等式实际应用(1) 课件(共35张PPT) 2024—2025学年人教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 09:25:17 | ||
图片预览








文档简介
(共35张PPT)
第十一章 不等式与不等式组
11.2 一元一次不等式
课时2 一元一次不等式的实际应用(一)
目
录
1. 学习目标
4. 知识点 一元一次不等式的实际应用(简单)
5. 课堂小结
6. 当堂小练
CONTENTS
2. 知识回顾
8. 拓展与延伸
7. 对接中考
3. 新课导入
掌握用一元一次不等式解决实际问题的步骤,会用一元一次不等式解简单的实际问题.
学习目标
知识回顾
解一元一次不等式的步骤:
① 去分母
② 去括号
③ 移项
④ 合并同类项
⑤ 系数化为 1
新课导入
一元一次方程解实际问题的步骤:
实际问题
设未知数
找相等关系
列出方程
检验解的合理性
解方程
【思考】那么如何用一元一次不等式解实际问题呢?
新课讲解
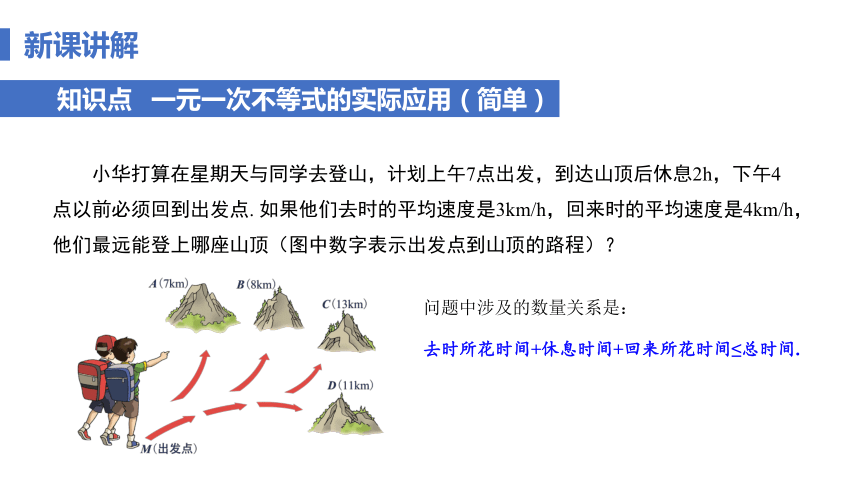
知识点 一元一次不等式的实际应用(简单)
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
新课讲解
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h,回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
新课讲解
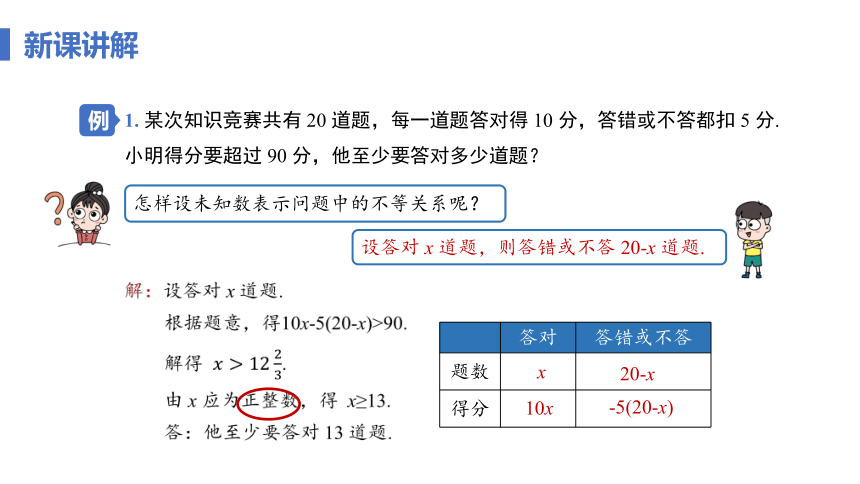
1. 某次知识竞赛共有 20 道题,每一道题答对得 10 分,答错或不答都扣 5 分.小明得分要超过 90 分,他至少要答对多少道题?
设答对 x 道题,则答错或不答 20-x 道题.
怎样设未知数表示问题中的不等关系呢?
答对 答错或不答
题数
得分
x
20-x
10x
-5(20-x)
解:设答对 x 道题.
根据题意,得10x-5(20-x)>90.
解得 .
由 x 应为正整数,得 x≥13.
答:他至少要答对 13 道题.
例
新课讲解
例
2. 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到 60%,如果明年(365天)这样的比值要超过 70%,那么明年空气质量良好的天数比去年至少要增加多少?
怎样设未知数表示问题中的不等关系呢?
设 x 表示明年增加的空气质量良好的天数,则明年空气质量良好的天数是 x+365×60%.
解:设明年比去年空气质量良好的天数增加了 x.
去年有 365×60% 天空气质量良好,明年有(x+365×60%)天空气质量良好,并且 .
去分母,得 x+219>255.5.
移项,合并同类项,得 x>36.5.
由 x 应为正整数,得 x≥37.
天数是整数,所以应该取 37.
这样就可以了吗?
答:明年空气质量良好的天数比去年至少要增加 37,才能使这一年空气质量良好的天数超过全年天数的70%.
新课讲解
例
解:设小明家每月用水x立方米.
∵5×1.8=9<15,
∴小明家每月用水超过5立方米,
则超出(x-5)立方米,按每立方米2元收费,
列出不等式为:5×1.8+(x-5)×2≥15,
解不等式得:x≥8.
答:小明家每月用水量至少是8立方米.
3. 小明家每月水费都不少于15元,自来水公司的收费标准如下:若每户每月用水不超过5立方米,则每立方米收费1.8元;若每户每月用水超过5立方米,则超出部分每立方米收费2元,小明家每月用水量至少是多少?
在利用一元一次不等式解决实际问题时一定根据实际情况取值.
注意
新课讲解
例
4. 我市某乡村振兴果蔬加工公司先后两次购买龙眼共21吨,第一次购买龙眼的价格为0.4万元/吨;因龙眼大量上市,价格下跌,第二次购买龙眼的价格为0.3万元/吨,两次购买龙眼共用了7万元.
(1)两次购买龙眼各是多少吨
解:(1)设第一次购买龙眼x吨,则第二次购买龙眼(21-x)吨,
由题意,得0.4x+0.3(21-x)=7,
解得x=7,所以21-x=21-7=14.
答:第一次购买龙眼7吨,第二次购买龙眼14吨.
新课讲解
例
4. 我市某乡村振兴果蔬加工公司先后两次购买龙眼共21吨,第一次购买龙眼的价格为0.4万元/吨;因龙眼大量上市,价格下跌,第二次购买龙眼的价格为0.3万元/吨,两次购买龙眼共用了7万元.
(2)公司把两次购买的龙眼加工成桂圆肉和龙眼干,1吨龙眼可加工成桂圆肉0.2吨或龙眼干0.5吨,桂圆肉和龙眼干的销售价格分别是10万元/吨和3万元/吨,若全部的销售额不少于39万元,则至少需要把多少吨龙眼加工成桂圆肉
解:(2)设把y吨龙眼加工成桂圆肉,则把(21-y)吨龙眼加工成龙眼干,
由题意,得10×0.2y+3×0.5(21-y)≥39,
解得y≥15.
答:至少需要把15吨龙眼加工成桂圆肉.
新课讲解
练一练
1. 一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小明答对了 x 道题,则他答错和不答的共有 (25-x)道题.
根据题意,得
4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
答:小明至少答对了22道题.
分析:本题涉及的数量关系是:总得分≥85.
新课讲解
练一练
2. 某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果至少要获得900元的纯利润,每套童装的售价至少是多少元?
解:设每套童装的售价是 x 元.
则40x-90×40-40x·10%≥900.
解得 x ≥ 125.
答:每套童装的售价至少是125元.
分析:本题涉及的数量关系是:销售额-成本-税费≥纯利润(900元).
新课讲解
练一练
分析:“今年万元地区生产总值能耗比去年的下降率不小于5%”是问题中蕴含的不等关系,转化为不等式:×100%≥5%.
3. 某市去年万元地区生产总值能耗为0.320t标准煤,如果计划使今年万元地区生产总值能耗比去年的下降率不小于5%,那么这个市今年万元地区生产总值能耗至多为多少
解:设这个市今年万元地区生产总值能耗为x t标准煤.
根据题意,列得不等式 ×100%≥5%.
解得 x≤0.304.
答:这个市今年万元地区生产总值能耗至多为0.304t标准煤.
4. 某水果店 5 月份购进甲、乙两种水果共花费 1 700 元,其中甲种水果 8 元/千克,乙种水果 18 元/千克.6 月份,这两种水果的进价上调为:甲种水果 10 元/千克,乙种水果 20 元/千克.
(1)若该店 6 月份购进两种水果的数量与5月份都相同,将多支付货款300元,求该店 5 月份购进甲、乙两种水果分别是多少千克;
新课讲解
练一练
解:(1)设 5 月份购进甲、乙两种水果分别为 x 千克和 y 千克.
根据题意,得 解得
答:该店 5 月份购进甲种水果 100 千克、乙种水果 50 千克.
5. 某水果店 5 月份购进甲、乙两种水果共花费 1 700 元,其中甲种水果 8 元/千克,乙种水果 18 元/千克.6 月份,这两种水果的进价上调为:甲种水果 10 元/千克,乙种水果 20 元/千克.
(2)若 6 月份这两种水果进货总量减少到 120 千克,且甲种水果不超过乙种
水果的 3 倍,则 6 月份该店需要支付这两种水果的货款最少应是多少元?
新课讲解
练一练
解:
(2)设 6 月份购进乙种水果 m 千克,则购进甲种水果(120-m)千克,该店需要支付这两种水果的货款为 W 元.
W=10(120-m)+20m=10m+1 200.
因为甲种水果不超过乙种水果的 3 倍,所以 120-m≤3m,解得 m≥30.
所以两种水果的货款最少应当是10×30+1 200=1 500(元).
课堂小结
认真审题,找出已知量和未知量,并找出它们之间的关系.
审
设出适当的未知数.
设
根据题中的不等关系列出不等式.
列
解不等式,求出其解集.
解
检验所求出的不等式的解集是否符合题意.
验
写出答案.
答
用一元一次不等式解决实际问题的步骤
当堂小练
1. 某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过95分,他至多可以答错或不答的试题道数为 ( )
A.5 B.6 C.7 D.8
解:设小玉答对了x道题目,则答错或不答的题目一共为(20-x)道.
由题意可得,10x-5(20-x)>95,
解得x>13,
所以小玉至少要答对14道题目,至多答错或不答20-14=6(道).
B
当堂小练
2. 某种商品的进价为每件 100 元,商场按进价提高 50% 后标价,为增加销量,准备打折销售,但要保证利润率不低于 20%,则至多可以打_____折.
八
标价:100(1+50%)
售价:100(1+20%)
100(1+50%)100(1+20%)
x≥8
当堂小练
3. 一种导火线的燃烧速度是 0.7 cm/s,一名爆破员点燃导火线后以 5 m/s 的速度跑到距爆破点 130 m 以外的安全地带,则导火线的长度至少应超过( )
A. 18 cm B. 18.2 cm C. 18.5 cm D. 19 cm
B
x >18.2
导火线燃烧完所用时间
人跑到安全地带所用时间
>
当堂小练
4. 小明准备用 40 元钱购买作业本和签字笔.已知每个作业本 6 元,每支签字笔 2.2 元,小明买了 7 支签字笔,他最多还可以买作业本的个数为( )
A.5 B.4 C.3 D.2
B
当堂小练
5. 某闹市区新建一个小吃城,设计一个进口和一个出口,内设 n 个摊位,预估进口和出口的客流量都是每分钟 10 人,每人消费 25 元,摊位的毛利润为 40%,若平均每个摊位一天(按 10 个小时计)的毛利润不低于 1 000 元,则n 的最大值为( )
A.30 B.40 C.50 D.60
D
n≤60
当堂小练
6. 某面馆购进A,B两种山西老陈醋,A种老陈醋每瓶12元,B种老陈醋每瓶 10元,该面馆购进A种老陈醋7瓶和B种老陈醋若干瓶,预算为205元,那么该面馆最多可以购进B种老陈醋 ( )
A.12瓶 B.10瓶 C.14瓶 D.16瓶
解:设该面馆可以购进B种老陈醋x瓶.
依题意,得12×7+10x≤205,
解得x≤12.1,
因为x为整数, 所以x最大取12.
A
当堂小练
设需要购买x块地板砖,则有
5×4≤0.6×0.6x
解得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
答:小明家至少要购买56块地板砖.
解:
7. 小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
当堂小练
8. 某林场计划购买甲、乙两种树苗共 6 000 棵,甲种树苗每棵 0.5 元,乙种树苗每棵 0.8 元,相关资料表明:甲、乙两种树苗的成活率分别为 90%和 95%.若要使这批树苗的成活率不低于 93%,且购买树苗的总费用最低,应选购乙种树苗( )
A.2 000棵 B.2 400棵 C.3 000棵 D.3 600棵
D
(6 000-x)90%+95%x≥93%×6 000
x≥3 600
当堂小练
9. 某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设小琴打了x分钟的电话,则有
0.22+ (x-3) ×0.11≤0.5
解得 x ≤
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
答:小琴最多打了5min的电话.
对接中考
1. 某商品进价 4 元,标价 5 元出售,商家准备打折销售,但其利润率不能少于 10%,则最多可打________折 .
8.8
对接中考
2. 为加强校园消防安全,学校计划购买某种型号的水基灭火器和干粉灭火器(如图)共50个 . 其中水基灭火器的单价为 540 元 / 个,干粉灭火器的单价为 380 元 / 个 . 若学校购买这两种灭火器的总价不超过 21 000 元,则最多可购买这种型号的水基灭火器多少个?
方法点拨:设购买其中一种灭火器 x 个,则可用含 x 的代数式表示出购买另一种灭火器的数量 . 根据总价不超过21 000 元建立一元一次不等式,解不等式即可得解 .
解:设可购买这种型号的水基灭火器 x 个,则购买干粉灭火器(50-x)个 .
根据题意,得 540x+380(50-x) ≤ 21 000,
解得 x ≤ 12.5.
∵ x 为整数, ∴ x 的最大值为 12.
答: 最多可购买这种型号的水基灭火器 12 个 .
对接中考
3. 今年五一小长假期间,我市迎来了一个短期旅游高峰. 某热门景点的门票价格规定见下表:
某旅行社接待的甲、乙两个旅游团
共102 人(甲团人数多于乙团),
在打算购买门票时,如果把两团联合作为一个团体购票会比两团分别各自购票节省730 元.
票的种类 A B C
购票人数/ 人 1~50 51~100 100以上
票价/ 元 50 45 40
(1)求两个旅游团各有多少人?
对接中考
3. 今年五一小长假期间,我市迎来了一个短期旅游高峰. 某热门景点的门票价格规定见下表:
某旅行社接待的甲、乙两个旅游团共
102 人(甲团人数多于乙团),在打
算购买门票时,如果把两团联合作为一个团体购票会比两团分别各自购票节省730 元.
票的种类 A B C
购票人数/ 人 1~50 51~100 100以上
票价/ 元 50 45 40
(1)求两个旅游团各有多少人?
(2)一个人数不足50人的旅游团,当游客人数最低为多少人时,购买B 种门票比购买A 种门票节省?
解:(2)设游客人数为a人时,购买B种门票比购买A种门票节省,
由题意得45×51<50a,解得a>45.9.
∵a为整数,∴a的最小值为46.
答:当游客人数最低为46人时,购买B种门票比购买A种门票节省.
对接中考
4. 刺绣是我国民间传统手工艺,湘绣作为中国四大刺绣之一,闻名中外,在巴黎奥运会倒计时 50 天之际,某国际旅游公司计划购买 A, B 两种奥运主题的湘绣作品作为纪念品 . 已知购买 1 件 A 种湘绣作品与 2 件 B 种湘绣作品共需要 700 元,购买 2 件 A 种湘绣作品与 3 件 B 种湘绣作品共需要 1 200 元 .
(1) A 种湘绣作品和 B 种湘绣作品的单价分别为多少元?
(2) 该国际旅游公司计划购买 A 种湘绣作品和 B 种湘绣作品共 200 件,总费用不超过 50 000 元,那么最多能购买 A 种湘绣作品多少件?
解:(1) 设 A 种湘绣作品的单价为 x元 / 件, B 种湘绣作品的单价为 y 元 / 件 .
根据题意,得解得
答: A 种湘绣作品的单价为 300 元 /件, B 种湘绣作品的单价为 200 元 / 件 .
(2) 设购买 A 种湘绣作品 m 件,则购买 B 种湘绣作品(200-m)件 .
根据题意,得300m+200(200-m) ≤50 000,
解得 m ≤ 100,∴ m 的最大值为 100.
答:最多能购买 100 件 A 种湘绣作品 .
拓展与延伸
1. 某校学生打算在星期天去登山,他们计划上午 8:30 出发,尽可能去登离驻地最远的山,如图所示,并且他们需在山顶开展 1.5 小时的文娱活动,于下午 3:00 以前必须返回驻地.如果去时平均速度为 3.2 千米/时,返回时平均速度为 4.5 千米/时,则能登上的最远的那座山是( )
A.A B.B C.C D.D
D
解:设从驻地到所登山的距离为 x 千米,
则 ,
解得 .
结合题图可知,能登上的最远的山为距离驻地 9 千米的 D.
拓展与延伸
2. 学校在“我和我的祖国”快闪拍摄活动中,为学生化妆. 其中 5 名男生和 3 名女生共需化妆费 190 元;3 名男生的化妆费用与 2 名女生的化妆费用相同.
(1)求每位男生和女生的化妆费分别为多少元;
(2)如果学校提供的化妆总费用为 2 000 元,根据活动需要至少应有 42 名女生化妆,那么男生最多有多少人化妆?
解:(1)设每位男生的化妆费是 x 元,每位女生的化妆费是 y 元.
依题意得 解得
答:每位男生的化妆费是 20 元,每位女生的化妆费是 30 元.
(2)设男生有 a 人化妆,依题意得 ,
解得 a≤37,即 a 的最大值是 37.
答:男生最多有 37 人化妆.
拓展与延伸
3. 为迎接“七一”党的生日,某校准备组织师生共 310 人参加一次大型公益活动,租用 4 辆大客车和 6 辆小客车恰好全部坐满,已知每辆大客车的座位数比小客车多 15 个.
(1)求每辆大客车和每辆小客车的座位数;
(2)经学校统计,实际参加活动的人数增加了 40 人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为使所有参加活动的师生均有座位,最多租用小客车多少辆?
解:(1)设每辆小客车的座位数是 x 个,每辆大客车的座位数是 y 个.根据题意,得 解得
答:每辆大客车的座位数是 40 个,每辆小客车的座位数是 25 个.
(2)设租用 a 辆小客车才能使所有参加活动的师生均有座位,则租用大客车(10-a)辆.
根据题意,得 25a+40(10-a)≥310+40,解得 a≤3.
因为 a 为非负整数,所以符合条件的 a 的最大值为 3.
答:最多租用小客车 3 辆.
第十一章 不等式与不等式组
11.2 一元一次不等式
课时2 一元一次不等式的实际应用(一)
目
录
1. 学习目标
4. 知识点 一元一次不等式的实际应用(简单)
5. 课堂小结
6. 当堂小练
CONTENTS
2. 知识回顾
8. 拓展与延伸
7. 对接中考
3. 新课导入
掌握用一元一次不等式解决实际问题的步骤,会用一元一次不等式解简单的实际问题.
学习目标
知识回顾
解一元一次不等式的步骤:
① 去分母
② 去括号
③ 移项
④ 合并同类项
⑤ 系数化为 1
新课导入
一元一次方程解实际问题的步骤:
实际问题
设未知数
找相等关系
列出方程
检验解的合理性
解方程
【思考】那么如何用一元一次不等式解实际问题呢?
新课讲解
知识点 一元一次不等式的实际应用(简单)
小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
新课讲解
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h,回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
新课讲解
1. 某次知识竞赛共有 20 道题,每一道题答对得 10 分,答错或不答都扣 5 分.小明得分要超过 90 分,他至少要答对多少道题?
设答对 x 道题,则答错或不答 20-x 道题.
怎样设未知数表示问题中的不等关系呢?
答对 答错或不答
题数
得分
x
20-x
10x
-5(20-x)
解:设答对 x 道题.
根据题意,得10x-5(20-x)>90.
解得 .
由 x 应为正整数,得 x≥13.
答:他至少要答对 13 道题.
例
新课讲解
例
2. 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到 60%,如果明年(365天)这样的比值要超过 70%,那么明年空气质量良好的天数比去年至少要增加多少?
怎样设未知数表示问题中的不等关系呢?
设 x 表示明年增加的空气质量良好的天数,则明年空气质量良好的天数是 x+365×60%.
解:设明年比去年空气质量良好的天数增加了 x.
去年有 365×60% 天空气质量良好,明年有(x+365×60%)天空气质量良好,并且 .
去分母,得 x+219>255.5.
移项,合并同类项,得 x>36.5.
由 x 应为正整数,得 x≥37.
天数是整数,所以应该取 37.
这样就可以了吗?
答:明年空气质量良好的天数比去年至少要增加 37,才能使这一年空气质量良好的天数超过全年天数的70%.
新课讲解
例
解:设小明家每月用水x立方米.
∵5×1.8=9<15,
∴小明家每月用水超过5立方米,
则超出(x-5)立方米,按每立方米2元收费,
列出不等式为:5×1.8+(x-5)×2≥15,
解不等式得:x≥8.
答:小明家每月用水量至少是8立方米.
3. 小明家每月水费都不少于15元,自来水公司的收费标准如下:若每户每月用水不超过5立方米,则每立方米收费1.8元;若每户每月用水超过5立方米,则超出部分每立方米收费2元,小明家每月用水量至少是多少?
在利用一元一次不等式解决实际问题时一定根据实际情况取值.
注意
新课讲解
例
4. 我市某乡村振兴果蔬加工公司先后两次购买龙眼共21吨,第一次购买龙眼的价格为0.4万元/吨;因龙眼大量上市,价格下跌,第二次购买龙眼的价格为0.3万元/吨,两次购买龙眼共用了7万元.
(1)两次购买龙眼各是多少吨
解:(1)设第一次购买龙眼x吨,则第二次购买龙眼(21-x)吨,
由题意,得0.4x+0.3(21-x)=7,
解得x=7,所以21-x=21-7=14.
答:第一次购买龙眼7吨,第二次购买龙眼14吨.
新课讲解
例
4. 我市某乡村振兴果蔬加工公司先后两次购买龙眼共21吨,第一次购买龙眼的价格为0.4万元/吨;因龙眼大量上市,价格下跌,第二次购买龙眼的价格为0.3万元/吨,两次购买龙眼共用了7万元.
(2)公司把两次购买的龙眼加工成桂圆肉和龙眼干,1吨龙眼可加工成桂圆肉0.2吨或龙眼干0.5吨,桂圆肉和龙眼干的销售价格分别是10万元/吨和3万元/吨,若全部的销售额不少于39万元,则至少需要把多少吨龙眼加工成桂圆肉
解:(2)设把y吨龙眼加工成桂圆肉,则把(21-y)吨龙眼加工成龙眼干,
由题意,得10×0.2y+3×0.5(21-y)≥39,
解得y≥15.
答:至少需要把15吨龙眼加工成桂圆肉.
新课讲解
练一练
1. 一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小明答对了 x 道题,则他答错和不答的共有 (25-x)道题.
根据题意,得
4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
答:小明至少答对了22道题.
分析:本题涉及的数量关系是:总得分≥85.
新课讲解
练一练
2. 某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果至少要获得900元的纯利润,每套童装的售价至少是多少元?
解:设每套童装的售价是 x 元.
则40x-90×40-40x·10%≥900.
解得 x ≥ 125.
答:每套童装的售价至少是125元.
分析:本题涉及的数量关系是:销售额-成本-税费≥纯利润(900元).
新课讲解
练一练
分析:“今年万元地区生产总值能耗比去年的下降率不小于5%”是问题中蕴含的不等关系,转化为不等式:×100%≥5%.
3. 某市去年万元地区生产总值能耗为0.320t标准煤,如果计划使今年万元地区生产总值能耗比去年的下降率不小于5%,那么这个市今年万元地区生产总值能耗至多为多少
解:设这个市今年万元地区生产总值能耗为x t标准煤.
根据题意,列得不等式 ×100%≥5%.
解得 x≤0.304.
答:这个市今年万元地区生产总值能耗至多为0.304t标准煤.
4. 某水果店 5 月份购进甲、乙两种水果共花费 1 700 元,其中甲种水果 8 元/千克,乙种水果 18 元/千克.6 月份,这两种水果的进价上调为:甲种水果 10 元/千克,乙种水果 20 元/千克.
(1)若该店 6 月份购进两种水果的数量与5月份都相同,将多支付货款300元,求该店 5 月份购进甲、乙两种水果分别是多少千克;
新课讲解
练一练
解:(1)设 5 月份购进甲、乙两种水果分别为 x 千克和 y 千克.
根据题意,得 解得
答:该店 5 月份购进甲种水果 100 千克、乙种水果 50 千克.
5. 某水果店 5 月份购进甲、乙两种水果共花费 1 700 元,其中甲种水果 8 元/千克,乙种水果 18 元/千克.6 月份,这两种水果的进价上调为:甲种水果 10 元/千克,乙种水果 20 元/千克.
(2)若 6 月份这两种水果进货总量减少到 120 千克,且甲种水果不超过乙种
水果的 3 倍,则 6 月份该店需要支付这两种水果的货款最少应是多少元?
新课讲解
练一练
解:
(2)设 6 月份购进乙种水果 m 千克,则购进甲种水果(120-m)千克,该店需要支付这两种水果的货款为 W 元.
W=10(120-m)+20m=10m+1 200.
因为甲种水果不超过乙种水果的 3 倍,所以 120-m≤3m,解得 m≥30.
所以两种水果的货款最少应当是10×30+1 200=1 500(元).
课堂小结
认真审题,找出已知量和未知量,并找出它们之间的关系.
审
设出适当的未知数.
设
根据题中的不等关系列出不等式.
列
解不等式,求出其解集.
解
检验所求出的不等式的解集是否符合题意.
验
写出答案.
答
用一元一次不等式解决实际问题的步骤
当堂小练
1. 某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过95分,他至多可以答错或不答的试题道数为 ( )
A.5 B.6 C.7 D.8
解:设小玉答对了x道题目,则答错或不答的题目一共为(20-x)道.
由题意可得,10x-5(20-x)>95,
解得x>13,
所以小玉至少要答对14道题目,至多答错或不答20-14=6(道).
B
当堂小练
2. 某种商品的进价为每件 100 元,商场按进价提高 50% 后标价,为增加销量,准备打折销售,但要保证利润率不低于 20%,则至多可以打_____折.
八
标价:100(1+50%)
售价:100(1+20%)
100(1+50%)100(1+20%)
x≥8
当堂小练
3. 一种导火线的燃烧速度是 0.7 cm/s,一名爆破员点燃导火线后以 5 m/s 的速度跑到距爆破点 130 m 以外的安全地带,则导火线的长度至少应超过( )
A. 18 cm B. 18.2 cm C. 18.5 cm D. 19 cm
B
x >18.2
导火线燃烧完所用时间
人跑到安全地带所用时间
>
当堂小练
4. 小明准备用 40 元钱购买作业本和签字笔.已知每个作业本 6 元,每支签字笔 2.2 元,小明买了 7 支签字笔,他最多还可以买作业本的个数为( )
A.5 B.4 C.3 D.2
B
当堂小练
5. 某闹市区新建一个小吃城,设计一个进口和一个出口,内设 n 个摊位,预估进口和出口的客流量都是每分钟 10 人,每人消费 25 元,摊位的毛利润为 40%,若平均每个摊位一天(按 10 个小时计)的毛利润不低于 1 000 元,则n 的最大值为( )
A.30 B.40 C.50 D.60
D
n≤60
当堂小练
6. 某面馆购进A,B两种山西老陈醋,A种老陈醋每瓶12元,B种老陈醋每瓶 10元,该面馆购进A种老陈醋7瓶和B种老陈醋若干瓶,预算为205元,那么该面馆最多可以购进B种老陈醋 ( )
A.12瓶 B.10瓶 C.14瓶 D.16瓶
解:设该面馆可以购进B种老陈醋x瓶.
依题意,得12×7+10x≤205,
解得x≤12.1,
因为x为整数, 所以x最大取12.
A
当堂小练
设需要购买x块地板砖,则有
5×4≤0.6×0.6x
解得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
答:小明家至少要购买56块地板砖.
解:
7. 小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
当堂小练
8. 某林场计划购买甲、乙两种树苗共 6 000 棵,甲种树苗每棵 0.5 元,乙种树苗每棵 0.8 元,相关资料表明:甲、乙两种树苗的成活率分别为 90%和 95%.若要使这批树苗的成活率不低于 93%,且购买树苗的总费用最低,应选购乙种树苗( )
A.2 000棵 B.2 400棵 C.3 000棵 D.3 600棵
D
(6 000-x)90%+95%x≥93%×6 000
x≥3 600
当堂小练
9. 某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元.她最多打了几分钟的电话?
解:设小琴打了x分钟的电话,则有
0.22+ (x-3) ×0.11≤0.5
解得 x ≤
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
答:小琴最多打了5min的电话.
对接中考
1. 某商品进价 4 元,标价 5 元出售,商家准备打折销售,但其利润率不能少于 10%,则最多可打________折 .
8.8
对接中考
2. 为加强校园消防安全,学校计划购买某种型号的水基灭火器和干粉灭火器(如图)共50个 . 其中水基灭火器的单价为 540 元 / 个,干粉灭火器的单价为 380 元 / 个 . 若学校购买这两种灭火器的总价不超过 21 000 元,则最多可购买这种型号的水基灭火器多少个?
方法点拨:设购买其中一种灭火器 x 个,则可用含 x 的代数式表示出购买另一种灭火器的数量 . 根据总价不超过21 000 元建立一元一次不等式,解不等式即可得解 .
解:设可购买这种型号的水基灭火器 x 个,则购买干粉灭火器(50-x)个 .
根据题意,得 540x+380(50-x) ≤ 21 000,
解得 x ≤ 12.5.
∵ x 为整数, ∴ x 的最大值为 12.
答: 最多可购买这种型号的水基灭火器 12 个 .
对接中考
3. 今年五一小长假期间,我市迎来了一个短期旅游高峰. 某热门景点的门票价格规定见下表:
某旅行社接待的甲、乙两个旅游团
共102 人(甲团人数多于乙团),
在打算购买门票时,如果把两团联合作为一个团体购票会比两团分别各自购票节省730 元.
票的种类 A B C
购票人数/ 人 1~50 51~100 100以上
票价/ 元 50 45 40
(1)求两个旅游团各有多少人?
对接中考
3. 今年五一小长假期间,我市迎来了一个短期旅游高峰. 某热门景点的门票价格规定见下表:
某旅行社接待的甲、乙两个旅游团共
102 人(甲团人数多于乙团),在打
算购买门票时,如果把两团联合作为一个团体购票会比两团分别各自购票节省730 元.
票的种类 A B C
购票人数/ 人 1~50 51~100 100以上
票价/ 元 50 45 40
(1)求两个旅游团各有多少人?
(2)一个人数不足50人的旅游团,当游客人数最低为多少人时,购买B 种门票比购买A 种门票节省?
解:(2)设游客人数为a人时,购买B种门票比购买A种门票节省,
由题意得45×51<50a,解得a>45.9.
∵a为整数,∴a的最小值为46.
答:当游客人数最低为46人时,购买B种门票比购买A种门票节省.
对接中考
4. 刺绣是我国民间传统手工艺,湘绣作为中国四大刺绣之一,闻名中外,在巴黎奥运会倒计时 50 天之际,某国际旅游公司计划购买 A, B 两种奥运主题的湘绣作品作为纪念品 . 已知购买 1 件 A 种湘绣作品与 2 件 B 种湘绣作品共需要 700 元,购买 2 件 A 种湘绣作品与 3 件 B 种湘绣作品共需要 1 200 元 .
(1) A 种湘绣作品和 B 种湘绣作品的单价分别为多少元?
(2) 该国际旅游公司计划购买 A 种湘绣作品和 B 种湘绣作品共 200 件,总费用不超过 50 000 元,那么最多能购买 A 种湘绣作品多少件?
解:(1) 设 A 种湘绣作品的单价为 x元 / 件, B 种湘绣作品的单价为 y 元 / 件 .
根据题意,得解得
答: A 种湘绣作品的单价为 300 元 /件, B 种湘绣作品的单价为 200 元 / 件 .
(2) 设购买 A 种湘绣作品 m 件,则购买 B 种湘绣作品(200-m)件 .
根据题意,得300m+200(200-m) ≤50 000,
解得 m ≤ 100,∴ m 的最大值为 100.
答:最多能购买 100 件 A 种湘绣作品 .
拓展与延伸
1. 某校学生打算在星期天去登山,他们计划上午 8:30 出发,尽可能去登离驻地最远的山,如图所示,并且他们需在山顶开展 1.5 小时的文娱活动,于下午 3:00 以前必须返回驻地.如果去时平均速度为 3.2 千米/时,返回时平均速度为 4.5 千米/时,则能登上的最远的那座山是( )
A.A B.B C.C D.D
D
解:设从驻地到所登山的距离为 x 千米,
则 ,
解得 .
结合题图可知,能登上的最远的山为距离驻地 9 千米的 D.
拓展与延伸
2. 学校在“我和我的祖国”快闪拍摄活动中,为学生化妆. 其中 5 名男生和 3 名女生共需化妆费 190 元;3 名男生的化妆费用与 2 名女生的化妆费用相同.
(1)求每位男生和女生的化妆费分别为多少元;
(2)如果学校提供的化妆总费用为 2 000 元,根据活动需要至少应有 42 名女生化妆,那么男生最多有多少人化妆?
解:(1)设每位男生的化妆费是 x 元,每位女生的化妆费是 y 元.
依题意得 解得
答:每位男生的化妆费是 20 元,每位女生的化妆费是 30 元.
(2)设男生有 a 人化妆,依题意得 ,
解得 a≤37,即 a 的最大值是 37.
答:男生最多有 37 人化妆.
拓展与延伸
3. 为迎接“七一”党的生日,某校准备组织师生共 310 人参加一次大型公益活动,租用 4 辆大客车和 6 辆小客车恰好全部坐满,已知每辆大客车的座位数比小客车多 15 个.
(1)求每辆大客车和每辆小客车的座位数;
(2)经学校统计,实际参加活动的人数增加了 40 人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为使所有参加活动的师生均有座位,最多租用小客车多少辆?
解:(1)设每辆小客车的座位数是 x 个,每辆大客车的座位数是 y 个.根据题意,得 解得
答:每辆大客车的座位数是 40 个,每辆小客车的座位数是 25 个.
(2)设租用 a 辆小客车才能使所有参加活动的师生均有座位,则租用大客车(10-a)辆.
根据题意,得 25a+40(10-a)≥310+40,解得 a≤3.
因为 a 为非负整数,所以符合条件的 a 的最大值为 3.
答:最多租用小客车 3 辆.
同课章节目录
