11.2课时2 一元一次不等式实际应用(2) 课件(共32张PPT) 2024—2025学年人教版七年级数学下册
文档属性
| 名称 | 11.2课时2 一元一次不等式实际应用(2) 课件(共32张PPT) 2024—2025学年人教版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 398.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
第十一章 不等式与不等式组
11.2 一元一次不等式
课时2 一元一次不等式的实际应用(二)
目
录
1. 学习目标
4. 知识点 一元一次不等式的实际应用(分类讨论)
5. 课堂小结
6. 当堂小练
CONTENTS
2. 知识回顾
8. 拓展与延伸
7. 对接中考
3. 新课导入
进一步学习通过列一元一次不等式解决生活中的实际问题,体会分类讨论思想在用不等式解决实际问题中的应用.
学习目标
知识回顾
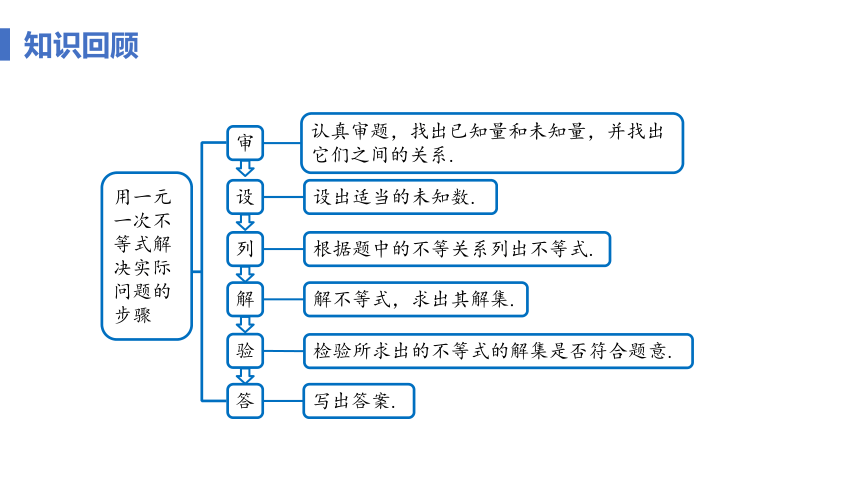
认真审题,找出已知量和未知量,并找出它们之间的关系.
审
设出适当的未知数.
设
根据题中的不等关系列出不等式.
列
解不等式,求出其解集.
解
检验所求出的不等式的解集是否符合题意.
验
写出答案.
答
用一元一次不等式解决实际问题的步骤
新课导入
上节课我们学习了运用不等式解决一些实际问题,这节课我们继续学习建立不等式模型解应用题.
新课讲解
知识点 一元一次不等式的实际应用(方案问题)
例
1. 某校组织学生参加“周末郊游”. 甲旅行社说:“只要一名学生买全票,那么其余学生可享受半价优惠.”乙旅行社说:“全体学生都可按6 折优惠.”已知全票价为240 元.
(1) 设学生数为x 人,甲旅行社收费为y甲元,乙旅行社收费为y乙元,用含x 的式子表示出y甲与y乙;
解:y甲=240+(x-1)×120=120x+120,
y乙=240×0.6x=144x.
新课讲解
例
1. 某校组织学生参加“周末郊游”. 甲旅行社说:“只要一名学生买全票,那么其余学生可享受半价优惠.”乙旅行社说:“全体学生都可按6 折优惠.”已知全票价为240 元.
(1) 设学生数为x 人,甲旅行社收费为y甲元,乙旅行社收费为y乙元,用含x 的式子表示出y甲与y乙;
y甲=120x+120,y乙=144x.
(2)讨论哪一家旅行社更优惠.
方法点拨:三种情况讨论:y 甲>y 乙,y 甲=y 乙,y 甲解:当y甲>y乙时,120x+120>144x,解得x<5.
∴当学生数少于5 人时,乙旅行社更优惠.
当y甲=y乙时,120x+120=144x,解得x=5.
∴当学生数正好为5 人时,两家旅行社一样优惠.
当y甲5.
∴当学生数超过5 人时,甲旅行社更优惠.
新课讲解
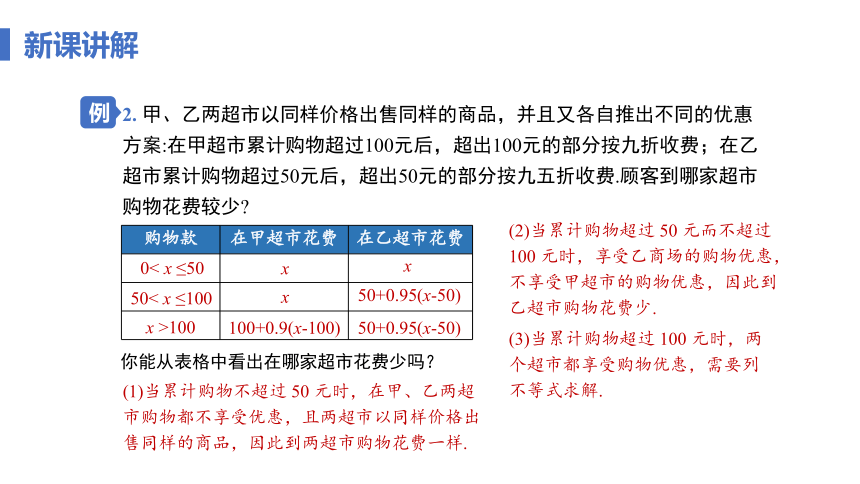
2. 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
例
分析:在甲超市购物超过100元后享受优惠,在乙超市购物超过50元后享受优惠,因此,需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元.
购物款 在甲超市花费 在乙超市花费
0< x ≤50
50< x ≤100
x >100
x
x
100+0.9(x-100)
x
50+0.95(x-50)
50+0.95(x-50)
你能从表格中看出在哪家超市花费少吗?
新课讲解
2. 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
例
购物款 在甲超市花费 在乙超市花费
0< x ≤50
50< x ≤100
x >100
x
x
100+0.9(x-100)
x
50+0.95(x-50)
50+0.95(x-50)
你能从表格中看出在哪家超市花费少吗?
(1)当累计购物不超过 50 元时,在甲、乙两超市购物都不享受优惠,且两超市以同样价格出售同样的商品,因此到两超市购物花费一样.
(2)当累计购物超过 50 元而不超过 100 元时,享受乙商场的购物优惠,不享受甲超市的购物优惠,因此到乙超市购物花费少.
(3)当累计购物超过 100 元时,两个超市都享受购物优惠,需要列不等式求解.
新课讲解
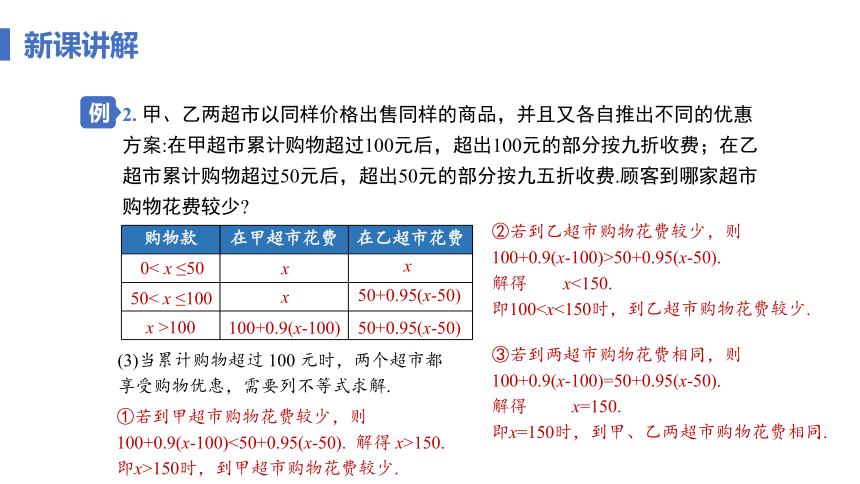
2. 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
例
购物款 在甲超市花费 在乙超市花费
0< x ≤50
50< x ≤100
x >100
x
x
100+0.9(x-100)
x
50+0.95(x-50)
50+0.95(x-50)
(3)当累计购物超过 100 元时,两个超市都享受购物优惠,需要列不等式求解.
①若到甲超市购物花费较少,则
100+0.9(x-100)<50+0.95(x-50). 解得 x>150.
即x>150时,到甲超市购物花费较少.
②若到乙超市购物花费较少,则
100+0.9(x-100)>50+0.95(x-50).
解得 x<150.
即100③若到两超市购物花费相同,则
100+0.9(x-100)=50+0.95(x-50).
解得 x=150.
即x=150时,到甲、乙两超市购物花费相同.
新课讲解
2. 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
例
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠,购物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元
①若50+0.95(x-50)>100+0.9(x-100) 即x>150在甲超市购物花费少;
②若50+0.95(x-50)<100+0.9(x-100) 即x<150在乙超市购物花费少;
③若50+0.95(x-50)=100+0.9(x-100) 即x=150在甲、乙两超市购物花费一样.
新课讲解
例
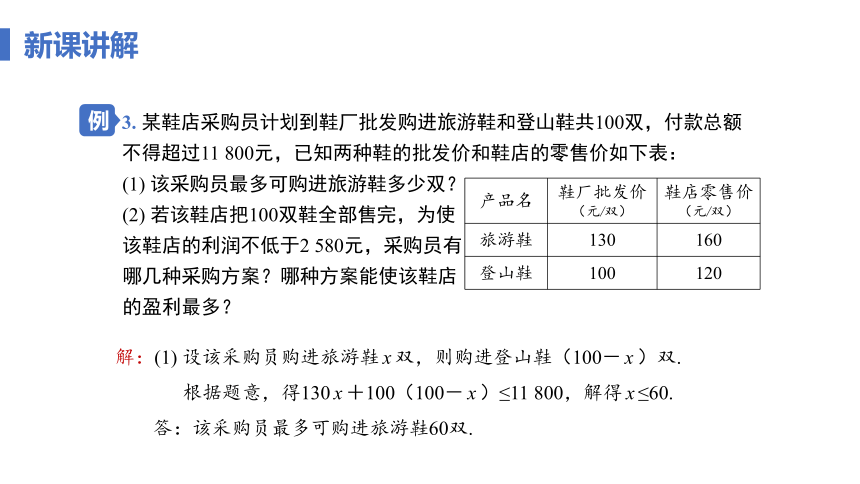
3. 某鞋店采购员计划到鞋厂批发购进旅游鞋和登山鞋共100双,付款总额不得超过11 800元,已知两种鞋的批发价和鞋店的零售价如下表:
产品名 鞋厂批发价(元/双) 鞋店零售价(元/双)
旅游鞋 130 160
登山鞋 100 120
(1) 该采购员最多可购进旅游鞋多少双?
(2) 若该鞋店把100双鞋全部售完,为使该鞋店的利润不低于2 580元,采购员有哪几种采购方案?哪种方案能使该鞋店的盈利最多?
解:(1) 设该采购员购进旅游鞋x双,则购进登山鞋(100-x)双.
根据题意,得130x+100(100-x)≤11 800,解得x≤60.
答:该采购员最多可购进旅游鞋60双.
新课讲解
例
3. 某鞋店采购员计划到鞋厂批发购进旅游鞋和登山鞋共100双,付款总额不得超过11 800元,已知两种鞋的批发价和鞋店的零售价如下表:
产品名 鞋厂批发价(元/双) 鞋店零售价(元/双)
旅游鞋 130 160
登山鞋 100 120
(1) 该采购员最多可购进旅游鞋多少双?
(2) 若该鞋店把100双鞋全部售完,为使该鞋店的利润不低于2 580元,采购员有哪几种采购方案?哪种方案能使该鞋店的盈利最多?
解:(2) 根据题意,得(160-130)x+(120-100)(100-x)≥2 580,解得x≥58.
∵x≤60,且x为正整数,∴x可取58,59,60,∴采购员共有3种采购方案.
方案1:购进旅游鞋58双,购进登山鞋42双;
方案2:购进旅游鞋59双,购进登山鞋41双;
方案3:购进旅游鞋60双,购进登山鞋40双.
选择方案1该鞋店的盈利为(160-130)×58+(120-100)×42=2 580 (元);
选择方案2该鞋店的盈利为(160-130)×59+(120-100)×41=2 590 (元);
选择方案3该鞋店的盈利为(160-130)×60+(120-100)×40=2 600 (元).
∵2 580<2 590<2 600,∴选择方案3能使该鞋店的盈利最多.
新课讲解
练一练
1. 某校一名老师将在假期带领学生去北京旅游,有两种购票方式:甲旅行社说:“老师买全票,其他人全部半价优惠.”乙旅行社说:“所有人按全票价的 6 折优惠.”已知全票价 240 元.设学生有 x 名,就学生人数讨论哪家旅行社更优惠.
旅行社 老师购票费用 学生购票费用
甲 240元 120x元
乙 144元 144x元
解:①若 240+120x=144x+144,解得 x=4,
此时两家旅行社收费一样;
②若 240+120x>144x+144,解得 x<4,
此时乙旅行社更优惠;
③若 240+120x<144x+144,解得 x>4,
此时甲旅行社更优惠.
新课讲解
2. 某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.
(1)符合公司要求的购买方案有哪几种?请说明理由;
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金收入不低于1500元,那么应选择以上哪种购买方案?
解:(1)设轿车要购买x辆,那么面包车要购买(10-x)辆,
7x+4(10-x)≤55,解得 x≤5,
又x≥3,则x=3,4,5,
∴有三种方案:①轿车3辆,面包车7辆;
②轿车4辆,面包车6辆;
③轿车5辆,面包车5辆.
(2)方案一的日租金为3×200+7×110=1370;
方案二的日租金为:4×200+6×110=1460;
方案三的日租金为:5×200+5×110=1550.
为保证日租金不低于1500元,应选方案三.
练一练
新课讲解
练一练
3. 某市打市内电话的收费标准是:每次3min以内(含3min)0.22元,以后每分钟0.11元(不足1min 部分按1min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元. 她最多打了几分钟的电话?
通话时间/min 电话费/元
x ≤3
x > 3
0.22
0.22+0.11(x-3)
解:设小琴打了 x min 的电话,则有
0.22+(x-3)×0.11≤0.5,
解得 x ≤ .
由于电话计时按照分钟计时,x 应是整数,
所以 x 的最大值为 5.
答:小琴最多打了 5 min 的电话.
新课讲解
练一练
4. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(1)购买一件原价为450元的健身器材时,选择哪种活动更合算
解:(1)∵450×=360(元),
450-80=370(元),
∴选择活动一更合算.
新课讲解
练一练
4. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价;
解:(2)设一件这种健身器材的原价为x元.
若x<300,则活动一按原价打八折,活动二按原价,
此时付款金额不可能相等,
∴300≤x<500.
由题意得,x=x-80,
解得x=400,
∴一件这种健身器材的原价是400元.
新课讲解
练一练
4. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算 设一件这种健身器材的原价为a元,请直接写出a的取值范围.
解:(3)当300≤a<600时,
a-80<0.8a,解得a<400,
∴300≤a<400;
当600≤a<900时,
a-160<0.8a,解得a<800,
∴600≤a<800.
综上所述,300≤a<400或600≤a<800.
课堂小结
检验
设未知数
列不等式
数学问题
(一元一次不等式)
实际问题
(包含不等关系)
数学问题的解
(不等式的解集)
实际问题的答案
解不等式
当堂小练
1. 某商店 5 月 1 日举行促销优惠活动,当天到该商店购买商品有两种方案.方案一:用 168 元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的 8 折优惠.方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的 9.5 折优惠.已知小敏 5月 1 日前不是该商店的会员.请帮小敏算一算,采用哪种方案更合算?
解:设所购买的商品的价格为 x 元时,
若采用方案一更合算,则 0.95x>0.8x+168,解得 x>1 120.
若采用方案二更合算,则 0.95x<0.8x+168,解得 x<1 120.
若采用两种方案一样,则 0.95x=0.8x+168,解得 x=1 120.
所以小敏所购买商品的价格超过 1 120 元时,采用方案一更合算.
当堂小练
2. 某通信公司升级了两种通信业务:“A 业务”使用者先缴 15 元月租费,然后每通话 1 分钟付话费 0.2 元;“B 业务”不缴月租费,每通话 1 分钟付费 0.3 元,你觉得选哪种业务更优惠?
业务类别 通话时长/分钟 话费/元
A
B
x
15+0.2x
x
0.3x
解:①若“A 业务”更优惠,则 15+0.2x<0.3x,解得 x>150;
②若“B 业务”更优惠,则 15+0.2x>0.3x,解得 x<150;
③若两种业务优惠一样,则 15+0.2x=0.3x,解得 x=150.
所以,当通话时间超过 150 分钟时,选“A 业务”更优惠;
当通话时间不足 150 分钟时,选“B 业务”更优惠;
当通话时间为 150 分钟时,两种业务优惠一样.
当堂小练
3. 友谊商店 A 型号笔记本电脑的售价是 a 元/台.最近,该商店对 A 型号笔记本电脑举行促销活动,有两种优惠方案.方案一:每台按售价的九折销售.方案二:若购买不超过 5 台,每台按售价销售;若超过 5 台,超过的部分每台按售价的八折销售.某公司一次性从友谊商店购买 A 型号笔记本电脑 x 台.
(1)当 x=8 时,应选择哪种方案,该公司购买费用最少?最少费用是多少元?
解:(1)当 x=8 时,方案一费用:0.9a·8=7.2a(元),
方案二费用:5a+0.8a×(8-5)=7.4a(元).
∵a>0,
∴7.2a<7.4a.
∴方案一费用最少,最少费用为 7.2a 元.
当堂小练
3. 友谊商店 A 型号笔记本电脑的售价是 a 元/台.最近,该商店对 A 型号笔记本电脑举行促销活动,有两种优惠方案.方案一:每台按售价的九折销售.方案二:若购买不超过 5 台,每台按售价销售;若超过 5 台,超过的部分每台按售价的八折销售.某公司一次性从友谊商店购买 A 型号笔记本电脑 x 台.
(2)若该公司采用方案二购买更合算,求 x 的取值范围.
购买台数 方案一 方案二
x ≤ 5
x > 5
0.9ax
0.9ax
ax
5a+0.8a(x-5)
解:(2)若 x≤5,方案一每台按售价的九折销售,方案二每台按售价销售.
∴采用方案一购买合算.
若 x>5,方案一的费用:0.9ax 元.
方案二的费用:5a+0.8a(x-5)=0.8ax+a(元).
由题意得 0.9ax>0.8ax+a,解得 x>10.
∴若该公司采用方案二购买更合算,x 的取值范围是 x>10 且 x 为正整数.
当堂小练
4.“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买 A,B 两种型号的垃圾处理设备共 10 台(每种型号至少买 1 台).已知每台 A 型设备日处理能力为 12 吨,每台 B 型设备日处理能力为 15 吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买 A,B 两种设备的方案.
解:(1)设购买 A 型设备 x 台,则购买 B 型设备(10-x)台.
根据题意,得 12x+15(10-x)≥140,
解得 x≤3.
∵ x 为正整数,∴ x=1,2,3.
∴ 该景区有三种购买方案:
方案一:购买 A 型设备 1 台,B 型设备 9 台.
方案二:购买 A 型设备 2 台,B 型设备 8 台.
方案三:购买 A 型设备 3 台,B 型设备 7 台.
当堂小练
4.“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买 A,B 两种型号的垃圾处理设备共 10 台(每种型号至少买 1 台).已知每台 A 型设备日处理能力为 12 吨,每台 B 型设备日处理能力为 15 吨,购回的设备日处理能力不低于140吨.
(2) 已知每台 A 型设备价格为 3 万元,每台 B 型设备价格为 4.4 万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠,问:采用(1)设计的哪种方案,可以使购买费用最少,为什么?
方案一:购买 A 型设备 1 台,B 型设备 9 台.
方案二:购买 A 型设备 2 台,B 型设备 8 台.
方案三:购买 A 型设备 3 台,B 型设备 7 台.
解:(2)各方案购买费用分别为:
方案一:3×1+4.4×9=42.6(万元)>40万元,
实际付款:42.6×0.9=38.34(万元);
方案二:3×2+4.4×8=41.2(万元)>40万元,
实际付款:41.2×0.9=37.08(万元).
当堂小练
5. 某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.
(1)符合公司要求的购买方案有哪几种?请说明理由;
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金收入不低于1500元,那么应选择以上哪种购买方案?
解:(1) 设轿车要购买x辆,那么面包车要购买(10-x)辆.
则有7x+4(10-x)≤55,解得 x≤5.
因为x≥3,所以整数x=3,4,5.
则有三种方案:①轿车3辆,面包车7辆;
②轿车4辆,面包车6辆;
③轿车5辆,面包车5辆.
(2) 方案一的日租金为3×200+7×110=1370(元);
方案二的日租金为4×200+6×110=1460(元);
方案三的日租金为5×200+5×110=1550(元).
为保证日租金不低于1500元,应选方案三.
对接中考
某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种 .
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满 300 元减 80 元 (如:所购商品原价为 300 元,可减 80 元,需付款 220 元;所购商品原价为 770 元,可减 160 元,需付款 610 元)
(1) 购买一件原价为 450 元的健身器材时,选择哪种活动更合算?请说明理由 .
解:(1) 购买一件原价为450元的健身器材时,选择活动一更合算.
理由:购买一件原价为450元的健身器材时,
活动一需付款为450×0.8=360(元),
活动二需付款为450-80=370(元).
∵360元<370元,
∴选择活动一更合算.
对接中考
某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种 .
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满 300 元减 80 元 (如:所购商品原价为 300 元,可减 80 元,需付款 220 元;所购商品原价为 770 元,可减 160 元,需付款 610 元)
(2) 购买一件原价在 500 元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价 .
解:(2) 设一件这种健身器材的原价是x元,
则0.8x=x-80,
解得x=400.
答:一件这种健身器材的原价是400元.
对接中考
(3) 购买一件原价在 900 元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算?设一件这种健身器材的原价为 a元,请求出 a 的取值范围 .
解:(3) 由题意,得活动一所需付款为0.8a元.
活动二:当0<a<300时,所需付款为a元;
当300≤a<600时,所需付款为(a-80)元;
当600≤a<900时,所需付款为(a-160)元.
①当0<a<300时,a>0.8a,此时无论a为何值,都是活动一更合算,不符合题意;
②当300≤a<600时,令a-80<0.8a,解得a<400,即当300≤a<400时,活动二更合算;
③当600≤a<900时,令a-160<0.8a,解得a<800,即当600≤a<800时,活动二更合算.
综上,当300≤a<400或600≤a<800时,活动二更合算.
某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种 .
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满 300 元减 80 元 (如:所购商品原价为 300 元,可减 80 元,需付款 220 元;所购商品原价为 770 元,可减 160 元,需付款 610 元)
拓展与延伸
小明同学三次到某超市购买 A,B 两种商品,其中仅有一次是有折扣的.购买数量及消费金额如下表:
购买 A 商品数量/件 购买 B 商品数量/件 消费金额/元
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
类别
次数
(1)第_____次购买有折扣;
三
(2)求A,B 两种商品的原价;
解:(2)设 A 种商品的原价为 x 元/件,B 种商品的原价为 y 元/件,根据题意,得 解得
答: A 种商品的原价为 30 元/件,B 种商品的原价为 40 元/件.
拓展与延伸
小明同学三次到某超市购买 A,B 两种商品,其中仅有一次是有折扣的.购买数量及消费金额如下表:
购买 A 商品数量/件 购买 B 商品数量/件 消费金额/元
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
类别
次数
(3)若购买 A,B 两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买 A,B
两种商品共 10 件,在(3)中折扣数的前提下,消费金额不超过 200 元,求至少购买 A 种商品多少件.
A 种商品的原价为 30 元/件,B 种商品的原价为 40 元/件.
解:(3)设折扣数为 z.根据题意,得
,
解得 z = 6,故折扣数为 6.
(4)设购买 A 种商品 m 件,则购买 B 种商品(10-m)件.根据题意,
得 ,
解得 .
因为 m 为正整数,所以 m 的最小值为 7.
故至少购买 A 种商品 7 件.
第十一章 不等式与不等式组
11.2 一元一次不等式
课时2 一元一次不等式的实际应用(二)
目
录
1. 学习目标
4. 知识点 一元一次不等式的实际应用(分类讨论)
5. 课堂小结
6. 当堂小练
CONTENTS
2. 知识回顾
8. 拓展与延伸
7. 对接中考
3. 新课导入
进一步学习通过列一元一次不等式解决生活中的实际问题,体会分类讨论思想在用不等式解决实际问题中的应用.
学习目标
知识回顾
认真审题,找出已知量和未知量,并找出它们之间的关系.
审
设出适当的未知数.
设
根据题中的不等关系列出不等式.
列
解不等式,求出其解集.
解
检验所求出的不等式的解集是否符合题意.
验
写出答案.
答
用一元一次不等式解决实际问题的步骤
新课导入
上节课我们学习了运用不等式解决一些实际问题,这节课我们继续学习建立不等式模型解应用题.
新课讲解
知识点 一元一次不等式的实际应用(方案问题)
例
1. 某校组织学生参加“周末郊游”. 甲旅行社说:“只要一名学生买全票,那么其余学生可享受半价优惠.”乙旅行社说:“全体学生都可按6 折优惠.”已知全票价为240 元.
(1) 设学生数为x 人,甲旅行社收费为y甲元,乙旅行社收费为y乙元,用含x 的式子表示出y甲与y乙;
解:y甲=240+(x-1)×120=120x+120,
y乙=240×0.6x=144x.
新课讲解
例
1. 某校组织学生参加“周末郊游”. 甲旅行社说:“只要一名学生买全票,那么其余学生可享受半价优惠.”乙旅行社说:“全体学生都可按6 折优惠.”已知全票价为240 元.
(1) 设学生数为x 人,甲旅行社收费为y甲元,乙旅行社收费为y乙元,用含x 的式子表示出y甲与y乙;
y甲=120x+120,y乙=144x.
(2)讨论哪一家旅行社更优惠.
方法点拨:三种情况讨论:y 甲>y 乙,y 甲=y 乙,y 甲
∴当学生数少于5 人时,乙旅行社更优惠.
当y甲=y乙时,120x+120=144x,解得x=5.
∴当学生数正好为5 人时,两家旅行社一样优惠.
当y甲
∴当学生数超过5 人时,甲旅行社更优惠.
新课讲解
2. 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
例
分析:在甲超市购物超过100元后享受优惠,在乙超市购物超过50元后享受优惠,因此,需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元.
购物款 在甲超市花费 在乙超市花费
0< x ≤50
50< x ≤100
x >100
x
x
100+0.9(x-100)
x
50+0.95(x-50)
50+0.95(x-50)
你能从表格中看出在哪家超市花费少吗?
新课讲解
2. 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
例
购物款 在甲超市花费 在乙超市花费
0< x ≤50
50< x ≤100
x >100
x
x
100+0.9(x-100)
x
50+0.95(x-50)
50+0.95(x-50)
你能从表格中看出在哪家超市花费少吗?
(1)当累计购物不超过 50 元时,在甲、乙两超市购物都不享受优惠,且两超市以同样价格出售同样的商品,因此到两超市购物花费一样.
(2)当累计购物超过 50 元而不超过 100 元时,享受乙商场的购物优惠,不享受甲超市的购物优惠,因此到乙超市购物花费少.
(3)当累计购物超过 100 元时,两个超市都享受购物优惠,需要列不等式求解.
新课讲解
2. 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
例
购物款 在甲超市花费 在乙超市花费
0< x ≤50
50< x ≤100
x >100
x
x
100+0.9(x-100)
x
50+0.95(x-50)
50+0.95(x-50)
(3)当累计购物超过 100 元时,两个超市都享受购物优惠,需要列不等式求解.
①若到甲超市购物花费较少,则
100+0.9(x-100)<50+0.95(x-50). 解得 x>150.
即x>150时,到甲超市购物花费较少.
②若到乙超市购物花费较少,则
100+0.9(x-100)>50+0.95(x-50).
解得 x<150.
即100
100+0.9(x-100)=50+0.95(x-50).
解得 x=150.
即x=150时,到甲、乙两超市购物花费相同.
新课讲解
2. 甲、乙两超市以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲超市累计购物超过100元后,超出100元的部分按九折收费;在乙超市累计购物超过50元后,超出50元的部分按九五折收费.顾客到哪家超市购物花费较少
例
解:(1)当购物不超过50元时,在甲、乙两超市都不享受优惠,购物花费一样;
(2)当购物超过50元而不超过100元时,在乙超市享受优惠,购物花费少;
(3)当累计购物超过100元后,设购物为x(x>100)元
①若50+0.95(x-50)>100+0.9(x-100) 即x>150在甲超市购物花费少;
②若50+0.95(x-50)<100+0.9(x-100) 即x<150在乙超市购物花费少;
③若50+0.95(x-50)=100+0.9(x-100) 即x=150在甲、乙两超市购物花费一样.
新课讲解
例
3. 某鞋店采购员计划到鞋厂批发购进旅游鞋和登山鞋共100双,付款总额不得超过11 800元,已知两种鞋的批发价和鞋店的零售价如下表:
产品名 鞋厂批发价(元/双) 鞋店零售价(元/双)
旅游鞋 130 160
登山鞋 100 120
(1) 该采购员最多可购进旅游鞋多少双?
(2) 若该鞋店把100双鞋全部售完,为使该鞋店的利润不低于2 580元,采购员有哪几种采购方案?哪种方案能使该鞋店的盈利最多?
解:(1) 设该采购员购进旅游鞋x双,则购进登山鞋(100-x)双.
根据题意,得130x+100(100-x)≤11 800,解得x≤60.
答:该采购员最多可购进旅游鞋60双.
新课讲解
例
3. 某鞋店采购员计划到鞋厂批发购进旅游鞋和登山鞋共100双,付款总额不得超过11 800元,已知两种鞋的批发价和鞋店的零售价如下表:
产品名 鞋厂批发价(元/双) 鞋店零售价(元/双)
旅游鞋 130 160
登山鞋 100 120
(1) 该采购员最多可购进旅游鞋多少双?
(2) 若该鞋店把100双鞋全部售完,为使该鞋店的利润不低于2 580元,采购员有哪几种采购方案?哪种方案能使该鞋店的盈利最多?
解:(2) 根据题意,得(160-130)x+(120-100)(100-x)≥2 580,解得x≥58.
∵x≤60,且x为正整数,∴x可取58,59,60,∴采购员共有3种采购方案.
方案1:购进旅游鞋58双,购进登山鞋42双;
方案2:购进旅游鞋59双,购进登山鞋41双;
方案3:购进旅游鞋60双,购进登山鞋40双.
选择方案1该鞋店的盈利为(160-130)×58+(120-100)×42=2 580 (元);
选择方案2该鞋店的盈利为(160-130)×59+(120-100)×41=2 590 (元);
选择方案3该鞋店的盈利为(160-130)×60+(120-100)×40=2 600 (元).
∵2 580<2 590<2 600,∴选择方案3能使该鞋店的盈利最多.
新课讲解
练一练
1. 某校一名老师将在假期带领学生去北京旅游,有两种购票方式:甲旅行社说:“老师买全票,其他人全部半价优惠.”乙旅行社说:“所有人按全票价的 6 折优惠.”已知全票价 240 元.设学生有 x 名,就学生人数讨论哪家旅行社更优惠.
旅行社 老师购票费用 学生购票费用
甲 240元 120x元
乙 144元 144x元
解:①若 240+120x=144x+144,解得 x=4,
此时两家旅行社收费一样;
②若 240+120x>144x+144,解得 x<4,
此时乙旅行社更优惠;
③若 240+120x<144x+144,解得 x>4,
此时甲旅行社更优惠.
新课讲解
2. 某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.
(1)符合公司要求的购买方案有哪几种?请说明理由;
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金收入不低于1500元,那么应选择以上哪种购买方案?
解:(1)设轿车要购买x辆,那么面包车要购买(10-x)辆,
7x+4(10-x)≤55,解得 x≤5,
又x≥3,则x=3,4,5,
∴有三种方案:①轿车3辆,面包车7辆;
②轿车4辆,面包车6辆;
③轿车5辆,面包车5辆.
(2)方案一的日租金为3×200+7×110=1370;
方案二的日租金为:4×200+6×110=1460;
方案三的日租金为:5×200+5×110=1550.
为保证日租金不低于1500元,应选方案三.
练一练
新课讲解
练一练
3. 某市打市内电话的收费标准是:每次3min以内(含3min)0.22元,以后每分钟0.11元(不足1min 部分按1min计).小琴一天在家里给同学打了一次市内电话,所用电话费没超过0.5元. 她最多打了几分钟的电话?
通话时间/min 电话费/元
x ≤3
x > 3
0.22
0.22+0.11(x-3)
解:设小琴打了 x min 的电话,则有
0.22+(x-3)×0.11≤0.5,
解得 x ≤ .
由于电话计时按照分钟计时,x 应是整数,
所以 x 的最大值为 5.
答:小琴最多打了 5 min 的电话.
新课讲解
练一练
4. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(1)购买一件原价为450元的健身器材时,选择哪种活动更合算
解:(1)∵450×=360(元),
450-80=370(元),
∴选择活动一更合算.
新课讲解
练一练
4. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价;
解:(2)设一件这种健身器材的原价为x元.
若x<300,则活动一按原价打八折,活动二按原价,
此时付款金额不可能相等,
∴300≤x<500.
由题意得,x=x-80,
解得x=400,
∴一件这种健身器材的原价是400元.
新课讲解
练一练
4. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)
(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算 设一件这种健身器材的原价为a元,请直接写出a的取值范围.
解:(3)当300≤a<600时,
a-80<0.8a,解得a<400,
∴300≤a<400;
当600≤a<900时,
a-160<0.8a,解得a<800,
∴600≤a<800.
综上所述,300≤a<400或600≤a<800.
课堂小结
检验
设未知数
列不等式
数学问题
(一元一次不等式)
实际问题
(包含不等关系)
数学问题的解
(不等式的解集)
实际问题的答案
解不等式
当堂小练
1. 某商店 5 月 1 日举行促销优惠活动,当天到该商店购买商品有两种方案.方案一:用 168 元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的 8 折优惠.方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的 9.5 折优惠.已知小敏 5月 1 日前不是该商店的会员.请帮小敏算一算,采用哪种方案更合算?
解:设所购买的商品的价格为 x 元时,
若采用方案一更合算,则 0.95x>0.8x+168,解得 x>1 120.
若采用方案二更合算,则 0.95x<0.8x+168,解得 x<1 120.
若采用两种方案一样,则 0.95x=0.8x+168,解得 x=1 120.
所以小敏所购买商品的价格超过 1 120 元时,采用方案一更合算.
当堂小练
2. 某通信公司升级了两种通信业务:“A 业务”使用者先缴 15 元月租费,然后每通话 1 分钟付话费 0.2 元;“B 业务”不缴月租费,每通话 1 分钟付费 0.3 元,你觉得选哪种业务更优惠?
业务类别 通话时长/分钟 话费/元
A
B
x
15+0.2x
x
0.3x
解:①若“A 业务”更优惠,则 15+0.2x<0.3x,解得 x>150;
②若“B 业务”更优惠,则 15+0.2x>0.3x,解得 x<150;
③若两种业务优惠一样,则 15+0.2x=0.3x,解得 x=150.
所以,当通话时间超过 150 分钟时,选“A 业务”更优惠;
当通话时间不足 150 分钟时,选“B 业务”更优惠;
当通话时间为 150 分钟时,两种业务优惠一样.
当堂小练
3. 友谊商店 A 型号笔记本电脑的售价是 a 元/台.最近,该商店对 A 型号笔记本电脑举行促销活动,有两种优惠方案.方案一:每台按售价的九折销售.方案二:若购买不超过 5 台,每台按售价销售;若超过 5 台,超过的部分每台按售价的八折销售.某公司一次性从友谊商店购买 A 型号笔记本电脑 x 台.
(1)当 x=8 时,应选择哪种方案,该公司购买费用最少?最少费用是多少元?
解:(1)当 x=8 时,方案一费用:0.9a·8=7.2a(元),
方案二费用:5a+0.8a×(8-5)=7.4a(元).
∵a>0,
∴7.2a<7.4a.
∴方案一费用最少,最少费用为 7.2a 元.
当堂小练
3. 友谊商店 A 型号笔记本电脑的售价是 a 元/台.最近,该商店对 A 型号笔记本电脑举行促销活动,有两种优惠方案.方案一:每台按售价的九折销售.方案二:若购买不超过 5 台,每台按售价销售;若超过 5 台,超过的部分每台按售价的八折销售.某公司一次性从友谊商店购买 A 型号笔记本电脑 x 台.
(2)若该公司采用方案二购买更合算,求 x 的取值范围.
购买台数 方案一 方案二
x ≤ 5
x > 5
0.9ax
0.9ax
ax
5a+0.8a(x-5)
解:(2)若 x≤5,方案一每台按售价的九折销售,方案二每台按售价销售.
∴采用方案一购买合算.
若 x>5,方案一的费用:0.9ax 元.
方案二的费用:5a+0.8a(x-5)=0.8ax+a(元).
由题意得 0.9ax>0.8ax+a,解得 x>10.
∴若该公司采用方案二购买更合算,x 的取值范围是 x>10 且 x 为正整数.
当堂小练
4.“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买 A,B 两种型号的垃圾处理设备共 10 台(每种型号至少买 1 台).已知每台 A 型设备日处理能力为 12 吨,每台 B 型设备日处理能力为 15 吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买 A,B 两种设备的方案.
解:(1)设购买 A 型设备 x 台,则购买 B 型设备(10-x)台.
根据题意,得 12x+15(10-x)≥140,
解得 x≤3.
∵ x 为正整数,∴ x=1,2,3.
∴ 该景区有三种购买方案:
方案一:购买 A 型设备 1 台,B 型设备 9 台.
方案二:购买 A 型设备 2 台,B 型设备 8 台.
方案三:购买 A 型设备 3 台,B 型设备 7 台.
当堂小练
4.“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买 A,B 两种型号的垃圾处理设备共 10 台(每种型号至少买 1 台).已知每台 A 型设备日处理能力为 12 吨,每台 B 型设备日处理能力为 15 吨,购回的设备日处理能力不低于140吨.
(2) 已知每台 A 型设备价格为 3 万元,每台 B 型设备价格为 4.4 万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠,问:采用(1)设计的哪种方案,可以使购买费用最少,为什么?
方案一:购买 A 型设备 1 台,B 型设备 9 台.
方案二:购买 A 型设备 2 台,B 型设备 8 台.
方案三:购买 A 型设备 3 台,B 型设备 7 台.
解:(2)各方案购买费用分别为:
方案一:3×1+4.4×9=42.6(万元)>40万元,
实际付款:42.6×0.9=38.34(万元);
方案二:3×2+4.4×8=41.2(万元)>40万元,
实际付款:41.2×0.9=37.08(万元).
当堂小练
5. 某汽车租赁公司要购买轿车和面包车共10辆,其中轿车至少要购买3辆,轿车每辆7万元,面包车每辆4万元,公司可投入的购车款不超过55万元.
(1)符合公司要求的购买方案有哪几种?请说明理由;
(2)如果每辆轿车的日租金为200元,每辆面包车的日租金为110元,假设新购买的这10辆车每日都可租出,要使这10辆车的日租金收入不低于1500元,那么应选择以上哪种购买方案?
解:(1) 设轿车要购买x辆,那么面包车要购买(10-x)辆.
则有7x+4(10-x)≤55,解得 x≤5.
因为x≥3,所以整数x=3,4,5.
则有三种方案:①轿车3辆,面包车7辆;
②轿车4辆,面包车6辆;
③轿车5辆,面包车5辆.
(2) 方案一的日租金为3×200+7×110=1370(元);
方案二的日租金为4×200+6×110=1460(元);
方案三的日租金为5×200+5×110=1550(元).
为保证日租金不低于1500元,应选方案三.
对接中考
某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种 .
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满 300 元减 80 元 (如:所购商品原价为 300 元,可减 80 元,需付款 220 元;所购商品原价为 770 元,可减 160 元,需付款 610 元)
(1) 购买一件原价为 450 元的健身器材时,选择哪种活动更合算?请说明理由 .
解:(1) 购买一件原价为450元的健身器材时,选择活动一更合算.
理由:购买一件原价为450元的健身器材时,
活动一需付款为450×0.8=360(元),
活动二需付款为450-80=370(元).
∵360元<370元,
∴选择活动一更合算.
对接中考
某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种 .
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满 300 元减 80 元 (如:所购商品原价为 300 元,可减 80 元,需付款 220 元;所购商品原价为 770 元,可减 160 元,需付款 610 元)
(2) 购买一件原价在 500 元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价 .
解:(2) 设一件这种健身器材的原价是x元,
则0.8x=x-80,
解得x=400.
答:一件这种健身器材的原价是400元.
对接中考
(3) 购买一件原价在 900 元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算?设一件这种健身器材的原价为 a元,请求出 a 的取值范围 .
解:(3) 由题意,得活动一所需付款为0.8a元.
活动二:当0<a<300时,所需付款为a元;
当300≤a<600时,所需付款为(a-80)元;
当600≤a<900时,所需付款为(a-160)元.
①当0<a<300时,a>0.8a,此时无论a为何值,都是活动一更合算,不符合题意;
②当300≤a<600时,令a-80<0.8a,解得a<400,即当300≤a<400时,活动二更合算;
③当600≤a<900时,令a-160<0.8a,解得a<800,即当600≤a<800时,活动二更合算.
综上,当300≤a<400或600≤a<800时,活动二更合算.
某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种 .
活动一:所购商品按原价打八折;
活动二:所购商品按原价每满 300 元减 80 元 (如:所购商品原价为 300 元,可减 80 元,需付款 220 元;所购商品原价为 770 元,可减 160 元,需付款 610 元)
拓展与延伸
小明同学三次到某超市购买 A,B 两种商品,其中仅有一次是有折扣的.购买数量及消费金额如下表:
购买 A 商品数量/件 购买 B 商品数量/件 消费金额/元
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
类别
次数
(1)第_____次购买有折扣;
三
(2)求A,B 两种商品的原价;
解:(2)设 A 种商品的原价为 x 元/件,B 种商品的原价为 y 元/件,根据题意,得 解得
答: A 种商品的原价为 30 元/件,B 种商品的原价为 40 元/件.
拓展与延伸
小明同学三次到某超市购买 A,B 两种商品,其中仅有一次是有折扣的.购买数量及消费金额如下表:
购买 A 商品数量/件 购买 B 商品数量/件 消费金额/元
第一次 4 5 320
第二次 2 6 300
第三次 5 7 258
类别
次数
(3)若购买 A,B 两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买 A,B
两种商品共 10 件,在(3)中折扣数的前提下,消费金额不超过 200 元,求至少购买 A 种商品多少件.
A 种商品的原价为 30 元/件,B 种商品的原价为 40 元/件.
解:(3)设折扣数为 z.根据题意,得
,
解得 z = 6,故折扣数为 6.
(4)设购买 A 种商品 m 件,则购买 B 种商品(10-m)件.根据题意,
得 ,
解得 .
因为 m 为正整数,所以 m 的最小值为 7.
故至少购买 A 种商品 7 件.
同课章节目录
