11.3课时1 一元一次不等式组及其解法 课件(共39张PPT) 2024—2025学年人教版七年级数学下册
文档属性
| 名称 | 11.3课时1 一元一次不等式组及其解法 课件(共39张PPT) 2024—2025学年人教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 09:31:31 | ||
图片预览










文档简介
(共39张PPT)
第十一章 不等式与不等式组
11.3 一元一次不等式组
课时1 一元一次不等式组及其解法
目
录
1. 学习目标
4. 知识点1 一元一次不等式组的概念
6. 课堂小结
7. 当堂小练
CONTENTS
2. 知识回顾
5. 知识点2 一元一次不等式组的解集
9. 拓展与延伸
8. 对接中考
3. 新课导入
1. 了解一元一次不等式组及其解集的含义.
2. 掌握一元一次不等式组的解法,会用数轴确定一元一次不等式组的解集,体会数形结合思想.
学习目标
知识回顾
解一元一次不等式的步骤:
① 去分母:不等式两边同时乘各分母的最小公倍数.
② 去括号:先去小括号,再去中括号,最后去大括号(也可以先去大括号,再去中括号,最后去小括号).
③ 移项:把含未知数的项都移到不等号的一边,常数项都移到不等号的另一边.
④ 合并同类项:系数相加,字母及字母的指数不变.
⑤ 系数化为 1:不等式的两边都除以未知数的系数(或乘未知数的系数的倒数),将不等式化为 或 的形式.
新课导入
嗨,我听管理员说,这头大象的体重不足5吨呢!
你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
若设大象的体重为x吨,请用不等式的知识分别表示上面两位同学谈话的内容:
x≥3 ①
x<5 ②
新课讲解
知识点1 一元一次不等式组的概念
【思考】某工程队用每小时可抽30 t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1 200 t而不足1 500 t,那么将污水抽完所用时间的范围是什么
设用x h将污水抽完,则x同时满足不等式:
30x>1 200,
30x<1 500.
新课讲解
类似于方程组,把这两个含有同一个未知数的一元一次不等式合起来,组成一个一元一次不等式组,记作
一元一次不等式组必须同时满足三个条件:
① 每个不等式都是一元一次不等式;
② 含有同一个未知数;
③ 不等式的个数不少于2.
新课讲解
例
1. 下列不等式组中,是一元一次不等式组的是________ .(填序号)
① ② ③
④ ⑤ ⑥
③④⑤
含有两个未知数
未知数的最高次数是2
不是整式
方法点拨: 判断一元一次不等式组的步骤
新课讲解
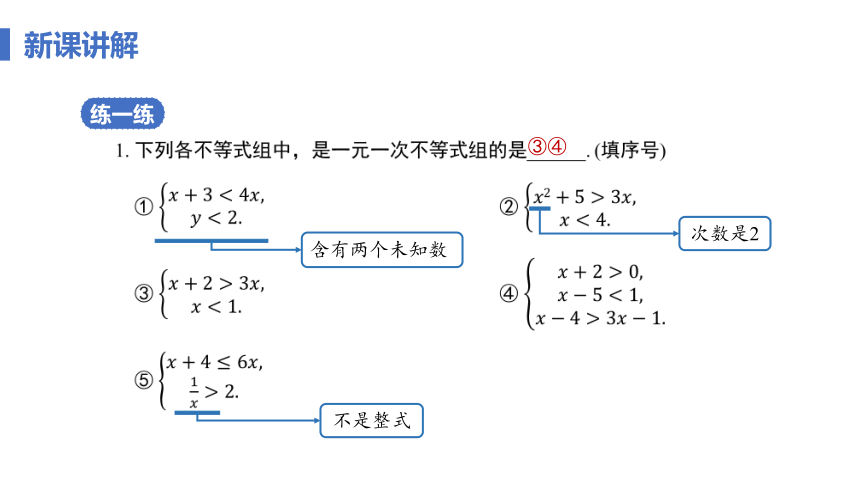
练一练
1. 下列各不等式组中,是一元一次不等式组的是______. (填序号)
① ②
③ ④
⑤
③④
含有两个未知数
次数是2
不是整式
新课讲解
练一练
2. 下列不等式组中,是一元一次不等式组的是( )
C
新课讲解
知识点2 一元一次不等式组的解集
【思考】怎样确定不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
一般地,几个不等式的解集的公共部分,叫作由它们所组成的不等式组的解集.
1. “公共部分”是指同时满足不等式组中每一个不等式的解集的部分.
2. 如果组成不等式组的各个不等式的解集没有公共部分,则这个不等式组无解.
注意
归纳
新课讲解
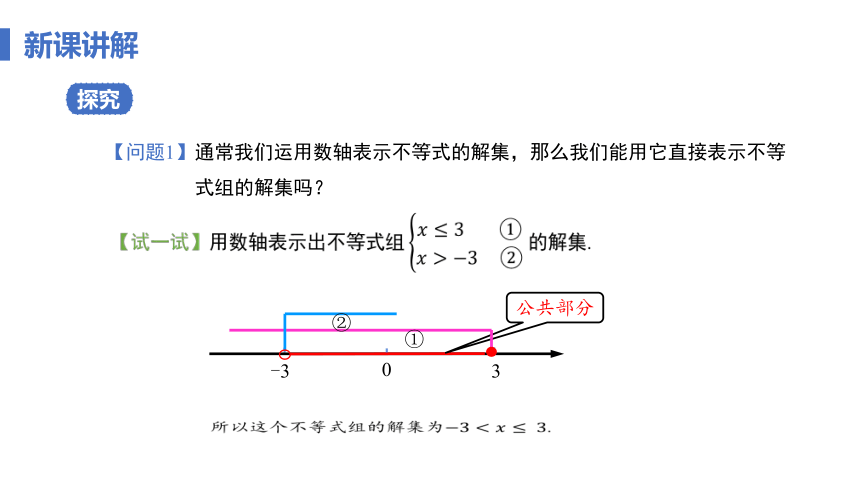
【问题1】通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
【试一试】用数轴表示出不等式组 的解集.
所以这个不等式组的解集为.
0
-3
3
公共部分
①
②
探究
新课讲解
【问题2】解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
xa无解
新课讲解
一元一次不等式组的解集有四种情况:
不等式组 (a>b)
各不等式的解集在数轴上的表示
不等式组的解集
巧记口诀
x>a
x无解
b同大取大
同小取小
大大小小无处找
大小小大中间找
b
a
b
a
b
a
b
a
新课讲解
例
解:(1)
(2)
(3)
(4)
2. 确定下列不等式组的解集.
(1) (2) (3) (4)
x>2
-3无解
x-3
新课讲解
【变式】关于x 的不等式组 的解集是x>-1, 则 m=______.
-3
方法点拨:根据不等式组解集的确定方法得出两个不等式解集端点值之间的数量关系.
解:∵ 2>-1,
∴ m+2>m-1.
∴关于x 的不等式组 的解集是x>m+2,
而题中给出其解集为x>-1,
∴ m+2=-1,∴ m=-3.
新课讲解
练一练
填表:
不等式组
不等式组的解集
x﹥-3
-5﹤x≤-3
x<-3
无解
新课讲解
确定一元一次不等式组的解集的两种方法:
1. 数轴法:即先把不等式组中每个不等式的解集在数轴上表示出来,找出它们的公共部分,就得到不等式组的解集,若无公共部分,则不等式组无解.
2. 口诀法:同大取大,同小取小,大小小大中间找,大大小小无处找.
当不等式组中含有“≥”或“≤”时,分界点处用实心原点,确定解集的方法不变.
注意
新课讲解
解:由不等式①,解得 x>40.
由不等式②,解得 x<50.
在同一数轴上表示不等式①②的解集,如下图所示.
50
30
0
10
20
40
60
从图中容易看出不等式①和②的解集的公共部分.
不等式组中x的取值范围是40【试一试】解上面问题中的不等式组
新课讲解
求不等式组的解集的过程叫做解不等式组.
解一元一次不等式组的一般步骤:
1. 分别求出不等式组中各个不等式的解集;
2. 利用数轴或“口诀”求出这些不等式解集的公共部分,即这个不等式组的解集;
3. 写出不等式组的解集.
新课讲解
例
解不等式②,得x <-3.
3. 解不等式组:(1)
解:(1)解不等式①,得x ≤ 3.
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是x<-3,所以这个不等式组的解集是 x<-3.
①
②
新课讲解
例
3. 解不等式组:(2)
①
②
解:(2)解不等式①,得x >-2.
解不等式②,得x >6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,
所以这个不等式组的解集是x>6.
新课讲解
【变式】若关于 x 的不等式组的解集为 x < m,则 m 的取值范围是( )
A. m < 3 B. m > 3 C. m ≤ 3 D. m ≥ 3
解:
解不等式①,得 x < m,
解不等式②,得 x < 3.
∵ 不等式组的解集为 x < m,
∴ m ≤ 3. 故选 C.
C
本题逆用口诀初步判断出 m 的取值范围后,需进一步考虑两个边界点相等时是否成立 .
注意
新课讲解
练一练
解下列不等式组:(1)
解:(1)解不等式①,得 x>2.
解不等式②,得 x>3.
把不等式①和②的解集在数轴上表示出来,如下图所示.
5
3
0
1
2
4
6
从图可以得不等式组的解集为 x>3.
所以这个不等式组的解集是 x>3.
新课讲解
练一练
解下列不等式组:(2)
解:(2)解不等式①,得 x≥8.
解不等式②,得 x<.
把不等式①和②的解集在数轴上表示出来,如图所示.
从图可以看到这两个不等式的解集没有公共部分,不等式组无解.
所以这个不等式组无解.
8
0
新课讲解
练一练
3. 若关于x 的不等式组 的解集为x > 3, 则a 的取值范围是( )
A. a > 3 B. a < 3 C. a ≥ 3 D. a ≤ 3
D
课堂小结
一元一次不等式组
不等式组中只含有同一个未知数
几个不等式的解集的公共部分
有两个或两个以上的一元一次不等式
由几个含有相同未知数的一元一次不等式组成
特征
解集
定义
分别求出不等式组中各个不等式的解集
确定解集的巧记口诀
解法
同大取大、同小取小、
大小小大中间找、大大小小无处找
将各个不等式的解集在数轴上表示出来
在数轴上找出各个不等式解集的公共部分
当堂小练
1. 不等式组 的解集是______.
x>1
1
0
2
x>1
x>
当堂小练
2. 解下列不等式组:
(1) (2)
解:(1)解不等式①,得 x>1.
解不等式②,得 x≤4.
将不等式①和②的解集在数轴上表示出来,
如图所示.
所以不等式组的解集为 14
2
-1
0
1
3
5
解:(2)解不等式①,得 x≥5.
解不等式②,得 x<4.
将不等式①和②的解集在数轴上表示出来,
如图所示.
所以不等式组无解.
5
4
2
-1
0
1
3
6
7
当堂小练
3. 小南解不等式组的过程如下:
解:由 ①, 得 x-3x >6, 第一步
∴ -2x > 6, 第二步
∴ x < -3. 第三步
由 ② , 得 2x-x+3 ≤ 1, 第四步
∴ x ≤ - 2. 第五步
∴原不等式组的解集为x < -3. 第六步
(1)老师批改时说小南的解题过程有错误,小南从第_____步开始出现错误 .
(2)请你写出正确的解答过程 .
四
解:正确的解答过程:
解:由①,得x-3x>6,
∴-2x>6,
∴x<-3.
由②,得2x-x-3≤2,
∴x≤5.
∴原不等式组的解集为x<-3.
当堂小练
4. 如果不等式组 有解,那么 m 的取值范围为( )
A. m > 3 B. m < 3
C. m ≥ 3 D. m ≤ 3
A
对接中考
1. 关于x 的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为__________.
0 ≤ x < 1
对接中考
2. 关于 x 的不等式组中,两个不等式的解集如图所示,则这个不等式组的解集是____________ .
x≥3
对接中考
3. 不等式组 的解集在数轴上表示为( )
B
对接中考
4. 解不等式组:
解:解不等式 ,得x < 7,
解不等式 < 2x,得 x >--1,
所以不等式组的解集为 -1 < x < 7.
对接中考
5. 若 2m-1, m,4-m 这三个实数在数轴上所对应的点从左到右依次排列,则 m 的取值范围是( )
A. m < 2 B. m < 1
C. 1 < m < 2 D. 1 < m <
B
对接中考
6. 若关于 x 的不等式组的解集为 x < 3,则 m 的取值范围是( )
A. m > 2 B. m ≥ 2 C. m < 2 D. m ≤ 2
B
解:解不等式 2x-1 < 5,得 x < 3.
∵ 关于 x 的不等式组的解集为 x < 3,
∴ m+1 ≥ 3,
∴ m ≥ 2.
拓展与延伸
1. 解不等式:.
解:原不等式可化为
解不等式①,得 .
解不等式②,得
所以不等式的解集为 .
还有其他解法吗?
解:对于 ,
去分母,得 6≤5-3x<12,
移项,得 6-5≤-3x<12-5,
合并同类项,得 1≤-3x<7,
系数.
对于只有中间部分含有未知数的连写形式的不等式也可以根据不等式的性质求解.
拓展与延伸
2. 解不等式组
解:解不等式①,得 x<1. 解不等式②,得 x≤-2.
解不等式③,得 x≥-4.
在同一数轴上表示不等式①②③的解集,如下图所示.
1
-1
-4
-3
-2
0
2
由图可知,该不等式组的解集为 -4≤x≤-2.
第十一章 不等式与不等式组
11.3 一元一次不等式组
课时1 一元一次不等式组及其解法
目
录
1. 学习目标
4. 知识点1 一元一次不等式组的概念
6. 课堂小结
7. 当堂小练
CONTENTS
2. 知识回顾
5. 知识点2 一元一次不等式组的解集
9. 拓展与延伸
8. 对接中考
3. 新课导入
1. 了解一元一次不等式组及其解集的含义.
2. 掌握一元一次不等式组的解法,会用数轴确定一元一次不等式组的解集,体会数形结合思想.
学习目标
知识回顾
解一元一次不等式的步骤:
① 去分母:不等式两边同时乘各分母的最小公倍数.
② 去括号:先去小括号,再去中括号,最后去大括号(也可以先去大括号,再去中括号,最后去小括号).
③ 移项:把含未知数的项都移到不等号的一边,常数项都移到不等号的另一边.
④ 合并同类项:系数相加,字母及字母的指数不变.
⑤ 系数化为 1:不等式的两边都除以未知数的系数(或乘未知数的系数的倒数),将不等式化为 或 的形式.
新课导入
嗨,我听管理员说,这头大象的体重不足5吨呢!
你能根据上图对话片断估计出这头大象的体重范围吗 请说说你的理由!
看,这头大象好大呀,体重肯定不少于3吨!
若设大象的体重为x吨,请用不等式的知识分别表示上面两位同学谈话的内容:
x≥3 ①
x<5 ②
新课讲解
知识点1 一元一次不等式组的概念
【思考】某工程队用每小时可抽30 t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1 200 t而不足1 500 t,那么将污水抽完所用时间的范围是什么
设用x h将污水抽完,则x同时满足不等式:
30x>1 200,
30x<1 500.
新课讲解
类似于方程组,把这两个含有同一个未知数的一元一次不等式合起来,组成一个一元一次不等式组,记作
一元一次不等式组必须同时满足三个条件:
① 每个不等式都是一元一次不等式;
② 含有同一个未知数;
③ 不等式的个数不少于2.
新课讲解
例
1. 下列不等式组中,是一元一次不等式组的是________ .(填序号)
① ② ③
④ ⑤ ⑥
③④⑤
含有两个未知数
未知数的最高次数是2
不是整式
方法点拨: 判断一元一次不等式组的步骤
新课讲解
练一练
1. 下列各不等式组中,是一元一次不等式组的是______. (填序号)
① ②
③ ④
⑤
③④
含有两个未知数
次数是2
不是整式
新课讲解
练一练
2. 下列不等式组中,是一元一次不等式组的是( )
C
新课讲解
知识点2 一元一次不等式组的解集
【思考】怎样确定不等式组中未知数的取值范围呢?
类比方程组的求解,不等式组中的各个不等式解集的公共部分,就是不等式组中的未知数的取值范围.
一般地,几个不等式的解集的公共部分,叫作由它们所组成的不等式组的解集.
1. “公共部分”是指同时满足不等式组中每一个不等式的解集的部分.
2. 如果组成不等式组的各个不等式的解集没有公共部分,则这个不等式组无解.
注意
归纳
新课讲解
【问题1】通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
【试一试】用数轴表示出不等式组 的解集.
所以这个不等式组的解集为.
0
-3
3
公共部分
①
②
探究
新课讲解
【问题2】解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
a b
a b
a b
a b
同大取大
同小取小
大小小大中间找
大大小小无处找
x>b
x
新课讲解
一元一次不等式组的解集有四种情况:
不等式组 (a>b)
各不等式的解集在数轴上的表示
不等式组的解集
巧记口诀
x>a
x
b
同小取小
大大小小无处找
大小小大中间找
b
a
b
a
b
a
b
a
新课讲解
例
解:(1)
(2)
(3)
(4)
2. 确定下列不等式组的解集.
(1) (2) (3) (4)
x>2
-3
x-3
新课讲解
【变式】关于x 的不等式组 的解集是x>-1, 则 m=______.
-3
方法点拨:根据不等式组解集的确定方法得出两个不等式解集端点值之间的数量关系.
解:∵ 2>-1,
∴ m+2>m-1.
∴关于x 的不等式组 的解集是x>m+2,
而题中给出其解集为x>-1,
∴ m+2=-1,∴ m=-3.
新课讲解
练一练
填表:
不等式组
不等式组的解集
x﹥-3
-5﹤x≤-3
x<-3
无解
新课讲解
确定一元一次不等式组的解集的两种方法:
1. 数轴法:即先把不等式组中每个不等式的解集在数轴上表示出来,找出它们的公共部分,就得到不等式组的解集,若无公共部分,则不等式组无解.
2. 口诀法:同大取大,同小取小,大小小大中间找,大大小小无处找.
当不等式组中含有“≥”或“≤”时,分界点处用实心原点,确定解集的方法不变.
注意
新课讲解
解:由不等式①,解得 x>40.
由不等式②,解得 x<50.
在同一数轴上表示不等式①②的解集,如下图所示.
50
30
0
10
20
40
60
从图中容易看出不等式①和②的解集的公共部分.
不等式组中x的取值范围是40
新课讲解
求不等式组的解集的过程叫做解不等式组.
解一元一次不等式组的一般步骤:
1. 分别求出不等式组中各个不等式的解集;
2. 利用数轴或“口诀”求出这些不等式解集的公共部分,即这个不等式组的解集;
3. 写出不等式组的解集.
新课讲解
例
解不等式②,得x <-3.
3. 解不等式组:(1)
解:(1)解不等式①,得x ≤ 3.
把不等式①、②的解集在数轴上表示出来,如图:
0
-3
3
由图可知,不等式①、②的解集的公共部分就是x<-3,所以这个不等式组的解集是 x<-3.
①
②
新课讲解
例
3. 解不等式组:(2)
①
②
解:(2)解不等式①,得x >-2.
解不等式②,得x >6.
把不等式①、②的解集在数轴上表示出来,如图:
0
-2
6
由图可知,不等式①、②的解集的公共部分就是x>6,
所以这个不等式组的解集是x>6.
新课讲解
【变式】若关于 x 的不等式组的解集为 x < m,则 m 的取值范围是( )
A. m < 3 B. m > 3 C. m ≤ 3 D. m ≥ 3
解:
解不等式①,得 x < m,
解不等式②,得 x < 3.
∵ 不等式组的解集为 x < m,
∴ m ≤ 3. 故选 C.
C
本题逆用口诀初步判断出 m 的取值范围后,需进一步考虑两个边界点相等时是否成立 .
注意
新课讲解
练一练
解下列不等式组:(1)
解:(1)解不等式①,得 x>2.
解不等式②,得 x>3.
把不等式①和②的解集在数轴上表示出来,如下图所示.
5
3
0
1
2
4
6
从图可以得不等式组的解集为 x>3.
所以这个不等式组的解集是 x>3.
新课讲解
练一练
解下列不等式组:(2)
解:(2)解不等式①,得 x≥8.
解不等式②,得 x<.
把不等式①和②的解集在数轴上表示出来,如图所示.
从图可以看到这两个不等式的解集没有公共部分,不等式组无解.
所以这个不等式组无解.
8
0
新课讲解
练一练
3. 若关于x 的不等式组 的解集为x > 3, 则a 的取值范围是( )
A. a > 3 B. a < 3 C. a ≥ 3 D. a ≤ 3
D
课堂小结
一元一次不等式组
不等式组中只含有同一个未知数
几个不等式的解集的公共部分
有两个或两个以上的一元一次不等式
由几个含有相同未知数的一元一次不等式组成
特征
解集
定义
分别求出不等式组中各个不等式的解集
确定解集的巧记口诀
解法
同大取大、同小取小、
大小小大中间找、大大小小无处找
将各个不等式的解集在数轴上表示出来
在数轴上找出各个不等式解集的公共部分
当堂小练
1. 不等式组 的解集是______.
x>1
1
0
2
x>1
x>
当堂小练
2. 解下列不等式组:
(1) (2)
解:(1)解不等式①,得 x>1.
解不等式②,得 x≤4.
将不等式①和②的解集在数轴上表示出来,
如图所示.
所以不等式组的解集为 1
2
-1
0
1
3
5
解:(2)解不等式①,得 x≥5.
解不等式②,得 x<4.
将不等式①和②的解集在数轴上表示出来,
如图所示.
所以不等式组无解.
5
4
2
-1
0
1
3
6
7
当堂小练
3. 小南解不等式组的过程如下:
解:由 ①, 得 x-3x >6, 第一步
∴ -2x > 6, 第二步
∴ x < -3. 第三步
由 ② , 得 2x-x+3 ≤ 1, 第四步
∴ x ≤ - 2. 第五步
∴原不等式组的解集为x < -3. 第六步
(1)老师批改时说小南的解题过程有错误,小南从第_____步开始出现错误 .
(2)请你写出正确的解答过程 .
四
解:正确的解答过程:
解:由①,得x-3x>6,
∴-2x>6,
∴x<-3.
由②,得2x-x-3≤2,
∴x≤5.
∴原不等式组的解集为x<-3.
当堂小练
4. 如果不等式组 有解,那么 m 的取值范围为( )
A. m > 3 B. m < 3
C. m ≥ 3 D. m ≤ 3
A
对接中考
1. 关于x 的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为__________.
0 ≤ x < 1
对接中考
2. 关于 x 的不等式组中,两个不等式的解集如图所示,则这个不等式组的解集是____________ .
x≥3
对接中考
3. 不等式组 的解集在数轴上表示为( )
B
对接中考
4. 解不等式组:
解:解不等式 ,得x < 7,
解不等式 < 2x,得 x >--1,
所以不等式组的解集为 -1 < x < 7.
对接中考
5. 若 2m-1, m,4-m 这三个实数在数轴上所对应的点从左到右依次排列,则 m 的取值范围是( )
A. m < 2 B. m < 1
C. 1 < m < 2 D. 1 < m <
B
对接中考
6. 若关于 x 的不等式组的解集为 x < 3,则 m 的取值范围是( )
A. m > 2 B. m ≥ 2 C. m < 2 D. m ≤ 2
B
解:解不等式 2x-1 < 5,得 x < 3.
∵ 关于 x 的不等式组的解集为 x < 3,
∴ m+1 ≥ 3,
∴ m ≥ 2.
拓展与延伸
1. 解不等式:.
解:原不等式可化为
解不等式①,得 .
解不等式②,得
所以不等式的解集为 .
还有其他解法吗?
解:对于 ,
去分母,得 6≤5-3x<12,
移项,得 6-5≤-3x<12-5,
合并同类项,得 1≤-3x<7,
系数.
对于只有中间部分含有未知数的连写形式的不等式也可以根据不等式的性质求解.
拓展与延伸
2. 解不等式组
解:解不等式①,得 x<1. 解不等式②,得 x≤-2.
解不等式③,得 x≥-4.
在同一数轴上表示不等式①②③的解集,如下图所示.
1
-1
-4
-3
-2
0
2
由图可知,该不等式组的解集为 -4≤x≤-2.
同课章节目录
