2.2利用同位角判定两条直线平行第1课时 课件(共35张PPT)
文档属性
| 名称 | 2.2利用同位角判定两条直线平行第1课时 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-31 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
北师大版数学七年级下册
第二章 相交线与平行线
汇报人:孙老师
汇报班级:X级X班
2.2 第1课时 利用同位角判定两条直线平行
2.2 探索直线平行的条件
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解并掌握同位角的概念,能够识别同位角.
2.能够运用同位角相等判定两直线平行.
3.理解并掌握平行公理及其推论,能够运用其解决实际问题.
第贰章节
新课导入
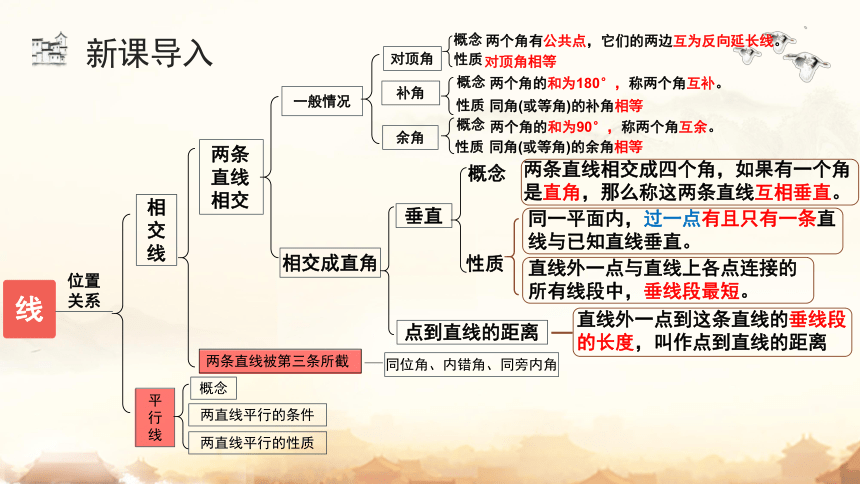
新课导入
线
平
行
线
相
交
线
两条
直线
相交
一般情况
补角
对顶角
相交成直角
垂直
位置
关系
余角
点到直线的距离
两条直线被第三条所截
同位角、内错角、同旁内角
概念
两直线平行的条件
两直线平行的性质
概念
性质
概念
性质
概念
性质
两个角有公共点,它们的两边互为反向延长线。
对顶角相等
两个角的和为180°,称两个角互补。
同角(或等角)的补角相等
两个角的和为90°,称两个角互余。
同角(或等角)的余角相等
概念
性质
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直。
同一平面内,过一点有且只有一条直线与已知直线垂直。
直线外一点与直线上各点连接的所有线段中,垂线段最短。
直线外一点到这条直线的垂线段的长度,叫作点到直线的距离
(1)如图2-13,装修工人要在墙上钉木条,如果木条b与竖直木条垂直, 那么木条a 与竖直木条所成的角为多少度时,才能使木条a与木条b平行?
图2-13
(2)如图2-14,如果木条b不与竖直木条垂直呢?
图2-14
b
a
创设情境,新课导入
在日常生活中, 人们经常用到平行线。
第叁章节
新知探究
新知探究
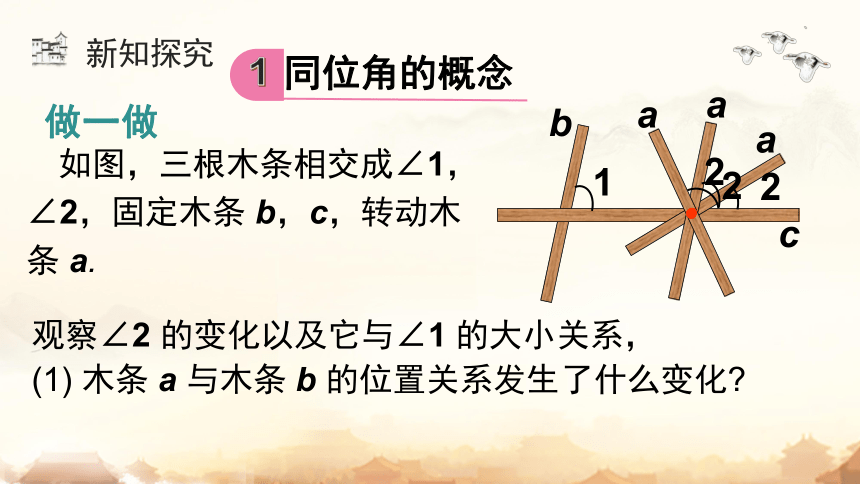
同位角的概念
如图,三根木条相交成∠1,∠2,固定木条 b,c,转动木条 a.
做一做
1
c
b
a
2
a
2
观察∠2 的变化以及它与∠1 的大小关系,
(1) 木条 a 与木条 b 的位置关系发生了什么变化
a
2
1
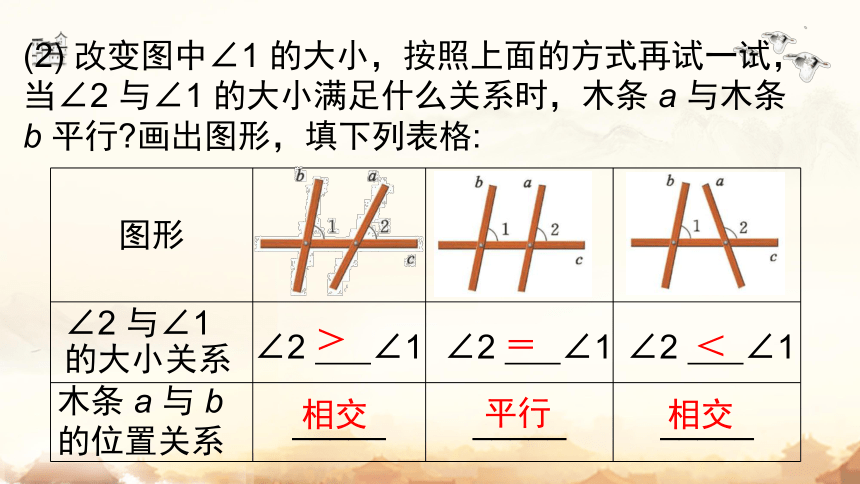
(2) 改变图中∠1 的大小,按照上面的方式再试一试,当∠2 与∠1 的大小满足什么关系时,木条 a 与木条 b 平行 画出图形,填下列表格:
图形
_____ _____ _____
∠2 与∠1
的大小关系
木条 a 与 b
的位置关系
∠2 ∠1
∠2 ∠1
∠2 ∠1
>
相交
=
平行
<
相交
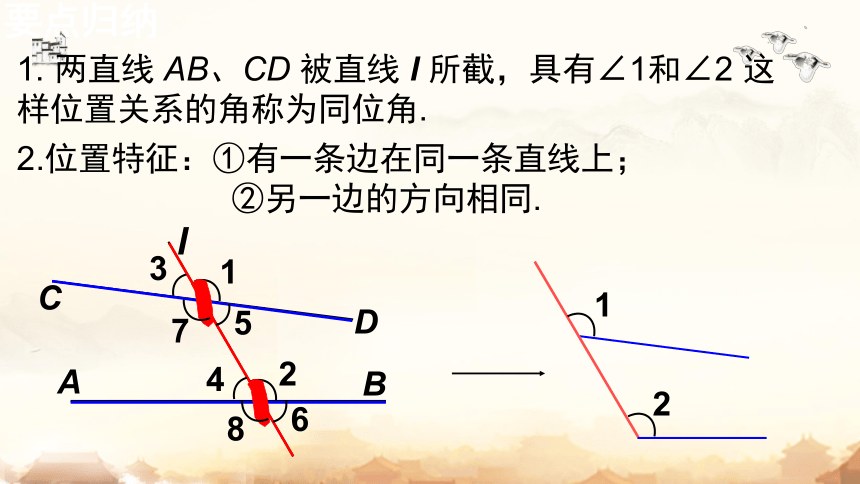
1. 两直线 AB、CD 被直线 l 所截,具有∠1和∠2 这样位置关系的角称为同位角.
A
C
B
D
l
1
2
6
8
4
7
3
1
2
5
要点归纳
2.位置特征:①有一条边在同一条直线上;
②另一边的方向相同.
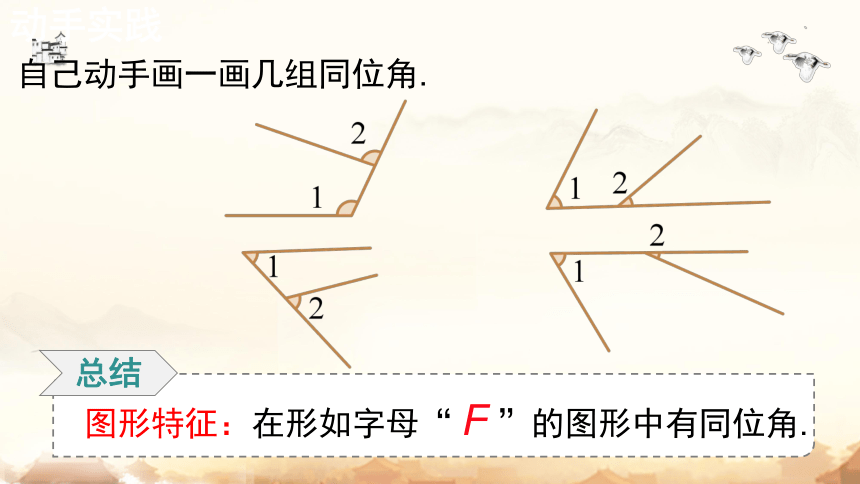
总结
图形特征:在形如字母“ F ”的图形中有同位角.
自己动手画一画几组同位角.
动手实践
想一想
活动1:你能借助三角尺画平行线吗
点击视频观看→
利用同位角判定两条直线平行
2
用三角尺和直尺画平行线的方法.
(1)放
(2)靠
(3)推
(4)画
●
b
A
2
1
a
B
(1) 画图过程中,三角尺起着什么作用?
(2) 直线 a,b 位置关系如何?
思考
a∥b
保持∠1跟∠2 相等
合作探究
简称为:同位角相等,两直线平行.
两直线平行,用“∥”表示.
如:a∥b .
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
因为∠1=∠2 ,
所以 a∥b.
判定方法1:
知识要点
同位角相等,两直线平行.
例1 如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
典例精析
例2 如图,直线 AB,CD 分别与 EF 相交于点 G,H,
已知∠1 = 70°,∠2 = 70°,试说明:AB∥CD.
解析:要说明AB∥CD,可转化为说明∠1 与其同位角相等,这由∠2 的对顶角容易得出.
解:因为∠2 = ∠EHD (对顶角相等),
∠2 = 70°,所以∠EHD = 70°.
因为 ∠1 = 70°,
所以∠EHD=∠1.
所以 AB∥CD (同位角相等,两直线平行).
典例精析
平行于同一条直线的两条直线平行
(1) 你能过直线 AB 外一点 P 画直线 AB 的平行线吗?能画出几条?
活动2:画一画
·
A
·
B
·
P
a
1 条
3
·
A
·
B
(2) 分别过点 C,D 画直线 AB 的平行线 EF,GH ,那么直线 EF,GH 平行吗?
·
·
E
D
平行
C
F
G
H
几何语言表达:
平行线的传递性:
平行于同一条直线的两条直线平行.
如果 b∥a,c∥a,
那么 b∥c.
经过直线外一点,有且只有一条直线与已知直线平行.
a
b
c
知识要点
例3 三条直线 a,b,c,若 a∥c,b∥c,
则 a 与 b 的位置关系是( )
A. a⊥b B. a∥b
C. a⊥b 或 a∥b D. 无法确定
B
典例精析
第肆章节
随堂练习
随堂练习
1.如图,直线a,b被直线c所截,下列各组角是同位角的是( ).
A.∠1与∠2
B.∠1与∠3
C.∠2与∠3
D.∠3与∠4
B
2.如图,下列四个条件:①∠1=∠5;②∠1=∠3;③∠4=∠8;
④∠2=∠6.其中能判定a∥b的条件共有( ).
A.1个
B.2个
C.3个
D.4个
C
3.如图,能判定EB∥AC的条件是( ).
A.∠C=∠ABE B.∠A=∠EBD
C.∠C=∠EBD D.∠A=∠ABC
C
(第4题)
4.如图,已知∠B=60°,当∠1= °时,DE∥BC,理由是
.
同位角相等,两直线平行
60
5.如图,已知直线AB,CD被直线EF所截,∠1=120°,∠2=60°,那么直线AB平行于CD吗?为什么?
解:AB∥CD.
理由如下:∵∠1+∠3=180°,∠1=120°,
∴∠3=60°.
∵∠2=60°,∴∠2=∠3,
∴AB∥CD(同位角相等,两直线平行).
6.如图,AB∥CD,∠1=∠2,可以判断哪些直线平行?并说明理由.
AB∥EF,CD∥EF.(同位角相等,两直线平行)
7.如图,已知∠ABC=∠ADE,若DF平分∠ADE,BG平分∠ABC,则DF与BG平行吗?为什么?
解:DF∥BG.
理由如下:∵DF平分∠ADE,BG平分∠ABC,
∴∠ADF=∠ADE,∠DBG=∠ABC.
∵∠ABC=∠ADE,
∴∠ADF=∠DBG,
∴DF∥BG(同位角相等,两直线平行).
8.如图,把一根筷子的一端放在水里,另一端露出水面,筷子变弯了.它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出∠2的同位角有哪些;
(2)若∠1=115°,测得∠BOM=145°,从水面
上看斜插入水中的筷子,水下部分向上折弯的
∠MOE的度数是多少?
解:(1)与∠2是同位角的有∠D,∠FOB.
(2)∵∠1+∠2=180°,∴∠2=180°-∠1=65°.
∵AB∥CD,∴∠BOF=∠2=65°.
又∠BOF+∠BOE=180°,
∴∠BOE=180°-∠BOF=115°.
∵∠BOM=145°,
∴∠MOE=∠BOM-∠BOE=145°-115°=30°.
第伍章节
课堂小结
课堂小结
探索直线平行的条件
过直线外一点有且只有一条直线与这条直线平行
平行于同一条直线的两条直线平行
同位角相等,两直线平行
过已知直线外一点画这条直线的平行线的画法:一放、二靠、三移、四画
位置特征:①在两条被截直线的同一方;②在截线的同侧.
两条直线平行的条件1
平行线的画法
(用三角尺和直尺)
同位角
平行线的基本
事实及其推论
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级下册
第二章 相交线与平行线
汇报人:孙老师
汇报班级:X级X班
2.2 第1课时 利用同位角判定两条直线平行
2.2 探索直线平行的条件
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解并掌握同位角的概念,能够识别同位角.
2.能够运用同位角相等判定两直线平行.
3.理解并掌握平行公理及其推论,能够运用其解决实际问题.
第贰章节
新课导入
新课导入
线
平
行
线
相
交
线
两条
直线
相交
一般情况
补角
对顶角
相交成直角
垂直
位置
关系
余角
点到直线的距离
两条直线被第三条所截
同位角、内错角、同旁内角
概念
两直线平行的条件
两直线平行的性质
概念
性质
概念
性质
概念
性质
两个角有公共点,它们的两边互为反向延长线。
对顶角相等
两个角的和为180°,称两个角互补。
同角(或等角)的补角相等
两个角的和为90°,称两个角互余。
同角(或等角)的余角相等
概念
性质
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直。
同一平面内,过一点有且只有一条直线与已知直线垂直。
直线外一点与直线上各点连接的所有线段中,垂线段最短。
直线外一点到这条直线的垂线段的长度,叫作点到直线的距离
(1)如图2-13,装修工人要在墙上钉木条,如果木条b与竖直木条垂直, 那么木条a 与竖直木条所成的角为多少度时,才能使木条a与木条b平行?
图2-13
(2)如图2-14,如果木条b不与竖直木条垂直呢?
图2-14
b
a
创设情境,新课导入
在日常生活中, 人们经常用到平行线。
第叁章节
新知探究
新知探究
同位角的概念
如图,三根木条相交成∠1,∠2,固定木条 b,c,转动木条 a.
做一做
1
c
b
a
2
a
2
观察∠2 的变化以及它与∠1 的大小关系,
(1) 木条 a 与木条 b 的位置关系发生了什么变化
a
2
1
(2) 改变图中∠1 的大小,按照上面的方式再试一试,当∠2 与∠1 的大小满足什么关系时,木条 a 与木条 b 平行 画出图形,填下列表格:
图形
_____ _____ _____
∠2 与∠1
的大小关系
木条 a 与 b
的位置关系
∠2 ∠1
∠2 ∠1
∠2 ∠1
>
相交
=
平行
<
相交
1. 两直线 AB、CD 被直线 l 所截,具有∠1和∠2 这样位置关系的角称为同位角.
A
C
B
D
l
1
2
6
8
4
7
3
1
2
5
要点归纳
2.位置特征:①有一条边在同一条直线上;
②另一边的方向相同.
总结
图形特征:在形如字母“ F ”的图形中有同位角.
自己动手画一画几组同位角.
动手实践
想一想
活动1:你能借助三角尺画平行线吗
点击视频观看→
利用同位角判定两条直线平行
2
用三角尺和直尺画平行线的方法.
(1)放
(2)靠
(3)推
(4)画
●
b
A
2
1
a
B
(1) 画图过程中,三角尺起着什么作用?
(2) 直线 a,b 位置关系如何?
思考
a∥b
保持∠1跟∠2 相等
合作探究
简称为:同位角相等,两直线平行.
两直线平行,用“∥”表示.
如:a∥b .
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
因为∠1=∠2 ,
所以 a∥b.
判定方法1:
知识要点
同位角相等,两直线平行.
例1 如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
典例精析
例2 如图,直线 AB,CD 分别与 EF 相交于点 G,H,
已知∠1 = 70°,∠2 = 70°,试说明:AB∥CD.
解析:要说明AB∥CD,可转化为说明∠1 与其同位角相等,这由∠2 的对顶角容易得出.
解:因为∠2 = ∠EHD (对顶角相等),
∠2 = 70°,所以∠EHD = 70°.
因为 ∠1 = 70°,
所以∠EHD=∠1.
所以 AB∥CD (同位角相等,两直线平行).
典例精析
平行于同一条直线的两条直线平行
(1) 你能过直线 AB 外一点 P 画直线 AB 的平行线吗?能画出几条?
活动2:画一画
·
A
·
B
·
P
a
1 条
3
·
A
·
B
(2) 分别过点 C,D 画直线 AB 的平行线 EF,GH ,那么直线 EF,GH 平行吗?
·
·
E
D
平行
C
F
G
H
几何语言表达:
平行线的传递性:
平行于同一条直线的两条直线平行.
如果 b∥a,c∥a,
那么 b∥c.
经过直线外一点,有且只有一条直线与已知直线平行.
a
b
c
知识要点
例3 三条直线 a,b,c,若 a∥c,b∥c,
则 a 与 b 的位置关系是( )
A. a⊥b B. a∥b
C. a⊥b 或 a∥b D. 无法确定
B
典例精析
第肆章节
随堂练习
随堂练习
1.如图,直线a,b被直线c所截,下列各组角是同位角的是( ).
A.∠1与∠2
B.∠1与∠3
C.∠2与∠3
D.∠3与∠4
B
2.如图,下列四个条件:①∠1=∠5;②∠1=∠3;③∠4=∠8;
④∠2=∠6.其中能判定a∥b的条件共有( ).
A.1个
B.2个
C.3个
D.4个
C
3.如图,能判定EB∥AC的条件是( ).
A.∠C=∠ABE B.∠A=∠EBD
C.∠C=∠EBD D.∠A=∠ABC
C
(第4题)
4.如图,已知∠B=60°,当∠1= °时,DE∥BC,理由是
.
同位角相等,两直线平行
60
5.如图,已知直线AB,CD被直线EF所截,∠1=120°,∠2=60°,那么直线AB平行于CD吗?为什么?
解:AB∥CD.
理由如下:∵∠1+∠3=180°,∠1=120°,
∴∠3=60°.
∵∠2=60°,∴∠2=∠3,
∴AB∥CD(同位角相等,两直线平行).
6.如图,AB∥CD,∠1=∠2,可以判断哪些直线平行?并说明理由.
AB∥EF,CD∥EF.(同位角相等,两直线平行)
7.如图,已知∠ABC=∠ADE,若DF平分∠ADE,BG平分∠ABC,则DF与BG平行吗?为什么?
解:DF∥BG.
理由如下:∵DF平分∠ADE,BG平分∠ABC,
∴∠ADF=∠ADE,∠DBG=∠ABC.
∵∠ABC=∠ADE,
∴∠ADF=∠DBG,
∴DF∥BG(同位角相等,两直线平行).
8.如图,把一根筷子的一端放在水里,另一端露出水面,筷子变弯了.它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出∠2的同位角有哪些;
(2)若∠1=115°,测得∠BOM=145°,从水面
上看斜插入水中的筷子,水下部分向上折弯的
∠MOE的度数是多少?
解:(1)与∠2是同位角的有∠D,∠FOB.
(2)∵∠1+∠2=180°,∴∠2=180°-∠1=65°.
∵AB∥CD,∴∠BOF=∠2=65°.
又∠BOF+∠BOE=180°,
∴∠BOE=180°-∠BOF=115°.
∵∠BOM=145°,
∴∠MOE=∠BOM-∠BOE=145°-115°=30°.
第伍章节
课堂小结
课堂小结
探索直线平行的条件
过直线外一点有且只有一条直线与这条直线平行
平行于同一条直线的两条直线平行
同位角相等,两直线平行
过已知直线外一点画这条直线的平行线的画法:一放、二靠、三移、四画
位置特征:①在两条被截直线的同一方;②在截线的同侧.
两条直线平行的条件1
平行线的画法
(用三角尺和直尺)
同位角
平行线的基本
事实及其推论
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
