2024-2025学年人教版七年级下期末专题复习专题一相交线与平行线(含解析)
文档属性
| 名称 | 2024-2025学年人教版七年级下期末专题复习专题一相交线与平行线(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 13.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年人教版七年级下期末专题复习
专题一 相交线与平行线
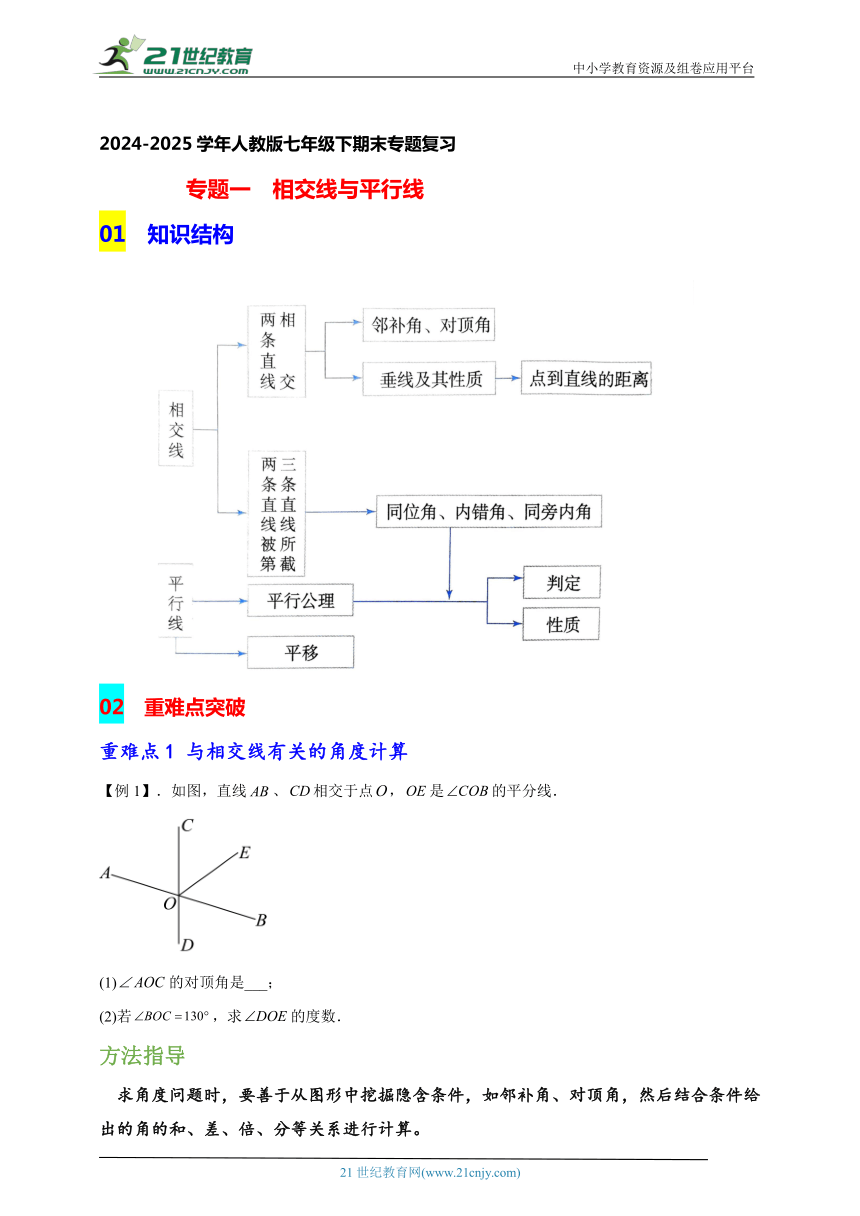
01 知识结构
02 重难点突破
重难点1 与相交线有关的角度计算
【例1】.如图,直线、相交于点,是的平分线.
(1)的对顶角是___;
(2)若,求的度数.
方法指导
求角度问题时,要善于从图形中挖掘隐含条件,如邻补角、对顶角,然后结合条件给出的角的和、差、倍、分等关系进行计算。
变式训练1
1.如图,把一张长方形纸片的一角任意折向长方形内,使点B落在点的位置,折痕为,再把折叠,使点C、D分别落在点的位置,折痕为,与在同一条直线上.
(1)分别直接写出与,与之间所满足的数量关系;
(2)与之间什么关系?
(3)是什么角?
2.如图,已知点为直线上一点,,,平分,.
(1)求的度数;
(2)试说明:平分;
(3)若改变的大小,其余条件不变,设,(2)中的结论是否依然成立?若成立,请说明理由;若不成立,请用表示.
3.如图,∠AOC=100°,∠BOE=80°,D,O,E三点在同一条直线上,∠AOD=37°,
(1)求∠COE的度数;
(2)请写出一组相等的角,并说明理由.(平角相等除外)
(3)若OM平分∠BOE,求∠COM的度数.
4.如图,直线相交于点D,.
(1)若,求证:;
(2)在(1)的条件下,若,求的度数.
5.如图,直线相交于点O,平分平分, ,H是射线上的一点.
(1)过点H画直线的垂线,垂足为F;
(2)在(1)问的基础上求的度数(用含的式子表示);
(3)探究的大小和的大小是否有关?若有,请写出的大小和的大小关系;若没有,请说明理由.
重难点2 平行线的性质和判定
【例2】.近年来,我国一直提倡“绿色环保、低碳生活”,健康骑行成为一种时尚、环保的运动,深受人们的青睐.小郑的自行车示意图如图所示,其中,,.
(1)求的度数;
(2)试判断与的位置关系,并说明理由.
方法指导
这类题目一般会综合考查平行线的性质与判定,即“由形推角”或“由角判形”,所以解决此类问题时要明确条件或结论,不要产生混淆,性质是由“形”得到“角”,判定是由“角”得到“形”。
变式训练2
1.综合与实践
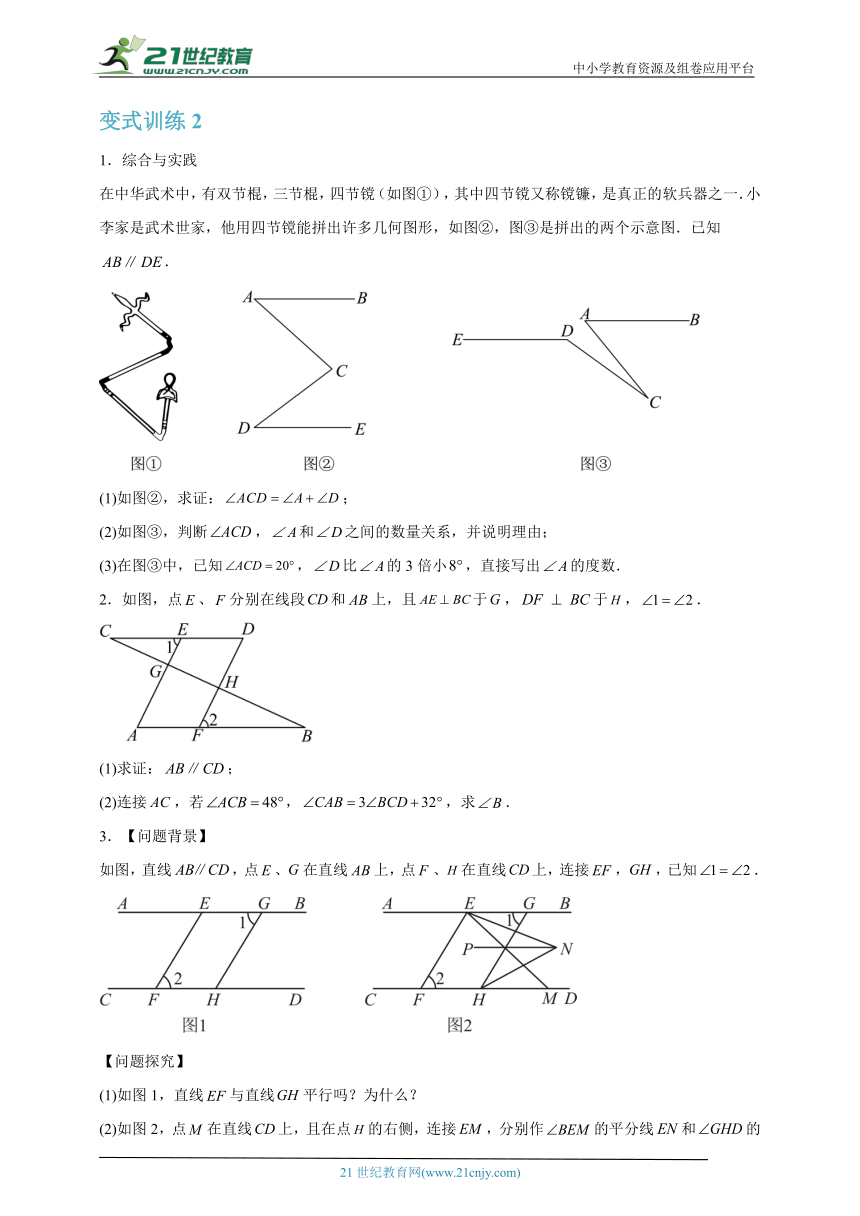
在中华武术中,有双节棍,三节棍,四节镋(如图①),其中四节镋又称镋镰,是真正的软兵器之一.小李家是武术世家,他用四节镋能拼出许多几何图形,如图②,图③是拼出的两个示意图.已知.
(1)如图②,求证:;
(2)如图③,判断,和之间的数量关系,并说明理由;
(3)在图③中,已知,比的3倍小,直接写出的度数.
2.如图,点、分别在线段和上,且于,于,.
(1)求证:;
(2)连接,若,,求.
3.【问题背景】
如图,直线,点、在直线上,点、在直线上,连接,,已知.
【问题探究】
(1)如图1,直线与直线平行吗?为什么?
(2)如图2,点在直线上,且在点的右侧,连接,分别作的平分线和的平分线相交于点,过点作,试探究与之间的数量关系,并说明理由.
4.如图所示,已知于,,,;求证:
5.如图,点D、E、H分别在线段上,连接,过点C画交的延长线于点F,且满足,若,,求证.
重难点3 命题
【例3】.黑板上写有3个命题:
①若,则;
②若是有理数,则;
③若与都是锐角,则这两个角的和是钝角.
(1)上述命题是真命题的是______(填序号),该命题的条件是______,结论是______;
(2)对于上述命题中的假命题,请各写出一个反例.
方法指导
要说明一个命题的正确性,可根据已有知识进行推理,论证,而判断一个命题是假命题,只需举一个反例即可。
变式训练3
1.判断下列语句是否是命题,如果是,改写成“如果……那么……”的形式,并分别指出它们的题设和结论,同时判断其真假
(1)作直线AB的垂线.
(2)相等的角是对顶角.
(3)你喜欢数学吗?
(4)OC平分∠AOB.
(5)两直线平行,内错角相等.
(6)同角的补角相等.
2.如图,有下列三个条件:①DE//BC;②;③.
(1)若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题?请你都写出来;
(2)你所写出的命题都是真命题吗?若是,请你就其中的一个真命题给出推理过程;若不是,请你对其中的假命题举出一个反例(温馨提示:)
3.如图,已知直线,给出下列信息:
①;②平分;③.
(1)请在上述3条信息中选择其中两条作为条件,其余的一条信息作为结论组成一个真命题,你选择的条件是 ,结论是 (只要填写序号),并说明理由.
(2)在(1)的条件下,若比的倍少度,求的度数.
4.如图,点D,E,F分别是三角形的边,,上的点,给定以下三个条件:①;②;③.请从这三个条件中选择两个作为条件(放在已知处),另一个作为结论(放在证明处)组成一个真命题,并进行证明.
已知:________,________.
求证:________.
证明:
5.如图,点在上,直线交于点.请从①,②平分,③中任选两个作为条件,余下一个作为结论,构造一个真命题,并求证.
已知:______,求证:______.(只须填写序号)
证明:
重难点4 平移的性质及应用
【例4】.如图,一个四边形经过平移后得到四边形.
(1)线段的对应线段是___________;
(2)的对应角是___________;
(3)线段和线段有何关系?
方法指导
解决平移有关问题,只需熟练掌握平移的性质即可,即(1)平移不改变图形的形状和大小;(2)经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
变式训练4
1.如图所示,是由沿箭头方向平移得到的.
(1)若,求的度数;
(2)若,求,的长.
2.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥,桥宽忽略不计.
(1)若荷塘的长为90米,宽为50米,则小桥总长为 米;
(2)若荷塘周长为米,则小桥总长为 米.
3.如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
4.如图所示,某商场重新装修后,准备在门前台阶上铺设地毯,已知这种地毯的批发价为每平方米50元,其台阶的尺寸如图所示,则购买地毯至少需要元.
5.已知的顶点A平移到顶点D,请用两种不同的方法,在图中作出平移后的图形.
重难点5 思想方法
构造法
【例5-1】.【阅读理解】两条平行线间的拐点问题经常可以通过作一条直线的平行线进行转化.例如:如图,直线,求证:
(1)阅读下面的解答过程,并填上适当的理由
解:过点作直线,
已知,,
【方法运用】
(2)如图2,直线,若,,求的度数.
方法指导
有“拐点”时,常常过拐点作平行线,构造平行线的性质解决问题。
变式训练5-1
1.已知直线,点,在直线上,点,在直线上,的平分线与的平分线交于点,,.
(1)如图1,点在点的左边,点在点的右边,求的度数;
(2)在(1)的条件下,求的度数;(用含的式子表示)
(3)将图1中的线段向左平移,使点落在点的左边,其他条件不变,在图2中画出符合题意的图形,并求出的值.
2.如图,若,,,求的度数.
3. 综合与实践:
【问题初探】
()数学活动课上,王老师给出如下问题:如图①,,点在之间且点在点右侧,求证:(提示:过点作);
【类比探究】
()小明对王老师给出的问题进行改编:如图②,,点在之间且点在点左侧,猜想,,之间的数量关系: ,并加以证明;
【学以致用】
()如图③是超市的购物车,图④是其侧面示意图,已知,,测量得知,,直接写出的度数 .
转化思想
【例5-2】.与是两个完全相同的直角三角形.将沿点B到点C的方向从的位置平移到如图所示的位置.若,图中阴影部分的面积为84,,求平移的距离.
方法指导
根据平移不改变图形的大小的性质,将零散的图形转化成规则图形面积。
变式训练5-2
1.如图,在三角形中,,,.将三角形沿向右平移,得到三角形,与交于点,连接.
(1)分别求和的度数;
(2)若,,求图中阴影部分的面积.
2.如图,将直角三角形沿方向平移线段的长度得到直角三角形,已知,,求图中四边形的面积.
3.如图,在三角形中,,,.将三角形沿向右平移,得到三角形,与交于点,连接.
(1)________,________;
(2)若,,求图中阴影部分的面积;
(3)已知点在三角形的内部,点经过相同平移后的对应点为,连接.若三角形的周长为,四边形的周长为,请直接写出的长度.
2024-2025学年人教版七年级下期末专题复习
专题一 相交线与平行线(解析版)
01 知识结构
02 重难点突破
重难点1 与相交线有关的角度计算
【例1】.如图,直线、相交于点,是的平分线.
(1)的对顶角是___;
(2)若,求的度数.
【答案】(1)
(2)
【分析】本题考查了几何图形中的角度计算、角平分线的定义、对顶角的定义、邻补角的性质,熟练掌握相关知识点是解题的关键.
(1)根据对顶角的定义即可解答;
(2)根据角平分线的定义得到,再根据邻补角的性质得到,即可求解.
【详解】(1)解:的对顶角是.
故答案为:.
(2)解:是的平分线,
,
,
.
方法指导
求角度问题时,要善于从图形中挖掘隐含条件,如邻补角、对顶角,然后结合条件给出的角的和、差、倍、分等关系进行计算。
变式训练1
1.如图,把一张长方形纸片的一角任意折向长方形内,使点B落在点的位置,折痕为,再把折叠,使点C、D分别落在点的位置,折痕为,与在同一条直线上.
(1)分别直接写出与,与之间所满足的数量关系;
(2)与之间什么关系?
(3)是什么角?
【答案】(1),
(2)与互余
(3)是直角
【分析】本题主要考查了轴对称的性质,邻补角的性质,互余的定义等知识点,熟练掌握轴对称的性质是解题的关键.
(1)根据邻补角的性质可得答案;
(2)由轴对称的性质可得,,进而可得,于是可得答案;
(3)由轴对称的性质可得,,进而可得,然后根据即可得出答案.
【详解】(1)解: 由邻补角的性质可得:
,;
(2)解:由轴对称的性质可得:,,
∴,
∴,
答:与互余;
(3)解:由轴对称的性质可得:,,
∴,
∴,
∴,
答:是直角.
2.如图,已知点为直线上一点,,,平分,.
(1)求的度数;
(2)试说明:平分;
(3)若改变的大小,其余条件不变,设,(2)中的结论是否依然成立?若成立,请说明理由;若不成立,请用表示.
【答案】(1)
(2)见解析
(3)(2)中的结论依然成立,理由见解答过程
【分析】此题主要考查了角平分线定义,垂直定义,邻补角定义,角的计算;
(1)先根据邻补角定义求出,再根据可得的度数;
(2)先根据及角平分线定义得,进而得,则,由此即可得出结论;
(3)根据邻补角定义得,根据得,再根据角平分线定义得,进而得,则,由此即可得出结论.
【详解】(1)解:点为直线上一点,,
,
,
,
;
(2),平分,
,
由(1)可知:,
,
,
,
,
平分;
(3)(2)中的结论依然成立,理由如下:
点为直线上一点,
,
,
,
,
平分,
,
,
,
,
,
平分.
3.如图,∠AOC=100°,∠BOE=80°,D,O,E三点在同一条直线上,∠AOD=37°,
(1)求∠COE的度数;
(2)请写出一组相等的角,并说明理由.(平角相等除外)
(3)若OM平分∠BOE,求∠COM的度数.
【答案】(1)117°;(2)∠DOB=∠AOC,理由见解析;(3)77°
【分析】(1)根据∠AOC=100°,∠AOD=37°先求出∠DOC=63°,再根据邻补角的定义即可求得答案;
(2)根据∠BOE=80°结合邻补角的定义可求得∠DOB=100°,进而可证得∠DOB=∠AOC;
(3)根据OM平分∠BOE,∠BOE=80°可得∠BOM=40°,再根据∠DOB=∠AOC可证得∠AOD=∠BOC=37°,最后根据∠COM=∠BOC+∠BOM即可求得答案.
【详解】解:(1)∵∠AOC=100°,∠AOD=37°,
∴∠DOC=∠AOC-∠AOD=63°,
∴∠COE=180°-63°=117°;
(2)∠DOB=∠AOC,理由如下:
∵∠BOE=80°,
∴∠DOB=180°-80°=100°,
∴∠DOB=∠AOC;
(3)∵OM平分∠BOE,∠BOE=80°,
∴∠BOM=40°,
∵∠DOB=∠AOC,
∴∠DOB-∠DOC =∠AOC-∠DOC,
∴∠AOD=∠BOC=37°,
∴∠COM=∠BOC+∠BOM=77°
【点睛】本题考查了角平分线定义和角的有关计算,能够熟练运用邻补角的定义是解此题的关键.
4.如图,直线相交于点D,.
(1)若,求证:;
(2)在(1)的条件下,若,求的度数.
【答案】(1)见解析
(2)
【分析】本题考查垂直的定义,几何中角度的计算.
(1)根据垂直的定义得到,结合,等量代换可得,即可证明;
(2)由,根据,可得,即可求出,由(1)知,由即可得出结果.
【详解】(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵,,
∴,
∴,
由(1)知,
,
∴.
5.如图,直线相交于点O,平分平分, ,H是射线上的一点.
(1)过点H画直线的垂线,垂足为F;
(2)在(1)问的基础上求的度数(用含的式子表示);
(3)探究的大小和的大小是否有关?若有,请写出的大小和的大小关系;若没有,请说明理由.
【答案】(1)见解析
(2)
(3)无关,理由见解析
【分析】本题考查了画垂线,互余与互补,角平分线的意义等知识.
(1)按照画垂线的方法进行即可;
(2)由对顶角相等及互余关系即可求解;
(3)由角平分线的意义及互补关系得,即可得的大小和的大小无关.
【详解】(1)解:如图,垂线即为所画;
(2)解:∵,
又∵,
∴,
∴;
(3)解:的大小和的大小无关.
理由如下:
∵平分平分,
∴,
∴
,
∵,
∴,
即的大小和的大小无关.
重难点2 平行线的性质和判定
【例2】.近年来,我国一直提倡“绿色环保、低碳生活”,健康骑行成为一种时尚、环保的运动,深受人们的青睐.小郑的自行车示意图如图所示,其中,,.
(1)求的度数;
(2)试判断与的位置关系,并说明理由.
【答案】(1)
(2).理由见解析
【分析】本题考查了平行线的判定和性质,熟练运用平行线的相关性质解题是关键.
(1)利用两直线平行,同旁内角互补,即可解答;
(2)证明,即可得到,即可解答.
【详解】(1)解:,
.
,
;
(2)解:.理由如下:
,
.
.
,
,
,
.
方法指导
这类题目一般会综合考查平行线的性质与判定,即“由形推角”或“由角判形”,所以解决此类问题时要明确条件或结论,不要产生混淆,性质是由“形”得到“角”,判定是由“角”得到“形”。
变式训练2
1.综合与实践
在中华武术中,有双节棍,三节棍,四节镋(如图①),其中四节镋又称镋镰,是真正的软兵器之一.小李家是武术世家,他用四节镋能拼出许多几何图形,如图②,图③是拼出的两个示意图.已知.
(1)如图②,求证:;
(2)如图③,判断,和之间的数量关系,并说明理由;
(3)在图③中,已知,比的3倍小,直接写出的度数.
【答案】(1)见解析
(2),理由见解析
(3)
【分析】本题主要考查了平行线的性质与判定,熟知平行线的性质与判定定理是解题的关键.
(1)过点C作,则,由平行线的性质可得,据此可证明结论;
(2)过点C作,则,由平行线的性质可得,再由即可推出结论 ;
(3)根据(2)的结论先得到,再由,计算求解即可.
【详解】(1)证明:如图所示,过点C作,
∵,
∴,
∴,
∵,
∴;
(2)解:,理由如下:
如图所示,过点C作,
∵,
∴,
∴,
∴,
∵,
∵,
∴;
(3)解:由(2)得,
∵,
∴,
∴,
∵比的3倍小,
∴,
∴,
∴.
2.如图,点、分别在线段和上,且于,于,.
(1)求证:;
(2)连接,若,,求.
【答案】(1)见解析
(2)
【分析】本题考查平行线的判定与性质,熟练掌握平行线的判定与性质是解题的关键.
(1)先证明得出,从而可证得,即可由平行线的判定定理得出结论;
(2)先由平行线的性质得出,再由,根据得出,即可求得,然后由平行线的性质求解即可.
【详解】(1)证明:,,
,
.
.
又,
,
.
(2)解:连接,如图,
,
.
,
.
又,
.
解得
又,
.
3.【问题背景】
如图,直线,点、在直线上,点、在直线上,连接,,已知.
【问题探究】
(1)如图1,直线与直线平行吗?为什么?
(2)如图2,点在直线上,且在点的右侧,连接,分别作的平分线和的平分线相交于点,过点作,试探究与之间的数量关系,并说明理由.
【答案】(1)平行,理由见解析
(2),理由见解析
【分析】本题考查平行线的判定和性质,与角平分线有关的计算,熟练掌握平行线的判定方法,是解题的关键:
(1)平行线的性质得到,进而得到,即可得出结果;
(2)根据平行线的性质,结合角平分线的定义,推出,即可得出结论.
【详解】(1)解:平行,理由如下:
∵,
∴,
∵,
∴,
∴;
(2)∵,
∴,
∴,
∵作的平分线和的平分线相交于点,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
4.如图所示,已知于,,,;求证:
【答案】证明见解析
【分析】本题主要考查平行线的判定与性质,解答的关键是明确平行线的判定定理与性质,并灵活运用. 由角的关系判定,通过平行线的性质找出角之间的关系,再利用角的关系判定其他直线平行,最终根据平行关系和已知垂直关系得出结论.
【详解】证明:,
.
,
.
.
,
.
,
.
,
.
.
.
5.如图,点D、E、H分别在线段上,连接,过点C画交的延长线于点F,且满足,若,,求证.
【答案】证明见解析
【分析】本题主要考查了平行线的性质与判定,先由平行线的性质和已知条件证明,则,再由平行线的性质和已知条件证明,则可证明.
【详解】证明:∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴.
重难点3 命题
【例3】.黑板上写有3个命题:
①若,则;
②若是有理数,则;
③若与都是锐角,则这两个角的和是钝角.
(1)上述命题是真命题的是______(填序号),该命题的条件是______,结论是______;
(2)对于上述命题中的假命题,请各写出一个反例.
【答案】(1)①,,
(2)②当时,,
③当,时,与都是锐角,
【分析】本题主要考查了命题的判定,掌握相关知识的运算,命题真假的判定是关键.
(1)根据平方,绝对值的性质,锐角、钝角的数量关系判定即可;
(2)根据命题的特点分别举出反例即可.
【详解】(1)解:若,则,是真命题,命题的条件是:,结论是:;
若是有理数,则不一定成立,是假命题;
若与都是锐角,则这两个角的和不一定是钝角,是假命题;
故答案为:①,,;
(2)解:反例:
②当时,,;
③当,时,与都是锐角,.
方法指导
要说明一个命题的正确性,可根据已有知识进行推理,论证,而判断一个命题是假命题,只需举一个反例即可。
变式训练3
1.判断下列语句是否是命题,如果是,改写成“如果……那么……”的形式,并分别指出它们的题设和结论,同时判断其真假
(1)作直线AB的垂线.
(2)相等的角是对顶角.
(3)你喜欢数学吗?
(4)OC平分∠AOB.
(5)两直线平行,内错角相等.
(6)同角的补角相等.
【答案】(1)是作图语言,不符合命题的定义,不是命题;(2)是命题;如果两个角相等,那么这两个角是对顶角;题设是两个角相等;结论是这两个角是对顶角;此命题是假命题;(3)表示疑问的句子,没有对事情做出判断,所以此语句不是命题;(4)陈述了一个事情,没有做出判断,不是命题;(5)是命题;如果两平行线被第三条直线所截,那么内错角相等;题设是两平行线被第三条直线所截,结论是内错角相等;此命题是真命题;(6)是命题;如果两个角是同一个角的补角,那么这两个角相等;题设是两个角是同一个角的补角,结论是这两个角相等;此命题是真命题.
【分析】判断语句是否为命题要紧扣两条:(1)命题必须是一个完整的陈述句;(2)必须对某件事情做出肯定或否定的判断.这二者缺一不可.
【详解】(1)是作图语言,不符合命题的定义,不是命题;
(2)是命题;
改写:如果两个角相等,那么这两个角是对顶角;
题设:两个角相等;结论:这两个角是对顶角;
此命题是假命题;
(3)表示疑问的句子,没有对事情做出判断,所以此语句不是命题;
(4)陈述了一个事情,没有做出判断,不是命题;
(5)是命题
改写:如果两平行线被第三条直线所截,那么内错角相等;
题设:两平行线被第三条直线所截;结论:内错角相等;
此命题是真命题;
(6)是命题
改写:如果两个角是同一个角的补角,那么这两个角相等;
题设:两个角是同一个角的补角;结论:这两个角相等;
此命题是真命题.
【点睛】本题考查了命题的概念,判断语句是否为命题的两个条件是做题的关键.
2.如图,有下列三个条件:①DE//BC;②;③.
(1)若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题?请你都写出来;
(2)你所写出的命题都是真命题吗?若是,请你就其中的一个真命题给出推理过程;若不是,请你对其中的假命题举出一个反例(温馨提示:)
【答案】(1)一共能组成三个命题,见解析
(2)都是真命题,推理见解析
【分析】(1)(1)根据两条件一结论组成命题,可得答案;
(2)根据平行线的性质,可判定①②,根据平行线的判定,可判定③,即可
【详解】(1)解:一共能组成三个命题:
①如果DE//BC,,那么;
②如果DE//BC,,那么;
③如果,,那么DE//BC ;
(2)解:都是真命题,
如果DE//BC,,那么,
理由如下:∵DE//BC,
∴,
∵,
∴.
如果DE//BC,,那么;
理由如下:∵DE//BC,
∴,,
∵,
∴;
如果,,那么DE//BC ;
理由如下:∵,
∴∠B+∠C=180°-∠BAC,
∵∠1+∠2+∠BAC=180°,
∴∠1+∠2=180°-∠BAC,
∴∠B+∠C=∠1+∠2,
∵,,
∴∠B=∠1,
∴DE//BC .
【点睛】本题考查了平行线的判定与性质,判断命题的真假,熟练掌握平行线的判定与性质是解题的关键.
3.如图,已知直线,给出下列信息:
①;②平分;③.
(1)请在上述3条信息中选择其中两条作为条件,其余的一条信息作为结论组成一个真命题,你选择的条件是 ,结论是 (只要填写序号),并说明理由.
(2)在(1)的条件下,若比的倍少度,求的度数.
【答案】(1)①②;③;理由见解析
(2)
【分析】(1)由角平分线的定义可得,再根据等角的余角相等可得出,再由平行线的性质可得,从而结论得证;
(2)由(1)得:,根据比的倍少度,可得关系式,求得,,再根据即可得到的度数.
【详解】(1)解:条件:①②,结论:③.理由如下:
∵平分,
∴,
∵,
∴,,
∴,
∵,
∴,
∴.
故答案为:①②;③.
(2)由(1)得:,
∵比的倍少度,
∴,
∴,
解得:,
∴,
∴.
∴的度数.
【点睛】本题考查了角平分线的定义,等角的余角相等,平行线的性质,解方程组等知识.理解和掌握平行线的性质,等角的余角相等是解题的关键.
4.如图,点D,E,F分别是三角形的边,,上的点,给定以下三个条件:①;②;③.请从这三个条件中选择两个作为条件(放在已知处),另一个作为结论(放在证明处)组成一个真命题,并进行证明.
已知:________,________.
求证:________.
证明:
【答案】见解析
【分析】本题考查平行线性质和判定,根据题意选择两个作为条件,另一个作为结论组成一个真命题,并结合平行线性质和判定进行证明,即可解题.
【详解】解:(答案不唯一)已知:,,
求证:.
证明:,
(两直线平行,内错角相等).
,
(两直线平行,同位角相等),
.
已知:,,
求证:.
证明:,
(两直线平行,内错角相等).
,
(等量代换),
(同位角相等,两直线平行).
已知:,,
求证:.
证明:,
(两直线平行,同位角相等).
,
(等量代换),
(内错角相等,两直线平行).
5.如图,点在上,直线交于点.请从①,②平分,③中任选两个作为条件,余下一个作为结论,构造一个真命题,并求证.
已知:______,求证:______.(只须填写序号)
证明:
【答案】①②,③,证明见解析.(答案不唯一)
【分析】根据平行线的性质可得,再由角平分线的性质可得,再利用等量代换可得
【详解】解:已知①②,求证∶③,
证明∶∵,
∴,
∵平分,
∴,
∴.
故答案为∶①②;③.
【点睛】此题主要考查了角平分线的定义、证明以及平行线的性质,关键是掌握两直线平行,内错角相等.
重难点4 平移的性质及应用
【例4】.如图,一个四边形经过平移后得到四边形.
(1)线段的对应线段是___________;
(2)的对应角是___________;
(3)线段和线段有何关系?
【答案】(1)
(2)
(3)
【分析】本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
(1)根据平移的性质解答即可;
(2)根据平移的性质解答即可;
(3)根据平移的性质解答即可.
【详解】(1)线段的对应线段是.
故答案为:;
(2)的对应角是.
故答案为:;
线段和线段有何关系为:.
方法指导
解决平移有关问题,只需熟练掌握平移的性质即可,即(1)平移不改变图形的形状和大小;(2)经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
变式训练4
1.如图所示,是由沿箭头方向平移得到的.
(1)若,求的度数;
(2)若,求,的长.
【答案】(1)
(2)5,5
【分析】本题考查了平移的性质,熟练掌握平行的性质是解题的关键.
(1)根据平移的性质即可得到结论;
(2)根据平移的性质即可得到结论.
【详解】(1)解:是由沿箭头方向平移得到的,,
.
(2)解:是由沿箭头方向平移得到的,
.
2.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥,桥宽忽略不计.
(1)若荷塘的长为90米,宽为50米,则小桥总长为 米;
(2)若荷塘周长为米,则小桥总长为 米.
【答案】(1)
(2)
【分析】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
(1)根据平移的性质可得:小桥总长就等于长方形荷塘的长与宽的和;
(2)由平移的性质得,小桥总长长方形周长的一半,据此即可求出答案.
【详解】(1)解:由平移的性质得,小桥总长就等于长方形荷塘的长与宽的和,
∴,
故答案为:.
(2)由平移的性质得,小桥总长长方形周长的一半,
∴,
故答案为:
3.如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
【答案】道路的宽为2米
【分析】本题考查一元二次方程的实际应用,设道路的宽为,利用平移得到草坪为一个长为,宽为的一个矩形,利用矩形的面积公式列出方程,进行求解即可.
【详解】解:设道路的宽为,由题意,得:,
解得:(舍去),;
答:道路的宽为2米.
4.如图所示,某商场重新装修后,准备在门前台阶上铺设地毯,已知这种地毯的批发价为每平方米50元,其台阶的尺寸如图所示,则购买地毯至少需要元.
【答案】元
【分析】本题考查了生活中的平移,熟记平移的性质并理解地毯长度的求法是解题的关键.
根据平移可知地毯的长度等于横向与纵向的长度之和求出地毯的长度,再根据矩形的面积列式求出地毯的面积,然后乘以单价计算即可得解.
【详解】解:解:地毯的长度至少为:(米);
(元).
答:铺设梯子的红地毯至少需要米,花费至少元.
5.已知的顶点A平移到顶点D,请用两种不同的方法,在图中作出平移后的图形.
【答案】见解析
【分析】本题涉及平移的知识.熟练掌握平移的定义是关键.
方法一:过点B作且使,过点C作且使,然后顺次连接D、E、F即可;
方法二:过点D作且使,过点D作且使,然后顺次连接D、E、F即可.
【详解】解:方法一,如图1;
方法2,如图2.
重难点5 思想方法
构造法
【例5-1】.【阅读理解】两条平行线间的拐点问题经常可以通过作一条直线的平行线进行转化.例如:如图,直线,求证:
(1)阅读下面的解答过程,并填上适当的理由
解:过点作直线,
已知,,
【方法运用】
(2)如图2,直线,若,,求的度数.
【答案】(1)见解析;(2)
【分析】本题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.
(1)根据平行线的判定与性质求解即可;
(2)根据(1)的方法过点作直线,进而根据平行线的判定与性质求解即可.
【详解】(1)解:过点作直线,
两直线平行,内错角相等
已知,,
平行于同一条直线的两条直线平行
两直线平行,内错角相等
(2)解:过点作直线
,
,
,,
,
,
,
,
°.
方法指导
有“拐点”时,常常过拐点作平行线,构造平行线的性质解决问题。
变式训练5-1
1.已知直线,点,在直线上,点,在直线上,的平分线与的平分线交于点,,.
(1)如图1,点在点的左边,点在点的右边,求的度数;
(2)在(1)的条件下,求的度数;(用含的式子表示)
(3)将图1中的线段向左平移,使点落在点的左边,其他条件不变,在图2中画出符合题意的图形,并求出的值.
【答案】(1)
(2)
(3)
【分析】本题主要考查了平行线的性质,角平分线的性质,解题的关键是熟练掌握相关性质进行灵活应用.
(1)利用角平分线的性质和平行线的性质即可解答本题;
(2)过点作,则,利用角平分线的性质表示,再根据平行线的性质及角的和差关系即可得答案;
(3)根据题目要求画出图形,过点作,利用拐点模型即可解答此题.
【详解】(1)解:平分,
,,
,
,
∴的度数为.
(2)解:如图,过点作,则,
平分,
,
∵,
∴,,
(3)解:如图所示,
平分,
过点作,
又
∴的值为
2.如图,若,,,求的度数.
【答案】
【分析】本题考查了平行线的性质与判定,过点作,得出,,进而即可求解.
【详解】解:如图,过点作
∴
∴
∵,
∴
∵,
∴
∴
3. 综合与实践:
【问题初探】
()数学活动课上,王老师给出如下问题:如图①,,点在之间且点在点右侧,求证:(提示:过点作);
【类比探究】
()小明对王老师给出的问题进行改编:如图②,,点在之间且点在点左侧,猜想,,之间的数量关系: ,并加以证明;
【学以致用】
()如图③是超市的购物车,图④是其侧面示意图,已知,,测量得知,,直接写出的度数 .
【答案】()证明见解析;(),证明见解析;()
【分析】()如图①,过点作,可得,,即得,进而即可求证;
()如图②,过点作,可得,,即得,进而即可求证;
()如图③,过点作,过点作,根据平行线的性质可得,,进而即可求解;
本题考查了平行线的判定和性质,正确作出辅助线是解题的关键.
【详解】()证明:如图①,过点作,则,
∵,
∴,
∴,
∵,
∴;
(),证明如下:
如图②,过点作,则,
∵,
∴,
∴,
∴,
即;
()解:如图③,过点作,过点作,
∴,,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故答案为:.
转化思想
【例5-2】.与是两个完全相同的直角三角形.将沿点B到点C的方向从的位置平移到如图所示的位置.若,图中阴影部分的面积为84,,求平移的距离.
【答案】平移的距离为.
【分析】本题考查了平移的性质,根据平移可得,,,得到,,再根据梯形的面积公式即可求解,掌握平移的性质是解题的关键.
【详解】解:根据平移可得:,,,
∴,,
∴,
∴,
∴,
∴平移的距离为.
方法指导
根据平移不改变图形的大小的性质,将零散的图形转化成规则图形面积。
变式训练5-2
1.如图,在三角形中,,,.将三角形沿向右平移,得到三角形,与交于点,连接.
(1)分别求和的度数;
(2)若,,求图中阴影部分的面积.
【答案】(1);
(2)10
【分析】(1)由平移的性质得,,,,,则,由此可得的度数;由得,由此可得的度数;
(2)先根据,得,再根据三角形的面积公式可求出图中阴影部分的面积;
此题主要考查了图形的平移变换及其性质,熟练掌握图形的平移变换及其性质是解决问题的关键.
【详解】(1)解:由平移性质得:,,,,,
∴,
∴,
∵,
∴,
∴;
(2)∵,,
∴,
又∵,
∴;
2.如图,将直角三角形沿方向平移线段的长度得到直角三角形,已知,,求图中四边形的面积.
【答案】9
【分析】本题考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.同时考查了梯形的面积公式.根据平移的性质可得,,在根据即可得到答案.
【详解】解:∵沿的方向平移距离得,
∴,
∵,
∴,
∴,
∴.
即四边形的面积为9.
3.如图,在三角形中,,,.将三角形沿向右平移,得到三角形,与交于点,连接.
(1)________,________;
(2)若,,求图中阴影部分的面积;
(3)已知点在三角形的内部,点经过相同平移后的对应点为,连接.若三角形的周长为,四边形的周长为,请直接写出的长度.
【答案】(1),
(2)
(3)
【分析】本题考查了平移的性质,平行线的性质;能熟练利用平移的性质进行求解是解题的关键.
(1)由平移的性质得,,由平行线的性质即可求解;
(2)由平移的性质得,由即可求解;
(3)由平移的性质得,,,,即可求解;
【详解】(1)解:由平移得,
,
,
,
,
,
,
故答案为:,;
(2)解:由平移得,
;
(3)解:由平移得
,,
,,
,
,
,
,
解得:,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024-2025学年人教版七年级下期末专题复习
专题一 相交线与平行线
01 知识结构
02 重难点突破
重难点1 与相交线有关的角度计算
【例1】.如图,直线、相交于点,是的平分线.
(1)的对顶角是___;
(2)若,求的度数.
方法指导
求角度问题时,要善于从图形中挖掘隐含条件,如邻补角、对顶角,然后结合条件给出的角的和、差、倍、分等关系进行计算。
变式训练1
1.如图,把一张长方形纸片的一角任意折向长方形内,使点B落在点的位置,折痕为,再把折叠,使点C、D分别落在点的位置,折痕为,与在同一条直线上.
(1)分别直接写出与,与之间所满足的数量关系;
(2)与之间什么关系?
(3)是什么角?
2.如图,已知点为直线上一点,,,平分,.
(1)求的度数;
(2)试说明:平分;
(3)若改变的大小,其余条件不变,设,(2)中的结论是否依然成立?若成立,请说明理由;若不成立,请用表示.
3.如图,∠AOC=100°,∠BOE=80°,D,O,E三点在同一条直线上,∠AOD=37°,
(1)求∠COE的度数;
(2)请写出一组相等的角,并说明理由.(平角相等除外)
(3)若OM平分∠BOE,求∠COM的度数.
4.如图,直线相交于点D,.
(1)若,求证:;
(2)在(1)的条件下,若,求的度数.
5.如图,直线相交于点O,平分平分, ,H是射线上的一点.
(1)过点H画直线的垂线,垂足为F;
(2)在(1)问的基础上求的度数(用含的式子表示);
(3)探究的大小和的大小是否有关?若有,请写出的大小和的大小关系;若没有,请说明理由.
重难点2 平行线的性质和判定
【例2】.近年来,我国一直提倡“绿色环保、低碳生活”,健康骑行成为一种时尚、环保的运动,深受人们的青睐.小郑的自行车示意图如图所示,其中,,.
(1)求的度数;
(2)试判断与的位置关系,并说明理由.
方法指导
这类题目一般会综合考查平行线的性质与判定,即“由形推角”或“由角判形”,所以解决此类问题时要明确条件或结论,不要产生混淆,性质是由“形”得到“角”,判定是由“角”得到“形”。
变式训练2
1.综合与实践
在中华武术中,有双节棍,三节棍,四节镋(如图①),其中四节镋又称镋镰,是真正的软兵器之一.小李家是武术世家,他用四节镋能拼出许多几何图形,如图②,图③是拼出的两个示意图.已知.
(1)如图②,求证:;
(2)如图③,判断,和之间的数量关系,并说明理由;
(3)在图③中,已知,比的3倍小,直接写出的度数.
2.如图,点、分别在线段和上,且于,于,.
(1)求证:;
(2)连接,若,,求.
3.【问题背景】
如图,直线,点、在直线上,点、在直线上,连接,,已知.
【问题探究】
(1)如图1,直线与直线平行吗?为什么?
(2)如图2,点在直线上,且在点的右侧,连接,分别作的平分线和的平分线相交于点,过点作,试探究与之间的数量关系,并说明理由.
4.如图所示,已知于,,,;求证:
5.如图,点D、E、H分别在线段上,连接,过点C画交的延长线于点F,且满足,若,,求证.
重难点3 命题
【例3】.黑板上写有3个命题:
①若,则;
②若是有理数,则;
③若与都是锐角,则这两个角的和是钝角.
(1)上述命题是真命题的是______(填序号),该命题的条件是______,结论是______;
(2)对于上述命题中的假命题,请各写出一个反例.
方法指导
要说明一个命题的正确性,可根据已有知识进行推理,论证,而判断一个命题是假命题,只需举一个反例即可。
变式训练3
1.判断下列语句是否是命题,如果是,改写成“如果……那么……”的形式,并分别指出它们的题设和结论,同时判断其真假
(1)作直线AB的垂线.
(2)相等的角是对顶角.
(3)你喜欢数学吗?
(4)OC平分∠AOB.
(5)两直线平行,内错角相等.
(6)同角的补角相等.
2.如图,有下列三个条件:①DE//BC;②;③.
(1)若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题?请你都写出来;
(2)你所写出的命题都是真命题吗?若是,请你就其中的一个真命题给出推理过程;若不是,请你对其中的假命题举出一个反例(温馨提示:)
3.如图,已知直线,给出下列信息:
①;②平分;③.
(1)请在上述3条信息中选择其中两条作为条件,其余的一条信息作为结论组成一个真命题,你选择的条件是 ,结论是 (只要填写序号),并说明理由.
(2)在(1)的条件下,若比的倍少度,求的度数.
4.如图,点D,E,F分别是三角形的边,,上的点,给定以下三个条件:①;②;③.请从这三个条件中选择两个作为条件(放在已知处),另一个作为结论(放在证明处)组成一个真命题,并进行证明.
已知:________,________.
求证:________.
证明:
5.如图,点在上,直线交于点.请从①,②平分,③中任选两个作为条件,余下一个作为结论,构造一个真命题,并求证.
已知:______,求证:______.(只须填写序号)
证明:
重难点4 平移的性质及应用
【例4】.如图,一个四边形经过平移后得到四边形.
(1)线段的对应线段是___________;
(2)的对应角是___________;
(3)线段和线段有何关系?
方法指导
解决平移有关问题,只需熟练掌握平移的性质即可,即(1)平移不改变图形的形状和大小;(2)经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
变式训练4
1.如图所示,是由沿箭头方向平移得到的.
(1)若,求的度数;
(2)若,求,的长.
2.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥,桥宽忽略不计.
(1)若荷塘的长为90米,宽为50米,则小桥总长为 米;
(2)若荷塘周长为米,则小桥总长为 米.
3.如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
4.如图所示,某商场重新装修后,准备在门前台阶上铺设地毯,已知这种地毯的批发价为每平方米50元,其台阶的尺寸如图所示,则购买地毯至少需要元.
5.已知的顶点A平移到顶点D,请用两种不同的方法,在图中作出平移后的图形.
重难点5 思想方法
构造法
【例5-1】.【阅读理解】两条平行线间的拐点问题经常可以通过作一条直线的平行线进行转化.例如:如图,直线,求证:
(1)阅读下面的解答过程,并填上适当的理由
解:过点作直线,
已知,,
【方法运用】
(2)如图2,直线,若,,求的度数.
方法指导
有“拐点”时,常常过拐点作平行线,构造平行线的性质解决问题。
变式训练5-1
1.已知直线,点,在直线上,点,在直线上,的平分线与的平分线交于点,,.
(1)如图1,点在点的左边,点在点的右边,求的度数;
(2)在(1)的条件下,求的度数;(用含的式子表示)
(3)将图1中的线段向左平移,使点落在点的左边,其他条件不变,在图2中画出符合题意的图形,并求出的值.
2.如图,若,,,求的度数.
3. 综合与实践:
【问题初探】
()数学活动课上,王老师给出如下问题:如图①,,点在之间且点在点右侧,求证:(提示:过点作);
【类比探究】
()小明对王老师给出的问题进行改编:如图②,,点在之间且点在点左侧,猜想,,之间的数量关系: ,并加以证明;
【学以致用】
()如图③是超市的购物车,图④是其侧面示意图,已知,,测量得知,,直接写出的度数 .
转化思想
【例5-2】.与是两个完全相同的直角三角形.将沿点B到点C的方向从的位置平移到如图所示的位置.若,图中阴影部分的面积为84,,求平移的距离.
方法指导
根据平移不改变图形的大小的性质,将零散的图形转化成规则图形面积。
变式训练5-2
1.如图,在三角形中,,,.将三角形沿向右平移,得到三角形,与交于点,连接.
(1)分别求和的度数;
(2)若,,求图中阴影部分的面积.
2.如图,将直角三角形沿方向平移线段的长度得到直角三角形,已知,,求图中四边形的面积.
3.如图,在三角形中,,,.将三角形沿向右平移,得到三角形,与交于点,连接.
(1)________,________;
(2)若,,求图中阴影部分的面积;
(3)已知点在三角形的内部,点经过相同平移后的对应点为,连接.若三角形的周长为,四边形的周长为,请直接写出的长度.
2024-2025学年人教版七年级下期末专题复习
专题一 相交线与平行线(解析版)
01 知识结构
02 重难点突破
重难点1 与相交线有关的角度计算
【例1】.如图,直线、相交于点,是的平分线.
(1)的对顶角是___;
(2)若,求的度数.
【答案】(1)
(2)
【分析】本题考查了几何图形中的角度计算、角平分线的定义、对顶角的定义、邻补角的性质,熟练掌握相关知识点是解题的关键.
(1)根据对顶角的定义即可解答;
(2)根据角平分线的定义得到,再根据邻补角的性质得到,即可求解.
【详解】(1)解:的对顶角是.
故答案为:.
(2)解:是的平分线,
,
,
.
方法指导
求角度问题时,要善于从图形中挖掘隐含条件,如邻补角、对顶角,然后结合条件给出的角的和、差、倍、分等关系进行计算。
变式训练1
1.如图,把一张长方形纸片的一角任意折向长方形内,使点B落在点的位置,折痕为,再把折叠,使点C、D分别落在点的位置,折痕为,与在同一条直线上.
(1)分别直接写出与,与之间所满足的数量关系;
(2)与之间什么关系?
(3)是什么角?
【答案】(1),
(2)与互余
(3)是直角
【分析】本题主要考查了轴对称的性质,邻补角的性质,互余的定义等知识点,熟练掌握轴对称的性质是解题的关键.
(1)根据邻补角的性质可得答案;
(2)由轴对称的性质可得,,进而可得,于是可得答案;
(3)由轴对称的性质可得,,进而可得,然后根据即可得出答案.
【详解】(1)解: 由邻补角的性质可得:
,;
(2)解:由轴对称的性质可得:,,
∴,
∴,
答:与互余;
(3)解:由轴对称的性质可得:,,
∴,
∴,
∴,
答:是直角.
2.如图,已知点为直线上一点,,,平分,.
(1)求的度数;
(2)试说明:平分;
(3)若改变的大小,其余条件不变,设,(2)中的结论是否依然成立?若成立,请说明理由;若不成立,请用表示.
【答案】(1)
(2)见解析
(3)(2)中的结论依然成立,理由见解答过程
【分析】此题主要考查了角平分线定义,垂直定义,邻补角定义,角的计算;
(1)先根据邻补角定义求出,再根据可得的度数;
(2)先根据及角平分线定义得,进而得,则,由此即可得出结论;
(3)根据邻补角定义得,根据得,再根据角平分线定义得,进而得,则,由此即可得出结论.
【详解】(1)解:点为直线上一点,,
,
,
,
;
(2),平分,
,
由(1)可知:,
,
,
,
,
平分;
(3)(2)中的结论依然成立,理由如下:
点为直线上一点,
,
,
,
,
平分,
,
,
,
,
,
平分.
3.如图,∠AOC=100°,∠BOE=80°,D,O,E三点在同一条直线上,∠AOD=37°,
(1)求∠COE的度数;
(2)请写出一组相等的角,并说明理由.(平角相等除外)
(3)若OM平分∠BOE,求∠COM的度数.
【答案】(1)117°;(2)∠DOB=∠AOC,理由见解析;(3)77°
【分析】(1)根据∠AOC=100°,∠AOD=37°先求出∠DOC=63°,再根据邻补角的定义即可求得答案;
(2)根据∠BOE=80°结合邻补角的定义可求得∠DOB=100°,进而可证得∠DOB=∠AOC;
(3)根据OM平分∠BOE,∠BOE=80°可得∠BOM=40°,再根据∠DOB=∠AOC可证得∠AOD=∠BOC=37°,最后根据∠COM=∠BOC+∠BOM即可求得答案.
【详解】解:(1)∵∠AOC=100°,∠AOD=37°,
∴∠DOC=∠AOC-∠AOD=63°,
∴∠COE=180°-63°=117°;
(2)∠DOB=∠AOC,理由如下:
∵∠BOE=80°,
∴∠DOB=180°-80°=100°,
∴∠DOB=∠AOC;
(3)∵OM平分∠BOE,∠BOE=80°,
∴∠BOM=40°,
∵∠DOB=∠AOC,
∴∠DOB-∠DOC =∠AOC-∠DOC,
∴∠AOD=∠BOC=37°,
∴∠COM=∠BOC+∠BOM=77°
【点睛】本题考查了角平分线定义和角的有关计算,能够熟练运用邻补角的定义是解此题的关键.
4.如图,直线相交于点D,.
(1)若,求证:;
(2)在(1)的条件下,若,求的度数.
【答案】(1)见解析
(2)
【分析】本题考查垂直的定义,几何中角度的计算.
(1)根据垂直的定义得到,结合,等量代换可得,即可证明;
(2)由,根据,可得,即可求出,由(1)知,由即可得出结果.
【详解】(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,
∴,
∵,,
∴,
∴,
由(1)知,
,
∴.
5.如图,直线相交于点O,平分平分, ,H是射线上的一点.
(1)过点H画直线的垂线,垂足为F;
(2)在(1)问的基础上求的度数(用含的式子表示);
(3)探究的大小和的大小是否有关?若有,请写出的大小和的大小关系;若没有,请说明理由.
【答案】(1)见解析
(2)
(3)无关,理由见解析
【分析】本题考查了画垂线,互余与互补,角平分线的意义等知识.
(1)按照画垂线的方法进行即可;
(2)由对顶角相等及互余关系即可求解;
(3)由角平分线的意义及互补关系得,即可得的大小和的大小无关.
【详解】(1)解:如图,垂线即为所画;
(2)解:∵,
又∵,
∴,
∴;
(3)解:的大小和的大小无关.
理由如下:
∵平分平分,
∴,
∴
,
∵,
∴,
即的大小和的大小无关.
重难点2 平行线的性质和判定
【例2】.近年来,我国一直提倡“绿色环保、低碳生活”,健康骑行成为一种时尚、环保的运动,深受人们的青睐.小郑的自行车示意图如图所示,其中,,.
(1)求的度数;
(2)试判断与的位置关系,并说明理由.
【答案】(1)
(2).理由见解析
【分析】本题考查了平行线的判定和性质,熟练运用平行线的相关性质解题是关键.
(1)利用两直线平行,同旁内角互补,即可解答;
(2)证明,即可得到,即可解答.
【详解】(1)解:,
.
,
;
(2)解:.理由如下:
,
.
.
,
,
,
.
方法指导
这类题目一般会综合考查平行线的性质与判定,即“由形推角”或“由角判形”,所以解决此类问题时要明确条件或结论,不要产生混淆,性质是由“形”得到“角”,判定是由“角”得到“形”。
变式训练2
1.综合与实践
在中华武术中,有双节棍,三节棍,四节镋(如图①),其中四节镋又称镋镰,是真正的软兵器之一.小李家是武术世家,他用四节镋能拼出许多几何图形,如图②,图③是拼出的两个示意图.已知.
(1)如图②,求证:;
(2)如图③,判断,和之间的数量关系,并说明理由;
(3)在图③中,已知,比的3倍小,直接写出的度数.
【答案】(1)见解析
(2),理由见解析
(3)
【分析】本题主要考查了平行线的性质与判定,熟知平行线的性质与判定定理是解题的关键.
(1)过点C作,则,由平行线的性质可得,据此可证明结论;
(2)过点C作,则,由平行线的性质可得,再由即可推出结论 ;
(3)根据(2)的结论先得到,再由,计算求解即可.
【详解】(1)证明:如图所示,过点C作,
∵,
∴,
∴,
∵,
∴;
(2)解:,理由如下:
如图所示,过点C作,
∵,
∴,
∴,
∴,
∵,
∵,
∴;
(3)解:由(2)得,
∵,
∴,
∴,
∵比的3倍小,
∴,
∴,
∴.
2.如图,点、分别在线段和上,且于,于,.
(1)求证:;
(2)连接,若,,求.
【答案】(1)见解析
(2)
【分析】本题考查平行线的判定与性质,熟练掌握平行线的判定与性质是解题的关键.
(1)先证明得出,从而可证得,即可由平行线的判定定理得出结论;
(2)先由平行线的性质得出,再由,根据得出,即可求得,然后由平行线的性质求解即可.
【详解】(1)证明:,,
,
.
.
又,
,
.
(2)解:连接,如图,
,
.
,
.
又,
.
解得
又,
.
3.【问题背景】
如图,直线,点、在直线上,点、在直线上,连接,,已知.
【问题探究】
(1)如图1,直线与直线平行吗?为什么?
(2)如图2,点在直线上,且在点的右侧,连接,分别作的平分线和的平分线相交于点,过点作,试探究与之间的数量关系,并说明理由.
【答案】(1)平行,理由见解析
(2),理由见解析
【分析】本题考查平行线的判定和性质,与角平分线有关的计算,熟练掌握平行线的判定方法,是解题的关键:
(1)平行线的性质得到,进而得到,即可得出结果;
(2)根据平行线的性质,结合角平分线的定义,推出,即可得出结论.
【详解】(1)解:平行,理由如下:
∵,
∴,
∵,
∴,
∴;
(2)∵,
∴,
∴,
∵作的平分线和的平分线相交于点,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
4.如图所示,已知于,,,;求证:
【答案】证明见解析
【分析】本题主要考查平行线的判定与性质,解答的关键是明确平行线的判定定理与性质,并灵活运用. 由角的关系判定,通过平行线的性质找出角之间的关系,再利用角的关系判定其他直线平行,最终根据平行关系和已知垂直关系得出结论.
【详解】证明:,
.
,
.
.
,
.
,
.
,
.
.
.
5.如图,点D、E、H分别在线段上,连接,过点C画交的延长线于点F,且满足,若,,求证.
【答案】证明见解析
【分析】本题主要考查了平行线的性质与判定,先由平行线的性质和已知条件证明,则,再由平行线的性质和已知条件证明,则可证明.
【详解】证明:∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴.
重难点3 命题
【例3】.黑板上写有3个命题:
①若,则;
②若是有理数,则;
③若与都是锐角,则这两个角的和是钝角.
(1)上述命题是真命题的是______(填序号),该命题的条件是______,结论是______;
(2)对于上述命题中的假命题,请各写出一个反例.
【答案】(1)①,,
(2)②当时,,
③当,时,与都是锐角,
【分析】本题主要考查了命题的判定,掌握相关知识的运算,命题真假的判定是关键.
(1)根据平方,绝对值的性质,锐角、钝角的数量关系判定即可;
(2)根据命题的特点分别举出反例即可.
【详解】(1)解:若,则,是真命题,命题的条件是:,结论是:;
若是有理数,则不一定成立,是假命题;
若与都是锐角,则这两个角的和不一定是钝角,是假命题;
故答案为:①,,;
(2)解:反例:
②当时,,;
③当,时,与都是锐角,.
方法指导
要说明一个命题的正确性,可根据已有知识进行推理,论证,而判断一个命题是假命题,只需举一个反例即可。
变式训练3
1.判断下列语句是否是命题,如果是,改写成“如果……那么……”的形式,并分别指出它们的题设和结论,同时判断其真假
(1)作直线AB的垂线.
(2)相等的角是对顶角.
(3)你喜欢数学吗?
(4)OC平分∠AOB.
(5)两直线平行,内错角相等.
(6)同角的补角相等.
【答案】(1)是作图语言,不符合命题的定义,不是命题;(2)是命题;如果两个角相等,那么这两个角是对顶角;题设是两个角相等;结论是这两个角是对顶角;此命题是假命题;(3)表示疑问的句子,没有对事情做出判断,所以此语句不是命题;(4)陈述了一个事情,没有做出判断,不是命题;(5)是命题;如果两平行线被第三条直线所截,那么内错角相等;题设是两平行线被第三条直线所截,结论是内错角相等;此命题是真命题;(6)是命题;如果两个角是同一个角的补角,那么这两个角相等;题设是两个角是同一个角的补角,结论是这两个角相等;此命题是真命题.
【分析】判断语句是否为命题要紧扣两条:(1)命题必须是一个完整的陈述句;(2)必须对某件事情做出肯定或否定的判断.这二者缺一不可.
【详解】(1)是作图语言,不符合命题的定义,不是命题;
(2)是命题;
改写:如果两个角相等,那么这两个角是对顶角;
题设:两个角相等;结论:这两个角是对顶角;
此命题是假命题;
(3)表示疑问的句子,没有对事情做出判断,所以此语句不是命题;
(4)陈述了一个事情,没有做出判断,不是命题;
(5)是命题
改写:如果两平行线被第三条直线所截,那么内错角相等;
题设:两平行线被第三条直线所截;结论:内错角相等;
此命题是真命题;
(6)是命题
改写:如果两个角是同一个角的补角,那么这两个角相等;
题设:两个角是同一个角的补角;结论:这两个角相等;
此命题是真命题.
【点睛】本题考查了命题的概念,判断语句是否为命题的两个条件是做题的关键.
2.如图,有下列三个条件:①DE//BC;②;③.
(1)若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题?请你都写出来;
(2)你所写出的命题都是真命题吗?若是,请你就其中的一个真命题给出推理过程;若不是,请你对其中的假命题举出一个反例(温馨提示:)
【答案】(1)一共能组成三个命题,见解析
(2)都是真命题,推理见解析
【分析】(1)(1)根据两条件一结论组成命题,可得答案;
(2)根据平行线的性质,可判定①②,根据平行线的判定,可判定③,即可
【详解】(1)解:一共能组成三个命题:
①如果DE//BC,,那么;
②如果DE//BC,,那么;
③如果,,那么DE//BC ;
(2)解:都是真命题,
如果DE//BC,,那么,
理由如下:∵DE//BC,
∴,
∵,
∴.
如果DE//BC,,那么;
理由如下:∵DE//BC,
∴,,
∵,
∴;
如果,,那么DE//BC ;
理由如下:∵,
∴∠B+∠C=180°-∠BAC,
∵∠1+∠2+∠BAC=180°,
∴∠1+∠2=180°-∠BAC,
∴∠B+∠C=∠1+∠2,
∵,,
∴∠B=∠1,
∴DE//BC .
【点睛】本题考查了平行线的判定与性质,判断命题的真假,熟练掌握平行线的判定与性质是解题的关键.
3.如图,已知直线,给出下列信息:
①;②平分;③.
(1)请在上述3条信息中选择其中两条作为条件,其余的一条信息作为结论组成一个真命题,你选择的条件是 ,结论是 (只要填写序号),并说明理由.
(2)在(1)的条件下,若比的倍少度,求的度数.
【答案】(1)①②;③;理由见解析
(2)
【分析】(1)由角平分线的定义可得,再根据等角的余角相等可得出,再由平行线的性质可得,从而结论得证;
(2)由(1)得:,根据比的倍少度,可得关系式,求得,,再根据即可得到的度数.
【详解】(1)解:条件:①②,结论:③.理由如下:
∵平分,
∴,
∵,
∴,,
∴,
∵,
∴,
∴.
故答案为:①②;③.
(2)由(1)得:,
∵比的倍少度,
∴,
∴,
解得:,
∴,
∴.
∴的度数.
【点睛】本题考查了角平分线的定义,等角的余角相等,平行线的性质,解方程组等知识.理解和掌握平行线的性质,等角的余角相等是解题的关键.
4.如图,点D,E,F分别是三角形的边,,上的点,给定以下三个条件:①;②;③.请从这三个条件中选择两个作为条件(放在已知处),另一个作为结论(放在证明处)组成一个真命题,并进行证明.
已知:________,________.
求证:________.
证明:
【答案】见解析
【分析】本题考查平行线性质和判定,根据题意选择两个作为条件,另一个作为结论组成一个真命题,并结合平行线性质和判定进行证明,即可解题.
【详解】解:(答案不唯一)已知:,,
求证:.
证明:,
(两直线平行,内错角相等).
,
(两直线平行,同位角相等),
.
已知:,,
求证:.
证明:,
(两直线平行,内错角相等).
,
(等量代换),
(同位角相等,两直线平行).
已知:,,
求证:.
证明:,
(两直线平行,同位角相等).
,
(等量代换),
(内错角相等,两直线平行).
5.如图,点在上,直线交于点.请从①,②平分,③中任选两个作为条件,余下一个作为结论,构造一个真命题,并求证.
已知:______,求证:______.(只须填写序号)
证明:
【答案】①②,③,证明见解析.(答案不唯一)
【分析】根据平行线的性质可得,再由角平分线的性质可得,再利用等量代换可得
【详解】解:已知①②,求证∶③,
证明∶∵,
∴,
∵平分,
∴,
∴.
故答案为∶①②;③.
【点睛】此题主要考查了角平分线的定义、证明以及平行线的性质,关键是掌握两直线平行,内错角相等.
重难点4 平移的性质及应用
【例4】.如图,一个四边形经过平移后得到四边形.
(1)线段的对应线段是___________;
(2)的对应角是___________;
(3)线段和线段有何关系?
【答案】(1)
(2)
(3)
【分析】本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
(1)根据平移的性质解答即可;
(2)根据平移的性质解答即可;
(3)根据平移的性质解答即可.
【详解】(1)线段的对应线段是.
故答案为:;
(2)的对应角是.
故答案为:;
线段和线段有何关系为:.
方法指导
解决平移有关问题,只需熟练掌握平移的性质即可,即(1)平移不改变图形的形状和大小;(2)经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
变式训练4
1.如图所示,是由沿箭头方向平移得到的.
(1)若,求的度数;
(2)若,求,的长.
【答案】(1)
(2)5,5
【分析】本题考查了平移的性质,熟练掌握平行的性质是解题的关键.
(1)根据平移的性质即可得到结论;
(2)根据平移的性质即可得到结论.
【详解】(1)解:是由沿箭头方向平移得到的,,
.
(2)解:是由沿箭头方向平移得到的,
.
2.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥,桥宽忽略不计.
(1)若荷塘的长为90米,宽为50米,则小桥总长为 米;
(2)若荷塘周长为米,则小桥总长为 米.
【答案】(1)
(2)
【分析】本题考查了生活中的平移现象,熟练掌握平移的性质是解题的关键.
(1)根据平移的性质可得:小桥总长就等于长方形荷塘的长与宽的和;
(2)由平移的性质得,小桥总长长方形周长的一半,据此即可求出答案.
【详解】(1)解:由平移的性质得,小桥总长就等于长方形荷塘的长与宽的和,
∴,
故答案为:.
(2)由平移的性质得,小桥总长长方形周长的一半,
∴,
故答案为:
3.如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
【答案】道路的宽为2米
【分析】本题考查一元二次方程的实际应用,设道路的宽为,利用平移得到草坪为一个长为,宽为的一个矩形,利用矩形的面积公式列出方程,进行求解即可.
【详解】解:设道路的宽为,由题意,得:,
解得:(舍去),;
答:道路的宽为2米.
4.如图所示,某商场重新装修后,准备在门前台阶上铺设地毯,已知这种地毯的批发价为每平方米50元,其台阶的尺寸如图所示,则购买地毯至少需要元.
【答案】元
【分析】本题考查了生活中的平移,熟记平移的性质并理解地毯长度的求法是解题的关键.
根据平移可知地毯的长度等于横向与纵向的长度之和求出地毯的长度,再根据矩形的面积列式求出地毯的面积,然后乘以单价计算即可得解.
【详解】解:解:地毯的长度至少为:(米);
(元).
答:铺设梯子的红地毯至少需要米,花费至少元.
5.已知的顶点A平移到顶点D,请用两种不同的方法,在图中作出平移后的图形.
【答案】见解析
【分析】本题涉及平移的知识.熟练掌握平移的定义是关键.
方法一:过点B作且使,过点C作且使,然后顺次连接D、E、F即可;
方法二:过点D作且使,过点D作且使,然后顺次连接D、E、F即可.
【详解】解:方法一,如图1;
方法2,如图2.
重难点5 思想方法
构造法
【例5-1】.【阅读理解】两条平行线间的拐点问题经常可以通过作一条直线的平行线进行转化.例如:如图,直线,求证:
(1)阅读下面的解答过程,并填上适当的理由
解:过点作直线,
已知,,
【方法运用】
(2)如图2,直线,若,,求的度数.
【答案】(1)见解析;(2)
【分析】本题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.
(1)根据平行线的判定与性质求解即可;
(2)根据(1)的方法过点作直线,进而根据平行线的判定与性质求解即可.
【详解】(1)解:过点作直线,
两直线平行,内错角相等
已知,,
平行于同一条直线的两条直线平行
两直线平行,内错角相等
(2)解:过点作直线
,
,
,,
,
,
,
,
°.
方法指导
有“拐点”时,常常过拐点作平行线,构造平行线的性质解决问题。
变式训练5-1
1.已知直线,点,在直线上,点,在直线上,的平分线与的平分线交于点,,.
(1)如图1,点在点的左边,点在点的右边,求的度数;
(2)在(1)的条件下,求的度数;(用含的式子表示)
(3)将图1中的线段向左平移,使点落在点的左边,其他条件不变,在图2中画出符合题意的图形,并求出的值.
【答案】(1)
(2)
(3)
【分析】本题主要考查了平行线的性质,角平分线的性质,解题的关键是熟练掌握相关性质进行灵活应用.
(1)利用角平分线的性质和平行线的性质即可解答本题;
(2)过点作,则,利用角平分线的性质表示,再根据平行线的性质及角的和差关系即可得答案;
(3)根据题目要求画出图形,过点作,利用拐点模型即可解答此题.
【详解】(1)解:平分,
,,
,
,
∴的度数为.
(2)解:如图,过点作,则,
平分,
,
∵,
∴,,
(3)解:如图所示,
平分,
过点作,
又
∴的值为
2.如图,若,,,求的度数.
【答案】
【分析】本题考查了平行线的性质与判定,过点作,得出,,进而即可求解.
【详解】解:如图,过点作
∴
∴
∵,
∴
∵,
∴
∴
3. 综合与实践:
【问题初探】
()数学活动课上,王老师给出如下问题:如图①,,点在之间且点在点右侧,求证:(提示:过点作);
【类比探究】
()小明对王老师给出的问题进行改编:如图②,,点在之间且点在点左侧,猜想,,之间的数量关系: ,并加以证明;
【学以致用】
()如图③是超市的购物车,图④是其侧面示意图,已知,,测量得知,,直接写出的度数 .
【答案】()证明见解析;(),证明见解析;()
【分析】()如图①,过点作,可得,,即得,进而即可求证;
()如图②,过点作,可得,,即得,进而即可求证;
()如图③,过点作,过点作,根据平行线的性质可得,,进而即可求解;
本题考查了平行线的判定和性质,正确作出辅助线是解题的关键.
【详解】()证明:如图①,过点作,则,
∵,
∴,
∴,
∵,
∴;
(),证明如下:
如图②,过点作,则,
∵,
∴,
∴,
∴,
即;
()解:如图③,过点作,过点作,
∴,,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故答案为:.
转化思想
【例5-2】.与是两个完全相同的直角三角形.将沿点B到点C的方向从的位置平移到如图所示的位置.若,图中阴影部分的面积为84,,求平移的距离.
【答案】平移的距离为.
【分析】本题考查了平移的性质,根据平移可得,,,得到,,再根据梯形的面积公式即可求解,掌握平移的性质是解题的关键.
【详解】解:根据平移可得:,,,
∴,,
∴,
∴,
∴,
∴平移的距离为.
方法指导
根据平移不改变图形的大小的性质,将零散的图形转化成规则图形面积。
变式训练5-2
1.如图,在三角形中,,,.将三角形沿向右平移,得到三角形,与交于点,连接.
(1)分别求和的度数;
(2)若,,求图中阴影部分的面积.
【答案】(1);
(2)10
【分析】(1)由平移的性质得,,,,,则,由此可得的度数;由得,由此可得的度数;
(2)先根据,得,再根据三角形的面积公式可求出图中阴影部分的面积;
此题主要考查了图形的平移变换及其性质,熟练掌握图形的平移变换及其性质是解决问题的关键.
【详解】(1)解:由平移性质得:,,,,,
∴,
∴,
∵,
∴,
∴;
(2)∵,,
∴,
又∵,
∴;
2.如图,将直角三角形沿方向平移线段的长度得到直角三角形,已知,,求图中四边形的面积.
【答案】9
【分析】本题考查了平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.同时考查了梯形的面积公式.根据平移的性质可得,,在根据即可得到答案.
【详解】解:∵沿的方向平移距离得,
∴,
∵,
∴,
∴,
∴.
即四边形的面积为9.
3.如图,在三角形中,,,.将三角形沿向右平移,得到三角形,与交于点,连接.
(1)________,________;
(2)若,,求图中阴影部分的面积;
(3)已知点在三角形的内部,点经过相同平移后的对应点为,连接.若三角形的周长为,四边形的周长为,请直接写出的长度.
【答案】(1),
(2)
(3)
【分析】本题考查了平移的性质,平行线的性质;能熟练利用平移的性质进行求解是解题的关键.
(1)由平移的性质得,,由平行线的性质即可求解;
(2)由平移的性质得,由即可求解;
(3)由平移的性质得,,,,即可求解;
【详解】(1)解:由平移得,
,
,
,
,
,
,
故答案为:,;
(2)解:由平移得,
;
(3)解:由平移得
,,
,,
,
,
,
,
解得:,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
