人教版高中物理必修第二册第七章万有引力与宇宙航行4宇宙航行课件(53页PPT)
文档属性
| 名称 | 人教版高中物理必修第二册第七章万有引力与宇宙航行4宇宙航行课件(53页PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-01 00:00:00 | ||
图片预览











文档简介
(共53张PPT)
第七章 万有引力与宇宙航行
4.宇宙航行
目标导航:1.知道三个宇宙速度及含义,了解卫星的分类.(物理观念) 2.会推导第 一宇宙速度,掌握人造卫星的线速度、角速度、周期与轨道半径的关系.(科学思 维) 3.了解人类在宇宙探索方面的重要成就,培养应用物理规律造福人类的意识. (科学态度与责任)
第*页
研习任务一
情境 导学
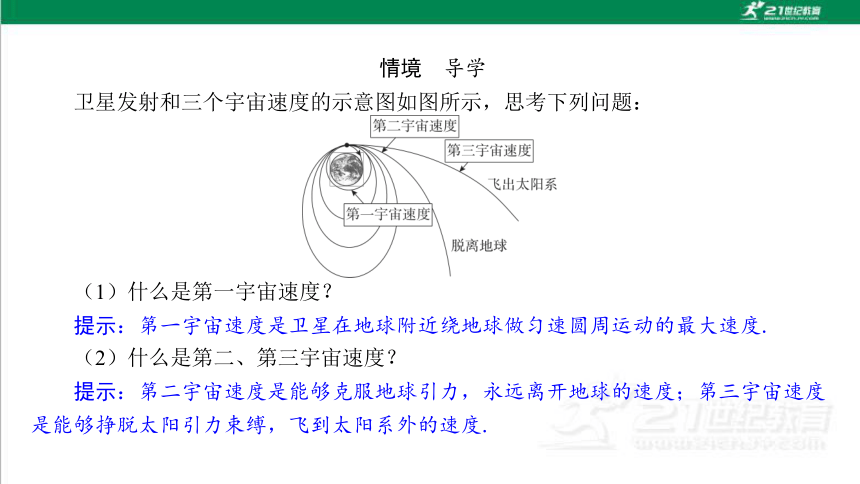
卫星发射和三个宇宙速度的示意图如图所示,思考下列问题:
(1)什么是第一宇宙速度?
提示:第一宇宙速度是卫星在地球附近绕地球做匀速圆周运动的最大速度.
(2)什么是第二、第三宇宙速度?
提示:第二宇宙速度是能够克服地球引力,永远离开地球的速度;第三宇宙速度 是能够挣脱太阳引力束缚,飞到太阳系外的速度.
知识 梳理
1. 第一宇宙速度
(1)定义:物体在地球附近绕地球做 运动的速度叫作第一宇宙速度.
(2)大小:v=7.9 km/s.
2. 第二宇宙速度
在地面附近发射飞行器,如果速度大于 ,又小于11.2 km/s,它绕地球运 行的轨迹就不是圆,而是椭圆.当飞行器的速度等于或大于11.2 km/s时,它就会克服 地球的引力,永远离开 .我们把 叫作第二宇宙速度.
3. 第三宇宙速度
在地面附近发射飞行器,如果要使其挣脱太阳引力的束缚,飞到太阳系外,必须使它 的速度等于或大于16.7 km/s,这个速度叫作第三宇宙速度.
匀速圆周
7.9 km/s
地球
11.2 km/s
深化 理解
1. 对第一宇宙速度的推导
2. 对宇宙速度的理解
(1)三个宇宙速度都是指发射速度,指在地面附近使航天器获得的速度,然后靠惯 性飞行.
(2)当发射速度达到第一宇宙速度,即v=7.9 km/s时,物体贴近地球表面做匀速圆 周运动,不再落回地面.当发射速度小于7.9 km/s时,物体最终落回地面,所以第一 宇宙速度是发射卫星的最小速度.
(3)当在地面的发射速度11.2 km/s>v>7.9 km/s时,卫星绕地球旋转的轨道是椭 圆,地球位于一个焦点上.
(4)当在地面的发射速度16.7 km/s>v≥11.2 km/s时,卫星脱离地球的束缚,成为 太阳系的一颗“小行星”或绕其他行星运动的卫星.
研习 经典
A. 16 km/s B. 32 km/s C. 4 km/s D. 2 km/s
[巧指导]
先推导行星上的第一宇宙速度与地球上的第一宇宙速度的关系,再利用地球上的第
一宇宙速度求解此行星上的第一宇宙速度.
A
对于任何天体,计算其近地卫星环绕速度时,都是根据万有引力提供向心力,近 地卫星的轨道半径等于天体的半径,然后利用牛顿第二定律列式计算.
A. 此卫星的发射速度大于第一宇宙速度
B. 此卫星在远地点的速度大于第一宇宙速度
C. 若想让卫星进入月球轨道,发射速度需大于第二宇宙速度
D. 若想让卫星进入太阳轨道,发射速度需大于第三宇宙速度
A
解析:第一宇宙速度是卫星的最小发射速度,要想发射卫星,发射速度至少为第一宇 宙速度,且轨道越高,发射速度越大,椭圆轨道为某卫星的运行轨道,则此卫星的发 射速度大于第一宇宙速度,A正确;第一宇宙速度是近地卫星绕地球表面做圆周运动 的运行速度,也是卫星绕地球做圆周运动的最大速度,此卫星在远地点做近心运动, 此卫星的速度小于在离地相同高度的圆轨道上做圆周运动的速度,故此卫星在远地点 的速度小于第一宇宙速度,B错误;卫星在月球轨道运行时还在地球吸引范围之内, 发射速度不能超过第二宇宙速度,C错误;发射速度大于第三宇宙速度时,卫星将脱 离太阳的束缚,飞到太阳系外,D错误.
第*页
研习任务二
情境 导学
图甲为不同轨道上的人造地球卫星,图乙为我国的天宫二号空间实验室.天 宫二号的轨道高度大约是393 km,同步卫星的轨道高度大约是3.6×104 km.思 考下列问题:
(1)天宫二号和同步卫星的周期相比较哪个更大?
提示:同步卫星的周期更大.
(2)天宫二号和同步卫星的运行速度、加速度哪个更大?
提示:天宫二号的运行速度、加速度更大.
深化 理解
1. 轨道及特点
(1)轨道:赤道轨道、极地轨道及其他轨道.如图所示.
(2)特点:所有轨道的圆心都在地心.
(2)卫星的各物理量随轨道半径变化的规律
3. 地球同步静止卫星
(1)概念:相对于地面静止且与地球自转具有相同周期的卫星,叫作地球同步静止 卫星.
(2)特点:六个“一定”
①转动方向一定:和地球自转方向一致;
②周期一定:和地球自转周期相同,即T=24 h;
③角速度一定:等于地球自转的角速度;
④轨道平面一定:所有的静止卫星都在赤道的正上方,其轨道平面必须与赤道平面成 0度角;
⑤高度一定:离地面高度固定不变(约3.6×104 km);
⑥速率一定:线速度大小一定(约3.1×103 m/s).
研习 经典
角度1 人造卫星的运行规律
A. 北斗-G5受到地球的引力小于北斗-M3受到地球的引力
B. 北斗-G5和北斗-M3绕地球运转的线速度均小于7.9 km/s
C. 北斗-M3绕地球运转的角速度小于北斗-G5的角速度
D. 北斗-M3绕地球运转的向心加速度小于北斗-G5的向心加速度
B
角度2 地球赤道上的物体、近地卫星、同步卫星的运动参量比较
A
A. ωA=ωC<ωB B. TA=TC<TB
C. vA=vC<vB D. aA=aC>aB
地球卫星的an、v、ω、T由地球的质量M和卫星的轨道半径r决定,当r确定后,卫 星的an、v、ω、T便确定了,与卫星的质量、形状等因素无关,俗称“一(r)定四 (an、v、ω、T)定”.
A. 飞船从1轨道变到2轨道要点火加速
B. 飞船在1轨道周期大于2轨道周期
C. 飞船在1轨道速度大于2轨道
D. 飞船在1轨道加速度大于2轨道
ACD
AD
知识 构建
第*页
课堂强研习 合作学习 精研重难
课后提素养
A. 人造卫星绕地球在圆轨道上运行时的速度大于或等于7.9 km/s、小于11.2 km/s
B. 火星探测卫星的发射速度大于16.7 km/s
C. 第三宇宙速度是在地面附近使物体可以挣脱地球引力束缚,成为绕太阳运行的人 造行星的最小发射速度
D. 第一宇宙速度7.9 km/s是人造地球卫星绕地球做圆周运动的最大运行速度
D
A. A、B两行星表面重力加速度之比等于它们的半径之比
B. 两卫星的线速度一定相等
C. 行星A、B的质量和半径一定相等
D. 行星A、B的密度一定相等
AD
A. 周期 B. 角速度
C. 线速度 D. 向心加速度
A
B
5. 已知地球半径为R,地球表面重力加速度为g,引力常量为G,不考虑地球自 转的影响.
(1)求地球的质量;
(2)试推导第一宇宙速度的表达式.
答案:见解析
第*页
课时作业(十三) 宇宙航行
[基础训练]
A. 第一宇宙速度是人造地球卫星在圆轨道运行时的最大速度
B. 第一宇宙速度是人造地球卫星在圆轨道运行时的最小速度
C. 人造地球卫星在圆轨道运行时的速度可以等于第二宇宙速度
D. 地球上的物体无论具有多大的速度都不可能脱离太阳的束缚
A
1
2
3
4
5
6
7
8
9
10
11
C
1
2
3
4
5
6
7
8
9
10
11
A. a、b的线速度大小之比是3∶2
D. a、b的向心加速度大小之比是9∶4
CD
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
A. 在轨道Ⅱ上处于受力平衡状态
B. 在轨道Ⅰ运行周期比在Ⅱ时短
C. 从轨道Ⅰ进入Ⅱ在P处要加速
D. 沿轨道Ⅰ向P飞近时速度增大
D
1
2
3
4
5
6
7
8
9
10
11
解析:“天问一号”探测器在轨道Ⅱ上做变速圆周运动,受力不平衡,故A错误;根 据开普勒第三定律可知,轨道Ⅰ的半长轴大于轨道Ⅱ的半长轴,故在轨道Ⅰ运行周期比 在Ⅱ时长,故B错误;“天问一号”探测器从轨道Ⅰ进入Ⅱ做近心运动,需要的向心力 要小于提供的向心力,故要在P点点火减速,故C错误;在轨道Ⅰ向P飞近时,由开普 勒第二定律知,速度增大,故D正确.
1
2
3
4
5
6
7
8
9
10
11
A. 3.3×103 km/s B. 7.9×103 km/s
C. 1.2×104 km/s D. 1.9×104 km/s
D
1
2
3
4
5
6
7
8
9
10
11
D
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
[能力提升]
A. a、c的加速度大小相等,且大于b的加速度
B. b、c的角速度大小相等,且小于a的角速度
C. a、c的线速度大小相等,且大于d的线速度
D. a、c存在相撞的危险
AC
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
A. 卫星在轨道Ⅰ上运动时,在P点的线速度大于在Q点的线速度
B. 卫星在轨道Ⅰ上运动时,在P点的加速度小于在Q点的加速度
C. 卫星沿轨道Ⅰ运动到P点时的加速度大于沿轨道Ⅱ运动到P点时的加速度
D. 卫星要从轨道Ⅰ进入轨道Ⅱ,需在P点减速
AD
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
A. 甲的向心加速度比乙的小
B. 甲的运行周期比乙的小
C. 甲的角速度比乙的大
D. 甲的线速度比乙的大
A
1
2
3
4
5
6
7
8
9
10
11
A. a的向心加速度等于g
B. 在相同时间内b转过的弧长最长
C. a的线速度等于b的线速度
D. d的运动周期可能是21 h
B
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
11. (2024·江苏镇江中学期中)航天员驾驶宇宙飞船绕质量分布均匀的一星球 做匀速圆周运动,测得飞船线速度大小的二次方与轨道半径的倒数的关系图像 如图中实线所示,该图线(直线)的斜率为k,图中r0(该星球的半径)为已知 量,引力常量为G. 求:
(1)该星球的密度;
1
2
3
4
5
6
7
8
9
10
11
(2)该星球的第一宇宙速度.
1
2
3
4
5
6
7
8
9
10
11
第七章 万有引力与宇宙航行
4.宇宙航行
目标导航:1.知道三个宇宙速度及含义,了解卫星的分类.(物理观念) 2.会推导第 一宇宙速度,掌握人造卫星的线速度、角速度、周期与轨道半径的关系.(科学思 维) 3.了解人类在宇宙探索方面的重要成就,培养应用物理规律造福人类的意识. (科学态度与责任)
第*页
研习任务一
情境 导学
卫星发射和三个宇宙速度的示意图如图所示,思考下列问题:
(1)什么是第一宇宙速度?
提示:第一宇宙速度是卫星在地球附近绕地球做匀速圆周运动的最大速度.
(2)什么是第二、第三宇宙速度?
提示:第二宇宙速度是能够克服地球引力,永远离开地球的速度;第三宇宙速度 是能够挣脱太阳引力束缚,飞到太阳系外的速度.
知识 梳理
1. 第一宇宙速度
(1)定义:物体在地球附近绕地球做 运动的速度叫作第一宇宙速度.
(2)大小:v=7.9 km/s.
2. 第二宇宙速度
在地面附近发射飞行器,如果速度大于 ,又小于11.2 km/s,它绕地球运 行的轨迹就不是圆,而是椭圆.当飞行器的速度等于或大于11.2 km/s时,它就会克服 地球的引力,永远离开 .我们把 叫作第二宇宙速度.
3. 第三宇宙速度
在地面附近发射飞行器,如果要使其挣脱太阳引力的束缚,飞到太阳系外,必须使它 的速度等于或大于16.7 km/s,这个速度叫作第三宇宙速度.
匀速圆周
7.9 km/s
地球
11.2 km/s
深化 理解
1. 对第一宇宙速度的推导
2. 对宇宙速度的理解
(1)三个宇宙速度都是指发射速度,指在地面附近使航天器获得的速度,然后靠惯 性飞行.
(2)当发射速度达到第一宇宙速度,即v=7.9 km/s时,物体贴近地球表面做匀速圆 周运动,不再落回地面.当发射速度小于7.9 km/s时,物体最终落回地面,所以第一 宇宙速度是发射卫星的最小速度.
(3)当在地面的发射速度11.2 km/s>v>7.9 km/s时,卫星绕地球旋转的轨道是椭 圆,地球位于一个焦点上.
(4)当在地面的发射速度16.7 km/s>v≥11.2 km/s时,卫星脱离地球的束缚,成为 太阳系的一颗“小行星”或绕其他行星运动的卫星.
研习 经典
A. 16 km/s B. 32 km/s C. 4 km/s D. 2 km/s
[巧指导]
先推导行星上的第一宇宙速度与地球上的第一宇宙速度的关系,再利用地球上的第
一宇宙速度求解此行星上的第一宇宙速度.
A
对于任何天体,计算其近地卫星环绕速度时,都是根据万有引力提供向心力,近 地卫星的轨道半径等于天体的半径,然后利用牛顿第二定律列式计算.
A. 此卫星的发射速度大于第一宇宙速度
B. 此卫星在远地点的速度大于第一宇宙速度
C. 若想让卫星进入月球轨道,发射速度需大于第二宇宙速度
D. 若想让卫星进入太阳轨道,发射速度需大于第三宇宙速度
A
解析:第一宇宙速度是卫星的最小发射速度,要想发射卫星,发射速度至少为第一宇 宙速度,且轨道越高,发射速度越大,椭圆轨道为某卫星的运行轨道,则此卫星的发 射速度大于第一宇宙速度,A正确;第一宇宙速度是近地卫星绕地球表面做圆周运动 的运行速度,也是卫星绕地球做圆周运动的最大速度,此卫星在远地点做近心运动, 此卫星的速度小于在离地相同高度的圆轨道上做圆周运动的速度,故此卫星在远地点 的速度小于第一宇宙速度,B错误;卫星在月球轨道运行时还在地球吸引范围之内, 发射速度不能超过第二宇宙速度,C错误;发射速度大于第三宇宙速度时,卫星将脱 离太阳的束缚,飞到太阳系外,D错误.
第*页
研习任务二
情境 导学
图甲为不同轨道上的人造地球卫星,图乙为我国的天宫二号空间实验室.天 宫二号的轨道高度大约是393 km,同步卫星的轨道高度大约是3.6×104 km.思 考下列问题:
(1)天宫二号和同步卫星的周期相比较哪个更大?
提示:同步卫星的周期更大.
(2)天宫二号和同步卫星的运行速度、加速度哪个更大?
提示:天宫二号的运行速度、加速度更大.
深化 理解
1. 轨道及特点
(1)轨道:赤道轨道、极地轨道及其他轨道.如图所示.
(2)特点:所有轨道的圆心都在地心.
(2)卫星的各物理量随轨道半径变化的规律
3. 地球同步静止卫星
(1)概念:相对于地面静止且与地球自转具有相同周期的卫星,叫作地球同步静止 卫星.
(2)特点:六个“一定”
①转动方向一定:和地球自转方向一致;
②周期一定:和地球自转周期相同,即T=24 h;
③角速度一定:等于地球自转的角速度;
④轨道平面一定:所有的静止卫星都在赤道的正上方,其轨道平面必须与赤道平面成 0度角;
⑤高度一定:离地面高度固定不变(约3.6×104 km);
⑥速率一定:线速度大小一定(约3.1×103 m/s).
研习 经典
角度1 人造卫星的运行规律
A. 北斗-G5受到地球的引力小于北斗-M3受到地球的引力
B. 北斗-G5和北斗-M3绕地球运转的线速度均小于7.9 km/s
C. 北斗-M3绕地球运转的角速度小于北斗-G5的角速度
D. 北斗-M3绕地球运转的向心加速度小于北斗-G5的向心加速度
B
角度2 地球赤道上的物体、近地卫星、同步卫星的运动参量比较
A
A. ωA=ωC<ωB B. TA=TC<TB
C. vA=vC<vB D. aA=aC>aB
地球卫星的an、v、ω、T由地球的质量M和卫星的轨道半径r决定,当r确定后,卫 星的an、v、ω、T便确定了,与卫星的质量、形状等因素无关,俗称“一(r)定四 (an、v、ω、T)定”.
A. 飞船从1轨道变到2轨道要点火加速
B. 飞船在1轨道周期大于2轨道周期
C. 飞船在1轨道速度大于2轨道
D. 飞船在1轨道加速度大于2轨道
ACD
AD
知识 构建
第*页
课堂强研习 合作学习 精研重难
课后提素养
A. 人造卫星绕地球在圆轨道上运行时的速度大于或等于7.9 km/s、小于11.2 km/s
B. 火星探测卫星的发射速度大于16.7 km/s
C. 第三宇宙速度是在地面附近使物体可以挣脱地球引力束缚,成为绕太阳运行的人 造行星的最小发射速度
D. 第一宇宙速度7.9 km/s是人造地球卫星绕地球做圆周运动的最大运行速度
D
A. A、B两行星表面重力加速度之比等于它们的半径之比
B. 两卫星的线速度一定相等
C. 行星A、B的质量和半径一定相等
D. 行星A、B的密度一定相等
AD
A. 周期 B. 角速度
C. 线速度 D. 向心加速度
A
B
5. 已知地球半径为R,地球表面重力加速度为g,引力常量为G,不考虑地球自 转的影响.
(1)求地球的质量;
(2)试推导第一宇宙速度的表达式.
答案:见解析
第*页
课时作业(十三) 宇宙航行
[基础训练]
A. 第一宇宙速度是人造地球卫星在圆轨道运行时的最大速度
B. 第一宇宙速度是人造地球卫星在圆轨道运行时的最小速度
C. 人造地球卫星在圆轨道运行时的速度可以等于第二宇宙速度
D. 地球上的物体无论具有多大的速度都不可能脱离太阳的束缚
A
1
2
3
4
5
6
7
8
9
10
11
C
1
2
3
4
5
6
7
8
9
10
11
A. a、b的线速度大小之比是3∶2
D. a、b的向心加速度大小之比是9∶4
CD
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
A. 在轨道Ⅱ上处于受力平衡状态
B. 在轨道Ⅰ运行周期比在Ⅱ时短
C. 从轨道Ⅰ进入Ⅱ在P处要加速
D. 沿轨道Ⅰ向P飞近时速度增大
D
1
2
3
4
5
6
7
8
9
10
11
解析:“天问一号”探测器在轨道Ⅱ上做变速圆周运动,受力不平衡,故A错误;根 据开普勒第三定律可知,轨道Ⅰ的半长轴大于轨道Ⅱ的半长轴,故在轨道Ⅰ运行周期比 在Ⅱ时长,故B错误;“天问一号”探测器从轨道Ⅰ进入Ⅱ做近心运动,需要的向心力 要小于提供的向心力,故要在P点点火减速,故C错误;在轨道Ⅰ向P飞近时,由开普 勒第二定律知,速度增大,故D正确.
1
2
3
4
5
6
7
8
9
10
11
A. 3.3×103 km/s B. 7.9×103 km/s
C. 1.2×104 km/s D. 1.9×104 km/s
D
1
2
3
4
5
6
7
8
9
10
11
D
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
[能力提升]
A. a、c的加速度大小相等,且大于b的加速度
B. b、c的角速度大小相等,且小于a的角速度
C. a、c的线速度大小相等,且大于d的线速度
D. a、c存在相撞的危险
AC
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
A. 卫星在轨道Ⅰ上运动时,在P点的线速度大于在Q点的线速度
B. 卫星在轨道Ⅰ上运动时,在P点的加速度小于在Q点的加速度
C. 卫星沿轨道Ⅰ运动到P点时的加速度大于沿轨道Ⅱ运动到P点时的加速度
D. 卫星要从轨道Ⅰ进入轨道Ⅱ,需在P点减速
AD
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
A. 甲的向心加速度比乙的小
B. 甲的运行周期比乙的小
C. 甲的角速度比乙的大
D. 甲的线速度比乙的大
A
1
2
3
4
5
6
7
8
9
10
11
A. a的向心加速度等于g
B. 在相同时间内b转过的弧长最长
C. a的线速度等于b的线速度
D. d的运动周期可能是21 h
B
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
11. (2024·江苏镇江中学期中)航天员驾驶宇宙飞船绕质量分布均匀的一星球 做匀速圆周运动,测得飞船线速度大小的二次方与轨道半径的倒数的关系图像 如图中实线所示,该图线(直线)的斜率为k,图中r0(该星球的半径)为已知 量,引力常量为G. 求:
(1)该星球的密度;
1
2
3
4
5
6
7
8
9
10
11
(2)该星球的第一宇宙速度.
1
2
3
4
5
6
7
8
9
10
11
