1.3 第2课时 三角形三边的垂直平分线及作图 课件(共366张PPT)
文档属性
| 名称 | 1.3 第2课时 三角形三边的垂直平分线及作图 课件(共366张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 20.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 10:58:27 | ||
图片预览








文档简介
(共36张PPT)
北师大版数学八年级下册
第一章 三角形的证明
汇报人:孙老师
汇报班级:X级X班
1.3 第2课时 三角形三边的垂直平分线及作图
3 线段的垂直平分线
目录
壹
课前复习
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
课前复习
课前复习
如图,在中,是 的垂直平分线,
且,分别交于点和, ,
,则 为( ).
C
A. B. C. D.
第贰章节
新课导入
新课导入
作三角形三条边的垂直平分线,你发现了什么?
P
三条边的垂直平分线交于一点P
第叁章节
新知探究
新知探究
三角形三边的垂直平分线的性质
1
合作探究
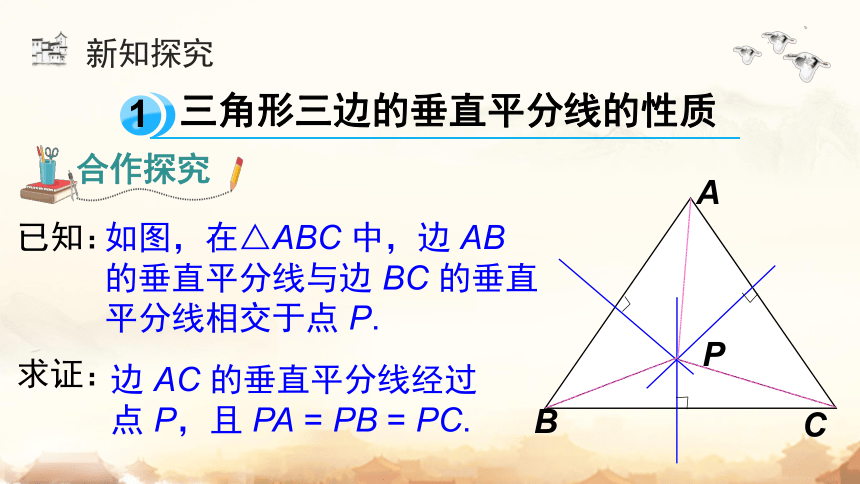
已知:
求证:
B
C
A
P
如图,在△ABC 中,边 AB 的垂直平分线与边 BC 的垂直平分线相交于点 P.
边 AC 的垂直平分线经过点 P,且 PA = PB = PC.
试试看,你会写出证明过程吗?
B
C
A
P
l
n
m
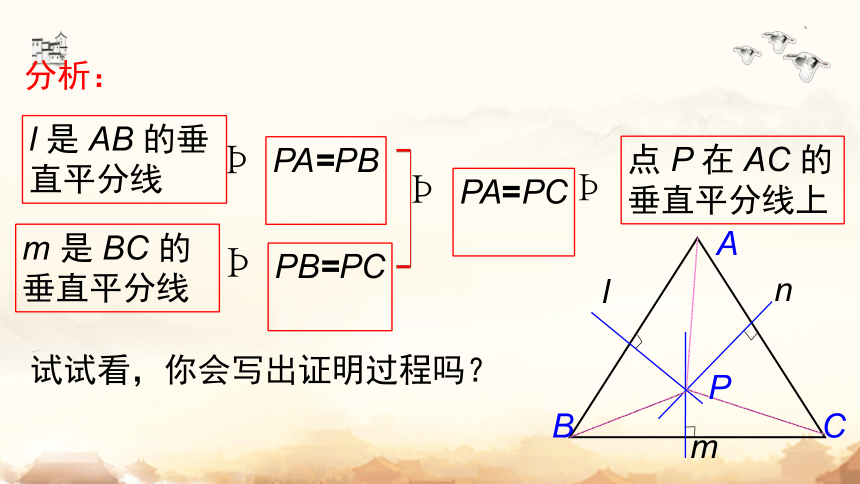
l 是 AB 的垂直平分线
m 是 BC 的垂直平分线
PA=PB
PB=PC
PA=PC
点 P 在 AC 的垂直平分线上
分析:
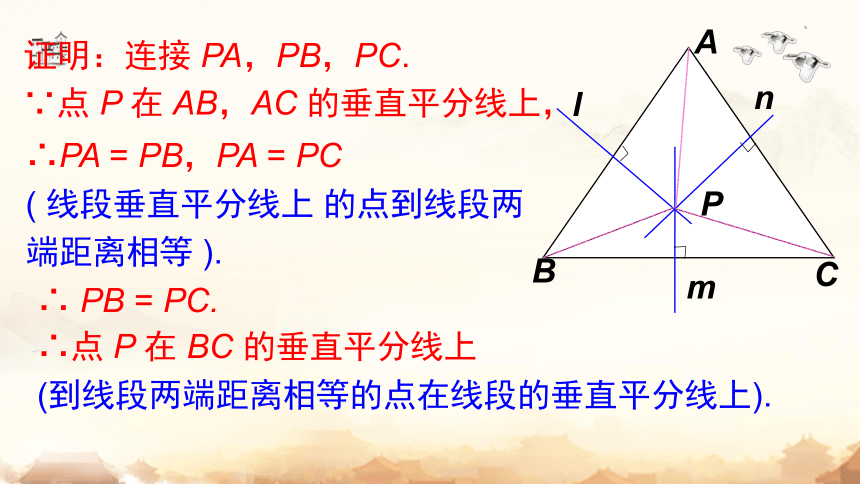
证明:连接 PA,PB,PC.
B
C
A
P
l
n
m
∴点 P 在 BC 的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
∴ PB = PC.
∴PA = PB,PA = PC
( 线段垂直平分线上 的点到线段两端距离相等 ).
∵点 P 在 AB,AC 的垂直平分线上,
应用格式:
∵ 点 P 为 △ABC 三边垂直平分线的交点,
∴ PA = PB = PC.
A
B
C
P
归纳总结
定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
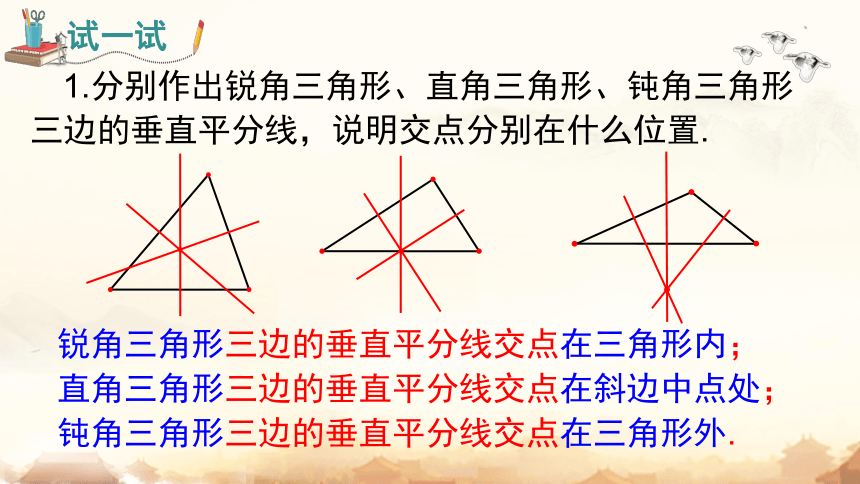
1.分别作出锐角三角形、直角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
锐角三角形三边的垂直平分线交点在三角形内;
直角三角形三边的垂直平分线交点在斜边中点处;
钝角三角形三边的垂直平分线交点在三角形外.
试一试
做一做: (1) 已知三角形的一条边及这条边上的高,你能作出三角形吗 如果能,能作几个 所作出的三角形都全等吗
已知:三角形的一条边 a 和这边上的高 h.
求作:△ABC,使 BC = a,BC 边上的高为 h.
Al
D
C
B
A
a
h
(D)
C
B
A
a
h
Al
D
C
B
A
a
h
Al
提示:能作出无数个这样的三角形,它们并不全等.
尺规作图
2
(2) 已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.
想一想:如何作出一个已知底及底边上的高的等腰三角形呢?
例 已知:线段 a,h.
求作:△ABC,使 AB = AC,BC = a,
高 AD = h.
l
D
C
B
a
h
A
作法:1. 作线段 BC = a;
2. 作线段 BC 的垂直平分线 l 交 BC
于点 D;
3. 在 l 上作线段 DA,使 DA=h .
4. 连接 AB,AC.
则△ABC 为所求的等腰三角形.
典例精析
(1) 先以 P 为圆心,大于点 P 到直线 l 的垂直距离 R 为半径作圆,交直线 l 于A,B.
B
A
作法:
2. 已知直线 l 和线外一点 P,利用尺规作 l 的垂线,使它经过点 P.
● P
C
D
(3) 过两交点作直线 l' ,此直线为 l
过 P 的垂线.
(2) 分别以 A、B 为圆心,大于 R 的长
为半径作圆,相交于 C、D 两点.
试一试
回顾导入
食堂应建在三个宿舍楼 A、B、C 的垂直平分线上,才能使得它到宿舍楼的距离相等.请画出这个位置.
解:如图所示,
连接 AB、BC、AC,分别作三条线段的垂直平分线,即点 P 为所求.
第肆章节
随堂练习
随堂练习
1.如图,在中, ,
, ,观察图中尺规作图的痕
迹,则 的长为( ).
C
A.1 B.2 C.3 D.4
2.如图,在中,, .
(1)用尺规作线段的垂直平分线,交于点,交于点 ;
(保留作图痕迹,不要求写作法)
解:如图,是 的垂直平分线.
(2)求 的周长.
解:是 的垂直平分线,
,
的周长 ,
的周长 ,
.
的周长是16.
3.如图是一块三角形的草坪,,, 点处各
种一棵树,现要在草坪上建一灌溉出水口,要
使出水口到三棵树的距离相等,则灌溉出水口
的位置应选在( ).
A
A.三边的垂直平分线的交点 B.三条角平分线的交点
C.三条高所在直线的交点 D.三条中线的交点
4.下列尺规作图,能判断是 边上的中线的是( ).
A
A. B. C. D.
5.如图,在中, , .
(1)尺规作图:作的垂直平分线交于点,交于点 ;
(不写作法,保留作图痕迹)
解:如图所示,就是要求作的 边上的中垂线;
(2)连接,求证:平分 .
证明: ,
,
,
,
是 边上的中垂线,
,
, ,
,
,平分 .
6.金秋十月,某校体育运动会顺利举行,运动员们
在赛场上奋力拼搏,老师们全力提供服务保障.如图,
过道上,两点相距,, 为两个班级,
于点,于点 ,为方便同学们接
取饮用水,现要在过道上临时设立一个饮水站,使得, 两个班级
到 站的距离相等.
(1)请用直尺(不带刻度)和圆规画出饮水站 的位置;
(不要求写作法,但要保留作图痕迹)
解:如图,连接,作线段的垂直平分线,交 于
点,则点 即为所求.
(2)已知,,求饮水站到点 的距离.
解:由题意得, ,
设,则 ,
, ,
,
在 中,
由勾股定理得 ,
在 中,
由勾股定理得 ,
, ,
,
即 ,
解得, .
答:饮水站到点的距离为 .
第伍章节
课堂小结
课堂小结
三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知一个等腰三角形的底边及底边上的高,作这个等腰三角形:
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学八年级下册
第一章 三角形的证明
汇报人:孙老师
汇报班级:X级X班
1.3 第2课时 三角形三边的垂直平分线及作图
3 线段的垂直平分线
目录
壹
课前复习
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
课前复习
课前复习
如图,在中,是 的垂直平分线,
且,分别交于点和, ,
,则 为( ).
C
A. B. C. D.
第贰章节
新课导入
新课导入
作三角形三条边的垂直平分线,你发现了什么?
P
三条边的垂直平分线交于一点P
第叁章节
新知探究
新知探究
三角形三边的垂直平分线的性质
1
合作探究
已知:
求证:
B
C
A
P
如图,在△ABC 中,边 AB 的垂直平分线与边 BC 的垂直平分线相交于点 P.
边 AC 的垂直平分线经过点 P,且 PA = PB = PC.
试试看,你会写出证明过程吗?
B
C
A
P
l
n
m
l 是 AB 的垂直平分线
m 是 BC 的垂直平分线
PA=PB
PB=PC
PA=PC
点 P 在 AC 的垂直平分线上
分析:
证明:连接 PA,PB,PC.
B
C
A
P
l
n
m
∴点 P 在 BC 的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上).
∴ PB = PC.
∴PA = PB,PA = PC
( 线段垂直平分线上 的点到线段两端距离相等 ).
∵点 P 在 AB,AC 的垂直平分线上,
应用格式:
∵ 点 P 为 △ABC 三边垂直平分线的交点,
∴ PA = PB = PC.
A
B
C
P
归纳总结
定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
1.分别作出锐角三角形、直角三角形、钝角三角形三边的垂直平分线,说明交点分别在什么位置.
锐角三角形三边的垂直平分线交点在三角形内;
直角三角形三边的垂直平分线交点在斜边中点处;
钝角三角形三边的垂直平分线交点在三角形外.
试一试
做一做: (1) 已知三角形的一条边及这条边上的高,你能作出三角形吗 如果能,能作几个 所作出的三角形都全等吗
已知:三角形的一条边 a 和这边上的高 h.
求作:△ABC,使 BC = a,BC 边上的高为 h.
Al
D
C
B
A
a
h
(D)
C
B
A
a
h
Al
D
C
B
A
a
h
Al
提示:能作出无数个这样的三角形,它们并不全等.
尺规作图
2
(2) 已知等腰三角形的底及底边上的高,你能用尺规作出等腰三角形吗?能作几个?
这样的等腰三角形只有两个,并且它们是全等的,分别位于已知底边的两侧.
想一想:如何作出一个已知底及底边上的高的等腰三角形呢?
例 已知:线段 a,h.
求作:△ABC,使 AB = AC,BC = a,
高 AD = h.
l
D
C
B
a
h
A
作法:1. 作线段 BC = a;
2. 作线段 BC 的垂直平分线 l 交 BC
于点 D;
3. 在 l 上作线段 DA,使 DA=h .
4. 连接 AB,AC.
则△ABC 为所求的等腰三角形.
典例精析
(1) 先以 P 为圆心,大于点 P 到直线 l 的垂直距离 R 为半径作圆,交直线 l 于A,B.
B
A
作法:
2. 已知直线 l 和线外一点 P,利用尺规作 l 的垂线,使它经过点 P.
● P
C
D
(3) 过两交点作直线 l' ,此直线为 l
过 P 的垂线.
(2) 分别以 A、B 为圆心,大于 R 的长
为半径作圆,相交于 C、D 两点.
试一试
回顾导入
食堂应建在三个宿舍楼 A、B、C 的垂直平分线上,才能使得它到宿舍楼的距离相等.请画出这个位置.
解:如图所示,
连接 AB、BC、AC,分别作三条线段的垂直平分线,即点 P 为所求.
第肆章节
随堂练习
随堂练习
1.如图,在中, ,
, ,观察图中尺规作图的痕
迹,则 的长为( ).
C
A.1 B.2 C.3 D.4
2.如图,在中,, .
(1)用尺规作线段的垂直平分线,交于点,交于点 ;
(保留作图痕迹,不要求写作法)
解:如图,是 的垂直平分线.
(2)求 的周长.
解:是 的垂直平分线,
,
的周长 ,
的周长 ,
.
的周长是16.
3.如图是一块三角形的草坪,,, 点处各
种一棵树,现要在草坪上建一灌溉出水口,要
使出水口到三棵树的距离相等,则灌溉出水口
的位置应选在( ).
A
A.三边的垂直平分线的交点 B.三条角平分线的交点
C.三条高所在直线的交点 D.三条中线的交点
4.下列尺规作图,能判断是 边上的中线的是( ).
A
A. B. C. D.
5.如图,在中, , .
(1)尺规作图:作的垂直平分线交于点,交于点 ;
(不写作法,保留作图痕迹)
解:如图所示,就是要求作的 边上的中垂线;
(2)连接,求证:平分 .
证明: ,
,
,
,
是 边上的中垂线,
,
, ,
,
,平分 .
6.金秋十月,某校体育运动会顺利举行,运动员们
在赛场上奋力拼搏,老师们全力提供服务保障.如图,
过道上,两点相距,, 为两个班级,
于点,于点 ,为方便同学们接
取饮用水,现要在过道上临时设立一个饮水站,使得, 两个班级
到 站的距离相等.
(1)请用直尺(不带刻度)和圆规画出饮水站 的位置;
(不要求写作法,但要保留作图痕迹)
解:如图,连接,作线段的垂直平分线,交 于
点,则点 即为所求.
(2)已知,,求饮水站到点 的距离.
解:由题意得, ,
设,则 ,
, ,
,
在 中,
由勾股定理得 ,
在 中,
由勾股定理得 ,
, ,
,
即 ,
解得, .
答:饮水站到点的距离为 .
第伍章节
课堂小结
课堂小结
三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知一个等腰三角形的底边及底边上的高,作这个等腰三角形:
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
