初中数学人教版八年级下册 第17章《勾股定理》 期末知识点复习题(含解析)
文档属性
| 名称 | 初中数学人教版八年级下册 第17章《勾股定理》 期末知识点复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-02 14:51:58 | ||
图片预览


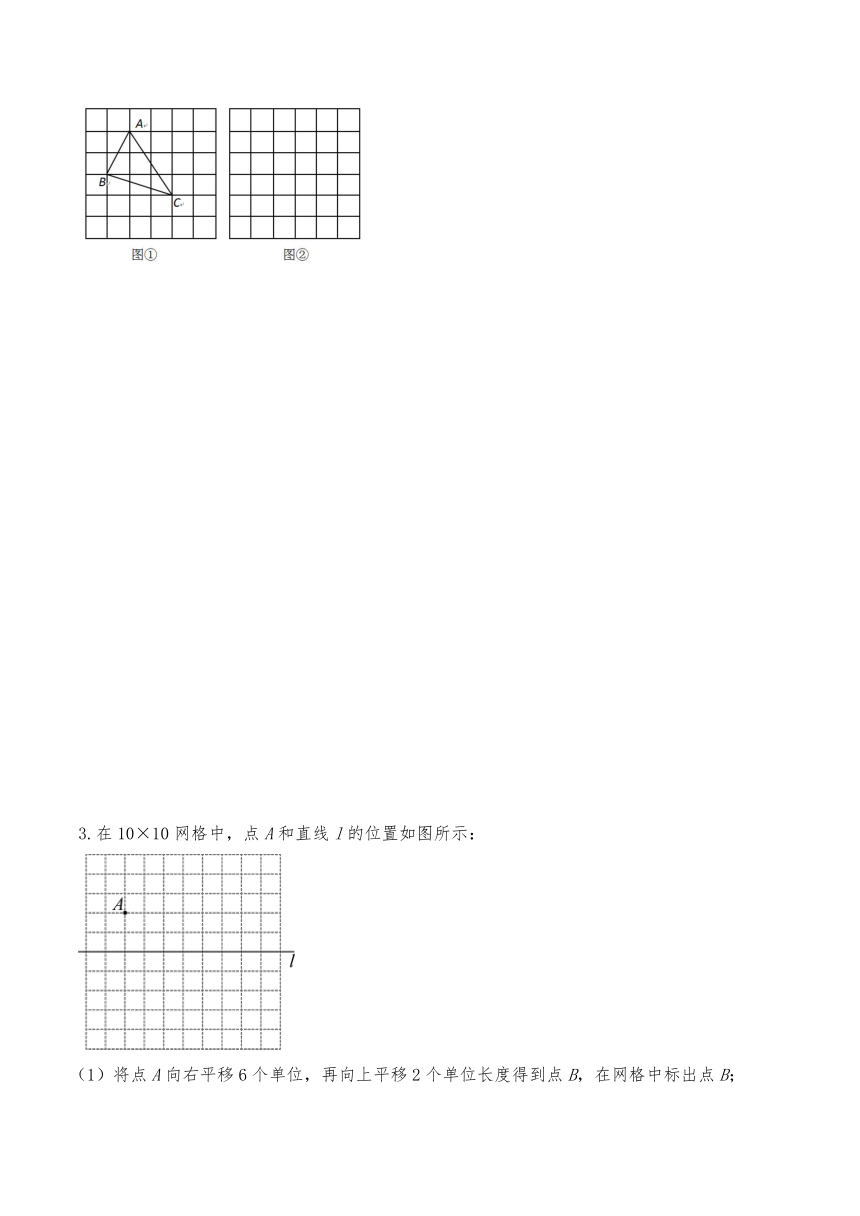

文档简介
第17章《勾股定理》 期末知识点复习题
【题型1 由勾股定理求两条线段的平方和(差)】
1.如图,射线于点、点、在、上,为线段的中点,且于点.
(1)若,直接写出的值;
(2)若,的周长为24,求的面积;
(3)若,点在射线上移动,问此过程中,的值是否为定值?若是,请求出这个定值;若不是,请求出它的取值范围.
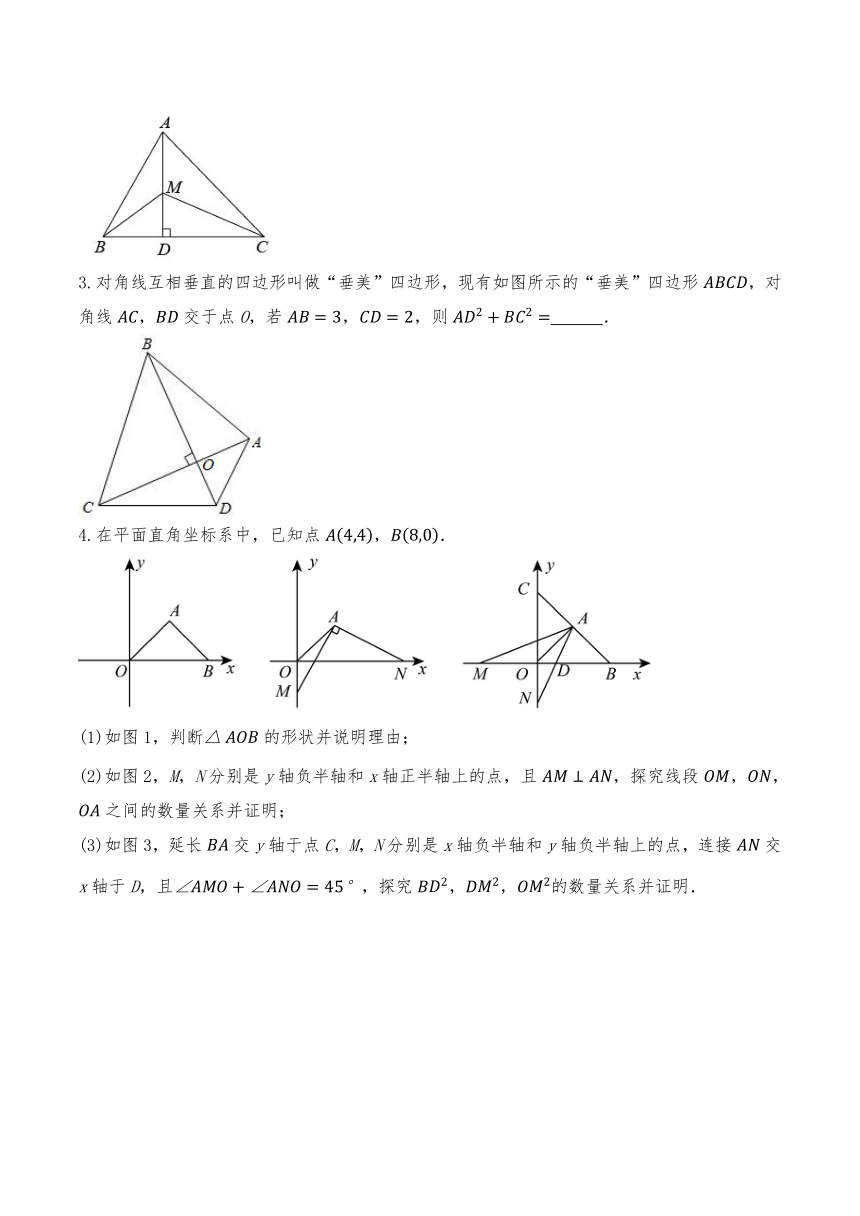
2.如图所示,已知中,,,于,为上任一点,则等于 .
3.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线,交于点O,若,,则 .
4.在平面直角坐标系中,已知点,.
(1)如图1,判断的形状并说明理由;
(2)如图2,M,N分别是y轴负半轴和x轴正半轴上的点,且,探究线段,,之间的数量关系并证明;
(3)如图3,延长交y轴于点C,M,N分别是x轴负半轴和y轴负半轴上的点,连接交x轴于D,且,探究,,的数量关系并证明.
【题型2 勾股定理在网格问题中的运用】
1.在每个小正方形的边长为1的网格图形中.每个小正方形的顶点称为格点.以顶点都是格点的正方形的边为斜边,向外作四个全等的直角三角形,使四个直角顶点都是格点,且四边形为正方形,我们把这样的图形称为格点弦图.例如,在图1所示的格点弦图中,正方形的边长为,此时正方形的面积为.问:当格点弦图中的正方形的边长为时,正方形的面积的所有可能值是 (不包括).
2.问题背景:在△ABC中,AB、BC、AC三边的长分别为,,,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上: ;
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为a,2a,a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新:
(3)若△ABC三边的长分别为(m>0,n>0,且m≠n),试运用构图法求出这三角形的面积.
3.在10×10网格中,点A和直线l的位置如图所示:
(1)将点A向右平移6个单位,再向上平移2个单位长度得到点B,在网格中标出点B;
(2)在(1)的条件下,在直线l上确定一点P,使PA+PB的值最小,保留画图痕迹,并直接写出PA+PB的最小值:______;
(3)结合(2)的画图过程并思考,直接写出+的最小值:____
4.如图,是由边长为1的小正方形构成的10×10网格,每个小正方形的顶点叫做格点.五边形ABCDE的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)五边形ABCDE的周长为 .
(2)在AB上找点F,使E,C两点关于直线DF对称;
(3)设DF交CE于点G,连接AG,直接写出四边形AEDG的面积;
(4)在直线DF上找点H,使∠AHB=135°.
【题型3 勾股定理在折叠问题中的运用】
1.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P是边AC上一动点,把△ABP沿直线BP折叠,使得点A落在图中点A′处,当△AA′C是直角三角形时,则线段CP的长是 .
2.定义:若a,b,c是△ABC的三边,且a2+b2=2c2,则称△ABC为“方倍三角形”.
(1)对于①等边三角形②直角三角形,下列说法一定正确的是 .
A.①一定是“方倍三角形”B.②一定是“方倍三角形”
C.①②都一定是“方倍三角形”D.①②都一定不是“方倍三角形”
(2)若Rt△ABC是“方倍三角形”,且斜边AB=,则该三角形的面积为 ;
(3)如图,△ABC中,∠ABC=120°,∠ACB=45°,P为AC边上一点,将△ABP沿直线BP进行折叠,点A落在点D处,连接CD,AD.若△ABD为“方倍三角形”,且AP=,求△PDC的面积.
3.如图1,在△ABC,AB=AC=10,BC=12.
(1)求BC边上的高线长.
(2)点E是BC边上的动点,点D在边AB上,且AD=4,连结DE.
①如图2,当点E是BC中点时,求△BDE的面积.
②如图3,沿DE将△BDE折叠得到△FDE,当DF与△ABC其中一边垂直时,求BE的长.
4.定义:若a,b,c是△ABC的三边,且,则称△ABC为“方倍三角形”.
(1)对于①等边三角形②直角三角形,下列说法一定正确的是___.
A. ①一定是“方倍三角形” B. ②一定是“方倍三角形”
C. ①②都一定是“方倍三角形” D. ①②都一定不是“方倍三角形”
(2)若Rt△ABC是“方倍三角形”,且斜边,则该三角形的面积为___;
(3)如图,△ABC中,,,P为AC边上一点,将△ABP沿直线BP进行折叠,点A落在点D处,连结CD,AD,若△ABD为“方倍三角形”,且AP=,求BC的长.
【题型4 以弦图为背景的计算】
1.在认识了勾股定理的赵爽弦图后,一位同学尝试将个全等的小正方形嵌入长方形内部,其中点,,,分别在长方形的边,,和上,若,,则小正方形的边长为( )
A. B. C. D.
2.如图,它是由弦图变化得到的,是由八个全等的直角三角形拼接而成的,将图中正方形、正方形、正方形的面积分别记为、、.
(1)若,,则 .
(2)若,则 .
3.如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成的.已知,正方形的面积为.连接AC,交于点P,交于点Q,连接.则图中阴影部分的面积之和为 .
4.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形,正方形,正方形的面积分别为,,,若,则的值是 .
【题型5 勾股定理的证明方法】
1.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.
(1)证明勾股定理
取4个与(图1)全等的三角形,其中,把它们拼成边长为的正方形,其中四边形是边长为c的正方形,如图2,请你利用以下图形验证勾股定理.
(2)应用勾股定理
①应用场景1:在数轴上画出表示无理数的点.
如图3,在数轴上找出表示1的点D和表示4的点A,过点A作直线l垂直于,在l上取点B,使,以点D为圆心,为半径作弧,则弧与数轴的交点C表示的数是______.
②应用场景2:解决实际问题.
如图4,某公园有一秋千,秋千静止时,踏板离地的垂直高度,将它往前推至C处时,水平距离,踏板离地的垂直高度,它的绳索始终拉直,求绳索的长.
2.计算图1的面积,把图1看作一个大正方形,它的面积是,如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为,由此得到:.
(1)如图2,正方形是由四个边长分别是a,b的长方形和中间一个小正方形组成的,用不同的方法对图2的面积进行计算,你发现的等式是______(用a,b表示)
(2)已知:两数x,y满足,,求的值.
(3)如图3,正方形的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,对图3的面积进行计算,你发现的等式是______.(用a,b,c表示,结果化到最简)
3.综合与实践
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得结论.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
【方法运用】千百年来,人们对勾股定理的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者.向常春在2010年构造发现了一个新的证法:把两个全等的直角三角形和如图2放置,其三边长分别为,,,,显然.
(1)请用,,分别表示出四边形,梯形,的面积,再探究这三个图形面积之间的关系,证明勾股定理.
(2)【方法迁移】请利用“双求法”解决下面的问题:如图3,小正方形边长为1,连接小正方形的三个顶点,可得,则边上的高为______.
(3)如图4,在中,是边上的高,,,,设,求的值.
4.如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形构造图3的图形,你能利用这个图形证明出题(1)的结论吗?如果能,请写出证明过程;
(3)当a=3,b=4时,将其中一个直角三角形放入平面直角坐标系中,使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合(如图4中Rt△AOB的位置).点C为线段OA上一点,将△ABC沿着直线BC翻折,点A恰好落在x轴上的D处.
①请写出C、D两点的坐标;
②若△CMD为等腰三角形,点M在x轴上,请直接写出符合条件的所有点M的坐标.
【题型6 勾股定理与全等综合】
1.如图,在中,,为底边上的高线,E是上一点,连接交于点F,且.
(1)求证:;
(2)如图1,若,,求的长;
(3)如图2,若,以,和为边,能围成直角三角形吗?请判断,并说明理由.
2.如图,把一张矩形纸片沿对角线折叠,若,,那么的长为 .
3.如图,正方形的边长为10,,,连接,则线段的长为( )
A. B. C. D.
4.在等腰中,,,是射线上的动点,过点作(始终在上方),且,连接.
(1)如图1,当点在线段上时,判断与的关系,并说明理由.
(2)如图2,若点为线段上的两个动点,且,连接,,求的长.
(3)若在点的运动过程中,,则___.
(4)如图3,若为中点,连接,在点的运动过程中,当__时,的长最小?最小值是___.
【题型7 由勾股定理确定在几何体中的最短距离】
1.如图,在墙角处放着一个长方体木柜(木柜与墙面和地面均没有缝腺),一只蚂蚁从柜角处沿着木柜表面爬到柜角处.若,,,则蚂蚁爬行的最短路程是( )
A. B. C. D.12
2.如图,一个圆柱形食品盒,它的高为,底面圆的周长为
(1)点A位于盒外底面的边缘,如果在A处有一只蚂蚁,它想吃到盒外表面对侧中点B处的食物,则蚂蚁需要爬行的最短路程是 ;
(2)将左图改为一个无盖的圆柱形食品盒,点C距离下底面,此时蚂蚁从C处出发,爬到盒内表面对侧中点B处(如右图),则蚂蚁爬行的最短路程是 .
3.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是 cm
4.初中几何的学习始于空间的“实物和具体模型”,聚焦平面的“几何图形的特征和运用”,形成了空间几何问题要转化为平面几何问题的解题策略.
问题提出:如图所示是放在桌面上的一个圆柱体,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,如何求最短路程呢?
(1)问题分析:蚂蚁从点出发沿着圆柱体的表面爬行到点,可以有几条路径?在图中画出来;
(2)问题探究:①若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;
②若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;
③若圆柱体的底面圆的半径为,高为,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程.
【题型8 由勾股定理构造图形解决实际问题】
1.如图所示,A、B两块试验田相距200m,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
2.2019年10月1日,中华人民共和国70年华诞之际,王梓涵和学校国旗护卫队的其他同学们赶到学校举行了简朴而降重的升旗仪式.倾听着雄壮的国歌声,目送着五星红旗缓缓升起,不禁心潮澎湃,爱国之情油然而生.爱动脑筋的王梓涵设计了一个方案来测量学校旗杆的高度.将升旗的绳子拉直到末端刚好接触地面,测得此时绳子末端距旗杆底端2米,然后将绳子末端拉直到距离旗杆5m处,测得此时绳子末端距离地面高度为1m,最后根据刚刚学习的勾股定理就能算出旗杆的高度为( )
A.10m B.11m C.12m D.13m
3.【问题探究】
(1)如图①,点E是正△ABC高AD上的一定点,请在AB上找一点F,使EF=AE,并说明理由;
(2)如图②,点M是边长为2的正△ABC高AD上的一动点,求AM+MC的最小值;
【问题解决】
(3)如图③,A、B两地相距600km,AC是笔直地沿东西方向向两边延伸的一条铁路,点B到AC的最短距离为360km.今计划在铁路线AC上修一个中转站M,再在BM间修一条笔直的公路。如果同样的物资在每千米公路上的运费是铁路上的两倍。那么,为使通过铁路由A到M再通过公路由M到B的总运费达到最小值,请确定中转站M的位置,并求出AM的长.(结果保留根号)
4.目前,某市正积极推进“五城联创”,其中扩充改造绿地是推进工作计划之一.现有一块直角三角形绿地,量得两直角边长分别为a=9m和b=12m,现要将此绿地扩充改造为等腰三角形,且扩充部分包含以b=12m为直角边的直角三角形,则扩充后等腰三角形的周长为 .
参考答案
【题型1 由勾股定理求两条线段的平方和(差)】
1.解:(1).
(2)因为,所以是直角三角形.
因为,的周长为,所以,
所以,解得,所以,
所以.
(3)在中,,在中,,
所以.
因为为线段的中点,所以,所以.
在中,,
所以(定值),
故在点移动的过程中,的值是定值,其值是.
2.
【分析】在和中,分别表示出和,在和中,表示出和,代入求解即可;
【详解】解:∵于,
∴,
在和中,
,,
在和中,
,
,
,
.
故答案为:.
3.13
【分析】在和中,根据勾股定理得,,进一步得,再根据,可求得的值.
【详解】解:,
,
在和中,根据勾股定理得,
,,
,
,,
.
故答案为:.
4.(1)解:为等腰直角三角形,理由如下:
过点A作,垂足为H,
∵点,,
∴,
∴,
∴,
∴, ,
∴为等腰直角三角形;
(2). 理由:过点A作,交x轴于点B,
由(1)可知是等腰直角三角形,
∴,,
∴,
∵, ∴,
∴,
在和中, ,
∴,
∴,
∴, 而是等腰直角三角形,可得,
∴;
(3),理由如下: 过A作 交y轴于G,连接,如图:
∵是等腰直角三角形,
∴,,,
∴,
∵,
∴,
在和中, ,
∴,
∴,,
而中,,
∴,
∵,,
∴,
∵,
∴, 即
∴,
在和中, ,
∴,
∴,
∴.
【题型2 勾股定理在网格问题中的运用】
1.或
【分析】设四个全等的直角三角形的直角边边长分别为a,b.利用分类讨论的思想,在格点上找出各点位置,即找出边的位置,即可求出面积.
【详解】设四个全等的直角三角形的直角边边长分别为a,b.则正方形EFGH的边长为a+b,
即 .
∴在网格中找出a和b的线段,且线段的端点都在格点上即可.
分情况讨论:
① ,如图,
此时.
② ,如图,
此时.
③,如图,
此时.
题干中不包括52,
故的值为36或50.
故答案为:36或50.
2.解:(1)的面积为,
故答案为:;
(2)如图,,,,
由图可得:;
故答案为:;
(3)构造所示,,
,
,
∴.
3.解:(1)如图所示:
(2)如图所示,PA+PB的最小值=;
故答案为:;
(3)如图,,,
∴PA+PB的最小值即为:,
∴+的最小值为,
故答案为:.
3.解:(1)由题意, ,,,
∴五边形ABCDE的周长=20+,
故答案为: .
(2)如图,连接EC,作DF⊥EC交AB于点F,点F即为所求作.
∵,DF⊥EC,
∴,
∴点D,G是CE垂直平分线上的点,
∴DF是CE的垂直平分线,
∴E,C两点关于直线DF对称;
(3)∵,,
∴,
∴是直角三角形;
∴.
(4)如图,过点A作AH⊥DF于H,连接BH,则点H即为所求作.
∵,,
∴.
∴是等腰直角三角形.
∴.
∴.
【题型3 勾股定理在折叠问题中的运用】
1.4或3
【分析】分类讨论分别当∠AA′C=90°时,当∠ACA′=90°时,根据折叠的性质函数直角三角形的性质即可得到结论.
【详解】解:如图1,当∠AA′C=90°时,
∵以直线BP为轴把△ABP折叠,使得点A落在图中点A′处,
∴AP=A′P,
∴∠PAA′=∠AA′P,
∵∠ACA′+∠PAA′=∠CA′P+∠AA′P=90°,
∴∠PCA′=∠PA′C,
∴PC=PA′,
∴PC=AC=4,
如图2,当∠ACA′=90°时,
∵在Rt△ABC中,∠ACB=90°,且AC=8,BC=6.
∴AB=10,
∵以直线BP为轴把△ABP折叠,使得点A落在图中点A′处,
∴A′B=AB=10,PA=PA′,
∴A′C=4,
设PC=x,
∴AP=8-x,
∵A′C2+PC2=PA′2,
∴42+x2=(8-x)2,
解得:x=3,
∴PC=3,
综上所述:当△AA′C是直角三角形时,则线段CP的长是4或3,
故答案为:4或3.
2.解:(1)对于①等边三角形,三边相等,
设边长为a,
则a2+a2=2a2,
根据“方倍三角形”定义可知:
等边三角形一定是“方倍三角形”;
对于②直角三角形,三边满足关系式:
a2+b2=c2,
根据“方倍三角形”定义可知:
直角三角形不一定是“方倍三角形”;
故答案为:A;
(2)设Rt△ABC其余两条边为a,b,
则满足a2+b2=3,
根据“方倍三角形”定义,还满足:
a2+3=2b2,
联立解得 ,
则Rt△ABC的面积为:;
故答案为:;
(3)由题意可知:
△ABP≌△DBP,
∴BA=BD,∠ABP=∠DBP,
根据“方倍三角形”定义可知:
BA2+BD2=2AD2=2BA2,
∴AD=AB=BD,
∴△ABD为等边三角形,∠BAD=60°,
∴∠ABP=∠DBP=30°,
∴∠PBC=90°,
∵∠CPB=45°,
∴∠APB=180°﹣45°=135°,
∴∠DPC=90°,
∵∠ABC=120°,∠ACB=45°,
∴∠BAC=15°,
∴∠CAD=45°,
∴△APD为等腰直角三角形,
∴AP=DP= ,
∴AD=2,
延长BP交AD于点E,如图,
∵∠ABP=∠PBD,
∴BE⊥AD,PE=AD=AE=1,
∴BE=,
∴PB=BE﹣PE= ﹣1,
∵∠CPB=∠PCB=45°,
∴△PBC为等腰直角三角形,
∴PC=PB=,
∴S△PDC=PC PD=()×=﹣1.
3.(1)解:如图,过作于
AB=AC=10,BC=12,
所以BC边上的高线长为
(2)解:①如图,连接
为的中点,
由(1)得:
则
②当时,由对折可得:
过作于 连接 过作于 过作于
由①得:
则
设
则
由
而
解得:
当于时,则
过作于 由对折可得
当时,如图,则
由对折可得 而 则
而
结合对折可得:
过作于
同理可得:
综上:当DF与△ABC其中一边垂直时,BE的长为或或.
4.(1)对于①等边三角形,三边相等,
设边长为a,
则,
根据“方倍三角形”定义可知:
等边三角形一定是“方倍三角形”;
对于②直角三角形,三边满足关系式:,
根据“方倍三角形”定义可知:
直角三角形不一定是“方倍三角形”;
故选:A
故答案为:A;
(2)设Rt△ABC其余两条边为a,b,
则满足,
根据“方倍三角形”定义,还满足:,
联立解得,
则Rt△ABC的面积为:;
故答案为:;
(3)由题意可知:,
∴,
根据“方倍三角形”定义可知:
,
∴,
∴△ABD为等边三角形,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴△APD为等腰直角三角形,
∴,
∴.
延长BP交AD于点E,如图,
∵,
∴,,
∴,
∴,
∵,
∴△PBC为等腰直角三角形,
∴.
【题型4 以弦图为背景的计算】
1.A
【分析】根据赵爽弦图,将小正方形分成4个全等的直角三角形,和一个最小的正方形,设直角三角形的短直角边长为,长直角边为,则正方形的水平宽度与垂直高度为,根据平移的性质,分别表示出,建立二元一次方程组,解方程组,进而勾股定理即可求解.
【详解】解:如图所示,根据赵爽弦图,将小正方形分成4个全等的直角三角形,和一个最小的正方形,
设直角三角形的短直角边长为,长直角边为,则正方形的水平宽度与垂直高度为,
依题意,
解得:
∴小正方形的边长为:,
故选:A.
2. 13 8
【分析】(1)首先结合题意求得正方形的边长,正方形的边长,由全等的直角三角的性质可得,,设,则,,然后可求得,,在中,由勾股定理可得,结合正方形面积公式即可获得答案;
(2)设每一个直角三角形面积为,则,,再结合即可获得答案.
【详解】解:(1)当,时,
正方形的边长,正方形的边长,
根据题意,该图形由八个全等的直角三角形拼接而成,
由全等的直角三角的性质可得,,
设,则,,
∴,解得,
∴,,
∴在中,,
∴正方形的面积;
故答案为:13;
(2)设每一个直角三角形面积为,
∴则,,
∵,
∴,
解得.
故答案为:8.
3.16
【分析】设,,根据正方形的面积公式和勾股定理可求得,再根据题意和三角形的面积公式可推导出,进而推出阴影部分的面积之和为梯形的面积,利用梯形面积公式求解即可.
【详解】解:由题意,,,,
∴,,,
∴,
∴,
∴,,
∵,
∴设,则,,
∴,
∴,
∴阴影部分的面积之和为
,
∵正方形的面积为,
∴即,
∴,
∴阴影部分的面积之和为16.
故答案为:16.
4.
【分析】由八个直角三角形全等,四边形,,为正方形,得出,,再根据三个正方形的面积公式列式相加:,求出的值,从而可以计算结论即可.
【详解】解:∵八个直角三角形全等,四边形,,为正方形,
∴,,
∴
,
,
∴,
∴,
∴,
故答案为:.
【题型5 勾股定理的证明方法】
1.(1)解:证明勾股定理:
由题意得,,,
∴,
∴.
(2)解:①在中,
,
,
点表示的数是.
故答案为:.
②,,
.
设秋千的绳索长为,根据题意可得,
利用勾股定理可得.
解得:.
答:绳索的长为.
2.(1)解:如图2,正方形的面积,
正方形的面积,
;
(2),且,,
,
即,
的值为.
(3)如图3,正方形的面积,
正方形的面积,
,
即.
3.(1)证明:∵,,,
∴
∴
∴
(2),
,
,
即AB边上的高是
(3)解:在中,由勾股定理得
∵,
∴
在中,由勾股定理得
∴,
∴
4.解:(1)∵S梯形ABCD=
S梯形ABCD=
.
(2)连接,
如图:
S四边形ABCD=,
S四边形ABCD=,
,
.
(3)①设,则,又,
根据翻折可知:
,,
.
在中,根据勾股定理,得
,
解得.
,.
答:、两点的坐标为,.
②如图:
当点在轴正半轴上时,
,
设,则,解得,
,
,;
,,,
,;
当点在轴负半轴上时,
,,
;
,,
,
,.
∴符合条件的所有点的坐标为:,、,、、,.
【题型6 勾股定理与全等综合】
1.(1)证明:在中,,,
∴,
由勾股定理得,
∴;
(2)解:由(1)可知,
在中,由勾股定理得,,
∵在中,,
∴是等腰直角三角形,
∴,
∴,
∴的长为3.5;
(3)解:能围成直角三角形,理由如下:
如图,在上取一点H,使,连接,,
∵,,
∴,
∴,
∵,,,
∴,
∴,,
∵,
∴,
∴,
∵,,
∴,,
∴,即,
又∵,
∴,
在中,由勾股定理,得,
∴,
∴以,和为边,能围成直角三角形.
2.
【分析】根据折叠的性质可得,设,则,在中,根据勾股定理即可求解.
【详解】解:矩形纸片沿对角线折叠,
∴,,,且,
∴,
∴,,
设,则,
在中,,
∴,解得,,
∴,
故答案为:.
3.B
【分析】延长交于点,根据正方形的性质证明,求出,,再证明,求出,,由勾股定理可得的长.
【详解】解:如图,延长交于点,
,,,
,,
和是直角三角形,
在和中,,
,
,,,
,,
,,
,,
在和中,,
,
,,,
,
同理可得,
在中,,
故选:B.
4.(1)解:当点在线段上时,
,,,
,
,
,
;
(2)解:,,
,
,
,
,
,
由(1)可知,,
,
设,
,
,
,
;
(3)解:如图1,当点在线段上,,设为边上的高,为垂足,
,
在等腰中,为的中点,,
,
,,
,
如图2,点在线段的延长线时,同理可得,
,
,
,
故答案为:或;
(4)解:点运动轨迹是过点,且垂直于的射线,根据垂线段最短的性质,当时,线段最短,如图3,
,
,,,
为等腰直角三角形,
,
由(1)知:,
,
此时,
故答案为:9,3.
【题型7 由勾股定理确定在几何体中的最短距离】
1.A
【分析】求出蚂蚁沿着木柜表面经线段到,以及蚂蚁沿着木柜表面经线段到的距离,再进行比较即可.
【详解】解:蚂蚁沿着木柜表面经线段到,
爬过的路径的长是,
蚂蚁沿着木柜表面经线段到,
爬过的路径的长是.
,最短路径的长是.
故选A.
2.
【分析】(1)把圆柱侧面展开,在中,利用勾股定理求解即可.
(2)将圆柱侧面展开,得到矩形,作点关于的对称点,构造,根据勾股定理求出即可解决问题.
【详解】(1)如图,把圆柱侧面展开,在中,
∵,
∴ ,
故答案为:.
(2)如图所示,点与点关于对称,可得,,
则最短路程为
故答案为:.
3.16
【分析】将正方形沿着翻折得到正方形 ,过点在正方形内部作,使,连接,过作于点,此时最小,运用勾股定理求解即可.
【详解】
如图,将正方形沿着翻折得到正方形 ,过点在正方形内部作,使,连接,过作于点,则四边形是矩形,四边形是平行四边形,
∴,,,,
此时最小,
∵点是中点,
∴cm,
∴cm,cm,
在中,cm,
∴cm,
故答案为:16.
4.(1)解:共有3条路径,如下图:
(2)解:①如图,连接,
根据题意得:,,
∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为;
②如图,连接,
根据题意得:,,
∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为;
③如图,连接,
根据题意得:,,
∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为.
【题型8 由勾股定理构造图形解决实际问题】
1.解:(1)△ABC是直角三角形;
理由如下:
∴AC2+BC2=1602+1202=40000,AB2=2002=40000,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)甲方案所修的水渠较短;
理由如下:
∵△ABC是直角三角形,
∴△ABC的面积=AB CH=AC BC,
∴CH=(m),
∵AC+BC=160+120=280(m),CH+AH+BH=CH+AB=96+200=296(m),
∴AC+BC<CH+AH+BH,
∴甲方案所修的水渠较短.
2.B
【分析】根据题意画出示意图,设旗杆高度为xm,可得AC=AD=xm,AB=(x﹣1)m,BC=5m,在Rt△ABC中利用勾股定理可求出x.
【详解】设旗杆高度为xm,可得AC=AD=xm,AB=(x﹣1)m,BC=5m,
根据勾股定理得,绳长的平方=x2+22,
如图,根据勾股定理得,绳长的平方=(x﹣1)2+52,
∴x2+22=(x﹣1)2+52,解得x=11,
故选:B.
3.解:(1)如图①,作EF⊥AB,垂足为点F,点F即为所求。
理由如下:∵点E是正△ABC高AD上的一定点,
∴∠BAD=30 ,
∵EF⊥AB,
∴EF=AE;
(2)如图②,作CN⊥AB,垂足为点N,交AD于点M,此时AM+MC最小,最小为CN的长。
∵△ABC是边长为2的正△ABC,
∴CN=BCsin60 =2×=
∴MN+CM=12AM+MC=
即AM+MC的最小值为
(3)如图③,作BD⊥AC,垂足为点D,在AC异于点B的一侧作∠CAN=30
作BF⊥AN,垂足为点F,交AC于点M,点M即为所求。
在Rt△ABD中,AD=(km)
在Rt△MBD中,∠MBD=∠MAF=30 ,得MD=BDtan30 =(km),
所以AM=(480 )km.
4.40米或48米或(30+6)米.
【详解】【分析】分三种情形讨论即可,①AB=BE1,②AB=AE3,③E2A=E2B,分别计算即可.
【详解】在Rt△ABC中,∵∠ACB=90°,BC=9,AC=12,∴AB==15,
①当BA=BE1=15时,CE1=6,
∴AE1==6,
∴△ABE1周长为(30+6)米;
②当AB=AE3=15时,CE3=BC=9,BE3=18,
∴△ABE3周长为48米;
③当E2A=E2B时,设E2C=x,则有E2A=BC+E2C=9+x,
∵∠ACE2=90°,∴AE22=CE22+AC2,
即(9+x)2=x2+122,
∴x=3.5,
∴E2A=E2B=9+3.5=12.5,
∴△ABE2周长为2×12.5+15=40米;
综上所述扩充后等腰三角形的周长为40米或48米或(30+6)米,
故答案为40米或48米或(30+6)米.
【题型1 由勾股定理求两条线段的平方和(差)】
1.如图,射线于点、点、在、上,为线段的中点,且于点.
(1)若,直接写出的值;
(2)若,的周长为24,求的面积;
(3)若,点在射线上移动,问此过程中,的值是否为定值?若是,请求出这个定值;若不是,请求出它的取值范围.
2.如图所示,已知中,,,于,为上任一点,则等于 .
3.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线,交于点O,若,,则 .
4.在平面直角坐标系中,已知点,.
(1)如图1,判断的形状并说明理由;
(2)如图2,M,N分别是y轴负半轴和x轴正半轴上的点,且,探究线段,,之间的数量关系并证明;
(3)如图3,延长交y轴于点C,M,N分别是x轴负半轴和y轴负半轴上的点,连接交x轴于D,且,探究,,的数量关系并证明.
【题型2 勾股定理在网格问题中的运用】
1.在每个小正方形的边长为1的网格图形中.每个小正方形的顶点称为格点.以顶点都是格点的正方形的边为斜边,向外作四个全等的直角三角形,使四个直角顶点都是格点,且四边形为正方形,我们把这样的图形称为格点弦图.例如,在图1所示的格点弦图中,正方形的边长为,此时正方形的面积为.问:当格点弦图中的正方形的边长为时,正方形的面积的所有可能值是 (不包括).
2.问题背景:在△ABC中,AB、BC、AC三边的长分别为,,,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上: ;
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为a,2a,a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新:
(3)若△ABC三边的长分别为(m>0,n>0,且m≠n),试运用构图法求出这三角形的面积.
3.在10×10网格中,点A和直线l的位置如图所示:
(1)将点A向右平移6个单位,再向上平移2个单位长度得到点B,在网格中标出点B;
(2)在(1)的条件下,在直线l上确定一点P,使PA+PB的值最小,保留画图痕迹,并直接写出PA+PB的最小值:______;
(3)结合(2)的画图过程并思考,直接写出+的最小值:____
4.如图,是由边长为1的小正方形构成的10×10网格,每个小正方形的顶点叫做格点.五边形ABCDE的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)五边形ABCDE的周长为 .
(2)在AB上找点F,使E,C两点关于直线DF对称;
(3)设DF交CE于点G,连接AG,直接写出四边形AEDG的面积;
(4)在直线DF上找点H,使∠AHB=135°.
【题型3 勾股定理在折叠问题中的运用】
1.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P是边AC上一动点,把△ABP沿直线BP折叠,使得点A落在图中点A′处,当△AA′C是直角三角形时,则线段CP的长是 .
2.定义:若a,b,c是△ABC的三边,且a2+b2=2c2,则称△ABC为“方倍三角形”.
(1)对于①等边三角形②直角三角形,下列说法一定正确的是 .
A.①一定是“方倍三角形”B.②一定是“方倍三角形”
C.①②都一定是“方倍三角形”D.①②都一定不是“方倍三角形”
(2)若Rt△ABC是“方倍三角形”,且斜边AB=,则该三角形的面积为 ;
(3)如图,△ABC中,∠ABC=120°,∠ACB=45°,P为AC边上一点,将△ABP沿直线BP进行折叠,点A落在点D处,连接CD,AD.若△ABD为“方倍三角形”,且AP=,求△PDC的面积.
3.如图1,在△ABC,AB=AC=10,BC=12.
(1)求BC边上的高线长.
(2)点E是BC边上的动点,点D在边AB上,且AD=4,连结DE.
①如图2,当点E是BC中点时,求△BDE的面积.
②如图3,沿DE将△BDE折叠得到△FDE,当DF与△ABC其中一边垂直时,求BE的长.
4.定义:若a,b,c是△ABC的三边,且,则称△ABC为“方倍三角形”.
(1)对于①等边三角形②直角三角形,下列说法一定正确的是___.
A. ①一定是“方倍三角形” B. ②一定是“方倍三角形”
C. ①②都一定是“方倍三角形” D. ①②都一定不是“方倍三角形”
(2)若Rt△ABC是“方倍三角形”,且斜边,则该三角形的面积为___;
(3)如图,△ABC中,,,P为AC边上一点,将△ABP沿直线BP进行折叠,点A落在点D处,连结CD,AD,若△ABD为“方倍三角形”,且AP=,求BC的长.
【题型4 以弦图为背景的计算】
1.在认识了勾股定理的赵爽弦图后,一位同学尝试将个全等的小正方形嵌入长方形内部,其中点,,,分别在长方形的边,,和上,若,,则小正方形的边长为( )
A. B. C. D.
2.如图,它是由弦图变化得到的,是由八个全等的直角三角形拼接而成的,将图中正方形、正方形、正方形的面积分别记为、、.
(1)若,,则 .
(2)若,则 .
3.如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成的.已知,正方形的面积为.连接AC,交于点P,交于点Q,连接.则图中阴影部分的面积之和为 .
4.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形,正方形,正方形的面积分别为,,,若,则的值是 .
【题型5 勾股定理的证明方法】
1.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要工具之一,也是数形结合的纽带之一.它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.
(1)证明勾股定理
取4个与(图1)全等的三角形,其中,把它们拼成边长为的正方形,其中四边形是边长为c的正方形,如图2,请你利用以下图形验证勾股定理.
(2)应用勾股定理
①应用场景1:在数轴上画出表示无理数的点.
如图3,在数轴上找出表示1的点D和表示4的点A,过点A作直线l垂直于,在l上取点B,使,以点D为圆心,为半径作弧,则弧与数轴的交点C表示的数是______.
②应用场景2:解决实际问题.
如图4,某公园有一秋千,秋千静止时,踏板离地的垂直高度,将它往前推至C处时,水平距离,踏板离地的垂直高度,它的绳索始终拉直,求绳索的长.
2.计算图1的面积,把图1看作一个大正方形,它的面积是,如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为,由此得到:.
(1)如图2,正方形是由四个边长分别是a,b的长方形和中间一个小正方形组成的,用不同的方法对图2的面积进行计算,你发现的等式是______(用a,b表示)
(2)已知:两数x,y满足,,求的值.
(3)如图3,正方形的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,对图3的面积进行计算,你发现的等式是______.(用a,b,c表示,结果化到最简)
3.综合与实践
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积有两种求法,一种是等于,另一种是等于四个直角三角形与一个小正方形的面积之和,即,从而得到等式,化简便得结论.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.
【方法运用】千百年来,人们对勾股定理的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者.向常春在2010年构造发现了一个新的证法:把两个全等的直角三角形和如图2放置,其三边长分别为,,,,显然.
(1)请用,,分别表示出四边形,梯形,的面积,再探究这三个图形面积之间的关系,证明勾股定理.
(2)【方法迁移】请利用“双求法”解决下面的问题:如图3,小正方形边长为1,连接小正方形的三个顶点,可得,则边上的高为______.
(3)如图4,在中,是边上的高,,,,设,求的值.
4.如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形构造图3的图形,你能利用这个图形证明出题(1)的结论吗?如果能,请写出证明过程;
(3)当a=3,b=4时,将其中一个直角三角形放入平面直角坐标系中,使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合(如图4中Rt△AOB的位置).点C为线段OA上一点,将△ABC沿着直线BC翻折,点A恰好落在x轴上的D处.
①请写出C、D两点的坐标;
②若△CMD为等腰三角形,点M在x轴上,请直接写出符合条件的所有点M的坐标.
【题型6 勾股定理与全等综合】
1.如图,在中,,为底边上的高线,E是上一点,连接交于点F,且.
(1)求证:;
(2)如图1,若,,求的长;
(3)如图2,若,以,和为边,能围成直角三角形吗?请判断,并说明理由.
2.如图,把一张矩形纸片沿对角线折叠,若,,那么的长为 .
3.如图,正方形的边长为10,,,连接,则线段的长为( )
A. B. C. D.
4.在等腰中,,,是射线上的动点,过点作(始终在上方),且,连接.
(1)如图1,当点在线段上时,判断与的关系,并说明理由.
(2)如图2,若点为线段上的两个动点,且,连接,,求的长.
(3)若在点的运动过程中,,则___.
(4)如图3,若为中点,连接,在点的运动过程中,当__时,的长最小?最小值是___.
【题型7 由勾股定理确定在几何体中的最短距离】
1.如图,在墙角处放着一个长方体木柜(木柜与墙面和地面均没有缝腺),一只蚂蚁从柜角处沿着木柜表面爬到柜角处.若,,,则蚂蚁爬行的最短路程是( )
A. B. C. D.12
2.如图,一个圆柱形食品盒,它的高为,底面圆的周长为
(1)点A位于盒外底面的边缘,如果在A处有一只蚂蚁,它想吃到盒外表面对侧中点B处的食物,则蚂蚁需要爬行的最短路程是 ;
(2)将左图改为一个无盖的圆柱形食品盒,点C距离下底面,此时蚂蚁从C处出发,爬到盒内表面对侧中点B处(如右图),则蚂蚁爬行的最短路程是 .
3.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是 cm
4.初中几何的学习始于空间的“实物和具体模型”,聚焦平面的“几何图形的特征和运用”,形成了空间几何问题要转化为平面几何问题的解题策略.
问题提出:如图所示是放在桌面上的一个圆柱体,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,如何求最短路程呢?
(1)问题分析:蚂蚁从点出发沿着圆柱体的表面爬行到点,可以有几条路径?在图中画出来;
(2)问题探究:①若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;
②若圆柱体的底面圆的周长为,高为,蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程;
③若圆柱体的底面圆的半径为,高为,一只蚂蚁从点出发沿着圆柱体的表面爬行到点,求最短路程.
【题型8 由勾股定理构造图形解决实际问题】
1.如图所示,A、B两块试验田相距200m,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
2.2019年10月1日,中华人民共和国70年华诞之际,王梓涵和学校国旗护卫队的其他同学们赶到学校举行了简朴而降重的升旗仪式.倾听着雄壮的国歌声,目送着五星红旗缓缓升起,不禁心潮澎湃,爱国之情油然而生.爱动脑筋的王梓涵设计了一个方案来测量学校旗杆的高度.将升旗的绳子拉直到末端刚好接触地面,测得此时绳子末端距旗杆底端2米,然后将绳子末端拉直到距离旗杆5m处,测得此时绳子末端距离地面高度为1m,最后根据刚刚学习的勾股定理就能算出旗杆的高度为( )
A.10m B.11m C.12m D.13m
3.【问题探究】
(1)如图①,点E是正△ABC高AD上的一定点,请在AB上找一点F,使EF=AE,并说明理由;
(2)如图②,点M是边长为2的正△ABC高AD上的一动点,求AM+MC的最小值;
【问题解决】
(3)如图③,A、B两地相距600km,AC是笔直地沿东西方向向两边延伸的一条铁路,点B到AC的最短距离为360km.今计划在铁路线AC上修一个中转站M,再在BM间修一条笔直的公路。如果同样的物资在每千米公路上的运费是铁路上的两倍。那么,为使通过铁路由A到M再通过公路由M到B的总运费达到最小值,请确定中转站M的位置,并求出AM的长.(结果保留根号)
4.目前,某市正积极推进“五城联创”,其中扩充改造绿地是推进工作计划之一.现有一块直角三角形绿地,量得两直角边长分别为a=9m和b=12m,现要将此绿地扩充改造为等腰三角形,且扩充部分包含以b=12m为直角边的直角三角形,则扩充后等腰三角形的周长为 .
参考答案
【题型1 由勾股定理求两条线段的平方和(差)】
1.解:(1).
(2)因为,所以是直角三角形.
因为,的周长为,所以,
所以,解得,所以,
所以.
(3)在中,,在中,,
所以.
因为为线段的中点,所以,所以.
在中,,
所以(定值),
故在点移动的过程中,的值是定值,其值是.
2.
【分析】在和中,分别表示出和,在和中,表示出和,代入求解即可;
【详解】解:∵于,
∴,
在和中,
,,
在和中,
,
,
,
.
故答案为:.
3.13
【分析】在和中,根据勾股定理得,,进一步得,再根据,可求得的值.
【详解】解:,
,
在和中,根据勾股定理得,
,,
,
,,
.
故答案为:.
4.(1)解:为等腰直角三角形,理由如下:
过点A作,垂足为H,
∵点,,
∴,
∴,
∴,
∴, ,
∴为等腰直角三角形;
(2). 理由:过点A作,交x轴于点B,
由(1)可知是等腰直角三角形,
∴,,
∴,
∵, ∴,
∴,
在和中, ,
∴,
∴,
∴, 而是等腰直角三角形,可得,
∴;
(3),理由如下: 过A作 交y轴于G,连接,如图:
∵是等腰直角三角形,
∴,,,
∴,
∵,
∴,
在和中, ,
∴,
∴,,
而中,,
∴,
∵,,
∴,
∵,
∴, 即
∴,
在和中, ,
∴,
∴,
∴.
【题型2 勾股定理在网格问题中的运用】
1.或
【分析】设四个全等的直角三角形的直角边边长分别为a,b.利用分类讨论的思想,在格点上找出各点位置,即找出边的位置,即可求出面积.
【详解】设四个全等的直角三角形的直角边边长分别为a,b.则正方形EFGH的边长为a+b,
即 .
∴在网格中找出a和b的线段,且线段的端点都在格点上即可.
分情况讨论:
① ,如图,
此时.
② ,如图,
此时.
③,如图,
此时.
题干中不包括52,
故的值为36或50.
故答案为:36或50.
2.解:(1)的面积为,
故答案为:;
(2)如图,,,,
由图可得:;
故答案为:;
(3)构造所示,,
,
,
∴.
3.解:(1)如图所示:
(2)如图所示,PA+PB的最小值=;
故答案为:;
(3)如图,,,
∴PA+PB的最小值即为:,
∴+的最小值为,
故答案为:.
3.解:(1)由题意, ,,,
∴五边形ABCDE的周长=20+,
故答案为: .
(2)如图,连接EC,作DF⊥EC交AB于点F,点F即为所求作.
∵,DF⊥EC,
∴,
∴点D,G是CE垂直平分线上的点,
∴DF是CE的垂直平分线,
∴E,C两点关于直线DF对称;
(3)∵,,
∴,
∴是直角三角形;
∴.
(4)如图,过点A作AH⊥DF于H,连接BH,则点H即为所求作.
∵,,
∴.
∴是等腰直角三角形.
∴.
∴.
【题型3 勾股定理在折叠问题中的运用】
1.4或3
【分析】分类讨论分别当∠AA′C=90°时,当∠ACA′=90°时,根据折叠的性质函数直角三角形的性质即可得到结论.
【详解】解:如图1,当∠AA′C=90°时,
∵以直线BP为轴把△ABP折叠,使得点A落在图中点A′处,
∴AP=A′P,
∴∠PAA′=∠AA′P,
∵∠ACA′+∠PAA′=∠CA′P+∠AA′P=90°,
∴∠PCA′=∠PA′C,
∴PC=PA′,
∴PC=AC=4,
如图2,当∠ACA′=90°时,
∵在Rt△ABC中,∠ACB=90°,且AC=8,BC=6.
∴AB=10,
∵以直线BP为轴把△ABP折叠,使得点A落在图中点A′处,
∴A′B=AB=10,PA=PA′,
∴A′C=4,
设PC=x,
∴AP=8-x,
∵A′C2+PC2=PA′2,
∴42+x2=(8-x)2,
解得:x=3,
∴PC=3,
综上所述:当△AA′C是直角三角形时,则线段CP的长是4或3,
故答案为:4或3.
2.解:(1)对于①等边三角形,三边相等,
设边长为a,
则a2+a2=2a2,
根据“方倍三角形”定义可知:
等边三角形一定是“方倍三角形”;
对于②直角三角形,三边满足关系式:
a2+b2=c2,
根据“方倍三角形”定义可知:
直角三角形不一定是“方倍三角形”;
故答案为:A;
(2)设Rt△ABC其余两条边为a,b,
则满足a2+b2=3,
根据“方倍三角形”定义,还满足:
a2+3=2b2,
联立解得 ,
则Rt△ABC的面积为:;
故答案为:;
(3)由题意可知:
△ABP≌△DBP,
∴BA=BD,∠ABP=∠DBP,
根据“方倍三角形”定义可知:
BA2+BD2=2AD2=2BA2,
∴AD=AB=BD,
∴△ABD为等边三角形,∠BAD=60°,
∴∠ABP=∠DBP=30°,
∴∠PBC=90°,
∵∠CPB=45°,
∴∠APB=180°﹣45°=135°,
∴∠DPC=90°,
∵∠ABC=120°,∠ACB=45°,
∴∠BAC=15°,
∴∠CAD=45°,
∴△APD为等腰直角三角形,
∴AP=DP= ,
∴AD=2,
延长BP交AD于点E,如图,
∵∠ABP=∠PBD,
∴BE⊥AD,PE=AD=AE=1,
∴BE=,
∴PB=BE﹣PE= ﹣1,
∵∠CPB=∠PCB=45°,
∴△PBC为等腰直角三角形,
∴PC=PB=,
∴S△PDC=PC PD=()×=﹣1.
3.(1)解:如图,过作于
AB=AC=10,BC=12,
所以BC边上的高线长为
(2)解:①如图,连接
为的中点,
由(1)得:
则
②当时,由对折可得:
过作于 连接 过作于 过作于
由①得:
则
设
则
由
而
解得:
当于时,则
过作于 由对折可得
当时,如图,则
由对折可得 而 则
而
结合对折可得:
过作于
同理可得:
综上:当DF与△ABC其中一边垂直时,BE的长为或或.
4.(1)对于①等边三角形,三边相等,
设边长为a,
则,
根据“方倍三角形”定义可知:
等边三角形一定是“方倍三角形”;
对于②直角三角形,三边满足关系式:,
根据“方倍三角形”定义可知:
直角三角形不一定是“方倍三角形”;
故选:A
故答案为:A;
(2)设Rt△ABC其余两条边为a,b,
则满足,
根据“方倍三角形”定义,还满足:,
联立解得,
则Rt△ABC的面积为:;
故答案为:;
(3)由题意可知:,
∴,
根据“方倍三角形”定义可知:
,
∴,
∴△ABD为等边三角形,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴△APD为等腰直角三角形,
∴,
∴.
延长BP交AD于点E,如图,
∵,
∴,,
∴,
∴,
∵,
∴△PBC为等腰直角三角形,
∴.
【题型4 以弦图为背景的计算】
1.A
【分析】根据赵爽弦图,将小正方形分成4个全等的直角三角形,和一个最小的正方形,设直角三角形的短直角边长为,长直角边为,则正方形的水平宽度与垂直高度为,根据平移的性质,分别表示出,建立二元一次方程组,解方程组,进而勾股定理即可求解.
【详解】解:如图所示,根据赵爽弦图,将小正方形分成4个全等的直角三角形,和一个最小的正方形,
设直角三角形的短直角边长为,长直角边为,则正方形的水平宽度与垂直高度为,
依题意,
解得:
∴小正方形的边长为:,
故选:A.
2. 13 8
【分析】(1)首先结合题意求得正方形的边长,正方形的边长,由全等的直角三角的性质可得,,设,则,,然后可求得,,在中,由勾股定理可得,结合正方形面积公式即可获得答案;
(2)设每一个直角三角形面积为,则,,再结合即可获得答案.
【详解】解:(1)当,时,
正方形的边长,正方形的边长,
根据题意,该图形由八个全等的直角三角形拼接而成,
由全等的直角三角的性质可得,,
设,则,,
∴,解得,
∴,,
∴在中,,
∴正方形的面积;
故答案为:13;
(2)设每一个直角三角形面积为,
∴则,,
∵,
∴,
解得.
故答案为:8.
3.16
【分析】设,,根据正方形的面积公式和勾股定理可求得,再根据题意和三角形的面积公式可推导出,进而推出阴影部分的面积之和为梯形的面积,利用梯形面积公式求解即可.
【详解】解:由题意,,,,
∴,,,
∴,
∴,
∴,,
∵,
∴设,则,,
∴,
∴,
∴阴影部分的面积之和为
,
∵正方形的面积为,
∴即,
∴,
∴阴影部分的面积之和为16.
故答案为:16.
4.
【分析】由八个直角三角形全等,四边形,,为正方形,得出,,再根据三个正方形的面积公式列式相加:,求出的值,从而可以计算结论即可.
【详解】解:∵八个直角三角形全等,四边形,,为正方形,
∴,,
∴
,
,
∴,
∴,
∴,
故答案为:.
【题型5 勾股定理的证明方法】
1.(1)解:证明勾股定理:
由题意得,,,
∴,
∴.
(2)解:①在中,
,
,
点表示的数是.
故答案为:.
②,,
.
设秋千的绳索长为,根据题意可得,
利用勾股定理可得.
解得:.
答:绳索的长为.
2.(1)解:如图2,正方形的面积,
正方形的面积,
;
(2),且,,
,
即,
的值为.
(3)如图3,正方形的面积,
正方形的面积,
,
即.
3.(1)证明:∵,,,
∴
∴
∴
(2),
,
,
即AB边上的高是
(3)解:在中,由勾股定理得
∵,
∴
在中,由勾股定理得
∴,
∴
4.解:(1)∵S梯形ABCD=
S梯形ABCD=
.
(2)连接,
如图:
S四边形ABCD=,
S四边形ABCD=,
,
.
(3)①设,则,又,
根据翻折可知:
,,
.
在中,根据勾股定理,得
,
解得.
,.
答:、两点的坐标为,.
②如图:
当点在轴正半轴上时,
,
设,则,解得,
,
,;
,,,
,;
当点在轴负半轴上时,
,,
;
,,
,
,.
∴符合条件的所有点的坐标为:,、,、、,.
【题型6 勾股定理与全等综合】
1.(1)证明:在中,,,
∴,
由勾股定理得,
∴;
(2)解:由(1)可知,
在中,由勾股定理得,,
∵在中,,
∴是等腰直角三角形,
∴,
∴,
∴的长为3.5;
(3)解:能围成直角三角形,理由如下:
如图,在上取一点H,使,连接,,
∵,,
∴,
∴,
∵,,,
∴,
∴,,
∵,
∴,
∴,
∵,,
∴,,
∴,即,
又∵,
∴,
在中,由勾股定理,得,
∴,
∴以,和为边,能围成直角三角形.
2.
【分析】根据折叠的性质可得,设,则,在中,根据勾股定理即可求解.
【详解】解:矩形纸片沿对角线折叠,
∴,,,且,
∴,
∴,,
设,则,
在中,,
∴,解得,,
∴,
故答案为:.
3.B
【分析】延长交于点,根据正方形的性质证明,求出,,再证明,求出,,由勾股定理可得的长.
【详解】解:如图,延长交于点,
,,,
,,
和是直角三角形,
在和中,,
,
,,,
,,
,,
,,
在和中,,
,
,,,
,
同理可得,
在中,,
故选:B.
4.(1)解:当点在线段上时,
,,,
,
,
,
;
(2)解:,,
,
,
,
,
,
由(1)可知,,
,
设,
,
,
,
;
(3)解:如图1,当点在线段上,,设为边上的高,为垂足,
,
在等腰中,为的中点,,
,
,,
,
如图2,点在线段的延长线时,同理可得,
,
,
,
故答案为:或;
(4)解:点运动轨迹是过点,且垂直于的射线,根据垂线段最短的性质,当时,线段最短,如图3,
,
,,,
为等腰直角三角形,
,
由(1)知:,
,
此时,
故答案为:9,3.
【题型7 由勾股定理确定在几何体中的最短距离】
1.A
【分析】求出蚂蚁沿着木柜表面经线段到,以及蚂蚁沿着木柜表面经线段到的距离,再进行比较即可.
【详解】解:蚂蚁沿着木柜表面经线段到,
爬过的路径的长是,
蚂蚁沿着木柜表面经线段到,
爬过的路径的长是.
,最短路径的长是.
故选A.
2.
【分析】(1)把圆柱侧面展开,在中,利用勾股定理求解即可.
(2)将圆柱侧面展开,得到矩形,作点关于的对称点,构造,根据勾股定理求出即可解决问题.
【详解】(1)如图,把圆柱侧面展开,在中,
∵,
∴ ,
故答案为:.
(2)如图所示,点与点关于对称,可得,,
则最短路程为
故答案为:.
3.16
【分析】将正方形沿着翻折得到正方形 ,过点在正方形内部作,使,连接,过作于点,此时最小,运用勾股定理求解即可.
【详解】
如图,将正方形沿着翻折得到正方形 ,过点在正方形内部作,使,连接,过作于点,则四边形是矩形,四边形是平行四边形,
∴,,,,
此时最小,
∵点是中点,
∴cm,
∴cm,cm,
在中,cm,
∴cm,
故答案为:16.
4.(1)解:共有3条路径,如下图:
(2)解:①如图,连接,
根据题意得:,,
∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为;
②如图,连接,
根据题意得:,,
∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为;
③如图,连接,
根据题意得:,,
∴,
即蚂蚁从点出发沿着圆柱体的表面爬行到点,最短路程为.
【题型8 由勾股定理构造图形解决实际问题】
1.解:(1)△ABC是直角三角形;
理由如下:
∴AC2+BC2=1602+1202=40000,AB2=2002=40000,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)甲方案所修的水渠较短;
理由如下:
∵△ABC是直角三角形,
∴△ABC的面积=AB CH=AC BC,
∴CH=(m),
∵AC+BC=160+120=280(m),CH+AH+BH=CH+AB=96+200=296(m),
∴AC+BC<CH+AH+BH,
∴甲方案所修的水渠较短.
2.B
【分析】根据题意画出示意图,设旗杆高度为xm,可得AC=AD=xm,AB=(x﹣1)m,BC=5m,在Rt△ABC中利用勾股定理可求出x.
【详解】设旗杆高度为xm,可得AC=AD=xm,AB=(x﹣1)m,BC=5m,
根据勾股定理得,绳长的平方=x2+22,
如图,根据勾股定理得,绳长的平方=(x﹣1)2+52,
∴x2+22=(x﹣1)2+52,解得x=11,
故选:B.
3.解:(1)如图①,作EF⊥AB,垂足为点F,点F即为所求。
理由如下:∵点E是正△ABC高AD上的一定点,
∴∠BAD=30 ,
∵EF⊥AB,
∴EF=AE;
(2)如图②,作CN⊥AB,垂足为点N,交AD于点M,此时AM+MC最小,最小为CN的长。
∵△ABC是边长为2的正△ABC,
∴CN=BCsin60 =2×=
∴MN+CM=12AM+MC=
即AM+MC的最小值为
(3)如图③,作BD⊥AC,垂足为点D,在AC异于点B的一侧作∠CAN=30
作BF⊥AN,垂足为点F,交AC于点M,点M即为所求。
在Rt△ABD中,AD=(km)
在Rt△MBD中,∠MBD=∠MAF=30 ,得MD=BDtan30 =(km),
所以AM=(480 )km.
4.40米或48米或(30+6)米.
【详解】【分析】分三种情形讨论即可,①AB=BE1,②AB=AE3,③E2A=E2B,分别计算即可.
【详解】在Rt△ABC中,∵∠ACB=90°,BC=9,AC=12,∴AB==15,
①当BA=BE1=15时,CE1=6,
∴AE1==6,
∴△ABE1周长为(30+6)米;
②当AB=AE3=15时,CE3=BC=9,BE3=18,
∴△ABE3周长为48米;
③当E2A=E2B时,设E2C=x,则有E2A=BC+E2C=9+x,
∵∠ACE2=90°,∴AE22=CE22+AC2,
即(9+x)2=x2+122,
∴x=3.5,
∴E2A=E2B=9+3.5=12.5,
∴△ABE2周长为2×12.5+15=40米;
综上所述扩充后等腰三角形的周长为40米或48米或(30+6)米,
故答案为40米或48米或(30+6)米.
