第17章《勾股定理》章节知识点复习题(含解析)八年级数学下册人教版
文档属性
| 名称 | 第17章《勾股定理》章节知识点复习题(含解析)八年级数学下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 10:18:55 | ||
图片预览



文档简介
第17章《勾股定理》章节知识点复习题
【题型1 勾股数的运用】
1.勾股定理最早出现在《周解算经》:“勾广三,股修四,弦隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点如下:勾为奇数,弦与股相差1,柏拉图研究了勾为偶数,弦与股相差2的一类勾股数,如:6,8,10;8,15,17;…若此类勾股数的勾为(,为正整数),则其弦是(结果用含的式子表示)( )
A. B. C. D.
2.下列各组是勾股数的是( )
A. B.
C.,,c= D.
3.当直角三角形的三边长都是正整数时,我们称这三个数为勾股数,如:3,4,5都是正整数,且,所以3,4,5是勾股数.观察下列各勾股数有哪些规律;
3,4,5; 9,40,41;
5,12,13; ……;
7,24,25; ,,.
(1)当时,求,的值
(2)判断10,24,26是否为一组勾股数?若是,请说明理由.
4.我们知道,如果直角三角形的三边的长都是正整数,这样的三个正整数就叫做一组勾股数.如果一个正整数c能表示为两个正整数a,b的平方和,即,那么称a,b,c为一组广义勾股数,c为广义斜边数,则下面的结论:①m为正整数,则3m,4m,5m为一组勾股数;②1,2,3是一组广义勾股数;③13是广义斜边数;④两个广义斜边数的和是广义斜边数;⑤若,其中k为正整数,则a,b,c为一组勾股数;⑥两个广义斜边数的积是广义斜边数.依次正确的是( )
A.①②③ B.①②④⑤ C.③④⑤ D.①③⑤
【题型2 勾股树的探究】
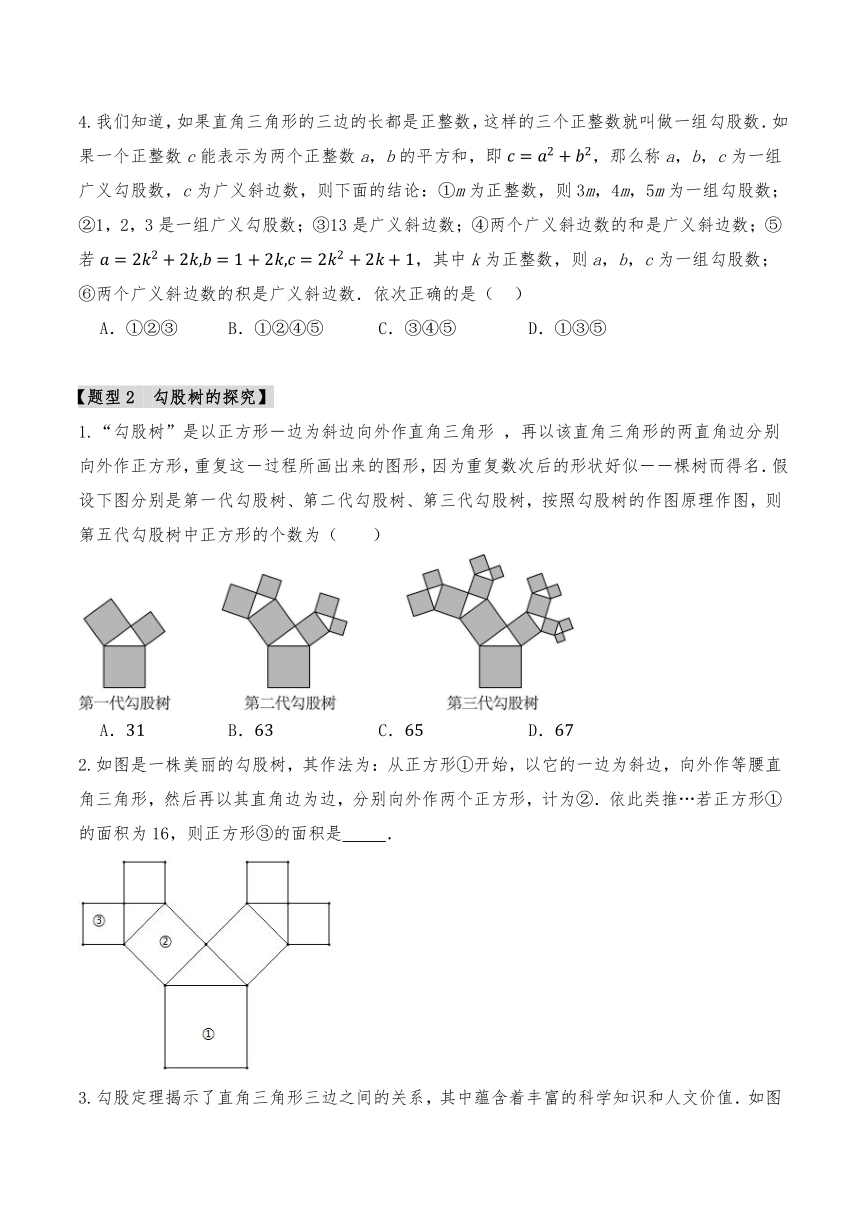
1.“勾股树”是以正方形-边为斜边向外作直角三角形 ,再以该直角三角形的两直角边分别向外作正方形,重复这-过程所画出来的图形,因为重复数次后的形状好似--棵树而得名.假设下图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第五代勾股树中正方形的个数为( )
A. B. C. D.
2.如图是一株美丽的勾股树,其作法为:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作两个正方形,计为②.依此类推…若正方形①的面积为16,则正方形③的面积是 .
3.勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为,第二个正方形和第二个直角三角形的面积之和为,…,第个正方形和第个直角三角形的面积之和为.
设第一个正方形的边长为1.
请解答下列问题:
(1) .
(2)通过探究,用含的代数式表示,则 .
4.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形(如图1),三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2022次后形成的图形中所有正方形的面积和是 .
【题型3 由勾股定理在坐标系中求距离】
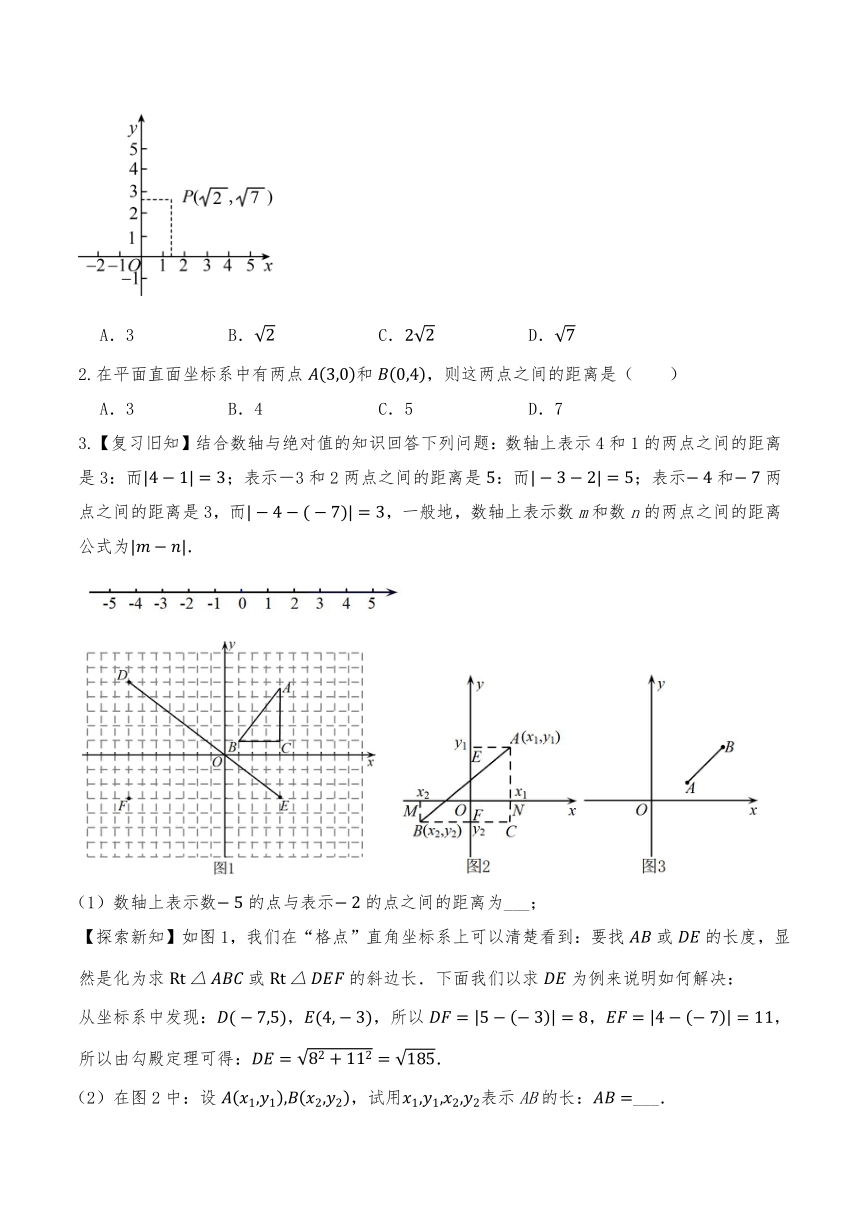
1.如图,点P是平面坐标系内一点,则点P到原点的距离是( )
A.3 B. C. D.
2.在平面直面坐标系中有两点和,则这两点之间的距离是( )
A.3 B.4 C.5 D.7
3.【复习旧知】结合数轴与绝对值的知识回答下列问题:数轴上表示4和1的两点之间的距离是3:而;表示-3和2两点之间的距离是:而;表示和两点之间的距离是3,而,一般地,数轴上表示数m和数n的两点之间的距离公式为.
(1)数轴上表示数的点与表示的点之间的距离为___;
【探索新知】如图1,我们在“格点”直角坐标系上可以清楚看到:要找或的长度,显然是化为求或的斜边长.下面我们以求为例来说明如何解决:
从坐标系中发现:,,所以,,所以由勾殿定理可得:.
(2)在图2中:设,试用表示AB的长:___.
得出的结论被称为“平面直角坐标系中两点间距离公式”;
【学以致用】请用此公式解决如下问题:
(3)如图3,已知:,,C为坐标轴上的点,且使得是以为底边的等腰三角形.请求出C点的坐标.
4.阅读材料,在平面直角坐标系中,已知x轴上两点、的距离记作,如果、是平面上任意两点,我们可以通过构造直角三角形来求间的距离.如下左图,过A、B分别向x轴、y轴作垂线、和、,垂足分别是、、、,直线交于点Q,在中,,,∴.
(1)由此得到平面直角坐标系内任意两点、间的距离公式为: ______.
(2)直接应用平面内两点间距离公式计算点,之间的距离为______.
利用上面公式解决下列问题:
(3)在平面直角坐标系中的两点,,P为x轴上任一点,求的最小值和此时点P的坐标;
(4)应用平面内两点间的距离公式,求代数式的最小值(直接写出答案).
【题型4 由勾股定理探究图形面积】
1.如图,在中,,,若以边和边向外作等腰直角三角形和等腰直角三角形.记的面积是,的面积是,则( )
A. B. C. D.
2.如果一个三角形,三条边的长度之比为,且周长为,那么这个三角形的面积是( )
A. B. C. D.
3.现有如图1的8张大小形状相同的直角三角形纸片,三边长分别是a、b、c.用其中4张纸片拼成如图2的大正方形(空白部分是边长分别为a和b的正方形);用另外4张纸片拼成如图3的大正方形(中间的空白部分是边长为c的正方形).
(1)观察:从整体看,整个图形的面积等于各部分面积的和.所以图2和图3的大正方形的面积都可以表示为,结论①;图2中的大正方形的面积又可以用含字母a、b的代数式表示为: ,结论②;图3中的大正方形的面积又可以用含字母a、b、c的代数式表示为: ,结论③;
(2)思考:结合结论①和结论②,可以得到一个等式 ;结合结论②和结论③,可以得到一个等式 ;
(3)应用:若分别以直角三角形三边为直径,向外作半圆(如图4),三个半圆的面积分别记作,且,求的值.
(4)延伸:若分别以直角三角形三边为直径,向上作三个半圆(如图5),直角边,,斜边,求图中阴影部分面积和.
4.在中, ,,则的面积是 .
【题型5 由勾股定理求线段长度】
1.如图,的周长为,其中,.
(1)______;
(2)判断是否为直角三角形,并说明理由.
(3)过点A作,,在上取一点D,使得,求的长度.
2.如图,,且,,,则DC的长度为( )
A.3 B.8 C.4 D.9
3.如图,在中,,线段的垂直平分线交于点O,则的长度为 .
4.如图,在等腰三角形中,底边,D是上一点,连接.
(1)求证:是直角三角形;
(2)求边的长度.
【题型6 由勾股定理证明线段之间的关系】
1.已知是等边三角形.
(1)如图1,也是等边三角形.点A、B、E三点不共线,求证:;
(2)如图2,点D是外一点,且,请证明结论;
(3)如图3,点D是等边三角形外一点,若.试求的度数.
2.如图,在平面直角坐标系中,点A在x轴上,且,点B在y轴上,且.
(1)求线段的长;
(2)若点E在线段上,,且,求的值;
(3)在(2)的条件下,过点O作,交于点M,试证明:
3.亲爱的同学们,在全等三角形中,我们见识了很多线段关系的论证题,下面请你用本阶段所学知识,分别完成下列题目.
(1)如图,已知:在中,,,直线经过点,直线,直线,垂足分别为点、.证明:;
(2)如图,和均为等腰直角三角形,,点、、在同一直线上,为中边上的高,连接.容易证明,则:
①的度数为______;
②直接写出、、之间的数量关系.
(3)如图,中,若,为的中点,交、于、,求证:.
4.如图,点A为x轴负半轴上一点,点B为y轴正半轴上一点,点C为x轴正半轴上一点,,,,且a、b、c满足有意义.
(1)若,求__________________;
(2)如图1,点P在x轴上(点P在点A左边),以为直角边在的上方作等腰直角三角形,求证:;
(3)如图2,点M为中点,点E为射线上一点,点F为射线上一点,且,设,,请求出的长度(用含m、n的代数式表示).
【题型7 勾股定理中的规律探究】
1.如图,为等腰直角三角形,,以斜边为直角边作等腰直角三角形,再以为直角边作等腰直角三角形,,按此规律作下去,则的长度为 .
2.如果正整数a、b、c满足等式,那么正整数a、b、c叫做勾股数.某同学将自探究勾股数的过程列成下表,观察表中每列数的规律,可知的值为( )
a b c
3 4 5
8 6 10
15 8 17
24 10 26
… … …
x 14 y
A.67 B.34 C.98 D.73
3.如图是第七届国际数学教育大会的会徽图案,它是由一串有公共顶点O的直角三角形组成的,图中的,按此规律,在线段,,,,中,长度为整数的线段有 条.
4.在平面直角坐标系中,将若干个边长为2个单位长度的等边三角形按如图所示的规律摆放,点P从原点O出发,以每秒2个单位长度的速度沿着等边三角形的边→→→→…的路线运动,设第n秒运动到点(n为正整数),则点的坐标是( )
A. B. C. D.
【题型8 由勾股定理求最值】
1.如图,已知,点为内的两个动点,且,,,点分别是上的动点,则的最小值是( )
A.5 B.7 C.8 D.10
2.如图,等腰和等腰的腰长分别为4和2,其中,M为边的中点.若等腰绕点A旋转,则点B到点M的距离的最大值为 .
3.如图,正方形的边长为6,线段在边上左右滑动,若,则的最小值为 .
4.如图,中,,,,点在上,将沿折叠,点落在点处,与相交于点,则的最大值为 .
参考答案
【题型1 勾股数的运用】
1.C
【分析】根据题意得为偶数,设其股是,则弦为,根据勾股定理列方程即可得到结论.
【详解】解:为正整数,
为偶数,设其股是,则弦为,
根据勾股定理得,,
解得,
弦是,
故选:C.
2.A
【分析】根据勾股数的概念对各选项进行逐一分析即可.
【详解】解:A、∵,
∴能构成勾股数,符合题意;
B、∵不是整数,
∴不能构成勾股数,不符合题意;
C、∵不是整数,
∴不能构成勾股数,不符合题意;
D、∵,
∴不能构成勾股数,不符合题意.
故选:A.
3.(1)解:观察已有的勾股数可得,
∴,
把代入,
解得(负值已舍掉),
∴;
(2)10,24,26是勾股数.
∵.
又∵10,24,26都是正整数
根据勾股数的定义,可知10,24,26是勾股数.
4.D
【分析】根据题目中所给的勾股数.广义勾股数,广义斜边数的定义,分析选项找出结论正确的即可.
【详解】解:由题意可知:
①m为正整数,则3m,4m,5m为一组勾股数;结论正确;
②1,2,3是一组广义勾股数;∵,∴不满足,不能成为广义勾股数,故结论不正确;
③13是广义斜边数;∵,∴结论正确;
④两个广义斜边数的和是广义斜边数;例如,,但是7不是广义斜边数,故结论不正确;
⑤若,其中k为正整数,则a,b,c为一组勾股数;∵,,满足:,故结论正确;
⑥两个广义斜边数的积是广义斜边数.例如,但是4不是广义斜边数,故结论不正确;
故正确的结论为:①③⑤.
故选:D
【题型2 勾股树的探究】
1.B
【分析】由已知图形观察规律,即可得到第五代勾股树中正方形的个数.
【详解】解:由题意可知第一代勾股树中正方形有(个),
第二代勾股树中正方形有(个),
第三代勾股树中正方形有(个),
由此推出第五代勾股树中正方形有(个)
故选:B.
2.4.
【分析】根据勾股定理可得两条直角边的平方和等于斜边的平方,即第①个正方形的面积=第②个正方形面积的两倍;同理,第③个正方形面积是第②个正方形面积的一半,依此类推即可解答.
【详解】解:第①个正方形的面积为16,
由分析可知:第②个正方形的面积为8,
第③个正方形的面积为4,
故答案为:4.
3. (为整数)
【分析】根据正方形的面积公式求出面积,再根据直角三角形三条边的关系运用勾股定理求出三角形的直角边,求出S1,然后利用正方形与三角形面积扩大与缩小的规律推导出公式.
【详解】解:(1)∵第一个正方形的边长为1,
∴正方形的面积为1,
又∵直角三角形一个角为30°,
∴三角形的一条直角边为,另一条直角边就是,
∴三角形的面积为,
∴S1=;
(2)∵第二个正方形的边长为,它的面积就是,也就是第一个正方形面积的,
同理,第二个三角形的面积也是第一个三角形的面积的,
∴S2=() ,
依此类推,S3=() ,
即S3=() ,
Sn=(n为整数).
故答案为:(1) ;(2)(为整数)
4.2023
【分析】根据勾股定理和正方形的面积公式,知“生长”1次后,以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,即所有正方形的面积和是2×1=2;“生长”2次后,所有的正方形的面积和是3×1=3,推而广之即可求出“生长”2022次后形成图形中所有正方形的面积之和.
【详解】设第一个直角三角形的是三条边分别是a,b,c.
根据勾股定理,得,
由图1可知,“生长”1次后,以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,即所有正方形的面积和是;
由图2可知,“生长”2次后,所有的正方形的面积和是,
···
“生长”了2022次后形成的图形中所有的正方形的面积和是.
故答案为:2023.
【题型3 由勾股定理在坐标系中求距离】
1.A
【分析】连接,在直角坐标系中,根据点P的坐标是,得,,然后利用勾股定理即可求解.
【详解】解:连接,
∵点P的坐标是,
∴,,
∴点P到原点的距离,
故选:A.
2.C
【分析】根据平面直角坐标系中,两点之间的距离公式,代值求解即可得到答案.
【详解】解:连接,如图所示:
∵,,
∴,
故选:C.
3.解:(1)数轴上表示数的点与表示的点之间的距离,
故答案为:3;
(2)结合图形可得:,,.
故答案为:;
(3)若点在轴上,设点的坐标为,
则,即,
解得:,
即点的坐标为;
若点在轴上,设点的坐标为,
则,即,
解得:,
即点的坐标为.
综上可得点的坐标为或.
4.(1)解:阅读材料可得:;
(2)平面直角坐标系内任意两点,,,间的距离公式为:,
点,之间的距离为:;
故答案为:5;
(3)作点关于轴对称的点,连接,直线于轴的交点即为所求的点,的最小值就是线段的长度,然后根据两点间的距离公式即可得到结论.
,
,
,
设直线的一次函数表达式为,
把代入 解得 ,
当时,解得,即,
,
即为的最小值为.
故答案为:;
(4)原式,
故原式表示点到和的距离之和.
由两点之间线段最短,点在以和为端点的线段上时,原式值最小.
利用公式可得,原式.
【题型4 由勾股定理探究图形面积】
1.B
【分析】由勾股定理求出,由等腰直角三角形的性质得出,,,即可得出结果.
【详解】解:,,
和为等腰直角三角形,
,,
,
故选:.
2.B
【分析】设这个三角形的三条边的长度分别为,根据周长为列出方程并求得三边长度;然后由勾股定理逆定理判定该三角形为直角三角形,由三角形的面积公式作答即可.
【详解】解:设这个三角形的三条边的长度分别为,
∵三角形的周长为,
则,
解得,
则该三角形的三条边的长度分别为,
∵,
则该三角形为直角三角形,两直角边长分别为,
∴面积为: ,
故选:B.
3.(1)解:图2:;
图3:;
(2)解:结合结论①和结论②,可以得到一个等式:;
结合结论②和结论③,可以得到一个等式:,
即,;
(3)解:,,,
,
,
,
,
解得;
(4)解:由“应用”的解答过程可知:
∴阴影部分面积和,
,,
阴影部分面积和.
4.或
【分析】作交于点,设,用勾股定理得出,再由可得是的倍列出方程可得的值,再根据三角形的面积公式可得答案.
【详解】解:作交于点,
设,则.
在中,
.
∵中,,
∴ ,即,
∴,
解得或.
∴ 或 ,
∴的面积 或 .
故答案为: 或 .
【题型5 由勾股定理求线段长度】
1.(1)解:∵的周长为,,,
∴,
故答案:;
(2)解:是直角三角形,理由如下:
∵,,
∴,
∴是直角三角形;
(3)解:∵,
∴,
∴.
2.A
【分析】在中先根据勾股定理求出的长,再在中根据勾股定理即可得出结论.
【详解】,,,
.
在中,
,,,
.
故选:A.
3.
【分析】连接,延长交于H,根据得,可得,根据等腰三角形的性质得到,根据勾股定理得到,在中,根据勾股定理求解即可.
【详解】解:如图:连接,延长交于H,
∵线段的垂直平分线交于点O,
∴,
∵,
,
在和中,,
,
∴,
∴平分,
∵
∴,
∴,
在中,,
解得:.
故答案为.
4.(1)解:,
,
是直角三角形;
(2)解:设腰长.
在中,,
,
解得,
即:.
【题型6 由勾股定理证明线段之间的关系】
1.(1)解:证明:如图1中,连接.
,都是等边三角形,
,,,
,
,
.
(2)如图2中,以为边向下作等边,连接.
,都是等边三角形,
,,,
,
,
,
,,
,
,
,,
.
(3)如图3中,以为边向下作等边,连接,作交的延长线于.
同法可证:,
,设,,
则有,
解得,
,
,
,
,
,
.
2.(1)在中,
∵,
∴.
(2)∵,
∴,
在和中,
,
∴,
∴,
∴.
(3)结论:,理由如下:
连接.∵,
∴垂直平分,
∴,
∵,
∴,
由(1)可知,
∴,
∴,
∴,
∴.
3.(1)证明:如图,
,直线,直线,
,
,
,
,
,
,,
;
(2)解:①和均为等腰直角三角形,,
,
,
,
,,
,
故答案为:;
②,理由如下:
为等腰直角三角形,为中边上的高,
,
,
;
(3)证明:如图,延长到点,使,连接,,
是的中点,
,
在和中,
,
,
,,
,
,
,即,
中,,
,,
,
.
4.(1)解:∵a、b满足有意义,
∴且,
∴,即,,
;
(2)证明:连接,由(1)可得,
∵两个坐标轴垂直,
∴,
∴,
又∵为等腰直角三角形,
∴,
∴,
在和中,
,
∴,
∴.,,
∵,
∴,
∴,
即,
∴即;
(3)当点E在线段上时,连接,如图所示:
∵,,点M为的中点,
∴,,,
∵,
∴,
∴,
∴,
∵,
∴,
根据勾股定理得:;
当点E在线段延长线上时,连接,如图所示:
同理可得:,
∴,
∵,
∴,
根据勾股定理得:;
综上分析可知,.
【题型7 勾股定理中的规律探究】
1.
【分析】利用等腰直角三角形的性质以及勾股定理分别求出各边长,依据规律即可得出答案.
【详解】解:为等腰直角三角形,,
,
为等腰直角三角形,
.
为等腰直角三角形,
.
为等腰直角三角形,
.
的长度为.
故答案为:.
2.C
【分析】依据每列数的规律,即可得到,,,进而得出的值.
【详解】解:由题可得,,,,
,,,(且n为正整数)
当时,
解得:,
,,
,
故选:C.
3.
【分析】,根据勾股定理可得,,找到的规律,即可得到结论.
【详解】解:∵如图是由一串有公共顶点O的直角三角形组成的,
图中的,
∴由勾股定理可得:
,
,
……
∴,
∴在线段,,,,中,完全平方数有,,.
∴故长度为整数的线段有条.
故答案为:.
4.C
【分析】通过观察可得,每6个点的纵坐标规律:,0,,0,,0,点的横坐标规律:1,2,3,4,5,6,…,n,点从原点出发,以每秒个单位长度的速度沿着等边三角形的边“…”的路线运动,1秒钟走一段,P运动每6秒循环一次,点P运动n秒的横坐标规律:1,2,3,4,5,6,…,n,点P的纵坐标规律:,0,,0,,0,…,确定循环的点即可.
【详解】解:过点作轴于B,
∵图中是边长为2个单位长度的等边三角形,
∴,
∴,
∴,,
同理,,
,,
,
…
∴中每6个点的纵坐标规律:,0,,0,,0,
点从原点出发,以每秒个单位长度的速度沿着等边三角形的边“…” 的路线运动,1秒钟走一段,
∴P运动每6秒循环一次,
∴点P的纵坐标规律:,0,,0,,0,…,
点P的横坐标规律: 1,2,3,4,5,6,…,,
∵,
∴点的纵坐标为,
∴点的横坐标为,
∴点的坐标,
故选C.
【题型8 由勾股定理求最值】
1.A
【分析】作点关于直线的对称点,连接,作点关于直线的对称点,连接,连接,可知,当,,,在同一条直线上时,可以取得最小值,最小值等于的长度,即的最小值等于的长度,利用勾股定理即可求得的长度.
【详解】如图所示,作点关于直线的对称点,连接,作点关于直线的对称点,连接,连接.
根据轴对称图形的性质可知,,
∴.
根据题意可知,当,,,在同一条直线上时,可以取得最小值,最小值等于的长度,即的最小值等于的长度.
根据轴对称图形的性质可知,,
∴.
∴.
根据轴对称图形的性质可知,,
∴.
∴的最小值等于.
故选:.
2.
【分析】连接.由三线合一得,利用勾股定理求出,然后利用三角形三条边的关系求解即可.
【详解】如图,连接.
∵M为边的中点,且为等腰直角三角形,
∴,.
在中,,
由勾股定理可知,即.
当A,B,M三点不共线时,由三角形的三边关系可知,
此时一定有;当A,B,M三点共线且点M不位于点A,B之间时,此时有,
∴,
即点B到点M的距离的最大值为.
3.13
【分析】如图,作A于对称点,则,在上截取,然后连接,当三点共线时,有值最小,然后利用勾股定理即可解答.
【详解】解:如图,作A于对称点,
∴,,
在上截取,然后连接,
∵
∴四边形是平行四边形,
∴,
∴,
∴当三点共线时,有值最小,
∵,
∴,
∴,
由勾股定理得:,即最小值为13.
故答案为13.
4.
【分析】首先利用勾股定理求出,然后确定取最大值时最小,然后利用垂线段最短解决问题.
【详解】解:在中,,,,
,
,,
当最小时,最大,
当时最小,
又 ,解得,
的最小值为,
的最大值为,
故答案为:.
【题型1 勾股数的运用】
1.勾股定理最早出现在《周解算经》:“勾广三,股修四,弦隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点如下:勾为奇数,弦与股相差1,柏拉图研究了勾为偶数,弦与股相差2的一类勾股数,如:6,8,10;8,15,17;…若此类勾股数的勾为(,为正整数),则其弦是(结果用含的式子表示)( )
A. B. C. D.
2.下列各组是勾股数的是( )
A. B.
C.,,c= D.
3.当直角三角形的三边长都是正整数时,我们称这三个数为勾股数,如:3,4,5都是正整数,且,所以3,4,5是勾股数.观察下列各勾股数有哪些规律;
3,4,5; 9,40,41;
5,12,13; ……;
7,24,25; ,,.
(1)当时,求,的值
(2)判断10,24,26是否为一组勾股数?若是,请说明理由.
4.我们知道,如果直角三角形的三边的长都是正整数,这样的三个正整数就叫做一组勾股数.如果一个正整数c能表示为两个正整数a,b的平方和,即,那么称a,b,c为一组广义勾股数,c为广义斜边数,则下面的结论:①m为正整数,则3m,4m,5m为一组勾股数;②1,2,3是一组广义勾股数;③13是广义斜边数;④两个广义斜边数的和是广义斜边数;⑤若,其中k为正整数,则a,b,c为一组勾股数;⑥两个广义斜边数的积是广义斜边数.依次正确的是( )
A.①②③ B.①②④⑤ C.③④⑤ D.①③⑤
【题型2 勾股树的探究】
1.“勾股树”是以正方形-边为斜边向外作直角三角形 ,再以该直角三角形的两直角边分别向外作正方形,重复这-过程所画出来的图形,因为重复数次后的形状好似--棵树而得名.假设下图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第五代勾股树中正方形的个数为( )
A. B. C. D.
2.如图是一株美丽的勾股树,其作法为:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作两个正方形,计为②.依此类推…若正方形①的面积为16,则正方形③的面积是 .
3.勾股定理揭示了直角三角形三边之间的关系,其中蕴含着丰富的科学知识和人文价值.如图所示,是一棵由正方形和含角的直角三角形按一定规律长成的勾股树,树的主干自下而上第一个正方形和第一个直角三角形的面积之和为,第二个正方形和第二个直角三角形的面积之和为,…,第个正方形和第个直角三角形的面积之和为.
设第一个正方形的边长为1.
请解答下列问题:
(1) .
(2)通过探究,用含的代数式表示,则 .
4.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形(如图1),三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”.在“生长”了2022次后形成的图形中所有正方形的面积和是 .
【题型3 由勾股定理在坐标系中求距离】
1.如图,点P是平面坐标系内一点,则点P到原点的距离是( )
A.3 B. C. D.
2.在平面直面坐标系中有两点和,则这两点之间的距离是( )
A.3 B.4 C.5 D.7
3.【复习旧知】结合数轴与绝对值的知识回答下列问题:数轴上表示4和1的两点之间的距离是3:而;表示-3和2两点之间的距离是:而;表示和两点之间的距离是3,而,一般地,数轴上表示数m和数n的两点之间的距离公式为.
(1)数轴上表示数的点与表示的点之间的距离为___;
【探索新知】如图1,我们在“格点”直角坐标系上可以清楚看到:要找或的长度,显然是化为求或的斜边长.下面我们以求为例来说明如何解决:
从坐标系中发现:,,所以,,所以由勾殿定理可得:.
(2)在图2中:设,试用表示AB的长:___.
得出的结论被称为“平面直角坐标系中两点间距离公式”;
【学以致用】请用此公式解决如下问题:
(3)如图3,已知:,,C为坐标轴上的点,且使得是以为底边的等腰三角形.请求出C点的坐标.
4.阅读材料,在平面直角坐标系中,已知x轴上两点、的距离记作,如果、是平面上任意两点,我们可以通过构造直角三角形来求间的距离.如下左图,过A、B分别向x轴、y轴作垂线、和、,垂足分别是、、、,直线交于点Q,在中,,,∴.
(1)由此得到平面直角坐标系内任意两点、间的距离公式为: ______.
(2)直接应用平面内两点间距离公式计算点,之间的距离为______.
利用上面公式解决下列问题:
(3)在平面直角坐标系中的两点,,P为x轴上任一点,求的最小值和此时点P的坐标;
(4)应用平面内两点间的距离公式,求代数式的最小值(直接写出答案).
【题型4 由勾股定理探究图形面积】
1.如图,在中,,,若以边和边向外作等腰直角三角形和等腰直角三角形.记的面积是,的面积是,则( )
A. B. C. D.
2.如果一个三角形,三条边的长度之比为,且周长为,那么这个三角形的面积是( )
A. B. C. D.
3.现有如图1的8张大小形状相同的直角三角形纸片,三边长分别是a、b、c.用其中4张纸片拼成如图2的大正方形(空白部分是边长分别为a和b的正方形);用另外4张纸片拼成如图3的大正方形(中间的空白部分是边长为c的正方形).
(1)观察:从整体看,整个图形的面积等于各部分面积的和.所以图2和图3的大正方形的面积都可以表示为,结论①;图2中的大正方形的面积又可以用含字母a、b的代数式表示为: ,结论②;图3中的大正方形的面积又可以用含字母a、b、c的代数式表示为: ,结论③;
(2)思考:结合结论①和结论②,可以得到一个等式 ;结合结论②和结论③,可以得到一个等式 ;
(3)应用:若分别以直角三角形三边为直径,向外作半圆(如图4),三个半圆的面积分别记作,且,求的值.
(4)延伸:若分别以直角三角形三边为直径,向上作三个半圆(如图5),直角边,,斜边,求图中阴影部分面积和.
4.在中, ,,则的面积是 .
【题型5 由勾股定理求线段长度】
1.如图,的周长为,其中,.
(1)______;
(2)判断是否为直角三角形,并说明理由.
(3)过点A作,,在上取一点D,使得,求的长度.
2.如图,,且,,,则DC的长度为( )
A.3 B.8 C.4 D.9
3.如图,在中,,线段的垂直平分线交于点O,则的长度为 .
4.如图,在等腰三角形中,底边,D是上一点,连接.
(1)求证:是直角三角形;
(2)求边的长度.
【题型6 由勾股定理证明线段之间的关系】
1.已知是等边三角形.
(1)如图1,也是等边三角形.点A、B、E三点不共线,求证:;
(2)如图2,点D是外一点,且,请证明结论;
(3)如图3,点D是等边三角形外一点,若.试求的度数.
2.如图,在平面直角坐标系中,点A在x轴上,且,点B在y轴上,且.
(1)求线段的长;
(2)若点E在线段上,,且,求的值;
(3)在(2)的条件下,过点O作,交于点M,试证明:
3.亲爱的同学们,在全等三角形中,我们见识了很多线段关系的论证题,下面请你用本阶段所学知识,分别完成下列题目.
(1)如图,已知:在中,,,直线经过点,直线,直线,垂足分别为点、.证明:;
(2)如图,和均为等腰直角三角形,,点、、在同一直线上,为中边上的高,连接.容易证明,则:
①的度数为______;
②直接写出、、之间的数量关系.
(3)如图,中,若,为的中点,交、于、,求证:.
4.如图,点A为x轴负半轴上一点,点B为y轴正半轴上一点,点C为x轴正半轴上一点,,,,且a、b、c满足有意义.
(1)若,求__________________;
(2)如图1,点P在x轴上(点P在点A左边),以为直角边在的上方作等腰直角三角形,求证:;
(3)如图2,点M为中点,点E为射线上一点,点F为射线上一点,且,设,,请求出的长度(用含m、n的代数式表示).
【题型7 勾股定理中的规律探究】
1.如图,为等腰直角三角形,,以斜边为直角边作等腰直角三角形,再以为直角边作等腰直角三角形,,按此规律作下去,则的长度为 .
2.如果正整数a、b、c满足等式,那么正整数a、b、c叫做勾股数.某同学将自探究勾股数的过程列成下表,观察表中每列数的规律,可知的值为( )
a b c
3 4 5
8 6 10
15 8 17
24 10 26
… … …
x 14 y
A.67 B.34 C.98 D.73
3.如图是第七届国际数学教育大会的会徽图案,它是由一串有公共顶点O的直角三角形组成的,图中的,按此规律,在线段,,,,中,长度为整数的线段有 条.
4.在平面直角坐标系中,将若干个边长为2个单位长度的等边三角形按如图所示的规律摆放,点P从原点O出发,以每秒2个单位长度的速度沿着等边三角形的边→→→→…的路线运动,设第n秒运动到点(n为正整数),则点的坐标是( )
A. B. C. D.
【题型8 由勾股定理求最值】
1.如图,已知,点为内的两个动点,且,,,点分别是上的动点,则的最小值是( )
A.5 B.7 C.8 D.10
2.如图,等腰和等腰的腰长分别为4和2,其中,M为边的中点.若等腰绕点A旋转,则点B到点M的距离的最大值为 .
3.如图,正方形的边长为6,线段在边上左右滑动,若,则的最小值为 .
4.如图,中,,,,点在上,将沿折叠,点落在点处,与相交于点,则的最大值为 .
参考答案
【题型1 勾股数的运用】
1.C
【分析】根据题意得为偶数,设其股是,则弦为,根据勾股定理列方程即可得到结论.
【详解】解:为正整数,
为偶数,设其股是,则弦为,
根据勾股定理得,,
解得,
弦是,
故选:C.
2.A
【分析】根据勾股数的概念对各选项进行逐一分析即可.
【详解】解:A、∵,
∴能构成勾股数,符合题意;
B、∵不是整数,
∴不能构成勾股数,不符合题意;
C、∵不是整数,
∴不能构成勾股数,不符合题意;
D、∵,
∴不能构成勾股数,不符合题意.
故选:A.
3.(1)解:观察已有的勾股数可得,
∴,
把代入,
解得(负值已舍掉),
∴;
(2)10,24,26是勾股数.
∵.
又∵10,24,26都是正整数
根据勾股数的定义,可知10,24,26是勾股数.
4.D
【分析】根据题目中所给的勾股数.广义勾股数,广义斜边数的定义,分析选项找出结论正确的即可.
【详解】解:由题意可知:
①m为正整数,则3m,4m,5m为一组勾股数;结论正确;
②1,2,3是一组广义勾股数;∵,∴不满足,不能成为广义勾股数,故结论不正确;
③13是广义斜边数;∵,∴结论正确;
④两个广义斜边数的和是广义斜边数;例如,,但是7不是广义斜边数,故结论不正确;
⑤若,其中k为正整数,则a,b,c为一组勾股数;∵,,满足:,故结论正确;
⑥两个广义斜边数的积是广义斜边数.例如,但是4不是广义斜边数,故结论不正确;
故正确的结论为:①③⑤.
故选:D
【题型2 勾股树的探究】
1.B
【分析】由已知图形观察规律,即可得到第五代勾股树中正方形的个数.
【详解】解:由题意可知第一代勾股树中正方形有(个),
第二代勾股树中正方形有(个),
第三代勾股树中正方形有(个),
由此推出第五代勾股树中正方形有(个)
故选:B.
2.4.
【分析】根据勾股定理可得两条直角边的平方和等于斜边的平方,即第①个正方形的面积=第②个正方形面积的两倍;同理,第③个正方形面积是第②个正方形面积的一半,依此类推即可解答.
【详解】解:第①个正方形的面积为16,
由分析可知:第②个正方形的面积为8,
第③个正方形的面积为4,
故答案为:4.
3. (为整数)
【分析】根据正方形的面积公式求出面积,再根据直角三角形三条边的关系运用勾股定理求出三角形的直角边,求出S1,然后利用正方形与三角形面积扩大与缩小的规律推导出公式.
【详解】解:(1)∵第一个正方形的边长为1,
∴正方形的面积为1,
又∵直角三角形一个角为30°,
∴三角形的一条直角边为,另一条直角边就是,
∴三角形的面积为,
∴S1=;
(2)∵第二个正方形的边长为,它的面积就是,也就是第一个正方形面积的,
同理,第二个三角形的面积也是第一个三角形的面积的,
∴S2=() ,
依此类推,S3=() ,
即S3=() ,
Sn=(n为整数).
故答案为:(1) ;(2)(为整数)
4.2023
【分析】根据勾股定理和正方形的面积公式,知“生长”1次后,以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,即所有正方形的面积和是2×1=2;“生长”2次后,所有的正方形的面积和是3×1=3,推而广之即可求出“生长”2022次后形成图形中所有正方形的面积之和.
【详解】设第一个直角三角形的是三条边分别是a,b,c.
根据勾股定理,得,
由图1可知,“生长”1次后,以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积,即所有正方形的面积和是;
由图2可知,“生长”2次后,所有的正方形的面积和是,
···
“生长”了2022次后形成的图形中所有的正方形的面积和是.
故答案为:2023.
【题型3 由勾股定理在坐标系中求距离】
1.A
【分析】连接,在直角坐标系中,根据点P的坐标是,得,,然后利用勾股定理即可求解.
【详解】解:连接,
∵点P的坐标是,
∴,,
∴点P到原点的距离,
故选:A.
2.C
【分析】根据平面直角坐标系中,两点之间的距离公式,代值求解即可得到答案.
【详解】解:连接,如图所示:
∵,,
∴,
故选:C.
3.解:(1)数轴上表示数的点与表示的点之间的距离,
故答案为:3;
(2)结合图形可得:,,.
故答案为:;
(3)若点在轴上,设点的坐标为,
则,即,
解得:,
即点的坐标为;
若点在轴上,设点的坐标为,
则,即,
解得:,
即点的坐标为.
综上可得点的坐标为或.
4.(1)解:阅读材料可得:;
(2)平面直角坐标系内任意两点,,,间的距离公式为:,
点,之间的距离为:;
故答案为:5;
(3)作点关于轴对称的点,连接,直线于轴的交点即为所求的点,的最小值就是线段的长度,然后根据两点间的距离公式即可得到结论.
,
,
,
设直线的一次函数表达式为,
把代入 解得 ,
当时,解得,即,
,
即为的最小值为.
故答案为:;
(4)原式,
故原式表示点到和的距离之和.
由两点之间线段最短,点在以和为端点的线段上时,原式值最小.
利用公式可得,原式.
【题型4 由勾股定理探究图形面积】
1.B
【分析】由勾股定理求出,由等腰直角三角形的性质得出,,,即可得出结果.
【详解】解:,,
和为等腰直角三角形,
,,
,
故选:.
2.B
【分析】设这个三角形的三条边的长度分别为,根据周长为列出方程并求得三边长度;然后由勾股定理逆定理判定该三角形为直角三角形,由三角形的面积公式作答即可.
【详解】解:设这个三角形的三条边的长度分别为,
∵三角形的周长为,
则,
解得,
则该三角形的三条边的长度分别为,
∵,
则该三角形为直角三角形,两直角边长分别为,
∴面积为: ,
故选:B.
3.(1)解:图2:;
图3:;
(2)解:结合结论①和结论②,可以得到一个等式:;
结合结论②和结论③,可以得到一个等式:,
即,;
(3)解:,,,
,
,
,
,
解得;
(4)解:由“应用”的解答过程可知:
∴阴影部分面积和,
,,
阴影部分面积和.
4.或
【分析】作交于点,设,用勾股定理得出,再由可得是的倍列出方程可得的值,再根据三角形的面积公式可得答案.
【详解】解:作交于点,
设,则.
在中,
.
∵中,,
∴ ,即,
∴,
解得或.
∴ 或 ,
∴的面积 或 .
故答案为: 或 .
【题型5 由勾股定理求线段长度】
1.(1)解:∵的周长为,,,
∴,
故答案:;
(2)解:是直角三角形,理由如下:
∵,,
∴,
∴是直角三角形;
(3)解:∵,
∴,
∴.
2.A
【分析】在中先根据勾股定理求出的长,再在中根据勾股定理即可得出结论.
【详解】,,,
.
在中,
,,,
.
故选:A.
3.
【分析】连接,延长交于H,根据得,可得,根据等腰三角形的性质得到,根据勾股定理得到,在中,根据勾股定理求解即可.
【详解】解:如图:连接,延长交于H,
∵线段的垂直平分线交于点O,
∴,
∵,
,
在和中,,
,
∴,
∴平分,
∵
∴,
∴,
在中,,
解得:.
故答案为.
4.(1)解:,
,
是直角三角形;
(2)解:设腰长.
在中,,
,
解得,
即:.
【题型6 由勾股定理证明线段之间的关系】
1.(1)解:证明:如图1中,连接.
,都是等边三角形,
,,,
,
,
.
(2)如图2中,以为边向下作等边,连接.
,都是等边三角形,
,,,
,
,
,
,,
,
,
,,
.
(3)如图3中,以为边向下作等边,连接,作交的延长线于.
同法可证:,
,设,,
则有,
解得,
,
,
,
,
,
.
2.(1)在中,
∵,
∴.
(2)∵,
∴,
在和中,
,
∴,
∴,
∴.
(3)结论:,理由如下:
连接.∵,
∴垂直平分,
∴,
∵,
∴,
由(1)可知,
∴,
∴,
∴,
∴.
3.(1)证明:如图,
,直线,直线,
,
,
,
,
,
,,
;
(2)解:①和均为等腰直角三角形,,
,
,
,
,,
,
故答案为:;
②,理由如下:
为等腰直角三角形,为中边上的高,
,
,
;
(3)证明:如图,延长到点,使,连接,,
是的中点,
,
在和中,
,
,
,,
,
,
,即,
中,,
,,
,
.
4.(1)解:∵a、b满足有意义,
∴且,
∴,即,,
;
(2)证明:连接,由(1)可得,
∵两个坐标轴垂直,
∴,
∴,
又∵为等腰直角三角形,
∴,
∴,
在和中,
,
∴,
∴.,,
∵,
∴,
∴,
即,
∴即;
(3)当点E在线段上时,连接,如图所示:
∵,,点M为的中点,
∴,,,
∵,
∴,
∴,
∴,
∵,
∴,
根据勾股定理得:;
当点E在线段延长线上时,连接,如图所示:
同理可得:,
∴,
∵,
∴,
根据勾股定理得:;
综上分析可知,.
【题型7 勾股定理中的规律探究】
1.
【分析】利用等腰直角三角形的性质以及勾股定理分别求出各边长,依据规律即可得出答案.
【详解】解:为等腰直角三角形,,
,
为等腰直角三角形,
.
为等腰直角三角形,
.
为等腰直角三角形,
.
的长度为.
故答案为:.
2.C
【分析】依据每列数的规律,即可得到,,,进而得出的值.
【详解】解:由题可得,,,,
,,,(且n为正整数)
当时,
解得:,
,,
,
故选:C.
3.
【分析】,根据勾股定理可得,,找到的规律,即可得到结论.
【详解】解:∵如图是由一串有公共顶点O的直角三角形组成的,
图中的,
∴由勾股定理可得:
,
,
……
∴,
∴在线段,,,,中,完全平方数有,,.
∴故长度为整数的线段有条.
故答案为:.
4.C
【分析】通过观察可得,每6个点的纵坐标规律:,0,,0,,0,点的横坐标规律:1,2,3,4,5,6,…,n,点从原点出发,以每秒个单位长度的速度沿着等边三角形的边“…”的路线运动,1秒钟走一段,P运动每6秒循环一次,点P运动n秒的横坐标规律:1,2,3,4,5,6,…,n,点P的纵坐标规律:,0,,0,,0,…,确定循环的点即可.
【详解】解:过点作轴于B,
∵图中是边长为2个单位长度的等边三角形,
∴,
∴,
∴,,
同理,,
,,
,
…
∴中每6个点的纵坐标规律:,0,,0,,0,
点从原点出发,以每秒个单位长度的速度沿着等边三角形的边“…” 的路线运动,1秒钟走一段,
∴P运动每6秒循环一次,
∴点P的纵坐标规律:,0,,0,,0,…,
点P的横坐标规律: 1,2,3,4,5,6,…,,
∵,
∴点的纵坐标为,
∴点的横坐标为,
∴点的坐标,
故选C.
【题型8 由勾股定理求最值】
1.A
【分析】作点关于直线的对称点,连接,作点关于直线的对称点,连接,连接,可知,当,,,在同一条直线上时,可以取得最小值,最小值等于的长度,即的最小值等于的长度,利用勾股定理即可求得的长度.
【详解】如图所示,作点关于直线的对称点,连接,作点关于直线的对称点,连接,连接.
根据轴对称图形的性质可知,,
∴.
根据题意可知,当,,,在同一条直线上时,可以取得最小值,最小值等于的长度,即的最小值等于的长度.
根据轴对称图形的性质可知,,
∴.
∴.
根据轴对称图形的性质可知,,
∴.
∴的最小值等于.
故选:.
2.
【分析】连接.由三线合一得,利用勾股定理求出,然后利用三角形三条边的关系求解即可.
【详解】如图,连接.
∵M为边的中点,且为等腰直角三角形,
∴,.
在中,,
由勾股定理可知,即.
当A,B,M三点不共线时,由三角形的三边关系可知,
此时一定有;当A,B,M三点共线且点M不位于点A,B之间时,此时有,
∴,
即点B到点M的距离的最大值为.
3.13
【分析】如图,作A于对称点,则,在上截取,然后连接,当三点共线时,有值最小,然后利用勾股定理即可解答.
【详解】解:如图,作A于对称点,
∴,,
在上截取,然后连接,
∵
∴四边形是平行四边形,
∴,
∴,
∴当三点共线时,有值最小,
∵,
∴,
∴,
由勾股定理得:,即最小值为13.
故答案为13.
4.
【分析】首先利用勾股定理求出,然后确定取最大值时最小,然后利用垂线段最短解决问题.
【详解】解:在中,,,,
,
,,
当最小时,最大,
当时最小,
又 ,解得,
的最小值为,
的最大值为,
故答案为:.
