专题4 一次函数与反比例函数(含解析)-2025年浙江省中考数学一模试题精编
文档属性
| 名称 | 专题4 一次函数与反比例函数(含解析)-2025年浙江省中考数学一模试题精编 |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 11:03:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题4 一次函数与反比例函数
一.选择题
1.(2025 杭州一模)如图为冰壶比赛场地示意图,由以P为圆心、半径分别为a,2a,3a,4a的同心圆组成.三只冰壶A,B,C的位置如图所示,∠APB=120°,CP的延长线平分∠APB,冰壶A,B分别表示为(4a,0°),(2a,120°),则冰壶C可表示为( )
A.(3a,120°) B.(4a,200°) C.(3a,240°) D.(3a,300°)
2.(2025 湖州一模)某地区某天的气温变化较大,如图表示该地区这天24小时的气温变化情况.下列说法正确的是( )
A.正午12点时,该地气温最高
B.这一天早上6点之后,该地气温一直在升高
C.该地这一天只有一个时刻的气温达到20℃
D.该地这一天的最高与最低气温差大约是25℃
3.(2025 浙江一模)若点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
4.(2025 湖州一模)在平面直角坐标系中,有A(﹣1,1),B(1,7),C(4,11),D(7,17)四个点,一次函数y=kx+b的图象恰好经过其中三个点,则该函数图象没有经过的点的坐标是( )
A.(﹣1,1) B.(1,7) C.(4,11) D.(7,17)
5.(2025 宁波一模)在平面直角坐标系中,点(a,a2+1)一定位于( )
A.一次函数y=x+1图象的上方 B.一次函数y=﹣x+1图象的下方
C.一次函数y=x图象的上方 D.一次函数y=﹣x图象的下方
6.(2025 温州一模)已知点(x1,y1),(x2,y2),(x3,y3)在反比例函数(k为常数)的图象上,x1<x2<x3,则下列说法中正确的是( )
A.若x1x2>0,则y1<y3 B.若x1x2<0,则y1<y3
C.若x2x3>0,则y1>y3 D.若x2x3<0,则y1>y3
7.(2025 龙泉市一模)若点A(m﹣3,y1),B(m﹣1,y2),C(m+1,y3)(其中1<m<3)都在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
8.(2025 滨江区一模)函数图象上有P(x1,t),Q(x2,t+4)两点.( )
A.若t>0,则0<x2<x1 B.若t>﹣4,则x2<0<x1
C.若t<0,则x2<0<x1 D.若t<﹣4,则0<x1<x2
9.(2025 定海区一模)如图,点B,C在反比例函数的图象上,点A在x轴上,连结AB交y轴于点E,延长BC交x轴于点D.已知点A(﹣2,0),且BC=CD,AE=BE.若△ABC面积为10,则k的值为( )
A.6 B.8 C.10 D.12
10.(2025 绍兴一模)如图,已知点A在函数y=(k是常数,k>0,x>0)图象上,点C在函数y=﹣(x>0)图象上,连结AC交x轴于点B,D是x轴上的点,若OA=AB,BC=CD,且△BCD的面积为1,则△AOB的面积为( )
A. B. C. D.
11.(2025 杭州一模)如图,矩形ABCO的两边分别在坐标轴上,OA=a,OC=b,点P在反比例函数(k为常数,k>0)的图象上,且在矩形ABCO内部,其横坐标为c.过点P作PE∥x轴交AC于点E,作PF∥y轴交AB于点F,连结EF,FC.记△EFC的面积为S,以下说法正确的是( )
A.S的值仅与a,b有关 B.S的值仅与c,k有关
C.S的值仅与k有关 D.S的值与a,b,c,k都有关
12.(2025 嘉善县一模)函数的图象经过P(m,y1),Q(m+2,y2)两点,则下列选项中正确的是( )
A.当m<0时,y1<y2 B.当﹣2<m<0时,y1>y2
C.当m>﹣2时,y1<y2 D.当m<﹣2或m>0时,y1>y2
13.(2025 宁波一模)已知A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数图象上的三个点,若x1<x2<0<x3,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
14.(2025 临安区一模)已知一次函数y1=k1(x﹣3)﹣2与反比例函数的图象交于A,B两点,与y轴交于点(0,k2),当x≥1时,总有y1<y2<0,则k1的值可以为( )
A.k1=1 B. C.k1=﹣1 D.k1=﹣2
15.(2025 宁波一模)已知一次函数y=x+a的图象与反比例函数交于M,N两点.当a=1时,△OMN的面积为1,则当a=﹣1时,△OMN的面积为( )
A. B.1 C. D.2
16.(2025 杭州模拟)综合实践小组的同学利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(cm)是液体的密度ρ(g/cm3)的反比例函数,其图象如图所示(ρ>0).下列说法正确的是( )
A.当液体密度ρ≥1g/cm3时,浸在液体中的高度h≥20cm
B.当液体密度ρ=2g/cm3时,浸在液体中的高度h=40cm
C.当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3
D.当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≤20cm
二.填空题
17.(2025 台州一模)已知一次函数y=kx+2(k是常数,k≠0)的图象过点(1,m)与(2,n),若m>0,n<0,则k的取值范围是 .
18.(2025 拱墅区一模)若一次函数y=kx+b的图象过点(1,m),(m,1),其中m≠1,则k= .
19.(2025 滨江区一模)甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示.当第一个人到达终点时,第二个人距离终点还剩 米.
20.(2025 定海区一模)世界各国的天气预报主要使用摄氏或华氏温标,学生查阅资料,得到两种温标计量值如表:
摄氏温度值x/℃ 0 10 20 30 40 50
华氏温度值y/℉ 32 50 68 86 104 122
请推算当摄氏温度为35℃时,华氏温度为 ℉.
21.(2025 富阳区一模)如图,一次函数y1=x﹣1与反比例函数y2=的图象交于点A(2,1),B(﹣1,﹣2),则使y1<y2的x的取值范围是 .
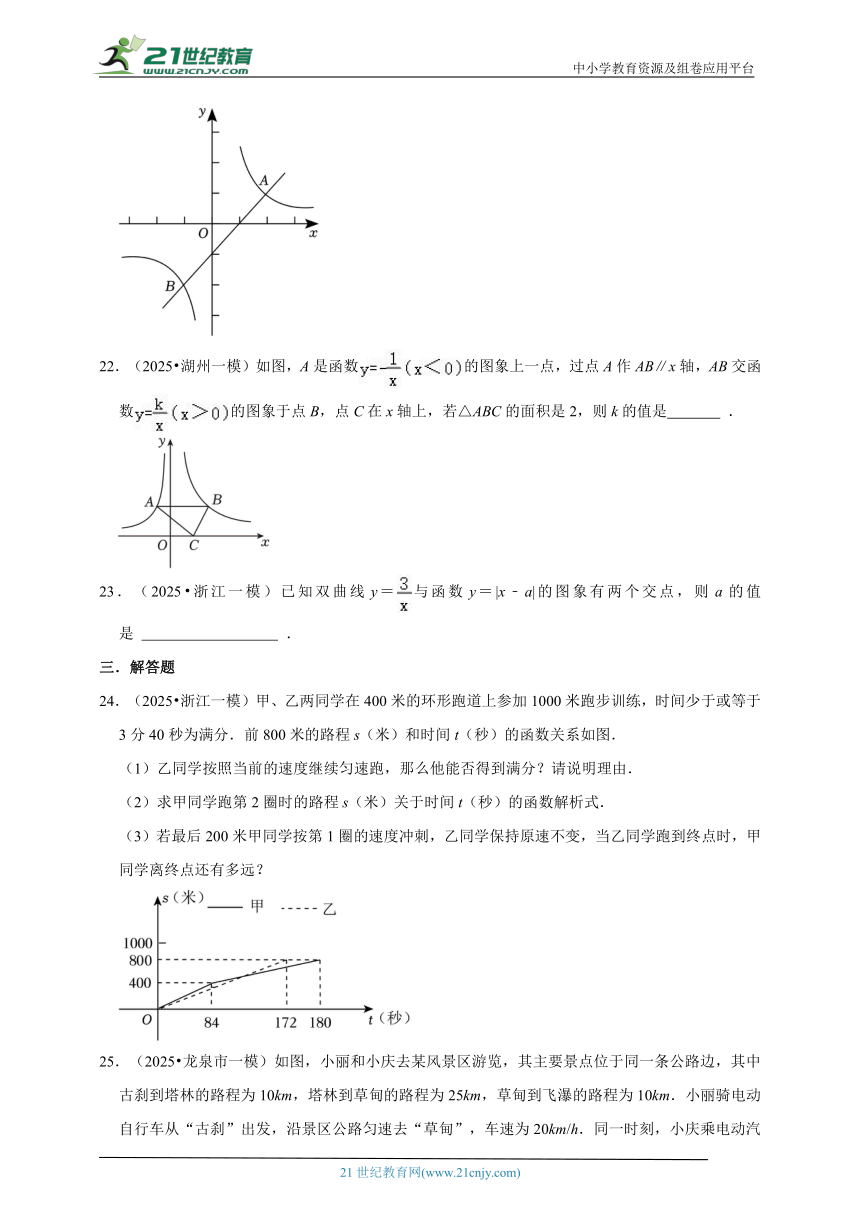
22.(2025 湖州一模)如图,A是函数的图象上一点,过点A作AB∥x轴,AB交函数的图象于点B,点C在x轴上,若△ABC的面积是2,则k的值是 .
23.(2025 浙江一模)已知双曲线y=与函数y=|x﹣a|的图象有两个交点,则a的值是 .
三.解答题
24.(2025 浙江一模)甲、乙两同学在400米的环形跑道上参加1000米跑步训练,时间少于或等于3分40秒为满分.前800米的路程s(米)和时间t(秒)的函数关系如图.
(1)乙同学按照当前的速度继续匀速跑,那么他能否得到满分?请说明理由.
(2)求甲同学跑第2圈时的路程s(米)关于时间t(秒)的函数解析式.
(3)若最后200米甲同学按第1圈的速度冲刺,乙同学保持原速不变,当乙同学跑到终点时,甲同学离终点还有多远?
25.(2025 龙泉市一模)如图,小丽和小庆去某风景区游览,其主要景点位于同一条公路边,其中古刹到塔林的路程为10km,塔林到草甸的路程为25km,草甸到飞瀑的路程为10km.小丽骑电动自行车从“古刹”出发,沿景区公路匀速去“草甸”,车速为20km/h.同一时刻,小庆乘电动汽车从“飞瀑”出发,沿景区公路匀速前往“古刹”.设两人相距的路程为s km,时间为t h,s关于t的部分函数图象如图所示.
(1)求小庆乘电动汽车的速度;
(2)求图中a的值;
(3)何时两人相距的路程等于5km?
26.(2025 衢州一模)2024年“有礼杯”衢州马拉松于11月24日开跑,小明和小聪一起报名参加了“迷你跑”的比赛.小明以一定的速度跑到3000米处的补给点休息了一段时间后,继续以原速前行,在距离终点500米处因体力不支,最终以100米/分的速度坚持跑到终点;小聪在途中休息了5分钟后,以原来的倍的速度冲向终点.如图是小明和小聪在比赛过程中所跑的路程s(米)和跑步时间t(分)的函数关系图.根据图象回答下列问题:
(1)求a的值;
(2)求图中线段BC对应的函数表达式;
(3)求小聪休息前的速度.
27.(2025 衢州一模)某科技公司在机器人展厅内的展台上举办了甲、乙两款机器人的表演、慢跑展示活动,展台的总长度是70米,如图1所示.甲机器人先从起点出发,匀速慢跑,到达指定的表演点后开始表演,表演结束后,立刻按原来速度继续向前慢跑,直到终点结束;乙机器人的起点在甲机器人起点前7米处,与甲机器人同时开始慢跑,一直前行,直到终点结束.已知甲、乙两款机器人距离甲机器人起点的距离y(米)与时间x(秒)之间的函数关系如图2所示.
(1)求甲、乙两款机器人各自的慢跑速度及甲机器人表演的时长.
(2)求当甲、乙两款机器人相遇时,相遇点离展示台终点的距离.
28.(2025 金华模拟)扎染古称“绞缬”,是我国一种古老的纺织品染色技艺.扎染工艺的发展带动了当地旅游相关产业的发展.某扎染坊第一次用3700元购进甲、乙两种布料共80件,其中两种布料的成本价和销售价如表:
单价类别 成本价/(元/件) 销售价/(元/件)
甲种布料 60 100
乙种布料 40 70
(1)该扎染坊第一次购进甲、乙两种布料各多少件?
(2)因热销,第一次购进的布料全部售完,该扎染坊第二次以相同的成本价再次购进甲、乙两种布料共100件.若此次购进甲种布料的数量不超过乙种布料数量的1.5倍,且以相同的销售价全部售完这批布料.设第二次购进甲种布料m件,第二次全部售完后获得的利润为W元.第二次应怎样进货,才能使第二次购进的布料全部售完后获得的利润最大?最大利润是多少元?
29.(2025 拱墅区一模)某社区推出智能可回收垃圾投放箱,居民投放可回收物可以赚取积分兑换生活用品.为了鼓励居民积极投放,超过一定投放质量后,奖励积分升级.其中塑料与纸张的奖励积分y(分)与投放质量x(kg)的函数关系如图所示.已知投放纸张超过10kg后,奖励积分为25分/kg.
(1)求投放8kg塑料的奖励积分.
(2)求a的值.
(3)若投放m kg的塑料的奖励积分是投放相同质量纸张的奖励积分的倍,求m的值.
30.(2025 杭州一模)为鼓励节约用水,某市实行了阶梯水价制度.设月用水量为x(吨),每月应交水费y(元),如表为每户的综合用水单价与月用水量的关系表,如图是y关于x的函数图象.
阶梯 月用水量(吨) 用水单价(元/吨)
第一阶梯 x≤10 a
第二阶梯 10<x≤20 b
第三阶梯 x>20 5
根据上述信息解决以下问题:
(1)求a,b的值.
(2)当x>10时,求y关于x的函数表达式.
(3)小红家6月份、7月份的用水量都为整数吨,且都超过了10吨,水费合计为90元,其中6月份用水量低于7月份用水量,求小红家6月份的用水量.
31.(2025 西湖区一模)在直角坐标系中,设函数y1=与函数y2=k2x+b(k1,k2,b是常数,k1k2≠0)的图象交于点A(1,4),B(﹣2,t).
(1)求函数y1,y2的表达式.
(2)当x>2时,比较y1与y2的大小.(直接写出结果)
(3)若点C在函数y2的图象上,将点C先向左平移1个单位,再向下平移6个单位得点D,点D恰好落在函数y1的图象上,求点C的坐标.
32.(2025 临安区一模)如图,反比例函数图象过点A(﹣2,a),直线x=4与该反比例函数图象和x轴分别交于点B和点D,连结AD.
(1)求△ADB的面积.
(2)若点P(m,n)(m>0)在反比例函数图象上,当PD⊥AD,求点P的坐标.
33.(2025 浙江模拟)如图,一次函数y=﹣2x+b的图象与反比例函数的图象相交于点A(﹣1,4).
(1)求b和k的值.
(2)横坐标为3的点B是反比例函数图象上的一点,现将点B向下平移.当点B落在一次函数图象上时,求向下平移的距离.
34.(2025 上城区一模)某项目学习小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地,当人和木板对湿地的压力F(单位:N)一定时,木板面积S(单位:m2)与人和木板对地面的压强P(单位:Pa)成反比例.当木板面积为0.2m2时,人和木板对地面的压强为3000Pa.
(1)求P关于S的函数表达式;
(2)当木板面积为0.3m2时,压强是多少?
(3)如果要求压强不超过1200Pa,木板面积至少要多大?请说明理由.
35.(2025 萧山区一模)科技创新为实现可持续发展赋能.某企业自2024年1月开始限产进行技术改造,其月利润y(万元)与月份x之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分.
(1)求反比例函数和一次函数的表达式.
(2)求当月利润不高于100万元时共经历了多少个月?
36.(2025 湖州一模)电磁波由振荡的电场和磁场构成,我国嫦娥六号探测器就是通过无线电波(电磁波的一种)与地球通信,电磁波的波长λ(单位:m)会随着电磁波的频率f(单位:MHz)的变化而变化.已知某段电磁波在同种介质中,波长λ与频率f的部分对应值如表:
频率f(MHz) 5 10 15 20 25 30
波长λ(m) 60 30 20 15 12 10
(1)根据表格中的数据,选择合适的函数模型,求出波长λ(m)关于频率f(MHz)的函数表达式.
(2)当该电磁波的频率为50MHz时,它的波长是多少m?
37.(2025 镇海区校级模拟)在平面直角坐标系中,直线y=﹣2x+4交x轴于点A,交y轴于点B,点C的坐标为(1,0).
(1)求直线BC的函数表达式.
(2)点D是x轴上一动点,连接BD、CD,当△BCD的面积是△AOB面积的时,求点D的坐标.
(3)点E坐标为(0,﹣2),连接CE,点P为直线AB上一点,若∠CEP=45°,求点P坐标.
答案与解析
一.选择题
1.(2025 杭州一模)如图为冰壶比赛场地示意图,由以P为圆心、半径分别为a,2a,3a,4a的同心圆组成.三只冰壶A,B,C的位置如图所示,∠APB=120°,CP的延长线平分∠APB,冰壶A,B分别表示为(4a,0°),(2a,120°),则冰壶C可表示为( )
A.(3a,120°) B.(4a,200°) C.(3a,240°) D.(3a,300°)
【点拨】设CP的延长线交冰壶场地的最外圈与D,根据题意求出图形和题意得出点C的位置.
【解析】解:设CP的延长线交冰壶场地的最外圈与D,如图:
∵∠APB=120°,CP的延长线平分∠APB,
∴∠APD=∠DPB=60°,
∴∠DPE=30°,
∴∠CPF=30°,
∴冰壶C可表示为(3a,240°),
故选:C.
【点睛】本题考查坐标定位置,关键是掌握平面直角坐标系中坐标的位置.
2.(2025 湖州一模)某地区某天的气温变化较大,如图表示该地区这天24小时的气温变化情况.下列说法正确的是( )
A.正午12点时,该地气温最高 B.这一天早上6点之后,该地气温一直在升高
C.该地这一天只有一个时刻的气温达到20℃ D.该地这一天的最高与最低气温差大约是25℃
【点拨】从图象中有效的获取信息,逐一进行判断即可.
【解析】解:由图象可知:
A、15点时,该地气温最高,原选项说法错误,不符合题意;
B、这一天早上6点至9点,该地气温在下降,原选项说法错误,不符合题意;
C、该地在12时至19时的气温达到20℃,原选项说法错误,不符合题意;
D、该地这一天的最高与最低气温差大约是:30﹣5=25(℃),说法正确,符合题意;
故选:D.
【点睛】本题考查的是函数的图象,能根据函数图象在坐标系中的增减性判断出函数的增减性是解答此题的关键.
3.(2025 浙江一模)若点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
【点拨】由k=﹣3<0,利用一次函数的性质,可得出y随x的增大而减小,再结合﹣2<1<3,即可得出y1>y3>y2.
【解析】解:∵k=﹣3<0,
∴y随x的增大而减小,
又∵点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,且﹣2<1<3,
∴y1>y3>y2.
故选:C.
【点睛】本题考查了一次函数的性质,牢记“k>0,y随x的增大而增大;k<0,y随x的增大而减小”是解题的关键.
4.(2025 湖州一模)在平面直角坐标系中,有A(﹣1,1),B(1,7),C(4,11),D(7,17)四个点,一次函数y=kx+b的图象恰好经过其中三个点,则该函数图象没有经过的点的坐标是( )
A.(﹣1,1) B.(1,7) C.(4,11) D.(7,17)
【点拨】根据题意,分别求出满足要求的一次函数的解析式,即可得出答案.
【解析】解:由题意,当一次函数y=kx+b的图象经过点A和点B时,
,
解得,
一次函数的解析式为y=3x+4;同理可得,
当一次函数y=kx+b的图象经过点A和点C时,一次函数的解析式为y=2x+3;
当一次函数y=kx+b的图象经过点B和点C时,一次函数的解析式为y=x+;
当一次函数y=kx+b的图象经过点B和点D时,一次函数的解析式为y=x+;
当一次函数y=kx+b的图象经过点C和点D时,一次函数的解析式为y=2x+3;
所以A、C、D都在一次函数y=2x+3的图象上,该函数图象没有经过的点的坐标是B(1,7).
故选:B.
【点睛】本题考查一次函数图象上点的坐标特征,分别求出满足要求的一次函数的解析式是解题的关键.
5.(2025 宁波一模)在平面直角坐标系中,点(a,a2+1)一定位于( )
A.一次函数y=x+1图象的上方 B.一次函数y=﹣x+1图象的下方
C.一次函数y=x图象的上方 D.一次函数y=﹣x图象的下方
【点拨】根据点(a,a2+1)在二次函数y=x2+1的图象上,画出函数图象判断即可.
【解析】解:点(a,a2+1)在二次函数y=x2+1的图象上,画出函数图象如下:
A、二次函数的图象与一次函数的图象有交点,所以点(a,a2+1)不一定位于一次函数y=x+1图象的上方,故A选项不符合题意;
B、二次函数的图象与一次函数的图象有交点,所以点(a,a2+1)不一定位于一次函数y=﹣x+1图象的下方,故B选项不符合题意;
C、二次函数的图象在一次函数y=x的上方,所以点(a,a2+1)一定位于一次函数y=x图象的上方,故C选项符合题意;
D、二次函数的图象在一次函数y=﹣x的上方,所以点(a,a2+1)一定位于一次函数y=x图象的上方,故D选项不符合题意;
故选:C.
【点睛】本题考查了二次函数和一次函数的图象,数形结合是关键.
6.(2025 温州一模)已知点(x1,y1),(x2,y2),(x3,y3)在反比例函数(k为常数)的图象上,x1<x2<x3,则下列说法中正确的是( )
A.若x1x2>0,则y1<y3 B.若x1x2<0,则y1<y3
C.若x2x3>0,则y1>y3 D.若x2x3<0,则y1>y3
【点拨】由k2+1>0可得反比例函数图象在第一、三象限,根据选项一一分析即可.
【解析】解:点(x1,y1),(x2,y2),(x3,y3)在反比例函数(k为常数)的图象上,x1<x2<x3,
∵k2+1>0,
∴图象在第一、三象限,在每个象限y随x增大而减小,
A、若x1x2>0,则点(x1,y1),(x2,y2)在同一象限,
如果点(x1,y1),(x2,y2),(x3,y3)都在第一象限,则y1>y3,故不合题意;
B、若x1x2<0,则点(x1,y1)在第三象限,(x2,y2),(x3,y3)在第一象限,则y1<y3,故符合题意;
C、若x2x3>0,则(x2,y2),(x3,y3)在同一象限,
如果点(x1,y1)在第三象限,点(x2,y2),(x3,y3)都在第一象限,则y1<y3,故不合题意;
D、若x2x3<0,则点(x1,y1),(x2,y2)在第三象限,(x3,y3)在第一象限,y1<y3,故不合题意.故选:B.
【点睛】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数的性质是解题的关键.
7.(2025 龙泉市一模)若点A(m﹣3,y1),B(m﹣1,y2),C(m+1,y3)(其中1<m<3)都在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
【点拨】根据反比例函数图象上点的坐标特征解答即可.
【解析】解:∵反比例函数的k=﹣3<0,
∴反比例函数图象分布在第二、四象限,在每个象限内,y随x的增大而增大,
∵1<m<3,
∴点A(m﹣3,y1)在第二象限,y1>0,B(m﹣1,y2)和C(m+1,y3)在第四象限,
∵m﹣1<m+1,
∴y2<y3<0,
∴y2<y3<y1.
故选:C.
【点睛】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数的增减性是关键.
8.(2025 滨江区一模)函数图象上有P(x1,t),Q(x2,t+4)两点.( )
A.若t>0,则0<x2<x1 B.若t>﹣4,则x2<0<x1
C.若t<0,则x2<0<x1 D.若t<﹣4,则0<x1<x2
【点拨】先根据反比例函数的解析式判断出函数图象所在的象限,再对各选项进行逐一判断即可.
【解析】解:∵反比例函数中,k=﹣4<0,
∴此函数图象的两个分支分别位于第二、四象限,在每一象限内y随x的增大而增大,
A、若t>0,则P(x1,t),Q(x2,t+4)在第二象限,且t<t+4,
∵t<t+4,
∴x1<x2<0,故错误,不符合题意;
B、若t>﹣4,则P(x1,t),Q(x2,t+4)有可能都在第四象限,故错误,不符合题意;
C、若t<0,则P(x1,t),Q(x2,t+4)有可能都在第二象限,故错误,不符合题意;
D、若t<﹣4,t+4<0,
∴P(x1,t),Q(x2,t+4)在第四象限,
∵t<t+4,
∴0<x1<x2,正确,符合题意.
故选:D.
【点睛】本题考查的是反比例函数图象上点的坐标特征,熟知反比例函数的图象与系数的关系是解题的关键.
9.(2025 定海区一模)如图,点B,C在反比例函数的图象上,点A在x轴上,连结AB交y轴于点E,延长BC交x轴于点D.已知点A(﹣2,0),且BC=CD,AE=BE.若△ABC面积为10,则k的值为( )
A.6 B.8 C.10 D.12
【点拨】根据反比例函数k值的几何意义解答即可.
【解析】解:如图,连接CE、OC,
∵AE=BE.△ABC面积为10,
∴S△AEC=S△ABC==5,
∵BC=CD,AE=BE.
∴CE是△ABD的中位线,
∴CE∥AD,
∴S△AEC=S△OEC=5,
∴k=2S△OEC=2×5=10,
故选:C.
【点睛】本题考查了反比例函数k值的几何意义、反比例函数图象上点的坐标特征,熟练掌握以上知识点是关键.
10.(2025 绍兴一模)如图,已知点A在函数y=(k是常数,k>0,x>0)图象上,点C在函数y=﹣(x>0)图象上,连结AC交x轴于点B,D是x轴上的点,若OA=AB,BC=CD,且△BCD的面积为1,则△AOB的面积为( )
A. B. C. D.
【点拨】作AE⊥x轴于E,CF⊥x轴于F,则AE∥CF,由题意设点A(m,),点C(n,﹣),则BE=OE=m,AE=,DF=BF=n﹣2m,CF=,通过证得△ABE∽△CBF,得到n=(+1)m,然后根据△BCD的面积为1,即可求得k的值.
【解析】解:作AE⊥x轴于E,CF⊥x轴于F,则AE∥CF,
∵OA=AB,BC=CD,
∴OE=BE,BF=DF,
由题意设点A(m,),点C(n,﹣),则BE=OE=m,AE=,DF=BF=n﹣2m,CF=,
∴BD=2(n﹣2m),
∵AE∥CF,
∴△ABE∽△CBF,
∴,即,
∴m2=n2﹣2mn,
∴2m2=(n﹣m)2,
∴n=(+1)m或n=(1﹣)m(舍去),
∴BD=2()m,CF=,
∵△BCD的面积为1,
∴=,
∴k=3+2,
∵S△AOE=,
∴S△AOB=2S△AOE=k=3+2.
故选:D.
【点睛】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,等腰三角形的性质,三角形相似的判定和性质,作出辅助线构建相似三角形是解题的关键.
11.(2025 杭州一模)如图,矩形ABCO的两边分别在坐标轴上,OA=a,OC=b,点P在反比例函数(k为常数,k>0)的图象上,且在矩形ABCO内部,其横坐标为c.过点P作PE∥x轴交AC于点E,作PF∥y轴交AB于点F,连结EF,FC.记△EFC的面积为S,以下说法正确的是( )
A.S的值仅与a,b有关 B.S的值仅与c,k有关
C.S的值仅与k有关 D.S的值与a,b,c,k都有关
【点拨】根据题意,先确定各点的坐标,C(b,0),B(b,a),A(0,a),P(c,),F(c,a),利用S△CEF=S△ABC﹣S△AEF﹣S△BCF=得到结论即可.
【解析】解:如图,
由条件可知C(b,0),B(b,a),A(0,a),
∵点P在反比例函数(k为常数,k>0)的图象上,且横坐标为c,
∴P(c,),F(c,a),
∴S△AEF= AF (a﹣)=(ac﹣k),
S△BCF===,
S△ABC==,
∴S△CEF=S△ABC﹣S△AEF﹣S△BCF=,
∴△EFC的面积为S仅与k值有关.
故选:C.
【点睛】本题考查了反比例函数k值的几何意义、反比例函数图象上点的坐标特征、矩形的性质,熟练掌握以上知识点是关键.
12.(2025 嘉善县一模)函数的图象经过P(m,y1),Q(m+2,y2)两点,则下列选项中正确的是( )
A.当m<0时,y1<y2 B.当﹣2<m<0时,y1>y2
C.当m>﹣2时,y1<y2 D.当m<﹣2或m>0时,y1>y2
【点拨】由于反比例函数y=﹣,可知函数位于第二、四象限,分情况讨论,根据反比例函数的增减性判断出y1与y2的大小.
【解析】解:由条件可知:函数位于第二、四象限,y随x的增大而增大,
当0<m<m+2时,即m>0时,y1<y2,
当m<m+2<0时,即m<﹣2时,y1<y2,
当m<0<m+2,即﹣2<m<0,y1>y2,
所以结合选项可知:B符合题意,
故选:B.
【点睛】本题考查了反比例函数图象上的点的坐标特征,掌握反比例函数的性质是解题的关键.
13.(2025 宁波一模)已知A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数图象上的三个点,若x1<x2<0<x3,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
【点拨】先根据函数解析式中的比例系数k确定函数图象所在的象限,再根据各象限内点的坐标特点及函数的增减性解答.
【解析】解:∵反比例函数中,k=﹣5<0,
∴此函数图象在二、四象限,在每个象限内y随x的增大而增大,
∵点A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数图象上的三个点,且x1<x2<0<x3,
∴点C(x3,y3)在第四象限,则y3<0,
∵点A(x1,y1),B(x2,y2)在第二象限,则y2>y1>0,
∴y1,y2,y3的大小关系为y3<y1<y2.
故选:D.
【点睛】此题考查的是反比例函数图象上点的坐标特点及平面直角坐标系中各象限内点的坐标特点,比较简单.
14.(2025 临安区一模)已知一次函数y1=k1(x﹣3)﹣2与反比例函数的图象交于A,B两点,与y轴交于点(0,k2),当x≥1时,总有y1<y2<0,则k1的值可以为( )
A.k1=1 B. C.k1=﹣1 D.k1=﹣2
【点拨】根据反比例函数与一次函数的交点问题解答即可.
【解析】解:∵一次函数与y轴交于点(0,k2),
∴k2=﹣3k1﹣2,
∵x≥1时,y2=<0,
∴k2<0,即﹣3k1﹣2<0,
∴k1>﹣,
∵当x=1时,y1<y2,
∴﹣2k1﹣2<﹣3k1﹣2,
∴k1<0,
∴﹣<k1<0,
四个选项,只有选项B符合条件.
故选:B.
【点睛】本题考查了反比例函数与一次函数的交点问题,熟练掌握交点坐标满足两个函数解析式是关键.
15.(2025 宁波一模)已知一次函数y=x+a的图象与反比例函数交于M,N两点.当a=1时,△OMN的面积为1,则当a=﹣1时,△OMN的面积为( )
A. B.1 C. D.2
【点拨】分别联立直线和反比例函数解析式得到两次的交点关于原点成中心对称,则△OMN的面积不变,即可求解.
【解析】解:当a=1时,联立得:x(x+1)=k,
解得:,
∴点,(顺序无关),
当a=﹣1联立得:x(x﹣1)=k,
解得:,
∴点,(顺序无关),
∴发现点M与点N′关于原点成中心对称,点N与点M′关于原点成中心对称,
∴S△OMN=S△OM′N′=1,
故选:B.
【点睛】本题考查了反比例函数与一次函数的交点问题,反比例函数的对称性,根据对称性求解是解题的关键.
16.(2025 杭州模拟)综合实践小组的同学利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(cm)是液体的密度ρ(g/cm3)的反比例函数,其图象如图所示(ρ>0).下列说法正确的是( )
A.当液体密度ρ≥1g/cm3时,浸在液体中的高度h≥20cm
B.当液体密度ρ=2g/cm3时,浸在液体中的高度h=40cm
C.当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3
D.当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≤20cm
【点拨】根据图象和反比例函数性质逐项分析判断即可.
【解析】解:根据题意得,反比例函数解析式为:h=,
A、当液体密度ρ≥1g/cm3时,浸在液体中的高度h≤20cm,故原说法错误,不符合题意;
B、当液体密度ρ=2g/cm3时,浸在液体中的高度h=10cm,故原说法错误,不符合题意;,
C、当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3,正确,符合题意;
D、当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≥20cm,故原说法错误,不符合题意;,
故选:C.
【点睛】本题考查了反比例函数的应用,熟练掌握反比例函数性质是关键.
二.填空题
17.(2025 台州一模)已知一次函数y=kx+2(k是常数,k≠0)的图象过点(1,m)与(2,n),若m>0,n<0,则k的取值范围是 ﹣2<k<﹣1 .
【点拨】根据y随x的增大而减小,即可得出答案.
【解析】解:∵一次函数y=kx+2的图象过点(1,m)与(2,n),m>0,n<0,
∴k+2>0,2k+2<0,
解得﹣2<k<﹣1.
故答案为:﹣2<k<﹣1.
【点睛】本题考查了一次函数图象与系数的关系,一次函数图象上点的坐标特征,熟练掌握一次函数的性质是解题的关键.
18.(2025 拱墅区一模)若一次函数y=kx+b的图象过点(1,m),(m,1),其中m≠1,则k= ﹣1 .
【点拨】利用一次函数图象上点的坐标特征,可得出关于k的方程组,解之即可得出结论.
【解析】解:∵一次函数y=kx+b的图象过点(1,m),(m,1),m≠1,
∴,
解得:k=﹣1.
故答案为:﹣1.
【点睛】本题考查了一次函数图象上点的坐标特征,牢记“直线上任意一点的坐标都满足函数关系式y=kx+b”是解题的关键.
19.(2025 滨江区一模)甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示.当第一个人到达终点时,第二个人距离终点还剩 4 米.
【点拨】根据图形列出算式,再求出即可.
【解析】解:100﹣=4(米),
即当第一个人到达终点时,第二个人距离终点还剩4米,
故答案为:4.
【点睛】本题考查了一次函数的应用,能根据图形得出正确的信息是解此题的关键,数形结合思想的应用.
20.(2025 定海区一模)世界各国的天气预报主要使用摄氏或华氏温标,学生查阅资料,得到两种温标计量值如表:
摄氏温度值x/℃ 0 10 20 30 40 50
华氏温度值y/℉ 32 50 68 86 104 122
请推算当摄氏温度为35℃时,华氏温度为 95 ℉.
【点拨】根据题意判断出函数的类型,再用待定系数法求解求出解析式,再代入数据计算即可.
【解析】解:由题意可得.x每增加10℃,y增加18℉,是一个均匀变化的过程,所以函数为一次函数,
设y=kx+b.
将(0,32)(10,50)代入解析式可得:
,
解得:.
∴y=1.8x+32,
当x=35°时,y=1.8×35+32=95,
故答案为:95.
【点睛】本题考查一次函数的应用,正确进行计算是解题关键.
21.(2025 富阳区一模)如图,一次函数y1=x﹣1与反比例函数y2=的图象交于点A(2,1),B(﹣1,﹣2),则使y1<y2的x的取值范围是 0<x<2或x<﹣1 .
【点拨】求得一次函数的图象在反比例函数的图象下方时,自变量x的取值即可.
【解析】解:∵一次函数y1=x﹣1与反比例函数y2=的图象交于点A(2,1),B(﹣1,﹣2),
∴从图象可知:使y1<y2的x的取值范围是x<﹣1或0<x<2,
故答案为0<x<2或x<﹣1.
【点睛】本题考查了反比例函数与一次函数的交点问题,利用数形结合是解题的关键.
22.(2025 湖州一模)如图,A是函数的图象上一点,过点A作AB∥x轴,AB交函数的图象于点B,点C在x轴上,若△ABC的面积是2,则k的值是 3 .
【点拨】依据题意,设点A的坐标为,其中a<0,又AB∥x轴,则点B的纵坐标与点A相同,故,代入(x>0),从而B的横坐标为,可得点B的坐标为,又△ABC的顶点C在x轴上,可设其坐标为(c,0),故S△ABC=AB h=(﹣ak﹣a) (﹣)=2,则,进而计算可以得解.
【解析】解:由题意,设点A的坐标为,其中a<0.
又∵AB∥x轴,
∴点B的纵坐标与点A相同.
∴,代入(x>0),
∴B的横坐标为.
∴点B的坐标为.
又∵△ABC的顶点C在x轴上,可设其坐标为(c,0).
∴S△ABC=AB h=(﹣ak﹣a) (﹣)=2.
∴.
∴k=3.
故答案为:3.
【点睛】本题主要考查了反比例函数系数k的几何意义、反比例函数图象上点的坐标特征,解题时要熟练掌握并能灵活运用反比例函数的性质是关键.
23.(2025 浙江一模)已知双曲线y=与函数y=|x﹣a|的图象有两个交点,则a的值是 .
【点拨】根据题意画出图象分析可得,一次函数y=﹣x+a的图象与y=的图象只有一个交点,且a>0,可得方程﹣x2+ax﹣3=0只有一个实数根,利用根的判别式即可求解.
【解析】解:如图,
∵双曲线y=与函数y=|x﹣a|的图象有两个交点,
∴由图可知,一次函数y=﹣x+a的图象与y=的图象只有一个交点,且a>0,
可得,
整理得:﹣x2+ax﹣3=0,
∴方程﹣x2+ax﹣3=0只有一个实数根,
∴Δ=b2﹣4ac=a2﹣12=0,
解得:a=或(舍去).
故答案为:.
【点睛】本题主要考查反比例函数与一次函数的交点问题、根的判别式,解题关键在于利用数形结合思想解决问题.
三.解答题
24.(2025 浙江一模)甲、乙两同学在400米的环形跑道上参加1000米跑步训练,时间少于或等于3分40秒为满分.前800米的路程s(米)和时间t(秒)的函数关系如图.
(1)乙同学按照当前的速度继续匀速跑,那么他能否得到满分?请说明理由.
(2)求甲同学跑第2圈时的路程s(米)关于时间t(秒)的函数解析式.
(3)若最后200米甲同学按第1圈的速度冲刺,乙同学保持原速不变,当乙同学跑到终点时,甲同学离终点还有多远?
【点拨】(1)求出乙同学路程s(米)关于时间t(秒)的函数解析式,然后令s=1000,求出t的值即可解答;
(2)设s=kt+b,用待定系数法求解即可;
(3)求出最后200米,乙跑到终点时,甲同学跑的时间是215﹣180=35(秒),速度是(米/秒),进而可求出甲同学离终点还有多远.
【解析】解:(1)设s=kt,
将(172,800)代入可得,800=172k,
解得:,
∴.
令s=1000,
解得:t=215.
∵3分40秒=220秒,215<220,
∴乙同学能够得到满分.
(2)由图象可知s是t的一次函数,设s=kt+b,
由题意可得:
解得:
∴.
(3)由(1)可知乙同学到终点的时间是215秒,
由图象可知甲同学跑前800米的时间是180秒,
所以最后200米,乙跑到终点时,甲同学跑的时间是215﹣180=35(秒).
速度是(米/秒).
路程是(米).
∴甲离终点的距离是(米).
【点睛】本题考查了从函数图象获取信息,一次函数的应用,数形结合是解答本题的关键.
25.(2025 龙泉市一模)如图,小丽和小庆去某风景区游览,其主要景点位于同一条公路边,其中古刹到塔林的路程为10km,塔林到草甸的路程为25km,草甸到飞瀑的路程为10km.小丽骑电动自行车从“古刹”出发,沿景区公路匀速去“草甸”,车速为20km/h.同一时刻,小庆乘电动汽车从“飞瀑”出发,沿景区公路匀速前往“古刹”.设两人相距的路程为s km,时间为t h,s关于t的部分函数图象如图所示.
(1)求小庆乘电动汽车的速度;
(2)求图中a的值;
(3)何时两人相距的路程等于5km?
【点拨】(1)根据“(出发时二之间的距离﹣二人相遇时小丽行驶的路程)÷相遇时间”计算小庆乘电动汽车的速度即可;
(2)根据“相遇后二人行驶的路程之和等于30km”列关于a的方程并求解即可;
(3)分别计算二人相遇前后两种情况下相距的路程等于5km时对应的时间即可.
【解析】解:(1)(45﹣20×0.9)÷0.9=30(km/h).
答:小庆乘电动汽车的速度为30km/h.
(2)根据图象,得(20+30)(a﹣0.9)=30,
解得a=1.5.
(3)相遇前,当两人相距的路程等于5km时,(45﹣5)÷(20+30)=0.8(h),
相遇后,当两人相距的路程等于5km时,0.9+5÷(20+30)=1(h),
∴两人出发后0.8h或1h相距的路程等于5km.
【点睛】本题考查一次函数的应用,掌握速度、时间和路程之间的关系是解题的关键.
26.(2025 衢州一模)2024年“有礼杯”衢州马拉松于11月24日开跑,小明和小聪一起报名参加了“迷你跑”的比赛.小明以一定的速度跑到3000米处的补给点休息了一段时间后,继续以原速前行,在距离终点500米处因体力不支,最终以100米/分的速度坚持跑到终点;小聪在途中休息了5分钟后,以原来的倍的速度冲向终点.如图是小明和小聪在比赛过程中所跑的路程s(米)和跑步时间t(分)的函数关系图.根据图象回答下列问题:
(1)求a的值;
(2)求图中线段BC对应的函数表达式;
(3)求小聪休息前的速度.
【点拨】(1)根据时间=路程÷速度求出CD所用时间,从而求出a的值即可;
(2)根据速度=路程÷时间求出小明在OA段的速度,亦即BC段的速度,设B(m,3000),根据路程=速度×时间列关于m的方程并求解,再根据路程=速度×时间求出线段BC对应的函数表达式即可;
(3)将t=32.5代入线段BC对应的函数表达式,求出对应s的值,设小聪休息前的速度为v米/分,则小聪休息后的速度为v米/分,用含v的代数式将点B的横坐标表示出来,再由路程=速度×时间列关于v的方程并求解即可.
【解析】解:(1)小明在跑完CD段用时500÷100=5(分),
37.5+5=42.5(分),
∴a=42.5.
(2)小明OA段和BC段的速度均为3000÷15=200(米/分),
设B(m,3000),则200(37.5﹣m)=5500﹣3000,
解得m=25,
s=3000+200(t﹣25)=200t﹣2000,
∴线段BC对应的函数表达式为s=200t﹣2000(25≤t≤37.5).
(3)当t=32.5时,s=200×32.5﹣2000=4500,
设小聪休息前的速度为v米/分,则小聪休息后的速度为v米/分,
∴点A的横坐标为,
∴点B的横坐标为+5,
根据图象,得4500+v[42.5﹣(+5)]=6000,
解得v=150.
答:小聪休息前的速度为150米/分.
【点睛】本题考查一次函数的应用、函数的图象,掌握速度、时间和路程之间的关系是解题的关键.
27.(2025 衢州一模)某科技公司在机器人展厅内的展台上举办了甲、乙两款机器人的表演、慢跑展示活动,展台的总长度是70米,如图1所示.甲机器人先从起点出发,匀速慢跑,到达指定的表演点后开始表演,表演结束后,立刻按原来速度继续向前慢跑,直到终点结束;乙机器人的起点在甲机器人起点前7米处,与甲机器人同时开始慢跑,一直前行,直到终点结束.已知甲、乙两款机器人距离甲机器人起点的距离y(米)与时间x(秒)之间的函数关系如图2所示.
(1)求甲、乙两款机器人各自的慢跑速度及甲机器人表演的时长.
(2)求当甲、乙两款机器人相遇时,相遇点离展示台终点的距离.
【点拨】(1)根据速度=路程÷时间分别计算甲、乙两款机器人各自的慢跑速度,由甲机器人表演的时长=甲机器人到达终点所用的时间﹣甲机器人到达终点通过的路程÷甲款机器人慢跑的速度计算甲机器人表演的时长即可;
(2)分别写出甲款机器人y与x之间的函数关系式(0≤x≤6)、乙款机器人y与x之间的函数关系式,分别计算两机器人相遇时对应y的值,从而求出相遇点离展示台终点的距离即可.
【解析】解:(1)甲款机器人慢跑的速度为30÷6=5(米/秒),
乙款机器人慢跑的速度为(70﹣7)÷18=3.5(米/秒),
甲款机器人表演的时长为18﹣70÷5=4(秒).
答:甲款机器人慢跑的速度为5米/秒,乙款机器人慢跑的速度为3.5米/秒,甲款机器人表演的时长为4秒.
(2)当0≤x≤6时,甲款机器人y与x之间的函数关系式为y=5x,
乙款机器人y与x之间的函数关系式为y=3.5x+7.
当0≤x≤6时,当甲、乙两款机器人相遇时,得,
解得,
此时相遇点离展示台终点的距离为70﹣=(米);
当6<x≤10时,当甲、乙两款机器人相遇时,y=30,
此时相遇点离展示台终点的距离为70﹣30=40(米);
当甲、乙两款机器人同时到达终点时,y=70,
此时相遇点离展示台终点的距离为70﹣70=0(米).
答:当甲、乙两款机器人相遇时,相遇点离展示台终点的距离为米或40米或0米.
【点睛】本题考查一次函数的应用,掌握速度、时间和路程之间的关系是解题的关键.
28.(2025 金华模拟)扎染古称“绞缬”,是我国一种古老的纺织品染色技艺.扎染工艺的发展带动了当地旅游相关产业的发展.某扎染坊第一次用3700元购进甲、乙两种布料共80件,其中两种布料的成本价和销售价如表:
单价类别 成本价/(元/件) 销售价/(元/件)
甲种布料 60 100
乙种布料 40 70
(1)该扎染坊第一次购进甲、乙两种布料各多少件?
(2)因热销,第一次购进的布料全部售完,该扎染坊第二次以相同的成本价再次购进甲、乙两种布料共100件.若此次购进甲种布料的数量不超过乙种布料数量的1.5倍,且以相同的销售价全部售完这批布料.设第二次购进甲种布料m件,第二次全部售完后获得的利润为W元.第二次应怎样进货,才能使第二次购进的布料全部售完后获得的利润最大?最大利润是多少元?
【点拨】(1)分别设该扎染坊第一次购进甲、乙两种布料的件数分别为未知数,根据题意列二元一次方程组并求解即可;
(2)根据题意,列关于m的一元一次不等式并求其解集,写出W关于m的函数关系式,根据一次函数的增减性和m的取值范围,确定当m取何值时W值最大,求出其最大值和此时100﹣m的值即可.
【解析】解:(1)设该扎染坊第一次购进甲种布料x件,购进乙种布料y件.
根据题意,得,
解得.
答:该扎染坊第一次购进甲种布料25件,购进乙种布料55件.
(2)根据题意,得m≤1.5(100﹣m),
解得m≤60,
W=(100﹣60)m+(70﹣40)(100﹣m)=10m+3000,
∵10>0,
∴W随m的增大而增大,
∵m≤60,
∴当m=60时W值最大,W最大=10×60+3000=3600,
100﹣60=40(件).
答:第二次购进甲种布料60件、乙种布料40件全部售完后获得的利润最,最大利润是3600元.
【点睛】本题考查一次函数的应用、二元一次方程组的应用,掌握二元一次方程组、一元一次不等式的解法和一次函数的增减性是解题的关键.
29.(2025 拱墅区一模)某社区推出智能可回收垃圾投放箱,居民投放可回收物可以赚取积分兑换生活用品.为了鼓励居民积极投放,超过一定投放质量后,奖励积分升级.其中塑料与纸张的奖励积分y(分)与投放质量x(kg)的函数关系如图所示.已知投放纸张超过10kg后,奖励积分为25分/kg.
(1)求投放8kg塑料的奖励积分.
(2)求a的值.
(3)若投放m kg的塑料的奖励积分是投放相同质量纸张的奖励积分的倍,求m的值.
【点拨】(1)求出投放塑料超过5kg后每千克的奖励积分,从而计算投放8kg塑料的奖励积分即可;
(2)根据题意列关于a的方程并求解即可;
(3)按照m不同的取值范围,根据题意列关于m的方程并求解即可.
【解析】解:(1)投放塑料超过5kg后,奖励积分为(300﹣100)÷(10﹣5)=40(分/kg),
100+40×(8﹣5)=220(分).
答:投放8kg塑料的奖励积分为220分.
(2)根据题意,得100+25(a﹣10)=300,
解得a=18.
(3)投放纸张不超过10kg,奖励积分为100÷10=10(分),
投放塑料不超过5kg,奖励积分为100÷5=20(分),
当0<m≤5时,得20m=×10m,
解得m=0(舍去),
当5<m≤10时,得100+40(m﹣5)=×10m,
解得m=,
当m>10时,得100+40(m﹣5)=[100+25(m﹣10)],
解得m=,
∴m=或.
【点睛】本题考查一次函数的应用,理解题意、从图象中获得必要的数学信息是解题的关键.
30.(2025 杭州一模)为鼓励节约用水,某市实行了阶梯水价制度.设月用水量为x(吨),每月应交水费y(元),如表为每户的综合用水单价与月用水量的关系表,如图是y关于x的函数图象.
阶梯 月用水量(吨) 用水单价(元/吨)
第一阶梯 x≤10 a
第二阶梯 10<x≤20 b
第三阶梯 x>20 5
根据上述信息解决以下问题:
(1)求a,b的值.
(2)当x>10时,求y关于x的函数表达式.
(3)小红家6月份、7月份的用水量都为整数吨,且都超过了10吨,水费合计为90元,其中6月份用水量低于7月份用水量,求小红家6月份的用水量.
【点拨】(1)依据题意得,,进而计算可以得解;
(2)依据题意,分当10<x≤20时和当x>20时,分别进行判断可以得解;
(3)依据题意,先判断6月用水量低于20吨,超过10吨,然后设6月份用水量为x吨,可得6月份的水费为3x﹣10,故7月份的水费为90﹣(3x﹣10)=100﹣3x,再分两种情形分析计算可以得解.
【解析】解:(1)由题意得,,
∴.
(2)由题意,①当10<x≤20时,y=20+3(x﹣10)=3x﹣10;
②当x>20时,y=50+5(x﹣20)=5x﹣50.
答:当x>10时,y关于x的函数表达式为y=.
(3)由题意,如果6月份、7月份的用水量均超过20吨,则总费用比超过100,不合题意,
又结合6月份用水量低于7月份用水量,
∴6月用水量低于20吨,超过10吨.
设6月份用水量为x吨,
∴6月份的水费为3x﹣10.
∴7月份的水费为90﹣(3x﹣10)=100﹣3x.
若7月份用水量低于20吨,则7月份的用水量为=﹣x,
又∵6月份、7月份的用水量都为整数吨,
∴7月份的用水量为﹣x,不合题意.
若7月份用水量大于20吨,则7月份的用水量为=30﹣x,
又∵6月份、7月份的用水量都为整数吨,
∴x为5的整数倍.
又∵10<x<30﹣x,
∴10<x<18.
∴x=15.
答:小红家6月份的用水量为15吨.
【点睛】本题主要考查了一次函数的应用、二元一次方程组的应用,解题时要熟练掌握并能灵活运用一次函数的性质是关键.
31.(2025 西湖区一模)在直角坐标系中,设函数y1=与函数y2=k2x+b(k1,k2,b是常数,k1k2≠0)的图象交于点A(1,4),B(﹣2,t).
(1)求函数y1,y2的表达式.
(2)当x>2时,比较y1与y2的大小.(直接写出结果)
(3)若点C在函数y2的图象上,将点C先向左平移1个单位,再向下平移6个单位得点D,点D恰好落在函数y1的图象上,求点C的坐标.
【点拨】(1)待定系数法求出两个函数解析式即可;
(2)画出图象,利用数形结合解答即可;
(3)根据点的平移法则设点C坐标为(m,2m+2),写出点D的坐标再代入反比例函数解析式求出m值即可点的点C坐标.
【解析】解:(1)∵两个函数图象交于点A(1,4),B(﹣2,t).
∴k1=1×4=﹣2t,
∴k1=4,t=﹣2,
∴y1=,
∵点A(1,4),B(﹣2,﹣2)在直线y2=k2x+b图象上,
,解得,
∴y2=2x+2.
(2)两个函数图象如图所示,
由图可知,当x>2时,y1<y2.
(3)设点C坐标为(m,2m+2),
∵将点C先向左平移1个单位,再向下平移6个单位得点D,
∴D(m﹣1,2m﹣4),
∵点D恰好落在函数y1的图象上,
∴(m﹣1)(2m﹣4)=4,
整理得m(m﹣3)=0,
∴m=3或m=0,
∴C(3,8)或(0,2).
【点睛】本题考查了一次函数与反比例函数的交点问题,交点坐标满足两个函数解析式是关键.
32.(2025 临安区一模)如图,反比例函数图象过点A(﹣2,a),直线x=4与该反比例函数图象和x轴分别交于点B和点D,连结AD.
(1)求△ADB的面积.
(2)若点P(m,n)(m>0)在反比例函数图象上,当PD⊥AD,求点P的坐标.
【点拨】(1)待定系数法求出a值,再利用解析式求出点B、D坐标,代入三角形面积公式计算即可.
(2)先求出直线AD的解析式得到kAD值,根据两直线垂直得到KPD,待定系数法求出直线PD解析式再与反比例函数解析式联立方程组即可求出点P的坐标.
【解析】解:(1)∵反比例函数图象过点A(﹣2,a),
∴a==﹣2,
∴A(﹣2,﹣2),
∵直线x=4与该反比例函数图象和x轴分别交于点B和点D,
∴B(4,1),D(4,0),
∴S△ABD=(4+2)=3;
(2)如图,
设直线AD的解析式为y=kx+b,代入点AD坐标可得:
,解得,
∵PD⊥AD,
∴kPD=﹣3,
设直线PD的解析式为y=﹣3x+m,代入点D坐标可得:m=12,
∴直线PD的解析式为y=﹣3x+12,
联立方程组得,解得,,
点P的坐标为(,6﹣2)或(,6+2).
【点睛】本题考查了一次函数与反比例函数的交点问题、三角形面积的计算,熟练掌握交点坐标求法是解答本题的关键.
33.(2025 浙江模拟)如图,一次函数y=﹣2x+b的图象与反比例函数的图象相交于点A(﹣1,4).
(1)求b和k的值.
(2)横坐标为3的点B是反比例函数图象上的一点,现将点B向下平移.当点B落在一次函数图象上时,求向下平移的距离.
【点拨】(1)把A(﹣1,4)代入一次函数,反比例函数解析式即可求解;
(2)根据题意得到,根据点的平移得到平移后,代入一次函数解析式即可求解.
【解析】解:(1)∵一次函数y=﹣2x+b的图象过点A(﹣1,4),
∴﹣2×(﹣1)+b=4,
解得b=2,
∴一次函数解析式为y=﹣2x+2,
∵与反比例函数的图象过点A(﹣1,4),
∴,
解得k=﹣4;
(2)由(1)知,k=﹣4,
∴反比例函数解析式为,
∵点B的横坐标为3,且点B在反比例函数图象上,
∴,即,
设点B向下平移了m个单位,
∴,
∴,
解得,
∴向下平移的距离为.
【点睛】本题主要考查的是反比例函数与一次函数的交点问题,待定系数法求一次函数的解析式,掌握以上知识是解题的关键.
34.(2025 上城区一模)某项目学习小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地,当人和木板对湿地的压力F(单位:N)一定时,木板面积S(单位:m2)与人和木板对地面的压强P(单位:Pa)成反比例.当木板面积为0.2m2时,人和木板对地面的压强为3000Pa.
(1)求P关于S的函数表达式;
(2)当木板面积为0.3m2时,压强是多少?
(3)如果要求压强不超过1200Pa,木板面积至少要多大?请说明理由.
【点拨】(1)压力一定时,压强和受力面积成反比,根据压力为600N写出解析式即可;
(2)在(1)的基础上可求出函数值p;
(3)压强不超过1200Pa,即p≤1200时,求相对应的自变量的范围.
【解析】解:(1)压力一定时,压强和受力面积成反比;
∵F=3000×0.2=600N,
∴P关于S的函数表达式为p=(s>0);
(2)当S=0.3时,p==2000(Pa),
故当木板面积为0.3m2时,压强为2000Pa;
(3)把p≤1200Pa代入解析式得:
≤1200,
解得:S≥0.5,
∴如果要求压强不超过1200Pa,木板面积至少要0.5m2.
【点睛】本题考查反比例函数的应用,涉及反比例函数的定义,反比例函数图象上点的特征以及反比例函数图象的性质,熟练掌握反比例函数的相关性质且能读懂题意,学以致用是解题的关键.
35.(2025 萧山区一模)科技创新为实现可持续发展赋能.某企业自2024年1月开始限产进行技术改造,其月利润y(万元)与月份x之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分.
(1)求反比例函数和一次函数的表达式.
(2)求当月利润不高于100万元时共经历了多少个月?
【点拨】(1)利用待定系数法先求出反比例函数解析式,再求出第4个月的利润,设出函数式,根据待定系数法即可求出函数解析式;
(2)把100万元代入函数解析式即可求出.
【解析】解:(1)根据图象,反比例函数图象经过(1,200),
设反比例函数为y=(k≠0),
则=200,
∴k=200,
∴反比例函数为y=(1≤x≤4),
把x=4代入y=得,y=50,
当x=6时,y=110,
设改造工程完工后函数解析式为y=mx+b,
则,
解得m=30,b=﹣70,
∴改造工程完工后函数解析式为y=30x﹣70(x>4且x取整数);
(2)当y=100时,30x﹣70=100,
解得x≈6.
6﹣2=4.
∴当月利润不高于100万元时共经历了4个月.
【点睛】本题主要考查反比例函数的应用,待定系数法求函数解析式和根据函数值求自变量,读懂图象信息对解本题比较关键.
36.(2025 湖州一模)电磁波由振荡的电场和磁场构成,我国嫦娥六号探测器就是通过无线电波(电磁波的一种)与地球通信,电磁波的波长λ(单位:m)会随着电磁波的频率f(单位:MHz)的变化而变化.已知某段电磁波在同种介质中,波长λ与频率f的部分对应值如表:
频率f(MHz) 5 10 15 20 25 30
波长λ(m) 60 30 20 15 12 10
(1)根据表格中的数据,选择合适的函数模型,求出波长λ(m)关于频率f(MHz)的函数表达式.
(2)当该电磁波的频率为50MHz时,它的波长是多少m?
【点拨】(1)根据变量的变化规律解答即可;
(2)将f=50代入(1)中求得的函数表达式,求出对应λ的值即可.
【解析】解:(1)由表格可知,fλ=300,
∴λ与f的函数表达式为λ=.
(2)当f=50时,λ==6,
答:当该电磁波的频率为50MHz时,它的波长是6m.
【点睛】本题考查反比例函数的应用,根据变量的变化规律写出函数关系式是解题的关键.
37.(2025 镇海区校级模拟)在平面直角坐标系中,直线y=﹣2x+4交x轴于点A,交y轴于点B,点C的坐标为(1,0).
(1)求直线BC的函数表达式.
(2)点D是x轴上一动点,连接BD、CD,当△BCD的面积是△AOB面积的时,求点D的坐标.
(3)点E坐标为(0,﹣2),连接CE,点P为直线AB上一点,若∠CEP=45°,求点P坐标.
【点拨】(1)解方程得到B(0,4),设直线BC的函数表达式为y=kx+b,解方程组得到直线BC的函数表达式为y=﹣4x+4;
(2)解方程得到A(2,0),求得OA=2,设D(m,0),则CD=|m﹣1|,根据三角形的面积公式列方程即可得到结论;
(3)过C作CH⊥EP于H,过H作KT∥y轴,过C作CK⊥KT于K,过E作ET⊥KT于T,设H(p,q),当P在EC下方时,当P在EC上方时,根据等腰直角三角形的性质得到∠CHE=90°,EH=CH,根据全等三角形的性质得到ET=HK=p,HT=CK=q﹣1,解方程即可得到结论.
【解析】解:(1)当x=0时,y=﹣2x+4=4,
∴B(0,4),
设直线BC的函数表达式为y=kx+b,
∵C的坐标为(1,0),
∴,
∴,
∴直线BC的函数表达式为y=﹣4x+4;
(2)当y=﹣2x+4=0,
∴x=2,
∴A(2,0),
∴OA=2,
设D(m,0),则CD=|m﹣1|,
∵△BCD的面积=△AOB面积的,
∴CD BO=×OA BO,|m﹣1|=×2=3,
解得m=﹣2或m=4,
∴点D的坐标为(﹣2,0)或(4,0);
(3)过C作CH⊥EP于H,过H作KT∥y轴,过C作CK⊥KT于K,过E作ET⊥KT于T,设H(p,q),
当P在EC下方时,如图:
∵∠CEP=45°,CH⊥EP,
∴△CEH是等腰直角三角形,
∴∠CHE=90°,EH=CH,
∴∠EHT=90°﹣∠CHK=∠HCK,
∵∠T=∠K=90°,
∴△EHT≌△HCK(AAS),
∴ET=HK=p,HT=CK=q﹣1,
∴,
解得p=,q=﹣,
∴H(,﹣),
由H(,﹣),E(0,﹣2)得直线EP解析式为y=x﹣2,
解得,
∴P(,﹣);
当P在EC上方时,如图:
同理可得△EHT≌△HCK(AAS),
∴ET=HK,HT=CK,
∴1﹣p=2+q,p=q,
解得p=﹣,q=﹣,
∴H(﹣,﹣),
∴直线EP解析式为y=﹣3x﹣2,
联立,
解得,
∴P(﹣6,16);
综上所述,P的坐标为(,﹣)或(﹣6,16).
【点睛】本题是一次函数的综合题,考查了待定系数法求函数的解析式,全等三角形的判定和性质,三角形的面积,正确的作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题4 一次函数与反比例函数
一.选择题
1.(2025 杭州一模)如图为冰壶比赛场地示意图,由以P为圆心、半径分别为a,2a,3a,4a的同心圆组成.三只冰壶A,B,C的位置如图所示,∠APB=120°,CP的延长线平分∠APB,冰壶A,B分别表示为(4a,0°),(2a,120°),则冰壶C可表示为( )
A.(3a,120°) B.(4a,200°) C.(3a,240°) D.(3a,300°)
2.(2025 湖州一模)某地区某天的气温变化较大,如图表示该地区这天24小时的气温变化情况.下列说法正确的是( )
A.正午12点时,该地气温最高
B.这一天早上6点之后,该地气温一直在升高
C.该地这一天只有一个时刻的气温达到20℃
D.该地这一天的最高与最低气温差大约是25℃
3.(2025 浙江一模)若点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
4.(2025 湖州一模)在平面直角坐标系中,有A(﹣1,1),B(1,7),C(4,11),D(7,17)四个点,一次函数y=kx+b的图象恰好经过其中三个点,则该函数图象没有经过的点的坐标是( )
A.(﹣1,1) B.(1,7) C.(4,11) D.(7,17)
5.(2025 宁波一模)在平面直角坐标系中,点(a,a2+1)一定位于( )
A.一次函数y=x+1图象的上方 B.一次函数y=﹣x+1图象的下方
C.一次函数y=x图象的上方 D.一次函数y=﹣x图象的下方
6.(2025 温州一模)已知点(x1,y1),(x2,y2),(x3,y3)在反比例函数(k为常数)的图象上,x1<x2<x3,则下列说法中正确的是( )
A.若x1x2>0,则y1<y3 B.若x1x2<0,则y1<y3
C.若x2x3>0,则y1>y3 D.若x2x3<0,则y1>y3
7.(2025 龙泉市一模)若点A(m﹣3,y1),B(m﹣1,y2),C(m+1,y3)(其中1<m<3)都在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
8.(2025 滨江区一模)函数图象上有P(x1,t),Q(x2,t+4)两点.( )
A.若t>0,则0<x2<x1 B.若t>﹣4,则x2<0<x1
C.若t<0,则x2<0<x1 D.若t<﹣4,则0<x1<x2
9.(2025 定海区一模)如图,点B,C在反比例函数的图象上,点A在x轴上,连结AB交y轴于点E,延长BC交x轴于点D.已知点A(﹣2,0),且BC=CD,AE=BE.若△ABC面积为10,则k的值为( )
A.6 B.8 C.10 D.12
10.(2025 绍兴一模)如图,已知点A在函数y=(k是常数,k>0,x>0)图象上,点C在函数y=﹣(x>0)图象上,连结AC交x轴于点B,D是x轴上的点,若OA=AB,BC=CD,且△BCD的面积为1,则△AOB的面积为( )
A. B. C. D.
11.(2025 杭州一模)如图,矩形ABCO的两边分别在坐标轴上,OA=a,OC=b,点P在反比例函数(k为常数,k>0)的图象上,且在矩形ABCO内部,其横坐标为c.过点P作PE∥x轴交AC于点E,作PF∥y轴交AB于点F,连结EF,FC.记△EFC的面积为S,以下说法正确的是( )
A.S的值仅与a,b有关 B.S的值仅与c,k有关
C.S的值仅与k有关 D.S的值与a,b,c,k都有关
12.(2025 嘉善县一模)函数的图象经过P(m,y1),Q(m+2,y2)两点,则下列选项中正确的是( )
A.当m<0时,y1<y2 B.当﹣2<m<0时,y1>y2
C.当m>﹣2时,y1<y2 D.当m<﹣2或m>0时,y1>y2
13.(2025 宁波一模)已知A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数图象上的三个点,若x1<x2<0<x3,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
14.(2025 临安区一模)已知一次函数y1=k1(x﹣3)﹣2与反比例函数的图象交于A,B两点,与y轴交于点(0,k2),当x≥1时,总有y1<y2<0,则k1的值可以为( )
A.k1=1 B. C.k1=﹣1 D.k1=﹣2
15.(2025 宁波一模)已知一次函数y=x+a的图象与反比例函数交于M,N两点.当a=1时,△OMN的面积为1,则当a=﹣1时,△OMN的面积为( )
A. B.1 C. D.2
16.(2025 杭州模拟)综合实践小组的同学利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(cm)是液体的密度ρ(g/cm3)的反比例函数,其图象如图所示(ρ>0).下列说法正确的是( )
A.当液体密度ρ≥1g/cm3时,浸在液体中的高度h≥20cm
B.当液体密度ρ=2g/cm3时,浸在液体中的高度h=40cm
C.当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3
D.当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≤20cm
二.填空题
17.(2025 台州一模)已知一次函数y=kx+2(k是常数,k≠0)的图象过点(1,m)与(2,n),若m>0,n<0,则k的取值范围是 .
18.(2025 拱墅区一模)若一次函数y=kx+b的图象过点(1,m),(m,1),其中m≠1,则k= .
19.(2025 滨江区一模)甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示.当第一个人到达终点时,第二个人距离终点还剩 米.
20.(2025 定海区一模)世界各国的天气预报主要使用摄氏或华氏温标,学生查阅资料,得到两种温标计量值如表:
摄氏温度值x/℃ 0 10 20 30 40 50
华氏温度值y/℉ 32 50 68 86 104 122
请推算当摄氏温度为35℃时,华氏温度为 ℉.
21.(2025 富阳区一模)如图,一次函数y1=x﹣1与反比例函数y2=的图象交于点A(2,1),B(﹣1,﹣2),则使y1<y2的x的取值范围是 .
22.(2025 湖州一模)如图,A是函数的图象上一点,过点A作AB∥x轴,AB交函数的图象于点B,点C在x轴上,若△ABC的面积是2,则k的值是 .
23.(2025 浙江一模)已知双曲线y=与函数y=|x﹣a|的图象有两个交点,则a的值是 .
三.解答题
24.(2025 浙江一模)甲、乙两同学在400米的环形跑道上参加1000米跑步训练,时间少于或等于3分40秒为满分.前800米的路程s(米)和时间t(秒)的函数关系如图.
(1)乙同学按照当前的速度继续匀速跑,那么他能否得到满分?请说明理由.
(2)求甲同学跑第2圈时的路程s(米)关于时间t(秒)的函数解析式.
(3)若最后200米甲同学按第1圈的速度冲刺,乙同学保持原速不变,当乙同学跑到终点时,甲同学离终点还有多远?
25.(2025 龙泉市一模)如图,小丽和小庆去某风景区游览,其主要景点位于同一条公路边,其中古刹到塔林的路程为10km,塔林到草甸的路程为25km,草甸到飞瀑的路程为10km.小丽骑电动自行车从“古刹”出发,沿景区公路匀速去“草甸”,车速为20km/h.同一时刻,小庆乘电动汽车从“飞瀑”出发,沿景区公路匀速前往“古刹”.设两人相距的路程为s km,时间为t h,s关于t的部分函数图象如图所示.
(1)求小庆乘电动汽车的速度;
(2)求图中a的值;
(3)何时两人相距的路程等于5km?
26.(2025 衢州一模)2024年“有礼杯”衢州马拉松于11月24日开跑,小明和小聪一起报名参加了“迷你跑”的比赛.小明以一定的速度跑到3000米处的补给点休息了一段时间后,继续以原速前行,在距离终点500米处因体力不支,最终以100米/分的速度坚持跑到终点;小聪在途中休息了5分钟后,以原来的倍的速度冲向终点.如图是小明和小聪在比赛过程中所跑的路程s(米)和跑步时间t(分)的函数关系图.根据图象回答下列问题:
(1)求a的值;
(2)求图中线段BC对应的函数表达式;
(3)求小聪休息前的速度.
27.(2025 衢州一模)某科技公司在机器人展厅内的展台上举办了甲、乙两款机器人的表演、慢跑展示活动,展台的总长度是70米,如图1所示.甲机器人先从起点出发,匀速慢跑,到达指定的表演点后开始表演,表演结束后,立刻按原来速度继续向前慢跑,直到终点结束;乙机器人的起点在甲机器人起点前7米处,与甲机器人同时开始慢跑,一直前行,直到终点结束.已知甲、乙两款机器人距离甲机器人起点的距离y(米)与时间x(秒)之间的函数关系如图2所示.
(1)求甲、乙两款机器人各自的慢跑速度及甲机器人表演的时长.
(2)求当甲、乙两款机器人相遇时,相遇点离展示台终点的距离.
28.(2025 金华模拟)扎染古称“绞缬”,是我国一种古老的纺织品染色技艺.扎染工艺的发展带动了当地旅游相关产业的发展.某扎染坊第一次用3700元购进甲、乙两种布料共80件,其中两种布料的成本价和销售价如表:
单价类别 成本价/(元/件) 销售价/(元/件)
甲种布料 60 100
乙种布料 40 70
(1)该扎染坊第一次购进甲、乙两种布料各多少件?
(2)因热销,第一次购进的布料全部售完,该扎染坊第二次以相同的成本价再次购进甲、乙两种布料共100件.若此次购进甲种布料的数量不超过乙种布料数量的1.5倍,且以相同的销售价全部售完这批布料.设第二次购进甲种布料m件,第二次全部售完后获得的利润为W元.第二次应怎样进货,才能使第二次购进的布料全部售完后获得的利润最大?最大利润是多少元?
29.(2025 拱墅区一模)某社区推出智能可回收垃圾投放箱,居民投放可回收物可以赚取积分兑换生活用品.为了鼓励居民积极投放,超过一定投放质量后,奖励积分升级.其中塑料与纸张的奖励积分y(分)与投放质量x(kg)的函数关系如图所示.已知投放纸张超过10kg后,奖励积分为25分/kg.
(1)求投放8kg塑料的奖励积分.
(2)求a的值.
(3)若投放m kg的塑料的奖励积分是投放相同质量纸张的奖励积分的倍,求m的值.
30.(2025 杭州一模)为鼓励节约用水,某市实行了阶梯水价制度.设月用水量为x(吨),每月应交水费y(元),如表为每户的综合用水单价与月用水量的关系表,如图是y关于x的函数图象.
阶梯 月用水量(吨) 用水单价(元/吨)
第一阶梯 x≤10 a
第二阶梯 10<x≤20 b
第三阶梯 x>20 5
根据上述信息解决以下问题:
(1)求a,b的值.
(2)当x>10时,求y关于x的函数表达式.
(3)小红家6月份、7月份的用水量都为整数吨,且都超过了10吨,水费合计为90元,其中6月份用水量低于7月份用水量,求小红家6月份的用水量.
31.(2025 西湖区一模)在直角坐标系中,设函数y1=与函数y2=k2x+b(k1,k2,b是常数,k1k2≠0)的图象交于点A(1,4),B(﹣2,t).
(1)求函数y1,y2的表达式.
(2)当x>2时,比较y1与y2的大小.(直接写出结果)
(3)若点C在函数y2的图象上,将点C先向左平移1个单位,再向下平移6个单位得点D,点D恰好落在函数y1的图象上,求点C的坐标.
32.(2025 临安区一模)如图,反比例函数图象过点A(﹣2,a),直线x=4与该反比例函数图象和x轴分别交于点B和点D,连结AD.
(1)求△ADB的面积.
(2)若点P(m,n)(m>0)在反比例函数图象上,当PD⊥AD,求点P的坐标.
33.(2025 浙江模拟)如图,一次函数y=﹣2x+b的图象与反比例函数的图象相交于点A(﹣1,4).
(1)求b和k的值.
(2)横坐标为3的点B是反比例函数图象上的一点,现将点B向下平移.当点B落在一次函数图象上时,求向下平移的距离.
34.(2025 上城区一模)某项目学习小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地,当人和木板对湿地的压力F(单位:N)一定时,木板面积S(单位:m2)与人和木板对地面的压强P(单位:Pa)成反比例.当木板面积为0.2m2时,人和木板对地面的压强为3000Pa.
(1)求P关于S的函数表达式;
(2)当木板面积为0.3m2时,压强是多少?
(3)如果要求压强不超过1200Pa,木板面积至少要多大?请说明理由.
35.(2025 萧山区一模)科技创新为实现可持续发展赋能.某企业自2024年1月开始限产进行技术改造,其月利润y(万元)与月份x之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分.
(1)求反比例函数和一次函数的表达式.
(2)求当月利润不高于100万元时共经历了多少个月?
36.(2025 湖州一模)电磁波由振荡的电场和磁场构成,我国嫦娥六号探测器就是通过无线电波(电磁波的一种)与地球通信,电磁波的波长λ(单位:m)会随着电磁波的频率f(单位:MHz)的变化而变化.已知某段电磁波在同种介质中,波长λ与频率f的部分对应值如表:
频率f(MHz) 5 10 15 20 25 30
波长λ(m) 60 30 20 15 12 10
(1)根据表格中的数据,选择合适的函数模型,求出波长λ(m)关于频率f(MHz)的函数表达式.
(2)当该电磁波的频率为50MHz时,它的波长是多少m?
37.(2025 镇海区校级模拟)在平面直角坐标系中,直线y=﹣2x+4交x轴于点A,交y轴于点B,点C的坐标为(1,0).
(1)求直线BC的函数表达式.
(2)点D是x轴上一动点,连接BD、CD,当△BCD的面积是△AOB面积的时,求点D的坐标.
(3)点E坐标为(0,﹣2),连接CE,点P为直线AB上一点,若∠CEP=45°,求点P坐标.
答案与解析
一.选择题
1.(2025 杭州一模)如图为冰壶比赛场地示意图,由以P为圆心、半径分别为a,2a,3a,4a的同心圆组成.三只冰壶A,B,C的位置如图所示,∠APB=120°,CP的延长线平分∠APB,冰壶A,B分别表示为(4a,0°),(2a,120°),则冰壶C可表示为( )
A.(3a,120°) B.(4a,200°) C.(3a,240°) D.(3a,300°)
【点拨】设CP的延长线交冰壶场地的最外圈与D,根据题意求出图形和题意得出点C的位置.
【解析】解:设CP的延长线交冰壶场地的最外圈与D,如图:
∵∠APB=120°,CP的延长线平分∠APB,
∴∠APD=∠DPB=60°,
∴∠DPE=30°,
∴∠CPF=30°,
∴冰壶C可表示为(3a,240°),
故选:C.
【点睛】本题考查坐标定位置,关键是掌握平面直角坐标系中坐标的位置.
2.(2025 湖州一模)某地区某天的气温变化较大,如图表示该地区这天24小时的气温变化情况.下列说法正确的是( )
A.正午12点时,该地气温最高 B.这一天早上6点之后,该地气温一直在升高
C.该地这一天只有一个时刻的气温达到20℃ D.该地这一天的最高与最低气温差大约是25℃
【点拨】从图象中有效的获取信息,逐一进行判断即可.
【解析】解:由图象可知:
A、15点时,该地气温最高,原选项说法错误,不符合题意;
B、这一天早上6点至9点,该地气温在下降,原选项说法错误,不符合题意;
C、该地在12时至19时的气温达到20℃,原选项说法错误,不符合题意;
D、该地这一天的最高与最低气温差大约是:30﹣5=25(℃),说法正确,符合题意;
故选:D.
【点睛】本题考查的是函数的图象,能根据函数图象在坐标系中的增减性判断出函数的增减性是解答此题的关键.
3.(2025 浙江一模)若点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y2>y1>y3 C.y1>y3>y2 D.y3>y2>y1
【点拨】由k=﹣3<0,利用一次函数的性质,可得出y随x的增大而减小,再结合﹣2<1<3,即可得出y1>y3>y2.
【解析】解:∵k=﹣3<0,
∴y随x的增大而减小,
又∵点A(﹣2,y1),B(3,y2),C(1,y3)在一次函数y=﹣3x+m(m是常数)的图象上,且﹣2<1<3,
∴y1>y3>y2.
故选:C.
【点睛】本题考查了一次函数的性质,牢记“k>0,y随x的增大而增大;k<0,y随x的增大而减小”是解题的关键.
4.(2025 湖州一模)在平面直角坐标系中,有A(﹣1,1),B(1,7),C(4,11),D(7,17)四个点,一次函数y=kx+b的图象恰好经过其中三个点,则该函数图象没有经过的点的坐标是( )
A.(﹣1,1) B.(1,7) C.(4,11) D.(7,17)
【点拨】根据题意,分别求出满足要求的一次函数的解析式,即可得出答案.
【解析】解:由题意,当一次函数y=kx+b的图象经过点A和点B时,
,
解得,
一次函数的解析式为y=3x+4;同理可得,
当一次函数y=kx+b的图象经过点A和点C时,一次函数的解析式为y=2x+3;
当一次函数y=kx+b的图象经过点B和点C时,一次函数的解析式为y=x+;
当一次函数y=kx+b的图象经过点B和点D时,一次函数的解析式为y=x+;
当一次函数y=kx+b的图象经过点C和点D时,一次函数的解析式为y=2x+3;
所以A、C、D都在一次函数y=2x+3的图象上,该函数图象没有经过的点的坐标是B(1,7).
故选:B.
【点睛】本题考查一次函数图象上点的坐标特征,分别求出满足要求的一次函数的解析式是解题的关键.
5.(2025 宁波一模)在平面直角坐标系中,点(a,a2+1)一定位于( )
A.一次函数y=x+1图象的上方 B.一次函数y=﹣x+1图象的下方
C.一次函数y=x图象的上方 D.一次函数y=﹣x图象的下方
【点拨】根据点(a,a2+1)在二次函数y=x2+1的图象上,画出函数图象判断即可.
【解析】解:点(a,a2+1)在二次函数y=x2+1的图象上,画出函数图象如下:
A、二次函数的图象与一次函数的图象有交点,所以点(a,a2+1)不一定位于一次函数y=x+1图象的上方,故A选项不符合题意;
B、二次函数的图象与一次函数的图象有交点,所以点(a,a2+1)不一定位于一次函数y=﹣x+1图象的下方,故B选项不符合题意;
C、二次函数的图象在一次函数y=x的上方,所以点(a,a2+1)一定位于一次函数y=x图象的上方,故C选项符合题意;
D、二次函数的图象在一次函数y=﹣x的上方,所以点(a,a2+1)一定位于一次函数y=x图象的上方,故D选项不符合题意;
故选:C.
【点睛】本题考查了二次函数和一次函数的图象,数形结合是关键.
6.(2025 温州一模)已知点(x1,y1),(x2,y2),(x3,y3)在反比例函数(k为常数)的图象上,x1<x2<x3,则下列说法中正确的是( )
A.若x1x2>0,则y1<y3 B.若x1x2<0,则y1<y3
C.若x2x3>0,则y1>y3 D.若x2x3<0,则y1>y3
【点拨】由k2+1>0可得反比例函数图象在第一、三象限,根据选项一一分析即可.
【解析】解:点(x1,y1),(x2,y2),(x3,y3)在反比例函数(k为常数)的图象上,x1<x2<x3,
∵k2+1>0,
∴图象在第一、三象限,在每个象限y随x增大而减小,
A、若x1x2>0,则点(x1,y1),(x2,y2)在同一象限,
如果点(x1,y1),(x2,y2),(x3,y3)都在第一象限,则y1>y3,故不合题意;
B、若x1x2<0,则点(x1,y1)在第三象限,(x2,y2),(x3,y3)在第一象限,则y1<y3,故符合题意;
C、若x2x3>0,则(x2,y2),(x3,y3)在同一象限,
如果点(x1,y1)在第三象限,点(x2,y2),(x3,y3)都在第一象限,则y1<y3,故不合题意;
D、若x2x3<0,则点(x1,y1),(x2,y2)在第三象限,(x3,y3)在第一象限,y1<y3,故不合题意.故选:B.
【点睛】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数的性质是解题的关键.
7.(2025 龙泉市一模)若点A(m﹣3,y1),B(m﹣1,y2),C(m+1,y3)(其中1<m<3)都在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
【点拨】根据反比例函数图象上点的坐标特征解答即可.
【解析】解:∵反比例函数的k=﹣3<0,
∴反比例函数图象分布在第二、四象限,在每个象限内,y随x的增大而增大,
∵1<m<3,
∴点A(m﹣3,y1)在第二象限,y1>0,B(m﹣1,y2)和C(m+1,y3)在第四象限,
∵m﹣1<m+1,
∴y2<y3<0,
∴y2<y3<y1.
故选:C.
【点睛】本题考查了反比例函数图象上点的坐标特征,熟练掌握反比例函数的增减性是关键.
8.(2025 滨江区一模)函数图象上有P(x1,t),Q(x2,t+4)两点.( )
A.若t>0,则0<x2<x1 B.若t>﹣4,则x2<0<x1
C.若t<0,则x2<0<x1 D.若t<﹣4,则0<x1<x2
【点拨】先根据反比例函数的解析式判断出函数图象所在的象限,再对各选项进行逐一判断即可.
【解析】解:∵反比例函数中,k=﹣4<0,
∴此函数图象的两个分支分别位于第二、四象限,在每一象限内y随x的增大而增大,
A、若t>0,则P(x1,t),Q(x2,t+4)在第二象限,且t<t+4,
∵t<t+4,
∴x1<x2<0,故错误,不符合题意;
B、若t>﹣4,则P(x1,t),Q(x2,t+4)有可能都在第四象限,故错误,不符合题意;
C、若t<0,则P(x1,t),Q(x2,t+4)有可能都在第二象限,故错误,不符合题意;
D、若t<﹣4,t+4<0,
∴P(x1,t),Q(x2,t+4)在第四象限,
∵t<t+4,
∴0<x1<x2,正确,符合题意.
故选:D.
【点睛】本题考查的是反比例函数图象上点的坐标特征,熟知反比例函数的图象与系数的关系是解题的关键.
9.(2025 定海区一模)如图,点B,C在反比例函数的图象上,点A在x轴上,连结AB交y轴于点E,延长BC交x轴于点D.已知点A(﹣2,0),且BC=CD,AE=BE.若△ABC面积为10,则k的值为( )
A.6 B.8 C.10 D.12
【点拨】根据反比例函数k值的几何意义解答即可.
【解析】解:如图,连接CE、OC,
∵AE=BE.△ABC面积为10,
∴S△AEC=S△ABC==5,
∵BC=CD,AE=BE.
∴CE是△ABD的中位线,
∴CE∥AD,
∴S△AEC=S△OEC=5,
∴k=2S△OEC=2×5=10,
故选:C.
【点睛】本题考查了反比例函数k值的几何意义、反比例函数图象上点的坐标特征,熟练掌握以上知识点是关键.
10.(2025 绍兴一模)如图,已知点A在函数y=(k是常数,k>0,x>0)图象上,点C在函数y=﹣(x>0)图象上,连结AC交x轴于点B,D是x轴上的点,若OA=AB,BC=CD,且△BCD的面积为1,则△AOB的面积为( )
A. B. C. D.
【点拨】作AE⊥x轴于E,CF⊥x轴于F,则AE∥CF,由题意设点A(m,),点C(n,﹣),则BE=OE=m,AE=,DF=BF=n﹣2m,CF=,通过证得△ABE∽△CBF,得到n=(+1)m,然后根据△BCD的面积为1,即可求得k的值.
【解析】解:作AE⊥x轴于E,CF⊥x轴于F,则AE∥CF,
∵OA=AB,BC=CD,
∴OE=BE,BF=DF,
由题意设点A(m,),点C(n,﹣),则BE=OE=m,AE=,DF=BF=n﹣2m,CF=,
∴BD=2(n﹣2m),
∵AE∥CF,
∴△ABE∽△CBF,
∴,即,
∴m2=n2﹣2mn,
∴2m2=(n﹣m)2,
∴n=(+1)m或n=(1﹣)m(舍去),
∴BD=2()m,CF=,
∵△BCD的面积为1,
∴=,
∴k=3+2,
∵S△AOE=,
∴S△AOB=2S△AOE=k=3+2.
故选:D.
【点睛】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,等腰三角形的性质,三角形相似的判定和性质,作出辅助线构建相似三角形是解题的关键.
11.(2025 杭州一模)如图,矩形ABCO的两边分别在坐标轴上,OA=a,OC=b,点P在反比例函数(k为常数,k>0)的图象上,且在矩形ABCO内部,其横坐标为c.过点P作PE∥x轴交AC于点E,作PF∥y轴交AB于点F,连结EF,FC.记△EFC的面积为S,以下说法正确的是( )
A.S的值仅与a,b有关 B.S的值仅与c,k有关
C.S的值仅与k有关 D.S的值与a,b,c,k都有关
【点拨】根据题意,先确定各点的坐标,C(b,0),B(b,a),A(0,a),P(c,),F(c,a),利用S△CEF=S△ABC﹣S△AEF﹣S△BCF=得到结论即可.
【解析】解:如图,
由条件可知C(b,0),B(b,a),A(0,a),
∵点P在反比例函数(k为常数,k>0)的图象上,且横坐标为c,
∴P(c,),F(c,a),
∴S△AEF= AF (a﹣)=(ac﹣k),
S△BCF===,
S△ABC==,
∴S△CEF=S△ABC﹣S△AEF﹣S△BCF=,
∴△EFC的面积为S仅与k值有关.
故选:C.
【点睛】本题考查了反比例函数k值的几何意义、反比例函数图象上点的坐标特征、矩形的性质,熟练掌握以上知识点是关键.
12.(2025 嘉善县一模)函数的图象经过P(m,y1),Q(m+2,y2)两点,则下列选项中正确的是( )
A.当m<0时,y1<y2 B.当﹣2<m<0时,y1>y2
C.当m>﹣2时,y1<y2 D.当m<﹣2或m>0时,y1>y2
【点拨】由于反比例函数y=﹣,可知函数位于第二、四象限,分情况讨论,根据反比例函数的增减性判断出y1与y2的大小.
【解析】解:由条件可知:函数位于第二、四象限,y随x的增大而增大,
当0<m<m+2时,即m>0时,y1<y2,
当m<m+2<0时,即m<﹣2时,y1<y2,
当m<0<m+2,即﹣2<m<0,y1>y2,
所以结合选项可知:B符合题意,
故选:B.
【点睛】本题考查了反比例函数图象上的点的坐标特征,掌握反比例函数的性质是解题的关键.
13.(2025 宁波一模)已知A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数图象上的三个点,若x1<x2<0<x3,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y2<y1 D.y3<y1<y2
【点拨】先根据函数解析式中的比例系数k确定函数图象所在的象限,再根据各象限内点的坐标特点及函数的增减性解答.
【解析】解:∵反比例函数中,k=﹣5<0,
∴此函数图象在二、四象限,在每个象限内y随x的增大而增大,
∵点A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数图象上的三个点,且x1<x2<0<x3,
∴点C(x3,y3)在第四象限,则y3<0,
∵点A(x1,y1),B(x2,y2)在第二象限,则y2>y1>0,
∴y1,y2,y3的大小关系为y3<y1<y2.
故选:D.
【点睛】此题考查的是反比例函数图象上点的坐标特点及平面直角坐标系中各象限内点的坐标特点,比较简单.
14.(2025 临安区一模)已知一次函数y1=k1(x﹣3)﹣2与反比例函数的图象交于A,B两点,与y轴交于点(0,k2),当x≥1时,总有y1<y2<0,则k1的值可以为( )
A.k1=1 B. C.k1=﹣1 D.k1=﹣2
【点拨】根据反比例函数与一次函数的交点问题解答即可.
【解析】解:∵一次函数与y轴交于点(0,k2),
∴k2=﹣3k1﹣2,
∵x≥1时,y2=<0,
∴k2<0,即﹣3k1﹣2<0,
∴k1>﹣,
∵当x=1时,y1<y2,
∴﹣2k1﹣2<﹣3k1﹣2,
∴k1<0,
∴﹣<k1<0,
四个选项,只有选项B符合条件.
故选:B.
【点睛】本题考查了反比例函数与一次函数的交点问题,熟练掌握交点坐标满足两个函数解析式是关键.
15.(2025 宁波一模)已知一次函数y=x+a的图象与反比例函数交于M,N两点.当a=1时,△OMN的面积为1,则当a=﹣1时,△OMN的面积为( )
A. B.1 C. D.2
【点拨】分别联立直线和反比例函数解析式得到两次的交点关于原点成中心对称,则△OMN的面积不变,即可求解.
【解析】解:当a=1时,联立得:x(x+1)=k,
解得:,
∴点,(顺序无关),
当a=﹣1联立得:x(x﹣1)=k,
解得:,
∴点,(顺序无关),
∴发现点M与点N′关于原点成中心对称,点N与点M′关于原点成中心对称,
∴S△OMN=S△OM′N′=1,
故选:B.
【点睛】本题考查了反比例函数与一次函数的交点问题,反比例函数的对称性,根据对称性求解是解题的关键.
16.(2025 杭州模拟)综合实践小组的同学利用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(cm)是液体的密度ρ(g/cm3)的反比例函数,其图象如图所示(ρ>0).下列说法正确的是( )
A.当液体密度ρ≥1g/cm3时,浸在液体中的高度h≥20cm
B.当液体密度ρ=2g/cm3时,浸在液体中的高度h=40cm
C.当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3
D.当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≤20cm
【点拨】根据图象和反比例函数性质逐项分析判断即可.
【解析】解:根据题意得,反比例函数解析式为:h=,
A、当液体密度ρ≥1g/cm3时,浸在液体中的高度h≤20cm,故原说法错误,不符合题意;
B、当液体密度ρ=2g/cm3时,浸在液体中的高度h=10cm,故原说法错误,不符合题意;,
C、当浸在液体中的高度0<h≤10cm时,该液体的密度ρ≥2g/cm3,正确,符合题意;
D、当液体的密度0<ρ≤1g/cm3时,浸在液体中的高度h≥20cm,故原说法错误,不符合题意;,
故选:C.
【点睛】本题考查了反比例函数的应用,熟练掌握反比例函数性质是关键.
二.填空题
17.(2025 台州一模)已知一次函数y=kx+2(k是常数,k≠0)的图象过点(1,m)与(2,n),若m>0,n<0,则k的取值范围是 ﹣2<k<﹣1 .
【点拨】根据y随x的增大而减小,即可得出答案.
【解析】解:∵一次函数y=kx+2的图象过点(1,m)与(2,n),m>0,n<0,
∴k+2>0,2k+2<0,
解得﹣2<k<﹣1.
故答案为:﹣2<k<﹣1.
【点睛】本题考查了一次函数图象与系数的关系,一次函数图象上点的坐标特征,熟练掌握一次函数的性质是解题的关键.
18.(2025 拱墅区一模)若一次函数y=kx+b的图象过点(1,m),(m,1),其中m≠1,则k= ﹣1 .
【点拨】利用一次函数图象上点的坐标特征,可得出关于k的方程组,解之即可得出结论.
【解析】解:∵一次函数y=kx+b的图象过点(1,m),(m,1),m≠1,
∴,
解得:k=﹣1.
故答案为:﹣1.
【点睛】本题考查了一次函数图象上点的坐标特征,牢记“直线上任意一点的坐标都满足函数关系式y=kx+b”是解题的关键.
19.(2025 滨江区一模)甲、乙两人在一次赛跑中,路程s(米)与时间t(秒)的关系如图所示.当第一个人到达终点时,第二个人距离终点还剩 4 米.
【点拨】根据图形列出算式,再求出即可.
【解析】解:100﹣=4(米),
即当第一个人到达终点时,第二个人距离终点还剩4米,
故答案为:4.
【点睛】本题考查了一次函数的应用,能根据图形得出正确的信息是解此题的关键,数形结合思想的应用.
20.(2025 定海区一模)世界各国的天气预报主要使用摄氏或华氏温标,学生查阅资料,得到两种温标计量值如表:
摄氏温度值x/℃ 0 10 20 30 40 50
华氏温度值y/℉ 32 50 68 86 104 122
请推算当摄氏温度为35℃时,华氏温度为 95 ℉.
【点拨】根据题意判断出函数的类型,再用待定系数法求解求出解析式,再代入数据计算即可.
【解析】解:由题意可得.x每增加10℃,y增加18℉,是一个均匀变化的过程,所以函数为一次函数,
设y=kx+b.
将(0,32)(10,50)代入解析式可得:
,
解得:.
∴y=1.8x+32,
当x=35°时,y=1.8×35+32=95,
故答案为:95.
【点睛】本题考查一次函数的应用,正确进行计算是解题关键.
21.(2025 富阳区一模)如图,一次函数y1=x﹣1与反比例函数y2=的图象交于点A(2,1),B(﹣1,﹣2),则使y1<y2的x的取值范围是 0<x<2或x<﹣1 .
【点拨】求得一次函数的图象在反比例函数的图象下方时,自变量x的取值即可.
【解析】解:∵一次函数y1=x﹣1与反比例函数y2=的图象交于点A(2,1),B(﹣1,﹣2),
∴从图象可知:使y1<y2的x的取值范围是x<﹣1或0<x<2,
故答案为0<x<2或x<﹣1.
【点睛】本题考查了反比例函数与一次函数的交点问题,利用数形结合是解题的关键.
22.(2025 湖州一模)如图,A是函数的图象上一点,过点A作AB∥x轴,AB交函数的图象于点B,点C在x轴上,若△ABC的面积是2,则k的值是 3 .
【点拨】依据题意,设点A的坐标为,其中a<0,又AB∥x轴,则点B的纵坐标与点A相同,故,代入(x>0),从而B的横坐标为,可得点B的坐标为,又△ABC的顶点C在x轴上,可设其坐标为(c,0),故S△ABC=AB h=(﹣ak﹣a) (﹣)=2,则,进而计算可以得解.
【解析】解:由题意,设点A的坐标为,其中a<0.
又∵AB∥x轴,
∴点B的纵坐标与点A相同.
∴,代入(x>0),
∴B的横坐标为.
∴点B的坐标为.
又∵△ABC的顶点C在x轴上,可设其坐标为(c,0).
∴S△ABC=AB h=(﹣ak﹣a) (﹣)=2.
∴.
∴k=3.
故答案为:3.
【点睛】本题主要考查了反比例函数系数k的几何意义、反比例函数图象上点的坐标特征,解题时要熟练掌握并能灵活运用反比例函数的性质是关键.
23.(2025 浙江一模)已知双曲线y=与函数y=|x﹣a|的图象有两个交点,则a的值是 .
【点拨】根据题意画出图象分析可得,一次函数y=﹣x+a的图象与y=的图象只有一个交点,且a>0,可得方程﹣x2+ax﹣3=0只有一个实数根,利用根的判别式即可求解.
【解析】解:如图,
∵双曲线y=与函数y=|x﹣a|的图象有两个交点,
∴由图可知,一次函数y=﹣x+a的图象与y=的图象只有一个交点,且a>0,
可得,
整理得:﹣x2+ax﹣3=0,
∴方程﹣x2+ax﹣3=0只有一个实数根,
∴Δ=b2﹣4ac=a2﹣12=0,
解得:a=或(舍去).
故答案为:.
【点睛】本题主要考查反比例函数与一次函数的交点问题、根的判别式,解题关键在于利用数形结合思想解决问题.
三.解答题
24.(2025 浙江一模)甲、乙两同学在400米的环形跑道上参加1000米跑步训练,时间少于或等于3分40秒为满分.前800米的路程s(米)和时间t(秒)的函数关系如图.
(1)乙同学按照当前的速度继续匀速跑,那么他能否得到满分?请说明理由.
(2)求甲同学跑第2圈时的路程s(米)关于时间t(秒)的函数解析式.
(3)若最后200米甲同学按第1圈的速度冲刺,乙同学保持原速不变,当乙同学跑到终点时,甲同学离终点还有多远?
【点拨】(1)求出乙同学路程s(米)关于时间t(秒)的函数解析式,然后令s=1000,求出t的值即可解答;
(2)设s=kt+b,用待定系数法求解即可;
(3)求出最后200米,乙跑到终点时,甲同学跑的时间是215﹣180=35(秒),速度是(米/秒),进而可求出甲同学离终点还有多远.
【解析】解:(1)设s=kt,
将(172,800)代入可得,800=172k,
解得:,
∴.
令s=1000,
解得:t=215.
∵3分40秒=220秒,215<220,
∴乙同学能够得到满分.
(2)由图象可知s是t的一次函数,设s=kt+b,
由题意可得:
解得:
∴.
(3)由(1)可知乙同学到终点的时间是215秒,
由图象可知甲同学跑前800米的时间是180秒,
所以最后200米,乙跑到终点时,甲同学跑的时间是215﹣180=35(秒).
速度是(米/秒).
路程是(米).
∴甲离终点的距离是(米).
【点睛】本题考查了从函数图象获取信息,一次函数的应用,数形结合是解答本题的关键.
25.(2025 龙泉市一模)如图,小丽和小庆去某风景区游览,其主要景点位于同一条公路边,其中古刹到塔林的路程为10km,塔林到草甸的路程为25km,草甸到飞瀑的路程为10km.小丽骑电动自行车从“古刹”出发,沿景区公路匀速去“草甸”,车速为20km/h.同一时刻,小庆乘电动汽车从“飞瀑”出发,沿景区公路匀速前往“古刹”.设两人相距的路程为s km,时间为t h,s关于t的部分函数图象如图所示.
(1)求小庆乘电动汽车的速度;
(2)求图中a的值;
(3)何时两人相距的路程等于5km?
【点拨】(1)根据“(出发时二之间的距离﹣二人相遇时小丽行驶的路程)÷相遇时间”计算小庆乘电动汽车的速度即可;
(2)根据“相遇后二人行驶的路程之和等于30km”列关于a的方程并求解即可;
(3)分别计算二人相遇前后两种情况下相距的路程等于5km时对应的时间即可.
【解析】解:(1)(45﹣20×0.9)÷0.9=30(km/h).
答:小庆乘电动汽车的速度为30km/h.
(2)根据图象,得(20+30)(a﹣0.9)=30,
解得a=1.5.
(3)相遇前,当两人相距的路程等于5km时,(45﹣5)÷(20+30)=0.8(h),
相遇后,当两人相距的路程等于5km时,0.9+5÷(20+30)=1(h),
∴两人出发后0.8h或1h相距的路程等于5km.
【点睛】本题考查一次函数的应用,掌握速度、时间和路程之间的关系是解题的关键.
26.(2025 衢州一模)2024年“有礼杯”衢州马拉松于11月24日开跑,小明和小聪一起报名参加了“迷你跑”的比赛.小明以一定的速度跑到3000米处的补给点休息了一段时间后,继续以原速前行,在距离终点500米处因体力不支,最终以100米/分的速度坚持跑到终点;小聪在途中休息了5分钟后,以原来的倍的速度冲向终点.如图是小明和小聪在比赛过程中所跑的路程s(米)和跑步时间t(分)的函数关系图.根据图象回答下列问题:
(1)求a的值;
(2)求图中线段BC对应的函数表达式;
(3)求小聪休息前的速度.
【点拨】(1)根据时间=路程÷速度求出CD所用时间,从而求出a的值即可;
(2)根据速度=路程÷时间求出小明在OA段的速度,亦即BC段的速度,设B(m,3000),根据路程=速度×时间列关于m的方程并求解,再根据路程=速度×时间求出线段BC对应的函数表达式即可;
(3)将t=32.5代入线段BC对应的函数表达式,求出对应s的值,设小聪休息前的速度为v米/分,则小聪休息后的速度为v米/分,用含v的代数式将点B的横坐标表示出来,再由路程=速度×时间列关于v的方程并求解即可.
【解析】解:(1)小明在跑完CD段用时500÷100=5(分),
37.5+5=42.5(分),
∴a=42.5.
(2)小明OA段和BC段的速度均为3000÷15=200(米/分),
设B(m,3000),则200(37.5﹣m)=5500﹣3000,
解得m=25,
s=3000+200(t﹣25)=200t﹣2000,
∴线段BC对应的函数表达式为s=200t﹣2000(25≤t≤37.5).
(3)当t=32.5时,s=200×32.5﹣2000=4500,
设小聪休息前的速度为v米/分,则小聪休息后的速度为v米/分,
∴点A的横坐标为,
∴点B的横坐标为+5,
根据图象,得4500+v[42.5﹣(+5)]=6000,
解得v=150.
答:小聪休息前的速度为150米/分.
【点睛】本题考查一次函数的应用、函数的图象,掌握速度、时间和路程之间的关系是解题的关键.
27.(2025 衢州一模)某科技公司在机器人展厅内的展台上举办了甲、乙两款机器人的表演、慢跑展示活动,展台的总长度是70米,如图1所示.甲机器人先从起点出发,匀速慢跑,到达指定的表演点后开始表演,表演结束后,立刻按原来速度继续向前慢跑,直到终点结束;乙机器人的起点在甲机器人起点前7米处,与甲机器人同时开始慢跑,一直前行,直到终点结束.已知甲、乙两款机器人距离甲机器人起点的距离y(米)与时间x(秒)之间的函数关系如图2所示.
(1)求甲、乙两款机器人各自的慢跑速度及甲机器人表演的时长.
(2)求当甲、乙两款机器人相遇时,相遇点离展示台终点的距离.
【点拨】(1)根据速度=路程÷时间分别计算甲、乙两款机器人各自的慢跑速度,由甲机器人表演的时长=甲机器人到达终点所用的时间﹣甲机器人到达终点通过的路程÷甲款机器人慢跑的速度计算甲机器人表演的时长即可;
(2)分别写出甲款机器人y与x之间的函数关系式(0≤x≤6)、乙款机器人y与x之间的函数关系式,分别计算两机器人相遇时对应y的值,从而求出相遇点离展示台终点的距离即可.
【解析】解:(1)甲款机器人慢跑的速度为30÷6=5(米/秒),
乙款机器人慢跑的速度为(70﹣7)÷18=3.5(米/秒),
甲款机器人表演的时长为18﹣70÷5=4(秒).
答:甲款机器人慢跑的速度为5米/秒,乙款机器人慢跑的速度为3.5米/秒,甲款机器人表演的时长为4秒.
(2)当0≤x≤6时,甲款机器人y与x之间的函数关系式为y=5x,
乙款机器人y与x之间的函数关系式为y=3.5x+7.
当0≤x≤6时,当甲、乙两款机器人相遇时,得,
解得,
此时相遇点离展示台终点的距离为70﹣=(米);
当6<x≤10时,当甲、乙两款机器人相遇时,y=30,
此时相遇点离展示台终点的距离为70﹣30=40(米);
当甲、乙两款机器人同时到达终点时,y=70,
此时相遇点离展示台终点的距离为70﹣70=0(米).
答:当甲、乙两款机器人相遇时,相遇点离展示台终点的距离为米或40米或0米.
【点睛】本题考查一次函数的应用,掌握速度、时间和路程之间的关系是解题的关键.
28.(2025 金华模拟)扎染古称“绞缬”,是我国一种古老的纺织品染色技艺.扎染工艺的发展带动了当地旅游相关产业的发展.某扎染坊第一次用3700元购进甲、乙两种布料共80件,其中两种布料的成本价和销售价如表:
单价类别 成本价/(元/件) 销售价/(元/件)
甲种布料 60 100
乙种布料 40 70
(1)该扎染坊第一次购进甲、乙两种布料各多少件?
(2)因热销,第一次购进的布料全部售完,该扎染坊第二次以相同的成本价再次购进甲、乙两种布料共100件.若此次购进甲种布料的数量不超过乙种布料数量的1.5倍,且以相同的销售价全部售完这批布料.设第二次购进甲种布料m件,第二次全部售完后获得的利润为W元.第二次应怎样进货,才能使第二次购进的布料全部售完后获得的利润最大?最大利润是多少元?
【点拨】(1)分别设该扎染坊第一次购进甲、乙两种布料的件数分别为未知数,根据题意列二元一次方程组并求解即可;
(2)根据题意,列关于m的一元一次不等式并求其解集,写出W关于m的函数关系式,根据一次函数的增减性和m的取值范围,确定当m取何值时W值最大,求出其最大值和此时100﹣m的值即可.
【解析】解:(1)设该扎染坊第一次购进甲种布料x件,购进乙种布料y件.
根据题意,得,
解得.
答:该扎染坊第一次购进甲种布料25件,购进乙种布料55件.
(2)根据题意,得m≤1.5(100﹣m),
解得m≤60,
W=(100﹣60)m+(70﹣40)(100﹣m)=10m+3000,
∵10>0,
∴W随m的增大而增大,
∵m≤60,
∴当m=60时W值最大,W最大=10×60+3000=3600,
100﹣60=40(件).
答:第二次购进甲种布料60件、乙种布料40件全部售完后获得的利润最,最大利润是3600元.
【点睛】本题考查一次函数的应用、二元一次方程组的应用,掌握二元一次方程组、一元一次不等式的解法和一次函数的增减性是解题的关键.
29.(2025 拱墅区一模)某社区推出智能可回收垃圾投放箱,居民投放可回收物可以赚取积分兑换生活用品.为了鼓励居民积极投放,超过一定投放质量后,奖励积分升级.其中塑料与纸张的奖励积分y(分)与投放质量x(kg)的函数关系如图所示.已知投放纸张超过10kg后,奖励积分为25分/kg.
(1)求投放8kg塑料的奖励积分.
(2)求a的值.
(3)若投放m kg的塑料的奖励积分是投放相同质量纸张的奖励积分的倍,求m的值.
【点拨】(1)求出投放塑料超过5kg后每千克的奖励积分,从而计算投放8kg塑料的奖励积分即可;
(2)根据题意列关于a的方程并求解即可;
(3)按照m不同的取值范围,根据题意列关于m的方程并求解即可.
【解析】解:(1)投放塑料超过5kg后,奖励积分为(300﹣100)÷(10﹣5)=40(分/kg),
100+40×(8﹣5)=220(分).
答:投放8kg塑料的奖励积分为220分.
(2)根据题意,得100+25(a﹣10)=300,
解得a=18.
(3)投放纸张不超过10kg,奖励积分为100÷10=10(分),
投放塑料不超过5kg,奖励积分为100÷5=20(分),
当0<m≤5时,得20m=×10m,
解得m=0(舍去),
当5<m≤10时,得100+40(m﹣5)=×10m,
解得m=,
当m>10时,得100+40(m﹣5)=[100+25(m﹣10)],
解得m=,
∴m=或.
【点睛】本题考查一次函数的应用,理解题意、从图象中获得必要的数学信息是解题的关键.
30.(2025 杭州一模)为鼓励节约用水,某市实行了阶梯水价制度.设月用水量为x(吨),每月应交水费y(元),如表为每户的综合用水单价与月用水量的关系表,如图是y关于x的函数图象.
阶梯 月用水量(吨) 用水单价(元/吨)
第一阶梯 x≤10 a
第二阶梯 10<x≤20 b
第三阶梯 x>20 5
根据上述信息解决以下问题:
(1)求a,b的值.
(2)当x>10时,求y关于x的函数表达式.
(3)小红家6月份、7月份的用水量都为整数吨,且都超过了10吨,水费合计为90元,其中6月份用水量低于7月份用水量,求小红家6月份的用水量.
【点拨】(1)依据题意得,,进而计算可以得解;
(2)依据题意,分当10<x≤20时和当x>20时,分别进行判断可以得解;
(3)依据题意,先判断6月用水量低于20吨,超过10吨,然后设6月份用水量为x吨,可得6月份的水费为3x﹣10,故7月份的水费为90﹣(3x﹣10)=100﹣3x,再分两种情形分析计算可以得解.
【解析】解:(1)由题意得,,
∴.
(2)由题意,①当10<x≤20时,y=20+3(x﹣10)=3x﹣10;
②当x>20时,y=50+5(x﹣20)=5x﹣50.
答:当x>10时,y关于x的函数表达式为y=.
(3)由题意,如果6月份、7月份的用水量均超过20吨,则总费用比超过100,不合题意,
又结合6月份用水量低于7月份用水量,
∴6月用水量低于20吨,超过10吨.
设6月份用水量为x吨,
∴6月份的水费为3x﹣10.
∴7月份的水费为90﹣(3x﹣10)=100﹣3x.
若7月份用水量低于20吨,则7月份的用水量为=﹣x,
又∵6月份、7月份的用水量都为整数吨,
∴7月份的用水量为﹣x,不合题意.
若7月份用水量大于20吨,则7月份的用水量为=30﹣x,
又∵6月份、7月份的用水量都为整数吨,
∴x为5的整数倍.
又∵10<x<30﹣x,
∴10<x<18.
∴x=15.
答:小红家6月份的用水量为15吨.
【点睛】本题主要考查了一次函数的应用、二元一次方程组的应用,解题时要熟练掌握并能灵活运用一次函数的性质是关键.
31.(2025 西湖区一模)在直角坐标系中,设函数y1=与函数y2=k2x+b(k1,k2,b是常数,k1k2≠0)的图象交于点A(1,4),B(﹣2,t).
(1)求函数y1,y2的表达式.
(2)当x>2时,比较y1与y2的大小.(直接写出结果)
(3)若点C在函数y2的图象上,将点C先向左平移1个单位,再向下平移6个单位得点D,点D恰好落在函数y1的图象上,求点C的坐标.
【点拨】(1)待定系数法求出两个函数解析式即可;
(2)画出图象,利用数形结合解答即可;
(3)根据点的平移法则设点C坐标为(m,2m+2),写出点D的坐标再代入反比例函数解析式求出m值即可点的点C坐标.
【解析】解:(1)∵两个函数图象交于点A(1,4),B(﹣2,t).
∴k1=1×4=﹣2t,
∴k1=4,t=﹣2,
∴y1=,
∵点A(1,4),B(﹣2,﹣2)在直线y2=k2x+b图象上,
,解得,
∴y2=2x+2.
(2)两个函数图象如图所示,
由图可知,当x>2时,y1<y2.
(3)设点C坐标为(m,2m+2),
∵将点C先向左平移1个单位,再向下平移6个单位得点D,
∴D(m﹣1,2m﹣4),
∵点D恰好落在函数y1的图象上,
∴(m﹣1)(2m﹣4)=4,
整理得m(m﹣3)=0,
∴m=3或m=0,
∴C(3,8)或(0,2).
【点睛】本题考查了一次函数与反比例函数的交点问题,交点坐标满足两个函数解析式是关键.
32.(2025 临安区一模)如图,反比例函数图象过点A(﹣2,a),直线x=4与该反比例函数图象和x轴分别交于点B和点D,连结AD.
(1)求△ADB的面积.
(2)若点P(m,n)(m>0)在反比例函数图象上,当PD⊥AD,求点P的坐标.
【点拨】(1)待定系数法求出a值,再利用解析式求出点B、D坐标,代入三角形面积公式计算即可.
(2)先求出直线AD的解析式得到kAD值,根据两直线垂直得到KPD,待定系数法求出直线PD解析式再与反比例函数解析式联立方程组即可求出点P的坐标.
【解析】解:(1)∵反比例函数图象过点A(﹣2,a),
∴a==﹣2,
∴A(﹣2,﹣2),
∵直线x=4与该反比例函数图象和x轴分别交于点B和点D,
∴B(4,1),D(4,0),
∴S△ABD=(4+2)=3;
(2)如图,
设直线AD的解析式为y=kx+b,代入点AD坐标可得:
,解得,
∵PD⊥AD,
∴kPD=﹣3,
设直线PD的解析式为y=﹣3x+m,代入点D坐标可得:m=12,
∴直线PD的解析式为y=﹣3x+12,
联立方程组得,解得,,
点P的坐标为(,6﹣2)或(,6+2).
【点睛】本题考查了一次函数与反比例函数的交点问题、三角形面积的计算,熟练掌握交点坐标求法是解答本题的关键.
33.(2025 浙江模拟)如图,一次函数y=﹣2x+b的图象与反比例函数的图象相交于点A(﹣1,4).
(1)求b和k的值.
(2)横坐标为3的点B是反比例函数图象上的一点,现将点B向下平移.当点B落在一次函数图象上时,求向下平移的距离.
【点拨】(1)把A(﹣1,4)代入一次函数,反比例函数解析式即可求解;
(2)根据题意得到,根据点的平移得到平移后,代入一次函数解析式即可求解.
【解析】解:(1)∵一次函数y=﹣2x+b的图象过点A(﹣1,4),
∴﹣2×(﹣1)+b=4,
解得b=2,
∴一次函数解析式为y=﹣2x+2,
∵与反比例函数的图象过点A(﹣1,4),
∴,
解得k=﹣4;
(2)由(1)知,k=﹣4,
∴反比例函数解析式为,
∵点B的横坐标为3,且点B在反比例函数图象上,
∴,即,
设点B向下平移了m个单位,
∴,
∴,
解得,
∴向下平移的距离为.
【点睛】本题主要考查的是反比例函数与一次函数的交点问题,待定系数法求一次函数的解析式,掌握以上知识是解题的关键.
34.(2025 上城区一模)某项目学习小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地,当人和木板对湿地的压力F(单位:N)一定时,木板面积S(单位:m2)与人和木板对地面的压强P(单位:Pa)成反比例.当木板面积为0.2m2时,人和木板对地面的压强为3000Pa.
(1)求P关于S的函数表达式;
(2)当木板面积为0.3m2时,压强是多少?
(3)如果要求压强不超过1200Pa,木板面积至少要多大?请说明理由.
【点拨】(1)压力一定时,压强和受力面积成反比,根据压力为600N写出解析式即可;
(2)在(1)的基础上可求出函数值p;
(3)压强不超过1200Pa,即p≤1200时,求相对应的自变量的范围.
【解析】解:(1)压力一定时,压强和受力面积成反比;
∵F=3000×0.2=600N,
∴P关于S的函数表达式为p=(s>0);
(2)当S=0.3时,p==2000(Pa),
故当木板面积为0.3m2时,压强为2000Pa;
(3)把p≤1200Pa代入解析式得:
≤1200,
解得:S≥0.5,
∴如果要求压强不超过1200Pa,木板面积至少要0.5m2.
【点睛】本题考查反比例函数的应用,涉及反比例函数的定义,反比例函数图象上点的特征以及反比例函数图象的性质,熟练掌握反比例函数的相关性质且能读懂题意,学以致用是解题的关键.
35.(2025 萧山区一模)科技创新为实现可持续发展赋能.某企业自2024年1月开始限产进行技术改造,其月利润y(万元)与月份x之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分.
(1)求反比例函数和一次函数的表达式.
(2)求当月利润不高于100万元时共经历了多少个月?
【点拨】(1)利用待定系数法先求出反比例函数解析式,再求出第4个月的利润,设出函数式,根据待定系数法即可求出函数解析式;
(2)把100万元代入函数解析式即可求出.
【解析】解:(1)根据图象,反比例函数图象经过(1,200),
设反比例函数为y=(k≠0),
则=200,
∴k=200,
∴反比例函数为y=(1≤x≤4),
把x=4代入y=得,y=50,
当x=6时,y=110,
设改造工程完工后函数解析式为y=mx+b,
则,
解得m=30,b=﹣70,
∴改造工程完工后函数解析式为y=30x﹣70(x>4且x取整数);
(2)当y=100时,30x﹣70=100,
解得x≈6.
6﹣2=4.
∴当月利润不高于100万元时共经历了4个月.
【点睛】本题主要考查反比例函数的应用,待定系数法求函数解析式和根据函数值求自变量,读懂图象信息对解本题比较关键.
36.(2025 湖州一模)电磁波由振荡的电场和磁场构成,我国嫦娥六号探测器就是通过无线电波(电磁波的一种)与地球通信,电磁波的波长λ(单位:m)会随着电磁波的频率f(单位:MHz)的变化而变化.已知某段电磁波在同种介质中,波长λ与频率f的部分对应值如表:
频率f(MHz) 5 10 15 20 25 30
波长λ(m) 60 30 20 15 12 10
(1)根据表格中的数据,选择合适的函数模型,求出波长λ(m)关于频率f(MHz)的函数表达式.
(2)当该电磁波的频率为50MHz时,它的波长是多少m?
【点拨】(1)根据变量的变化规律解答即可;
(2)将f=50代入(1)中求得的函数表达式,求出对应λ的值即可.
【解析】解:(1)由表格可知,fλ=300,
∴λ与f的函数表达式为λ=.
(2)当f=50时,λ==6,
答:当该电磁波的频率为50MHz时,它的波长是6m.
【点睛】本题考查反比例函数的应用,根据变量的变化规律写出函数关系式是解题的关键.
37.(2025 镇海区校级模拟)在平面直角坐标系中,直线y=﹣2x+4交x轴于点A,交y轴于点B,点C的坐标为(1,0).
(1)求直线BC的函数表达式.
(2)点D是x轴上一动点,连接BD、CD,当△BCD的面积是△AOB面积的时,求点D的坐标.
(3)点E坐标为(0,﹣2),连接CE,点P为直线AB上一点,若∠CEP=45°,求点P坐标.
【点拨】(1)解方程得到B(0,4),设直线BC的函数表达式为y=kx+b,解方程组得到直线BC的函数表达式为y=﹣4x+4;
(2)解方程得到A(2,0),求得OA=2,设D(m,0),则CD=|m﹣1|,根据三角形的面积公式列方程即可得到结论;
(3)过C作CH⊥EP于H,过H作KT∥y轴,过C作CK⊥KT于K,过E作ET⊥KT于T,设H(p,q),当P在EC下方时,当P在EC上方时,根据等腰直角三角形的性质得到∠CHE=90°,EH=CH,根据全等三角形的性质得到ET=HK=p,HT=CK=q﹣1,解方程即可得到结论.
【解析】解:(1)当x=0时,y=﹣2x+4=4,
∴B(0,4),
设直线BC的函数表达式为y=kx+b,
∵C的坐标为(1,0),
∴,
∴,
∴直线BC的函数表达式为y=﹣4x+4;
(2)当y=﹣2x+4=0,
∴x=2,
∴A(2,0),
∴OA=2,
设D(m,0),则CD=|m﹣1|,
∵△BCD的面积=△AOB面积的,
∴CD BO=×OA BO,|m﹣1|=×2=3,
解得m=﹣2或m=4,
∴点D的坐标为(﹣2,0)或(4,0);
(3)过C作CH⊥EP于H,过H作KT∥y轴,过C作CK⊥KT于K,过E作ET⊥KT于T,设H(p,q),
当P在EC下方时,如图:
∵∠CEP=45°,CH⊥EP,
∴△CEH是等腰直角三角形,
∴∠CHE=90°,EH=CH,
∴∠EHT=90°﹣∠CHK=∠HCK,
∵∠T=∠K=90°,
∴△EHT≌△HCK(AAS),
∴ET=HK=p,HT=CK=q﹣1,
∴,
解得p=,q=﹣,
∴H(,﹣),
由H(,﹣),E(0,﹣2)得直线EP解析式为y=x﹣2,
解得,
∴P(,﹣);
当P在EC上方时,如图:
同理可得△EHT≌△HCK(AAS),
∴ET=HK,HT=CK,
∴1﹣p=2+q,p=q,
解得p=﹣,q=﹣,
∴H(﹣,﹣),
∴直线EP解析式为y=﹣3x﹣2,
联立,
解得,
∴P(﹣6,16);
综上所述,P的坐标为(,﹣)或(﹣6,16).
【点睛】本题是一次函数的综合题,考查了待定系数法求函数的解析式,全等三角形的判定和性质,三角形的面积,正确的作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
