2024-2025学年甘肃省定西市渭源县第二中学高一下学期第二次阶段考试数学试卷(人教版2019,湘教版2019均可用)(含答案)
文档属性
| 名称 | 2024-2025学年甘肃省定西市渭源县第二中学高一下学期第二次阶段考试数学试卷(人教版2019,湘教版2019均可用)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 270.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-03 10:00:28 | ||
图片预览

文档简介
2024-2025甘肃省定西市渭源县第二中学高一下学期第二次阶段考试
数学 试卷
一、单选题:本大题共8小题,每小题5分,共40分,每小题只有一个正确选项.
1.若(2+i) z=5i,则z的虚部为( )
A.﹣2i B.2i C.﹣2 D.2
2.若m,n为两条直线,α为一个平面,则下列结论中正确的是( )
A.若m∥α,n α,则m∥n
B.若m∥α,n∥α,则m∥n
C.若m∥α,n⊥α,则m⊥n
D.若m∥α,n⊥α,则m与n相交
3.若底面半径为r,母线长为l的圆锥的表面积与直径为l的球的表面积相等,则( )
A. B. C. D.
4.在△ABC中,a=6,c=10,,则边b=( )
A.6 B.10 C.14 D.
5.已知向量,则在方向上的投影向量的坐标为( )
A.(3,1)
B.
C.
D.
6.已知一组数据x1,x2,x3,x4,x5满足x1<x2<x3<x4<x5,则下列说法正确的是( )
A.这组数据的40%分位数是x2
B.x2,x3,x4的平均数小于x1,x2,x3,x4,x5的平均数
C.x2,x3,x4的方差大于x1,x2,x3,x4,x5的方差
D.x2,x3,x4的极差小于x1,x2,x3,x4,x5的极差
7.已知事件A,B满足P(A)=0.5,P(B)=0.2,则( )
A.若B A,则P(AB)=0.5
B.若A,B互斥,则P(A+B)=0.7
C.若A与B相互独立,则
D.若P(B)+P(C)=1,则C与B相互对立
8.在△ABC中,M为边BC中点,N为AM的中点,,则λ+2μ=( )
A. B. C. D.1
二、多选题:本大题共3小题,每小题6分,共18分.
9.在△ABC中,角A,B,C所对的边分别为a,b,c,能确定∠C为锐角的有( )
A.a2+b2>c2 B.
C.A,B均为锐角,且sinA>cosB D.sinA=2sinC
10.已知复数z1,z2,则下列结论正确的是( )
A.|z1+z2|=|z1|+|z2| B.|z1 z2|=|z1| |z2|
C.若|z1|=|z2|,则 D.若|z1|=|z2|,则z1 z2
11.如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,M为B1C1边的中点,点P在底面ABCD内运动(包括边界),则下列说法正确的有( )
A.不存在点P,使得D1P⊥AD1
B.点B到平面ACM的距离为
C.点A1到直线AM的距离为1
D.点N在棱BB1上,且B1N=4NB,存在点P,使得D1P⊥NP
三、填空题:本题共3个小题,每小题5分,共15分。将答案直接填在答题卷相应的横线上。
12.如图所示,圆锥SO的底面圆半径OA=1,侧面的平面展开图的面积为3π,则此圆锥的体积为 .
13.已知向量,则 .
14.长方形ABCD中,AB=4,AD=3,沿对角线AC把平面ACD折起,使平面ACD⊥平面ABC,则折叠后∠BCD的余弦值为 .
四、解答题:本题共5小题,第15题13分,第16、17小题15分,第18、19小题17分,共77分。解答应写出文字说明、证明过程或演算步骤。
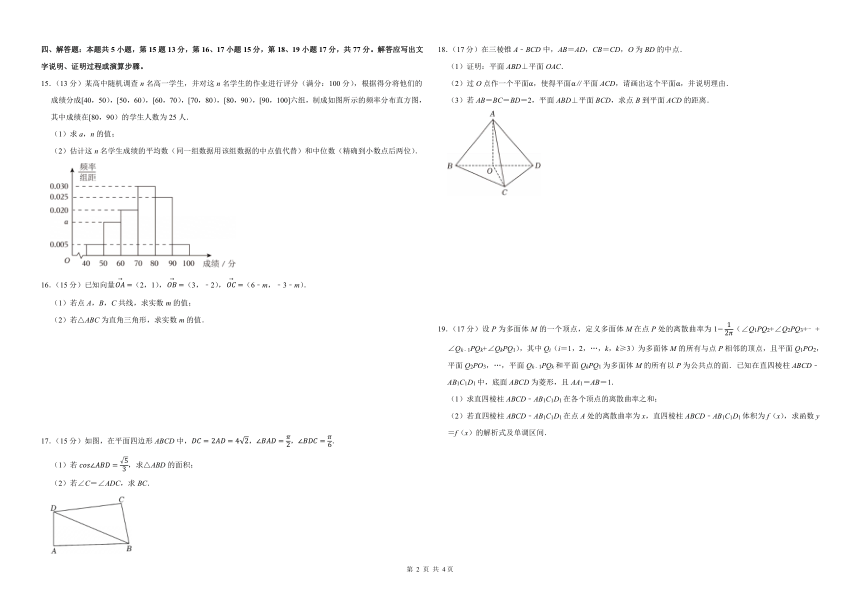
15.(13分)某高中随机调查n名高一学生,并对这n名学生的作业进行评分(满分:100分),根据得分将他们的成绩分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组,制成如图所示的频率分布直方图,其中成绩在[80,90)的学生人数为25人.
(1)求a,n的值;
(2)估计这n名学生成绩的平均数(同一组数据用该组数据的中点值代替)和中位数(精确到小数点后两位).
16.(15分)已知向量(2,1),(3,﹣2),(6﹣m,﹣3﹣m).
(1)若点A,B,C共线,求实数m的值;
(2)若△ABC为直角三角形,求实数m的值.
17.(15分)如图,在平面四边形ABCD中,,,.
(1)若,求△ABD的面积;
(2)若∠C=∠ADC,求BC.
18.(17分)在三棱锥A﹣BCD中,AB=AD,CB=CD,O为BD的中点.
(1)证明:平面ABD⊥平面OAC.
(2)过O点作一个平面α,使得平面α∥平面ACD,请画出这个平面α,并说明理由.
(3)若AB=BC=BD=2,平面ABD⊥平面BCD,求点B到平面ACD的距离.
19.(17分)设P为多面体M的一个顶点,定义多面体M在点P处的离散曲率为1(∠Q1PQ2+∠Q2PQ3+ +∠Qk﹣1PQk+∠QkPQ1),其中Qi(i=1,2,…,k,k≥3)为多面体M的所有与点P相邻的顶点,且平面Q1PO2,平面Q2PO3,…,平面Qk﹣1PQk和平面QkPQ1为多面体M的所有以P为公共点的面.已知在直四棱柱ABCD﹣AB1C1D1中,底面ABCD为菱形,且AA1=AB=1.
(1)求直四棱柱ABCD﹣AB1C1D1在各个顶点的离散曲率之和;
(2)若直四棱柱ABCD﹣AB1C1D1在点A处的离散曲率为x,直四棱柱ABCD﹣AB1C1D1体积为f(x),求函数y=f(x)的解析式及单调区间.
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D C B C D D B C
二.多选题(共3小题)
题号 9 10 11
答案 ACD BD ABD
三.填空题(共3小题)
12..
13.14.
.
四.解答题(共5小题)
15.解:(1)由题意得n100,
10×(0.005+a+0.02+0.03+0.025+0.005)=1,
解得a=0.015.
(2)平均数为:
(45×0.005+55×0.015+65×0.02+75×0.03+85×0.025+95×0.005)×10=72,
∵(0.005+0.015+0.02)×10=0.4,
(0.005+0.02+0.03)×10=0.7,
∴中位数在[70,80)之间,设中位数为x,
则(0.005+0.015+0.02)×10+(x﹣70)×0.03=0.5,
解得x≈73.33.
16.解:(1)向量(2,1),(3,﹣2),(6﹣m,﹣3﹣m).
故,,
故,
整理得:﹣1﹣m+3(3﹣m)=0,
故m=2.
(2)由于向量(2,1),(3,﹣2),(6﹣m,﹣3﹣m).
故,,,
①当∠A为直角时,
所以,
故4﹣m+3(4+m)=0,解得m=﹣8;
②当∠B为直角时,
,
故4﹣m+2+3m=0,解得m=﹣3;
③当∠C为直角时,
所以,
故2m2﹣2m+17=0,无解.
由①②③可知:m=﹣3或﹣8.
17.解:(1)因为0,所以sin∠ABD,
所以tan∠ABD,
在Rt△ABD中,tan∠ABD,
所以AB,
所以△ABD的面积SAB AD2.
(2)设∠CBD=α,则∠ADC=∠Cα,
因为,所以∠ADB=∠ADC﹣∠BDCα,
在Rt△ABD中,cos∠ADB,所以BD,
在△BCD中,由正弦定理知,,
所以(*),
所以,
即sinα=2×(sin2αcos2α)sin2α(1﹣sin2α)=2sin2α,
整理得4sin2α﹣2sinα﹣1=0,解得sinα(舍负),
代入(*)式得,BC2().
18.解:(1)证明:因为AB=AD,CB=CD,O为BD的中点,
所以OA⊥BD,OC⊥BD,
又因为OA,OC 平面OAC,OA∩OC=O,所以BD⊥平面OAC,
又因为BD 平面ABD,所以平面ABD⊥平面OAC;
(2)取AB的中点E,BC的中点F,连接OE,OF,EF,
又因为O为BD的中点,所以OE∥AD,
又因为OE 平面ACD,AD 平面ACD,所以OE∥平面ACD,
同理可得OF∥平面ACD,
因为OE∩OF=O,OE,OF 平面OEF,所以平面OEF∥平面ACD,
所以平面OEF即为所求的平面α.
(3)因为平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,OA⊥BD,OA 平面ABD,
所以OA⊥平面BCD,
因为AB=BC=BD=2,所以△ABD,△BCD均为等边三角形,
所以,所以,
所以,
因为OA⊥平面BCD,OC 平面BCD,所以OA⊥OC,
由勾股定理得:,
取AC的中点H,连接DH,
因为在△ACD中,,所以DH⊥AC,
所以,,
设点B到平面ACD的距离为d,VB﹣ACD=VA﹣BCD,
所以,解得.
所以点B到平面ACD的距离为.
19.解:(1)在直四棱柱ABCD﹣A1B1C1D1中,,底面ABCD为菱形,
由离散曲率的定义知:A,A1,C,C1的离散曲率相等,B,B1,D,D1的离散曲率相等,
∴A处的曲率为,
又D处的曲率为,∠BAD+∠ADC=π,
∴A、D两处的曲率和为,
∴直四棱柱ABCD﹣AB1C1D1在各个顶点的离散曲率之和;
(2)根据题意可知A处的曲率,
∴∠BAD=π(1﹣2x),
∴直四棱柱底面面积为,
∴直四棱柱ABCD﹣AB1C1D1高为1,∴体积为f(x)=sin2πx,
令,k∈Z,
∴,k∈Z,
即,k∈Z上f(x)递增;
令,k∈Z,
∴,k∈Z,
即,k∈Z上f(x)递减;
∴f(x)增区间为,减区间为,k∈Z.
数学 试卷
一、单选题:本大题共8小题,每小题5分,共40分,每小题只有一个正确选项.
1.若(2+i) z=5i,则z的虚部为( )
A.﹣2i B.2i C.﹣2 D.2
2.若m,n为两条直线,α为一个平面,则下列结论中正确的是( )
A.若m∥α,n α,则m∥n
B.若m∥α,n∥α,则m∥n
C.若m∥α,n⊥α,则m⊥n
D.若m∥α,n⊥α,则m与n相交
3.若底面半径为r,母线长为l的圆锥的表面积与直径为l的球的表面积相等,则( )
A. B. C. D.
4.在△ABC中,a=6,c=10,,则边b=( )
A.6 B.10 C.14 D.
5.已知向量,则在方向上的投影向量的坐标为( )
A.(3,1)
B.
C.
D.
6.已知一组数据x1,x2,x3,x4,x5满足x1<x2<x3<x4<x5,则下列说法正确的是( )
A.这组数据的40%分位数是x2
B.x2,x3,x4的平均数小于x1,x2,x3,x4,x5的平均数
C.x2,x3,x4的方差大于x1,x2,x3,x4,x5的方差
D.x2,x3,x4的极差小于x1,x2,x3,x4,x5的极差
7.已知事件A,B满足P(A)=0.5,P(B)=0.2,则( )
A.若B A,则P(AB)=0.5
B.若A,B互斥,则P(A+B)=0.7
C.若A与B相互独立,则
D.若P(B)+P(C)=1,则C与B相互对立
8.在△ABC中,M为边BC中点,N为AM的中点,,则λ+2μ=( )
A. B. C. D.1
二、多选题:本大题共3小题,每小题6分,共18分.
9.在△ABC中,角A,B,C所对的边分别为a,b,c,能确定∠C为锐角的有( )
A.a2+b2>c2 B.
C.A,B均为锐角,且sinA>cosB D.sinA=2sinC
10.已知复数z1,z2,则下列结论正确的是( )
A.|z1+z2|=|z1|+|z2| B.|z1 z2|=|z1| |z2|
C.若|z1|=|z2|,则 D.若|z1|=|z2|,则z1 z2
11.如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,M为B1C1边的中点,点P在底面ABCD内运动(包括边界),则下列说法正确的有( )
A.不存在点P,使得D1P⊥AD1
B.点B到平面ACM的距离为
C.点A1到直线AM的距离为1
D.点N在棱BB1上,且B1N=4NB,存在点P,使得D1P⊥NP
三、填空题:本题共3个小题,每小题5分,共15分。将答案直接填在答题卷相应的横线上。
12.如图所示,圆锥SO的底面圆半径OA=1,侧面的平面展开图的面积为3π,则此圆锥的体积为 .
13.已知向量,则 .
14.长方形ABCD中,AB=4,AD=3,沿对角线AC把平面ACD折起,使平面ACD⊥平面ABC,则折叠后∠BCD的余弦值为 .
四、解答题:本题共5小题,第15题13分,第16、17小题15分,第18、19小题17分,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)某高中随机调查n名高一学生,并对这n名学生的作业进行评分(满分:100分),根据得分将他们的成绩分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组,制成如图所示的频率分布直方图,其中成绩在[80,90)的学生人数为25人.
(1)求a,n的值;
(2)估计这n名学生成绩的平均数(同一组数据用该组数据的中点值代替)和中位数(精确到小数点后两位).
16.(15分)已知向量(2,1),(3,﹣2),(6﹣m,﹣3﹣m).
(1)若点A,B,C共线,求实数m的值;
(2)若△ABC为直角三角形,求实数m的值.
17.(15分)如图,在平面四边形ABCD中,,,.
(1)若,求△ABD的面积;
(2)若∠C=∠ADC,求BC.
18.(17分)在三棱锥A﹣BCD中,AB=AD,CB=CD,O为BD的中点.
(1)证明:平面ABD⊥平面OAC.
(2)过O点作一个平面α,使得平面α∥平面ACD,请画出这个平面α,并说明理由.
(3)若AB=BC=BD=2,平面ABD⊥平面BCD,求点B到平面ACD的距离.
19.(17分)设P为多面体M的一个顶点,定义多面体M在点P处的离散曲率为1(∠Q1PQ2+∠Q2PQ3+ +∠Qk﹣1PQk+∠QkPQ1),其中Qi(i=1,2,…,k,k≥3)为多面体M的所有与点P相邻的顶点,且平面Q1PO2,平面Q2PO3,…,平面Qk﹣1PQk和平面QkPQ1为多面体M的所有以P为公共点的面.已知在直四棱柱ABCD﹣AB1C1D1中,底面ABCD为菱形,且AA1=AB=1.
(1)求直四棱柱ABCD﹣AB1C1D1在各个顶点的离散曲率之和;
(2)若直四棱柱ABCD﹣AB1C1D1在点A处的离散曲率为x,直四棱柱ABCD﹣AB1C1D1体积为f(x),求函数y=f(x)的解析式及单调区间.
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D C B C D D B C
二.多选题(共3小题)
题号 9 10 11
答案 ACD BD ABD
三.填空题(共3小题)
12..
13.14.
.
四.解答题(共5小题)
15.解:(1)由题意得n100,
10×(0.005+a+0.02+0.03+0.025+0.005)=1,
解得a=0.015.
(2)平均数为:
(45×0.005+55×0.015+65×0.02+75×0.03+85×0.025+95×0.005)×10=72,
∵(0.005+0.015+0.02)×10=0.4,
(0.005+0.02+0.03)×10=0.7,
∴中位数在[70,80)之间,设中位数为x,
则(0.005+0.015+0.02)×10+(x﹣70)×0.03=0.5,
解得x≈73.33.
16.解:(1)向量(2,1),(3,﹣2),(6﹣m,﹣3﹣m).
故,,
故,
整理得:﹣1﹣m+3(3﹣m)=0,
故m=2.
(2)由于向量(2,1),(3,﹣2),(6﹣m,﹣3﹣m).
故,,,
①当∠A为直角时,
所以,
故4﹣m+3(4+m)=0,解得m=﹣8;
②当∠B为直角时,
,
故4﹣m+2+3m=0,解得m=﹣3;
③当∠C为直角时,
所以,
故2m2﹣2m+17=0,无解.
由①②③可知:m=﹣3或﹣8.
17.解:(1)因为0,所以sin∠ABD,
所以tan∠ABD,
在Rt△ABD中,tan∠ABD,
所以AB,
所以△ABD的面积SAB AD2.
(2)设∠CBD=α,则∠ADC=∠Cα,
因为,所以∠ADB=∠ADC﹣∠BDCα,
在Rt△ABD中,cos∠ADB,所以BD,
在△BCD中,由正弦定理知,,
所以(*),
所以,
即sinα=2×(sin2αcos2α)sin2α(1﹣sin2α)=2sin2α,
整理得4sin2α﹣2sinα﹣1=0,解得sinα(舍负),
代入(*)式得,BC2().
18.解:(1)证明:因为AB=AD,CB=CD,O为BD的中点,
所以OA⊥BD,OC⊥BD,
又因为OA,OC 平面OAC,OA∩OC=O,所以BD⊥平面OAC,
又因为BD 平面ABD,所以平面ABD⊥平面OAC;
(2)取AB的中点E,BC的中点F,连接OE,OF,EF,
又因为O为BD的中点,所以OE∥AD,
又因为OE 平面ACD,AD 平面ACD,所以OE∥平面ACD,
同理可得OF∥平面ACD,
因为OE∩OF=O,OE,OF 平面OEF,所以平面OEF∥平面ACD,
所以平面OEF即为所求的平面α.
(3)因为平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,OA⊥BD,OA 平面ABD,
所以OA⊥平面BCD,
因为AB=BC=BD=2,所以△ABD,△BCD均为等边三角形,
所以,所以,
所以,
因为OA⊥平面BCD,OC 平面BCD,所以OA⊥OC,
由勾股定理得:,
取AC的中点H,连接DH,
因为在△ACD中,,所以DH⊥AC,
所以,,
设点B到平面ACD的距离为d,VB﹣ACD=VA﹣BCD,
所以,解得.
所以点B到平面ACD的距离为.
19.解:(1)在直四棱柱ABCD﹣A1B1C1D1中,,底面ABCD为菱形,
由离散曲率的定义知:A,A1,C,C1的离散曲率相等,B,B1,D,D1的离散曲率相等,
∴A处的曲率为,
又D处的曲率为,∠BAD+∠ADC=π,
∴A、D两处的曲率和为,
∴直四棱柱ABCD﹣AB1C1D1在各个顶点的离散曲率之和;
(2)根据题意可知A处的曲率,
∴∠BAD=π(1﹣2x),
∴直四棱柱底面面积为,
∴直四棱柱ABCD﹣AB1C1D1高为1,∴体积为f(x)=sin2πx,
令,k∈Z,
∴,k∈Z,
即,k∈Z上f(x)递增;
令,k∈Z,
∴,k∈Z,
即,k∈Z上f(x)递减;
∴f(x)增区间为,减区间为,k∈Z.
同课章节目录
