2024-2025学年七年级下学期数学期考末模拟卷(浙江台州市专用)[答案+解析]
文档属性
| 名称 | 2024-2025学年七年级下学期数学期考末模拟卷(浙江台州市专用)[答案+解析] |  | |
| 格式 | docx | ||
| 文件大小 | 554.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 12:18:09 | ||
图片预览




文档简介
保密★启用前
2024-2025学年七年级下册期末模拟卷(台州市专用)
数 学
(考试范围:七下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列学校校徽可以看成是由图案自身的一部分经平移后得到的为( )
A. B.
C. D.
2.下列是二元一次方程的是( )
A. B. C. D.
3.关于的分式方程无解,则的值是( )
A.1 B.3 C.或 D.或
4.要调查某校七年级学生周一到周五平均每天的睡眠时间,选取调查对象最合适的是( )
A.选取该校七年级一个班级的学生
B.选取60名该校的七年级女生
C.选取60名该校的七年级男生
D.随机选取60名该校的七年级学生
5.如图,已知直线a与直线b被第三条直线c所截,则的内错角是( )
A. B. C. D.
6.若,则等于( )
A.1 B. C. D.6
7.一个宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团25人准备同时租用这三种客房共9间,如果每个房间都住满,则租房方案共有( )
A.4种 B.3种 C.2种 D.1种
8.某电瓶车厂根据去年第三、四季度各月产量,制作了统计图.根据图中信息,可以判断相邻两个月中,月产量增长最大的是( )
A.月到月 B.月到月 C.月到月 D.月到月
9.如图,,点在上,,的延长线交的延长线于点,则图中与相等的角(不含)共有( )
A.7个 B.6个 C.5个 D.4个
10.下列计算正确的是( )
A. B. C. D.
二、填空题(本题有6小题,每小题3分,共18分)
11.若是一个完全平方式,则的值为 .
12.如图,若,则、、之间的关系为 .
13.光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,在水中平行的光线,在空气中也是平行的.如图是从玻璃杯底部发出的一束平行光线经过水面折射形成的光线示意图.若,,则 .
14.某校举行运动会时,由若干名同学组成一个13列的长方形彩旗队阵.如果原队阵中增加16人,能组成一个正方形队阵;如果原队阵中减少16人,也能组成一个正方形队阵,则原长方形彩旗队阵中有同学 人.
15.将45个数据分成6组,第一到第四组的频数分别为9,7,8,6,第五组的频率为0.2,则第六组的频数是 .
16.如图,长为,宽为的大长方形被分割为5小块,除阴影外,其余3块都是正方形,若阴影周长为10,下列结论:①的值为5;②若阴影的周长为8,则正方形的面积为1;③若大长方形的面积为30,则三个正方形周长的和为24.其中正确的是 .
三、解答题 (本题有 8 小题, 第17-21题每题 8 分, 第 22,23 题每题 10 分, 第 24 题 12 分, 共 72 分)
17.计算:
(1).
(2).
18.解方程组:
(1);
(2).
19.请将下列证明过程补充完整.
如图,已知,.
求证:.
证明:∵( ),
∴ (同旁内角互补,两直线平行).
∴( ).
又∵(已知),
∴(等量代换).
∴(内错角相等,两直线平行),
∴( ).
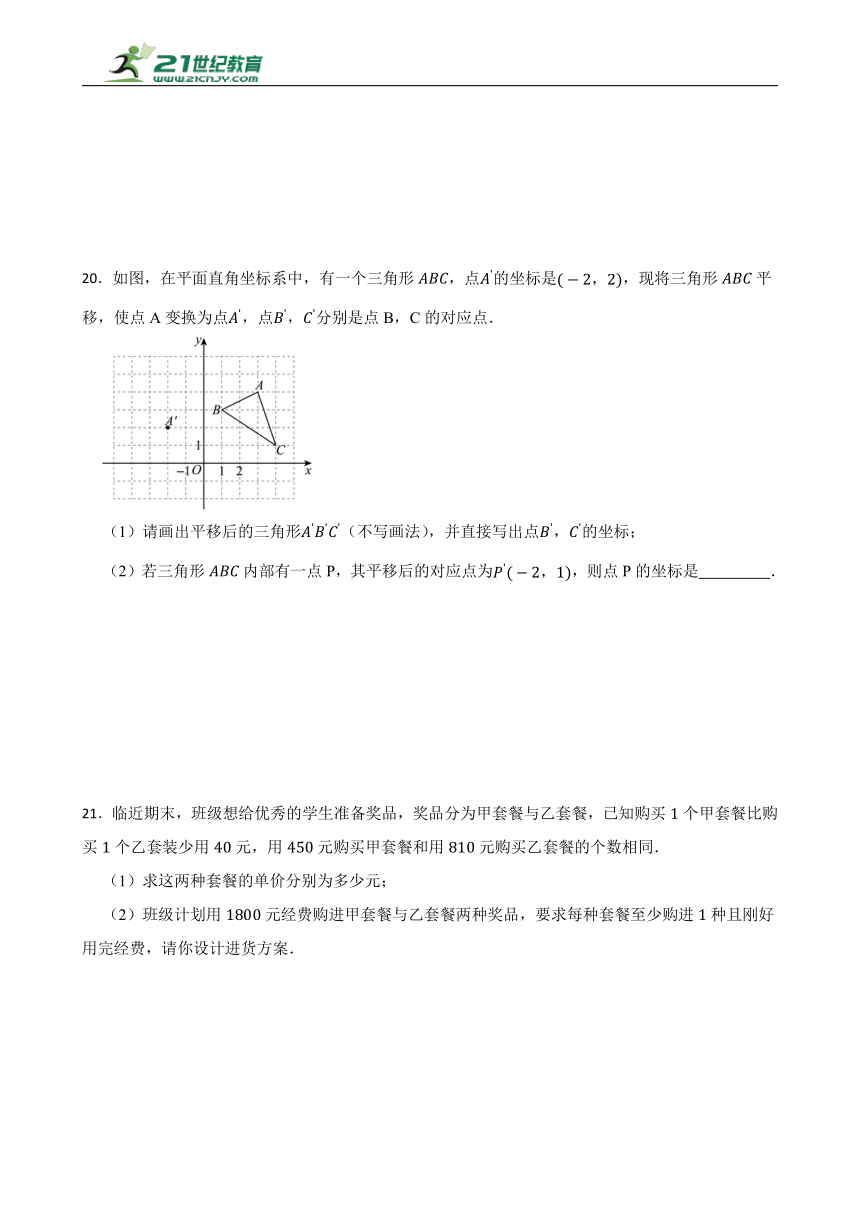
20.如图,在平面直角坐标系中,有一个三角形,点的坐标是,现将三角形平移,使点A变换为点,点,分别是点B,C的对应点.
(1)请画出平移后的三角形(不写画法),并直接写出点,的坐标;
(2)若三角形内部有一点P,其平移后的对应点为,则点P的坐标是 .
21.临近期末,班级想给优秀的学生准备奖品,奖品分为甲套餐与乙套餐,已知购买个甲套餐比购买个乙套装少用元,用元购买甲套餐和用元购买乙套餐的个数相同.
(1)求这两种套餐的单价分别为多少元;
(2)班级计划用元经费购进甲套餐与乙套餐两种奖品,要求每种套餐至少购进种且刚好用完经费,请你设计进货方案.
22.某校在市卫生健康局、教育局联合举办的“5.20中国学生营养日”活动带领下举行了七年级学生“健康菜谱”设计活动,让学生能设计一份健康菜谱,菜谱需符合“减油、增豆、加奶”的原则.现收集了七年级2班同学们设计的菜谱,并将菜中的主要食材分类、整理成图表,下面给出了部分信息:
根据以上信息回答下列问题:
(1)七年级2班共有______人,并补全条形统计图
(2)“谷物”所对应的扇形圆心角度数为______度.
(3)若该校七年级学生共1200人,则选择“蔬果”作为主要食材的学生约有多少人?
23.如图1,将长方形纸片沿直线折叠,点,的对应点分别为点,,折叠后与交于点.
(1)若,直接写出的度数.
(2)如图2,设.
①若,求的度数.
②若,求的值.
24.根据素材,完成任务.
如何设计雪花模型材料采购方案?
素 材 一 学校组织同学参与甲、乙两款雪花模型的制作.每款雪花模型都需要用到长、短两种管子材料.某同学用6根长管子、48根短管子制作了1个甲雪花模型与1个乙雪花模型.已知制作一个甲、乙款雪花模型需要的长、短管子数分别为与.
素 材 二 某商店的店内广告牌如右所示.5月,学校花费320元向该商店购得的长管子数量比花200元购得的短管子数量少80根. 1.短管子售价:a元/根,长管子售价:元/根 2.6月1日起,购买3根长管子赠送1根短管子. 3.本店库存数量有限,长管子仅剩267根,短管子仅剩2130根,先到先得!
素 材 三 6月,学校有活动经费1280元,欲向该商店采购长、短管子各若干根全部用来制作甲、乙雪花模型(材料无剩余),且采购经费恰好用完.
问题解决
任 务 一 分析雪花模型结构 求制作一个甲、乙款雪花模型分别需要长、短管子多少根?
任 务 二 确定采购费用 试求a的值并求出假如6月只制作一个甲款雪花模型的材料采购费.
任 务 三 拟定采购方案 求出所有满足条件的采购方案,并指出哪种方案得到的雪花总数最多.
答案解析部分
1.C
解:A、是一个轴对称图形,可以看成是由图案自身的一部分经轴对称得到,故不符合题意;
B、是一个没有规律的图形,故不可以看成是由图案自身的一部分经平移后得到,故不符合题意;
C、可以看做是图案自身的一部分沿着直线运动得到,故符合题意;
D、是一个轴对称图形,可以看成是由图案自身的一部分经轴对称得到,故不符合题意;
故答案为:C.
根据平移的定义和平移不改变图形的形状和大小的性质,结合图案,对选项逐一分析,即可排除错误答案.
2.B
A.是分式方程,不是二元一次方程,不符合题意;
B.是二元一次方程,符合题意;
C.含未知数项的最高次数为二次,不是二元一次方程,不符合题意;
D.含未知数项的最高次数为二次,不是二元一次方程,不符合题意.
故答案为:B.
二元一次方程是指含有两个未知数,并且所含未知数的项的次数都是1的整式方程,据此判断.
3.D
解:去分母得:,
,
当,即时,,此时整式方程无解,分式方程无解,
当,即时,由得,
把代入得:,
解得:,
关于的分式方程无解时,或,
故选:D.
去分母化为整式方程,根据分整式方程无解、整式方程的解是分式方程的增根两种情况解答即可.
4.D
解:只选取一个班级的学生不具有代表性,故A不符合题意;
只选取女生不具有代表性,故B不符合题意;
只选取男生不具有代表性,故C不符合题意;
随机选取该校七年级60名学生,符合抽样调查的样本要求,故D符合题意.
故答案为:D.
根据抽样调查的意义,对四个选项逐一分析,再作出判断.
5.B
6.C
解:,
.
故选:C.
根据同底数幂的除法和幂的乘方的逆算解答即可.
7.B
解:设宾馆有客房:二人间x间、三人间y间、四人间z间,根据题意得:
解得:y+2z=7,
y=7﹣2z,
∵x,y,z都是小于9的正整数,
当z=1时,y=5,x=3;
当z=2时,y=3,x=4;
当z=3时,y=1,x=5
当z=4时,y=﹣1(不符合题意,舍去)
∴租房方案有3种.
故选:B.
首先设宾馆有客房:二人间x间、三人间y间、四人间z间,根据题意可得方程组:,解此方程组可得y+2z=7,又由x,y,z是非负整数,即可求得答案.
8.D
、月到月增加了(辆),
、月到月增加了(辆),
、月到月增加了(辆),
、月到月增加了(辆),
∴月产量增长最大的是月到月,
故答案为:.
根据统计图,计算相邻两个月销售额的差,然后比较解题.
9.B
∵AB∥EF, ∴∠AGE=∠GEF, ∠GBP=∠BPF
∵EF∥CD, ∴∠GEF=∠EHC, ∠PCD=∠EPC=∠BPF,
∵GE∥BC, ∴∠EHC=∠BCD,
∴∠AGE =∠GEF=∠EHC=∠BCD=∠EPC=∠BPF=∠GBP.
共6个角与∠AGE相等.
故选:B
两直线平行、同位角相等、内错角相等,则∠AGE=∠GEF=∠EHC=∠BCD=∠EPC=∠BPF=∠GBP.
10.C
解:A.,故选项错误,不符合题意;
B.,故选项错误,不符合题意;
C.,故选项正确,符合题意;
D.与不是同类项,不能合并,故选项错误,不符合题意.
故答案为:A.
分别根据同底数幂的乘法、同底数幂的除法、积的乘方和幂的乘方、合并同类项的基本算理计算即可判断.
11.或
解:,
,解得:或.
故答案为:或.
根据完全平方公式的结构特征列方程,求出的值即可.
12.
解:过点E作EF∥AB,如图所示.
∵AB∥CD,EF∥AB,
∴EF∥CD∥AB,
∴∠α+∠AEF=180°,∠γ=∠CEF.
∴∠α+∠AEF+∠CEF=180°+∠γ,
又∵∠AEF+∠CEF=∠β,
∴∠α+∠β ∠γ=180°.
故答案为:∠α+∠β ∠γ=180°.
由平行线公理“平行于同一直线的两直线互相平行”可得出EF∥CD∥AB,再根据“两直线平行,内错角相等(同旁内角互补)”得∠α+∠AEF=180°,∠γ=∠CEF,根据整式性质将两式相加得∠α+∠AEF+∠CEF=180°+∠γ,再将∠AEF+∠CEF=∠β整体代入变形即可得出结论.
13.
14.
解:设原长方形队阵中有同学(为正整数)人,则由已知与均为完全平方数,
设正方形方阵的边长分别为m,n,可得其中m,n为正整数.
两式相减,得,
即.
∵,
和同奇或同偶,
∴或,
解得或
当时,,,
当时,,,不合题意,舍去;
故原长方形队阵中有同学人.
故答案为:.
设原长方形队阵中有同学(为正整数)人,设正方形方阵的边长分别为m,n列关系式,然后两式相减得到,根据平方差公式分解因式解题即可.
15.
16.①②
解:设正方形的边长为,正方形的边长为,正方形的边长为,
,
阴影的长为,宽为,
阴影的长为,宽为,
∵阴影的周长为10,
,
,
即,故①正确;
∵阴影周长为8,
,
解得:,
,
,
即正方形的面积为1,故②正确;
∵大长方形的面积为30,
,
,
,
,
假设三个正方形的周长为24,
,
,
(不成立),
∴若大长方形的面积为30,则三个正方形周长的和为24.故③错误,
故答案为:①②.
设正方形的边长为,正方形的边长为,正方形的边长为,即可得到,表示阴影、阴影的长和宽,根据阴影的周长求出值判定①;根据阴影周长求出值,进而得到的值判定②;根据大长方形的面积为30,得到,设三个正方形的周长为24,解得判定③解题.
17.(1)6
(2)
18.(1)解:,
将代入得:,
解得:,
将代入得:,
原方程组的解为:;
(2)解:整理得:,
由得:,
解得:,
将代入得:,
解得:,
原方程组的解为:.
本题考查解二元一次方程组.
(1)根据方程组中②方程的特点,此题使用代入消元法较为简单,首先将②代入①消去x求出y的值,再将y的值代入②方程可求出x的值,从而即可求出方程组的解;
(2)先将方程组整理成一般形式,观察可得y的系数互为相反数,利用加减消元法两个方程相加,可消去y,求出x的值,进而将x的值代入①方程求出y的值,从而即可解出二元一次方程组.
19.已知;;两直线平行,同位角相等;两直线平行,内错角相等.
证明:∵(已知),
∴(同旁内角互补,两直线平行).
∴(两直线平行,同位角相等).
又∵(已知),
∴(等量代换).
∴(内错角相等,两直线平行),
∴(两直线平行,内错角相等).
故答案为:已知;;两直线平行,同位角相等;两直线平行,内错角相等.
根据平行线的判定和性质进行填空即可解决问题.
20.(1)解:由直角坐标系可知,、,
三角形ABC向左平移5个单位长度,再向下平移2个单位长度,得到平移后的三角形A'B'C',
、,
,,
三角形A'B'C'即为所求;
(2)
解:(2)设P(a,b),则P′(a-5,b-2).
∵P′(-2,1),
∴a-5=-2,b-2=1,
∴a=3,b=3,
∴P(3,3).
故答案为:(3,3).
(1)根据点A、A′的坐标可得平移步骤为:先向左平移5个单位长度,再向下平移2个单位长度,据此找出点B′、C′的位置,顺次连接可得△A′B′C′,进而可得点B′、C′的坐标;
(2)设P(a,b),根据点的坐标的平移规律“横坐标左减右加,纵坐标上加下减”可得P′(a-5,b-2),然后结合点P′的坐标可得a、b的值,据此可得点P的坐标.
21.(1)解:设甲种套餐的单价为元,则乙种套餐的单价为元,
根据题意得:,
解得,
经检验,是原方程的解,
,
甲种套餐的单价为元,乙种套餐的单价为元;
(2)解:设甲种套餐购进套,乙种套餐购进套,
根据题意得,
,
,为正整数,
或或,
有三种进货方案:甲种套餐购进套,乙种套餐购进套或甲种套餐购进套,乙种套餐购进套或甲种套餐购进套,乙种套餐购进套.
(1)设甲种套餐的单价为x元,根据用450元购买甲套餐和用810元购买乙套餐的个数相同列出分式方程得:,解方程并检验得出答案;
(2)设甲种套餐购进m套,乙种套餐购进n套,根据题意列出二元一次方程得50m+90n=1800,求出方程的正整数解即可
22.(1)50,图见解析
(2)100.8
(3)解:人.
答:选择“蔬果”作为主要食材的学生约有144人.
【解答 】(1)七年级2班学生总人数为(人),
高蛋白人数为(人),
补全图形如下:
故答案为:50;
(2)
“谷物”所对应的扇形圆心角度数为,
故答案为:100.8;
(1)观察两个统计图,可由豆类人数及其所占百分比求得总人数,再用总人数乘以高蛋白对应百分比求出其人数,从而补全图形;
(2)用乘以谷物数量所占比例即可;
(3)总人数乘以样本中蔬果数量所占比例即可.
(1)七年级2班学生总人数为(人),
高蛋白人数为(人),
补全图形如下:
故答案为:50;
(2)“谷物”所对应的扇形圆心角度数为,
故答案为:100.8;
(3)人.
答:选择“蔬果”作为主要食材的学生约有144人.
23.(1)
(2)解:①∵长方形纸片沿直线折叠,∴
∵,
∵CN∥DM
即70°+70°+∠AMD=180°
∴∠AMD=40°
②由①知:
∵,
在三角形MNE中
∴
解:(1)∵长方形纸片沿直线折叠,
∴AD∥BC,∠MEN=∠ CNE=90°,
∴;
故答案为:45°.
(1)根据垂直的定义,平行线的性质,得到,再根据折痕是角平分线,求出的度数即可;
(2)①折叠的性质,得到,平行得到=,,再根据角的和差关系进行求解即可;
②根据问题①中得到和三角形的内角和定理求解即可.
(1)解:∵长方形纸片沿直线折叠,
∴,
∵,
∴,
∴,
∴;
(2)①∵折叠,
∴,,
∵,
∴,
∴;
②由①知:,
∵,且,
∴,
∴.
24.解:任务一:设制作一个甲款雪花模型需要长管子x根,制作一个乙款雪花模型需要长管子y根,根据题意得:
,
解得:,
∴,,
答:制作一个甲款雪花模型需要长管子3根,短管子21根;制作一个乙款雪花模型需要长管子3根,短管子根;
任务二:由题意得:
∴,
解得:,
经检验是原方程的根;
∵制作一个甲款雪花模型需要长管子3根,短管子21根,且6月1日起购买3根长管子赠送一根短管子,
∴制作一个甲款雪花模型需要的费用为:(元);
任务三:设学校中采购了m根长管子,n根短管子,根据题意得:
,
解得:,
∵一款甲款雪花和一款乙款雪花都需要3根长管子,
∴m根长管子可制作两款雪花模型共个,
∴需要的短管子数量最少为个,最多为个,可得,
∵商店中长管子仅剩267根,短管子仅剩2130根,
∴,
解得:,
∵m必须能被3整除,
∴,,264,267.
当时,,,
∴可以购买258根长管子,2130根短管子,能制作甲、乙两款雪花模型共86个;
当时,,,
∴可以购买261根长管子,2125根短管子,能制作甲、乙两款雪花模型共87个;
当时,,,
∴可以购买264根长管子,2120根短管子,能制作甲、乙两款雪花模型共88个;
当时,,,
∴可以购买267根长管子,2115根短管子,能制作甲、乙两款雪花模型共89个;
86<87<88<89,
∴当购买267根长管子,2115根短管子时,制作的雪花模型最多.
任务一:设制作一个甲款雪花模型需要长管子x根,制作一个乙款雪花模型需要长管子y根,根据题意“6根长管子、48根短管子制作了1个甲雪花模型与1个乙雪花模型”,“ 制作一个甲、乙款雪花模型需要的长、短管子数分别为与 ”,列出方程组并求解即可;
任务二:根据题意得等量关系:花费320元购得的长管子数量+80=花200元购得的短管子数量,据此列出关于a的方程,解方程即可得a的值;根据a的值和6月份的优惠方案即可求出制作一个甲款雪花模型需要的费用即可;
任务三:设学校中采购了m根长管子,n根短管子,根据总费用1280元可列出方程,得出, 制作一个甲、乙款雪花模型需要的长、短管子数分别为与 ”可得;再根据商店中长管子仅剩267根,短管子仅剩2130根,可列出不等式组,求出,根据m必须能被3整除,得出m的能取得的值,再分别计算对应的n和的值,即可得出所有的购买方案.
2024-2025学年七年级下册期末模拟卷(台州市专用)
数 学
(考试范围:七下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列学校校徽可以看成是由图案自身的一部分经平移后得到的为( )
A. B.
C. D.
2.下列是二元一次方程的是( )
A. B. C. D.
3.关于的分式方程无解,则的值是( )
A.1 B.3 C.或 D.或
4.要调查某校七年级学生周一到周五平均每天的睡眠时间,选取调查对象最合适的是( )
A.选取该校七年级一个班级的学生
B.选取60名该校的七年级女生
C.选取60名该校的七年级男生
D.随机选取60名该校的七年级学生
5.如图,已知直线a与直线b被第三条直线c所截,则的内错角是( )
A. B. C. D.
6.若,则等于( )
A.1 B. C. D.6
7.一个宾馆有二人间、三人间、四人间三种客房供游客租住,某旅行团25人准备同时租用这三种客房共9间,如果每个房间都住满,则租房方案共有( )
A.4种 B.3种 C.2种 D.1种
8.某电瓶车厂根据去年第三、四季度各月产量,制作了统计图.根据图中信息,可以判断相邻两个月中,月产量增长最大的是( )
A.月到月 B.月到月 C.月到月 D.月到月
9.如图,,点在上,,的延长线交的延长线于点,则图中与相等的角(不含)共有( )
A.7个 B.6个 C.5个 D.4个
10.下列计算正确的是( )
A. B. C. D.
二、填空题(本题有6小题,每小题3分,共18分)
11.若是一个完全平方式,则的值为 .
12.如图,若,则、、之间的关系为 .
13.光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,在水中平行的光线,在空气中也是平行的.如图是从玻璃杯底部发出的一束平行光线经过水面折射形成的光线示意图.若,,则 .
14.某校举行运动会时,由若干名同学组成一个13列的长方形彩旗队阵.如果原队阵中增加16人,能组成一个正方形队阵;如果原队阵中减少16人,也能组成一个正方形队阵,则原长方形彩旗队阵中有同学 人.
15.将45个数据分成6组,第一到第四组的频数分别为9,7,8,6,第五组的频率为0.2,则第六组的频数是 .
16.如图,长为,宽为的大长方形被分割为5小块,除阴影外,其余3块都是正方形,若阴影周长为10,下列结论:①的值为5;②若阴影的周长为8,则正方形的面积为1;③若大长方形的面积为30,则三个正方形周长的和为24.其中正确的是 .
三、解答题 (本题有 8 小题, 第17-21题每题 8 分, 第 22,23 题每题 10 分, 第 24 题 12 分, 共 72 分)
17.计算:
(1).
(2).
18.解方程组:
(1);
(2).
19.请将下列证明过程补充完整.
如图,已知,.
求证:.
证明:∵( ),
∴ (同旁内角互补,两直线平行).
∴( ).
又∵(已知),
∴(等量代换).
∴(内错角相等,两直线平行),
∴( ).
20.如图,在平面直角坐标系中,有一个三角形,点的坐标是,现将三角形平移,使点A变换为点,点,分别是点B,C的对应点.
(1)请画出平移后的三角形(不写画法),并直接写出点,的坐标;
(2)若三角形内部有一点P,其平移后的对应点为,则点P的坐标是 .
21.临近期末,班级想给优秀的学生准备奖品,奖品分为甲套餐与乙套餐,已知购买个甲套餐比购买个乙套装少用元,用元购买甲套餐和用元购买乙套餐的个数相同.
(1)求这两种套餐的单价分别为多少元;
(2)班级计划用元经费购进甲套餐与乙套餐两种奖品,要求每种套餐至少购进种且刚好用完经费,请你设计进货方案.
22.某校在市卫生健康局、教育局联合举办的“5.20中国学生营养日”活动带领下举行了七年级学生“健康菜谱”设计活动,让学生能设计一份健康菜谱,菜谱需符合“减油、增豆、加奶”的原则.现收集了七年级2班同学们设计的菜谱,并将菜中的主要食材分类、整理成图表,下面给出了部分信息:
根据以上信息回答下列问题:
(1)七年级2班共有______人,并补全条形统计图
(2)“谷物”所对应的扇形圆心角度数为______度.
(3)若该校七年级学生共1200人,则选择“蔬果”作为主要食材的学生约有多少人?
23.如图1,将长方形纸片沿直线折叠,点,的对应点分别为点,,折叠后与交于点.
(1)若,直接写出的度数.
(2)如图2,设.
①若,求的度数.
②若,求的值.
24.根据素材,完成任务.
如何设计雪花模型材料采购方案?
素 材 一 学校组织同学参与甲、乙两款雪花模型的制作.每款雪花模型都需要用到长、短两种管子材料.某同学用6根长管子、48根短管子制作了1个甲雪花模型与1个乙雪花模型.已知制作一个甲、乙款雪花模型需要的长、短管子数分别为与.
素 材 二 某商店的店内广告牌如右所示.5月,学校花费320元向该商店购得的长管子数量比花200元购得的短管子数量少80根. 1.短管子售价:a元/根,长管子售价:元/根 2.6月1日起,购买3根长管子赠送1根短管子. 3.本店库存数量有限,长管子仅剩267根,短管子仅剩2130根,先到先得!
素 材 三 6月,学校有活动经费1280元,欲向该商店采购长、短管子各若干根全部用来制作甲、乙雪花模型(材料无剩余),且采购经费恰好用完.
问题解决
任 务 一 分析雪花模型结构 求制作一个甲、乙款雪花模型分别需要长、短管子多少根?
任 务 二 确定采购费用 试求a的值并求出假如6月只制作一个甲款雪花模型的材料采购费.
任 务 三 拟定采购方案 求出所有满足条件的采购方案,并指出哪种方案得到的雪花总数最多.
答案解析部分
1.C
解:A、是一个轴对称图形,可以看成是由图案自身的一部分经轴对称得到,故不符合题意;
B、是一个没有规律的图形,故不可以看成是由图案自身的一部分经平移后得到,故不符合题意;
C、可以看做是图案自身的一部分沿着直线运动得到,故符合题意;
D、是一个轴对称图形,可以看成是由图案自身的一部分经轴对称得到,故不符合题意;
故答案为:C.
根据平移的定义和平移不改变图形的形状和大小的性质,结合图案,对选项逐一分析,即可排除错误答案.
2.B
A.是分式方程,不是二元一次方程,不符合题意;
B.是二元一次方程,符合题意;
C.含未知数项的最高次数为二次,不是二元一次方程,不符合题意;
D.含未知数项的最高次数为二次,不是二元一次方程,不符合题意.
故答案为:B.
二元一次方程是指含有两个未知数,并且所含未知数的项的次数都是1的整式方程,据此判断.
3.D
解:去分母得:,
,
当,即时,,此时整式方程无解,分式方程无解,
当,即时,由得,
把代入得:,
解得:,
关于的分式方程无解时,或,
故选:D.
去分母化为整式方程,根据分整式方程无解、整式方程的解是分式方程的增根两种情况解答即可.
4.D
解:只选取一个班级的学生不具有代表性,故A不符合题意;
只选取女生不具有代表性,故B不符合题意;
只选取男生不具有代表性,故C不符合题意;
随机选取该校七年级60名学生,符合抽样调查的样本要求,故D符合题意.
故答案为:D.
根据抽样调查的意义,对四个选项逐一分析,再作出判断.
5.B
6.C
解:,
.
故选:C.
根据同底数幂的除法和幂的乘方的逆算解答即可.
7.B
解:设宾馆有客房:二人间x间、三人间y间、四人间z间,根据题意得:
解得:y+2z=7,
y=7﹣2z,
∵x,y,z都是小于9的正整数,
当z=1时,y=5,x=3;
当z=2时,y=3,x=4;
当z=3时,y=1,x=5
当z=4时,y=﹣1(不符合题意,舍去)
∴租房方案有3种.
故选:B.
首先设宾馆有客房:二人间x间、三人间y间、四人间z间,根据题意可得方程组:,解此方程组可得y+2z=7,又由x,y,z是非负整数,即可求得答案.
8.D
、月到月增加了(辆),
、月到月增加了(辆),
、月到月增加了(辆),
、月到月增加了(辆),
∴月产量增长最大的是月到月,
故答案为:.
根据统计图,计算相邻两个月销售额的差,然后比较解题.
9.B
∵AB∥EF, ∴∠AGE=∠GEF, ∠GBP=∠BPF
∵EF∥CD, ∴∠GEF=∠EHC, ∠PCD=∠EPC=∠BPF,
∵GE∥BC, ∴∠EHC=∠BCD,
∴∠AGE =∠GEF=∠EHC=∠BCD=∠EPC=∠BPF=∠GBP.
共6个角与∠AGE相等.
故选:B
两直线平行、同位角相等、内错角相等,则∠AGE=∠GEF=∠EHC=∠BCD=∠EPC=∠BPF=∠GBP.
10.C
解:A.,故选项错误,不符合题意;
B.,故选项错误,不符合题意;
C.,故选项正确,符合题意;
D.与不是同类项,不能合并,故选项错误,不符合题意.
故答案为:A.
分别根据同底数幂的乘法、同底数幂的除法、积的乘方和幂的乘方、合并同类项的基本算理计算即可判断.
11.或
解:,
,解得:或.
故答案为:或.
根据完全平方公式的结构特征列方程,求出的值即可.
12.
解:过点E作EF∥AB,如图所示.
∵AB∥CD,EF∥AB,
∴EF∥CD∥AB,
∴∠α+∠AEF=180°,∠γ=∠CEF.
∴∠α+∠AEF+∠CEF=180°+∠γ,
又∵∠AEF+∠CEF=∠β,
∴∠α+∠β ∠γ=180°.
故答案为:∠α+∠β ∠γ=180°.
由平行线公理“平行于同一直线的两直线互相平行”可得出EF∥CD∥AB,再根据“两直线平行,内错角相等(同旁内角互补)”得∠α+∠AEF=180°,∠γ=∠CEF,根据整式性质将两式相加得∠α+∠AEF+∠CEF=180°+∠γ,再将∠AEF+∠CEF=∠β整体代入变形即可得出结论.
13.
14.
解:设原长方形队阵中有同学(为正整数)人,则由已知与均为完全平方数,
设正方形方阵的边长分别为m,n,可得其中m,n为正整数.
两式相减,得,
即.
∵,
和同奇或同偶,
∴或,
解得或
当时,,,
当时,,,不合题意,舍去;
故原长方形队阵中有同学人.
故答案为:.
设原长方形队阵中有同学(为正整数)人,设正方形方阵的边长分别为m,n列关系式,然后两式相减得到,根据平方差公式分解因式解题即可.
15.
16.①②
解:设正方形的边长为,正方形的边长为,正方形的边长为,
,
阴影的长为,宽为,
阴影的长为,宽为,
∵阴影的周长为10,
,
,
即,故①正确;
∵阴影周长为8,
,
解得:,
,
,
即正方形的面积为1,故②正确;
∵大长方形的面积为30,
,
,
,
,
假设三个正方形的周长为24,
,
,
(不成立),
∴若大长方形的面积为30,则三个正方形周长的和为24.故③错误,
故答案为:①②.
设正方形的边长为,正方形的边长为,正方形的边长为,即可得到,表示阴影、阴影的长和宽,根据阴影的周长求出值判定①;根据阴影周长求出值,进而得到的值判定②;根据大长方形的面积为30,得到,设三个正方形的周长为24,解得判定③解题.
17.(1)6
(2)
18.(1)解:,
将代入得:,
解得:,
将代入得:,
原方程组的解为:;
(2)解:整理得:,
由得:,
解得:,
将代入得:,
解得:,
原方程组的解为:.
本题考查解二元一次方程组.
(1)根据方程组中②方程的特点,此题使用代入消元法较为简单,首先将②代入①消去x求出y的值,再将y的值代入②方程可求出x的值,从而即可求出方程组的解;
(2)先将方程组整理成一般形式,观察可得y的系数互为相反数,利用加减消元法两个方程相加,可消去y,求出x的值,进而将x的值代入①方程求出y的值,从而即可解出二元一次方程组.
19.已知;;两直线平行,同位角相等;两直线平行,内错角相等.
证明:∵(已知),
∴(同旁内角互补,两直线平行).
∴(两直线平行,同位角相等).
又∵(已知),
∴(等量代换).
∴(内错角相等,两直线平行),
∴(两直线平行,内错角相等).
故答案为:已知;;两直线平行,同位角相等;两直线平行,内错角相等.
根据平行线的判定和性质进行填空即可解决问题.
20.(1)解:由直角坐标系可知,、,
三角形ABC向左平移5个单位长度,再向下平移2个单位长度,得到平移后的三角形A'B'C',
、,
,,
三角形A'B'C'即为所求;
(2)
解:(2)设P(a,b),则P′(a-5,b-2).
∵P′(-2,1),
∴a-5=-2,b-2=1,
∴a=3,b=3,
∴P(3,3).
故答案为:(3,3).
(1)根据点A、A′的坐标可得平移步骤为:先向左平移5个单位长度,再向下平移2个单位长度,据此找出点B′、C′的位置,顺次连接可得△A′B′C′,进而可得点B′、C′的坐标;
(2)设P(a,b),根据点的坐标的平移规律“横坐标左减右加,纵坐标上加下减”可得P′(a-5,b-2),然后结合点P′的坐标可得a、b的值,据此可得点P的坐标.
21.(1)解:设甲种套餐的单价为元,则乙种套餐的单价为元,
根据题意得:,
解得,
经检验,是原方程的解,
,
甲种套餐的单价为元,乙种套餐的单价为元;
(2)解:设甲种套餐购进套,乙种套餐购进套,
根据题意得,
,
,为正整数,
或或,
有三种进货方案:甲种套餐购进套,乙种套餐购进套或甲种套餐购进套,乙种套餐购进套或甲种套餐购进套,乙种套餐购进套.
(1)设甲种套餐的单价为x元,根据用450元购买甲套餐和用810元购买乙套餐的个数相同列出分式方程得:,解方程并检验得出答案;
(2)设甲种套餐购进m套,乙种套餐购进n套,根据题意列出二元一次方程得50m+90n=1800,求出方程的正整数解即可
22.(1)50,图见解析
(2)100.8
(3)解:人.
答:选择“蔬果”作为主要食材的学生约有144人.
【解答 】(1)七年级2班学生总人数为(人),
高蛋白人数为(人),
补全图形如下:
故答案为:50;
(2)
“谷物”所对应的扇形圆心角度数为,
故答案为:100.8;
(1)观察两个统计图,可由豆类人数及其所占百分比求得总人数,再用总人数乘以高蛋白对应百分比求出其人数,从而补全图形;
(2)用乘以谷物数量所占比例即可;
(3)总人数乘以样本中蔬果数量所占比例即可.
(1)七年级2班学生总人数为(人),
高蛋白人数为(人),
补全图形如下:
故答案为:50;
(2)“谷物”所对应的扇形圆心角度数为,
故答案为:100.8;
(3)人.
答:选择“蔬果”作为主要食材的学生约有144人.
23.(1)
(2)解:①∵长方形纸片沿直线折叠,∴
∵,
∵CN∥DM
即70°+70°+∠AMD=180°
∴∠AMD=40°
②由①知:
∵,
在三角形MNE中
∴
解:(1)∵长方形纸片沿直线折叠,
∴AD∥BC,∠MEN=∠ CNE=90°,
∴;
故答案为:45°.
(1)根据垂直的定义,平行线的性质,得到,再根据折痕是角平分线,求出的度数即可;
(2)①折叠的性质,得到,平行得到=,,再根据角的和差关系进行求解即可;
②根据问题①中得到和三角形的内角和定理求解即可.
(1)解:∵长方形纸片沿直线折叠,
∴,
∵,
∴,
∴,
∴;
(2)①∵折叠,
∴,,
∵,
∴,
∴;
②由①知:,
∵,且,
∴,
∴.
24.解:任务一:设制作一个甲款雪花模型需要长管子x根,制作一个乙款雪花模型需要长管子y根,根据题意得:
,
解得:,
∴,,
答:制作一个甲款雪花模型需要长管子3根,短管子21根;制作一个乙款雪花模型需要长管子3根,短管子根;
任务二:由题意得:
∴,
解得:,
经检验是原方程的根;
∵制作一个甲款雪花模型需要长管子3根,短管子21根,且6月1日起购买3根长管子赠送一根短管子,
∴制作一个甲款雪花模型需要的费用为:(元);
任务三:设学校中采购了m根长管子,n根短管子,根据题意得:
,
解得:,
∵一款甲款雪花和一款乙款雪花都需要3根长管子,
∴m根长管子可制作两款雪花模型共个,
∴需要的短管子数量最少为个,最多为个,可得,
∵商店中长管子仅剩267根,短管子仅剩2130根,
∴,
解得:,
∵m必须能被3整除,
∴,,264,267.
当时,,,
∴可以购买258根长管子,2130根短管子,能制作甲、乙两款雪花模型共86个;
当时,,,
∴可以购买261根长管子,2125根短管子,能制作甲、乙两款雪花模型共87个;
当时,,,
∴可以购买264根长管子,2120根短管子,能制作甲、乙两款雪花模型共88个;
当时,,,
∴可以购买267根长管子,2115根短管子,能制作甲、乙两款雪花模型共89个;
86<87<88<89,
∴当购买267根长管子,2115根短管子时,制作的雪花模型最多.
任务一:设制作一个甲款雪花模型需要长管子x根,制作一个乙款雪花模型需要长管子y根,根据题意“6根长管子、48根短管子制作了1个甲雪花模型与1个乙雪花模型”,“ 制作一个甲、乙款雪花模型需要的长、短管子数分别为与 ”,列出方程组并求解即可;
任务二:根据题意得等量关系:花费320元购得的长管子数量+80=花200元购得的短管子数量,据此列出关于a的方程,解方程即可得a的值;根据a的值和6月份的优惠方案即可求出制作一个甲款雪花模型需要的费用即可;
任务三:设学校中采购了m根长管子,n根短管子,根据总费用1280元可列出方程,得出, 制作一个甲、乙款雪花模型需要的长、短管子数分别为与 ”可得;再根据商店中长管子仅剩267根,短管子仅剩2130根,可列出不等式组,求出,根据m必须能被3整除,得出m的能取得的值,再分别计算对应的n和的值,即可得出所有的购买方案.
同课章节目录
