2024-2025学年七年级下学期数学期考末模拟卷(浙江温州市专用)[答案+解析]
文档属性
| 名称 | 2024-2025学年七年级下学期数学期考末模拟卷(浙江温州市专用)[答案+解析] |  | |
| 格式 | docx | ||
| 文件大小 | 397.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 12:29:20 | ||
图片预览



文档简介
保密★启用前
2024-2025学年七年级下册期末模拟卷(温州市专用)
数 学
(考试范围:七下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列方程中,是二元一次方程的是( )
A. B. C. D.
2.如图.已知直线,将一块含角的直角三角板按如图方式放置()其中点A,B分别落在直线a、b上.若,则的度数为( )
A. B. C. D.
3.已知直线 , 将一块含 角的直角三角板按如图方式放置, 其中 角的顶点在直线 上, 角的顶点在直线 上, 若 , 则 的度数是( )
A. B. C. D.
4.为配合大阅读活动,学校对全校学生阅读兴趣调查的数据进行整理,要反映学生感兴趣的各类图书所占百分比,最适合的统计图是( )
A.条形统计图 B.频数直方图 C.折线统计图 D.扇形统计图
5.已知,,则的值为( )
A.16 B.4 C. D.
6.要使分式有意义,的取值应满足( )
A. B. C. D.
7.已知是二元一次方程的一个解,则a的值为( )
A.-1 B.1 C.-2 D.2
8.已知关于 的二次三项式 分解因式的结果为 , 则 和 的值分别是( )
A. B. C. D.
9.科学家发现人体最小的细胞是淋巴细胞, 直径约为 0.0000061 米, 将数据 0.0000061 用科学记数法表示正确的是 ( )
A. B. C. D.
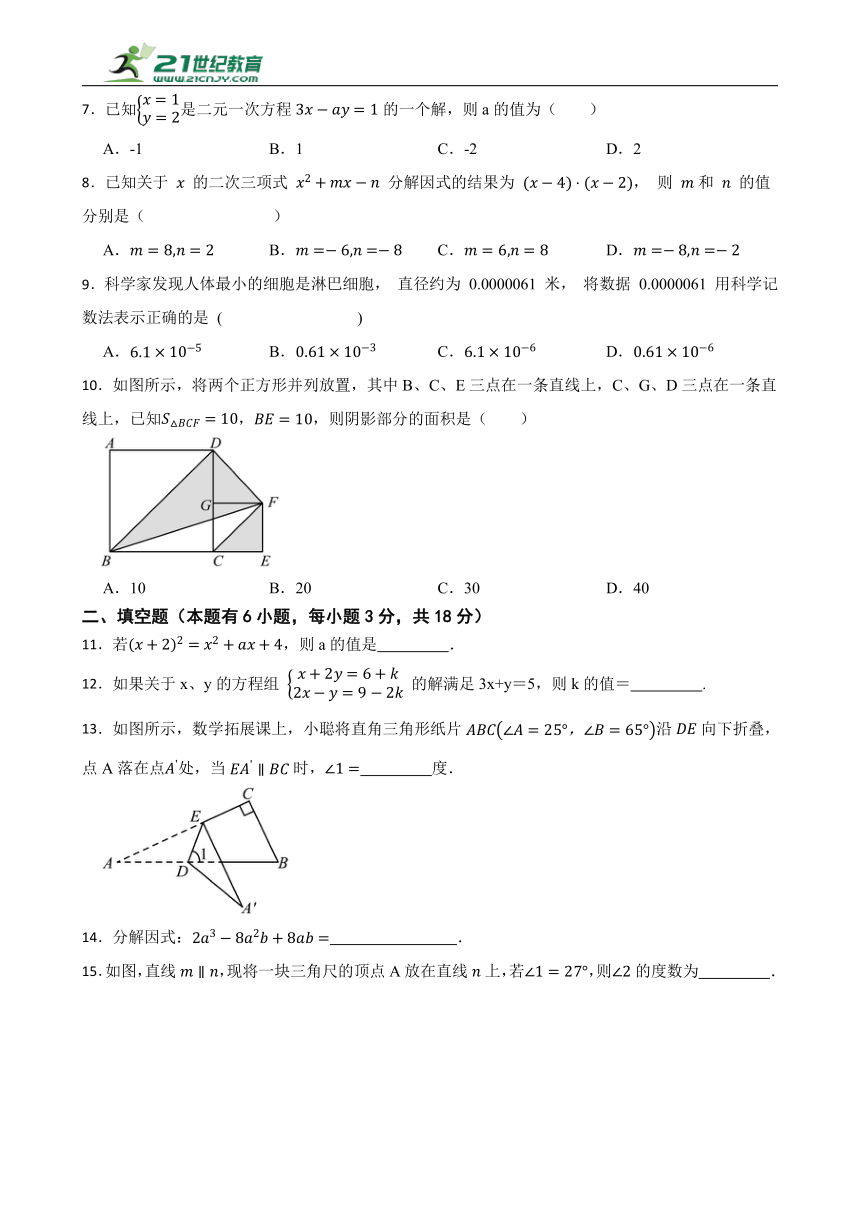
10.如图所示,将两个正方形并列放置,其中B、C、E三点在一条直线上,C、G、D三点在一条直线上,已知,,则阴影部分的面积是( )
A.10 B.20 C.30 D.40
二、填空题(本题有6小题,每小题3分,共18分)
11.若,则a的值是 .
12.如果关于x、y的方程组 的解满足3x+y=5,则k的值= .
13.如图所示,数学拓展课上,小聪将直角三角形纸片沿向下折叠,点A落在点处,当时, 度.
14.分解因式: .
15.如图,直线,现将一块三角尺的顶点A放在直线上,若,则的度数为 .
16. A, B 两市相距 200 km , 甲车从 A 市到 B 市, 乙车从 B 市到 A 市, 两车同时出发, 已知甲车速度比乙车速度快 , 且甲车比乙车早半小时到达目的地, 若设乙车的速度是 x , 则根据题意, 可列方程为 .
三、解答题(本题有7小题,共72分. 解答需写出必要的文字说明、演算步骤或说理过程)
17.计算:
(1);
(2).
18.解方程 (组)
(1)
(2) .
19.已知关于x的分式方程.
(1)当时,求这个分式方程的解;
(2)若此分式方程无解,求的值.
20.临近期末,班级想给优秀的学生准备奖品,奖品分为甲套餐与乙套餐,已知购买个甲套餐比购买个乙套装少用元,用元购买甲套餐和用元购买乙套餐的个数相同.
(1)求这两种套餐的单价分别为多少元;
(2)班级计划用元经费购进甲套餐与乙套餐两种奖品,要求每种套餐至少购进种且刚好用完经费,请你设计进货方案.
21.如图,在中,平分,.
(1)试判断与的位置关系,并说明理由.
(2)若,且,求的度数.
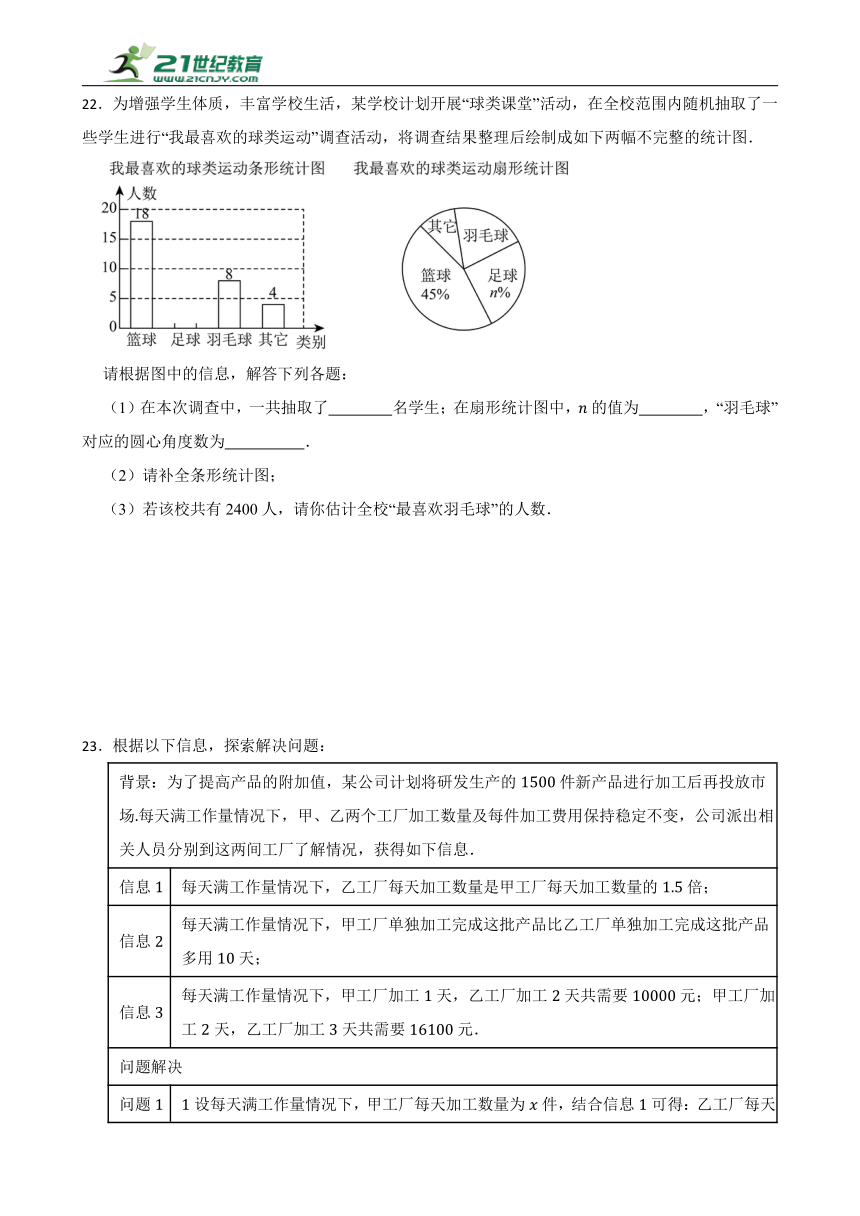
22.为增强学生体质,丰富学校生活,某学校计划开展“球类课堂”活动,在全校范围内随机抽取了一些学生进行“我最喜欢的球类运动”调查活动,将调查结果整理后绘制成如下两幅不完整的统计图.
请根据图中的信息,解答下列各题:
(1)在本次调查中,一共抽取了 名学生;在扇形统计图中,的值为 ,“羽毛球”对应的圆心角度数为 .
(2)请补全条形统计图;
(3)若该校共有2400人,请你估计全校“最喜欢羽毛球”的人数.
23.根据以下信息,探索解决问题:
背景:为了提高产品的附加值,某公司计划将研发生产的件新产品进行加工后再投放市场每天满工作量情况下,甲、乙两个工厂加工数量及每件加工费用保持稳定不变,公司派出相关人员分别到这两间工厂了解情况,获得如下信息.
信息 每天满工作量情况下,乙工厂每天加工数量是甲工厂每天加工数量的倍;
信息 每天满工作量情况下,甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用天;
信息 每天满工作量情况下,甲工厂加工天,乙工厂加工天共需要元;甲工厂加工天,乙工厂加工天共需要元.
问题解决
问题 设每天满工作量情况下,甲工厂每天加工数量为件,结合信息可得:乙工厂每天加工数量为 件请用的代数式表示.
问题 每天满工作量情况下,求甲工厂每天能加工多少件新产品?
问题 公司将件新产品交给甲、乙两工厂一起加工,发现这批新产品的平均加工费用为整数,两工厂加工的时间之和不是整数请问交给甲工厂多少件新产品进行加工?
答案解析部分
1.A
解:A、含有两个未知数,且未知数的次数都是1,是二元一次方程,故符合题意;
B、不是整式方程,故不符合题意;
C、含有两个未知数,未知数的最高次数是2,不是二元一次方程,故不符合题意;
D、未知数的最高次数是2,不是二元一次方程,故不符合题意;
故答案为:A.
依据二元一次方程的定义“含有两个未知数,且含未知数的项的次数是1次的方程称为二元一次方程”,逐一判断即可.
2.B
解:如图所示,
根据题意可知:,(已知),
∴∠1+∠3=90°,
∵,
∴,
∵(已知),
∴(两直线平行,同位角相等),
故答案为:B.
根据平角的定义求出,然后利用两直线平行,同位角相等,得出∠2=∠3,即可得出答案.
3.C
解:如图:作直线c∥a
∴∠1=∠4=40°
∴∠3=90°-∠4=90°-40°=50°
∵a∥b
∴c∥b
∴∠2=∠3=50°
故答案为:C.
作直线c∥a,得到∠1=∠4=40°,再根据∠3+∠4=90°,求出∠3的度数,再根据平行于同一条直线的两条直线也平行,得出:c∥b,从而∠2=∠3=50°.
4.D
解: 要反映学生感兴趣的各类图书所占百分比,最适合的统计图是 扇形统计图
故选C.
扇形统计图反映了部分占总体的百分比.
5.D
6.D
解:由题意,得:,
∴;
故选:D.
根据分式的分母不为0时,分式有意义,即进行求解即可
7.B
解:∵是二元一次方程3x-ay=1的一个解,
∴3×1-2a=1,
解得a=1.
故答案为:B.
根据方程解的概念,将x=1、y=2代入方程中进行计算就可求出a的值.
8.B
解:∵
∴m=-6,-n=8
∴m=-6,n=-8
故答案为:B.
根据题意,先把进行展开,得到:,故=,得出:.
9.C
解: 0.0000061 =,故答案为A.
绝对值小于1的数科学记数法可以表示为:,其中1≤a∠10,n取从左边数第一个非0数前0的个数,包括小数点前面的0.
10.C
解:设小正方形的边长为x,大正方形的边长为y,
,,
,,
∴阴影部分的面积等于,
∴,
,
故答案为:C.
先得出,,再利用几何图形得到阴影部分的面积等于,列出算式,利用完全平方公式变形后求解.
11.4
12.10
解: ,①+②得:3x+y=15-k,∴15-k=5,解得:k=10.故答案为10.
将两方程相加可得3x+y=15-k,结合3x+y=5,可得15-k=5,求出k值即可.
13.70
解:如图所示:
∵,
∴,∠B=∠2,
∵∠B=65°,
∴∠2=65°,
由折叠可知:==45°,
∴∠1=180°-∠A'ED-∠2=180°-45°-65°=70°,
故答案为:70.
根据易得,∠B=∠2,然后根据折叠可知:=45°,最后利用三角形内角和即可求出∠1.
14.
解:
,
,
故答案为:.
运用提取公因式的方法进行因式分解即可,因式分解常用的方法有:①提公因式法;②公式法;③十字相乘法;④分组分解法.因式分解必须分解到每个因式都不能再分解为止.
15.
解:如图,作,
∴,
∵,
∴,
∵ ,
∴,
∵,
∴,
∴,
故答案为:.
作,利用平行线的性质可知,根据平行公理的推论证明得到,得到,进而得到,即可求出.
16..
解:由题意可列:
故答案为:.
设乙车的速度是 x , 则甲车的速度为(x+15),根据等量关系:,列出方程即可.
17.(1)解:原式
;
(2)解:原式
.
18.(1)解:
①+②得:4x=8,解得:x=2
把x=2代入②得:2+2y=6,解得y=2
∴是原方程组的解.
(2)解:
∴3x=9
∴x=3
把x=3代入x-3中得:3-3=0
∴原方程无解.
19.(1)解:当m=-1时,
原方程为:
方程两边同乘(1-x),得:2=x-2(1-x),
去括号,得:,
移项、合并同类项,得:,
解得:,
检验:将代入(1-x)得:,
是原分式方程的解;
(2)解:
方程两边同乘(1-x),得:2=-mx-2(1-x),
整理得:(2-m)x=4,
∴当2-m=0时,即m=2时,原分式方程无解,
当2-m≠0时,即m≠2时,原分式方程无解,
则x-1=0,即x=1,
此时,m=-2,
综上所述,当m=2或m=-2时,原分式方程无解.
(1)利用去分母将分式方程转化为整式方程,求出的值后进行检验即;
(2)用去分母将分式方程转化为整式方程,然后根据分式方程无解进行分类讨论即可.
(1)解:把代入分式方程得:,
整理得:,
去分母,得:,
去括号,得:,
移项、合并同类项,得:,
解得:,
检验:把代入得:,
是分式方程的解;
(2)分式方程变形得:,
去分母,得:,即,
若,即时,此方程无解,即分式方程无解;
若,即时,
分式方程无解,
,即,
把代入整式方程得:,
综上所述,或.
20.(1)解:设甲种套餐的单价为元,则乙种套餐的单价为元,
根据题意得:,
解得,
经检验,是原方程的解,
,
甲种套餐的单价为元,乙种套餐的单价为元;
(2)解:设甲种套餐购进套,乙种套餐购进套,
根据题意得,
,
,为正整数,
或或,
有三种进货方案:甲种套餐购进套,乙种套餐购进套或甲种套餐购进套,乙种套餐购进套或甲种套餐购进套,乙种套餐购进套.
(1)设甲种套餐的单价为x元,根据用450元购买甲套餐和用810元购买乙套餐的个数相同列出分式方程得:,解方程并检验得出答案;
(2)设甲种套餐购进m套,乙种套餐购进n套,根据题意列出二元一次方程得50m+90n=1800,求出方程的正整数解即可
21.(1)解:,理由见如下:
平分,
,
∴,
,
,
;
(2)解:,
,
,
,
,
,
.
(1)先根据角平分线的定义得出,结合,推出,即可证明;
(2)由得到,结合,推出,进而证明,得到,最后根据平角的定义即可求解.
22.(1)40,25,
(2)补全条形图如下:
(3)解:(人),
答:全校“最喜欢羽毛球”的人数为480人.
解:(1)(人),
喜欢足球的人:(人),
,
,
“羽毛球”对应的圆心角度数为,
故答案为:40,25,;
(1)根据喜欢篮球的有18人,占,求出抽取总人数,进而求出足球的人数即可得到n的值,用羽毛球的人数除以抽取的总人数乘以360度即可求圆心角;
(2)根据(1)中求出的足球人数补全条形统计图即可;
(3)用样本所占百分比来估计总体,即可求得.
(1)解:由条形统计图与扇形统计图可知:喜欢篮球的有18人,占,
一共抽取的人数为(人),
喜欢足球的人有:(人),
,
,
“羽毛球”对应的圆心角度数为,
故答案为:40,25,;
(2)补全条形图如下:
(3)(人),
估计全校“最喜欢羽毛球”的人数为480人.
23.解:问题:1.5x;问题:设 甲工厂每天能加工x件新产品,根据题意得:,解得:x=50,经检验,x=50是所列方程的解,其符合题意.答:每天满工作量情况下,甲工厂每天能加工50件新产品;问题:设每天满工作量情况下,甲工厂加工1天所需费用为a元,乙工厂加工1天所需费用为b元,根据题意得:,解得:,每天满工作量情况下,甲工厂加工新产品的单价为元件,乙工厂加工新产品的单价为元件.设交给甲工厂y件新产品进行加工,则交给乙工厂(1500-y)件新产品进行加工,根据题意得:,且为整数,.为正整数,可以为,,,当时,,此时天,符合题意;当时,,此时天,不符合题意,舍去;当时,,此时天,符合题意.答:交给甲工厂1125或375件新产品进行加工.
问题1:设每天满工作量情况下,甲工厂每天加工数量为x件,可得乙工厂每天加工数量为1.5x件;
问题2:基本关系:工作时间=工作量÷工作效率,利用“甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天”,列出方程,即可求解;
问题3:基本关系:金额=价格×时间,设甲工厂加工1天需要a元,乙工厂加工1天需要b元,根据题意,列出方程组,求出a,b的值,再设甲工厂加工y件,则乙工厂加工(1500-y)件,于是有,n为平均匀单价,确定n的取值范围,逐一尝试即可求解.
2024-2025学年七年级下册期末模拟卷(温州市专用)
数 学
(考试范围:七下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.下列方程中,是二元一次方程的是( )
A. B. C. D.
2.如图.已知直线,将一块含角的直角三角板按如图方式放置()其中点A,B分别落在直线a、b上.若,则的度数为( )
A. B. C. D.
3.已知直线 , 将一块含 角的直角三角板按如图方式放置, 其中 角的顶点在直线 上, 角的顶点在直线 上, 若 , 则 的度数是( )
A. B. C. D.
4.为配合大阅读活动,学校对全校学生阅读兴趣调查的数据进行整理,要反映学生感兴趣的各类图书所占百分比,最适合的统计图是( )
A.条形统计图 B.频数直方图 C.折线统计图 D.扇形统计图
5.已知,,则的值为( )
A.16 B.4 C. D.
6.要使分式有意义,的取值应满足( )
A. B. C. D.
7.已知是二元一次方程的一个解,则a的值为( )
A.-1 B.1 C.-2 D.2
8.已知关于 的二次三项式 分解因式的结果为 , 则 和 的值分别是( )
A. B. C. D.
9.科学家发现人体最小的细胞是淋巴细胞, 直径约为 0.0000061 米, 将数据 0.0000061 用科学记数法表示正确的是 ( )
A. B. C. D.
10.如图所示,将两个正方形并列放置,其中B、C、E三点在一条直线上,C、G、D三点在一条直线上,已知,,则阴影部分的面积是( )
A.10 B.20 C.30 D.40
二、填空题(本题有6小题,每小题3分,共18分)
11.若,则a的值是 .
12.如果关于x、y的方程组 的解满足3x+y=5,则k的值= .
13.如图所示,数学拓展课上,小聪将直角三角形纸片沿向下折叠,点A落在点处,当时, 度.
14.分解因式: .
15.如图,直线,现将一块三角尺的顶点A放在直线上,若,则的度数为 .
16. A, B 两市相距 200 km , 甲车从 A 市到 B 市, 乙车从 B 市到 A 市, 两车同时出发, 已知甲车速度比乙车速度快 , 且甲车比乙车早半小时到达目的地, 若设乙车的速度是 x , 则根据题意, 可列方程为 .
三、解答题(本题有7小题,共72分. 解答需写出必要的文字说明、演算步骤或说理过程)
17.计算:
(1);
(2).
18.解方程 (组)
(1)
(2) .
19.已知关于x的分式方程.
(1)当时,求这个分式方程的解;
(2)若此分式方程无解,求的值.
20.临近期末,班级想给优秀的学生准备奖品,奖品分为甲套餐与乙套餐,已知购买个甲套餐比购买个乙套装少用元,用元购买甲套餐和用元购买乙套餐的个数相同.
(1)求这两种套餐的单价分别为多少元;
(2)班级计划用元经费购进甲套餐与乙套餐两种奖品,要求每种套餐至少购进种且刚好用完经费,请你设计进货方案.
21.如图,在中,平分,.
(1)试判断与的位置关系,并说明理由.
(2)若,且,求的度数.
22.为增强学生体质,丰富学校生活,某学校计划开展“球类课堂”活动,在全校范围内随机抽取了一些学生进行“我最喜欢的球类运动”调查活动,将调查结果整理后绘制成如下两幅不完整的统计图.
请根据图中的信息,解答下列各题:
(1)在本次调查中,一共抽取了 名学生;在扇形统计图中,的值为 ,“羽毛球”对应的圆心角度数为 .
(2)请补全条形统计图;
(3)若该校共有2400人,请你估计全校“最喜欢羽毛球”的人数.
23.根据以下信息,探索解决问题:
背景:为了提高产品的附加值,某公司计划将研发生产的件新产品进行加工后再投放市场每天满工作量情况下,甲、乙两个工厂加工数量及每件加工费用保持稳定不变,公司派出相关人员分别到这两间工厂了解情况,获得如下信息.
信息 每天满工作量情况下,乙工厂每天加工数量是甲工厂每天加工数量的倍;
信息 每天满工作量情况下,甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用天;
信息 每天满工作量情况下,甲工厂加工天,乙工厂加工天共需要元;甲工厂加工天,乙工厂加工天共需要元.
问题解决
问题 设每天满工作量情况下,甲工厂每天加工数量为件,结合信息可得:乙工厂每天加工数量为 件请用的代数式表示.
问题 每天满工作量情况下,求甲工厂每天能加工多少件新产品?
问题 公司将件新产品交给甲、乙两工厂一起加工,发现这批新产品的平均加工费用为整数,两工厂加工的时间之和不是整数请问交给甲工厂多少件新产品进行加工?
答案解析部分
1.A
解:A、含有两个未知数,且未知数的次数都是1,是二元一次方程,故符合题意;
B、不是整式方程,故不符合题意;
C、含有两个未知数,未知数的最高次数是2,不是二元一次方程,故不符合题意;
D、未知数的最高次数是2,不是二元一次方程,故不符合题意;
故答案为:A.
依据二元一次方程的定义“含有两个未知数,且含未知数的项的次数是1次的方程称为二元一次方程”,逐一判断即可.
2.B
解:如图所示,
根据题意可知:,(已知),
∴∠1+∠3=90°,
∵,
∴,
∵(已知),
∴(两直线平行,同位角相等),
故答案为:B.
根据平角的定义求出,然后利用两直线平行,同位角相等,得出∠2=∠3,即可得出答案.
3.C
解:如图:作直线c∥a
∴∠1=∠4=40°
∴∠3=90°-∠4=90°-40°=50°
∵a∥b
∴c∥b
∴∠2=∠3=50°
故答案为:C.
作直线c∥a,得到∠1=∠4=40°,再根据∠3+∠4=90°,求出∠3的度数,再根据平行于同一条直线的两条直线也平行,得出:c∥b,从而∠2=∠3=50°.
4.D
解: 要反映学生感兴趣的各类图书所占百分比,最适合的统计图是 扇形统计图
故选C.
扇形统计图反映了部分占总体的百分比.
5.D
6.D
解:由题意,得:,
∴;
故选:D.
根据分式的分母不为0时,分式有意义,即进行求解即可
7.B
解:∵是二元一次方程3x-ay=1的一个解,
∴3×1-2a=1,
解得a=1.
故答案为:B.
根据方程解的概念,将x=1、y=2代入方程中进行计算就可求出a的值.
8.B
解:∵
∴m=-6,-n=8
∴m=-6,n=-8
故答案为:B.
根据题意,先把进行展开,得到:,故=,得出:.
9.C
解: 0.0000061 =,故答案为A.
绝对值小于1的数科学记数法可以表示为:,其中1≤a∠10,n取从左边数第一个非0数前0的个数,包括小数点前面的0.
10.C
解:设小正方形的边长为x,大正方形的边长为y,
,,
,,
∴阴影部分的面积等于,
∴,
,
故答案为:C.
先得出,,再利用几何图形得到阴影部分的面积等于,列出算式,利用完全平方公式变形后求解.
11.4
12.10
解: ,①+②得:3x+y=15-k,∴15-k=5,解得:k=10.故答案为10.
将两方程相加可得3x+y=15-k,结合3x+y=5,可得15-k=5,求出k值即可.
13.70
解:如图所示:
∵,
∴,∠B=∠2,
∵∠B=65°,
∴∠2=65°,
由折叠可知:==45°,
∴∠1=180°-∠A'ED-∠2=180°-45°-65°=70°,
故答案为:70.
根据易得,∠B=∠2,然后根据折叠可知:=45°,最后利用三角形内角和即可求出∠1.
14.
解:
,
,
故答案为:.
运用提取公因式的方法进行因式分解即可,因式分解常用的方法有:①提公因式法;②公式法;③十字相乘法;④分组分解法.因式分解必须分解到每个因式都不能再分解为止.
15.
解:如图,作,
∴,
∵,
∴,
∵ ,
∴,
∵,
∴,
∴,
故答案为:.
作,利用平行线的性质可知,根据平行公理的推论证明得到,得到,进而得到,即可求出.
16..
解:由题意可列:
故答案为:.
设乙车的速度是 x , 则甲车的速度为(x+15),根据等量关系:,列出方程即可.
17.(1)解:原式
;
(2)解:原式
.
18.(1)解:
①+②得:4x=8,解得:x=2
把x=2代入②得:2+2y=6,解得y=2
∴是原方程组的解.
(2)解:
∴3x=9
∴x=3
把x=3代入x-3中得:3-3=0
∴原方程无解.
19.(1)解:当m=-1时,
原方程为:
方程两边同乘(1-x),得:2=x-2(1-x),
去括号,得:,
移项、合并同类项,得:,
解得:,
检验:将代入(1-x)得:,
是原分式方程的解;
(2)解:
方程两边同乘(1-x),得:2=-mx-2(1-x),
整理得:(2-m)x=4,
∴当2-m=0时,即m=2时,原分式方程无解,
当2-m≠0时,即m≠2时,原分式方程无解,
则x-1=0,即x=1,
此时,m=-2,
综上所述,当m=2或m=-2时,原分式方程无解.
(1)利用去分母将分式方程转化为整式方程,求出的值后进行检验即;
(2)用去分母将分式方程转化为整式方程,然后根据分式方程无解进行分类讨论即可.
(1)解:把代入分式方程得:,
整理得:,
去分母,得:,
去括号,得:,
移项、合并同类项,得:,
解得:,
检验:把代入得:,
是分式方程的解;
(2)分式方程变形得:,
去分母,得:,即,
若,即时,此方程无解,即分式方程无解;
若,即时,
分式方程无解,
,即,
把代入整式方程得:,
综上所述,或.
20.(1)解:设甲种套餐的单价为元,则乙种套餐的单价为元,
根据题意得:,
解得,
经检验,是原方程的解,
,
甲种套餐的单价为元,乙种套餐的单价为元;
(2)解:设甲种套餐购进套,乙种套餐购进套,
根据题意得,
,
,为正整数,
或或,
有三种进货方案:甲种套餐购进套,乙种套餐购进套或甲种套餐购进套,乙种套餐购进套或甲种套餐购进套,乙种套餐购进套.
(1)设甲种套餐的单价为x元,根据用450元购买甲套餐和用810元购买乙套餐的个数相同列出分式方程得:,解方程并检验得出答案;
(2)设甲种套餐购进m套,乙种套餐购进n套,根据题意列出二元一次方程得50m+90n=1800,求出方程的正整数解即可
21.(1)解:,理由见如下:
平分,
,
∴,
,
,
;
(2)解:,
,
,
,
,
,
.
(1)先根据角平分线的定义得出,结合,推出,即可证明;
(2)由得到,结合,推出,进而证明,得到,最后根据平角的定义即可求解.
22.(1)40,25,
(2)补全条形图如下:
(3)解:(人),
答:全校“最喜欢羽毛球”的人数为480人.
解:(1)(人),
喜欢足球的人:(人),
,
,
“羽毛球”对应的圆心角度数为,
故答案为:40,25,;
(1)根据喜欢篮球的有18人,占,求出抽取总人数,进而求出足球的人数即可得到n的值,用羽毛球的人数除以抽取的总人数乘以360度即可求圆心角;
(2)根据(1)中求出的足球人数补全条形统计图即可;
(3)用样本所占百分比来估计总体,即可求得.
(1)解:由条形统计图与扇形统计图可知:喜欢篮球的有18人,占,
一共抽取的人数为(人),
喜欢足球的人有:(人),
,
,
“羽毛球”对应的圆心角度数为,
故答案为:40,25,;
(2)补全条形图如下:
(3)(人),
估计全校“最喜欢羽毛球”的人数为480人.
23.解:问题:1.5x;问题:设 甲工厂每天能加工x件新产品,根据题意得:,解得:x=50,经检验,x=50是所列方程的解,其符合题意.答:每天满工作量情况下,甲工厂每天能加工50件新产品;问题:设每天满工作量情况下,甲工厂加工1天所需费用为a元,乙工厂加工1天所需费用为b元,根据题意得:,解得:,每天满工作量情况下,甲工厂加工新产品的单价为元件,乙工厂加工新产品的单价为元件.设交给甲工厂y件新产品进行加工,则交给乙工厂(1500-y)件新产品进行加工,根据题意得:,且为整数,.为正整数,可以为,,,当时,,此时天,符合题意;当时,,此时天,不符合题意,舍去;当时,,此时天,符合题意.答:交给甲工厂1125或375件新产品进行加工.
问题1:设每天满工作量情况下,甲工厂每天加工数量为x件,可得乙工厂每天加工数量为1.5x件;
问题2:基本关系:工作时间=工作量÷工作效率,利用“甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天”,列出方程,即可求解;
问题3:基本关系:金额=价格×时间,设甲工厂加工1天需要a元,乙工厂加工1天需要b元,根据题意,列出方程组,求出a,b的值,再设甲工厂加工y件,则乙工厂加工(1500-y)件,于是有,n为平均匀单价,确定n的取值范围,逐一尝试即可求解.
同课章节目录
