2024-2025学年七年级下学期数学期考末模拟卷(浙江舟山市专用)[答案+解析]
文档属性
| 名称 | 2024-2025学年七年级下学期数学期考末模拟卷(浙江舟山市专用)[答案+解析] |

|
|
| 格式 | docx | ||
| 文件大小 | 498.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-01 00:00:00 | ||
图片预览




文档简介
保密★启用前
2024-2025学年七年级下册期末模拟卷(舟山市专用)
数 学
(考试范围:七下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.(2024七下·慈溪期末) 下列调查中,适合全面调查的是 ( )
A.某班级学生的视力水平
B.端午节期间市场上粽子的质量情况
C.新城河的水质情况
D.一批日光灯的使用寿命
2.(2024七下·奉化期末)甲骨文主要流行于商周时期,是迄今为止中国发现的年代最早的成熟文字系统,是汉字的源头和中华优秀传统文化的根脉,下列甲骨文中,能用其中一部分平移得到的是( )
A.杯 B.立 C.比 D.曲
3.(2024七下·滨江期末)将长方形纸片按图所示方式进行折叠,且满足.若增大10°,则( )
A.增大 B.减少 C.不变 D.增大
4.(2021七下·萧山期末)下列各式从左到右的变形属于因式分解的是( )
A. B.x2-9=(x-3)(x+3)
C. D.(x+2)(x-3)=x2-x-6
5.(2024七下·余姚期末)下列运算正确的是( )
A.a2 a3=a6 B.(﹣a2)3=﹣a6
C.(ab)2=ab2 D.a8÷a4=a2
6.(2022七下·上虞期末)下列各组数中,是二元一次方程的解的是( )
A. B. C. D.
7.(2024七下·义乌期末)已知某细菌直径为 0.000000072 豪米,其中数 0.000000072 用科学记数法表示为( )
A. B. C. D.
8.(2024七下·东阳期末)端午节来临,某社区计划制作380份粽子送给社区孤寡老人.由于青年志愿者的加入,每小时比原计划多做,结果提前3小时就完成任务.设志愿者未加入前每小时做份粽子,则所列方程为( )
A. B.
C. D.
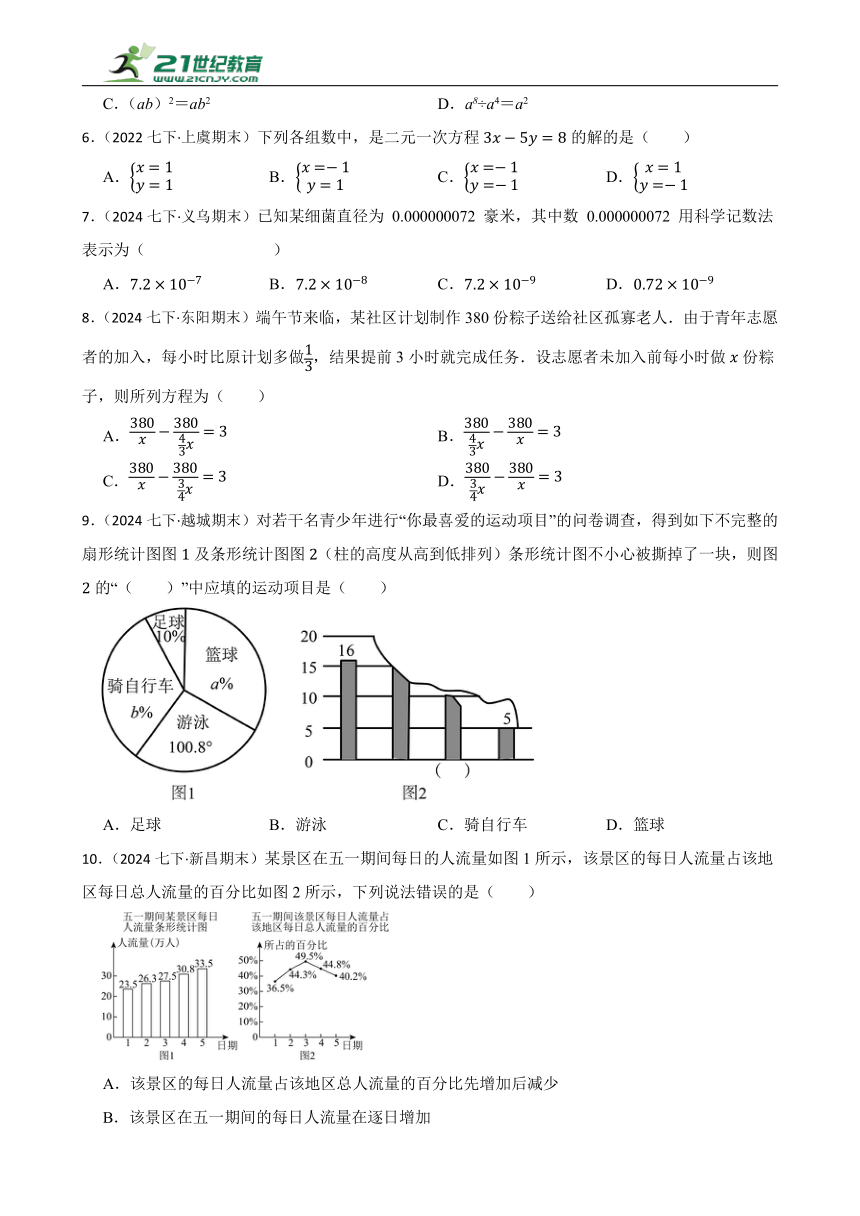
9.(2024七下·越城期末)对若干名青少年进行“你最喜爱的运动项目”的问卷调查,得到如下不完整的扇形统计图图及条形统计图图(柱的高度从高到低排列)条形统计图不小心被撕掉了一块,则图的“( )”中应填的运动项目是( )
A.足球 B.游泳 C.骑自行车 D.篮球
10.(2024七下·新昌期末)某景区在五一期间每日的人流量如图1所示,该景区的每日人流量占该地区每日总人流量的百分比如图2所示,下列说法错误的是( )
A.该景区的每日人流量占该地区总人流量的百分比先增加后减少
B.该景区在五一期间的每日人流量在逐日增加
C.该景区在5月3日人流量占该地区总人流量的百分比达到最高
D.该地区5月4日的总人流量比5月5日的总人流量多1.2
二、填空题(本题有6小题,每小题3分,共18分)
11.(2023七下·吴兴期末)要使分式有意义,则x的取值范围为 .
12.(2024八下·仁寿期末)已知,则的值为 .
13.(2024七下·龙湖期末)如图,直线,现将一块三角尺的顶点A放在直线上,若,则的度数为 .
14.(2024七下·东阳期末)如果一个两位正整数,(,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为,若为2376,那么我们称这个数为“最美数”,则这个“最美数”为 .
15.(2024七下·越城期末) 《九章算术》中记载: “今有五雀、六燕, 集称之衡, 雀俱重, 燕俱轻. 一雀一燕交而处, 衡适平. 并燕、雀重一斤. 问燕、雀一枚各重几何 ” 其大意如下: “今有 5 只雀、6 只燕, 分别放一起用衡器称, 聚在一起的雀重, 燕轻. 将 1 只雀、 1 只燕交换位置而放, 两边重量相等. 5 只雀、 6 只燕重量为 1 斤. 问雀、燕各重多少斤 ” 若设雀、燕每只各重 斤、 斤. 根据题意可列方程组为 .
16.(2024七下·越城期末)如图,有A、B、C三种不同型号的卡片,每种各10张.A型卡片是边长为a的正方形,B型卡片是相邻两边长分别为a,b的长方形,C型卡片是边长为b的正方形.从中取出若干张卡片(每种卡片至少取一张),把取出的这些卡片拼成一个正方形,则所有符合要求能够拼成的正方形的个数有 个.
三、解答题(本题有8小题,共72分. 解答需写出必要的文字说明、演算步骤或说理过程)
17.(2024七下·钱塘期末)计算:
(1).
(2).
18.(2024七下·嵊州期末)分解因式:
(1)
(2)
19.(2024七下·新昌期末)某学习小组以“学生上学的主要交通方式”为主题,对全校学生进行抽样调查,根据结果绘制了如下不完整的条形统计图和扇形统计图(每位同学必选且仅选一项):
请根据图表信息,解答下列问题:
(1)求本次抽样调查的学生人数,并补全条形统计图.
(2)若该校有1200名学生,则以电瓶车为主要交通方式的学生约有多少人?
20.(2024七下·路桥期末)如图,已知,.
(1)求证:;
(2)若,,求的度数.
21.(2024七下·鄞州期末) 先阅读下边的解题过程,再回答问题.
(1) 右边的解答有错误,错误步骤的序号是 .
(2)请你给出正确的解答.
22.(2024七下·平湖期末)已知,两地相距150千米,甲、乙两车分别从,两地同时出发,相向而行,其终点分别为,两地.两车均先以每小时千米的速度行驶,再以每小时千米的速度行驶,且甲车以两种速度行驶的路程相等,乙车以两种速度行驶的时间相等.
(1)若,且甲车行驶的总时间为小时,求和的值;
(2)若,且乙车行驶的总时间为2小时.
①求和的值;②求两车相遇时,离地多少千米.
23.(2024七下·东阳期末)如图1,一块三角板如图放置,,直线分别交于点,的角平分线交于点,交于点是线段上的一点(不与重合),连接交于点.
(1)判断之间的关系,并说明理由;
(2)若.
①用含的代数式表示的度数;
②当时,将绕着点以每秒的速度逆时针旋转,旋转时间为,当边与射线重合时停止,则在旋转过程中,当的其中一边与的某一边平行时,求出此时的值.
24.(2024七下·绍兴期末)某危险品工厂采用甲型、乙型两种机器人代替人力搬运产品.甲型机器人比乙型机器人每小时多搬运,甲型机器人搬运所用时间与乙型机器人搬运所用时间相等.问乙型机器人每小时搬运多少产品?
根据以上信息,解答下列问题.
(1)小华同学设乙型机器人每小时搬运产品,则甲型机器人每小时搬运_____产品,根据“甲型机器人搬运所用时间与乙型机器人搬运所用时间相等”,可列方程为_______.
(2)小惠同学设甲型机器人搬运所用时间为小时,则甲型机器人每小时搬______产品,根据“甲型机器人比乙型机器人每小时多搬运”,可列方程为________.
(3)请你按照(1)中小华同学的解题思路,写出完整的解答过程.
答案解析部分
1.A
解:A、某班级学生的视力水平,适合全面调查,A符合题意;
B、端午节期间市场上粽子的质量情况,适合抽样调查,B不符合题意;
C、新城河的水质情况,适合抽样调查,C不符合题意;
D、一批日光灯的使用寿命,适合抽样调查,D不符合题意;
故答案为:A.
根据全面调查、抽样调查的特点逐项判断即可.
2.C
解:由平移的性质知,只有C是利用图形的平移得到的,
故答案为:C.
根据图形的平移的定义逐一判断求解. 某一基本的平面图形沿着一定的方向移动,这种图形的平行移动,简称为平移 .
3.B
4.B
解:A.从左到右的变形不属于因式分解,故本选项不符合题意;
B.从左到右的变形属于因式分解,故本选项符合题意;
C.从左到右的变形不属于因式分解,故本选项不符合题意;
D.从左到右的变形属于整式乘法,不属于因式分解,故本选项不符合题意;
故答案为:B.
利用因式分解的定义:把一个多项式分解成几个整式的乘积形式,再对各选项逐一判断即可.
5.B
解:、,该选项错误,不合题意;
、,该选项正确,符合题意;
、,该选项错误,不合题意;
、,该选项错误,不合题意.
故答案为:B.
据同底数幂的乘法、幂的乘方、积的乘方、同底数幂的除法分别计算即可判断求解,掌握整式的运算法则是解题的关键.
6.D
解:A、把代入方程得:左边,右边,
左边右边,
不是方程的解;
B、把代入方程得:左边,右边,
左边右边,
不是方程的解;
C、把代入方程得:左边,右边,
左边右边,
不是方程的解;
D、把代入方程得:左边,右边,
左边右边,
是方程的解.
故答案为:D.
所谓方程的解,就是使方程的左边和右边相等的未知数的值,据此分别将各个选项中给出的x、y的值代入3x-5y中求出相应的值,然后与8进行比较即可.
7.B
解:0.000000072=7.2×10-8.
故答案为:B.
绝对值小于1且大于0的数用科学记数法表示为:a×10﹣n,其中1≤|a|<10,n=从左向右第一个不是0的数字前的0的个数,根据科学记数法的意义可求解.
8.A
解:设志愿者未加入前每小时做份粽子.根据题意,得
.
故选:A.
设志愿者未加入前每小时做份粽子,根据“ 每小时比原计划多做,结果提前3小时就完成任务 ”列分式方程解题.
9.B
根据题意可得足球人数最少,占比,
故总人数为:(人),
游泳的百分比是:,
游泳的人数是:(人),
剩余的人数是: (人),
∵柱的高度从高到低排列,
∴图中前两个柱一个为自行车,一个为篮球,应填的游泳,第三个柱为游泳,
故选:B.
根据足球的频数和百分比得到总人数,求出游泳的百分比是,即可得到骑自行车和篮球的人数为和,然后从高到低排列解答即可.
10.D
解:A. 该景区的每日人流量占该地区总人流量的百分比先增加后减少,故该选项正确,不符合题意;
B. 该景区在五一期间的每日人流量在逐日增加,故该选项正确,不符合题意;
C. 该景区在5月3日人流量占该地区总人流量的百分比达到最高,故该选项正确,不符合题意;
D. 该地区5月5日的总人流量比5月4日的总人流量多,万人,故该选项不正确,符合题意;
故答案为:D.
分析统计图得到相关信息,逐项判断解答.
11.
12.4
解:∵,
∴a2-2a+1+b2+b+1=0
∴(a-1)2+(b+1)2=0
∴a-1=0且b+1=0
解之:a=1,b=-2,
∴.
故答案为:4
利用完全平方公式,将等式转化为(a-1)2+(b+1)2=0,再利用几个非负数之和为0,则每一个数都为0,可得到关于a,b的方程,解方程求出a,b的值,然后将a,b的值代入代数式进行计算.
13.
解:如图,作,
∴,
∵,
∴,
∵ ,
∴,
∵,
∴,
∴,
故答案为:.
作,利用平行线的性质可知,根据平行公理的推论证明得到,得到,进而得到,即可求出.
14.57或15
解:,
,
∵,
∴,
∴,
∵,x,y为自然数,
∴,,且
∴或,,
解得或,,
∵x,y为自然数,
∴或,
∴这个“最美数”是57或15.
故答案为:57或15.
根据题意得到,,根据题意得到,然后利用,求得符合条件的x、y的值即可解题.
15.
解:设雀、燕每只各重 斤、 斤,由题意得,
故答案为:
设雀、燕每只各重 斤、 斤,根据“雀、燕每只各重 斤、 斤,则 5 只雀、 6 只燕重量为 1 斤 得5x+6y=1,而4只雀和1只燕与5只燕和1只雀重量相等即有4x+y=5y+x”即可列出二元一次方程组,从而即可求解。
16.6
解:由题意得,A正方形的面积为,B长方形的面积为,C正方形的面积为,
∵A、B、C三种不同型号的卡片,每种各10张,从中取出若干张卡片(每种卡片至少取一张),把取出的这些卡片拼成一个正方形,
因此有:,需要A卡片1张,B卡片2张,C卡片1张;
,需要A卡片4张,B卡片4张,C卡片1张;
,需要A卡片1张,B卡片4张,C卡片4张;
,需要A卡片9张,B卡片6张,C卡片1张;
,需要A卡片1张,B卡片6张,C卡片9张;
,需要A卡片4张,B卡片8张,C卡片4张;
综上所述,符合条件的正方形有6个,
故答案为:6.
根据完全平方公式解答即可.
17.(1)解:原式=1+(-2)=-1
(2)解:原式=y-2x
(1)根据零指数幂和负整数指数幂计算后,再求和即可;
(2)先计算积的平方,再根据多项式除以单项式计算即可.
(1)解:原式
;
(2)解:原式
.
18.(1)解:
;
(2)解:
.
(1)运用平方差公式即可分解因式;
(2)运用提公因式法即可分解因式.
(1)解:
;
(2)解:
.
19.(1)解:本次抽样调查的学生人数为(人).
公共汽车的人数为(人),
统计图补全如图所示.
(2)解:.
(人).
答:以电瓶车为主要交通方式的学生人数约有人.
(1)运用私家车人数除以占比得到总人数,用总人数乘以公共汽车占比求出其人数,补全条形统计图即可;
(2)利用1200×电瓶车的占比解答即可.
20.(1)证明:,
,
又,
,
(2)解:,,
∴ ∠2=∠CBE=180°-136°=44°,
,
,
21.(1)③
(2)解:
(1)解:解答有错误,错误步骤的序号是③;(1)分式的加减运算不能去分母,从而可得错误步骤的序号是③;
(2)先通分化为同分母分式,再计算即可.
22.(1)解:根据题意得,,
将②代入①可得x=100,
∴ y=75,
经检验,,是原分式方程的解
答:x和y的值分别为75和100;
(2)解:①根据题意得,,
解得,,
答:x和y的值分别为60和90;
②当行驶1h时,两车的路程和为60×1+60×1=120<150;
当75÷60=1.25h,75+60+0.25×90=157.5>150;
∴ 两车相遇时甲车速度为60km/h,而乙车速度为90km/h,
即相遇时甲车行驶的时间为,
乙离地的距离即为甲行驶的距离,
(千米).
两车相遇时,离地72千米.
(1)由甲车以两种速度行驶的路程相等,可得,再结合即可求出、的值;
(2)①由乙车以两种速度行驶时间相等可得,再由,可求、的值;②先判断出相遇时两车的速度,并计算出相遇时甲车行驶的时间,最后计算出甲的行驶路程即可.
(1)解:由已知甲车以两种速度行驶的路程相等,
甲车行驶的时间为,即
甲车行驶的总时间为小时,
,
∵,
,;
经检验:,是原分式方程的解
(2)解:①乙车以两种速度行驶的时间相等,且乙车行驶的总时间为2小时,
,
,
∵,
∴
,
②相遇时甲车行驶的时间为,
乙离地的距离即为甲行驶的距离,
(千米).
两车相遇时,离地72千米.
23.(1)解:.
理由如下:
作,
∵,
∴,
∴,
∴.
(2)解:①设,则,,∵,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴,
由(1)得;
②解:当时,,,,
(i)当时,延长交边于P,
∵,
∴,
∵,
∴,
∴,
∴当绕E点旋转时,,
∴;
(ii)当时,
∴,
∴,
∴,
∴,
∴当绕点E旋转时,,
∴;
(iii)当时,即与在同一直线上时,
∴,
∴当绕点E旋转时,,
∴,
(iv)当时,
∵,
∴.
∴当旋转时,.
∴;
(v)当时,
∵,,
∴.
∴当旋转时,.
∴,
当的其中一边与的某一边平行时t的值为5秒或秒或秒或秒或秒.
(1)作,即可得到,然后利用平行线的性质可得,然后根据角的和差解题即可;
(2)①设,根据,可以得到,根据角平分线的定义和垂直的定义可得,求出x的值,利用(1)的结论解答即可;
②当时,分为,,,和与五种情况,分别画图根据平行线的性质解答即可.
24.(1),
(2),
(3)解:设乙型机器人每小时搬运产品,则甲型机器人每小时搬运产品,根据题意得:
;
解得:,
经检验得:是原方程的解,且符合题意,
答:乙型机器人每小时搬运产品.
(1)解:设乙型机器人每小时搬运产品,则甲型机器人每小时搬运产品,根据题意得:
;
故答案为:;
(2)解:设甲型机器人搬运所用时间为小时,根据题意得:
;
故答案为:;
(1)设乙型机器人每小时搬运产品,根据“甲型机器人搬运所用时间与乙型机器人搬运所用时间相等”列分式方程;
(2)设甲型机器人搬运所用时间为小时,表示甲型机器人的工作效率,根据题意列分式方程即可;
(3)根据解析(1)中列的分式方程,求出x值检验解题即可.
2024-2025学年七年级下册期末模拟卷(舟山市专用)
数 学
(考试范围:七下全册 考试时间:100分钟 分值:120分)
卷首语:同学们,展开智慧的翅膀,细心浇灌每一题,笔墨生花,收获成长的喜悦!
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本题有10小题,每小题3分,共30分. 每小题只有一个选项是正确的,不选、多选、错选,均不给分)
1.(2024七下·慈溪期末) 下列调查中,适合全面调查的是 ( )
A.某班级学生的视力水平
B.端午节期间市场上粽子的质量情况
C.新城河的水质情况
D.一批日光灯的使用寿命
2.(2024七下·奉化期末)甲骨文主要流行于商周时期,是迄今为止中国发现的年代最早的成熟文字系统,是汉字的源头和中华优秀传统文化的根脉,下列甲骨文中,能用其中一部分平移得到的是( )
A.杯 B.立 C.比 D.曲
3.(2024七下·滨江期末)将长方形纸片按图所示方式进行折叠,且满足.若增大10°,则( )
A.增大 B.减少 C.不变 D.增大
4.(2021七下·萧山期末)下列各式从左到右的变形属于因式分解的是( )
A. B.x2-9=(x-3)(x+3)
C. D.(x+2)(x-3)=x2-x-6
5.(2024七下·余姚期末)下列运算正确的是( )
A.a2 a3=a6 B.(﹣a2)3=﹣a6
C.(ab)2=ab2 D.a8÷a4=a2
6.(2022七下·上虞期末)下列各组数中,是二元一次方程的解的是( )
A. B. C. D.
7.(2024七下·义乌期末)已知某细菌直径为 0.000000072 豪米,其中数 0.000000072 用科学记数法表示为( )
A. B. C. D.
8.(2024七下·东阳期末)端午节来临,某社区计划制作380份粽子送给社区孤寡老人.由于青年志愿者的加入,每小时比原计划多做,结果提前3小时就完成任务.设志愿者未加入前每小时做份粽子,则所列方程为( )
A. B.
C. D.
9.(2024七下·越城期末)对若干名青少年进行“你最喜爱的运动项目”的问卷调查,得到如下不完整的扇形统计图图及条形统计图图(柱的高度从高到低排列)条形统计图不小心被撕掉了一块,则图的“( )”中应填的运动项目是( )
A.足球 B.游泳 C.骑自行车 D.篮球
10.(2024七下·新昌期末)某景区在五一期间每日的人流量如图1所示,该景区的每日人流量占该地区每日总人流量的百分比如图2所示,下列说法错误的是( )
A.该景区的每日人流量占该地区总人流量的百分比先增加后减少
B.该景区在五一期间的每日人流量在逐日增加
C.该景区在5月3日人流量占该地区总人流量的百分比达到最高
D.该地区5月4日的总人流量比5月5日的总人流量多1.2
二、填空题(本题有6小题,每小题3分,共18分)
11.(2023七下·吴兴期末)要使分式有意义,则x的取值范围为 .
12.(2024八下·仁寿期末)已知,则的值为 .
13.(2024七下·龙湖期末)如图,直线,现将一块三角尺的顶点A放在直线上,若,则的度数为 .
14.(2024七下·东阳期末)如果一个两位正整数,(,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为,若为2376,那么我们称这个数为“最美数”,则这个“最美数”为 .
15.(2024七下·越城期末) 《九章算术》中记载: “今有五雀、六燕, 集称之衡, 雀俱重, 燕俱轻. 一雀一燕交而处, 衡适平. 并燕、雀重一斤. 问燕、雀一枚各重几何 ” 其大意如下: “今有 5 只雀、6 只燕, 分别放一起用衡器称, 聚在一起的雀重, 燕轻. 将 1 只雀、 1 只燕交换位置而放, 两边重量相等. 5 只雀、 6 只燕重量为 1 斤. 问雀、燕各重多少斤 ” 若设雀、燕每只各重 斤、 斤. 根据题意可列方程组为 .
16.(2024七下·越城期末)如图,有A、B、C三种不同型号的卡片,每种各10张.A型卡片是边长为a的正方形,B型卡片是相邻两边长分别为a,b的长方形,C型卡片是边长为b的正方形.从中取出若干张卡片(每种卡片至少取一张),把取出的这些卡片拼成一个正方形,则所有符合要求能够拼成的正方形的个数有 个.
三、解答题(本题有8小题,共72分. 解答需写出必要的文字说明、演算步骤或说理过程)
17.(2024七下·钱塘期末)计算:
(1).
(2).
18.(2024七下·嵊州期末)分解因式:
(1)
(2)
19.(2024七下·新昌期末)某学习小组以“学生上学的主要交通方式”为主题,对全校学生进行抽样调查,根据结果绘制了如下不完整的条形统计图和扇形统计图(每位同学必选且仅选一项):
请根据图表信息,解答下列问题:
(1)求本次抽样调查的学生人数,并补全条形统计图.
(2)若该校有1200名学生,则以电瓶车为主要交通方式的学生约有多少人?
20.(2024七下·路桥期末)如图,已知,.
(1)求证:;
(2)若,,求的度数.
21.(2024七下·鄞州期末) 先阅读下边的解题过程,再回答问题.
(1) 右边的解答有错误,错误步骤的序号是 .
(2)请你给出正确的解答.
22.(2024七下·平湖期末)已知,两地相距150千米,甲、乙两车分别从,两地同时出发,相向而行,其终点分别为,两地.两车均先以每小时千米的速度行驶,再以每小时千米的速度行驶,且甲车以两种速度行驶的路程相等,乙车以两种速度行驶的时间相等.
(1)若,且甲车行驶的总时间为小时,求和的值;
(2)若,且乙车行驶的总时间为2小时.
①求和的值;②求两车相遇时,离地多少千米.
23.(2024七下·东阳期末)如图1,一块三角板如图放置,,直线分别交于点,的角平分线交于点,交于点是线段上的一点(不与重合),连接交于点.
(1)判断之间的关系,并说明理由;
(2)若.
①用含的代数式表示的度数;
②当时,将绕着点以每秒的速度逆时针旋转,旋转时间为,当边与射线重合时停止,则在旋转过程中,当的其中一边与的某一边平行时,求出此时的值.
24.(2024七下·绍兴期末)某危险品工厂采用甲型、乙型两种机器人代替人力搬运产品.甲型机器人比乙型机器人每小时多搬运,甲型机器人搬运所用时间与乙型机器人搬运所用时间相等.问乙型机器人每小时搬运多少产品?
根据以上信息,解答下列问题.
(1)小华同学设乙型机器人每小时搬运产品,则甲型机器人每小时搬运_____产品,根据“甲型机器人搬运所用时间与乙型机器人搬运所用时间相等”,可列方程为_______.
(2)小惠同学设甲型机器人搬运所用时间为小时,则甲型机器人每小时搬______产品,根据“甲型机器人比乙型机器人每小时多搬运”,可列方程为________.
(3)请你按照(1)中小华同学的解题思路,写出完整的解答过程.
答案解析部分
1.A
解:A、某班级学生的视力水平,适合全面调查,A符合题意;
B、端午节期间市场上粽子的质量情况,适合抽样调查,B不符合题意;
C、新城河的水质情况,适合抽样调查,C不符合题意;
D、一批日光灯的使用寿命,适合抽样调查,D不符合题意;
故答案为:A.
根据全面调查、抽样调查的特点逐项判断即可.
2.C
解:由平移的性质知,只有C是利用图形的平移得到的,
故答案为:C.
根据图形的平移的定义逐一判断求解. 某一基本的平面图形沿着一定的方向移动,这种图形的平行移动,简称为平移 .
3.B
4.B
解:A.从左到右的变形不属于因式分解,故本选项不符合题意;
B.从左到右的变形属于因式分解,故本选项符合题意;
C.从左到右的变形不属于因式分解,故本选项不符合题意;
D.从左到右的变形属于整式乘法,不属于因式分解,故本选项不符合题意;
故答案为:B.
利用因式分解的定义:把一个多项式分解成几个整式的乘积形式,再对各选项逐一判断即可.
5.B
解:、,该选项错误,不合题意;
、,该选项正确,符合题意;
、,该选项错误,不合题意;
、,该选项错误,不合题意.
故答案为:B.
据同底数幂的乘法、幂的乘方、积的乘方、同底数幂的除法分别计算即可判断求解,掌握整式的运算法则是解题的关键.
6.D
解:A、把代入方程得:左边,右边,
左边右边,
不是方程的解;
B、把代入方程得:左边,右边,
左边右边,
不是方程的解;
C、把代入方程得:左边,右边,
左边右边,
不是方程的解;
D、把代入方程得:左边,右边,
左边右边,
是方程的解.
故答案为:D.
所谓方程的解,就是使方程的左边和右边相等的未知数的值,据此分别将各个选项中给出的x、y的值代入3x-5y中求出相应的值,然后与8进行比较即可.
7.B
解:0.000000072=7.2×10-8.
故答案为:B.
绝对值小于1且大于0的数用科学记数法表示为:a×10﹣n,其中1≤|a|<10,n=从左向右第一个不是0的数字前的0的个数,根据科学记数法的意义可求解.
8.A
解:设志愿者未加入前每小时做份粽子.根据题意,得
.
故选:A.
设志愿者未加入前每小时做份粽子,根据“ 每小时比原计划多做,结果提前3小时就完成任务 ”列分式方程解题.
9.B
根据题意可得足球人数最少,占比,
故总人数为:(人),
游泳的百分比是:,
游泳的人数是:(人),
剩余的人数是: (人),
∵柱的高度从高到低排列,
∴图中前两个柱一个为自行车,一个为篮球,应填的游泳,第三个柱为游泳,
故选:B.
根据足球的频数和百分比得到总人数,求出游泳的百分比是,即可得到骑自行车和篮球的人数为和,然后从高到低排列解答即可.
10.D
解:A. 该景区的每日人流量占该地区总人流量的百分比先增加后减少,故该选项正确,不符合题意;
B. 该景区在五一期间的每日人流量在逐日增加,故该选项正确,不符合题意;
C. 该景区在5月3日人流量占该地区总人流量的百分比达到最高,故该选项正确,不符合题意;
D. 该地区5月5日的总人流量比5月4日的总人流量多,万人,故该选项不正确,符合题意;
故答案为:D.
分析统计图得到相关信息,逐项判断解答.
11.
12.4
解:∵,
∴a2-2a+1+b2+b+1=0
∴(a-1)2+(b+1)2=0
∴a-1=0且b+1=0
解之:a=1,b=-2,
∴.
故答案为:4
利用完全平方公式,将等式转化为(a-1)2+(b+1)2=0,再利用几个非负数之和为0,则每一个数都为0,可得到关于a,b的方程,解方程求出a,b的值,然后将a,b的值代入代数式进行计算.
13.
解:如图,作,
∴,
∵,
∴,
∵ ,
∴,
∵,
∴,
∴,
故答案为:.
作,利用平行线的性质可知,根据平行公理的推论证明得到,得到,进而得到,即可求出.
14.57或15
解:,
,
∵,
∴,
∴,
∵,x,y为自然数,
∴,,且
∴或,,
解得或,,
∵x,y为自然数,
∴或,
∴这个“最美数”是57或15.
故答案为:57或15.
根据题意得到,,根据题意得到,然后利用,求得符合条件的x、y的值即可解题.
15.
解:设雀、燕每只各重 斤、 斤,由题意得,
故答案为:
设雀、燕每只各重 斤、 斤,根据“雀、燕每只各重 斤、 斤,则 5 只雀、 6 只燕重量为 1 斤 得5x+6y=1,而4只雀和1只燕与5只燕和1只雀重量相等即有4x+y=5y+x”即可列出二元一次方程组,从而即可求解。
16.6
解:由题意得,A正方形的面积为,B长方形的面积为,C正方形的面积为,
∵A、B、C三种不同型号的卡片,每种各10张,从中取出若干张卡片(每种卡片至少取一张),把取出的这些卡片拼成一个正方形,
因此有:,需要A卡片1张,B卡片2张,C卡片1张;
,需要A卡片4张,B卡片4张,C卡片1张;
,需要A卡片1张,B卡片4张,C卡片4张;
,需要A卡片9张,B卡片6张,C卡片1张;
,需要A卡片1张,B卡片6张,C卡片9张;
,需要A卡片4张,B卡片8张,C卡片4张;
综上所述,符合条件的正方形有6个,
故答案为:6.
根据完全平方公式解答即可.
17.(1)解:原式=1+(-2)=-1
(2)解:原式=y-2x
(1)根据零指数幂和负整数指数幂计算后,再求和即可;
(2)先计算积的平方,再根据多项式除以单项式计算即可.
(1)解:原式
;
(2)解:原式
.
18.(1)解:
;
(2)解:
.
(1)运用平方差公式即可分解因式;
(2)运用提公因式法即可分解因式.
(1)解:
;
(2)解:
.
19.(1)解:本次抽样调查的学生人数为(人).
公共汽车的人数为(人),
统计图补全如图所示.
(2)解:.
(人).
答:以电瓶车为主要交通方式的学生人数约有人.
(1)运用私家车人数除以占比得到总人数,用总人数乘以公共汽车占比求出其人数,补全条形统计图即可;
(2)利用1200×电瓶车的占比解答即可.
20.(1)证明:,
,
又,
,
(2)解:,,
∴ ∠2=∠CBE=180°-136°=44°,
,
,
21.(1)③
(2)解:
(1)解:解答有错误,错误步骤的序号是③;(1)分式的加减运算不能去分母,从而可得错误步骤的序号是③;
(2)先通分化为同分母分式,再计算即可.
22.(1)解:根据题意得,,
将②代入①可得x=100,
∴ y=75,
经检验,,是原分式方程的解
答:x和y的值分别为75和100;
(2)解:①根据题意得,,
解得,,
答:x和y的值分别为60和90;
②当行驶1h时,两车的路程和为60×1+60×1=120<150;
当75÷60=1.25h,75+60+0.25×90=157.5>150;
∴ 两车相遇时甲车速度为60km/h,而乙车速度为90km/h,
即相遇时甲车行驶的时间为,
乙离地的距离即为甲行驶的距离,
(千米).
两车相遇时,离地72千米.
(1)由甲车以两种速度行驶的路程相等,可得,再结合即可求出、的值;
(2)①由乙车以两种速度行驶时间相等可得,再由,可求、的值;②先判断出相遇时两车的速度,并计算出相遇时甲车行驶的时间,最后计算出甲的行驶路程即可.
(1)解:由已知甲车以两种速度行驶的路程相等,
甲车行驶的时间为,即
甲车行驶的总时间为小时,
,
∵,
,;
经检验:,是原分式方程的解
(2)解:①乙车以两种速度行驶的时间相等,且乙车行驶的总时间为2小时,
,
,
∵,
∴
,
②相遇时甲车行驶的时间为,
乙离地的距离即为甲行驶的距离,
(千米).
两车相遇时,离地72千米.
23.(1)解:.
理由如下:
作,
∵,
∴,
∴,
∴.
(2)解:①设,则,,∵,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴,
由(1)得;
②解:当时,,,,
(i)当时,延长交边于P,
∵,
∴,
∵,
∴,
∴,
∴当绕E点旋转时,,
∴;
(ii)当时,
∴,
∴,
∴,
∴,
∴当绕点E旋转时,,
∴;
(iii)当时,即与在同一直线上时,
∴,
∴当绕点E旋转时,,
∴,
(iv)当时,
∵,
∴.
∴当旋转时,.
∴;
(v)当时,
∵,,
∴.
∴当旋转时,.
∴,
当的其中一边与的某一边平行时t的值为5秒或秒或秒或秒或秒.
(1)作,即可得到,然后利用平行线的性质可得,然后根据角的和差解题即可;
(2)①设,根据,可以得到,根据角平分线的定义和垂直的定义可得,求出x的值,利用(1)的结论解答即可;
②当时,分为,,,和与五种情况,分别画图根据平行线的性质解答即可.
24.(1),
(2),
(3)解:设乙型机器人每小时搬运产品,则甲型机器人每小时搬运产品,根据题意得:
;
解得:,
经检验得:是原方程的解,且符合题意,
答:乙型机器人每小时搬运产品.
(1)解:设乙型机器人每小时搬运产品,则甲型机器人每小时搬运产品,根据题意得:
;
故答案为:;
(2)解:设甲型机器人搬运所用时间为小时,根据题意得:
;
故答案为:;
(1)设乙型机器人每小时搬运产品,根据“甲型机器人搬运所用时间与乙型机器人搬运所用时间相等”列分式方程;
(2)设甲型机器人搬运所用时间为小时,表示甲型机器人的工作效率,根据题意列分式方程即可;
(3)根据解析(1)中列的分式方程,求出x值检验解题即可.
同课章节目录
